Reaction pathways on N-substituted carbon catalysts during the electrochemical reduction of nitrate to ammonia

Abstract

Electrochemical reduction of nitrate into ammonia is one potential strategy to valorize pollutants needed to close the nitrogen cycle. The understanding of carbonaceous materials as metal-free representatives of electrocatalysts is of high importance to ensure sufficient activity and target selectivity. We report on the role of defects in cellulose-derived nitrogen-doped carbon (NDC) materials, produced by ammonolysis at different temperatures, to obtain efficient electrocatalysts for the nitrate reduction reaction (NO₃RR). Carbon catalyst ammonolysis at 800 °C (NDC-800) yields the highest electrochemical performance, exhibiting 73.1% NH₄⁺ selectivity and nearly 100% NO₃⁻ reduction efficiency with a prolonged NO₃RR time (48 h) at −1.5 V vs. Ag/AgCl in a 0.1 M Na₂SO₄ electrolyte. We provide support to our findings by undertaking complementary structural analyses with scanning electron microscopy (SEM), transmission electron microscopy (TEM), powder X-ray diffraction (PXRD), X-ray photoelectron spectroscopy (XPS), Raman spectroscopy, low-temperature N₂ adsorption, and theoretical studies based on multi-scale/level calculations. Atomistic molecular dynamics simulations based on a reactive force field combined with quantum chemistry (QC) calculations on representative model systems suggest possible realistic scenarios of the material structure and reaction mechanisms of the NO₃⁻ reduction routes.

---

Introduction

Low-cost, high-performance carbon-based materials are metal-free catalysts that have the potential to challenge, as sustainable substitutes, established metal-based nanoparticle catalysts.^1–11 The most significant carbon-based materials are made from natural resources, and very often, cellulose is the preferential choice being the most abundant, renewable biopolymer on earth.^12–20 The cellulose macromolecule exists as a structural component of the primary cell wall in green plants, algae, and oomycetes, and is easily obtained from low-cost natural sources.²¹ Notably, owing to its unique structure, it can be transformed by an environmentally friendly decomposition process at high temperatures, with low or even almost zero carbon emission, into cellulose-derived carbon substances.^12,16

These products are then treated further to improve/maximize their performance in specific applications. Since the incorporation of heteroatoms could alter the properties of metal-free carbon materials, chemical doping with nitrogen was used to tailor their physicochemical properties effectively.^22–27 It was reported, in fact, that the incorporation of nitrogen improved their surface wettability, electron donor properties, conductivity, and reactivity.^3,28,29 Notwithstanding the successful results, a judicious choice of tailored functional modification is mandatory and crucial for manufacturing porous NDC materials as functional novel carbon materials.^3,30 As a matter of fact, the carbonization temperature and environmental conditions play essential roles in the tailored functional transformation, and their variation can drive the formation of porous structures and modulate the distribution of the incorporated nitrogen.^16,27

The electrochemical NO₃RR, being characterized by much faster kinetics than the nitrogen reduction reaction (NRR), provides an attractive strategy to produce ammonia under ambient conditions and is considered a promising alternative to the Haber–Bosch process. Generally, the NO₃RR to ammonia is more favorable than the NRR to ammonia due to the lower dissociation energy of the N=O bond (204 kJ mol⁻¹) than that of the N≡N bond (941 kJ mol⁻¹), as well as the higher solubility of nitrate in aqueous solution as compared to nitrogen gas.^31–43 The replacement of ion exchange, reverse osmosis, or bacterial denitrification with the electrochemical NO₃RR to ammonia is one of the most promising strategies to tackle nitrate degradation.^40–55 This methodology is based on the transformation of nitrate into ammonia that can be more easily recovered from its aqueous solution through regeneration of resins and converted into fertilizer.^44,52 The nitrate can also be turned into recyclable and valuable ammonia through renewable electricity inputs such as solar or wind sources. Nonetheless, the present electrocatalytic performance of the NO₃RR still suffers from a low ammonia yield rate at low at nitrate concentrations (<100 mg L⁻¹) due to the mass transfer.^31,32,35,39 On the other hand, the electrochemical NO₃RR involves complicated nine-proton and eight-electron transfer processes.³² Numerous intermediates, such as toxic nitrous oxide, hydroxylamine, and diamine, may leak as by-products.³² Consequently, the development of efficient catalysts should overcome current limitations, e.g. as low selectivity, low Faradaic efficiency, and release of toxic by-products.

To date, various metal-based catalysts have been reported for the electrochemical NO₃RR to ammonia.^31,56,57 The metal-free cellulose-derived NDC material as a perspective green electrocatalyst has received particular attention for electrocatalytic applications due to its significant electrical conductivity and catalytic activity that can be applied in the NO₃RR.^12,15,58 We have recently shown that graphitic N is important for NDC-800 in the electrochemical reduction of nitrite anions,⁵⁹ but the role of defects and the potential mechanisms in reduction of nitrate anions on carbon catalysts still remain elusive.

In this work, we disclose the reaction mechanisms for the electrochemical NO₃RR to ammonia on various NDC catalysts. The final optimized NDC electrocatalyst, under given conditions, exhibits high selectivity toward the ammonia synthesis from NO₃⁻ electroreduction with outstanding NO₃⁻ reduction efficiency.

Resorting to an efficient computational strategy based on reactive force field (ReaxFF) MD simulations at the atomic level as developed earlier⁶⁰ to create amorphous carbonaceous materials with different degrees of graphitization, we push the methodology steps forward, above the state of the art, by reproducing not only the whole carbonization of realistic cellulose fiber assemblies but also the N-doping process of the material. We have obtained representative models nicely matching the experimental results in terms of material density, graphitic character, and percentage of N and O atomic species. Then, we have identified the most critical NO₃⁻ binding sites by simulating the dynamics of the ion adsorption, which turn out to occur mainly in the defective regions. Then, as done before,^56,61,62 we have focused on small portions of the system. Indeed, we extracted a few representative locations and investigated them further through QC calculations to evaluate the energies involved in all the NO₃⁻ reduction reaction steps. Our findings match the literature extremely well, suggesting that nitrogen atoms in the defective regions could improve the reaction conditions.

Experimental section

Materials

Cellulose (microcrystalline, Sigma Aldrich) was used to prepare the NDC by the following steps. 3 g of cellulose was dried in a tube furnace under a 40 mL min⁻¹ flow of N₂ at 250 °C for 6 h and then oxidized by soaking it in a 30 mL of 40 wt% HNO₃ aqueous solution at 50 °C for 3 h. Next, the resulting sample was centrifuged and washed with deionized water several times and subsequently dried overnight at 120 °C. The obtained materials were carbonized under a 20 mL min⁻¹ flow of NH₃ and H₂ mixture at a constant temperature within the range of 500–900 °C for 2 h, with heating and cooling rates of 10 °C min⁻¹. The flow ratio of NH₃ and H₂ was selected to be 3 : 1 based on previous experience,^63,64 whilst the addition of H₂ was conducive to the equilibrium of the reversible reaction between NH₃ and H₂ with N₂ toward NH₃ at high temperatures. The resulting modified carbons were marked as NDC-500, NDC-600, NDC-700, NDC-800 and NDC-900 according to the carbonization temperatures of 500, 600, 700, 800, and 900 °C, respectively.

Structural characterization

N₂ adsorption. Analyses were conducted at −196 °C using an ASAP 2020 instrument (Micrometrics). The samples were degassed at 250 °C for 4 h under a dynamic vacuum before the measurement. The recorded data were analyzed using the following models: Brunauer–Emmett–Teller surface area (S_BET), Langmuir surface area (S_Langmuir), t-plot micropore volume (V_micro), and Barrett–Joyner–Halenda mesopore volume (V_meso). Moreover, the total pore volume (V_total) was determined by the single-point method (p/p₀ ∼ 0.99).

PXRD. The diffraction patterns of the samples were recorded in transmission mode on a STOE STADI-P diffractometer using a Cu K_α1 radiation source, with a DECTRIS Mythen 1K detector. The measured 2θ range was detected from 10° to 60° with a scanning rate of 1° min⁻¹.

Raman spectroscopy. Spectra were recorded on a LabRAM HR 800 Raman instrument under excitation of 532 nm laser light with a power of 50 mW, where the laser was an air-cooled and double frequency Nd:YAG laser, and the intensity was adjusted using a filter wheel equipped with software-controlled 6ND filters.

Electron microscopy. SEM was performed on a Leo Supra 35VP SMT (Zeiss) thermal field emission scanning electron microscope and a JEOL JSM-7000F microscope. Copper tape was used for sample preparation for the SEM analysis. TEM was conducted on a JEOL-2100F.

Elemental analysis. Inductively coupled plasma optical emission spectrometry (ICP-OES) and a Flash 2000 elemental analyzer containing a thermal conductivity detector with an auto-sampler were used to determine the metal content and the C, H and N contents in the carbon materials, respectively.

XPS. Measurements were performed using a hemispherical analyzer (VG SCIENTA R3000) and monochromatized aluminum Al K_α radiation as an excitation source (E = 1486.6 eV). All the peaks were calibrated with an Au 4f reference peak at a binding energy of 84.0 eV. The recorded data were analyzed using the CasaXPS software.

Electrochemical measurements

For the preparation of the electrodes, typically, a carbon fiber (Toray carbon-paper TP-030, Quintech) was used as a substrate after ultrasonic cleaning with deionized water and ethanol for 15 min and drying under ambient atmosphere. The electrocatalyst ink was prepared by adding 6 mg of sample, 270 μL of ethanol, and 30 μL of Nafion (D-520 dispersion 5 wt%, Alfa Aesar) into a glass bottle, followed by treatment with ultrasound for 50 min. Subsequently, 100 mL of electrocatalyst ink was loaded onto each side of the carbon fiber in a multiple drop manner. The electrode was obtained after drying under ambient atmosphere for 2 h.

The electrochemical measurements were carried out using a potentiostat (Gamry Instruments) operating in a three-electrode setup. The prepared electrode, a platinum wire, and a 1 M Ag/AgCl electrode were used as the working electrode, counter electrode, and reference electrode, respectively. A relative-sealed typical H-type electrolytic cell separated by a Nafion 117 membrane was used as a reaction device. All the applied potentials were recorded against 1 M Ag/AgCl owing to the continuous change of the pH value during the electrochemical process. Milli-Q water (18.3 Ω cm) was used for the preparation of the electrolytes. Cyclic voltammetry (CV) and linear sweep voltammetry (LSV) were performed at a scan rate of 10 mV s⁻¹, and chronoamperometry (CA) was recorded at a stirring rate of 400 rpm for the NO₃RR. Before collecting data of the NO₃RR, the working electrode yielded a stable polarization curve and was cleaned with electrolyte while the fresh electrolyte of the electrolytic cell was bubbled with N₂ for 1 h.

Quantitative analysis

The concentrations of NO₃⁻, NO₂⁻ and NH₄⁺ were determined by spectrophotometry using an ultraviolet-visible (UV-vis) spectrophotometer (Genesys 10S) after diluting the samples to an appropriate concentration to match the range of the calibration curve. The following are the detailed methods and processes.

Determination of the nitrate concentration. An amount of electrolyte was taken out from the cathodic chamber and diluted to 5 mL. 0.1 mL of HCl (1 mol L⁻¹) and 0.01 mL of sulfamic acid solution (0.8 wt%) were successively added into the diluted electrolyte solution under shaking before being left to stand for 15 min. The calibration curve was achieved using different concentrations of NaNO₃ standard solutions and their corresponding absorbances (Fig. S1†). The absorbance was calculated according to the following formula:⁴⁴

A = A_220nm − 2A_275nm

where A is the absorbance of nitrate, and A_220nm and A_275nm are the absorbances of nitrate at wavelengths of 220 nm and 275 nm, respectively.

Determination of the nitrite concentration. An amount of electrolyte was taken out from the cathodic chamber and diluted to 5 mL. One level microspoon reagent (114 658, MColortestTM) was added into the diluted electrolyte solution under shaking before being left to stand for 5 min. The absorbance was measured at a wavelength of 520 nm at 25 °C. The calibration curve was achieved using different concentrations of NaNO₂ standard solutions and their corresponding absorbances (Fig. S2†).

Determination of the ammonia concentration. 5 mL of electrolyte was taken out from the cathodic chamber to determine the ammonia concentration using 114 423 test kits (Merck Spectroquant). 0.4 mL of NH₄-1 reagent and 1 level microspoon NH₄-2 reagent were successively added into the solution under shaking before being left to stand for 5 min. Subsequently, 4 drops of NH₄-3 reagent were added before shaking for 10 s and being left to stand for 7 min. After that, the absorbance was measured at a wavelength of 655 nm at 25 °C. The calibration curve could be achieved using different concentrations of NH₄Cl standard solutions and their corresponding absorbances (Fig. S3†).

¹⁵N isotope labelling experiments. The isotope labelling nitrate reduction experiments were carried out to clarify the source of ammonia. The above-mentioned electrochemical nitrate reduction methodology was used, except for the replacement of the N source with Na¹⁵NO₃ (≥99%, Sigma Aldrich) at a concentration of 100 ppm of ¹⁵NO₃⁻. The pH value of the electrolyte after the reaction was adjusted to weakly acidic with diluted H₂SO₄, and D₂O was added as an internal standard for further quantification by means of ¹H nuclear magnetic resonance (NMR) (400 MHz).

Calculation of the nitrate conversion, selectivity, Faradaic efficiency, and NH₄⁺ yield. The NO₃⁻ conversion efficiency, NH₄⁺ selectivity, NH₄⁺ Faradaic efficiency, and NH₄⁺ yield were calculated according to the following equations:

NO₃⁻ reduction efficiency = ΔC_NO3⁻/C₀ × 100%

NH₄⁺ selectivity = (C_NH4⁺/18) × (ΔC_NO3⁻/62) × 100%

NH₄⁺ Faradaic efficiency = (8F × C_NH4⁺ × V) × 18Q × 100%

NH₄⁺ yield = (C_NH4⁺ × V) × (18 × t × m) × 100%

where C₀ is the initial concentration of NO₃⁻ (100 ppm); ΔC_NO3⁻ is the concentration difference of NO₃⁻ between the initial and final electrolyte (ppm); C_NH4⁺ is the final concentration of NH₄⁺ (ppm); V is the electrolyte volume (50 mL); F is the Faradaic constant (96 485 C mol⁻¹); Q is the total charge used for the carbon (C); t is the time of electrolysis (h); m is the mass of the catalyst (2 mg).

Multi-level/scale calculations

Molecular dynamics simulations. To disclose the chemical evolution and dynamics of the different materials during carbonization in terms of the degree of graphitization, general morphology, the content of hydrogen, nitrogen, and oxygen, their hybridization, and distribution, we designed a specific computational strategy, which could mimic the different stages of the process starting from the original preassembled components in agreement with the experiments. The molecular model used as a starting material consisted of cellulose fibers parallelly packed in a rectangular parallelepiped box.

Eight cellulose fibers, made of sixteen chains with sixteen glucosyl residues each, arranged as a parallelepiped rod (84 × 25 × 25 ų), were assembled parallelly close to each other on two parallel planes (four fibers on each plane – Fig. S4†) and used as the carbon source in the carbonization process. This was reproduced through all-atom reactive molecular dynamics (RMD) simulations based on a pre-parametrized force field using the MD-ReaxFF code implemented in the Amsterdam Density Functional (ADF)/ReaxFF package.^65,66 The size of the simulation box was fixed at 100 × 100 × 100 ų. Carbonization was simulated through RMD runs at high and low temperatures in the NVT ensemble, applying periodic boundary conditions in all directions (Fig. S5 and S6†). Then, nitrogen atoms were introduced in the simulation box, and the dynamics run was extended to thermalize and stabilize the new system at a high temperature and induce the internalization of the N atoms (Fig. S7–S9†).⁶⁰ This was useful for estimating the capacity of adsorption of the carbonized material and possible types of insertion. The final equilibrated model (Fig. S7†) was selected for the subsequent simulations in the presence of NO₃⁻ ions.

A stable carbonized N-doped configuration extracted from the final portion of the RMD trajectory was surrounded by NO₃⁻ ions, equilibrated in the NVT ensemble at ambient temperature and simulated for about 200 ps. The final configuration was used to identify probable locations of the ions close to the graphitic regions (Fig. S10 and S11†). No restraints were applied to the systems, and reactivity was always on to simulate bond breaking and formation in response to the surrounding environment. All the details of the simulations are reported in the ESI.†

QC calculations. After explorative QC optimizations of various model systems extracted from the simulations and modified to comply with the QC requirements (see ESI† – Fig. S12–S14), which were meant to provide qualitative descriptions of the chains of reactions taking place on the catalyst, we opted for a more systematic approach to provide quantitative estimates of the energies that came into play. Thus, selected portions of the RMD configurations were used to build the QC models aimed at reconstructing the whole mechanism of the NO₃RR under realistic conditions. All QC calculations were carried out with the Quantum Espresso package⁶⁷ in conjunction with the GGA-PBE xc-functional,⁶⁸ the Grimme-D2 corrections (to account for van der Waals dispersion interactions),⁶⁹ and ultrasoft pseudo-potentials. Local relaxations were performed spin-polarized, applying 40 Ry and 400 Ry cut-offs on the one-electron wave functions and density, respectively. The single-particle KS levels were broadened by Gaussian smearing of 0.002 Ry. The first Brillouin zone was sampled at the Γ point only, as the selected systems were intrinsically non-periodic; for this purpose, a minimum empty space of 10–15 Å in all directions was selected in order to decouple the system from its replicas. Our approach and the process analysis were inspired by previous investigations focused on similar processes.^56,61 Reaction energies were calculated referring to a gas-phase HNO₃ molecule and the hydrogen electrode method,⁶² which assumes that the chemical potential of an electron–proton pair is equal to that of 1/2H₂ in the gas phase. The limiting potential of each mechanism was calculated by taking the negative of the maximum energy difference between every two successive steps in the mechanism diagram. Reaction energies were calculated in the gas phase by considering the effects played by the insertion of solvation models negligible.

Results and discussion

Characterization

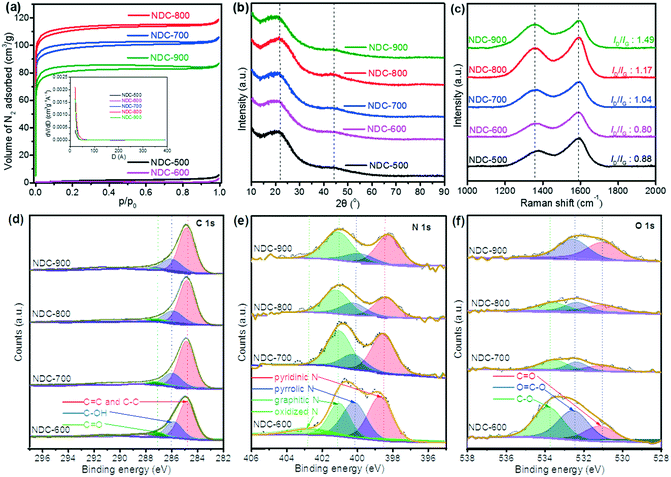
As a carbon-based material formed by the oxidation of cellulose by HNO₃ and then carbonization under an NH₃/H₂ flow, NDC has a porous structure with a large surface area. Irregular shapes and disordered open pores of the particles are visible in the SEM and TEM micrographs (Fig. 1) of the five NDC materials, i.e., NDC-500, NDC-600, NDC-700, NDC-800 and NDC-900. Further analysis of these porous materials by means of N₂ adsorption (Fig. 2a) revealed that the shape of the isotherms strongly depends on the carbonization temperature. The N₂ uptake for NDC-500 and NDC-600 is very low, suggesting the non-porous character of these materials, whereas the samples carbonized at higher temperatures show adsorption isotherms of type I according to the IUPAC classification.⁷⁰ This type of isotherm assesses microporous materials where the limiting adsorbate uptake is governed by the accessible micropore volume rather than by the internal surface area. As shown in Table 1, NDC-800 had a higher total pore volume (V_total = 0.184 cm³ g⁻¹) and BET surface area (S_BET = 413 m² g⁻¹) than the others. The surface area and porosity could decrease due to the material shrinkage at high temperatures (900 °C).⁷⁰

Fig. 1 SEM micrographs of (a) NDC-500, (b) NDC-600, (c) NDC-700, (d) NDC-800 and (e) NDC-900; (f) TEM image of NDC-800.

Fig. 2 (a) N₂ adsorption–desorption isotherms, (b) PXRD patterns and (c) Raman spectra of NDC-500, NDC-600, NDC-700, NDC-800 and NDC-900 materials; XPS (d) C 1s, (e) N 1s and (f) O 1s spectra of NDC-600, NDC-700, NDC-800 and NDC-900 materials.

Table 1 Textural parameters from the five NDC materials after carbonization at different temperatures in a flow of NH₃/H₂

Sample	S BET (m^2 g^−1)	S Langmuir (m^2 g^−1)	V total (cm^3 g^−1)	V meso (cm^3 g^−1)	V micro (cm^3 g^−1)
NDC-500	6	12	0.009	0.006	0.001
NDC-600	3	5	0.005	0.001	0.001
NDC-700	357	437	0.164	0.136	0.017
NDC-800	413	494	0.184	0.154	0.019
NDC-900	304	362	0.135	0.113	0.012

---

These observations well compare with the final morphology of the atomistic model extracted from the carbonization doping RMD simulations. The typical structures (Fig. S7–S9†) consist of an extended network of graphene-like sheets with nonlinear bending deformations, several contortions, defects, and vacancies. These became more randomly twisted, rugged, and packed in the central region of the simulation box, where the material was accumulated and formed a sort of a long carbon fiber (visible through periodicity). The combination of these atomistic shapes might generate the macroscopic morphology shown in Fig. 1. Planar motifs (graphitized sheets) interconnecting the fibers were found at the boundaries (Fig. 3). We could estimate the degree of graphitization considering the bond orders of the atoms in the structure, and we found that the ratio between the graphitic-like and diamond-like carbon was about 1.44, confirming the dominant graphitic character of the ensemble. The composition of the final structured configurations is approximately C 88%, N 6%, and O 1%. Most of the O and N atoms are on the edges of the pores. O is bound as C=O and C–O–C, whereas N is more prone to ring insertion. 10% of the total number of nitrogen is inserted in carbon rings. 25% is found in five-membered-rings, 45% in six-membered-rings, 21% in seven-membered-rings and 8% in eight-membered-rings. These rings could be inside the core of the structure or at the edges of the pores. Only 6% of the nitrogen is inside the graphitic sheets, while the other nitrogen atoms are bonded to carbon chains at the boundaries of the fibers. The analysis of the pore size distribution, evaluated with the CAVER software, revealed the presence of pores in the range of 2–3 nm (Fig. S9†) inside the fiber, which is in good agreement with the experimental findings.

Fig. 3 (a) The final carbonized-N-doped atomistic configuration obtained through RMD (periodic replica), (b) graphitic-like structure with N at the edges of the pores, and (c) identification of the tunnels and cavities by CAVER's sphere filling (stick models and spheres colored according to the atom type: C gray, O red, N blue).

Indeed, the determination of the chemical composition of the five NDC materials via elemental analysis reveals that the materials consist mainly of C, N, and H (Table 2). It should be noted that these samples also contain significant amounts of oxygen, which cannot be determined by this method. A downward trend of the resultant N and H contents was observed with the increase in the carbonization temperature since pyrolysis at high temperature accelerates the break-up of the N-containing networks. The increase in N content at 900 °C can be explained by the reaction of the material with nitrogen due to the presence of ammonia during calcination at high temperatures.^16,22,27,30 In addition, further analysis with ICP revealed the low concentrations (<10 ppm) for Cr, Mn, Ni, Co, Cu, Mo, V, W, Pt, and Pd in the NDC materials.

Table 2 C, H, and O and their relative contents in the five NDC materials

Sample	C%	N%	H%
NDC-500	71.9	8.0	3.6
NDC-600	76.5	9.0	2.6
NDC-700	82.4	7.7	1.8
NDC-800	84.0	5.7	1.4
NDC-900	82.1	6.3	1.4

---

The structural identification of the NDC materials through multiple analytical techniques showed that the PXRD patterns present two broad diffraction feature peaks at 23° and 44° assigned to the graphite facets (002) and (101) of carbon (Fig. 2b).⁹ Raman spectral analysis reveals D and G bands at 1340 cm⁻¹ and 1590 cm⁻¹ (Fig. 2c), respectively. Both D and G bands arise from the disordered sp² hybridized carbon and the crystalline graphitic carbon, respectively.⁷¹ The ratio intensity of the D and G bands (I_D/I_G) is considered an essential asset to evaluate the degree of graphitization of carbon materials. A trend of higher ratios was observed upon increasing the carbonization temperature, whilst NDC-900 had the highest I_D/I_G ratio (1.49), implying more defects and disordered structures than the others.⁷² XPS disclosed the surface composition of the materials (Fig. 2d–f), which showed that the ratio of resultant pyrrolic N decreased while that of total graphitic and pyridinic N increased with the increase of carbonization temperature. Graphitic N and pyridinic N are considered efficient and stable metal-free active sites, which are closely related to the electrocatalysis properties of NDC materials.^3,28,29

Catalysis

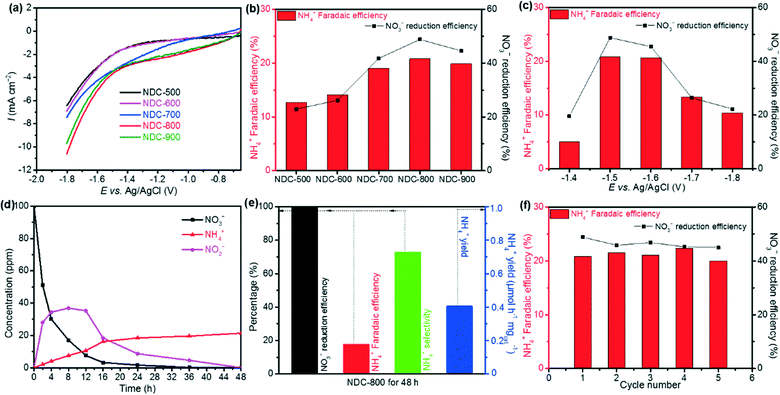
Since the carbonization temperature can affect the formation of the carbon-based catalyst structure and thus its electrocatalytic activities, we tested various carbonization temperatures to select the best conditions and prepared a series of cellulose-derived NDC samples, namely NDC-500, NDC-600, NDC-700, NDC-800, and NDC-900.

Then, we measured the electrochemical NO₃RR in a 0.1 M Na₂SO₄ electrolyte with 100 ppm NO₃⁻ (pH 5.6). The results are depicted in Fig. 4a. Among the five NDC materials, the highest electrocatalytic activity was achieved for the NDC-800 catalyst. This trend was also typical for the hydrogen evolution reaction (HER) at lower potentials (Fig. S15†) and the oxygen evolution reaction (OER) at higher potentials (Fig. S16†) in a 0.1 M NaOH electrolyte. Furthermore, NDC-800 yielded 28.1 ppm NO₂⁻ and 2.09 ppm NH₄⁺ from the NO₃RR in CA at −1.5 V vs. Ag/AgCl for 2 h, with the highest NH₄⁺ Faradaic and NO₃⁻ reduction efficiencies (Fig. 4b). Although the five NDC materials had similar textural properties, the presented electrocatalytic activity of the electrochemical NO₃RR climbs up first and then declines when the carbonization temperature increases from 500 °C to 900 °C (Fig. 4b). From these findings, we could speculate that the significant activity of NDC-800 in the electrochemical NO₃RR is related to its higher microporosity and a more substantial number of active sites rather than a higher amount of nitrogen. This is demonstrated by the computational multi-scale approach that not only identified the active sites as the defective regions where undercoordinated/open valence atoms were present but also reproduced the dynamics of the NO₃⁻ ions towards these locations and the whole reaction mechanisms. In summary, the experiments indicate that ammonolysis at 800 °C can create an optimum NDC structure for the efficient electrochemical NO₃RR to ammonia.

Fig. 4 (a) LSV curves of NDC-500, NDC-600, NDC-700, NDC-800 and NDC-900 for the NO₃RR; (b) NH₄⁺ Faradaic and NO₃⁻ reduction efficiencies of NDC-500, NDC-600, NDC-700, NDC-800 and NDC-900 at −1.5 V vs. Ag/AgCl for 2 h CA; (c) NH₄⁺ Faradaic and NO₃⁻ reduction efficiencies of NDC-800 at various applied potentials for 2 h CA; (d) time-dependent concentrations of NO₃⁻, NO₂⁻ and NH₄⁺ over NDC-800 CA at −1.5 V vs. Ag/AgCl; (e) NO₃⁻ reduction efficiency, NH₄⁺ Faradaic efficiency, NH₄⁺ selectivity and NH₄⁺ yield of NDC-800 at −1.5 V vs. Ag/AgCl for 48 h CA; (f) NO₃⁻ reduction and NH₄⁺ Faradaic efficiencies of NDC-800 at −1.5 V vs. Ag/AgCl for 2 h CA after consecutive recycling tests. Measurements were performed in a 0.1 M Na₂SO₄ aqueous electrolyte with 100 ppm of NO₃⁻.

Thus, we chose NDC-800 to identify the optimum applied potential for the catalytic activity for the NO₃RR. The measurements were performed in a 0.1 M Na₂SO₄ electrolyte with 100 ppm NO₃⁻ on CA for 2 h, at constant potentials of −1.4, −1.5, −1.6, −1.7, and −1.8 V vs. Ag/AgCl. As shown in Fig. 4c, the yield of NH₄⁺ and the current density increased upon increasing the applied potentials. Due to the competition with competitive reactions, such as the HER and nitrite reduction reaction (NO₂RR), both NO₃⁻ reduction and NH₄⁺ Faradaic efficiencies showed a volcanic shape curve with a maximum value of 48.8% and 20.8% at −1.5 V vs. Ag/AgCl, respectively.

Unveiling the electrocatalytic decay rate of the NO₃⁻ concentration with reaction time could provide crucial information on removed NO₃⁻ for the NDC-800 material toward the possibility of using it in NO₃RR application. Therefore, further studies in this system and CA measurements were performed at −1.5 V vs. Ag/AgCl in a 0.1 M Na₂SO₄ electrolyte with 100 ppm NO₃⁻ for 2, 4, 8, 12, 16, 24, 36, and 48 h. The results of time-dependent NO₃⁻, NO₂⁻ and NH₄⁺ concentrations are shown in Fig. 4d. As the reaction time increased, better effective reduction efficiency of NO₃⁻ was observed and reached nearly 100% when prolonging to 48 h, while the intermediate by-product NO₂⁻ concentration increased first and was further almost completely electrochemically reduced to NH₄⁺ after 48 h. The concentration of NH₄⁺ increased, with an NH₄⁺ faradaic efficiency of 17.8%, selectivity of 73.1%, and NH₄⁺ yield rate of 0.42 μmol h⁻¹ mg_cat.⁻¹ (Fig. 4e). The metal-free NDC-800 exhibited high selectivity toward the ammonia synthesis from NO₃⁻ electroreduction with outstanding reduction efficiency.

The stability of the NDC-800 catalyst during the NO₃RR was estimated by means of consecutive recycling tests using the same electrode before cleaning and drying. Each cycle of tests was carried out for 2 h using CA at −1.5 V vs. Ag/AgCl in a 0.1 M Na₂SO₄ electrolyte with 100 ppm NO₃⁻. The results of five cycling tests are depicted in Fig. 4f. Notably, the CA plots showed only a slight fluctuation and no apparent downward trend. Meanwhile, the remaining amount of NO₃⁻, the yield of NO₂⁻ and NH₄⁺, the NO₃⁻ reduction efficiency, and the NH₄⁺ Faradaic efficiency revealed small changes but no evident trend of decrease after each test. These results imply good catalytic stability during the NO₃RR for the NDC-800 catalyst, which is consistent with previous carbon-based materials studies.^59,73

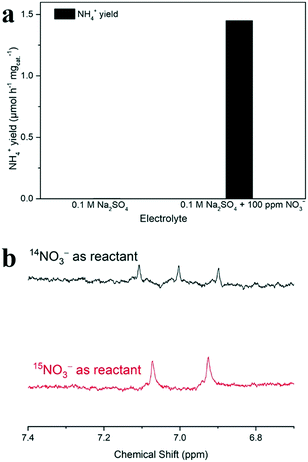
To verify the source of ammonia, the electrolyte without NO₃⁻ was also tested as a control experiment for the electrochemical NO₃RR. The result showed that the electrochemical NO₃RR measured in blank Na₂SO₄ electrolyte yielded a negligible concentration of NH₄⁺ (Fig. 5). Meanwhile, ¹⁵N isotope labeling ¹H NMR spectra were acquired to further verify the source of ammonia. The ¹H NMR spectra of the electrolyte after the NO₃RR with Na¹⁵NO₃ at −1.5 V vs. ref for 2 h show typical double peaks of ¹⁵NH₄⁺, which is different from the triple peaks of ¹⁴NH₄⁺ from the ¹H NMR spectra with Na¹⁴NO₃ as the reactant (Fig. 6).⁷⁴ This result further confirms that the produced NH₄⁺ originates from the electrochemical reduction of NO₃⁻.

Fig. 5 (a) NH₄⁺ yield of NDC-800 in 0.1 M Na₂SO₄ electrolyte with and without 100 ppm NO₃⁻ for 2 h CA; (b) ¹H NMR spectra of the electrolyte after the electrocatalytic NO₃RR using ¹⁵NO₃⁻ and ¹⁴NO₃⁻ as the nitrogen sources.

Fig. 6 Energy profile of the NO₃RR mechanism leading to the formation of NH₃ and three water molecules and the corresponding configurations. These were obtained through energy minimizations at the QC level (using a reduced model system terminated with hydrogen atoms). C gray, N blue, O red, H light blue. Note that the first step is the spontaneous dissociation of HNO₃ at the carbon surface.

Reaction mechanisms by multi-scale/level calculations

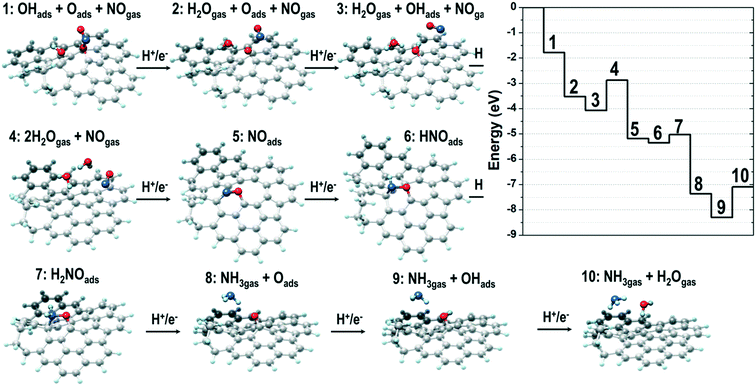
To investigate the reaction mechanism and unravel the origin of NDC's high performance in the NO₃RR, we performed density functional theory (DFT) calculations starting from the RMD supramolecular model described above. Considering that nitrate reduction to ammonia can take place according to several mechanisms and that only defects (low-coordinated sites) resulted as active centers towards nitrate reduction,^56,75 we carefully scrutinized the process against a typical defect site of the NDC material identified in the RMD simulations. The analysis of the corresponding energy profiles (Fig. S17 and S18†) allowed the identification of a promising reduction pathway with limiting potentials in a range of the experimental onset potentials at −1.50 V vs. Ag/AgCl accompanied by eight proton/electron transfers and the generation of ammonia (and water molecules). The detailed steps of such a pathway are shown in Fig. 6. It is easy to notice that the initially two O atoms of HNO₃ (under acidic conditions, RMD simulations predicted the stabilization of the nitrate ion as undissociated nitric acid) strongly interact with the defect and spontaneously dissociate nitric acid into NO (not in direct contact with the surface), an oxygen atom and a hydroxyl group anchored to the defect borders (step 1 in Fig. 6). The addition of a proton/electron pair leads to the spontaneous generation (downhill energy variation) of a water molecule released into the environment (step 2). The oxygen atom firmly bound to the defect can generate a second water molecule via the addition of two further proton/electron pairs (steps 3 and 4) via an uphill variation characterized by a limiting potential of about −1.2 eV.

Interestingly, a modification of the defect borders, achieved by inserting a nitrogen atom, as shown in Fig. 7, can decrease (in absolute value) the limiting potential of such a step to about −0.6 eV. The reduction proceeds via the adsorption of NO in the surface defects. We simulate this scenario by considering the adsorption of NO on the most strongly interacting carbon atom of the defective region (the atom with only two first neighbors). It is worth mentioning that this is a very subtle step as the adsorption could be via the N or the O atom, and thus the reduction could proceed through different mechanisms. More specifically, the adsorption via the N atoms evolves by those mechanisms labeled in the literature as O-distal, O-alternating, N-distal, and N-alternating. Such mechanisms, whose energy plots are reported in the ESI,† are characterized by downhill steps up to the stabilization of the NH₂ species strongly interacting with the defect borders and characterized by limiting potentials (larger than −1.8 eV in absolute values) that are too high for the generation of ammonia.

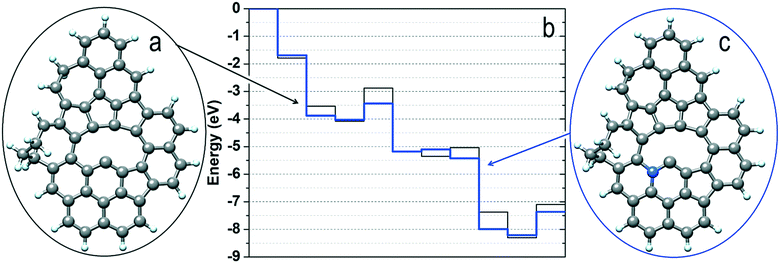Fig. 7 (a) Structure of the bare defect sampled as the catalytic site in the mechanism shown in Fig. 6; (b) energy profiles for the NO₃RR mechanism characterizing sites (a) and (c); (c) same structure of panel (a) where one C atom next to the defect border has been replaced with a nitrogen atom.

Instead, if the adsorption of NO takes place according to the configuration depicted in step 5 of Fig. 6 (where it is the O atom that is connected to the carbon with the most robust interaction), the reduction can proceed according to other mechanisms labeled N-first, N-enzymatic, O-first, and O-enzymatic, which are more convenient. Among these, it is the N-first that results as the most promising mechanism, and it corresponds to the mechanism depicted in Fig. 6. Starting from configuration 5, NO can adsorb two H atoms via the addition of two proton/electron pairs, resulting in the adsorbed HNO and H₂NO species (steps 6 and 7); the first step is downhill in energy, whereas the second one is characterized by a relatively low (about −0.4 eV) limiting potential. Further proton/electron addition produces ammonia (step 8) and leaves on the surface an adsorbed O atom in an analogous configuration to that of step 2. In fact, the generation of the last water molecule (steps 9 and 10) proceeds via the addition of the final two proton/electron pairs with a profile very similar to that observed in steps 3 and 4 and a limiting potential of about −1.2 eV. If we consider the defect in the presence of the N atom at the border of the defect, Fig. 7, this last limiting potential is decreased (in absolute value) to about −0.8 eV, analogous to what was observed for the generation of the second water molecule.

We want to point out that here we do not present the precise topology of the defect as the only candidate for promoting nitrate reduction, and the models we used are aimed at demonstrating the presence of a family of localized surface defects (whose formation derives from the chosen synthetic procedure) with catalytic properties associated to limiting potentials in agreement with the experimentally observed onset potentials. A further degree of freedom is given by the composition of the final cellulose-derived NDC material, as it has been explicitly shown that the presence of N atoms can modulate the catalytic properties of the neighboring sites. Furthermore, the described N-first mechanism is characterized by limiting potentials in the range of −0.6/−1.2 eV, corresponding to water evolution and the polishing of the surface borders from adsorbed O atoms or OH groups. The production of NH₃ is achieved at much lower (in absolute values) limiting potentials, corresponding, in the aforementioned case, to about −0.4 eV. This means that working at −1.5 V vs. Ag/AgCl does not guarantee (according to our analysis) the removal of oxygen species from the defect borders but guarantees the evolution of ammonia via an N-first mechanism.

We could speculate that the active site, besides binding oxygen and nitrogen, can also modulate the interaction of intermediates, thus optimizing the reaction pathway and hindering the formation of by-products. This is consistent with the experimental results that identified NDC-800, which displayed more active sites, as the more active catalyst.

Conclusions

In summary, metal-free cellulose-derived NDC materials were synthesized as electrocatalysts. NDC-500, NDC-600, NDC-700, NDC-800, and NDC-900 were prepared from cellulose with a combination of HNO₃ treatment and carbonization with NH₃/H₂ at 500, 600, 700, 800, and 900 °C, respectively. For the electrochemical NO₃RR performed at the optimal potential of −1.5 V vs. Ag/AgCl in a 0.1 M Na₂SO₄ electrolyte with 100 ppm NO₃⁻, the NDC-800 material exhibited higher electrocatalytic activity in comparison with the other materials, showing 73.1% NH₄⁺ selectivity toward the ammonia synthesis from NO₃⁻ electroreduction and nearly 100% NO₃⁻ reduction efficiency when prolonging to 48 h, with outstanding electrochemical stability. We have provided a complete computational description of the NDC material, from the formation to the catalytic activity. This has not been carried out yet for these types of amorphous systems due to their complex nature and organization. Using ReaxFF MD simulations, we have simulated all the processes leading to the carbonized-N-doped morphologies starting from the cellulose fibers and obtained realistic models of the NDC catalyst corresponding to the experimental findings (as confirmed by analysis of the structures). We have described, at the atomic level and on the nanoscale region, the behavior of the system in terms of morphology, distinct reactive regions, and ion adsorption. We have identified the most active portions and explored through QC calculations (at the sub-nanoscale) the reaction mechanisms there to disclose the role played by the N-doping action and the energies involved in the formation of the final products. The results suggest that defective regions containing nitrogen atoms are fundamental to improving the material response and agree with the general picture that emerged from the experimental characterization. This synergistic combination of all the experimental techniques and computational modeling can be used effectively for careful design of efficient carbon-based catalysts for the electrochemical NO₃⁻ reduction to ammonia.

Data availability

The datasets supporting this article have been uploaded as part of the ESI.†

Author contributions

Z. C. synthesized the materials and performed the Raman analysis. J. C. performed the electrochemical and TEM experiments. S. M and G. B. performed the theoretical calculations and analyzed the work. A. R. and P. K. performed the N₂ adsorption, CHN analysis and XPS measurements. R. D. co-supervised the synthesis and analysis. A. S. and S. M. supervised the project and designed the experiments and calculations. All authors contributed to the writing of the manuscript. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Swedish Energy Agency (project nr: 50501-1). Z. C. would like to thank the China Scholarship Council for a PhD scholarship. P. K. acknowledges the European Regional Development Fund in the framework of the Polish Innovation Operational Program (contract no. POIG.02.01.00-12-023/08) for financial support. T. M. B. acknowledges the Swedish Research Council for Sustainable Development Formas (project reg. nr: 2020-02321) for financial support. S. B. thanks the “Austrian COMET-Program” (project InTribology1, no. 872176) via the Austrian Research Promotion Agency (FFG) and the federal states of Niederösterreich and Vorarlberg, which was carried out within the “Excellence Centre of Tribology” (AC2T research GmbH).

Notes and references

1. D. Liu, L. Dai, X. Lin, J. F. Chen, J. Zhang, X. Feng, K. Müllen, X. Zhu and S. Dai, Adv. Mater., 2019, 31, 1804863.
2. Y. Song, W. Chen, C. Zhao, S. Li, W. Wei and Y. Sun, Angew. Chem., Int. Ed., 2017, 56, 10840–10844.
3. Y. Yang, L. Gu, S. Guo, S. Shao, Z. Li, Y. Sun and S. Hao, Front. Chem., 2019, 7, 1–18.
4. Y. Zhao, R. Nakamura, K. Kamiya, S. Nakanishi and K. Hashimoto, Nat. Commun., 2013, 4, 1–7.
5. Q. Lv, W. Si, J. He, L. Sun, C. Zhang, N. Wang, Z. Yang, X. Li, X. Wang, W. Deng, Y. Long, C. Huang and Y. Li, Nat. Commun., 2018, 9, 1–11.
6. C. Zhang, N. Mahmood, H. Yin, F. Liu and Y. Hou, Adv. Mater., 2013, 25, 4932–4937.
7. K. Tian, J. Wang, L. Cao, W. Yang, W. Guo, S. Liu, W. Li, F. Wang, X. Li, Z. Xu, Z. Wang, H. Wang and Y. Hou, Nat. Commun., 2020, 11, 2–11.
8. X. Wang, A. Vasileff, Y. Jiao, Y. Zheng and S. Z. Qiao, Adv. Mater., 2019, 31, 1803625.
9. H. Jiang, J. Gu, X. Zheng, M. Liu, X. Qiu, L. Wang, W. Li, Z. Chen, X. Ji and J. Li, Energy Environ. Sci., 2019, 12, 322–333.
10. R. Pawlak, X. Liu, S. Ninova, P. D'Astolfo, C. Drechsel, S. Sangtarash, R. Häner, S. Decurtins, H. Sadeghi, C. J. Lambert, U. Aschauer, S. X. Liu and E. Meyer, J. Am. Chem. Soc., 2020, 142, 12568–12573.
11. T. Zhang, W. Schilling, S. U. Khan, H. Y. V. Ching, C. Lu, J. Chen, A. Jaworski, G. Barcaro, S. Monti, K. De Wael and A. Slabon, ACS Catal., 2021, 11, 14087–14101.
12. R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994.
13. X. Wu, Z. Shi, R. Tjandra, A. J. Cousins, S. Sy, A. Yu, R. M. Berry and K. C. Tam, J. Mater. Chem. A, 2015, 3, 23768–23777.
14. P. Song, B. Liu, C. Liang, K. Ruan, H. Qiu, Z. Ma, Y. Guo and J. Gu, Nano-Micro Lett., 2021, 13, 1–17.
15. X. Du, Z. Zhang, W. Liu and Y. Deng, Nano Energy, 2017, 35, 299–320.
16. H. Wang, Y. Shao, S. Mei, Y. Lu, M. Zhang, J. K. Sun, K. Matyjaszewski, M. Antonietti and J. Yuan, Chem. Rev., 2020, 120, 9363–9419.
17. T. Bai, Y. Guo, D. Wang, H. Liu, G. Song, Y. Wang, Z. Guo, C. Liu and C. Shen, J. Mater. Chem. A, 2021, 9, 5566–5577.
18. B. P. Chhetri, D. Soni, A. B. Rangumagar, C. M. Parnell, H. Wayland, F. Watanabe, G. Kannarpady, A. S. Biris and A. Ghosh, J. Environ. Chem. Eng., 2017, 5, 2586–2596.
19. C. Chen, Y. Kuang, S. Zhu, I. Burgert, T. Keplinger, A. Gong, T. Li, L. Berglund, S. J. Eichhorn and L. Hu, Nat. Rev. Mater., 2020, 5, 642–666.
20. R. Huang, C. Cao, J. Liu, D. Sun and W. Song, Chem. Commun., 2019, 55, 1935–1938.
21. T. Li, C. Chen, A. H. Brozena, J. Y. Zhu, L. Xu, C. Driemeier, J. Dai, O. J. Rojas, A. Isogai, L. Wågberg and L. Hu, Nature, 2021, 590, 47–56.
22. Z. Qiang, Y. Xia, X. Xia and B. D. Vogt, Chem. Mater., 2017, 29, 10178–10186.
23. D. Deng, X. Pan, L. Yu, Y. Cui, Y. Jiang, J. Qi, W. X. Li, Q. Fu, X. Ma, Q. Xue, G. Sun and X. Bao, Chem. Mater., 2011, 23, 1188–1193.
24. Y. Cao, S. Mao, M. Li, Y. Chen and Y. Wang, ACS Catal., 2017, 7, 8090–8112.
25. X. Y. Wang, X. Yao, A. Narita and K. Müllen, Acc. Chem. Res., 2019, 52, 2491–2505.
26. T. Schiros, D. Nordlund, L. Pálová, D. Prezzi, L. Zhao, K. S. Kim, U. Wurstbauer, C. Gutiérrez, D. Delongchamp, C. Jaye, D. Fischer, H. Ogasawara, L. G. M. Pettersson, D. R. Reichman, P. Kim, M. S. Hybertsen and A. N. Pasupathy, Nano Lett., 2012, 12, 4025–4031.
27. W. Luo, B. Wang, C. G. Heron, M. J. Allen, J. Morre, C. S. Maier, W. F. Stickle and X. Ji, Nano Lett., 2014, 14, 2225–2229.
28. Z. Zhang, L. Yu, Y. Tu, R. Chen, L. Wu, J. Zhu and D. Deng, Cell Rep. Phys. Sci., 2020, 1, 100145.
29. N. Zhou, N. Wang, Z. Wu and L. Li, Catalysts, 2018, 8, 509.
30. Y. Liu, Y. Su, X. Quan, X. Fan, S. Chen, H. Yu, H. Zhao, Y. Zhang and J. Zhao, ACS Catal., 2018, 8, 1186–1191.
31. P. H. van Langevelde, I. Katsounaros and M. T. M. Koper, Joule, 2021, 5, 290–294.
32. W. J. Sun, H. Q. Ji, L. X. Li, H. Y. Zhang, Z. K. Wang, J. H. He and J. M. Lu, Angew. Chem., Int. Ed., 2021, 60, 22933–22939.
33. H. Niu, Z. Zhang, X. Wang, X. Wan, C. Shao and Y. Guo, Adv. Funct. Mater., 2021, 31, 2008533.
34. N. C. Kani, J. A. Gauthier, A. Prajapati, J. Edgington, I. Bordawekar, W. Shields, M. Shields, L. C. Seitz, A. R. Singh and M. R. Singh, Energy Environ. Sci., 2021, 14, 6349–6359.
35. P. Gao, Z. H. Xue, S. N. Zhang, D. Xu, G. Y. Zhai, Q. Y. Li, J. S. Chen and X. H. Li, Angew. Chem., Int. Ed., 2021, 60, 20711–20716.
36. Q. Hu, Y. Qin, X. Wang, Z. Wang, X. Huang, H. Zheng, K. Gao, H. Yang, P. Zhang, M. Shao and C. He, Energy Environ. Sci., 2021, 14, 4989–4997.
37. M. Li, X. Liu, L. Wang, F. Hou, S. X. Dou and J. Liang, EcoMat, 2021, 3, 1–26.
38. Y. Wang, A. Xu, Z. Wang, L. Huang, J. Li, F. Li, J. Wicks, M. Luo, D. H. Nam, C. S. Tan, Y. Ding, J. Wu, Y. Lum, C. T. Dinh, D. Sinton, G. Zheng and E. H. Sargent, J. Am. Chem. Soc., 2020, 142, 5702–5708.
39. G. F. Chen, Y. Yuan, H. Jiang, S. Y. Ren, L. X. Ding, L. Ma, T. Wu, J. Lu and H. Wang, Nat. Energy, 2020, 5, 605–613.
40. S. B. Patil, T. R. Liu, H. L. Chou, Y. Bin Huang, C. C. Chang, Y. C. Chen, Y. S. Lin, H. Li, Y. C. Lee, Y. J. Chang, Y. H. Lai, C. Y. Wen and D. Y. Wang, J. Phys. Chem. Lett., 2021, 12, 8121–8128.
41. S. B. Patil, H. L. Chou, Y. M. Chen, S. H. Hsieh, C. H. Chen, C. C. Chang, S. R. Li, Y. C. Lee, Y. S. Lin, H. Li, Y. J. Chang, Y. H. Lai and D. Y. Wang, J. Mater. Chem. A, 2021, 9, 1230–1239.
42. S. B. Patil and D. Y. Wang, Small, 2020, 16, 1–44.
43. C. C. Chang, S. R. Li, H. L. Chou, Y. C. Lee, S. Patil, Y. S. Lin, C. C. Chang, Y. J. Chang and D. Y. Wang, Small, 2019, 15, 1–7.
44. R. Jia, Y. Wang, C. Wang, Y. Ling, Y. Yu and B. Zhang, ACS Catal., 2020, 10, 3533–3540.
45. S. Xu, D. C. Ashley, H. Y. Kwon, G. R. Ware, C. H. Chen, Y. Losovyj, X. Gao, E. Jakubikova and J. M. Smith, Chem. Sci., 2018, 9, 4950–4958.
46. I. Taniguchi, N. Nakashima, K. Matsushita and K. Yasukouchi, J. Electroanal. Chem. Interfacial Electrochem., 1987, 224, 199–209.
47. S. Guo, K. Heck, S. Kasiraju, H. Qian, Z. Zhao, L. C. Grabow, J. T. Miller and M. S. Wong, ACS Catal., 2018, 8, 503–515.
48. J. Liu, T. Cheng, L. Jiang, A. Kong and Y. Shan, ACS Appl. Mater. Interfaces, 2020, 12, 33186–33195.
49. Y. Wang, Y. Yu, R. Jia, C. Zhang and B. Zhang, Natl. Sci. Rev., 2019, 6, 730–738.
50. S. Garcia-Segura, M. Lanzarini-Lopes, K. Hristovski and P. Westerhoff, Appl. Catal., B, 2018, 236, 546–568.
51. J. Gao, B. Jiang, C. Ni, Y. Qi, Y. Zhang, N. Oturan and M. A. Oturan, Appl. Catal., B, 2019, 254, 391–402.
52. J. M. McEnaney, S. J. Blair, A. C. Nielander, J. A. Schwalbe, D. M. Koshy, M. Cargnello and T. F. Jaramillo, ACS Sustainable Chem. Eng., 2020, 8, 2672–2681.
53. A. Thornton, P. Pearce and S. A. Parsons, J. Hazard. Mater., 2007, 147, 883–889.
54. J. H. Jang, A. Gaur, H. J. Song and J. Park, Chem. Pap., 2011, 65, 437–446.
55. L. Su, D. Han, G. Zhu, H. Xu, W. Luo, L. Wang, W. Jiang, A. Dong and J. Yang, Nano Lett., 2019, 19, 5423–5430.
56. Z. Y. Wu, M. Karamad, X. Yong, Q. Huang, D. A. Cullen, P. Zhu, C. Xia, Q. Xiao, M. Shakouri, F. Y. Chen, J. Y. Kim, Y. Xia, K. Heck, Y. Hu, M. S. Wong, Q. Li, I. Gates, S. Siahrostami and H. Wang, Nat. Commun., 2021, 12, 1–10.
57. J. Li, G. Zhan, J. Yang, F. Quan, C. Mao, Y. Liu, B. Wang, F. Lei, L. Li, A. W. M. Chan, L. Xu, Y. Shi, Y. Du, W. Hao, P. K. Wong, J. Wang, S. X. Dou, L. Zhang and J. C. Yu, J. Am. Chem. Soc., 2020, 142, 7036–7046.
58. A. Wütscher, T. Eckhard, D. Hiltrop, K. Lotz, W. Schuhmann, C. Andronescu and M. Muhler, ChemElectroChem, 2019, 6, 514–521.
59. Z. Chen, A. Jaworski, J. Chen, T. M. Budnyak, I. Szewczyk, A. Rokicińska, R. Dronskowski, N. Hedin, P. Kuśtrowski and A. Slabon, Dalton Trans., 2021, 50, 6857–6866.
60. S. Monti, G. Barcaro, W. A. Goddard and A. Fortunelli, ACS Nano, 2021, 15, 6369–6385.
61. F. Calle-Vallejo, M. Huang, J. B. Henry, M. T. M. Koper and A. S. Bandarenka, Phys. Chem. Chem. Phys., 2013, 15, 3196–3202.
62. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Appl. Catal., B, 2004, 108, 17886–17892.
63. Z. Ma, T. Thersleff, A. L. Görne, N. Cordes, Y. Liu, S. Jakobi, A. Rokicinska, Z. G. Schichtl, R. H. Coridan, P. Kustrowski, W. Schnick, R. Dronskowski and A. Slabon, ACS Appl. Mater. Interfaces, 2019, 11, 19077–19086.
64. Z. Ma, A. Jaworski, J. George, A. Rokicinska, T. Thersleff, T. M. Budnyak, G. Hautier, A. J. Pell, R. Dronskowski, P. Kuśtrowski and A. Slabon, J. Phys. Chem. C, 2019, 124, 152–160.
65. C. Zhu, S. Monti and A. P. Mathew, ACS Nano, 2018, 12, 7028–7038.
66. Scientific Computing & Modelling NV, ADF Manual Amsterdam Modeling Suite 2019, 2019.
67. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
68. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
69. G. Stefan, J. Comput. Chem., 2006, 27, 1787–1799.
70. K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603–619.
71. P. P. Sharma, J. Wu, R. M. Yadav, M. Liu, C. J. Wright, C. S. Tiwary, B. I. Yakobson, J. Lou, P. M. Ajayan and X.-D. Zhou, Angew. Chem., 2015, 127, 13905–13909.
72. A. C. Ferrari, Solid State Commun., 2007, 143, 47–57.
73. I. Szewczyk, A. Rokicińska, M. Michalik, J. Chen, A. Jaworski, R. Aleksis, A. J. Pell, N. Hedin, A. Slabon and P. Kuśtrowski, Chem. Mater., 2020, 32, 7263–7273.
74. L. Zhang, L. Ding, G. Chen, X. Yang and H. Wang, Angew. Chem., 2019, 131, 2638–2642.
75. J. Lim, C. Y. Liu, J. Park, Y. H. Liu, T. P. Senftle, S. W. Lee and M. C. Hatzell, ACS Catal., 2021, 11, 7568–7577.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cy00050d

‡ These authors contributed equally to this work.

---