Open Access Article
Open Access ArticlePhotochemical carbon–sulfur bond cleavage in thioethers mediated via excited state Rydberg-to-valence evolution†
Nikoleta
Kotsina‡
 a,
Sebastian L.
Jackson‡
a,
Sebastian L.
Jackson‡
 a,
Thomas
Malcomson
a,
Thomas
Malcomson
 b,
Martin J.
Paterson
b,
Martin J.
Paterson
 c and
Dave
Townsend
c and
Dave
Townsend
 *ac
*ac
aInstitute of Photonics & Quantum Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK
bDepartment of Chemistry, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
cInstitute of Chemical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. E-mail: d.townsend@hw.ac.uk
First published on 1st December 2022
Abstract
Time-resolved photoelectron imaging and supporting ab initio quantum chemistry calculations were used to investigate non-adiabatic excess energy redistribution dynamics operating in the saturated thioethers diethylsulfide, tetrahydrothiophene and thietane. In all cases, 200 nm excitation leads to molecular fragmentation on an ultrafast (<100 fs) timescale, driven by the evolution of Rydberg-to-valence orbital character along the S–C stretching coordinate. The C–S–C bending angle was also found to be a key coordinate driving initial internal conversion through the excited state Rydberg manifold, although only small angular displacements away from the ground state equilibrium geometry are required. Conformational constraints imposed by the cyclic ring structures of tetrahydrothiophene and thietane do not therefore influence dynamical timescales to any significant extent. Through use of a high-intensity 267 nm probe, we were also able to detect the presence of some transient (bi)radical species. These are extremely short lived, but they appear to confirm the presence of two competing excited state fragmentation channels – one proceeding directly from the initially prepared 4p manifold, and one involving non-adiabatic population of the 4s state. This is in addition to a decay pathway leading back to the S0 electronic ground state, which shows an enhanced propensity in the 5-membered ring system tetrahydrothiophene over the other two species investigated.
I. Introduction
Thioethers are abundant in nature, such as the tens of teragrams per year released into the atmosphere due to biogenic emissions from marine plankton.1–3 They are also found as a structural motif in biological molecules, for instance, the amino acid methionine, which is essential for human growth. Anthropogenic thioethers from petrochemicals represent a significant pollution concern, due to their similarity to chemical weapons such as mustard gas, and their serious impact on health at very low concentrations.4 Additionally, it has been shown that the health effects of atmospheric pollutants are worsened due to photochemical reactions after exposure to ultraviolet (UV) light.5From a more fundamental perspective, aliphatic thioethers potentially provide excellent model candidates for the detailed study of non-adiabatic excess energy redistribution dynamics following absorption of a UV photon. This is particularly true in relation to the time-resolved photoelectron imaging (TRPEI) technique, which provides a highly differential energy- and angle-resolved picture of the transient behaviour.6–9 In general, aliphatic thioethers have excited states that are predominantly Rydberg in character, which are expected to yield well-resolved photoelectron bands and highly anisotropic angular distributions. Furthermore, they typically exhibit relatively low (<9 eV) ionization potentials (IPs) and high vapour pressures, making them convenient for gas-phase studies using the TRPEI approach. They also have low-lying electronic absorption bands that are accessible without the need for vacuum ultraviolet or multi-photon excitation – something that is a complicating factor in related experiments on analogous ether species.10,11
In a wide range of molecules, the coupling between nuclear and electronic degrees of freedom within the excited state manifold is often significant following UV absorption. This leads to a rapid intramolecular redistribution of the excess energy – typically on ultrafast (i.e. sub picosecond) timescales. The TRPEI approach, in conjunction with high-level quantum chemistry calculations, permits detailed insight into the dynamics of such non-adiabatic processes. This has been a recurring theme in several previous studies conducted on saturated secondary and tertiary aliphatic amines,12–19 which may be viewed as the N-atom centre analogues of mercaptans and thioethers, respectively. Of particular interest is the dynamical role played by low-lying states of mixed Rydberg/valence composition, which are now recognized as common features in a broad range of small hetero-atom containing systems.20–23 Although exhibiting a dominant Rydberg orbital character in the Franck–Condon region, increased πσ* or nσ* valence contributions may develop along extended N–X, O–X, or S–X stretching coordinates. Such behaviour then provides a potential pathway for interaction with the S0 electronic ground state at large bond lengths. Radiationless nonadiabatic population transfer to the S0 state may then impart an effective (condensed phase) photoprotective mechanism based on efficient dissipation of excess vibrational energy into the surroundings.24
Rydberg-to-valence evolution is often observed in excited states that may be designated as predominantly s-type in Rydberg character (at molecular geometries close to that of the electronic ground state).20–23 Previous TRPEI measurements have concluded, however, that long (>10 ps) excited state lifetimes seen in various tertiary aliphatic amines are a consequence of the 3s state maintaining Rydberg character at extended N–C distances. In contrast, secondary and primary aliphatic amines exhibit a sub-picosecond decay of the 3s state, as valence character readily develops along the N-H bond. This is illustrated, for example, when contrasting the dynamical timescales observed in piperidine (a secondary aliphatic amine) and N-methylpyrrolidine (a tertiary species).14,15,25 Excitation to the 3p Rydberg manifold occurs in both cases following 200 nm absorption, and rapid (<400 fs) internal conversion then populates the 3s state. This subsequently survives for less than 200 fs in piperidine, but in N-methylpyrrolidine the lifetime is 160 ps. Supporting ab initio calculations add more detail to this observation, revealing that in both systems, members of the 3p manifold (but not the 3s state) appear to develop nσ* character upon N–C bond extension – a factor mediating the initial 3p to 3s internal conversion. In contrast, 3s to nσ* evolution is only seen along the N–H bond of piperidine (a coordinate absent in N-methylpyrrolidine). Such differences between primary/secondary vs. tertiary aliphatic amines raise questions about related behavioural trends in analogues of these species containing other heteroatom centres. Although relevant time-resolved measurements on such systems are limited, Röder et al. have recently reported a comprehensive TRPEI study on a series of small cyclic ethers using a 160 nm pump.10 This excites into the 3d Rydberg manifold and leads to an extremely rapid (<150 fs) non-adiabatic cascade via the 3p manifold to the 3s state, which then develops nσ* valence character as the C–O bond extends – a picture reinforced by accompanying quantum chemistry calculations. Internal conversion to the vibrationally hot electronic ground state was then thought to lead to C–O bond fission. Interestingly, this overall picture indicates that ethers exhibit similar transitory Rydberg-to-valence behaviour to that seen in primary/secondary aliphatic amines, rather than tertiary species.
Here we present a TRPEI study conducted on a series of systematically varied aliphatic thioethers to learn more about the excited state excess energy redistribution pathways and the influence of geometry constraints in these systems. The specific species chosen for investigation were thietane (THI, 4 membered ring), tetrahydrothiophene (THT, 5 membered ring); and diethyl sulfide (DES, a linear chain species). Schematic structures are presented in Fig. 1. The similar density of states in THT and DES offers an interesting comparison between cyclic and acyclic systems, while THI serves as an instructive additional inclusion since there is a greater body of photochemically relevant pre-existing literature for this system.
Our experimental pump–probe measurements utilized a 200 nm excitation step (see Section II for more details). In all three systems under study, this induces an electronic transition from a non-bonding orbital localized on the sulfur atom directly to the 4p Rydberg manifold – as documented in various spectroscopic reports.26–31 Our own UV absorption spectra of THT and DES are included in the ESI,† for direct comparison. For the subsequent probe step, we explored the use of 267 nm light under two different sets of experimental conditions: a “lower-intensity” regime at approx. 3 × 1012 W cm−2 and “higher-intensity” regime at approx. 5 × 1013 W cm−2. Both scenarios have a Keldysh parameter >1, indicating that strong field effects (e.g. tunnel ionization) are not expected to contribute to our observed photoelectron signals.32 This is a relatively limited approximation for molecular ionization,33 but still serves as a simple starting benchmark when considering our experimental parameters. As illustrated in detail elsewhere,34 it is often desirable to undertake TRPEI measurements with probes that project as deeply into the ionization continuum as possible. This maximizes the view along the reaction coordinate(s) connecting optically prepared states to final photoproducts. Given the complex, multi-step nature of such pathways, this improved observation window is extremely valuable. As a general point-of-principle, a single-photon VUV probe is typically preferred. Careful use of a (more experimentally convenient) multiphoton probe step is, however, also instructive – particularly when photoelectron bands originating from different photon-order processes (e.g. 1 + 1′ vs. 1 + 2′ ionization) are spectrally well-resolved (as will be the case here).
II. Experimental methodology
Pump and probe pulses for our TRPEI measurements were derived from a 1 kHz regeneratively amplified Ti:Sapphire laser system (Spectra-Physics, Spitfire Pro) operating with a fundamental wavelength centred at 800 nm. The 200 nm pump beam was the fourth harmonic of this output, generated in a three-step non-linear optical scheme. Initially, a portion of the 800 nm fundamental was passed through a thin beta barium borate (BBO) crystal to produce the 400 nm second harmonic. A calcite crystal was used for timing compensation between the co-propagating 400 nm and residual 800 nm pulses and a dual λ/2 waveplate was then used to match the linear polarisation directions before generation of the third harmonic (267 nm) in a second BBO crystal. This output and a further portion of the 800 nm fundamental beam were then temporally and spatially overlapped in a third BBO crystal producing the fourth harmonic at 200 nm (∼1.3 μJ per pulse). During this final step, the two beams were aligned to travel with a narrow angular convergence that produced a spatial intersection only within the BBO crystal itself. This non-colinear geometry leads to generation of the 200 nm output along a different propagation axis to the input beams, providing a clean spectral separation without the need for specialist dichroic mirrors. The probe beam (267 nm) was produced independently in a similar manner to the first two stages of the pump generation scheme. This beamline also incorporated a computer-controlled linear translation stage fitted with a retroreflector for precise, automated adjustment of the temporal pump–probe delay, and a neutral density filter for variable attenuation of the 800 nm starting energy. Under our experimental focussing conditions, TRPEI measurements could then performed under either lower-intensity (3 × 1012 W cm−2) or higher-intensity (5 × 1013 W cm−2) probe regimes, as already highlighted in the Introduction.Liquid samples of the various aliphatic sulphides (all >96% purity or higher) were purchased from Sigma-Aldrich and used without further refinement. Samples were placed in a small bubbler vessel and helium (1.25 bar) was used as a carrier gas to the source chamber of our differentially pumped ultrahigh vacuum photoelectron imaging spectrometer (described in more detail elsewhere35). Expansion through a small (ϕ = 150 μm) pinhole generated a continuous molecular beam. This then entered the main interaction chamber via a skimmer (ϕ = 0.8 mm) before passing along the central axis of a multi-electrode annular electrostatic lens set-up optimised for velocity-map imaging (VMI).36 Co-propagating 200 nm pump and 267 nm probe pulses were also directed into this electrode assembly, moving along an axis perpendicular to that of the molecular beam. The unfocused light initially travelled straight through the VMI set-up before reflecting off a curved UV enhanced aluminium mirror (f = 10 cm) attached to a high-precision x–y–z manipulator. The tightly focussed pump and probe then ionized the sample on a second optical pass back through the VMI electrodes. Photoelectrons generated in this process were accelerated towards a 40 mm diameter dual micro-channel plate/P47 phosphor screen detector positioned at the end of a short flight tube (directed parallel to the molecular beam propagation axis). A CCD camera (640 × 480 pixels) positioned external to the vacuum chamber then captured a 2D projection of the spatial distribution image. Prior to commencing photoelectron acquisition, the spectrometer was switched to ion time-of-flight detection mode to confirm no unwanted cluster formation was apparent. Photoelectron data collection repeatedly scanned the pump–probe delay between −450 fs to 450 fs in 30 fs increments, 450 fs to 3030 fs in 60 fs steps and 20 exponentially increasing time intervals beyond this point to 50 ps. At each delay position, time-invariant pump-alone and probe-alone images were recorded for subsequent background subtraction, in addition to the pump–probe data. TRPEI measurements were conducted on DES and THT under both the lower and higher intensity probe regimes, while THI was investigated only under higher probe intensity conditions.
A fast matrix inversion method (documented in detail elsewhere35) was used for processing the raw experimental images. As with other inversion methods, this approach recovers the centre slice through the 3D charged particle distribution. The full velocity distribution may then be obtained by applying an rsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ weighting to each pixel in the reconstructed image (where r is the pixel radius, and the angular co-ordinate system is defined with θ = 0° and 180° lying along the laser polarization axis). Data for pixel-to-kinetic energy image calibration was obtained from 1 + 1′ multiphoton ionization of butadiene and this measurement also provided a good estimate for the optical Gaussian cross-correlation (200 ± 10 fs FWHM). For the case of ionization using linearly polarized light, the evolution of the angular anisotropy as a function of pump–probe delay Δt and photoelectron kinetic energy E is described by the following expression:9,37
θ weighting to each pixel in the reconstructed image (where r is the pixel radius, and the angular co-ordinate system is defined with θ = 0° and 180° lying along the laser polarization axis). Data for pixel-to-kinetic energy image calibration was obtained from 1 + 1′ multiphoton ionization of butadiene and this measurement also provided a good estimate for the optical Gaussian cross-correlation (200 ± 10 fs FWHM). For the case of ionization using linearly polarized light, the evolution of the angular anisotropy as a function of pump–probe delay Δt and photoelectron kinetic energy E is described by the following expression:9,37
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) are Legendre polynomial functions, and the βl(E,Δt) anisotropy parameter terms dictate the overall shape of the observed angular forms. As expanded upon later, processes up to and including a total of either two (lmax = 4) or three (lmax = 6) photons were considered in any fits to our experimental data.
θ) are Legendre polynomial functions, and the βl(E,Δt) anisotropy parameter terms dictate the overall shape of the observed angular forms. As expanded upon later, processes up to and including a total of either two (lmax = 4) or three (lmax = 6) photons were considered in any fits to our experimental data.
Temporal analysis of the transient information was conducted using a series of exponentially decaying functions fi(Δt) convolved with the experimentally determined Gaussian cross-correlation function g(Δt):
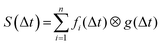 | (2) |
 | (3) |
III. Quantum chemistry calculations
Ab initio calculations were undertaken using the Gaussian16 software package and visualized with GaussView.38,39 Ground state geometries of all three molecules under study were optimized using density functional theory with the B3LYP functional and augmented correlation-consistent basis set aug-cc-pVTZ. Vertical singlet state excitation energies and orbital-relaxed linear response oscillator strengths were calculated using the equation-of-motion coupled-cluster method with single and double excitations (EOM-CCSD).40 The double-zeta aug-cc-pVDZ basis set was applied to all carbon and hydrogen atoms and the triple-zeta aug-cc-pVTZ to the sulfur atom. A similar general approach has previously proved instructive when tackling excited state problems in other structurally related species.14,15,25 The lowest four excited states incorporating excitations predominantly to the 4s orbital along with the x, y and z components of the 4p manifold are of direct interest to the present study. This data is summarized in Table 1. The character of the individual excited states generally contains contributions from several different Rydberg-type orbitals, but the dominant component is unambiguous.Relaxed scans along a single S–C bond were carried out for THT and DES by fixing this coordinate at incremented extensions, optimizing the ground stage geometry, and then calculating the vertical excited state transitions. All energies were plotted relative to the ground state equilibrium geometry. This output is presented in Fig. 2, where the state character is denoted using the relevant Rydberg label in the vertical Frank-Condon region (i.e. when the excited state geometry is similar to that of the S0 ground state). An important caveat here is that the use of the excited state Rydberg character as a simple identification label is only valid in this initial limit. Over the more extended range of nuclear geometries that a system may subsequently sample following UV absorption, an expanded mixed Rydberg/valence picture is needed for a fully comprehensive description. Such Rydberg-to-valence evolution is particularly evident in the 4s and 4py states, which become dissociative as the S–C bond extends. This behaviour is further illustrated in the orbital plots shown in Fig. 3. In the interests of clarity, the use of simple (e.g. 4s, 4px) labels will be retained throughout, although drawing on a more extensive mixed state picture will prove essential in interpreting some aspects of our TRPEI data in subsequent sections. Adding more detail here, the excited states start vertically with a dominant single particle-hole character, where the nature of the particle orbital is dominated by diffuse basis functions of a given angular momentum. Upon proceeding along the reaction coordinate there is mixing of further basis functions into the particle orbitals, in addition to further multi-electron character developing (i.e. multiple particle–hole configurations of importance). Careful consideration of local wavefunction composition and molecular properties enables these changes to be tracked along the reaction coordinate, allowing us to effectively retain the original vertical state label across the entire potential. Note that the complexity of this diabatic picture away from equilibrium reflects the inherent breakdown of the (qualitative) single-particle description of excited electronic states and is different from the actual crossing of adiabatic potential surfaces, which happens additionally at longer range and introduces further mixing of the orbital character.
 | ||
| Fig. 2 EOM-CCSD potential energy cuts for the S0, 4s and 4p states of DES (left) and THT (right) along the S–C stretching coordinate and C–S–C bending coordinate. Rydberg state labels are formally only valid close to the S0 equilibrium geometry but serve as a useful reference for general discussion – see main text and Fig. 3 for additional detail. An equivalent cut along the C–S–C bond angle in THI is presented in Fig. S3 of the ESI.† | ||
Scans along the S–C bond were terminated at a separation just beyond 3 Å to avoid inaccuracies introduced by the growing open-shell character observed at longer bond lengths (for which single-reference methods such as EOM-CCSD start to break down). The 4s state of DES converges upon the same dissociation limit as S0, yielding C2H5S(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) + C2H5(
) + C2H5(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radical products, while the 4py state asymptotically converges to C2H5S(Ã) + C2H5(
) radical products, while the 4py state asymptotically converges to C2H5S(Ã) + C2H5(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ). In THT, biradical ring-opened products are formed in the corresponding
). In THT, biradical ring-opened products are formed in the corresponding ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) or à states, respectively. Scans along the C–S–C bond angle of DES and THT are also included in Fig. 2. This degree of freedom was targeted for specific inspection at it exhibits the most obvious differences in terms of constraint between cyclic and acyclic systems. Of note here is the point of electronic degeneracy reached by a member of the 4p manifold and the 4s state when the angular coordinate undergoes relatively small displacements from the ground state equilibrium geometry (∼6°). This suggests that the C–S–C angle may be important in mediating internal conversion between the 4p manifold and 4s states, although such a process is likely to proceed extremely rapidly – even where constraints on this specific motion are imposed by a closed ring geometry.
or à states, respectively. Scans along the C–S–C bond angle of DES and THT are also included in Fig. 2. This degree of freedom was targeted for specific inspection at it exhibits the most obvious differences in terms of constraint between cyclic and acyclic systems. Of note here is the point of electronic degeneracy reached by a member of the 4p manifold and the 4s state when the angular coordinate undergoes relatively small displacements from the ground state equilibrium geometry (∼6°). This suggests that the C–S–C angle may be important in mediating internal conversion between the 4p manifold and 4s states, although such a process is likely to proceed extremely rapidly – even where constraints on this specific motion are imposed by a closed ring geometry.
IV. Results and discussion
A. Lower probe intensity regime
Fig. 4 presents time-resolved photoelectron spectra of THT and DES under lower probe intensity conditions. Representative photoelectron images close to zero pump–probe delay are also inset. Data for both molecules display very similar features, with the raw images exhibiting two bright rings that show a pronounced spatial anisotropy peaking along the direction of the pump and probe laser polarization. A much weaker signal with reduced anisotropy also extends through the images – something that is more readily seen in the angle-integrated photoelectron spectra at kinetic energies extending below 1.4 eV. The accompanying narrow bands centred at 1.7–1.9 eV and 2.4–2.5 eV correlate with the two rings in the raw image data, and the temporal onset of the peak at lower energy is slightly delayed with respect to the higher energy one. This is more clearly revealed for the case of THT in Fig. 5, which also includes a fit to the transient data using the model described by eqn (2) and (3). The overall dynamics appear to be extremely rapid, with no signals persisting beyond 400 fs. Additionally, no significant spectral features are observed in Fig. 4 at photoelectron kinetic energies exceeding ∼2.5 eV, which is in agreement with expectations based on the total (central wavelength) pump + probe energy for (1 + 1′) ionization (10.85 eV) and the adiabatic D0 IPs of 8.43 eV (DES) and 8.38 eV (THT).41,42 The D1 cation state is also (just) energetically accessible in both molecules given the laser bandwidth used in our measurements,43,44 and we attribute the bright spot seen in the centre of our raw image data to ionization into this continuum (most likely from the 4s state). Given the inherent difficulties associated with extracting reliable angular and intensity information from signals projecting over a small number of central image pixels, however, we do not consider these very low (<0.1 eV) energy photoelectrons further in our analysis. | ||
| Fig. 4 Time-dependent 200/267 nm pump/probe photoelectron spectra of DES and THT obtained under a lower probe intensity regime (∼3 × 1012 W cm−2). Note the non-linear scaling of the time axis (see main text for details). Photoelectron images at Δt = 0 are inset. Time-invariant pump- and probe-alone background signals have been subtracted and the images are 4-fold symmetrized (i.e. the raw data in four individual quadrants defined by horizontal and vertical axes passing though the image centre have been averaged together – which is valid given the symmetry of the photoelectron angular distribution described by eqn (1)). | ||
 | ||
| Fig. 5 Data points: scaled 200/267 nm pump/probe transient photoelectron signals integrated over narrow energy regions corresponding to 4p (2.4–2.6 eV) and 4s (1.8–2.0 eV) state ionization in THT under lower probe intensity conditions. Solid lines: Fit to the data using the procedure described by eqn (2) and (3). The 4p transient was fitted with a single exponential to extract τ1. This was then included as the rising term in a sequential bi-exponential fit to the 4s transient to yield τ2. 1σ uncertainties in the quoted τ1 and τ2 values are ±5 fs and ±10 fs, respectively. Identical transitory behaviour is seen in DES. | ||
On the basis of previously reported absorption spectra26,27 and the quantum chemistry calculations presented in Section III, the peaks centred at 1.7–1.9 eV and 2.4–2.5 eV in Fig. 4 may be attributed to ionization from the 4s Rydberg state and the 4p Rydberg manifold, respectively. In further support of this assignment, the narrow width of the peaks reflects a strong propensity for diagonal transitions to the cation (i.e. Δν = 0, where ν is a generalized, non–mode-specific vibrational quantum number) – as would typically be expected for Rydberg state ionization. The 4p manifold is accessed directly by the 200 nm pump step and internal conversion to the 4s state occurs within 100 fs (as seen in Fig. 5). Internal conversion between individual members of the 4p manifold may also occur during this time, as revealed previously in some amine systems,17,18 but this process (if occurring) is not resolved in our present measurements. As presented in Fig. 2, a likely key coordinate in the 4p to 4s internal conversion process is a widening of the C–S–C bond angle relative to that at the ground state equilibrium geometry. This brings members of the 4p manifold and the 4s state to a point of electronic degeneracy and may ultimately facilitate rapid non-adiabatic population transfer via a conical intersection. Furthermore, the small angular change required here means that conformational restrictions imposed by the ring structure in THT do not impact significantly on the overall timescale for this process relative to DES (as evident in Fig. 4). Assuming modest (T ≤ 100 K) internal cooling in our molecular beam expansion and given previously reported frequencies for the C–S–C bend/ring deformation modes in both species (∼300 cm−1),45,46 we may reasonably assume any effects due to vibrationally excited population in the ground state are negligible. Once populated, the 4s state is then unbound along the S–C stretching coordinate, giving rise to an extremely short (<100 fs) lifetime. As the S–C bond extends, the 4s state begins to develop increasing nσ* valence character – as illustrated for DES in Fig. 3. Given our instrument response function of 200 fs, we are not able to temporally resolve this extremely rapid evolution in our experiments (i.e. the pump–probe signature of this broader feature appears matched that of the 4s state within experimental uncertainty – see Fig. S2 in the ESI†). We suggest, however, that our data does appear to reflect this transitory behaviour in a spectrally averaged way, since increasing nσ* valence character can lead to a reduction in the propensity for diagonal ionization. This gives rise to the much broader feature seen in the photoelectron spectra below 1.4 eV, with the shift to lower energies reflecting an increase in the energy separation between the 4s/nσ* and D0 cation states along the S–C stretch. We note that similar arguments relating to N–H and N–C bond extensions have previously been put forward to explain comparable spectral features in other TRPEI data.15,47
Given the above discussion, a concomitant reduction in the photoelectron anisotropy associated with ionization from a state with increased nσ* character at more extended S–C distances would also be expected. This is a consequence of the angular momentum being more poorly defined than for a predominantly Rydberg-like composition (i.e. the state is no longer well-described by a single s-type basis orbital). Such an effect is quantified in Fig. 6, which shows polar plots of the photoelectron angular distributions (PADs) obtained for DES averaged over three different energy bands corresponding to 4p, 4s and nσ* ionization in the region close to zero pump–probe delay (see Fig. 4). Fits to this data using an appropriately time- and energy-integrated form of eqn (1) are also overlaid. Here the summation in eqn (1) was truncated at lmax = 4 as we may be confident that (1 + 1′) ionization is the dominant contribution to all signals in our low probe intensity regime. The PAD associated with nσ* ionization tends towards isotropic (β2 = 0.18 and β4 = −0.20), whereas the PADs relating to Rydberg state ionization exhibit a pronounced anisotropy. Notably, however, the β2 and β4 parameters associated with 4s and 4p ionization are very similar (1.22 and 0.25 vs. 1.31 and 0.34, respectively). The β4 value for the 4s state also deviates significantly from the value of zero that would typically be expected in a “first approximation” picture of single photon ionization from an Rydberg orbital possessing no inherent alignment.20 Furthermore, no temporal variation in the anisotropy parameters was distinguishable upon analysing their transient behaviour. Such observations appear consistent with the extremely rapid internal conversion between the 4p Rydberg manifold and the 4s state, which occurs on a timescale approaching the limit of our experimental pump–probe resolution. Coupling between excited states induces mixing of their electronic character and this may often be reflected in the temporal evolution of the anisotropy seen in PAD measurements.14,25,47–49 In the present measurements, however, any state mixing is too rapid to effectively be distinguished in the time domain.
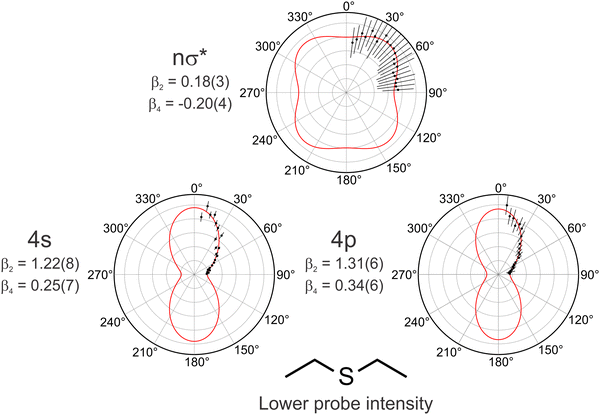 | ||
| Fig. 6 Normalized polar PAD plots showing low probe intensity angular data for DES averaged over energy regions corresponding predominantly to 4p (2.4–2.6 eV), 4s (1.8–2.0 eV) and nσ* (0.2–1.6 eV) ionization in the region close to zero pump–probe delay. Error bars denote 1σ uncertainties. Red solid lines are the corresponding fits to the data obtained using a time- and energy-integrated form of eqn (1). The anisotropy parameters obtained from these fits are also shown, with values in parentheses denoting 1σ uncertainties in the final significant figure. | ||
Based on the experimental data discussed so far, we suggest that ultrafast S–C bond cleavage occurring on the 4s excited state potential energy surface is likely to be an important photochemical pathway in saturated thioether systems. The evolution of Rydberg-to-valence character within the 4s state of both DES and THT displays clear similarities to that seen in the 3s state of primary/secondary amine systems while differing from that of tertiary species – as discussed previously in the Introduction. In DES this leads asymptotically to two radical fragments (C2H5 and C2H5S), both of which will be formed in their respective ground electronic states (see Section III). Such a picture is consistent with the highly anisotropic recoil seen in CH3 fragments produced from the related species dimethylsulfide following direct excitation to the first absorption band (i.e. what we denote here as the 4s state).50–53 The equivalent C–S bond fission step in THT is expected to lead initially to a ring-opened biradical species. This process may, however, potentially also occur during repopulation of the S0 ground state rather than exclusively on 4s potential energy surface – as suggested by Röder et al. in their aforementioned study of analogous cyclic ether systems.10 A more expanded discussion of the photofragmentation mechanism will form a central theme of the following section.
B. Higher probe intensity regime: general features
Fig. 7 presents time-resolved photoelectron spectra of THT and DES under higher probe intensity conditions. Photoelectron images close to zero pump–probe delay are also inset. In contrast to the lower probe intensity regime (Fig. 4), an additional sharp, anisotropic ring feature is now clearly visible, appearing at a smaller radius/photoelectron energy than the two peaks previously assigned as 4p and 4s ionization. Ionization into the D1 continuum is also seen slightly more strongly in the centre of the images. Between the various sharp features, there is still a broad background signal at pump–probe delays close to zero, indicative of nσ* ionization resulting from S–C bond extension in the 4s state. In the case of THT, a much longer-lived transient signal is now also evident, persisting out to the 50 ps limit of our pump–probe observation window. This is seen with improved contrast in the energy-integrated form of the data, as presented in Fig. S4 of the ESI.†Fig. 7 also includes data obtained for THI, which appears to display very similar overall spectral signatures to DES – although there is a subtle difference in the transient dynamics that will be expanded upon shortly. | ||
| Fig. 7 Time-dependent 200/267 nm pump/probe photoelectron spectra of DES, THT and THI obtained under a higher probe intensity regime (∼5 × 1013 W cm−2). Note the non-linear scaling of the time axis (see main text for details). Photoelectron images at Δt = 0 are inset. As in Fig. 4, time-invariant pump- and probe-alone background signals have been subtracted and the images are 4-fold symmetrized. The laser polarization is vertical with respect to the inset. | ||
Before discussing the new spectral features appearing under higher probe intensity conditions, it is important to highlight that the 4p and 4s peaks in the THT and DES data are not appreciably shifted in position, width or relative intensity when compared with the lower probe intensity regime. This offers good evidence that the higher probe intensity conditions do not actively modify the excited state dynamics. Further support of this assertion is also provided by the PAD data for DES presented in Fig. 8. Here eqn (1) was used with a form including terms up lmax = 6 as there is a possibility that some underlying photoelectron signals may now originate from two-photon probe ionization (i.e. a 1 + 2′ process overall). For the case of the 4s and 4p states, however, the β6 terms returned by the fit are very close to zero and the β2 and β4 parameters are similar to those obtained under lower probe intensity conditions (Fig. 6). Table S1 in the ESI† includes equivalent fitted anisotropy parameters for THT and THI, which are broadly comparable.
 | ||
| Fig. 8 Normalized polar PAD plots showing higher probe intensity angular data for DES averaged over energy regions corresponding predominantly to 4p (2.4–2.6 eV), 4s (1.8–2.0 eV), radical intermediate (0.8–1.0 eV) and nσ* (0.2–0.6 eV) ionization in the region close to zero pump–probe delay. Error bars denote 1σ uncertainties. Red solid lines are the corresponding fits to the data obtained using a time- and energy-integrated form of eqn (1). The anisotropy parameters obtained from these fits are also shown, with values in parentheses denoting 1σ uncertainties in the final significant figure. See the ESI,† for additional anisotropy parameter data relating to other systems. | ||
The new spectral feature seen in Fig. 7 at 0.8–1.0 eV for both DES and THT must originate from a higher order photon process than the peaks attributable to ionization of the 4p and 4s states. A similar argument also holds, by extension, in THI (where the equivalent feature sits in the 0.6–0.8 eV region). The new peak has a delayed temporal onset with a rise time matched to that seen in the 4s state, suggesting a link to decay within the 4p manifold. This is more clearly seen in Fig. 9, which plots the transient signals from DES and THI for the various narrow peaks appearing in the photoelectron spectrum along with a sequential fit using the model described by eqn (2) and (3). Fig. 9 also reveals a clear difference in the transitory behaviour of these two systems, with THI displaying additional “tail” features extending to longer pump–probe delay times than DES. This necessitates the use of two separate exponentially decaying functions to obtain a satisfactory fit to the data in some spectral regions (and is also a requirement in THT), whereas only a single exponential decay is required for the equivalent regions in DES. Numerical time-constant information extracted for all systems across various individual photoelectron band features is summarized in Table 2.
 | ||
| Fig. 9 Data points: scaled 200/267 nm pump/probe transient photoelectron signals integrated over narrow energy regions corresponding to 4p, 4s and radical fragment ionization in DES and THI under higher probe intensity conditions. Solid lines: fit to the data points using the procedure described by eqn (2) and (3). The 4p transient was fitted with a single exponential term. This was then included as a rise time in independent fits to the 4s and radical transients. The clear tails extending to longer delay times in the THI data necessitates the use of two separate functions to accurately model the decay in both 4s and radical channels. In contrast, only a single exponential is required for each of these regions in DES. See Table 2 for numerical values and main text for discussion. | ||
C. Higher probe intensity regime: assignment of narrow peak <1.0 eV
When compared to the spectral features already attributed to (1 + 1′) ionization in Section IV A, the relatively large signal strength seen in the new (higher photon order) peak sitting below 1.0 eV leads us to speculate that it may originate via an additional resonantly enhanced step (i.e. a 1 + 1′ + 1′ process rather than 1 + 2′). This would eliminate the possibility of the signal originating from an ionization out of the 4s state that projects directly to a very high-lying cation state. Furthermore, based on the peak position and the overall photon energetics, such a high-lying cation state would be required to sit somewhere in the region of 6 eV above the ionization onset threshold yet exhibit a similar electronic configuration to D0 to preserve efficient Koopmans’ correlations.54,55 This seems unlikely and, where relevant calculations are available (for the case of THI31), such a state has not been observed. Energetic considerations also appear to eliminate the possibility of this peak resulting from triplet state ionization following intersystem crossing (ISC) from the 4p manifold – even though there is a growing body of evidence to support ISC on such ultrafast timescales in other systems.56 To help verify this, we evaluated the vertical triplet state energies for DES using the same computational approach as discussed in Section III. Calculated values for the 4s state (4.98 eV) and members of the 4p manifold (5.53, 6.14, and 6.21 eV) sit in an approximate range only 0.1–0.4 eV below their respective singlet counterparts (listed in Table 1). This implies that any populated triplet states should already be observable in the lower intensity 1 + 1′ ionization regime or, alternatively, any 1 + 2′ ionization would lead to photoelectron bands at kinetic energies well above 1.0 eV. Finally, here, we also consider the potential role of electronic autoionization from short-lived super-excited neutral states sitting above the D0 continuum. Such autoionization processes have previously been implicated in contributing to the experimental VUV threshold photoelectron spectrum of THI,31 and could conceivably yield photoelectrons with kinetic energies in the region below 1.0 eV, as seen in our data. Although supporting calculations in this earlier work (and also for the related 3-membered ring system ethylene sulfide57) suggest a relatively dense manifold of super-excited states extending up to around 14 eV (∼5.5 eV above the D0 IP), our combined (1 × 200 nm + 2 × 267 nm) photon energy of 15.5 eV exceeds this predicted range by some margin. Given this finding, and the fact that similar observations would also likely be expected in DES and THT, we therefore discount autoionization mechanisms as a contributing factor in our photoelectron data.Having ruled out the various possibilities considered above; we suggest the most likely origin of the narrow peak appearing below 1.0 eV in the Fig. 9 data is two-photon (1′ + 1′) probe ionization of a very short-lived radical intermediate. This is formed via ultrafast dissociation/ring-opening of the neutral parent molecule following initial absorption of the 200 nm pump. We begin by considering the case of DES before extending the discussion to the two cyclic systems. Given that the delayed temporal onset of the 0.8–1.0 eV peak indicates a fragment originating from dissociation within the 4p manifold (Fig. 9), the expected DES photoproducts are C2H5S(Ã) and C2H5(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ), as already highlighted in Section III. Since the IP of C2H5(
), as already highlighted in Section III. Since the IP of C2H5(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) lies in the range 8.2–8.5 eV,58,59 this species initially seems like a plausible candidate, as ionization using two 267 nm probe photons (9.3 eV in total) could therefore yield a photoelectron peak close to 0.8–1.0 eV. On the other hand, the barrier to C2H5(
) lies in the range 8.2–8.5 eV,58,59 this species initially seems like a plausible candidate, as ionization using two 267 nm probe photons (9.3 eV in total) could therefore yield a photoelectron peak close to 0.8–1.0 eV. On the other hand, the barrier to C2H5(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) dissociation exceeds 37 kcal mol−1 (1.6 eV) and so dissociation in <100 fs seems unlikely – even factoring in any internal vibrational excitation imparted in the initial fragmentation of the DES parent.60,61 Furthermore, formation of C2H5(
) dissociation exceeds 37 kcal mol−1 (1.6 eV) and so dissociation in <100 fs seems unlikely – even factoring in any internal vibrational excitation imparted in the initial fragmentation of the DES parent.60,61 Furthermore, formation of C2H5(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) is also expected following dissociation via the 4s state and we see no evidence of the radical peak being associated with this channel (Fig. 9). Finally, the first excited electronic state of C2H5 is not energetically accessible upon absorption of a single 267 nm photon and so no resonant (1′ + 1′) enhancement of the overall two-photon radical ionization process is possible.62 This enhancement would likely be a requirement here given the relatively low (<8 Mb) single-photon ionization cross-section of C2H5 reported at energies close to threshold.60
) is also expected following dissociation via the 4s state and we see no evidence of the radical peak being associated with this channel (Fig. 9). Finally, the first excited electronic state of C2H5 is not energetically accessible upon absorption of a single 267 nm photon and so no resonant (1′ + 1′) enhancement of the overall two-photon radical ionization process is possible.62 This enhancement would likely be a requirement here given the relatively low (<8 Mb) single-photon ionization cross-section of C2H5 reported at energies close to threshold.60
The electronic spectroscopy of the C2H5S radical has been studied in detail following generation via photolysis of neutral precursors, with the à ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state origin identified at 440.0 nm (2.82 eV).63 The à state was also reported to be strongly pre-dissociated, with 1/e lifetimes decreasing from 75 ns at the origin band to 15 ns when exciting just 0.3 eV higher in energy. A similar picture has also been reported in the related CH3S radical, where ab initio quantum chemistry calculations have revealed several unbound electronic states crossing the à state potential energy surface close to energy minimum and at relatively modest C–S bond extensions.64 Given this evidence, it therefore seems likely that the short-lived 0.8–1.0 eV peak seen in our data at higher probe intensities arises due to (1′ + 1′) ionization of the C2H2S radical à state formed following 200 nm dissociation directly within the 4p manifold of the parent DES molecule. This pathway acts in competition with internal conversion from the 4p manifold to the 4s state (as already observed in the lower probe intensity regime). The internal vibrational energy deposited into the C2H5S(Ã) radical species during photolysis is then sufficient to bring about further ultrafast fragmentation, liberating sulphur atoms and further ethyl radical products (which we do not detect). Due to the energy gap between the à state origin (2.82 eV) and the lowest experimentally determined IP of C2H5S (9.08 eV),65 two 267 nm photons are required for the ionization step and there is a strong possibility of enhancement due to the dense manifold of high-lying resonances that would be reasonably be expected in the region 1–2 eV below the onset of the continuum. Our calculations also indicate that the electronic configuration of the excited C2H5S à state is built predominantly on a transition between the HOMO−2 and HOMO orbitals. Based on simple Koopmans’ correlation arguments,54,55 the à state is therefore not expected to project strongly into any of the three energetically lowest-lying states of the C2H5S cation, which are all built on removal of an electron from either the HOMO or HOMO−1 orbitals of the neutral radical upon ionization.65 This provides a strong rationale for the peak associated with C2H5S à state ionization appearing below 1.0 eV in Fig. 9, rather than at much higher kinetic energies (as might otherwise be expected). Our interpretation/assignment of the higher probe intensity spectral feature in DES is also consistent with photofragment REMPI studies conducted on the related dimethylsuflide molecule following excitation at 201 nm.66 Here a bimodal CH3 translational energy distribution was observed, with both components exhibiting strong recoil anisotropy (indicating dissociation on a timescale faster than the period of molecular rotation). The higher kinetic energy feature was attributed to S–C bond cleavage within the parent molecule, while the lower kinetic energy feature was thought to be prompt secondary dissociation of the resulting SCH3 co-fragment.
state origin identified at 440.0 nm (2.82 eV).63 The à state was also reported to be strongly pre-dissociated, with 1/e lifetimes decreasing from 75 ns at the origin band to 15 ns when exciting just 0.3 eV higher in energy. A similar picture has also been reported in the related CH3S radical, where ab initio quantum chemistry calculations have revealed several unbound electronic states crossing the à state potential energy surface close to energy minimum and at relatively modest C–S bond extensions.64 Given this evidence, it therefore seems likely that the short-lived 0.8–1.0 eV peak seen in our data at higher probe intensities arises due to (1′ + 1′) ionization of the C2H2S radical à state formed following 200 nm dissociation directly within the 4p manifold of the parent DES molecule. This pathway acts in competition with internal conversion from the 4p manifold to the 4s state (as already observed in the lower probe intensity regime). The internal vibrational energy deposited into the C2H5S(Ã) radical species during photolysis is then sufficient to bring about further ultrafast fragmentation, liberating sulphur atoms and further ethyl radical products (which we do not detect). Due to the energy gap between the à state origin (2.82 eV) and the lowest experimentally determined IP of C2H5S (9.08 eV),65 two 267 nm photons are required for the ionization step and there is a strong possibility of enhancement due to the dense manifold of high-lying resonances that would be reasonably be expected in the region 1–2 eV below the onset of the continuum. Our calculations also indicate that the electronic configuration of the excited C2H5S à state is built predominantly on a transition between the HOMO−2 and HOMO orbitals. Based on simple Koopmans’ correlation arguments,54,55 the à state is therefore not expected to project strongly into any of the three energetically lowest-lying states of the C2H5S cation, which are all built on removal of an electron from either the HOMO or HOMO−1 orbitals of the neutral radical upon ionization.65 This provides a strong rationale for the peak associated with C2H5S à state ionization appearing below 1.0 eV in Fig. 9, rather than at much higher kinetic energies (as might otherwise be expected). Our interpretation/assignment of the higher probe intensity spectral feature in DES is also consistent with photofragment REMPI studies conducted on the related dimethylsuflide molecule following excitation at 201 nm.66 Here a bimodal CH3 translational energy distribution was observed, with both components exhibiting strong recoil anisotropy (indicating dissociation on a timescale faster than the period of molecular rotation). The higher kinetic energy feature was attributed to S–C bond cleavage within the parent molecule, while the lower kinetic energy feature was thought to be prompt secondary dissociation of the resulting SCH3 co-fragment.
Having established the origin of the 0.8–1.0 eV peak in DES, we may, by extension, start to apply a similar reasoning to the cyclic thioethers we have investigated. This is valid given the similar spectral and temporal nature of the equivalent feature seen in their respective TRPEI data (Fig. 7). The main difference here is that cleavage of the S–C bond directly via the 4p manifold following 200 nm excitation now initially leads to a ring-opened biradical species – something previously suggested in earlier studies of THI and THT photoproducts following UV excitation over a range of different wavelengths.67–70 This biradical intermediate will be formed in the (short-lived) à state when accessed directly from the 4p manifold and – as in DES – will then undergo ultrafast fission of the second S–C bond to yield S atom products. In thietane, this is known to be almost exclusively S(1D) following 193 nm excitation, with a C3H6 co-fragment (cyclopropane and/or propene).71,72 No final photoproducts are observed in our TRPEI data, however, even though the relatively low S(1D) IP of 9.21 eV means it could, in principle, be observed (non-resonantly) via two-photon probe ionization. This earlier THI work has also suggested that simultaneous breaking of both S–C bonds may lead to S atom release. Such a concerted process does not, though, seem to be supported by our present measurements. In all three molecules under study, a lack of relevant ionization cross-section data means we are unable to determine the relative branching between the direct dissociation pathway within the optically prepared 4p manifold and internal conversion to the 4s state. Given the considerable size of the (higher overall photon order) signal attributed to ionization of the (bi)radical à state, we may, however, speculate that the direct 4p dissociation pathway is a significant factor. This significance also seems to be suggested in studies carried out on THI by Dorer et al. that reveal a dominant C3H6 product channel following absorption at 214 nm.67 The emergence of this specific channel was also linked to the onset of excitation to the second absorption band (i.e. the 4p manifold in our notation).
D. Higher probe intensity regime: longer-time dynamics
As noted earlier and summarized in Table 2, the 4s and radical intermediate ionization channels in the cyclic THI and THT systems exhibit a biexponential decay, whereas the equivalent features in DES exhibit single exponential lifetimes. This is in addition to the much longer 42 ps dynamics observed exclusively in THT. To explain the biexponential behaviour, we start by making analogies with some amine-based species. Following UV excitation of morpholine over the 250–193 nm region, Ashfold and co-workers have previously reported two distinct H atom kinetic energy release channels.73 This was attributed to subsets of dissociating molecules exhibiting either (i) a planar geometry about the N atom centre upon first encountering a conical intersection with the S0 ground state at extended N–H distances (and rapidly passing straight through it) or (ii) a non-planar geometry at this point leading to a more ‘‘frustrated’’ fragmentation where the upper cone of the conical intersection is repeatedly resampled until the correct region of phase space is achieved. More recent TRPEI studies conducted by our own group indicated a similar behaviour in the structurally related piperidine system.15 Here the observation of two distinct lifetimes in our data (180 fs and 1.7 ps) were attributed to a prompt decay of the 3s state, and a more extended process where excited state population remained effectively trapped at large N–H distances for short period before population transfer to S0 takes place. The spectral signature of the more extended process (1.7 ps) was observed to span a broad range of photoelectron kinetic energies, indicative of the increased valence character of the 3s state at a geometry far from that of ground state equilibrium. We also highlight that similar trapping phenomena have been invoked to explain dynamical observations in the excited states of several other systems.74–79Based on the discussion outlined above, we tentatively suggest a similar frustrated mechanism may operate in the case of THT and THI. Here a sizable fraction of molecules within the 4s state may be temporarily trapped at large S–C distances before undergoing either dissociation, or internal conversion to the S0 ground state. Such behaviour is captured in the time constants of order 270–300 fs and 470–560 fs seen in THT and THI, respectively (see Table 2), and this is due to a broad spectral feature that energetically spans across the individual narrow photoelectron bands seen in our data. It is a consequence of constraints imposed by the cyclic structure of these two molecules (as it is absent in DES) and operates in addition to a prompt S–C bond cleavage associated with the <100 fs decay of the 4s state (something DES does also clearly exhibit). This then leads the discussion to the relatively weak, but much longer-lived signal with a 42 ps decay that is seen in THT (Fig. 7, Table 2, and Fig. S4, ESI†). We suggest the most likely origin of this feature is two-photon probe ionization of the re-populated S0 ground state, which then undergoes some form of statistical fragmentation due to extremely high levels of concomitant vibrational excitation. As already discussed, the S0 state may be accessed by a conical intersection with the 4s state at highly extended S–C bond extensions (beyond the 3 Å limit of our EOM-CCSD calculations in Fig. 2). Similar pathways to the ground state have also been discussed in related cyclic ether systems, as highlighted in the Introduction.10 The clear difference in the propensity for S–C bond cleavage on the excited 4s potential surface vs. S0 recovery seen in THT and DES might then be rationalized through angular geometry constraints imposed by the 5-membered ring of the former species, and the influence this then exerts at the relevant conical intersection. On the other hand, this argument does not explain why the behaviour seen in THT is notably different to that in THI. In THI, however, excitation directly to the 4s state is known to yield ethene and thioformaldehyde products (the reverse Thia-Paternò-Büchi reaction).67,68,70 Furthermore, this process may be assumed to take place extremely rapidly by analogy with 193 nm excitation studies conducted on oxetane (the ether analogue of THI), where ethene and formaldehyde products formed via ground state repopulation exhibit a high degree of recoil anisotropy.80 This raises a second possibility that the 270–300 fs and 470–560 fs lifetimes seen in THT and THI are, in fact, associated with a rapid decay of S0 following the internal conversion from the 4s state. In this scenario, there may be two competing fragmentation pathways from the ground state of THT (with associated time constants of 270–300 fs and 42 ps) – presumably arising due to subsets of molecules sampling different initial regions of phase space within S0 during the internal conversion process. Conversely, in THI only one such pathway (with an associated time constant of 470–560 fs) is of significance. Clearly more experimental data is required to investigate these possibilities further, and we suggest that time-resolved measurements conducted using complementary techniques with different associated observables (e.g. transient absorption spectroscopy, time-resolved X-ray scattering) may prove particularly instructive in this regard. This is in addition to time-resolved photoionization experiments conducted with probes that specifically target the resonant transitions of specific products or, alternatively, exploit VUV probes that project much more deeply into the ionization continuum.
V. Conclusion
The non-adiabatic excess energy redistribution dynamics operating in a series of saturated thioethers were investigated using the TRPEI approach, supported by quantum chemistry calculations. Experimental measurements employed a 200 nm pump in conjunction with a 267 nm probe operating under two different intensity regimes. In the lower probe intensity case (∼3 × 1012 W cm−2) the straight chain molecule DES and the 5-membered ring system THT were observed to undergo extremely rapid (<100 fs) internal conversion between the initially excited 4p Rydberg manifold and the 4s state. The C–S–C bending angle was found to potentially be a key coordinate driving this internal conversion step, although only very small angular displacements away from the ground state equilibrium geometry are required. Conformational constraints imposed by cyclic ring structures therefore do not influence the dynamical timescale to any significant extent. The resulting 4s state is unbound along the S–C stretching coordinate and exhibits an extremely short (<100 fs) lifetime. Under higher probe intensities (∼5 × 1013 W cm−2), additional features appear in the photoelectron spectra. These are attributed to ionization of short-lived excited state (bi)radical intermediates formed following direct dissociation within the 4p manifold and indicate the presence of a second decay channel that acts in competition with 4p → 4s internal conversion. We also observe a much higher propensity for re-population of the S0 ground state via the 4s pathway in THT over other systems studied (where the 4s state predominantly dissociates). Utilizing a higher level of theory, e.g. complete active space self-consistent field (CASSCF) calculations, may in future reveal much more about the 4s/S0 conical intersection at highly extended S–C bond distances. Our findings also illustrate the value of projecting more deeply into the ionization continuum to reveal pathways to which TRPEI measurements would otherwise be otherwise blind. In this regard, we suggest that future time-resolved studies conducted on thioether systems using VUV probes (and other complementary techniques) will reveal much more mechanistic detail, and we hope and anticipate that this present work will serve as a stimulus for such an undertaking.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Engineering and Physical Sciences Research Council (EPSRC) grants EP/P001459, EP/R030448/, EP/T021675, and EP/V006746. MJP thanks the Leverhulme trust for support through project grant RPG-2020-208. Heriot-Watt University are also acknowledged for providing PhD funding to S. L. J.References
- J. Bock, M. Michou, P. Nabat, M. Abe, J. P. Mulcahy, D. J. L. Olivié, J. Schwinger, P. Suntharalingam, J. Tjiputra, M. van Hulten, M. Watanabe, A. Yool and R. Séférian, Biogeosciences, 2021, 18, 3823 CrossRef CAS.
- A. Lana, T. G. Bell, R. Simó, S. M. Vallina, J. Ballabrera-Poy, A. J. Kettle, J. Dachs, L. Bopp, E. S. Saltzman, J. Stefels, J. E. Johnson and P. S. Liss, Global Biogeochem. Cycles, 2011, 25, GB1004 CrossRef.
- R. Simó and J. Dachs, Global Biogeochem. Cycles, 2002, 16, 1078 CrossRef.
- C.-L. Lee and P. Brimblecombe, Earth-Sci. Rev., 2016, 160, 1 CrossRef CAS.
- C. A. Weitekamp, T. Stevens, M. J. Stewart, P. Bhave and M. I. Gilmour, Sci. Total Environ., 2020, 704, 135772 CrossRef CAS PubMed.
- N. Kotsina and D. Townsend, Phys. Chem. Chem. Phys., 2021, 23, 10736 RSC.
- H. H. Fielding and G. A. Worth, Chem. Soc. Rev., 2018, 47, 309 RSC.
- G. Wu, P. Hockett and A. Stolow, Phys. Chem. Chem. Phys., 2011, 13, 18447 RSC.
- T. Suzuki, Annu. Rev. Phys. Chem., 2006, 57, 555 CrossRef CAS PubMed.
- A. Röder, A. B. Skov, A. E. Boguslavskiy, R. Lausten and A. Stolow, Phys. Chem. Chem. Phys., 2020, 22, 26241 RSC.
- A. A. Scala, E. W.-G. Diau, Z. H. Kim and A. H. Zewail, J. Chem. Phys., 1998, 108, 7933 CrossRef CAS.
- M. D. J. Waters, A. B. Skov, M. A. B. Larsen, C. M. Clausen, P. M. Weber and T. I. Sølling, Phys. Chem. Chem. Phys., 2019, 21, 2283 RSC.
- Y. Zhang, H. Jónsson and P. M. Weber, Phys. Chem. Chem. Phys., 2017, 19, 26403 RSC.
- J. O. F. Thompson, L. B. Klein, T. I. Sølling, M. J. Paterson and D. Townsend, Chem. Sci., 2016, 7, 1826 RSC.
- L. B. Klein, J. O. F. Thompson, S. W. Crane, L. Saalbach, T. I. Sølling, M. J. Paterson and D. Townsend, Phys. Chem. Chem. Phys., 2016, 18, 25070 RSC.
- L. B. Klein, T. J. Morsing, R. A. Livingstone, D. Townsend and T. I. Sølling, Phys. Chem. Chem. Phys., 2016, 18, 9715 RSC.
- S. Deb, B. A. Bayes, M. P. Minitti and P. M. Weber, J. Phys. Chem. A, 2011, 115, 1804 CrossRef CAS PubMed.
- J. D. Cardoza, F. M. Rudakov and P. M. Weber, J. Phys. Chem. A, 2008, 112, 10736 CrossRef CAS.
- J. L. Gosselin, M. P. Minitti, F. M. Rudakov, T. I. Sølling and P. M. Weber, J. Phys. Chem. A, 2006, 110, 4251 CrossRef CAS PubMed.
- M. J. Paterson and D. Townsend, Int. Rev. Phys. Chem., 2020, 39, 517 Search PubMed.
- H. S. You, S. Han, J.-H. Yoon, J. S. Lim, J. Lee, S.-Y. Kim, D.-S. Ahn, J. S. Lim and S. K. Kim, Int. Rev. Phys. Chem., 2015, 34, 429 Search PubMed.
- G. M. Roberts and V. G. Stavros, Chem. Sci., 2014, 5, 1698 RSC.
- M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218 RSC.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093 RSC.
- M. M. Zawadzki, M. Candelaresi, L. Saalbach, S. W. Crane, M. J. Paterson and D. Townsend, Faraday Discuss., 2016, 194, 185 RSC.
- L. B. Clark and W. T. Simpson, J. Chem. Phys., 1965, 43, 3666 CrossRef CAS.
- D. D. Altenloh and B. R. Russell, J. Phys. Chem., 1982, 86, 1960 CrossRef CAS.
- I. Tokue, A. Hiraya and K. Shobatake, J. Chem. Phys., 1989, 91, 2808 CrossRef CAS.
- A. A. Planckaert, J. Doucet and C. Sandorfly, J. Chem. Phys., 1974, 60, 4846 CrossRef CAS.
- C. H. Hearn, E. Turcu and J. A. Joens, Atmos. Environ., 1990, 24A, 1939 CrossRef CAS.
- D. M. P. Holland, D. A. Shaw, I. C. Walker, I. J. McEwen and M. F. Guest, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 035102 CrossRef.
- L. V. Keldysh, Sov. Phys. JETP, 1965, 20, 1307 Search PubMed.
- M. J. DeWitt and R. J. Levis, Phys. Rev. Lett., 1998, 81, 5101 CrossRef CAS.
- N. Kotsina, M. Candelaresi, L. Saalbach, M. M. Zawadzki, S. W. Crane, C. Sparling and D. Townsend, Phys. Chem. Chem. Phys., 2020, 22, 4647 RSC.
- R. A. Livingstone, J. O. F. Thompson, M. Iljina, R. J. Donaldson, B. J. Sussman, M. J. Paterson and D. Townsend, J. Chem. Phys., 2012, 137, 184304 CrossRef PubMed.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477 CrossRef CAS.
- K. L. Reid, Annu. Rev. Phys. Chem., 2003, 54, 397 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029 CrossRef CAS.
- J. J. Butler and T. Baer, Org. Mass Spectrom, 1983, 18, 248 CrossRef CAS.
- K. Watanabe, T. Nakayama and J. Mottl, J. Quant. Spectrosc. Radiat. Transfer, 1962, 2, 369 CrossRef.
- G. Wagner and H. Bock, Chem. Ber., 1974, 107, 68 CrossRef CAS.
- H. Schmidt and A. Schweig, Tetrahedron Lett., 1973, 14, 1437 CrossRef.
- M. G. Giorgini, G. Paliani and R. Cataliotti, Spectrochim. Acta, 1977, 33A, 1083 CrossRef.
- S. D. Christesen, J. Raman Spectrosc., 1991, 22, 459 CrossRef CAS.
- J. O. F. Thompson, L. Saalbach, S. W. Crane, M. J. Paterson and D. Townsend, J. Chem. Phys., 2015, 142, 114309 CrossRef PubMed.
- D. A. Horke, H. M. Watts, A. D. Smith, E. Jager, E. Springate, O. Alexander, C. Cacho, R. T. Chapman and R. S. Minns, Phys. Rev. Lett., 2016, 117, 163002 CrossRef CAS PubMed.
- C. Z. Bisgaard, O. J. Clarkin, G. Wu, A. M. D. Lee, O. Gessner, C. C. Hayden and A. Stolow, Science, 2009, 323, 1464 CrossRef CAS.
- P. Quintana, R. F. Delmdah, D. H. Parker, B. Martínez-Haya, F. J. Aoiz, L. Bañares and E. Verdasco, Chem. Phys. Lett., 2000, 325, 146 CrossRef CAS.
- B. Martínez-Haya, P. Quintana, L. Bañares, P. Samartzis, D. J. Smith and T. N. Kitsopoulos, J. Chem. Phys., 2001, 114, 4450 CrossRef.
- J.-H. Yoon, K. C. Woo and S. K. Kim, Phys. Chem. Chem. Phys., 2014, 16, 8949 RSC.
- M. Bain, C. S. Hansen and M. N. R. Ashfold, J. Chem. Phys., 2018, 149, 081103 CrossRef PubMed.
- V. Blanchet, M. Z. Zgierski and A. Stolow, J. Chem. Phys., 2001, 114, 1194–1205 CrossRef CAS.
- V. Blanchet, M. Z. Zgierski and A. Stolow, Nature, 1999, 401, 52–54 CrossRef CAS.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS.
- D. M. P. Holland, D. A. Shaw, I. C. Walker, I. J. McEwen and M. F. Guest, Chem. Phys., 2008, 344, 227 CrossRef CAS.
- J. M. Dyke, A. R. Ellis, N. Keddar and A. Morris, J. Phys. Chem., 1984, 88, 2565 CrossRef CAS.
- F. A. Houle and J. L. Beauchamp, J. Am. Chem. Soc., 1979, 101, 4067 CrossRef CAS.
- B. L. FitzPatrick, M. Maienschein-Cline, L. J. Butler, S.-H. Lee and J. J. Lin, J. Phys. Chem. A, 2007, 111, 12417 CrossRef CAS PubMed.
- W. L. Hase, H. B. Schlegel, V. Balbyshev and M. Page, J. Phys. Chem., 1996, 100, 5354 CrossRef CAS.
- H. R. Wendt and H. E. Hunziker, J. Chem. Phys., 1984, 81, 717 CrossRef CAS.
- G. Black and L. E. Jusinski, Chem. Phys. Lett., 1987, 136, 241 CrossRef CAS.
- A. Bouallagui, A. Zanchet, O. Yazidi, N. Jaïdane, L. Bañares, M. L. Senent and A. García-Vela, Phys. Chem. Chem. Phys., 2017, 19, 31245 RSC.
- M. Ge, J. Wang, X. Zhu, Z. Sun and D. Wang, J. Chem. Phys., 2000, 113, 1866 CrossRef CAS.
- D. V. Chicharro, S. M. Poullain, L. Rubio-Lago and L. Bañares, J. Phys. Chem. A, 2019, 123, 8552 CrossRef CAS PubMed.
- F. H. Dorer, M. E. Okazaki and K. E. Salomon, J. Phys. Chem., 1981, 85, 2671 CrossRef CAS.
- D. R. Dice and R. P. Steer, J. Phys. Chem., 1973, 77, 434 CrossRef CAS.
- S. Braslavsky and J. Heicklen, Can. J. Chem., 1971, 49, 1316 CrossRef CAS.
- H. A. Wiebe and J. Heicklen, J. Am. Chem. Soc., 1970, 92, 7031 CrossRef.
- F. Qi, L. Sheng, M. Ahmed, D. S. Peterka and T. Baer, Chem. Phys. Lett., 2002, 357, 204 CrossRef CAS.
- A. G. Suits and F. Qi, J. Electron Spectros. Relat. Phenomena, 2001, 119, 127 CrossRef CAS.
- T. A. A. Oliver, G. A. King and M. N. R. Ashfold, Chem. Sci., 2010, 1, 89 RSC.
- M. M. Zawadzki, J. O. F. Thompson, E. A. Burgess, M. J. Paterson and D. Townsend, Phys. Chem. Chem. Phys., 2015, 17, 26659 RSC.
- J. D. Rodríguez, M. G. González, L. Rubio-Lago and L. Bañares, Phys. Chem. Chem. Phys., 2014, 16, 406 RSC.
- A. S. Chatterley, G. M. Roberts and V. G. Stavros, J. Chem. Phys., 2013, 139, 034318 CrossRef.
- J. S. Lim and S. K. Kim, Nat. Chem., 2010, 2, 627 CrossRef CAS PubMed.
- D.-S. Ahn, J. Lee, J.-M. Choi, K.-S. Lee, S. J. Baek, K. Lee, K.-K. Baek and S. K. Kim, J. Chem. Phys., 2008, 128, 224305 CrossRef.
- J. Biesner, L. Schnieder, G. Ahlers, X. Xie, K. H. Welge, M. N. R. Ashfold and R. N. Dixon, J. Chem. Phys., 1989, 91, 2901–2911 CrossRef CAS.
- S.-H. Lee, J. Chem. Phys., 2009, 131, 224309 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental & theoretical data. See DOI: https://doi.org/10.1039/d2cp04789f |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2022 |