Electrostatic interactions and physisorption: mechanisms of passive cesium adsorption on Prussian blue

Abstract

The dangers posed by nuclear accidents necessitate developments in techniques for cesium removal. One such is the adsorption of cesium cations in Prussian blue (PB) materials, on which adsorption can be a substation process or pure physisorption. The underlying mechanism of the latter is not well understood, although a Langmuir isotherm is frequently used to model experimental results. In this work, we exploit tight-binding density-functional theory (DFTB) methods to probe the atomic interactions in the physisorption process. The results show that there is a diminishing return for the energy of adsorption as more sites are filled. This means that the adsorption sites are not independent, as stipulated by the ideal Langmuir isotherm. Instead, the results indicate that electrostatic effects need to be considered to explain the theoretical and experimental results. Therefore, an electrostatic Langmuir (EL) model is introduced, which contains an electrostatic ideality correction to the classic Langmuir isotherm. For future materials development, these physical insights indicate that shielding effects as well as the number of independent physical sites must be considered when synthesizing effective Prussian blue analogs (PBA). In conclusion, the study provides insights into the limiting mechanisms in the physisorption of cesium cations on PB.

---

Introduction

Accidents at nuclear power plants can have long-lasting hazardous consequences, including contamination with radioactive isotopes.¹ One such is cesium (Cs-137).² Potential contamination by these elements necessitates the development of effective materials^3–8 for decontamination. Because of the chemical nature of the element cesium, it is typically found in the form of cesium salts with relatively high solubilities in water. Therefore, Prussian Blue (PB) represents a highly suitable candidate material for cation adsorption and thus decontamination.^9,10

PB is part of a larger family of metal hexacyanoferrates (MHCF).^11–14 Its standard molecular structure is KFe[Fe(CN)₆],¹⁰ although there is usually a high density of defects mainly caused by missing hexacyanoferrate units.^2,15,16 In addition, the nanoporous PB structure may contain various amounts of incorporated water, as well as absorbed cations in the internal cavities. Notably, PB forms crystals with wide lattice spacing.¹⁰ This makes PB systems adept for a variety of applications, such as sensing,¹⁷ carbon capture,¹⁸ bio-medicine,^19,20 and intercalation in capacitive deionization (CDI).^21–33 Importantly for this work, it means that K⁺ ions that are part of the PB material but interstitially present in the crystal framework can be replaced by other cations, such as cesium ions.² Thus, replacement is one way of removing cesium ions from water using PB materials. Multiple studies have investigated the diffusion and replacement mechanisms to better understand this process.^2,34 However, PB can also adsorb cesium ions passively.³⁵

Passive adsorption of cesium ions is commonly described using a Langmuir isotherm, which works reasonably well.^35–39 However, the details of the adsorption mechanisms are usually not discussed. A fundamental prerequisite in the Langmuir isotherm model is that the adsorption occurs on a finite number of physical sites, and another is that the sites are independent and energetically equal.^40,41 However, cesium cations are charged, and therefore we should expect interactions between adsorbed cesium ions unless the charges are well shielded. Such effects are not included in the standard Langmuir isotherm. This study will thus investigate the relationship between the Langmuir isotherm and the adsorption of charged species, exemplified through the adsorption of cesium cations on PB (Fig. 1).

Fig. 1 A unit cell of PB. This illustration shows a model structure containing a central defect, where a hexacyanoferrate group is missing and instead is replaced by water molecules coordinated to neighboring Fe ions. Vacancies exist in all PB materials, and this is a commonly used model for so-called insoluble PB.¹⁰

Specifically, in this work, we use tight-binding density-functional theory (DFTB)⁴² to simulate atomic-scale properties of PB including the effects of cesium adsorption. The semi-empirical DFTB approach represents a compromise between classical and full ab initio molecular dynamics (aiMD), allowing larger systems to be explicitly modeled than with aiMD and at the same time retain the covalent bond interaction effects of the more advanced models. The simulations were performed to estimate how the adsorption energy changes depending on the adsorption quantity and adsorption configuration. To start, the goal is to obtain deeper insights into the mechanisms behind the adsorption process with the main objective to identify guidelines on how to modify the PB materials to enhance the specific cesium ion adsorption properties. Finally, we introduce an electrostatic Langmuir (EL) model to explain and quantify the deviation from the classic Langmuir isotherm in this system.

Methods

DFTB calculations

Because the central interactions of adsorption are on a molecular level, the fundamental method in this study involves atomistic simulations. The approach will be to build a representative model of the PB crystal structure and observe how it performs as an adsorption target when the number of cesium ions is increased.

The model system constructed includes a unit cell of PB with a central defect (a model of so-called insoluble PB, Fe₄[Fe(CN)₆]₃·6H₂O).¹⁰ To generate reasonable surface properties, we completed the first coordination shells of all hexacyanoferrate complexes at the six interfaces by adding the necessary cyanide ligands (Fig. 2). That is, the model crystal is no longer a perfect cube, but rather contains hexacyanoferrate and metal-ion groups with complete coordination shells. This leads to a rather high net negative charge of the model, which was compensated by adding cations (cesium) near the outside surface to make the overall system charge-neutral. In addition, the Packmol program was employed to generate a water droplet around the unit cell.⁴³ To keep the droplet intact, we put the model in a spherical cavity, restricting the atoms to reside inside the droplet using a restraining force. Also, we constrained the distance between the Fe, N, and C atoms to ensure that the PB unit cells retained the same shape as in a real crystal. When probing the cesium adsorption properties, we added excess cesium ions in the water droplet hydration shell near the PB surface (N = 0–4, denoting the excess number of added cesium ions per unit cell).

Fig. 2 A PB model of cesium ion adsorption. (a) The core model corresponds to an isolated unit cell of PB, but the first coordination shells of all the hexacyanoferrate groups have been completed by the necessary number of additional cyanide ligands. Cesium cations were located around the surface to generate net charge neutrality. (b) The solvated version of the model. Water molecules were placed to solvate the PB unit cell model.

The simulations were performed using the xTB program, which provides semi-empirical simulations based on DFTB.^42,44,45 Specifically, the GFN-FF method was applied as a compromise between accuracy and reasonable computation times.⁴² We employ the default settings in the simulations, except that the MD step time was reduced to 0.5 fs. Room temperature was assumed and retained using an NVT ensemble and a Berendsen thermostat. Also, the adsorption will depend on the change in Gibbs free energy for different numbers of excess cesium ions in the model. This can be calculated from the Hessian in the simulation (xTB provides the total free energy through a rigid-rotor-harmonic-oscillator approach⁴⁶). However, the total model system contains many local energy minima, which makes it difficult to identify a single representative geometry. To overcome this problem of a static approach, we instead used molecular dynamics (MD) to simulate the system behavior over 2 ns. The trajectories were sampled every ps, and we used the snapshots from 100 ps to 1999 ps of the simulations, representing equilibrated systems, to generate a statistical average of the free energy.

To get a wider data range, the initial MD simulations were followed by Monte–Carlo-style⁴⁷ single-point simulations of different cesium ion configurations. We first introduced a 2 × 2 × 2 supercell of PB to generate more realistic surface properties. Subsequently, 0–39 excess cesium ions were introduced (along with their excess charge). Each cesium ion was assigned to a random adsorption site on the surface (the surface sites corresponding to the center of the cavities if they had been inside the unit cell) The calculation for each excess cesium was repeated 25 times, yielding 1000 data points for the each of the numbers of excess cesium ions and configurations of the surface. To estimate the net energy of adsorption, we evaluated the total internal-energy difference between a water droplet and a droplet with an added cesium ion. That represents the baseline cesium ion energy. We subsequently subtracted N times the baseline energy from the total internal energy in the model systems with N excess cesium ions.

Finally, linear and quadratic regression models were introduced to quantify the energy contributions from the number of excess cesium ions, the first-neighbor adsorption sites, and the second-neighbor adsorption sites. Previous works on the Langmuir isotherm in gas systems have indicated that these interactions can be important for quantifying non-ideal behavior.⁴⁷ The overall goal here is to understand why there would be deviations from the standard Langmuir isotherm.

The MD simulations and Hessian estimates were performed on the Tegner and Dardel cluster computers at PDC.⁴⁸ These supercomputers have 24 and 128 cores, respectively. The MD calculations typically required 5 days in terms of wall-time per simulation. One simulation was performed for each number of excess cesium ions going stepwise from 0 to 4 ions in excess. The Hessian calculations typically only took a few minutes. However, the total calculation time was much longer, since we extracted structural snapshots every ps of the MD simulations between 100 ps and 2000 ps and repeated the Hessian calculation for them to generate sufficiently low statistical errors.

NEDA analysis

A Natural Energy Decomposition Analysis (NEDA) analysis was performed using NBO 7.0 as interfaced with Gaussian 16 (Rev. C.01).^49,50 The full unit cell of the PB material with amended cyanide ligands and cesium cations turned out to be too big for a rational NEDA analysis. Therefore, the structural model was reduced to approximately 1/8 unit cell together with two cesium ions of the formal composition Cs₂[Fe₇(CN)₂₄(H₂O)₃]⁴⁻ (66 atoms in total, see Fig. 3) in a singlet electronic state. The model was divided into two fragments, of which one comprised the cesium ions and the other the remaining atoms. Fe and the lighter elements were analyzed using 6-31G basis sets, and Cs invoked the Stuttgart–Dresden–Cologne effective-core potential basis set as implemented in Gaussian 16 (SDD keyword), and the B3LYP hybrid functional was used to generate the molecular orbitals for the energy decomposition analysis.

Fig. 3 The structural model used in the NEDA analysis. Fe (whitish blue), C (grey), N (blue), O (red), H (white) and Cs (purple).

Isotherm modeling

The standard Langmuir isotherm is shown in eqn (1). Here, q is the equilibrium adsorption level, K_L is the equilibrium constant of adsorption, c is the equilibrium concentration, and q_m is the maximum adsorption level. Also, K_L = k_ads/k_des wherein the latter are constants of adsorption and desorption rates. The expression can be rewritten in a linear form (eqn (2)). This form makes it possible to model the unknown parameters K_L and q_m through linear regression to the experimental data. Specifically, the q_m parameter can be deduced from the intercept and K_L can be determined from the slope of the linear fit.

We will now derive an algorithm for modeling the adsorption isotherm in cases when K_L is not constant with respect to any model parameter, such as the excess level of cesium cations. Specifically, the case when there is a quadratic energy dependence will be relevant for this work. Because the quadratic energy dependence can originate from repulsive electrostatic interactions among the adsorbed cations, we will denote this as the electrostatic Langmuir model, or the EL model. Normally, the energy of adsorption in the Langmuir framework is proportional to the adsorption. That is, E(q) = aq or E(q)/q = a for some constant a. If there is a quadratic energy dependence, that would instead correspond to E(q) = aq + bq², or E(q)/q = a + bq.

In this framework, three types of energies need to be taken into account. These are the energy of an ion in the solution, the height of the energy barrier of adsorption, and the energy in the adsorbed configuration. The solution and barrier energies affect the adsorption rate constant, while the barrier and adsorbed energies affect the desorption rate constant. The quadratic energy dependence on the adsorbed side should thus primarily affect the desorption rate. Because rates are proportional to the exponential of the energy, we get k_des,q = k_des exp(k_qq). Here, the subscript q indicates that the parameter is related to the isotherm with a quadratic dependence. Also, k_q is a constant corresponding to the quadratic correction. This means K_L,q = K_L exp(−k_qq). The system would thus have three parameters to be estimated in a regression model: K_L, q_m, and k_q (eqn (3)).

If k_q = 0, the result becomes the same as for the standard Langmuir isotherm, and therefore the extra parameter can be regarded as an ideality factor. Because this factor will be quite small, the relevant parameter values are expected to be close to zero. Thus, the exponential can be expanded to the first order using a Taylor expansion (eqn (4)).

This expression can be handled in the same way as the standard Langmuir equation. To be explicit, the expression can be rewritten in matrix form, as in eqn (5). Here, bold font denotes vector properties. That is, q is the vector of observed equilibrium adsorption for experiments with concentrations listed in c (N × 1 vector, corresponding to the N experiments). In addition, “./” (with a dot) indicates element-wise division. The matrix components are listed in eqn (6)–(8). In this formulation, there is a standard least-squares solution for β, [small beta, Greek, circumflex] = (X^TX)⁻¹X^Ty. We thus arrive at q_m = 1/[small beta, Greek, circumflex]₃, K_L = 1/[small beta, Greek, circumflex]₁q_m, and k_q = [small beta, Greek, circumflex]₂K_Lq_m. Here, the numbers in subscripts denote the vector elements.

y = Xβ (5)

y ≡ c./q (6)

X ≡ [1qc] (7)

β ≡ [1/(q_mK_L)k_q/(q_mK_L)1/q_m]^T (8)

An extended discussion can be found in the ESI.† That section also shows how to model and estimate the three system parameters without introducing the Taylor approximation of exp(k_qq). Still, we have chosen to show the expansion approximation here because it is simpler and more stable to model. Additional options, such as ridge regression or boundaries on the parameters, could also be introduced to facilitate the regression step. Programs such as MATLAB have built-in routines for these methods. However, the graphs in the results section have been produced based on the standard least-squares solution shown above.

Results and discussion

Preliminaries

Studies that provide an estimate of the physisorption of cesium ions on PB are usually based on the Langmuir isotherm.^35–39 Because of this, we would expect some agreement between the system conditions and the underlying premises of the Langmuir isotherm. The Langmuir isotherm relies on two basic presumptions: that there is adsorption at a finite number of physical sites, and that all sites are characterized by the same energy of adsorption. The question is how well these hold on the detailed level.

For instance, previous DFT studies on gas adsorption employing the Langmuir isotherm have reported significant deviations by considering the interactions between neighboring adsorbates.⁴⁷ Such interactions disfavor close packing of adsorbed entities. This leads to a more stepwise behavior than the classic isotherm.

Probing with molecular dynamics

We started the investigation using MD simulations. The reason is to gain an understanding of how cesium ion moves and interacts with the PB material, including the stability and variation in adsorption sites. Such simulations may also reveal unexpected transport mechanisms in the system. The results from 2 ns simulations show that the Gibbs free energy can be regarded as stable over time (Fig. 4(a) and the ESI†). The system energy displays natural fluctuations. This can be attributed to the movement of a large number of water molecules together with the crystal unit cell comprising the system. The trends are the same for all the model systems containing different numbers of excess cesium.

Fig. 4 (a) The Gibbs free energy as estimated from the Hessian and exemplified for 4 cesium ions in excess. The abscissa shows the simulation time, and one snapshot was extracted every ps. The ordinate shows the Gibbs free energy normalized by the average Gibbs energy in the time series. (b) The snapshots were used to generate a statistical average of the Gibbs free energy of the system. The graph shows the interaction energy for N excess Cs⁺, as calculated with the Gibbs-free-energy difference between 0 and N cesium, minus N times the baseline energy for 1 excess cesium ion. The ordinate shows the interaction energy as a percentage of the baseline energy (0 added cesium ions). (c) and (d) Trajectories for a cesium ion during the MD simulations (top-down and inside cavity views). The dots show the host PB structure at the 100 ps snapshot with one excess cesium. Solvating water and other cesium ions have been omitted for sake of clarity. The isosurface plot shows a 95% probability of the cesium ion positions centered on the statistical mean position. The color in the isosurface plot indicates the crystallographic z-coordinate. Because the host structure also moves slightly within the solvation droplet during the simulation, all snapshots have been rotated and shifted to align the crystal matrices before generating the cesium trajectory.

A large number of water molecules in the systems makes it difficult to extract exact Gibbs free energy from individual configurations. However, long MD simulations will allow the estimation of stable mean energies that can be used as reliable energy estimates. Adding cesium ions to the model will always add to the Gibbs free energy (the system has been expanded). But, the energy difference emerging from each added excess ion can be compared to discern if there are any trends. These initial results indicate that the energy gained by adsorbing more cesium ions is less favorable if there are cesium ions already adsorbed on the surface (Fig. 4(b)). At this point, we can only speculate on what type of effect causes this observation. However, the trend suggests that there is a repulsive interaction effect between the adsorbed cesium ions. That is an interesting observation since it contradicts the prerequisites of the standard Langmuir isotherm. Later sections of this work will investigate this deviation in more detail.

Looking at the trajectory plots of the 2 ns MD simulations, it is notable that the cesium ions remain in the proximity of a stable position during the entire simulation time (Fig. 4(c) and (d)). This position is close to the hollow area at the surface. That is, the position that would have represented an inner wall center in a cavity if it had been inside the unit cell structure instead of at the surface. Also, most of the movement is diagonal, parallel to the closest cyanide groups that protrude from the surface. These preferred positions of adsorption will be used in the coming sections, when we more deeply investigate the interaction effects between adsorbed cesium ions.

Identifying the non-ideal interactions

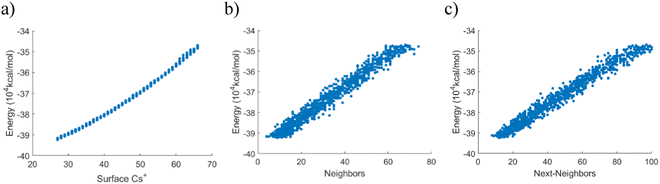
The previous section suggested that the ion adsorption sites are not fully independent at the atomic level. More specifically, adsorption becomes less energetically favorable the more ions that are already adsorbed on the surface. One study on gas adsorption and the Langmuir isotherm found that this type of non-ideal behavior could be attributed to interactions between neighboring adsorbed atoms.⁴⁷ Thus, a question is if neighboring adsorbed cesium ions could exhibit similar interaction effects.

The results in Fig. 5 show a more thorough scan of the total internal energy depending on the number of excess cesium ions, including their configuration. The Monte–Carlo-inspired scan includes 25 randomized positions for each of the systems containing between 0 and 39 excess cesium ions, yielding a total of 1000 data points. The ions were randomly distributed among the preferred surface areas, as described previously. In each configuration, the number of each type of interaction was recorded (number of cesium ions, first-order neighbors, and second-order neighbors). Because of the random sampling, a regression can reveal the impact of each interaction type. This is only the total internal energy of the PB system with adsorbed ions and does not include the energy difference when taking the ions from the solution into account, to this point. The internal energy difference can be described as predominantly linear, although the results confirm the findings in the previous section concerning the non-linear energy increase with an increasing number of interactions. In this context, it should be emphasized that an increase in energy here corresponds to a weakening of the adsorption energy for the cesium ions. Just plotting the total internal energy versus the number of first (Fig. 5(b)) or second (Fig. 5(c)) nearest neighbor interactions suggests a strong linear correlation for both these factors.

Fig. 5 The total system energy plotted against the number of a single interaction type. (a) The abscissa shows the total number of cesium ions on the PB surface. The leftmost data point corresponds to the charge-neutral case of 0 ions in excess. Every additional ion makes the system more positively charged. (b) The abscissa shows the number of first-order interactions; that is, the number of pair-wise interactions between adjacent adsorbed cesium ions. (c) These are the number of second neighbor interactions, showing the number of pair-wise adsorbed cesium ions that are two adsorption sites apart.

To investigate further, we used a linear model for the data and included all these factors. Interestingly, a linear model with only the number of excess cesium ions could properly describe the energy changes with an R² value of 0.991. Adding the first-order neighbor interactions raised this marginally to 0.994. Adding the second-order neighbor interactions raised the value to 0.995. In summary, the results indicate that the next-nearest neighbors have a negligible effect on the modeling accuracy. This suggests that their impact on the physical system is small.

Another observation is that the total internal energy of the PB system increases with more ions included, because the total number of ions increases in the system. In reality, the excess cesium ions added to the model must come from the surrounding solution. We will thus calculate the net energy by subtracting N times the energy of having a cesium ion in a solution from the adsorption model with N excess cesium. These results indicate that some adsorption is energetically favorable even if it leads to a higher net charge for the system. However, adsorption is counteracted by the non-linear energy effects when the number of excess cesium ions is increased. That is clearly seen in Fig. 6, where the energy differences go from negative to positive after some 10–15 cesium ions have been adsorbed.

If this correction is introduced, the linear model that aims to explain the total internal energy in terms of nearest neighbor interactions becomes less suitable. That supports the idea that neighbor interactions cannot be the source of the non-ideal energies obtained. On the other hand, a near-perfect (R² = 0.999) fit can be obtained when instead applying a quadratic model (Fig. 6). A model with quadratic energy dependence makes sense if electrostatic effects are the cause of the non-linear behavior. This is because every excess ion experiences electrostatic repulsion from all the other excess ions. The ESI† contains a section with an extended discussion around the principles of the electrostatic repulsion behavior in adsorption.

Fig. 6 The net adsorption energies (Fig. 5(a)), i.e. the net energy from N cesium ions in the solution subtracted from the energy from N cesium ions adsorbed to the PB surface. The axes have been shifted so that the (0,0) point is the system energy with zero cesium ions in excess.

NEDA analysis

The previous section suggested that electrostatic effects are the main cause of the increase in interaction (adsorption) energy between the adsorbed cesium ions and the rest of the system. To test this idea, we performed a NEDA analysis, as described in the methods section. Based on the NEDA analysis of the interaction between the adsorbed Cs⁺ cations and the reduced PB unit cell model, it is clear that electrostatics profoundly dominates the interactions. The electrostatics amount to −611 kcal mol⁻¹, whereas charge transfer (essentially covalent interactions) only to about 58 kcal mol⁻¹. Of the electrostatics about 93 kcal mol⁻¹ arise from polarization, thus showing that static electrostatics predominate the interaction between the Cs⁺ cations and the host PB material.

In summary, the results have demonstrated that electrostatic interactions are present that counteract the prerequisites of the standard Langmuir isotherm. Furthermore, there is a quadratic dependency between the adsorption energy and the number of adsorbed ions. The next section will demonstrate how to construct a modified Langmuir isotherm based on the results obtained from the simulations.

Construction of a non-ideal Langmuir isotherm

So far, the results show that there is a weak repulsive interaction between neighboring adsorbed cesium ions. Therefore, the standard Langmuir model should work reasonably well. On the other hand, the main cause of non-ideal adsorption energy originates from long-range repulsive electrostatic interactions. The exact magnitude of these effects should depend on the shielding effects from the host material and the surrounding solution. Thus, a quadratic ideality correction to the energy can account for these deviations. We will therefore implement these corrections in an electrostatic Langmuir model – the EL model outlined in the methods section.

Fig. 7(a) shows the results from modeling using the Langmuir isotherm and the EL isotherm, respectively. Because the standard Langmuir isotherm represents a special case of the EL model, the EL model should always describe the simulation results at least as well. This expectation is consistent with the results obtained. The difference is most pronounced in Fig. 7(d). Here, the modified EL isotherm better captures the early rise in adsorption level at low concentrations. A possible reason for the larger difference here is that the concentration range is expanded with respect to the cases in Fig. 7a–c. A good model must thus be able to accurately encompass the behavior at both high and low concentrations.

Fig. 7 Standard and electrostatic (EL) Langmuir isotherms. (a)–(c) Experimental data from ref. 51. This is the adsorption of cesium ions on three types of Prussian blue embedded magnetic hydrogel beads (PB-MHBs). The beads will adsorb cesium and then be magnetically extracted from the solution. (d) Experiment data from ref. 52. This is the adsorption trend of cesium ions on a material with PBA anchored on a 3D reduced graphene aerogel.

Outlook

The results have shown that electrostatic effects can influence adsorption behavior. An analogy can be found in the field of electrically mediated adsorption on porous materials, such as sodium ions on activated carbon cloths.^53–55 These systems have traditionally been modeled through the formation of electrical double layers (EDLs).^56,57 However, the Langmuir adsorption isotherm has also worked surprisingly well to model the results in many studies.^58–64 A reason for this could be that the pore sizes are so small that the EDLs are overlapping.³³ The charges therefore accumulate in the tightly packed Stern layers on the pore wall,³³ somewhat like in monolayer adsorption.⁶⁵ The limiting factor for electrosorption, in that case, is the effect of repulsive forces between the adsorbed ions. Based on this, studies have shown that surface modifications, such as the introduction of ZnO rods, can increase the overall adsorption capacity due to their strong dielectric properties.^66,67 There, the adsorption was observed to be higher even though the total surface area was smaller after the ZnO coating. Similarly, we hypothesize that charge shielding is important in the adsorption of cesium ions on PB.

We also hypothesize that the EL isotherm has wider applicability beyond cesium ions and PB. The only assumptions in deriving the model were (i) the premises of the standard Langmuir isotherm hold approximately well; (ii) the overall electrostatic interactions between adsorbed species have an impact on the adsorption energy. These basic assumptions should, in principle, be applicable to a wide range of systems. Future research could thus be dedicated to investigating the relevance of the new EL isotherm also for other systems.

Sensitivity analysis

Because this study mainly focuses on simulations, it is appropriate to discuss the validity of the general conclusions. The major finding in this study is that electrostatic interactions lead to a quadratic correction term to the Langmuir isotherm.

There are limitations to how accurate individual calculations are. In the PB simulations, the random variations from water alignment caused by hydrogen bonding create significant fluctuations in energy. In the long MD simulation shown in Fig. 4(a), the estimated error in the adsorption energy per excess cesium ion is approximately 3 kcal mol⁻¹. A similar value is obtained for the simulations including a wider range of excess cesium ions in Fig. 5. Most likely, systematic errors originating from the limited system sizes and representability have a larger influence on the results and conclusions. We used a 2 × 2 × 2 supercell and many simulations to generate reliable results. In addition, simulation conditions were as much as possible kept constant, except for the number and positioning of the excess cesium ions. Still, the absolute energies from any single simulation should be taken with some reservation. However, the trends are more reliable, and different types of tests have been combined to prove the fundamental points. The collected findings that validate the ideas of electrostatic effects and a quadratic correction are summarized below.

The presumption that electrostatic effects can cause non-ideal adsorption energies is reasonable from the perspective of Coulomb's law. Alike charges should repel each other, and net charges should repel other charges of the same sign. In addition, the typical adsorption distances (ion to host material) in our systems are around 5 Å are significantly longer than in typical reported gas-adsorption systems. Such a long distance will reduce orbital overlap and thus the contribution from covalent interactions. Furthermore, the NEDA analysis demonstrated that electrostatic effects are dominating the adsorption interactions. The simulation results confirm this by showing that neighbor interactions have no added value for explaining the observed energy variations.

Because all excess cesium ions will repel all other cesium ions, the electrostatic effects should have a quadratic dependence on the number of excess cesium ions. Even if long-range electrostatic effects are damped by the water solvent and the dielectric properties of the host material, local clusters of cesium ions will still exhibit the expected quadratic interaction behavior. These results are confirmed by the energy trends in the calculations. Also, the EL isotherm works well for describing macroscopic behavior.

Conclusions

In this work, we have investigated the atomic-level interactions that underpin the Langmuir isotherm for cesium ion adsorption on PB host materials. The results show that there is a diminishing return with respect to the energy of adsorption. Interactions between pairs of neighboring cesium ions could not explain this result. In fact, the limited effect of repulsive interactions between neighboring sites can explain why the Langmuir isotherm works well. Instead, repulsive electrical forces from the collective adsorbed cesium ions limit how many ions can be accommodated on the surface. This goes against the fundamental prerequisites of the Langmuir isotherm model.

We have constructed an EL model to include such electrostatic effects. It could describe the macroscopic experimental data accurately and provides a more robust atomic-level description of the adsorption interactions, including insights into the main interactions at play in the adsorption process. Also, the electrostatic interactions point to analogies to electrically mediated adsorption. We thus hypothesize that dielectric shielding of charges could have an impact on the efficacy of the PB materials as hosts for cesium ion adsorption.

While the study focuses on cesium ion adsorption on PB, physisorption of charged species is common in many other applications as well. Hence, the EL isotherm could become more widely relevant. Future research will therefore be conducted to further investigate the applicability of the EL isotherm to other systems.

Author contributions

Conceptualization, J. N. and L. K.; methodology, J. N. and L. K.; software, J. N.; validation, J. N.; formal analysis, J. N.; investigation, J. N. and L. K.; resources, J. N.; data curation, J. N.; writing—original draft preparation, J. N.; writing—review and editing, J. N and L. K.; visualization, J. N.; supervision, L. K.; project administration, L. K.; funding acquisition, J. N. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors would like to thank the Swedish Research Council (Diary No. 2018-05387) and J. Gust. Richert foundation (Diary No. 2020-00584) for funding the work, and the SNIC PDC supercomputing center (PDC-2021-56) for providing computing resources.

References

1. S. Hashimoto, S. Ugawa, K. Nanko and K. Shichi, The total amounts of radioactively contaminated materials in forests in Fukushima, Japan, Sci. Rep., 2012, 2, 1–5.
2. A. Takahashi, H. Tanaka, K. Minami, K. Noda, M. Ishizaki, M. Kurihara, H. Ogawa and T. Kawamoto, Unveiling Cs-adsorption mechanism of Prussian blue analogs: Cs⁺-percolation: Via vacancies to complete dehydrated state, RSC Adv., 2018, 8, 34808–34816.
3. A. Abusafa and H. Yücel, Removal of 137Cs from aqueous solutions using different cationic forms of a natural zeolite: Clinoptilolite, Sep. Purif. Technol., 2002, 28, 103–116.
4. Y. Ikarashi, H. Mimura, T. Nakai, Y. Niibori, E. Ishizaki and M. Matsukura, Selective cesium uptake behavior of insoluble ferrocyanide loaded zeolites and development of stable solidification method, J. Ion Exch., 2014, 25, 212–219.
5. V. Lamare, J. F. Dozol, S. Fuangswasdi, F. Arnaud-Neu, P. Thuéry, M. Nierlich, Z. Asfari and J. Vicens, A new calix[4]arene-bis(crown ether) derivative displaying an improved caesium over sodium selectivity: Molecular dynamics and experimental investigation of alkali-metal ion complexation, J. Chem. Soc., Perkin Trans. 2, 1999, 271–284.
6. A. Casnati, A. Pochini, R. Ungaro, F. Ugozzoli, F. Arnaud, S. Fanni, M. Schwing, R. J. M. Egberink, F. De Jong and D. N. Reinhoudt, Synthesis, complexation, and membrane transport studies of 1,3-altemate calix[4]arene-crown-6 conformers: A new class of cesium selective ionophores, J. Am. Chem. Soc., 1995, 117, 2767–2777.
7. B. Aguila, D. Banerjee, Z. Nie, Y. Shin, S. Ma and P. K. Thallapally, Selective removal of cesium and strontium using porous frameworks from high level nuclear waste, Chem. Commun., 2016, 52, 5940–5942.
8. R. G. Anthony, R. G. Dosch, D. Gu and C. V. Philip, Use of silicotitanates for removing cesium and strontium from defense waste, Ind. Eng. Chem. Res., 1994, 33, 2702–2705.
9. A. Kraft, On the history of Prussian blue: Thomas Everitt (1805-1845) and Everitt's salt, Bull. Hist. Chem., 2014, 39, 18–25.
10. M. J. P. Muñoz and E. C. Martínez, Prussian Blue Based Batteries, Springer, Cham, 2018, vol. 3.
11. S. Kjeldgaard, I. Dugulan, A. Mamakhel, M. Wagemaker, B. B. Iversen and A. Bentien, Strategies for synthesis of Prussian blue analogues, R. Soc. Open Sci., 2021, 8, 201779.
12. F. S. Hegner, J. R. Galán-Mascarós and N. López, A Database of the structural and electronic properties of Prussian blue, Prussian white, and berlin green compounds through density functional theory, Inorg. Chem., 2016, 55, 12851–12862.
13. S. Vafakhah, L. Guo, D. Sriramulu, S. Huang, M. Saeedikhani and H. Y. Yang, Efficient sodium-ion intercalation into the freestanding Prussian blue/graphene aerogel anode in a hybrid capacitive deionization system, ACS Appl. Mater. Interfaces, 2019, 11, 5989–5998.
14. G. Du and H. Pang, Recent advancements in Prussian blue analogues: Preparation and application in batteries, Energy Storage Mater., 2021, 36, 387–408.
15. A. Simonov, T. De Baerdemaeker, H. L. B. Boström, M. L. Ríos Gómez, H. J. Gray, D. Chernyshov, A. Bosak, H. B. Bürgi and A. L. Goodwin, Hidden diversity of vacancy networks in Prussian blue analogues, Nature, 2020, 578, 256–260.
16. M. Qin, W. Ren, R. Jiang, Q. Li, X. Yao, S. Wang, Y. You and L. Mai, Highly crystallized Prussian blue with enhanced kinetics for highly efficient sodium storage, ACS Appl. Mater. Interfaces, 2021, 13, 3999–4007.
17. A. A. Karyakin, Prussian blue and its analogues: Electrochemistry and analytical applications, Electroanalysis, 2001, 13, 813–819.
18. P. K. Thallapally, R. K. Motkuri, C. A. Fernandez, B. P. McGrail and G. S. Behrooz, Prussian blue analogues for CO₂ and SO₂ capture and separation applications, Inorg. Chem., 2010, 49, 4909–4915.
19. C. R. Patra, Prussian blue nanoparticles and their analogues for application to cancer theranostics, Nanomedicine, 2016, 11, 569–572.
20. Z. Qin, Y. Li and N. Gu, Progress in applications of Prussian blue nanoparticles in biomedicine, Adv. Healthcare Mater., 2018, 7, 1–13.
21. S. Porada, R. Zhao, A. van der Waals, V. Presser and P. M. Biesheuvel, Review on the science and technology of water desalination by capacitive deionization, Prog. Mater. Sci., 2013, 58, 1388–1442.
22. J. Nordstrand and J. Dutta, Flexible modeling and control of capacitive-deionization processes through a linear-state-space dynamic-Langmuir model, npj Clean Water, 2021, 4, 1–7.
23. W. Tang, J. Liang, D. He, J. Gong, L. Tang, Z. Liu, D. Wang and G. Zeng, Various cell architectures of capacitive deionization: Recent advances and future trends, Water Res., 2019, 150, 225–251.
24. J. Nordstrand, K. Laxman, M. T. Z. Myint and J. Dutta, An easy-to-use tool for modeling the dynamics of capacitive deionization, J. Phys. Chem. A, 2019, 123, 6628–6634.
25. X. Zhao, H. Wei, H. Zhao, Y. Wang and N. Tang, Electrode materials for capacitive deionization: A review, J. Electroanal. Chem., 2020, 873, 114416.
26. E. Toledo-Carrillo, X. Zhang, K. Laxman and J. Dutta, Asymmetric electrode capacitive deionization for energy efficient desalination, Electrochim. Acta, 2020, 358, 136939.
27. S. Ahualli and G. R. Iglesias, Principles and theoretical models of CDI: Experimental approaches, Interface Sci. Technol., 2018, 24, 169–192.
28. J. Nordstrand and J. Dutta, Predicting and enhancing the ion selectivity in multi-ion capacitive deionization, Langmuir, 2020, 36, 8476–8484.
29. J. Choi, P. Dorji, H. K. Shon and S. Hong, Applications of capacitive deionization: Desalination, softening, selective removal, and energy efficiency, Desalination, 2019, 449, 118–130.
30. A. Kalfa, B. Shapira, A. Shopin, I. Cohen, E. Avraham and D. Aurbach, Capacitive deionization for wastewater treatment: Opportunities and challenges, Chemosphere, 2020, 241, 125003.
31. C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, A review of electrolyte materials and compositions for electrochemical supercapacitors, Chem. Soc. Rev., 2015, 44, 7484–7539.
32. J. Nordstrand and J. Dutta, Langmuir-based modeling produces steady two-dimensional simulations of capacitive deionization via relaxed adsorption-flow coupling, Langmuir, 2022, 38, 3350–3359.
33. A. Hemmatifar, M. Stadermann and J. G. Santiago, Two-dimensional porous electrode model for capacitive deionization, J. Phys. Chem. C, 2015, 119, 24681–24694.
34. J. Nordstrand, E. Toledo-Carrillo, S. Vafakhah, L. Guo, H. Y. Yang, L. Kloo and J. Dutta, Ladder mechanisms of ion transport in Prussian blue analogues, ACS Appl. Mater. Interfaces, 2022, 14, 1102–1113.
35. I. Lee, C. W. Park, S. S. Yoon and H. M. Yang, Facile synthesis of copper ferrocyanide-embedded magnetic hydrogel beads for the enhanced removal of cesium from water, Chemosphere, 2019, 224, 776–785.
36. H. Wi, H. Kim, D. Oh, S. Bae and Y. Hwang, Surface modification of poly(vinyl alcohol) sponge by acrylic acid to immobilize Prussian blue for selective adsorption of aqueous cesium, Chemosphere, 2019, 226, 173–182.
37. J. Wang, S. Zhuang and Y. Liu, Metal hexacyanoferrates-based adsorbents for cesium removal, Coord. Chem. Rev., 2018, 374, 430–438.
38. A. K. Vipin, B. Fugetsu, I. Sakata, A. Isogai, M. Endo, M. Li and M. S. Dresselhaus, Cellulose nanofiber backboned Prussian blue nanoparticles as powerful adsorbents for the selective elimination of radioactive cesium, Sci. Rep., 2016, 6, 1–14.
39. H. A. Alamudy and K. Cho, Selective adsorption of cesium from an aqueous solution by a montmorillonite-Prussian blue hybrid, Chem. Eng. J., 2018, 349, 595–602.
40. I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40, 1361–1403.
41. S. Azizian, S. Eris and L. D. Wilson, Re-evaluation of the century-old Langmuir isotherm for modeling adsorption phenomena in solution, Chem. Phys., 2018, 513, 99–104.
42. S. Spicher and S. Grimme, Robust atomistic modeling of materials, organometallic, and biochemical systems, Angew. Chem., Int. Ed., 2020, 59, 15665–15673.
43. L. M. Marinez, R. Andrade, E. G. Birgin and J. M. Martinez, Packmol: A package for building initial configurations for molecular dynamics simulations L, J. Comput. Chem., 2009, 30, 2157–2164.
44. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended tight-binding quantum chemistry methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, 1–49.
45. C. Bannwarth, S. Ehlert and S. Grimme, GFN_2−xTB – An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671.
46. Grimme group, xTB Documentation, https://xtb-docs.readthedocs.io/en/latest/setup.html, (accessed 22 April 2022).
47. F. O. Sanchez-Varretti, E. del, V. Gómez, L. B. Avalle, F. M. Bulnes, M. C. Gimenez and A. J. Ramirez-Pastor, Monte Carlo simulations and cluster-exact approximation applied to H/Cu(100),H/Ag(100) and O/Cu(100) systems, Appl. Surf. Sci., 2020, 500, 144034.
48. SNIC, Dardel, https://www.snic.se/resources/compute-resources/dardel/, (accessed 7 April 2022).
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016.
50. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, 2018.
51. H. M. Yang, J. R. Hwang, D. Y. Lee, K. B. Kim, C. W. Park, H. R. Kim and K. W. Lee, Eco-friendly one-pot synthesis of Prussian blue-embedded magnetic hydrogel beads for the removal of cesium from water, Sci. Rep., 2018, 8, 1–10.
52. J. Huo, G. Yu and J. Wang, Selective adsorption of cesium(i) from water by Prussian blue analogues anchored on 3D reduced graphene oxide aerogel, Sci. Total Environ., 2021, 761, 143286.
53. J. Nordstrand and J. Dutta, An extended randles circuit and a systematic model-development approach for capacitive deionization, J. Electrochem. Soc., 2021, 168, 013502.
54. J. Nordstrand, L. Zuili, E. Alejandro, T. Carrillo and J. Dutta, Predicting capacitive deionization processes using an electrolytic-capacitor (ELC) model, Desalination, 2022, 525, 115493.
55. J. Nordstrand and J. Dutta, Simplified prediction of ion removal in capacitive deionization of multi-ion solutions, Langmuir, 2020, 36, 1338–1344.
56. D. Brogioli and F. La Mantia, Interface Science and Technology, Elsevier Ltd., San Diego, 1st edn, 2018, vol. 24, pp.87–117.
57. J. Nordstrand and J. Dutta, A new automated model brings stability to finite-element simulations of capacitive deionization, Nano Sel., 2022, 3, 1021–1035.
58. H. Li, L. Pan, T. Lu, Y. Zhan, C. Nie and Z. Sun, A comparative study on electrosorptive behavior of carbon nanotubes and graphene for capacitive deionization, J. Electroanal. Chem., 2011, 653, 40–44.
59. M. W. Ryoo, J. H. Kim and G. Seo, Role of titania incorporated on activated carbon cloth for capacitive deionization of NaCl solution, J. Colloid Interface Sci., 2003, 264, 414–419.
60. C. J. Gabelich, T. D. Tran and I. H. “Mel” Suffet, Electrosorption of inorganic salts from aqueous solution using carbon aerogels, Environ. Sci. Technol., 2002, 36, 3010–3019.
61. G. Wang, B. Qian, Q. Dong, J. Yang, Z. Zhao and J. Qiu, Highly mesoporous activated carbon electrode for capacitive deionization, Sep. Purif. Technol., 2013, 103, 216–221.
62. H. Li, T. Lu, L. Pan, Y. Zhang and Z. Sun, Electrosorption behavior of graphene in NaCl solutions, J. Mater. Chem., 2009, 19, 6773–6779.
63. L. Wang, M. Wang, Z.-H. Huang, T. Cui, X. Gui, F. Kang, K. Wang and D. Wu, Capacitive deionization of NaCl solutions using carbon nanotube sponge electrodes, J. Mater. Chem., 2011, 21, 18295.
64. H. Li, L. Pan, Y. Zhang, L. Zou, C. Sun, Y. Zhan and Z. Sun, Kinetics and thermodynamics study for electrosorption of NaCl onto carbon nanotubes and carbon nanofibers electrodes, Chem. Phys. Lett., 2010, 485, 161–166.
65. J. Nordstrand and J. Dutta, Basis and prospects of combining electroadsorption modeling approaches for capacitive deionization, Physics, 2020, 2, 309–324.
66. K. Laxman, M. T. Z. Myint, R. Khan, T. Pervez and J. Dutta, Effect of a semiconductor dielectric coating on the salt adsorption capacity of a porous electrode in a capacitive deionization cell, Electrochim. Acta, 2015, 166, 329–337.
67. K. Laxman, D. Kimoto, A. Sahakyan and J. Dutta, Nanoparticulate dielectric overlayer for enhanced electric fields in a capacitive deionization device, ACS Appl. Mater. Interfaces, 2018, 10, 5941–5948.

---

Footnote

† Electronic supplementary information (ESI) available: Derivation of EL without Taylor approximation (S1); time-series data from the MD simulations (S2). Extended discussion on electrostatics and adsorption (S3). See DOI: https://doi.org/10.1039/d2cp04317c

---