Tailoring the optoelectronic properties and dielectric profiles of few-layer S-doped MoO₃ and O-doped MoS₂ nanosheets: a first-principles study

Abstract

To gain insights into few layer (FL) van der Waals MoO_3−xS_x/MoS_2−xO_x heterostructures for photocatalytic applications, we analyze how the concentration (x) and location of anionic isovalent atom (S or O) substitutions impact their opto-electronic properties and high frequency dielectric constant profiles. By using density functional theory (DFT) calculations within the HSE06 functional, we show that the electronic band gap of FL MoO_3−xS_x decreases with increasing x, while the dielectric constant profile and absorption coefficient in the UV-vis range increase. The stronger band gap reductions are obtained when S-atoms are located in the internal bulk region of FL MoO_3−xS_x and in interaction with O-atoms of the neighboring layer. Moreover, the conduction and valence band (CB/VB) levels are shifted to higher energy values in the case of the edge location (external surface) of these S-atoms. Thanks to the determination of the thermodynamic diagrams of 4L MoO_3−xS_x and 6L MoS_2−xO_x, we propose optimal heterojunctions made of 4L MoO_3−xS_x with either single-layer (SL) or FL MoS₂ with CB/VB levels compatible with a Z-scheme working principle and with potentials required for photocatalysis applications such as the photolysis of water into O₂ and H₂. This study combined with our previous theoretical investigations on bulk materials and SL provides a thorough analysis of SL–FL MoO_3−xS_x/MoS₂ heterojunctions where the concentration and location of S-atoms in MoO_3−xS_x are key to design efficient materials for water photolysis.

---

1. Introduction

Two-dimensional (2D) materials are the subject of numerous research studies. Among these materials not only graphene¹ but also many other 2D materials such as h-BN,² silicen,³ germanen,⁴ transition metal oxides (TMOs),^5,6 transition metal dichalcogenides (TMDs),⁷ MXenes,⁸ and phospherene⁹ are of keen interest for numerous applications in physics and chemistry. In particular, 2D TMDs and TMOs are actively investigated, and recently, their thin films and nanosheets have been realized experimentally.^6,7 2D TMOs exhibit various structures depending on their elemental compositions and configurations while 2D TMDs are typically made of a layer of transition metal atoms sandwiched between two rows of chalcogen atoms. The availability of various transition metals and their binding states in 2D TMDs and TMOs enables them to show a wide spectrum of properties such as metals to wide band gap semiconductors. The electronic, optical and catalytic properties of TMDs can be significantly tuned by oxidation. In particular, because TMOs are promising hole injection layers, a TMD−TMO heterostructure can potentially be applied as a p-type semiconductor¹⁰ for applications in p-type FETs^11–13 and gas sensors.¹⁴

Molybdenum disulfide (MoS₂) and trioxide (MoO₃), as frontrunners of TMD and TMO families, have opened up new horizons because of numerous attractive properties such as tunable band gaps, high surface-to-volume ratio and mechanical robustness.¹⁵ They are layered materials with strong intralayer iono-covalent bonding and weak van der Waals interlayer coupling, which provides an opportunity for tuning the number of stacked layers. α-MoO₃ with an orthorhombic layered crystal structure and a Pnma space group is thermodynamically the most stable phase of molybdenum trioxide which is an n-type semiconductor with a wide experimental band gap of ∼3.2 eV.^16,17 On the other hand, the 2H-phase of MoS₂ with a hexagonal crystal system and a P6₃/mmc space group exhibits an indirect band gap of about 1.23 eV, which may be valuable for photocatalytic applications.¹⁸ In particular, TiO₂ supported MoS₂ has been found to catalyze hydrogen production from water^19,20 or alcohol.²¹ However, a margin of improvement is expected for such MoS₂ based photocatalysts depending on the targeted reaction.

Compared to their bulk counterparts, 2D α-MoO₃ and 2H-MoS₂ with mono- and few-layer thicknesses could exhibit different physical and chemical properties (such as the band gap, charge transport, and catalytic activity), originating from the confinement in the ultrathin plane. Such single- or few-layer MoO₃ and MoS₂ materials can be obtained by using various experimental synthesis methods such as mechanical exfoliation, molecular beam epitaxy and chemical/physical vapor deposition.^22–25 MoS₂ becomes a direct band gap semiconductor with an electronic band gap of 1.8 eV when it is thinned down to a single-layer.²⁶ In the case of TiO₂ supported MoS₂, density functional theory (DFT) calculations have shown that the SL interacting with TiO₂ surfaces through van der Waals may lead to the formation of type II heterojunctions providing the potential Z-scheme.²⁷ In contrast, the value and indirect nature of the α-MoO₃ band gap keep almost unchanged from few layers (FLs) to a single-layer (SL).²⁸ Hence, 2D/2D heterojunctions involving MoS₂ and other materials have been explored^20,29 in the field of photocatalysis. However, numerous properties of such heterojunctions remain to be optimized to improve the photocatalytic performances of these supported MoS₂ materials depending on the targeted reaction water dissociation or CO₂ reduction. If one focuses on the optoelectronic properties, a systematic theoretical prediction of band gaps, levels of the conduction/valence bands (CB/VB) and the mobility and separation of charge carriers is expected.³⁰ This is particularly crucial for the design of relevant 2D/2D heterostructures with appealing optical properties providing an optimal charge transfer and separation between both 2D semiconductors such as obtained in the Z-scheme heterojunction.³¹ To address this challenge, it is mandatory to simulate the evolution of the properties of these 2D materials (MoS₂ and MoO₃) not only in their pristine state but also after O or S chemical doping of the heterostructure.

In our previous theoretical works, we showed that the optoelectronic properties of α-MoO₃ and 2H-MoS₂ bulk systems can be tuned with anionic isovalent-atom substitutions.³² By using DFT calculations within the HSE06 functional, we first revealed that S-doping of α-MoO₃ may significantly reduce the band gaps and increase the charge carrier mobility of the pristine material, while 2H-MoS₂ properties are less sensitive to O-doping. In addition, we identified the potential interest of creating a 2D heterojunction between S-doped α-MoO₃ layers and 2H-MoS₂ layers.³³ While the MoO₃/MoS₂ 2D heterostructure belongs to the type III heterojunction associated with a metallic character, substituting oxygen atoms by sulfur atoms in the MoO₃ SL enables us to switch from a type III heterojunction to a type II heterojunction.³³ Moreover, it was highlighted that the band gap and charge transfer within the heterostructure are intimately correlated with the S concentration at the interface of MoO₃/MoS₂. This previous finding may open new routes for the design of 2D MoO₃/2D MoS₂ SL heterojunctions with the potential Z-scheme behavior. However, the formation of such controlled 2D stacked SLs is challenging to synthesize experimentally, whereas FLs could be formed more easily. Therefore, it is legitimate to investigate how the opto-electronic properties of such MoO₃/MoS₂ FL heterostructures differ from SLs. Moreover, forming such FL structures increase the number of possible configurations depending on S-doping element positions inside the MoO₃ layered structure which may lead to different opto-electronic properties for a given dopant concentration. As a consequence, one key question for the photocatalysis application is to determine which configurations must be favored to generate the most appropriate optoelectronic properties and which configurations may be detrimental. Hence, the present report aims at addressing the structural and opto-electronic properties of S-doped MoO₃ FLs and O-doped MoS₂ FLs in order to assess the future potential of harnessing novel 2D nanomaterials as more efficient visible-light-driven photocatalysts. We will particularly pay attention to various properties: electronic band gaps, valence and CB/VB edge positions and optical absorption coefficients in the UV-vis range. Also, high frequency dielectric constants will be determined since they are important and challenging properties not so often addressed in the literature for these 2D materials. We will show how these properties of individual MoO₃ and MoS₂ components can be effectively modulated by S- and O-substitution and which optimal MoO_3−xS_x/MoS_2−xO_x heterostructures could be proposed in order to match some targeted parameters required for the water photolysis reaction. Before this, the next section will present the details of the methodology and computational setup used to compute the crystal structures and the electronic properties, the optical properties and the high frequency dielectric constant.

2. Methods

2.1. Geometry optimizations and electronic properties

The two reference supercells used for the non-doped 6L MoS₂ and 4L MoO₃ slabs are reported in Fig. 1. This choice of the number of layers of MoO₃ and MoS₂ slabs results from the best compromise for MoO₃ and MoS₂ according to the 3 following parameters. First, the slab should be thick enough to have different edges, pre-edges and bulk sites for impurity substitution. Then, the physical properties of the slabs such as the binding energy, electronic band gap and dielectric constant do not change with the increase in the number of layers. In this case, the properties of few-layered materials are close to their bulk phase (see Table S1, ESI†). Lastly, the hybrid functional makes the calculations rather CPU time consuming. Hence, we must select a minimum number of layers that fulfills the two previous conditions for both systems.

Fig. 1 The unit cells of (a) 4L α-MoO₃ and (b) 6L 2H-MoS₂. The purple, red and yellow balls in the geometrical models represent the Mo, O and S atoms, respectively.

The geometry optimizations of all pristine and substituted MoO₃ and MoS₂ layered structures were performed by using the ab initio CRYSTAL17 code³⁴ within periodic boundary conditions and localized Gaussian-type function basis sets (BSs). The convergence criterion for the geometry optimization was fixed at 10⁻¹⁰ Ha per unit cell. The following BSs were used: Mo_SC_HAYWSC-311(d31)G_cora_1997³⁵ (for Mo atoms), S_86-311G*_lichanot_1993³⁶ (for S atoms) and O_8-411d11G_valenzano_2006³⁷ (for O atoms). For the exchange-correlation potential, the PBE functional³⁸ has been adopted and the van der Waals contributions were described by using the semi-empirical Grimme D3 approach³⁹ with optimized scaling factors.³² The tolerances for the evaluation of Coulomb and exchange series were set to 8 × 8 × 8 × 8 × 16.³⁴ Since ordinary DFT within the PBE/GGA functional underestimates the electronic band gap, all the electronic properties were computed via single-point calculations by using the range separated hybrid Heyd–Scuseria–Ernzerhof (HSE06) exchange correlation functional^40,41 on the PBE optimized geometries using CRYSTAL17. The wave functions were converged with a SCF energy convergence criterion of 10⁻¹⁰ Ha per unit-cell and the reciprocal space for the unit-cell of pristine FL MoS₂ and FL MoO₃ systems is sampled according to a sublattice with a 12 × 12 k-point mesh. The k-point mesh sampling was progressively reduced as the size of the SL and FL unit cells increases for the doped materials (Tables S2 and S3, ESI†).

Due to the large number of structures and their large number of atoms, it was not possible to make systematic phonon analyses. However, to check for the relevance of the various FL MoO_3−xS_x and MoS_2−xO_x systems simulated, their relative thermodynamic stability was analyzed through three types of descriptors: (i) binding energy (Tables S1 and S2, ESI†), (ii) reaction energy and (iii) thermodynamic phase diagram. The equations for the reaction energy of S/O exchanges in FL MoO_3−xS_x and MoS_2−xO_x with H₂S/H₂O and for the grand potential approach used for the determination of thermodynamic phase diagrams of FL MoO_3−xS_x and MoS_2−xO_x as a function of T and are reported in the ESI,† 2.2. The approach follows the original one proposed in ref. 42 and applied earlier for the sulfo-reduction of MoS₂ slabs⁴³ and more recently for the MoO_3−xS_x and MoS_2−xO_x bulk materials.³²

2.2. Optical properties

The absorption coefficient is evaluated from the dielectric matrix ε_αβ(ω) using the Kramers–Kronig transformation.⁴⁴ The optical properties were evaluated within the HSE06 functional by using the Vienna ab initio simulation package (VASP)^45–47 with a kinetic energy cut-off of 500 eV for the plane wave basis set and the project augmented wave (PAW)⁴⁸ pseudopotentials for Mo, O and S atoms. The previously PBE optimized structures with CRYSTAL were used for the optical calculations with a 20 Å vacuum distance in order to avoid interactions with images of the systems along the thickness of the nanosheets. We set a denser k-point mesh size of 24 × 24 × 1 Γ-centered Monkhorst–Pack⁴⁹ to evaluate optical properties. For more details about the calculations of optical properties, see our previous studies.^32,33

2.3. High frequency dielectric constant profile ε_∞(z)

In order to extract the optical (high frequency) dielectric constant profile along the out-of-plane direction (z-axis) in 2D systems, we followed a DFT scheme based on polarization variations in response to a finite electric field.^50–52 This method was performed^51–55 to calculate the dielectric constant profile using the local orbital SIESTA⁵⁶ code within the simple LDA⁵⁷ or GGA³⁸ functionals so far. For the first time, in our previous work, we performed this method using the CRYSTAL results of the electronic density within the range separated the hybrid functional HSE06.⁴¹ As detailed in ref. 50 and 52, the calculation of the microscopic dielectric profile requires applying an external electric field, we analyzed the band gap evolution of each 2D layered MoO₃ and MoS₂ structures as a function of this external electric field applied perpendicularly to the layer planes (Fig. S1, ESI†). Then, we checked that the induced dipole in 2D MoO₃ and MoS₂ layered structures scales linearly with the number of layers for very small external electric field, E_ext = 0.025 eV Å⁻¹, as shown in Fig. S2 (ESI†). Hence, all dielectric constant profiles (ε_∞) are calculated for E_ext = 0.025 eV Å⁻¹. For more details about the calculations of the dielectric constant profile, the reader should refer to our previous work.³³

3. Results

3.1 Pristine structures of few-layer MoO₃ and MoS₂

3.1.1 Structural and electronic properties. To model the FL MoO₃ and MoS₂ structures, the primitive cell of 2D layers was directly cut from the optimized 3D bulk structures along the direction of the van der Waals interactions of [100] for MoO₃ and [001] for MoS₂ (Fig. 1). In our previous work,³³ we analyzed the optimized lattice parameters and band structures of the primitive cells of the SL and FL of MoO₃ and MoS₂ with the aim at focusing on the building of the SL heterojunction. As detailed in ref. 33, the indirect band gap of MoO₃ systems is relatively constant with respect to the number of layers, ranging from 2.83 to 2.96 eV. Moreover, the VB and CB edges of MoO₃ nanosheets remain almost unchanged from SL to 5 layers and do not satisfy the required band positions for overall water splitting. On the other hand, SL MoS₂ exhibits a direct band gap with the computed values of 2.38 eV. The optical band gap of SL MoS₂ has been obtained to be about 1.8 eV from the photoluminescence and optical absorption experiments^7,18 while its fundamental electronic band gap from STM/STS experiments is 2.40 eV both values differing by the exciton binding energy.⁵⁸ In contrast, all the FL MoS₂ structures exhibit an indirect band gap as in the bulk. As mentioned in ref. 33, the fundamental band gap of MoS₂ layers increases monotonically when the number of layers decreases, which is due to a large confinement of electrons in the slab.^26,59,60 More specifically, in MoS₂ nanosheets, the CB edge positions remain almost constant while the VB edge position shifts to higher energies by increasing the number of layers, in which these 2D layers possess suitable band edge positions that correctly bracket the water redox potentials for visible-light-driven overall water splitting reactions.

3.1.2 High frequency dielectric constant and absorption coefficient. In Fig. 2, the dielectric constant profiles (ε_∞) are calculated for 1L, 3L and 5L of MoO₃ and of MoS₂ along out-of-plane (in the interlayer direction). Due to the atomic displacements in the plane of layered materials (within the layer) in response to external fields, there is a negligible change in the in-plane dielectric constant from SL to the bulk, compared to the out-of-plane dielectric constant.⁶¹ These in-plane displacements are practically unaltered by the interaction between the FLs.^51,52 The electronic dielectric constant (ε_∞) values averaged along in-plane for α-MoO₃ and 2H-MoS₂ bulk systems are 5.6 and 14.5, respectively.³² The maximum values of the dielectric profiles are identical (4.1) for any number of MoO₃ layers whereas the reduction of the number of layers in MoS₂ leads to a decrease of the dielectric profile maximum values from 11.3 in 3L to 9.5 in 1L. The resulting effective dielectric constant, ε_eff, (Fig. 2) is also enhanced with the increasing number of MoO₃ layers from 2.85 in 1L to 4.3 in the bulk. Increasing the number of layers in the MoS₂ structure leads to a band gap reduction and consequently an increase of an effective dielectric constant from 4.96 in 1L to 6.3 in the bulk phase.

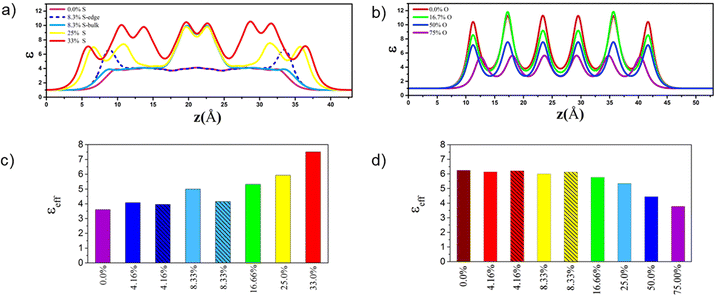
Fig. 2 Dielectric constant profiles (ε) along out-of-plane for 1L, 3L and 5L MoO₃ (a) and 1L, 3L and 5L MoS₂ (b). The effective dielectric constant along out-of-plane for 1L–5L and bulk MoO₃ (c) and 1L–6L and bulk MoS₂ (d). The effective dielectric constants for 3D bulk phases are also included according to our previous work.³²

In addition, the calculated optical absorption coefficients confirm the highly anisotropic optical properties of both pristine MoO₃ and MoS₂ systems considering in-plane and out-of-plane absorption coefficients (Fig. S3, ESI†). For both layered structures, the in-plane absorption coefficient is greater than that of the out-of-plane one. The absorption spectra increase in the UV-vis range, notably for the out-of-plane direction, by increasing the number of layers, whereas the electronic band gaps for layered MoO₃ systems remain in the same range.³³ These results also show that by increasing the number of layers the absorption coefficient of the MoS₂ nanosheets increases more significantly than that of MoO₃ and is enhanced in the UV-vis range, while the band gaps increase continuously with the number of layers.³³ Furthermore, high absorption coefficients were achieved for all MoO₃ and MoS₂ FLs, in particular along the in-plane direction, which is higher than the typical optical absorption for direct band gap semiconductors in the UV-vis range.^32,62

3.2 S-doped 4L MoO₃ and O doped 6L MoS₂

3.2.1 Structures and thermodynamic stability. There are three distinct types of oxygen atoms in the orthorhombic lattice of the MoO₃ system: terminal (O_t), asymmetrical (O_a), and symmetrical (O_s) oxygen atoms,³² while all S atoms in the hexagonal MoS₂ system are equivalent (Fig. 1). Previous studies dedicated to the bulk MoO₃ material showed that O_t can be easily (from a thermodynamic point of view) substituted by S atoms.^32,33,63 Hence, we also consider the O_t position for the oxygen-substituted 4L MoO₃ system. In order to compare the electronic properties of the two slabs for the same dopant concentrations (4.16%, 8.33%, 16.66%, 25% and 33%), we chose different supercell sizes of (1 × 1) for S-doped MoO₃ and (2 × 2) for O doped MoS₂. Considering the finite size character of both FL MoO₃ and MoS₂ systems, two different substitutional configurations must be considered: either at the topmost layers (edge and pre-edge, see Fig. 1) or at the inner layers (bulk, see Fig. 1). The calculated lattice parameters and binding energies of S-substituted 4L MoO₃ and O-substituted 6L MoS₂ systems for different concentrations are reported in Tables S1 and S2 (ESI†), respectively.

Fig. 3 and Fig. S7a (ESI†) illustrate the thermodynamic phase diagrams of substituted 4L MoO_3−xS_x and 6L MoS_2−xO_x systems with respect to the pristine structures considering the H₂S/H₂O reservoir by using the Grand potential approach. It is conspicuous that the sulfidation of pristine 4L MoO₃ nanosheets requires a value of as high as −0.36 eV. For in the range between −0.36 eV and −0.19 eV, the structure with 4.16% S is thermodynamically favored and for it is higher than −0.19 eV, the 4L MoS_xO_3−x system with 33% S is the most stable. These results are different from those obtained on bulk materials, where the value required for sulfide MoO₃ was significantly greater (∼0.1 eV). As shown in Fig. 3, this trend is mainly induced by the easier sulfidation of O_t located at edges, exhibiting lower Grand potential values than the ones corresponding to bulk substitution. Generally, the O/S exchange process is exergonic when O_t located at edges are involved, whereas it was endergonic for the bulk materials.³² This shows that FL MoO₃ materials are much easier to sulfide than bulk materials. The most stable compositions correspond to 4.16% S and 33% S although one cannot exclude the 8.33%S and 16.66% S ones according to the methodology accuracy. All these systems will be considered for the opto-electronic analyses. From an experimental point of view, it has been shown that it is possible to reach high S-doping concentrations which would require to substitute not only top-oxo but also bridging-oxo species leading to more complex reconstructed Mo oxy-sulfides.^64,65 Hence, it seems relevant to propose the S-dopant concentration as high as 33%. This doping process is all the easier as the material will expose many edges and near edge sites exchangeable with S.

Fig. 3 Thermodynamic phase stability of the S-substituted 4L MoO₃ considering the H₂S/H₂O reservoir. The dashed and dotted lines denote the results for impurity-substituted only in the edge and the bulk of layered systems, respectively.

Regarding the 6L MoS₂ material, the free energies for oxidation (Fig. S6a, ESI†) are all endergonic. Hence, oxidation starts for higher than ∼0.75 eV, and the oxidized structure with the highest O concentration (75%) should be the least unfavored. The value obtained for the bulk MoS₂ material was at ∼0.75 eV.³² Fig. S6a (ESI†) shows that edge doped systems are nearly superimposed to the bulk doped ones meaning that almost no energy gain is obtained. Hence, the impact of edge oxidation is negligible for this system: the intrinsic unfavorable S/O exchange is due to the poor lability of tri-coordinated S-atoms present in MoS₂. Although the chemical systems are different, this trend seems to be qualitatively comparable with previous experimental results having shown that only a very low concentration of SnS₂ can be oxidized into SnO₂.⁶⁶

As a consequence, this analysis reveals that the sulfidation of 4L MoO₃ is thermodynamically more favorable than the oxidation of 6L MoS₂ when we consider H₂S/H₂O as reactants or products. Moreover, the sulfidation of 4L MoO₃ is enhanced at edges which may also impact the electronic properties investigated in the following section.

3.2.2 Electronic structures and absorption coefficients. The band structures and the projected density of states (PDOS) of all S- and O-concentrations in 4L MoO₃ and 6L MoS₂ are reported in Fig. S7 and S8 (ESI†), respectively. The corresponding band gap values for all doped systems are reported in Fig. 4, Tables S1 and S2 (ESI†). Substituting oxygen atoms with sulfur atoms in 4L MoO₃ significantly decreases the band gap while the indirect character of the band gap remains unchanged. The band gap reduction for sulfur substituted of 4L MoO₃ depends obviously on the position of the S-atoms. From a general trend, the reduction is more significant for S-substitution in the bulk than at the edge (Fig. 4 and Table S1, ESI†).

Fig. 4 (a and b) Computed electronic band gap values (in eV) and (c and d) absorption coefficients (α, in cm⁻¹) along in-plane and out-of-plane of the most stable S-substituted 4L MoO₃ (a and c) and O-substituted 6L MoS₂ (b and d) for different S- and O-concentrations. The hatching patterns in the bar graphs and dashed lines in the absorption spectra are related to those structures in which impurities substituted at the edge.

Moreover, as it is illustrated by the various configurations simulated for MoS_0.25O_2.75 (x_s = 8.33%) and MoS_0.5O_2.5 (x_s = 16.7%), the interaction between the S atoms and O atoms at the nearest layers leads to a decrease in the electronic band gap (Fig. S7, ESI†). A relevant example for which the band gap evolves in three different configurations is illustrated in Fig. 5 for MoS_0.5O_2.5 (x_s = 16.7%). The band gap is maximized (1.85 eV) when S-atoms are not located in close vicinity of the O-atoms of the nearest layer (configuration of Fig. 5c), whereas it is significantly reduced when 2 S atoms are facing 2 O atoms located either at the pre-edge (configuration of Fig. 5a) or at the inner layer (Fig. 5b). The corresponding PDOS reported in Fig. 5 highlights how the occupied 3p-states of S atoms (either in the bulk or at the pre-edge) located at the top of the VB are pushing down the unoccupied 2p-states of O atoms (either at the pre-edge or in the bulk, respectively) at the bottom of the CB upon interaction. This induces a downward shift of the CB band (as illustrated later) and a closure of the band gap in the extreme case as shown in Fig. 5a. The configuration of Fig. 5a where the two central layers are sulfided and sandwiched between two MoO₃ layers is qualitatively comparable to previous calculations on the SL MoO₃/MoS₂ heterojunction which has a metallic character because of the proximity of S and O at the interface of two layers,³³ while for S-doped MoO₃ at the interface of MoO₃/MoS₂ with concentrations equal to or greater than 5.6%, a metal–semiconductor transition occurs.³³ Lastly, it is interesting to notice that all S-doped 4L MoO₃ systems exhibit a significant decrease of the band gap (by at least 0.74 eV) with respect to their homologous doped SL MoO₃ system, while the band gap of the non-doped MoO₃ system does not depend on the number of layers.³³

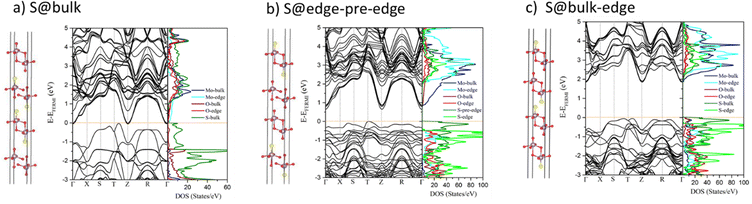Fig. 5 Optimized structures, electronic band structures and PDOS of 4L MoS_0.5O_2.5 (x_s = 16.66%) for 3 different S substitution positions calculated by using HSE06: (a) inside the bulk only, (b) at edge and pre-edge, (c) at edge and in the bulk. The Fermi level is set to zero. The corresponding structures, band structures and PDOS for these systems are also reported in Fig. S3 and S5 (ESI†) configurations h, i, and j, respectively.

In contrast, the indirect band gap feature in 6L MoS₂ also remains unchanged within substituting sulfur atoms by oxygen atoms. The band gap value of 6L MoO_xS_2−x is first decreased by minimum O doping and then begins to enhance by increasing the O concentration of up to 75% (Fig. 4 and Table S2, ESI†). However, from a general point of view, either bulk or edge sites used for the substitution of O atoms in 6L MoS_2−xO_x produce very similar electronic properties as illustrated by PDOS analysis (Fig. S8, ESI†). This trend is similar to the analysis already made on bulk MoS_2−xO_x.³² Due to the Mott insulator character of MoS₂, the nature of the CB/VB bands are dominated by Mo 4d states induced by a_1g–e_g splitting in the trigonal prismatic Mo environment. The 2p states of the O dopants are thus located at energy levels which do not impact strongly the evolution of the band gaps and the CB/VB of the pristine 6L MoS₂ system.

The optical property analysis (Fig. 4) of these FL materials confirms that by increasing the S concentration on 4L MoO₃ the in-plane and out-of-plane absorption coefficients are enhanced in the UV-vis range while it is reduced monotonically in 6L MoS₂ by increasing the O concentration. Moreover, the S-doped 4L MoO₃ materials clearly reveal a stronger absorption in the visible range than the previously studied S-doped SL MoO₃ materials.³³ The different impurity sites (bulk and edge) for the low concentration level produce nearly the same absorption coefficient along the in-plane direction in both materials while edge substitutions lead to enhanced adsorption spectra along the out-of-plane direction. All doped FL structures have an indirect band gap feature, and their absorption coefficient is thus notably low for the photon energy close to the bandgap. However, for wavelengths below 500 nm, direct transitions are possible allowing to reach high absorption coefficients (∼10⁵ cm⁻¹) and comparable to those of organic perovskite solar cells.^67,68 These results indicate that these systems possess significant light-harvesting capabilities for the solar spectrum in the UV-visible range of light.^32,62

3.2.3 Absolute valence and conduction band positions. Fig. 6 shows the valence and conduction band-edge positions of S-substituted 4L MoO₃ and O-substituted 6L MoS₂ for different concentrations and configurations. Fig. 6a reveals a direct effect of the location of S-atoms on the CB/VB positions either at edges or in the bulk of S-substituted 4L MoO₃. As a consequence of the previous PDOS analysis, the CB/VB edge positions depend on the relative positions of S and O atoms in the structure. For 33%S where S-atoms are all located at the edge and in the bulk, the CB/VB positions do not strongly differ from those of 16.66%S where S-atoms are located at edges only. However, for 25%S where a fraction of bulk O-atoms is not replaced by S, the CB/VB positions and band gap strongly differ from the two previous cases. As underlined in PDOS analysis, the proximity of S-atoms and O-atoms in the nearest layers implies a band gap reduction, and it also strongly impacts the absolute CB/VB positions. In the case of close vicinity between the S-dopant and O-atoms of two neighboring layers (such as 8.33%S in the bulk and 25%S), there is a strong downward shift of the O states located in the CB pushing the CB energy downwards with respect to structures where S atoms are located on the edge or S atoms (8.33%S at the edge) are facing other S-atoms (16.66%S bulk–edge, Fig. 5c, 33%S). Regarding the VB, we observe a different magnitude in its upper shift which is predominantly driven by the presence of S atoms located at the edge. Indeed, the comparison of the structures with 8.33%S where S is either at the edge or in the bulk (with S in close vicinity of another S atom), the electronic states of the sulfido species located at the edge push up the Fermi level (and thus the VB). For the other structures with higher S-concentrations, a weaker fluctuation of the VB level exists which might be induced by the presence of vicinal S and O atoms. However, this effect is less pronounced.

Fig. 6 Calculated conduction and valence band-edge positions of (a) S-substituted 4L MoO₃ (only for the most stable cases) and (b) O-substituted 6L MoS₂ with respect to the vacuum level and the standard hydrogen electrode. The band edge position for SL MoS₂ is also presented in (a). The lower edge of the conduction band (orange color) and the upper edge of the valence band (blue color) are presented along with the band gap in electron volts. The dashed green lines indicate the water stability limits for the hydrogen and oxygen evolution reactions. The absolute potential of the standard hydrogen electrode was taken as 4.44 eV at a pH = 0.

Hence, to generate a good material for water oxidation and O₂ evolution, either the edges must be covered by S-atoms or all top oxo-species (at edges and in the bulk) must be replaced by S. In contrast, isolated top-oxo species remaining inside the partially S-doped MoO₃ bulk are detrimental. The CB levels of the S-doped MoO₃ 4L systems with 8.33%S (edge), 16.66% (edge + bulk) and 33% (edge + bulk) are predicted to be at the same level as the water photo-oxidation potential for O₂ evolution only, which is not enough to overcome the expected overpotential. Hence, to tackle the challenge of water photolysis, the S-doped MoO₃ FL systems cannot be used alone but it must be involved within a heterostructure involving either SL or ML MoS₂ as analyzed in the following.

As a result of the previous PDOS analysis, the location of O substituted in 6L MoS₂ does not produce any significant change in the VB edge positions (Fig. 6b). The CB edge positions for these O-doped systems slightly shift to lower energies (even lower to the required level for H₂ evolution). Hence they possess suitable band edge positions only for water oxidation and O₂ evolution.

In our recent paper,³³ we proposed strategies to tune the transitions from type III to type II band alignment of materials made of the 2D SL MoO_3−xS_x/SL MoS₂ heterostructure. Here, since the CB edge positions of FL MoO_3−xS_x (with S at edges) shift to higher energy levels, we can extend our previous proposals by considering heterostructures made of 4L MoS_xO_3−x/SL MoS₂ and 4L MoS_xO_3−x/FL MoS₂ to optimize at best the composite material as a function of stacking. One should underline that one strong advantage of the 4L MoS_xO_3−x material with respect to the previously studied SL MoS_xO_3−x is its stronger absorption coefficient in the visible range as previously shown in Fig. 4.

By analyzing first the VB and CB edge levels of 4L MoS_xO_3−x and SL MoS₂ layers (Fig. 6a), we identify potential 2D heterojunctions made of 4L MoS_xO_3−x and SL MoS₂ layers that would lead to the type II band alignment with targeted concentrations and locations of S into MoO₃ layers: 8.33% (at the edge of layers), 16.66% and 33%. For 16.66%S, the control of the precise positions of S atoms located inside the bulk should make this system difficult to handle experimentally. These proposed type II heterostructures could thus be good candidates for photocatalytic applications since they may potentially generate a direct Z-scheme due to the proximity of the CB of 4L MoS_xO_3−x to the VB of SL MoS₂, although the band gaps of the heterostructures with 8.33%, 16.66% and 33% are larger (∼0.83 eV) than those in the case of the SL MoS_xO_3−x/MoS₂ heterojunction (0.4 eV).³³ For all other S concentrations, these interfaces are type III heterojunction resulting from the lower CB positions of 4L MoS_xO_3−x layers rather than the VB position of SL MoS₂.

Finally, the CB positions in 4L MoS_xO_3−x doped with 8.33%S (at the edge) and 16.66%S are ∼0.6 and ∼0.7 eV, respectively, higher than those of the SL MoS_xO_3−x doped with a similar S concentration.³³ For 4L MoS_xO_3−x doped with 33%S, the CB position is quite high too, similar to the SL case. This implies that it is potentially more efficient to combine these 3 structures with the non-doped MoS₂ SL materials to build a type II heterojunction or a Z-scheme system. Indeed, the CB positions of these 4L MoS_xO_3−x are slightly above the VB of the non-doped MoS₂ SL materials leading to a small band gap heterostructure which may be in favor of a charge transfer from MoS₂ to MoS_xO_3−x before illumination as analyzed in ref. 33 for the SL heterostructure. In addition, the 4L MoS_xO_3−x structures doped with 8.33%S (at the edge), 16.66%S and 33%S are compatible with the non-doped MoS₂ FL structure.

As a general consequence, to optimize the band gap and charge transfer, the best heterojunctions should be either the SL MoS_xO_3−x/SL MoS₂ heterostructure with 8.3%S doping in MoS_xO_3−x as previously invoked³³ or alternatively FL MoS_xO_3−x with edge S-doping of 8.3, 16.7 or 33% and SL or FL MoS₂ as proposed in the present work. Since the 4L MoS_xO_3−x doped with 33%S is thermodynamically stable (Fig. 3), this structure may be a good candidate for building a heterojunction with a FL MoS₂ material (such as the 6L one studied here). These optimal heterostructures lead to type II heterojunctions as proposed for other systems.^69,70 In this case, the CB position of FL MoS_xO_3−x is located just above the VB of FL MoS₂ which may also provide an optimal situation for a Z-scheme behavior where the electrons photogenerated at the CB of FL MoS_xO_3−x recombine with the hole generated on the VB of FL or SL MoS₂. At the same time, the electrons generated at the CB of FL or SL MoS₂ will reduce the proton into H₂, while the hole of the VB of FL MoS_xO_3−x will oxidize the water into O₂.

3.2.4 High frequency dielectric profile ε_∞(z). In order to analyze the ability of the material to screen the photo-generated charges, we plotted the high frequency dielectric profiles ε_∞(z) of S-substituted 4L MoO₃ and O-substituted 6L MoS₂ for different S- and O-concentrations along the out-of-plane direction. The electronic dielectric constant profiles ε_∞ of S doped 4L MoO₃ and O doped 6L MoS₂ are depicted in Fig. 7, respectively. These results indicate that S doping into 4L MoO₃ enhances the peak height of the dielectric profile increasing from 4.1 in 4L MoO₃ to 10.5 for 4L MoSO₂ (for x_s = 33%). This enhancement is more significant for S-substituted at the center of 4L MoO₃ than for S doped at the edge due to the further reduction of the electronic band gap. In contrast, O doping into 6L MoS₂ reduces the peak height of the dielectric profile which reach from 11.3 for pristine 6L MoS₂ to 5.1 for 6L MoO_1.5S_0.5 (for x_O = 75%). We also calculated the effective dielectric constant (ε_eff) of S-doped 4L MoO₃ and O-doped 6L MoS₂ nanosheets as depicted in Fig. 7. The ε_eff of 4L MoS_xO_3−x systems enhances monotonically by increasing the S concentration from 3.6 for the pristine structure to 7.5 for 4L MoSO₂ while for 6L MoO_xS_2−x systems it reduces by increasing the O concentration from 6.3 for pristine 6L MoS₂ to 4.1 for 6L MoO_1.5S_0.5. As it is eminent by increasing the sulfur concentration in these FL systems the frequency dielectric constant is enhanced because of two intricate effects: sulfur is more polarizable than O and the Mo–S bond is more covalent than the Mo–O bond, as discussed in our previous work.³²

Fig. 7 Dielectric constant profiles (ε) along out-of-plane of S-substituted 4L MoO₃ (a) and O-substituted 6L MoS₂ (b) for different S- and O-concentrations. The effective dielectric constants along out-of-plane of S-substituted 4L MoO₃ (c) and O-substituted 6L MoS₂ (d) for different S- and O-concentrations. The hatching patterns in the bar graphs and dashed lines in the dielectric profile are related to those structures in which impurities substituted at the edge only.

4. Conclusion

We used DFT calculations within the HSE06 functional to characterize the opto-electronic properties and high frequency dielectric constant profiles of sulfur doped MoO₃ and oxygen doped MoS₂ FL structures. The thermodynamic phase diagram for various concentrations of S doped 4L MoO₃ structures in the H₂S/H₂O environment revealed that the structures with 4.16%S at the edge, 8.33%S at the edge, and 16.66 and 33%S concentrations can be stabilized with a reasonable ratio. Moreover, we showed that the MoO_3−xS_x structures with S-impurities at the edge of nanolayers are more stable than those having impurities in the bulk. This specific edge location is beneficial for the opto-electronic properties (band gaps and CB/VP levels) and the absorption spectrum. The sulfur doping of 4L MoO₃ induces a decrease of the electronic band gap (from 2.92 eV to 1.44 eV). The stronger band gap reductions are obtained when S-atoms are located inside the bulk and interact with O-atoms located in neighboring layers, while the CB and VB positions are shifted to lower potential values in the case of the edge location of S-atoms. This doping induces an increase of the dielectric constant profile and absorption coefficient in the UV-vis range, which is significantly enhanced in the visible range when compared with the previous S-doped SL MoO₃ material.³³

In contrast, it is less favorable to substitute S atoms by O atoms in 6L MoS₂ under the same conditions. Moreover, substituting sulfur atoms by oxygen atoms on 6L MoS₂ for the 4.16% O concentration abruptly decreases the electronic band gap from 1.73 eV in the pristine material to around 1.2 eV. Then the electronic band gap of 6L MoS_2−xO_x begins to enhance with the increasing O concentration which induces a decrease of the dielectric constant profile and absorption coefficient in the UV-vis range. Hence, O-doping of MoS₂ either as the SL, FL or bulk does not provide significant improvements of the properties of the MoS₂ material.

As a consequence, to reach the targeted properties for water photocatalytic dissociation into O₂ and H₂, we proposed relevant heterostructures leading to type II heterojunctions which may contain either FL or SL components. In particular, we identified the stable 4L MoS_xO_3−x doped with 8.33%S at the edge and 16.66%S (edge + bulk) and 33%S in combination with the FL or SL MoS₂ as potential good candidates for the Z-scheme formalism. Moreover since the 4L MoS_xO_3−x doped with 33% S provides the largest effective dielectric constant, we suggest that this system should be particularly appealing for screening the photogenerated charges. Hence, the present work provides additional relevant heterostructures supplementing our previous work devoted mainly to SL MoS_xO_3−x/SL MoS₂ systems.³³ This finding is of practical interest for experimental implementation because it allows more flexibility for the number of layers to be targeted at the synthesis steps without being limited to the SL MoS_xO_3−x/MoS₂ heterojunction. It also highlights the great versatility of heterostructures made of a variable number of layers of MoS_xO_3−x and MoS₂ usable in photocatalytic applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is part of the “RatiOnAl Design for CATalysis” (ROAD4CAT) industrial chair, project IDEXLYON funded by the French National Research Agency (ANR-16-IDEX-0005) and the Commissariat-General for Investment (CGI) within the framework of Investissements d’Avenir program (“Investment for the future”). The authors thank the SYSPROD project and AXELERA Pôle de Compétitivité for financial support (PSMN Data Center). This work was granted access to the HPC resources of CINES, IDRIS and TGCC under the allocation 2018-080609 made by GENCI.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306, 666.
2. Y. Kubota, K. Watanabe, O. Tsuda and T. Taniguchi, Deep Ultraviolet Light-Emitting Hexagonal Boron Nitride Synthesized at Atmospheric Pressure, Science, 2007, 317, 932.
3. P. Vogt, P. de Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Silicene: compelling experimental evidence for graphene like two-dimensional silicon, Phys. Rev. Lett., 2012, 108, 155501.
4. S. Balendhran, S. Walia, H. Nili, S. Sriram and M. Bhaskaran, Elemental Analogues of Graphene: Silicene, Germanene, Stanene, and Phosphorene, Small, 2015, 11, 640–652.
5. J. Miao, C. Chen, L. Meng and Y. S. Lin, Self-Assembled Monolayer of Metal Oxide Nanosheet and Structure and Gas-Sensing Property Relationship, ACS Sens., 2019, 4, 1279–1290.
6. T. Yang, T. T. Song, M. Callsen, J. Zhou, J. W. Chai, Y. P. Feng, S. J. Wang and M. Yang, Atomically Thin 2D Transition Metal Oxides: Structural Reconstruction, Interaction with Substrates, and Potential Applications, Adv. Mater. Interfaces, 2019, 6, 1801160.
7. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Atomically Thin MoS₂: A New Direct-Gap Semiconductor, Phys. Rev. Lett., 2010, 105, 136805.
8. M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, 25^th Anniversary Article: MXenes: A New Family of Two-Dimensional Materials, Adv. Mater., 2014, 26, 992–1005.
9. H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility, ACS Nano, 2014, 8, 4033–4041.
10. M. M. Furchi, A. Pospischil, F. Libisch, J. Burgdörfer and T. Mueller, Photovoltaic Effect in an Electrically Tunable van der Waals Heterojunction, Nano Lett., 2014, 14, 4785–4791.
11. K. Xu, Y. Wang, Y. Zhao and Y. Chai, Modulation doping of transition metal dichalcogenide/oxide heterostructures, J. Mater. Chem. C, 2017, 5, 376–381.
12. S. KC, R. C. Longo, R. Addou, R. M. Wallace and K. Cho, Electronic properties of MoS₂/MoO_x interfaces: Implications in Tunnel Field Effect Transistors and Hole Contacts, Sci. Rep., 2016, 6, 33562.
13. Z. Gao, Z. Zhou and D. Tománek, Degenerately Doped Transition Metal Dichalcogenides as Ohmic Homojunction Contacts to Transition Metal Dichalcogenide Semiconductors, ACS Nano, 2019, 13, 5103–5111.
14. B. Wang, H. Luo, X. Wang, E. Wang, Y. Sun, Y.-C. Tsai, J. Dong, P. Liu, H. Li, Y. Xu, S. Tongay, K. Jiang, S. Fan and K. Liu, Direct laser patterning of two-dimensional lateral transition metal disulfide-oxide-disulfide heterostructures for ultrasensitive sensors, Nano Res., 2020, 13, 2035–2043.
15. J. Azadmanjiri, P. Kumar, V. K. Srivastava and Z. Sofer, Surface Functionalization of 2D Transition Metal Oxides and Dichalcogenides via Covalent and Non-covalent Bonding for Sustainable Energy and Biomedical Applications, ACS Appl. Nano Mater., 2020, 3, 3116–3143.
16. P. Carcia and E. McCarron, Synthesis and properties of thin film polymorphs of molybdenum trioxide, Thin Solid Films, 1987, 155, 53–63.
17. M. Kröger, S. Hamwi, J. Meyer, T. Riedl, W. Kowalsky and A. Kahn, Role of the deep-lying electronic states of MoO₃ in the enhancement of hole-injection in organic thin films, Appl. Phys. Lett., 2009, 95, 123301.
18. K. K. Kam and B. A. Parkinson, Detailed photocurrent spectroscopy of the semiconducting group VIB transition metal dichalcogenides, J. Phys. Chem., 1982, 86, 463–467.
19. Y.-J. Yuan, Z.-J. Ye, H.-W. Lu, B. Hu, Y.-H. Li, D.-Q. Chen, J.-S. Zhong, Z.-T. Yu and Z.-G. Zou, Constructing Anatase TiO₂ Nanosheets with Exposed (001) Facets/Layered MoS₂ Two-Dimensional Nanojunctions for Enhanced Solar Hydrogen Generation, ACS Catal., 2016, 6, 532–541.
20. Y. Li, Y.-L. Li, B. Sa and R. Ahuja, Review of two-dimensional materials for photocatalytic water splitting from a theoretical perspective, Catal. Sci. Technol., 2017, 7, 545–559.
21. C. Maheu, E. Puzenat, C. Geantet, L. Cardenas and P. Afanasiev, Titania - Supported transition metals sulfides as photocatalysts for hydrogen production from propan-2-ol and methanol, Int. J. Hydrogen Energy, 2019, 44, 18038–18049.
22. B. Zheng, Z. Wang, Y. Chen, W. Zhang and X. Li, Centimeter-sized 2D α-MoO₃ single crystal: growth, Raman anisotropy, and optoelectronic properties, 2D Mater., 2018, 5, 45011.
23. F. Rahman, T. Ahmed, S. Walia, E. Mayes, S. Sriram, M. Bhaskaran and S. Balendhran, Two-dimensional MoO₃ via a top-down chemical thinning route, 2D Mater., 2017, 4, 35008.
24. J. Sun, X. Li, W. Guo, M. Zhao, X. Fan, Y. Dong, C. Xu, J. Deng and Y. Fu, Synthesis Methods of Two-Dimensional MoS₂: A Brief Review, Crystals, 2017, 7, 198.
25. Y.-H. Lee, X.-Q. Zhang, W. Zhang, M.-T. Chang, C.-T. Lin, K.-D. Chang, Y.-C. Yu, J. T.-W. Wang, C.-S. Chang, L.-J. Li and T.-W. Lin, Synthesis of Large-Area MoS₂ Atomic Layers with Chemical Vapor Deposition, Adv. Mater., 2012, 24, 2320–2325.
26. S. L. Howell, D. Jariwala, C.-C. Wu, K.-S. Chen, V. K. Sangwan, J. Kang, T. J. Marks, M. C. Hersam and L. J. Lauhon, Investigation of Band-Offsets at Monolayer–Multilayer MoS₂ Junctions by Scanning Photocurrent Microscopy, Nano Lett., 2015, 15, 2278–2284.
27. R. Favre, P. Raybaud and T. Le Bahers, Electronic structures of the MoS₂/TiO₂ (anatase) heterojunction: influence of physical and chemical modifications at the 2D- or 1D-interfaces, Phys. Chem. Chem. Phys., 2022, 24, 2646–2655.
28. F. Li and Z. Chen, Tuning electronic and magnetic properties of MoO₃ sheets by cutting, hydrogenation, and external strain: a computational investigation, Nanoscale, 2013, 5, 5321–5333.
29. T. Su, Q. Shao, Z. Qin, Z. Guo and Z. Wu, Role of Interfaces in Two-Dimensional Photocatalyst for Water Splitting, ACS Catal., 2018, 8, 2253–2276.
30. T. Le Bahers, M. Rérat and P. Sautet, Semiconductors Used in Photovoltaic and Photocatalytic Devices: Assessing Fundamental Properties from DFT, J. Phys. Chem. C, 2014, 118, 5997–6008.
31. X. Li, C. Garlisi, Q. Guan, S. Anwer, K. Al-Ali, G. Palmisano and L. Zheng, A review of material aspects in developing direct Z-scheme photocatalysts, Mater. Today, 2021, 47, 75–107.
32. M. Shahrokhi, P. Raybaud and T. Le Bahers, On the understanding of the optoelectronic properties of S-doped MoO₃ and O-doped MoS₂ bulk systems: a DFT perspective, J. Mater. Chem. C, 2020, 8, 9064–9074.
33. M. Shahrokhi, P. Raybaud and T. Le Bahers, 2D MoO_3−xS_x/MoS₂ van der Waals Assembly: A Tunable Heterojunction with Attractive Properties for Photocatalysis, ACS Appl. Mater. Interfaces, 2021, 13, 36465–36474.
34. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
35. F. Corà, A. Patel, N. M. Harrison, C. Roetti and C. R. A. Catlow, Anab initio Hartree–Fock study of α- MoO₃, J. Mater. Chem., 1997, 7, 959–967.
36. A. Lichanot, E. Aprà and R. Dovesi, Quantum Mechnical Hartree-Fock Study of the Elastic Properties of Li₂S and Na₂S, Phys. Status Solidi B, 1993, 177, 157–163.
37. L. Valenzano, F. J. Torres, K. Doll, F. Pascale, C. M. Zicovich-Wilson and R. Dovesi, Ab Initio Study of the Vibrational Spectrum and Related Properties of Crystalline Compounds; the Case of CaCO₃ Calcite, Z. Phys. Chem., 2006, 220, 893–912.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
40. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215.
41. J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)], J. Chem. Phys., 2006, 124, 219906.
42. M. Scheffler and J. Dabrowski, Parameter-free calculations of total energies, interatomic forces and vibrational entropies of defects in semiconductors, Philos. Mag. A, 1988, 58, 107–121.
43. P. Raybaud, J. Hafner, G. Kresse, S. Kasztelan and H. Toulhoat, Ab Initio Study of the H₂–H₂S/MoS₂ Gas–Solid Interface: The Nature of the Catalytically Active Sites, J. Catal., 2000, 189, 129–146.
44. F. Wooten, Optical Properties of Solids, Elsevier Science, Burlington, 2013.
45. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
46. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
47. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
48. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
49. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
50. F. Giustino, P. Umari and A. Pasquarello, Dielectric Discontinuity at Interfaces in the Atomic-Scale Limit: Permittivity of Ultrathin Oxide Films on Silicon, Phys. Rev. Lett., 2003, 91, 267601.
51. D. Sapori, M. Kepenekian, L. Pedesseau, C. Katan and J. Even, Quantum confinement and dielectric profiles of colloidal nanoplatelets of halide inorganic and hybrid organic–inorganic perovskites, Nanoscale, 2016, 8, 6369–6378.
52. J. Even, L. Pedesseau and M. Kepenekian, Electronic surface states and dielectric self-energy profiles in colloidal nanoscale platelets of CdSe, Phys. Chem. Chem. Phys., 2014, 16, 25182–25190.
53. R. Ramprasad and N. Shi, Dielectric properties of nanoscale HfO₂ slabs, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 52107.
54. N. Shi and R. Ramprasad, Dielectric properties of ultrathin SiO₂ slabs, Appl. Phys. Lett., 2005, 87, 262102.
55. N. Shi and R. Ramprasad, Atomic-scale dielectric permittivity profiles in slabs and multilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 45318.
56. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The SIESTA method forab initioorder-Nmaterials simulation, J. Condens. Matter Phys., 2002, 14, 2745–2779.
57. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138.
58. Y. Li Huang, Y. Chen, W. Zhang, S. Y. Quek, C.-H. Chen, L.-J. Li, W.-T. Hsu, W.-H. Chang, Y. J. Zheng, W. Chen and A. T. S. Wee, Bandgap tunability at single-layer molybdenum disulphide grain boundaries, Nat. Commun., 2015, 6, 6298.
59. E. J. G. Santos and E. Kaxiras, Electric-Field Dependence of the Effective Dielectric Constant in Graphene, Nano Lett., 2013, 13, 898–902.
60. J. Koo, S. Gao, H. Lee and L. Yang, Vertical dielectric screening of few-layer van der Waals semiconductors, Nanoscale, 2017, 9, 14540–14547.
61. A. Laturia, M. L. van de Put and W. G. Vandenberghe, Dielectric properties of hexagonal boron nitride and transition metal dichalcogenides: from monolayer to bulk, npj 2D Mater. Appl., 2018, 2, 6.
62. T. Le Bahers, M. Rérat and P. Sautet, Semiconductors Used in Photovoltaic and Photocatalytic Devices: Assessing Fundamental Properties from DFT, J. Phys. Chem. C, 2014, 118, 5997–6008.
63. X.-R. Shi, J. Wang and K. Hermann, Theoretical Cluster Studies on the Catalytic Sulfidation of MoO₃, J. Phys. Chem. C, 2010, 114, 6791–6801.
64. T. Weber, J. C. Muijsers, J. H. M. C. van Wolput, C. P. J. Verhagen and J. W. Niemantsverdriet, Basic Reaction Steps in the Sulfidation of Crystalline MoO₃ to MoS₂, As Studied by X-ray Photoelectron and Infrared Emission Spectroscopy, J. Phys. Chem., 1996, 100, 14144–14150.
65. D. Genuit, I. Bezverkhyy and P. Afanasiev, Solution preparation of the amorphous molybdenum oxysulfide MoOS₂ and its use for catalysis, J. Solid State Chem., 2005, 178, 2759–2765.
66. X. Jiao, X. Li, X. Jin, Y. Sun, J. Xu, L. Liang, H. Ju, J. Zhu, Y. Pan, W. Yan, Y. Lin and Y. Xie, Partially Oxidized SnS₂ Atomic Layers Achieving Efficient Visible-Light-Driven CO2 Reduction, J. Am. Chem. Soc., 2017, 139, 18044–18051.
67. N. J. Jeon, J. H. Noh, Y. C. Kim, W. S. Yang, S. Ryu and S. I. Seok, Solvent engineering for high-performance inorganic–organic hybrid perovskite solar cells, Nat. Mater., 2014, 13, 897–903.
68. M. Shirayama, H. Kadowaki, T. Miyadera, T. Sugita, M. Tamakoshi, M. Kato, T. Fujiseki, D. Murata, S. Hara, T. N. Murakami, S. Fujimoto, M. Chikamatsu and H. Fujiwara, Optical Transitions in Hybrid Perovskite Solar Cells: Ellipsometry, Density Functional Theory, and Quantum Efficiency Analyses for CH₃NH₃PbI₃, Phys. Rev. Appl., 2016, 5, 14012.
69. X. Niu, X. Bai, Z. Zhou and J. Wang, Rational Design and Characterization of Direct Z-Scheme Photocatalyst for Overall Water Splitting from Excited State Dynamics Simulations, ACS Catal., 2020, 10, 1976–1983.
70. Y. Fan, X. Song, H. Ai, W. Li and M. Zhao, Highly Efficient Photocatalytic CO₂ Reduction in Two-Dimensional Ferroelectric CuInP₂S₆ Bilayers, ACS Appl. Mater. Interfaces, 2021, 13, 34486–34494.

---

Footnote

† Electronic supplementary information (ESI) available: S1. Optoelectronic properties of non-doped 4L MoO₃ and O-doped 6L MoS₂. S2. S-doped 4L MoO₃ and O-doped 6L MoS₂: structural, thermodynamic and electronic properties. See DOI: https://doi.org/10.1039/d2cp03410g

---