Full-dimensional potential energy surface development and dynamics for the HBr + C₂H₅ → Br(²P_3/2) + C₂H₆ reaction

Abstract

We report a full-dimensional spin–orbit-corrected analytical potential energy surface (PES) for the HBr + C₂H₅ → Br + C₂H₆ reaction and a quasi-classical dynamics study on the new PES. For the PES development, the ROBOSURFER program package is applied and the ManyHF-based UCCSD(T)-F12a/cc-pVDZ-F12(-PP) energy points are fitted using the permutationally-invariant monomial symmetrization approach. The spin–orbit coupling at the level of MRCI-F12+Q(5,3)/cc-pVDZ-F12(-PP) is taken into account, since it has a significant effect in the exit channel of this reaction. Our simulations show that in the 1–40 kcal mol⁻¹ collision energy (E_coll) range the b = 0 reaction probability increases first and then decreases with increasing E_coll, reaching around 15% at the medium E_coll. No significant E_coll dependence is observed in the range of 5–20 kcal mol⁻¹. The reaction probabilities decrease monotonically with increasing b and the maximum b where reactivity vanishes is smaller and smaller as E_coll increases. Unlike in the case of HBr + CH₃, the integral cross-section decays sharply as E_coll changes from 5 to 1 kcal mol⁻¹. Scattering angle distributions usually show forward scattering preference, indicating the dominance of the direct stripping mechanism. The reaction clearly favors H-side attack over side-on HBr and the least-preferred Br-side approach, and favors side-on CH₃CH₂ attack over the CH₂-side and the least-preferred CH₃-side approach. The initial translational energy turns out to convert mostly into product recoil, whereas the reaction energy excites the C₂H₆ vibration. The vibrational and rotational distributions of the C₂H₆ product slightly blue-shift as E_coll increases, and very few reactive trajectories violate zero-point energy.

---

1. Introduction

Detailed dynamical investigations of the bimolecular reaction started in the 1970s for three-atom reactions.^1–3 As the computer performance and methodology improved during the last half centuries, the size of the studied chemical reactions has grown into much bigger systems. However, compared to the experiment, which turned out to be more feasible in the case of larger systems than the accurate computational methods of dynamics investigations, the theory was not capable of performing accurate dynamics simulations of nine-atomic systems until around 2020.^4–11

The dynamics of two other similar chemical reactions have been theoretically investigated in our group: the study on the Cl + C₂H₆ reaction provided unprecedented agreement with the experiment for the rotational state distribution of the HCl product.⁷ In the meanwhile the vibrationally-resolved rotational state distributions of the HF product obtained from the computations agree well with the single-collision experimental data for the v = 1, 2, and 3 states, in the case of the F + C₂H₆ reaction.⁶ The HBr + C₂H₅ reaction has been the subject of both theoretical and experimental investigations due to their supposedly non-Arrhenius behavior.^12–17 Experimentally, Seetula¹² investigated the kinetics of the title reaction under pseudo-first-order conditions in a heatable tubular reactor and fitted the pressure-independent rate constants determined by the Arrhenius expression: k = (1.87 ± 0.14) × 10⁻¹² exp[+(3.7 ± 0.2) kJ mol⁻¹/RT]. They also reported the formation values of entropy (244 ± 6 J K⁻¹ mol⁻¹) and enthalpy (120.7 ± 2.1 kJ mol⁻¹) for the radical studied at 298 K using the above kinetic data in a second-law procedure. Leplat et al.¹³ performed a reinvestigation of the absolute rate constants and led to the following Arrhenius expressions: k = 3.69(±0.95) × 10⁻¹¹ exp(−10.62(±0.66) kJ mol⁻¹/RT) in the temperature range of 293–623 K using a Knudsen reactor coupled to a single-photon photoionization mass spectrometer. They recommended the standard heat of formation of C₂H₅ to be 117.3 ± 3.1 kJ mol⁻¹ resulting from an average of “third law” evaluations using S_298^°(C₂H₅) = 242.9 ± 4.6 J K⁻¹ mol⁻¹. Theoretical investigations began with the evaluation of absolute rate constants and kinetic isotope effects by transition state theory and RRKM theory as applied to the dissociation of the intermediate complex at the (U)MP4/6-311G**//(U)MP2/6-31G* level.¹⁴ Seetula¹⁵ calculated the enthalpy of formation of C₂H₅ at 298 K to be 120.4 ± 2.7 kJ mol⁻¹ by optimizing the transition state of the reaction HBr + C₂H₅ → Br + C₂H₆ at the MP2(fc)/6-31G(d,p) level of theory, and studied the chemical nature of the transition state by localizing it along the minimum energy path of the reaction. Sheng et al.¹⁶ studied the reaction over the temperature range from 200 to 1400 K. They calculated the electronic structure information at the BHLYP/6-311+G(d,p) and QCISD/6-31+G(d) levels, and further refined the energies along the minimum energy paths at both levels by performing the single-point calculations at the PMP4(SDTQ)/6-311+G(3df,2p)//BHLYP and QCISD(T)/6-311++G(2df,2pd)//QCISD levels. Their computed results further indicated that the title reaction has a negative temperature dependence at T < 850 K, but clearly shows a positive temperature dependence at T > 850 K, and predicted that the kinetic isotope effect for the title reaction is inverse in the temperature range from 200 to 482 K. Golden et al.¹⁷ employed RRKM theory to analyze the kinetics of the title reaction. They characterized the stationary points along the reaction coordinate with coupled cluster theory combined with basis set extrapolation to the complete basis set limit, and located a shallow minimum bound by 9.7 kJ mol⁻¹ relative to the reactants, with a very small energy barrier to dissociation to the products. They reported that the transition state is tight compared to the adduct, explored the influence of vibrational anharmonicity on the kinetics and thermochemistry of the title reaction, and suggested that with adjustment of the adduct binding energy by around 4 kJ mol⁻¹, the computed rate constants may be brought into agreement with most experimental data in the literature. They indicated that at temperatures above those studied experimentally, the activation energy may switch from negative to positive. As an initial step for the dynamics study reported here, in 2019 our group¹⁸ determined benchmark geometries and energies for the stationary points of the backward reaction Br + C₂H₆, also considering the H-substitution and the methyl-substitution reaction pathways, by augmenting the CCSD(T)-F12b/aug-cc-pVQZ energies by core-correlation, post-CCSD(T) and spin–orbit corrections. Taking these correction terms into account turns out to be essential to reach subchemical, i.e. 0.5 kcal mol⁻¹, accuracy.

In 2013 one of us worked out the potential energy function of a similar but smaller reactive system, Br + CH₄.¹⁹ Later, using the quasi-classical trajectory (QCT) method in combination with an improved version of the high-level ab initio PES, Góger et al.²⁰ also provided reliable rate coefficients for the HBr + CH₃ → Br + CH₄ reaction at combustion temperatures where no experimental data are available. The QCT calculations had been validated by reproducing the experimental rate coefficients at room temperature. At temperatures between 600 and 3200 K, the QCT rate coefficients display positive activation energies. Very recently, Gao et al.²¹ performed quantum and quasi-classical dynamics calculations for this reaction and very good agreement was found between the two approaches. The cross-sections were found to diverge when E_coll decreases, indicating that the reactant attraction is responsible for the dynamics at low E_coll. The quantum mechanical and the quasi-classical rate constants also agree very well and almost exactly reproduce the experimental results at low temperatures up to 540 K. The negative activation energy observed experimentally is confirmed by the calculations and is a consequence of the long-range attraction between the reactants. They found that at very low E_coll, the reactive system crosses the potential barrier because the forces within the complex guide them. When E_coll increases, the system does not follow the most favorable path and the reactants are, with increasing probability, reflected from the repulsive walls of the nonreactive parts of the reactants, providing a picture beyond the decreasing excitation function.

In this study, we aim to give a better understanding of how the HBr + C₂H₅ → Br + C₂H₆ reaction proceeds step-by-step at the atomic and molecular level. A full-dimensional ab initio PES for the title reaction is developed to provide a correct description. The spin–orbit coupling is taken explicitly into account in our computations, since it has a significant effect in the exit channel of this reaction, especially when the products are far from each other. Using this PES, we carry out QCT simulations, and discuss detailed dynamics results of the title reaction.

2. Computational details

2.1. Potential energy surface development

The initial candidate of the geometry set is obtained by randomly displacing the Cartesian coordinates of the stationary points,¹⁸ optimized at the ROHF-UCCSD(T)-F12b/aug-cc-pVTZ^22,23 level of theory, of the backward reaction Br + C₂H₆, in the 0–0.4 Å interval. For the Br atom a small-core relativistic effective core potential (ECP)²⁴ is used with the corresponding aug-cc-pVTZ-PP basis set. In addition, the reactants and products are randomly scattered around each other in the range of 3–8 Å (for three product channels: hydrogen-abstraction, methyl-substitution, hydrogen-substitution). At these initial geometries single-point quantum chemical computations are performed at the ManyHF-based²⁵ RMP2/aug-cc-pVDZ²⁶ (aug-cc-pVDZ-PP for Br atom) level of theory using the MOLPRO program package.²⁷ It is important to note that, in regions far from equilibrium, in our case, the reactant and product regions of HBr + C₂H₅ → Br + C₂H₆, one is often plagued by Hartree–Fock (HF) convergence issues, and even if convergence is achieved, self-consistent field procedures that are used to obtain HF solutions offer no guarantee that the solution found is the lowest-energy solution, resulting in erratic post-HF energies and regions where no energy is obtained.²⁵ Therefore, here we use the ManyHF method recently developed in our group for automatically finding better HF solutions to compute all the energies in this work. First, five different Kohn–Sham DFT computations, an ordinary ROHF/AVDZ calculation, and an MCSCF calculation started from the final orbitals of the ordinary ROHF/AVDZ were performed, leading to the first seven ROHF/AVDZ primary candidates for the best HF solution. Second, we pass the primary candidates through the MCSCF module in ROHF mode providing secondary candidates. Finally, the lowest energy solution among the primary and secondary candidates is then used as the reference wavefunction for the desired correlation method.²⁵ The data set is then cut by excluding the geometries with higher than 100 kcal mol⁻¹ relative energy with respect to the global minimum of the set. After the cut the initial data set consists of 6313 geometries, and is used to start the PES development with the ROBOSURFER program package²⁸ developed in our group.

For the fitting of the energy points of the PES we utilize the Monomial Symmetrization Approach (MSA).²⁹ Within this approach the PES is fitted using a full-dimensional analytical function which is inherently invariant under the permutations of like atoms. This function is an expansion of polynomials of the y_ij = exp(−r_ij/a) Morse-like variables, where r_ij are the inter-atomic distances and the a parameter, set to 2.0 bohr based on careful tests, controls the asymptotic behavior of the PES. The highest order of the polynomials is 5. The energy points are fitted using a least-squares fit with an E₀/(E + E₀) weighing factor, where E is the actual energy relative to the global minimum of the fitting set, and E₀ = 0.04 hartree. The fifth order expansion requires 3234 fitting coefficients.

In the ROBOSURFER program a hard energy limit of 150 kcal mol⁻¹ relative to the energy of the free reactants is applied, above which no energy point is added. A hard energy limit of 30 kcal mol⁻¹ below the reactants is set to avoid spurious minima. A 0.5 kcal mol⁻¹ target accuracy of the fitting is set. These parameter values are chosen to obtain the best possible description of the HBr + C₂H₅ reaction. The ManyHF-based RMP2/aug-cc-pVDZ (aug-cc-pVDZ-PP for Br atom) level of theory is used for the initial PES development, which consists of 128 ROBOSURFER iterations in total. During the PES development QCT computations³⁰ are run to obtain new geometries, where the E_coll is set from 1 to 60 kcal mol⁻¹, which is enough to cover the energies in the PES we are interested in. We use both sides of the reaction, i.e., HBr + C₂H₅ and Br + C₂H₆, as the starting points of the QCTs. At the end we have 12 819 geometries and the energies of them are recomputed at the following composite level of theory: ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for Br atom), where “SO_corr” is the spin–orbit (SO) correction to each energy point. In free halogen atoms the non-relativistic ²P ground electronic state splits due to the relativistic spin–orbit interaction, and the relativistic ²P_3/2 ground state (where the total angular momentum quantum number, J = 3/2) is lower by one third of the splitting energy with respect to the non-relativistic ground state. Thus, this energy-lowering effect is especially relevant in the exit (Br + C₂H₆) channel of the reactive PES, where the Br atom is far from and thus unbound to the ethane molecule. The SO correction is determined at the MRCI-F12+Q(5,3)/cc-pVDZ-F12(-PP)³¹ level of theory for each geometry. The multireference computations utilize a minimal active space of 5 electrons on 3 spatial 4p-like orbitals, and the Q Davidson-correction³² estimates higher-order correlation energy effects. The SO computations make use of the Breit–Pauli operator in the interacting-states approach,³³ where the SO eigenstates are determined by diagonalizing the 6 × 6 SO matrix whose diagonal elements are replaced by the Davidson-corrected MRCI energies.

The MSA is used again for the fitting of the geometries with new energies of the PES. The final PES is built from 11 364 geometries and the corresponding composite energies, whose distribution is shown in Fig. 1, and features small root mean square (RMS) errors in the chemically interesting energy ranges as shown in Table 1.

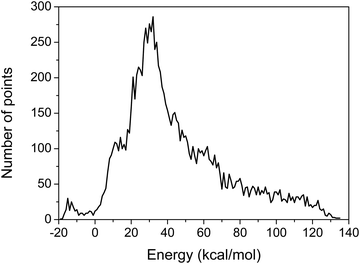Fig. 1 Distribution of the final sampling points. Energies are given with respect to the asymptote of reactants.

Table 1 RMS errors in the chemically interesting regions of the PES (energy intervals are given relative to the global minimum of the fitting set)

Energy range (kcal mol^−1)	0–20	20–40	40–100
RMS (kcal mol^−1)	0.248	0.487	1.015

---

2.2. Quasi-classical trajectory simulations

QCT simulations are carried out at E_coll = 1, 2, 5, 10, 20, and 40 kcal mol⁻¹ for the title reaction. At the beginning of the trajectories, the zero-point energies (ZPEs) of HBr and C₂H₅ are set by standard normal-mode sampling³⁰ and the initial rotational angular momentum of each reactant is adjusted to zero. The spatial orientations of the reactants are randomly sampled. The initial distance between the center of mass of HBr and the center of mass of C₂H₅ is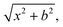 where x = 28 bohr and the impact parameter is varied between 0 and b_max (where the reaction probability vanishes) with a step size of 0.5 bohr. 1000 trajectories are run at each b value. The trajectories are propagated with a 0.0726 fs time step until the largest interatomic distance becomes larger than the largest initial one by 1 bohr. Less than 0.1% of the trajectories failed and gave unphysical results.

Integral cross-sections (σ) for the title reaction are calculated by a b-weighted numerical integration of the P(b) opacity functions at each E_coll. The product ZPE-constraint, i.e., the classical vibrational energy of C₂H₆ has to be greater than its ZPE on the present PES, only rules out 8 trajectories from the 5793 reactive trajectories. So from now on we can safely ignore the differences between features with and without ZPE constraint.

The scattering angle distributions are obtained by binning the cosine of the angle (θ) of the relative velocity vectors of the center of masses of the products and those of the reactants into 10 equidistant bins from −1 to 1. cos(θ) = 1 (θ = 0°) corresponds to forward scattering and cos(θ) = −1 (θ = 180°) corresponds to backward scattering. The initial attack angle distributions for the reactants are calculated by binning the cosine of the angle (α for HBr and β for C₂H₅) of the velocity vector of center of mass of the examined reactant and an interatomic vector that is considered as the Br–H bond for HBr and the C–C bond for C₂H₅. We also use 10 equidistant bins between −1 to 1 like in the case of scattering angle distributions. For HBr cos(α) = −1 means that HBr approaches with its Br atom side and in the situation of cos(α) = 1 HBr goes with its H atom towards C₂H₅. While for C₂H₅ cos(β) = −1 means that C₂H₅ approaches HBr with its CH₃ side and in the situation of cos(β) = 1 C₂H₅ goes with its CH₂ side towards the HBr. Rotational quantum numbers of C₂H₆ are obtained by rounding the lengths of classical rotational angular momentum vectors to the nearest integer values.

3. Results and discussion

3.1. The potential energy surface

The schematic energy diagram of the title reaction is shown in Fig. 2. The C_s-symmetry transition state (TS) structure with a 175° bent C–H–Br arrangement and with a large H–C distance of 1.74 is clearly reactant-like.¹⁸ A pre-reaction minimum is located very near to the TS. The reaction is exothermic, in accordance with its early-barrier nature.³⁴Fig. 2 also shows the comparison of the classical relative energies of the stationary points of the title reaction obtained on the newly-developed PES, the ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for Br atom) energies computed at the geometries optimized on the PES, and the previously determined benchmark results.¹⁸ The comparison of the former two indicates low (0.2 kcal mol⁻¹) fitting errors of the full-dimensional PES, consistent with the small RMS values of Table 1. The relative energy of the TS obtained on the PES reproduces well the benchmark value (<0.1 kcal mol⁻¹ difference). The classical relative energies of the pre-reaction minimum (premin) structure and the products are about 0.2 and 0.3 kcal mol⁻¹ higher than the benchmark energies. The energies on the PES are fortuitously accurate for this system compared to the similar F + C₂H₆ and Cl + C₂H₆ systems,^6,7 due probably to the cancellation of errors in the present calculations.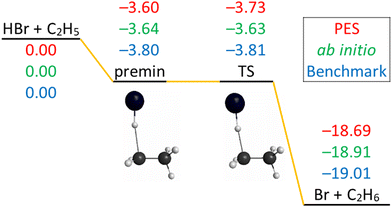

Fig. 2 Schematic potential energy diagram of the HBr + C₂H₅ → Br + C₂H₆ reaction comparing the classical relative energies obtained on the present PES, ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for Br atom) energies at geometries optimized on the PES, and the relativistic all-electron CCSDT(Q)/complete-basis-set-quality benchmark relative energies¹⁸ of the stationary points, in kcal mol⁻¹.

The imaginary frequency of the TS is only 162 cm⁻¹ so it is a soft TS, which means the energy is a little higher than nearby. The lowest normal mode of premin has a wavenumber of 61 cm⁻¹ so it is a shallow minimum, its energy is a little lower than nearby. It is possible that the TS lies below the premin, as shown at the benchmark level and on the PES. Note that at the ab initio level used for the PES development this trend is reversed, but with only 0.1 kcal mol⁻¹ difference. Actually in this reaction the TS and the premin have very similar energies and their relative energy is within our error bar.

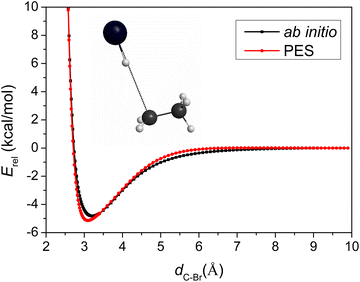
Besides the comparison of the stationary-point energies, the one-dimensional potential energy curve as a function of the C–Br distance obtained on the PES, compared to that obtained using the ab initio method, is another good tool to evaluate the accuracy of the PES. The PES describes the entrance channel potential accurately as shown in Fig. 3.

Fig. 3 One-dimensional potential energy curve for CH₃CH₂⋯HBr as a function of the C–Br distance obtained on the PES, compared to that obtained using the composite ab initio method describing the pre-reaction minimum of the HBr + C₂H₅ → Br + C₂H₆ reaction.

To capture the properties near TS, we took the TS geometry, elongated and shortened the C–Br distance, while freezing the other degrees of the two parts, CH₃CH₂ and HBr. The asymptote in Fig. 3 is not the reactants in equilibrium, but bent over a little, so its energy is higher than that of the reactants, leading to a deeper well with −5.1 and −4.8 kcal mol⁻¹ relative energies with respect to the asymptote in the case of the PES and the direct ab initio method, respectively. The comparison of the two minima indicates low (0.3 kcal mol⁻¹) fitting errors of the full-dimensional PES, again consistent with the small RMS values of Table 1. The positions of the two minima located at C–Br distances of 3.10 and 3.22 Å, only differ by 0.12 Å, showing good behavior of the analytical PES.

3.2. Reaction probabilities

Using the newly developed PES, we carried out QCT simulations at six E_coll (1, 2, 5, 10, 20 and 40 kcal mol⁻¹) for the title reaction, and the opacity functions (reaction probabilities as a function of the impact parameter) obtained at the different E_coll are shown in Fig. 4.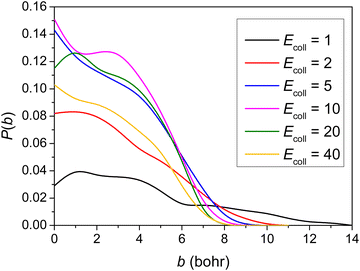

Fig. 4 Reaction probabilities as a function of the b impact parameter for the title reaction at different collision energies (given in kcal mol⁻¹).

As seen in Fig. 4, no threshold energy above 1.0 kcal mol⁻¹ can be observed for the title reaction to proceed, in accordance with the negative barrier height relative to the reactants. It is clear that the opacity function at 1 kcal mol⁻¹E_coll has a much smaller reaction probability and much further distance where the reaction can still occur. The b = 0 reaction probability increases first and then decreases with increasing E_coll, reaching around 15% in the medium E_coll. No significant E_coll dependence is observed in the range of 5–20 kcal mol⁻¹. The reaction probabilities decrease monotonically with increasing b and the maximum b where reactivity vanishes decreases as E_coll increases. The b_max value is the largest (14 bohr) at 1 kcal mol⁻¹E_coll, due presumably to the fact that the dipole–dipole interaction between the reactants is the least counteracted by translational momenta. Considering ZPE (41 kcal mol⁻¹ for reactants and 43 kcal mol⁻¹ for TS), the sub-barrier energy is −1.7 kcal mol⁻¹. In shallow sub-barrier reactions, the reaction probability could be small at low E_coll.^6,10

3.3. Integral cross-sections

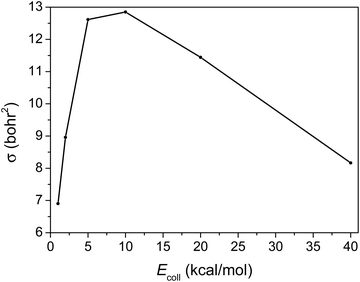
The integral cross-section (σ) as a function of E_coll of the title reaction, presented in Fig. 5, reflects a big jump from 1 to 5 kcal mol⁻¹E_coll, but a slightly efficient inhibition of the reaction by the increase in the initial translational energy from 10 to 40 kcal mol⁻¹.

Fig. 5 Integral cross-sections for the title reaction as a function of the collision energy.

The integral cross-section reaches its highest value at around 5 to 10 kcal mol⁻¹E_coll. At the high E_coll part it decreases slowly, consistent with the HBr + CH₃ → Br + CH₄ reaction.¹⁹ However when E_coll is low it decreases sharply with decreasing E_coll, due probably to the fact that the reactants’ interaction is more anisotropic in the case of C₂H₅.

3.4. Scattering and initial attack angle distributions

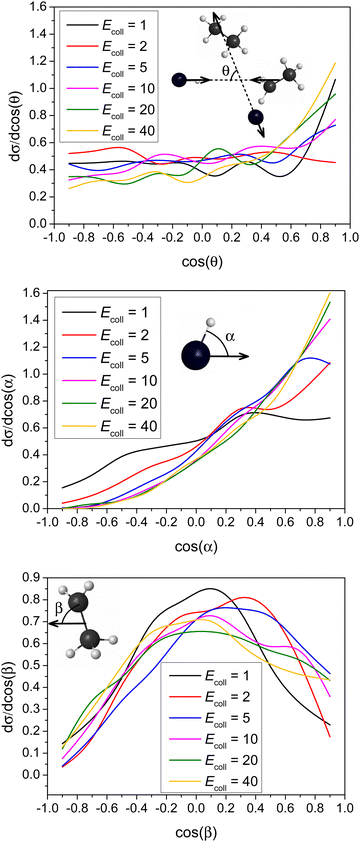
Differential cross-sections showing the scattering and initial attack angle distributions of the title reaction at different E_coll are shown in Fig. 6.

Fig. 6 Normalized scattering and initial attack angle distributions for the title reaction at different collision energies (given in kcal mol⁻¹). The attack angles are defined at the beginning of each reactive trajectory. θ is the scatting angle for the two products, while α and β are calculated by the velocity vector of the center of mass of the examined reactant and an interatomic vector that is considered as the Br–H bond for HBr and the C–C bond for C₂H₅, respectively.

It is clear that forward scattering is favored at high E_coll (40 and 20 kcal mol⁻¹) indicating the dominance of the direct stripping mechanism. As E_coll decreases (10 and 5 kcal mol⁻¹), the distributions are less anisotropic. The DCS is almost isotropic for 2 kcal mol⁻¹. However, it is quite surprising that the DCS at E_coll = 1 kcal mol⁻¹ shows a forward peak, which may indicate a different mechanism at low E_coll. Nevertheless, this forward scattering is consistent with the significantly larger b_max value at low E_coll (see Fig. 4), because at large b usually stripping occurs resulting in forward scattering. The title reaction favors H-side attack over side-on HBr and the least-preferred Br-side approach, as expected, because an H–C bond forms in the abstraction process, and favors side-on CH₃CH₂ attack over CH₂-side and the least-preferred CH₃-side approach. None of these attack characters shows any significant E_coll dependence, except that the HBr attack angle distribution is more isotropic at the lowest E_coll.

In order to provide more insight into the scattering dynamics, we present the correlation diagrams of the impact parameters and scattering angles in Fig. 7. At higher collision energies the reaction with direct forward scattering is favored for large b while backward scatting is favored for small b as expected. At low E_coll some correlation between b and cos(θ) still exists showing that the isotropic scattering angle distribution at E_coll = 2 kcal mol⁻¹ rather originates from the balance of direct rebound and stripping than from indirect dynamics. At E_coll = 1 kcal mol⁻¹ the b − cos(θ) correlation is less significant showing some indirect feature. Furthermore, the forward-scattered trajectories at b > 9.5 bohr, which are not present at E_coll = 2 kcal mol⁻¹, boost the forward-scattered peak of the scattering angle distribution at E_coll = 1 kcal mol⁻¹ due to the b-weighted integration over the impact parameters.

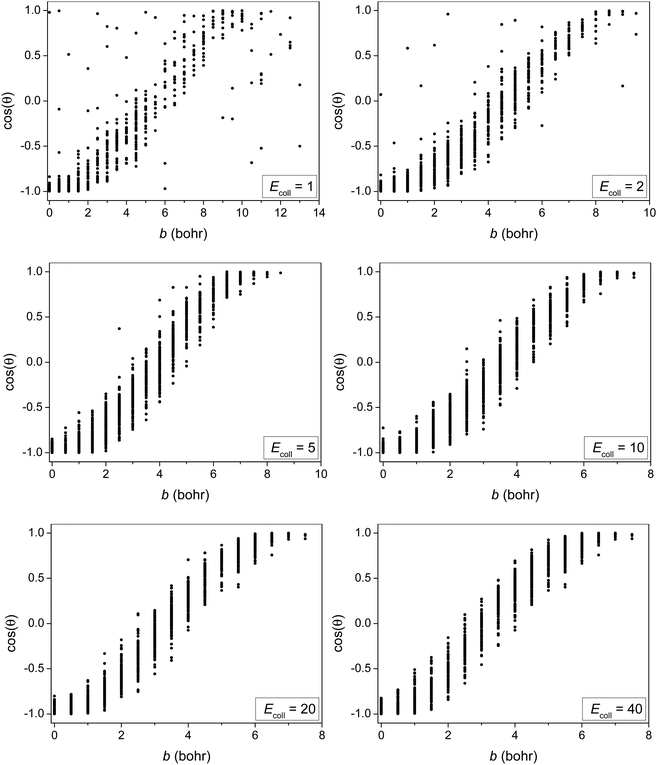Fig. 7 Correlation diagrams of the impact parameters and scattering angles for the title reaction at different collision energies (given in kcal mol⁻¹).

3.5. The post-reaction distribution of energy

Differential cross-sections showing the distribution of the relative translational energy of the products at different E_coll are plotted in Fig. 8.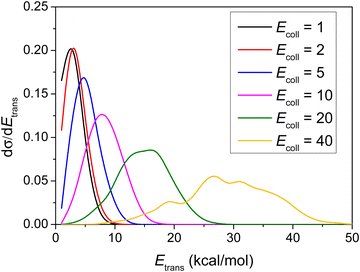

Fig. 8 Normalized product relative translational energy distributions for the title reaction at different collision energies (given in kcal mol⁻¹).

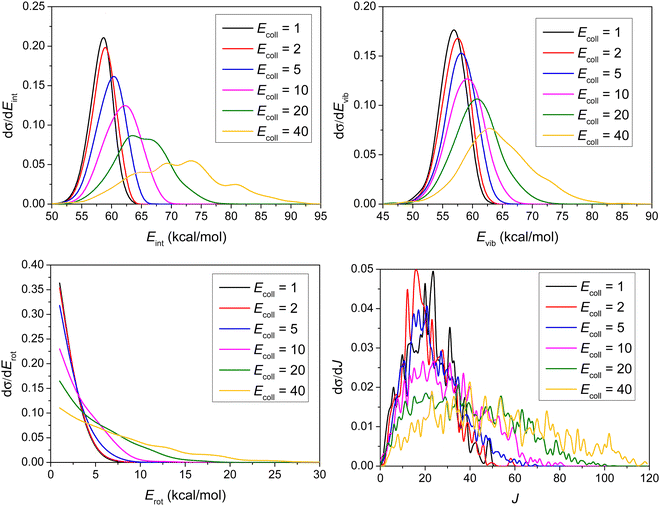
As shown in Fig. 8, the distributions become broader as the E_coll increases, and their maxima are shifted by almost the total increment of the E_coll, indicating that the major part of the initial translational energy ends up in translational recoil in all cases.

Consistent with the above observation, the E_coll dependence of the internal energy distribution of ethane, plotted in Fig. 9, also suggests that only a small portion of the collision energy is transferred into the vibrational and rotational degrees of freedom of ethane, since the peaks of the distributions are less affected by the change in the initial translational energy than those of the product relative translational energy distributions. The internal energy excitations of the product ethane mainly come from the reaction energy.

Fig. 9 Normalized internal energy (E_int), vibrational energy (E_vib), rotational energy (E_rot), and rotational quantum number (J) value distributions for the product ethane of the title reaction at different collision energies (given in kcal mol⁻¹).

As shown in Fig. 9, considering that the ZPE of ethane is 47 kcal mol⁻¹, very few trajectories are ZPE-violating, consistent with our previous points arguing that ZPE-constraint only rules out 8 reactive trajectories.

4. Conclusion

We have developed a full-dimensional spin–orbit-corrected PES for the nine-atomic HBr + C₂H₅ → Br + C₂H₆ reaction using the ROBOSURFER program package and the MSA of the permutationally invariant polynomial method for fitting the ab initio energy points and studied its dynamics in detail by performing QCT simulations. The ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) (cc-pVDZ-PP-F12 for Br atom) level of theory used for the PES development is necessary to correctly describe the reaction and also reflects well the negative barrier height. The energies on the PES agree fortuitously well with the benchmark data, due probably to the cancellation of errors in the present calculations. Quasi-classical dynamics simulations on this PES show substantial probabilities of this H-abstraction reaction in a wide range of E_coll. Scattering angle distributions of the products indicate a dominance of the direct stripping mechanism. Relative translational energy distributions of the products and internal energy distributions of ethane suggest that most of the E_coll ends up in product translational recoil, and only a small amount of the initial translational energy excites the rotational and vibrational modes of ethane. The substantial reaction energy excites the vibration of the product. The vibrational and rotational distributions of the C₂H₆ product slightly blue-shift as E_coll increases, and surprisingly very few reactive trajectories violate zero-point energy. The accurate theoretical simulation of the present reaction may motivate future experiments and classical, semi-classical or reduced-dimensional quantum kinetics and dynamics computations.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Tibor Győri for the tips and discussion. This work was supported by the National Research, Development and Innovation Office-NKFIH, K-125317, the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT, Project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme, and the Momentum (Lendület) Program of the Hungarian Academy of Sciences.

References

1. G. C. Schatz and A. Kuppermann, J. Chem. Phys., 1975, 62, 2502.
2. G. C. Schatz and A. Kuppermann, J. Chem. Phys., 1976, 65, 4642.
3. A. Persky, J. Chem. Phys., 1977, 66, 2932.
4. J. Espinosa-Garcia, M. Garcia-Chamorro and J. C. Corchado, Phys. Chem. Chem. Phys., 2019, 21, 13347.
5. J. Espinosa-Garcia, C. Rangel, J. C. Corchado and M. Garcia-Chamorro, Phys. Chem. Chem. Phys., 2020, 22, 22591.
6. D. Papp and G. Czakó, J. Chem. Phys., 2020, 153, 064305.
7. D. Papp, V. Tajti, T. Győri and G. Czakó, J. Phys. Chem. Lett., 2020, 11, 4762.
8. B. Bastian, T. Michaelsen, L. Li, M. Ončák, J. Meyer, D. H. Zhang and R. Wester, J. Phys. Chem. A, 2020, 124, 1929.
9. J. Meyer, V. Tajti, E. Carrascosa, T. Győri, M. Stei, T. Michaelsen, B. Bastian, G. Czakó and R. Wester, Nat. Chem., 2021, 13, 977.
10. D. Gao and D. Wang, Phys. Chem. Chem. Phys., 2021, 23, 26911.
11. X. Lu, L. Li, X. Zhang, B. Fu, X. Xu and D. H. Zhang, J. Phys. Chem. Lett., 2022, 13, 5253.
12. J. A. Seetula, J. Chem. Soc., Faraday Trans., 1998, 94, 891.
13. N. Leplat, A. Wokaun and M. J. Rossi, J. Phys. Chem. A, 2013, 117, 11383.
14. Y. H. Chen and E. Tschuikow-Roux, J. Phys. Chem., 1993, 97, 3742.
15. J. A. Seetula, Phys. Chem. Chem. Phys., 2000, 2, 3807.
16. L. Sheng, Z. S. Li, J. Y. Liu, J. F. Xiao and C. C. Sun, J. Comput. Chem., 2004, 25, 423.
17. D. M. Golden, J. P. Peng, A. Goumri, J. Yuan and P. Marshall, J. Phys. Chem. A, 2012, 116, 5847.
18. D. Papp, B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 396.
19. G. Czakó, J. Chem. Phys., 2013, 138, 134301.
20. S. Góger, P. Szabó, G. Czakó and G. Lendvay, Energy Fuels, 2018, 32, 10100.
21. D. Gao, X. Xin, D. Wang, P. Szabó and G. Lendvay, Phys. Chem. Chem. Phys., 2022, 24, 10548.
22. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
23. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007.
24. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
25. T. Győri and G. Czakó, J. Chem. Phys., 2022, 156, 071101.
26. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
27. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net.
28. T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51.
29. Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26.
30. W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399–407.
31. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
32. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
33. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
34. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334.

---