Structure and stability of 7-mercapto-4-methylcoumarin self-assembled monolayers on gold: an experimental and computational analysis

Abstract

Self-assembled monolayers (SAM) of 7-mercapto-4-methylcoumarin (MMC) on a flat gold surface were studied by molecular dynamics (MD) simulations, reference-free grazing incidence X-ray fluorescence (GIXRF) and X-ray photoelectron spectroscopy (XPS), to determine the maximum monolayer density and to investigate the nature of the molecule/surface interface. In particular, the protonation state of the sulfur atom upon adsorption was analyzed, since some recent literature presented evidence for physisorbed thiols (preserving the S–H bond), unlike the common picture of chemisorbed thiyls (losing the hydrogen). MD with a specifically tailored force field was used to simulate either thiol or thiyl monolayers with increasing number of molecules, to determine the maximum dynamically stable densities. This result was refined by computing the monolayer chemical potential as a function of the density with the bennet acceptance ratio method, based again on MD simulations. The monolayer density was also measured with GIXRF, which provided the absolute quantification of the number of sulfur atoms in a dense self-assembled monolayer (SAM) on flat gold surfaces. The sulfur core level binding energies in the same monolayers were measured by XPS, fitting the recorded spectra with the binding energies proposed in the literature for free or adsorbed thiols and thiyls, to get insight on the nature of the molecular species present in the layer. The comparison of theoretical and experimental SAM densities, and the XPS analysis strongly support the picture of a monolayer formed by chemisorbed, dissociated thiyls.

---

Introduction

Since their first description,¹ thiol self-assembled monolayers (SAM) on gold surfaces and nanoparticles have been widely used in a variety of technological applications,^2–13 and studied with a wealth of diffraction,^14–18 spectroscopic^8,19–23 and other surface science techniques.²⁴ In addition, thiol SAMs have been modeled theoretically by several ab initio (mainly density functional theory, DFT)^25–32 and molecular mechanics^{27,28,33–38} studies.

Despite such a widespread interest, many key features of thiol/gold monolayers are still debated: even for some fundamental characteristics of the interface, as the nature of sulfur–gold bond or the weight of intermolecular interactions inside the organic layer, different models have been proposed with no unique interpretation of the experimental data. For instance, the protonation state of the sulfur atom bonded to the metal surface is not unanimously accepted:^30,32,39 though most researchers assume that the S–H bond is dissociated and de-protonated sulfur is covalently bound to gold atoms,^2,40–42 some evidences have been presented showing that the layers can also be formed by undissociated thiol molecules.^43–46 (The former model is also referred to as “chemisorption”, in contrast with the latter described as “physisorption” to stress the absence of a typical covalent bond between protonated sulfur and gold).

The present work contributes to this investigation, comparing the structure and stability of different SAMs of 7-mercapto-4-methylcoumarin (MMC) on gold (111) surfaces. A number of monolayers, formed either by undissociated thiol or radical thiyl MMC units (Fig. 1), have been modeled theoretically, and the results compared with the absolute quantification of MMC surface density obtained by means of reference-free grazing incidence X-ray fluorescence (GIXRF) in SAMs prepared on 100 nm-thick gold layers. Moreover, X-ray photoelectron spectroscopy (XPS) characterization was performed to determine the nature of the thiol/thiyl S–Au chemical bond.

Fig. 1 7-Mercapto-4-methylcoumarin (MMC) thiol molecule (A) and thiyl radical (B).

(A note on the terminology: since nearly all the proposed models for the dissociation of the S–H bond are based on a homolytic cleavage, eventually leading to H₂ formation, we prefer to consider the dissociated species as a radical thiyl rather than a thiolate ion, unlike many published studies. Whether the R–S unit has to be seen as a radical or an ion depends on the charge distribution in the S–Au bond, and appears as a rather unessential question in this context.)

Methods and models

Theoretical modeling

Some models of thiol and thiyl SAM with different densities were prepared, to study their kinetic and thermodynamic stability with molecular dynamics (MD). Our goal is to determine the highest stable density and evaluate the chemical potential and the order degree for SAMs of both species: if thiol and thiyl SAM models exhibit different characteristics, the comparison with the experiments performed on the same system could shed some light on the protonation state of the sulfur atoms and in general on the structure of the SAM.

The gold (111) surface was modeled by cleaving a three layers thick slab out of the metal bulk structure: the periodic unit cell comprises 24 × 24 atoms in each layer and its surface area, considering an atomic radius for gold of 0.1385 nm, is 38.2 nm².

All the MD runs were carried out with GROMACS2020 package,⁴⁷ while the single point energy calculations needed for FF parameterization were performed with LAMMPS package.⁴⁸ The initial force field was GROMOS 54A7, provided by the Automated Topology Builder (ATB)⁴⁹ website, and used as such to reproduce MMC bonded interactions and intermolecular energies.

The interactions between MMC (molecule and radical) with the gold surface were parameterized against DFT calculations on small model systems, with an incremental procedure. First, the parameters for the interactions of aromatic C and H atoms with gold were determined for benzene on the Au surface; then the parameters for the –SH group were optimized using benzenethiol (keeping the previous parameters fixed); aliphatic C and H parameters were added by considering methyl–benzenethiol, and finally oxygen and radical S parameters were obtained with MMC.

All the details of the FF parameterization, along with the results of the benchmarking and checking, and the optimized parameters are reported in the ESI.† We are also providing in the ESI† the complete FF in the GROMACS format.

After an initial energy minimization, to remove spurious close contacts, the MD simulations were performed with 2 × 10⁶ steps of 0.5 fs for equilibration, and 2 × 10⁶ steps of 1 fs for production runs. A 2 nm cut-off was used for the van der Waals and electrostatic interactions, using the PME method for longer distances; during all the simulations, Au positions were kept frozen.

The MMC chemical potential in the monolayers at various densities was computed as the free energy of decoupling⁵⁰ of one thiol or thiyl from the gold slab and the rest of the layer, using the bennet acceptance ratio (BAR) method⁵¹ implemented in GROMACS (gmx BAR procedure), and sketched in the ESI.†

Sample preparation

Silicon substrates were cleaned in acetone and isopropanol and deposited with a layer of 100 nm of gold by RF sputtering. The resulting gold surface, continuous and polycrystalline, was characterized by atomic force microscopy (AFM) with tapping mode measurements performed on 25 μm² areas. These allowed to determine the ratio between its surface area and its theoretical flat area, i.e. the factor k in eqn (1) (see below). A complete description of the AFM measurement and uncertainty budget is available in the ESI.† The preparation of the MMC SAM was conducted with a standard protocol.⁵² MMC powder (Merck) was diluted in ethanol at 1 mM concentration (20 mL per each sample). The gold-coated substrates were then immersed in the MMC solution for two hours, then abundantly rinsed with EtOH to remove any excess molecules not bounded to the gold surface.

GIXRF characterization

The quantitative characterization of the areal density of MMC in SAM was conducted by reference-free grazing incidence X-ray fluorescence (GIXRF)⁵³ at the BESSY II synchrotron radiation facility. More details on the experimental conditions used are reported in the ESI.† In GIXRF, the angle of incidence of the X-ray beam is varied around the critical angle for total external reflection allowing the formation of an X-ray standing wave (XSW) interference field just above the sample surface. The XSW field enhances the fluorescence emitted by the atom inside it. Furthermore, the grazing incidence conditions allow to significantly attenuate X-ray fluorescence and other background contributions originating from the bulk volume of the sample.⁵⁴ A SI-traceable quantification of the mass deposition of sulfur can be performed, without any calibration standard, through the following equation,⁵⁵ as previously reported in ref. 54 and 56.

The element-specific fluorescence photon count rate P_e,K is obtained by a spectral deconvolution procedure (details in the ESI†) and then converted to the mass of the element of interest per unit area σ_e, expressed in g cm⁻², by combining the atomic fundamental parameters and calibrated instrumental parameters. The radiometrically calibrated instrumental parameters, i.e. the sine of the incidence angle θ, the incident photon flux Φ₀, the solid angle of detection Ω/4π, are known due to the use of the well-known physically calibrated instrumentation⁵⁶ and are used to correct P_e,K. The factor 1/k corrects the photon count P_e,K for the deviation from a non-flat distribution of the target element, through the analysis of the surface area and its ratio to the theoretical area. Another correction factor accounts for the SDD's detection efficiency ε_(Ee,K) at the photon energy of the fluorescence line K for the element e and the incident photon energy E₀ and angular dependent relative intensity of the XSW field I_XSW(E₀, θ).⁵⁷ Finally, the tabulated fundamental parameters τ_e,K(E₀) and ω_e,K are the partial photoionization cross section and fluorescence yield related to the K-shell of the target atom e, respectively. They form the production cross section for fluorescence radiation of the element of interest.

XPS characterization

A PHI 5000 Versaprobe Scanning X-ray Photoelectron Spectrometer (Physical Electronics, Chanhassen, MN, USA) has been involved in this study to get information regarding the relative atomic concentration (at%) of each element present on the surface of functionalized Au thin film, and also to have further evidence regarding the bonds established between the MMC molecule and the golden surface. The X-ray source was a monochromatic Al Kα radiation (1486.6 eV, 15 kV voltage and 1 mA anode current). All samples were subjected to a combined electron and Ar ion gun neutralizer system, to decrease the electrical charging effect during the analysis.

Powder sample has been loaded directly on a steel mask by attaching it on a double-sided conductive tape. The Au thin film deposited on Si substrate and functionalized with MMC has been attached on the 2-inches sample holder surface by means of double-sided conductive tape. Working pressure, inside the main chamber, reached a maximum value of 10⁻⁶ Pa. Details about the signal analysis provided in the ESI.†

Results and discussion

Molecular dynamics modeling

Several models were defined placing an increasing number of thiol or thiyl units randomly onto the gold slab: then, after a MM minimization to remove close-contacts and spurious structures, MD simulations were run at 298 K until equilibration, and then for further 2 ns dynamics to check the monolayer stability. In the densest layers some of the organic molecules or radicals detached from the slab during the dynamics, remaining in contact with the other MMC units, in a sort of disordered double layer. We consider that such molecules, not interacting with the gold surface, would be washed away during the SAM preparation, so did not include them in the calculation of the SAM density.

The MD evidenced substantially different behaviors for thiols and thiyls. In the former case, when the SAM density reached 2.05 molecules per nm² some thiols began to leave the surface during the dynamics, being readsorbed in the SAM later, in a sort of exchange with the double layer mentioned above; for number densities larger than 3.72 nm⁻² the second layer became stable and every new molecule added to the SAM was expelled during the MD, floating above it, so we consider this density value as an upper bound for thiol SAMs.

On the other hand, thiyls can be packed more closely than thiols and form denser SAMs, as expected for their much larger interaction energy with gold, which balances the intermolecular repulsions in the crowded layers. Indeed no radical was observed to leave the monolayer during the MD up to a density of 4.84 radicals per nm²: above this value, all the newly added thiyls were expelled from the SAM during the dynamics, forming also in this case a second layer above it. Clearly, while a second layer is likely to be formed above dense enough thiol SAMs, the existence of radical thiyls floating outside the layer is much less reliable, and one would simply expect that no further thiyls can be formed in a too crowded layer: in this sense, the present result indicates the maximum number density dynamically stable in these conditions.

Besides investigating the density limit of stable monolayers, MD can provide some insights also about the SAM structure at various coverages. Apart from the units leaving the surface at high densities, mentioned above, molecules and radicals were found either in ‘horizontal’ or ‘vertical’ arrangement: in the former (related to the “striped phase” observed in many STM images,⁵⁸ even if in our case the thermal motions produce disordered layers) the units lie down on the slab maximizing the interaction of all the atoms with the surface, in the latter sulfur interacts strongly with gold, while the rest of the organic atoms are involved mainly in side intermolecular interactions, which can be overall attractive or repulsive, depending on the SAM density. A number of STM and theoretical (mainly ab initio) studies² have shown that at low temperature dense SAMs of alkylthiols tend to form ordered structures, with a well defined tilting angle between the alkyl chains and the gold surface: our FF is not constructed to reproduce this detail of the structure, since we are interested in the overall stability of the layer, with a reliable calculation of molecule/surface and molecule/molecule interactions, including the strong thermal motions at room temperature.

Some representative snapshots of the simulated thiol and thiyl SAMs are shown in Fig. 2: clearly the position and orientation of the organic units change during the dynamics, but we found that the number of horizontal and vertical arrangements at the various densities is remarkably stable at 298 K.

Fig. 2 MD snapshots (top and side views) of: thiol (A) and thiyl (B) SAMs with different number densities (nm⁻²) (indicated below each image). In red/green molecules in horizontal/vertical arrangement.

The simulations show that at low coverage the organic units prefer to lie on the surface, because the interactions with the gold atoms are favored with respect to the intermolecular ones. As the SAM density increases, more and more molecules and radicals stand vertically, in agreement with the mechanism of the monolayer formation often proposed in the literature.^59–62 Thiol SAMs are less ordered then thiyl layers: in the former numerous molecules remain in horizontal position even at high densities competing with their vertical counterparts for the gold surface. As noted above, it is not possible to simulate an all-vertical thiol SAM, since the molecules prefer to leave a too crowded layer.

On the other hand, the vertical arrangement is easier in thiyl SAMs, since it allows a better interaction between the sulfur and gold atoms (which is markedly stronger than the analogous interaction in thiols) compensating the partial loss of stabilization when the molecule/surface interactions are substituted by side-side intermolecular ones. As a consequence, thiyl SAMs can be denser and more ordered: at high densities, almost all the radicals are in vertical position, allowing a closer packing. A picture of the ordered patterns established in a dense thiyl SAM, with several MMC phenyl rings stacked in lines is shown in the ESI.†

Chemical potential calculations

The MD simulations discussed above provide useful insights about the SAM dynamical stability: however, this approach is not completely satisfactory, since the dynamics risk to be biased by the initial conformations, unless they can be run for a very long time and possibly with reasonable temperature annealings, to refine the exploration of the potential surfaces.

The information obtained with MD, however, can be complemented by the calculation of the monolayer chemical potentials as a function of the SAM density. The chemical potentials μ_SH(n), μ_S(n) are defined as the free energy changes associated to the addition of a MMC unit to an already formed SAM of (n − 1) molecules or radicals, respectively. In the practice, these quantities are computed by removing one molecule or radical from a n-units SAM: since various molecules/radicals can experience different interactions inside the SAM, the calculations are repeated for 5 random units and averaged.

The calculation of the chemical potentials was performed with the method illustrated in the Section “Methods” on the SAMs previously modeled and equilibrated with MD: the values obtained for thiol and thiyl at the various densities are collected in Table 1. Such potentials are referred to an isolated molecule or radical in ideal gas state; μ_SH(n) and μ_S(n) cannot be directly compared to each other, nor used to estimate the ΔG of SAM formation, unless other contributions are included, for instance for desolvation and S–H bond dissociation. This thermodynamic analysis is beyond the scope of this paper, and will be considered in a future work.

Table 1 Chemical potential (μ, kJ mol⁻¹) of MMC monolayers on Au(111) surfaces; n is the number of molecules or radicals per model slab; ρ (nm⁻²) the SAM number density. The potentials are averaged over 5 different molecules/radicals decoupled from the SAM; standard errors are reported as well

Thiol			Thiyl
n	ρ	μ SH(n)	n	ρ	μ S(n)
24	0.50	−226 ± 1	24	0.50	−352 ± 2
99	2.05	−136 ± 9	103	2.12	−310 ± 15
147	3.04	−121 ± 10	171	3.53	−255 ± 3
171	3.54	−109 ± 7	190	3.93	−196 ± 11
180	3.72	−108 ± 7	196	4.06	−137 ± 17
			205	4.24	−86 ± 11
			215	4.45	+22 ± 5
			234	4.84	+298 ± 29

---

The data show that the chemical potential of thiol SAMs remains negative even at the highest densities attainable with the MD equilibration. One could wonder why it is not possible to simulate SAMs with higher densities, then: as mentioned above, when the monolayer density grows, an increasing number of thiols leave the gold surface during the MD and form a sort of second layer, strongly interacting with the underlying molecules still in the SAM. The chemical potential of one molecule belonging to this second layer, computed with the same technique as above, falls in the range −102/−112 kJ mol⁻¹, depending on the position, very close to the thiol potential in the SAMs with 100 to 145 molecules. Then the dynamical instability of denser SAMs, observed in the MD runs, can derive from the competition of the second layer, favoring the shift from the crowded SAM to the spacious layer floating above it.

On the other hand, in the case of thiyl layers we see that the densest SAM, with number density 4.84 nm⁻², is not thermodynamically favored, though stable during the MD. Evidently, in this case the MD could not lead to a complete equilibration, since no radicals left the surface despite the thermodynamic advantage that could have been gained, because of the very high energy needed to break the strong S–Au bond, which “trapped” the SAM in a less favorable conformation. The chemical potential of the SAM at density 4.24 nm⁻² is still largely negative, while the SAM at 4.45 nm⁻² is slightly unfavored, considering the uncertainty associated to the average potential. So the chemical potential calculation refines the MD analysis, lowering the highest density predicted for a thiyl SAM to around 4.4 nm⁻².

Experimental quantification of the molecular density

The surface density of the MMC molecules in the SAMs formed on a flat reflecting gold surface was determined by performing a reference-free GIXRF experiment,⁵³ sketched in Fig. 3a.

Fig. 3 (a) Schematic representation of the GIXRF measurement where the X-ray beam impinges on the reflecting sample surface at θ angle and excites the fluorescence radiation detected at 90. (b) Deconvolution of the spectrum acquired at θ = 0.5.

For the quantification of MMC, the GIXRF measurements were perfomed by selecting sulfur as target element. The experiment was carried out on a gold-coated substrate incubated in the MMC solution to determine the sulfur mass per unit area ascribable to the SAM. On each probed sample, the fluorescence photon count rate of the sulfur K fluorescence line, obtained through spectral deconvolution (Fig. 3b), was converted to its mass per unit area using eqn (1) and tabulated values of the sulfur K-shell fluorescence yield ω_S,K = 0.08038 with a relative uncertainty of 7.5% estimated in ref. 63 and of the partial photoionization cross section τ_S,K(E₀ = 2.6 keV) = 1737 cm² g⁻¹ with a relative uncertainty of 5%.⁶⁴ The ratio k between the effective surface area of the gold surface area, characterized by AFM on a non-functionalized surface (more details in the ESI†), and the theoretical projected area was found to be k = (1.0076 ± 0.0014), so that the correcting factor 1/k = (0.9925 ± 0.0014).

The mass of sulfur per unit area was found to be σ_SMMC = (24.3 ± 4.0) ng cm⁻², the overall uncertainty of 11% derived mainly from the fundamental parameter uncertainties, already reported, and additional 4% relative uncertainty on the determination of solid angle of detection, 1.5% relative uncertainty on the incident photon flux and 2% on the XSW field intensity above the sample surface. From σ_SMMC, the numerical density of sulfur atom is easily derived through the element atomic weight and the Avogadro number. Since there is only one sulfur atom per each MMC (molecule or radical), its numerical density corresponds to the number of self-assembled MMC per unit area which is (4.5 ± 0.7) nm⁻². The total uncertainty associated to every reported value is due to the propagation of uncertainties for independent variables including statistical uncertainty on repeated measurements and the uncertainty contributions in eqn (1).

XPS analysis of the bond chemistry

The nature of bonds between gold surfaces and organic thiols has been widely studied in the last decades. XPS is one of the most used techniques to investigate such bonds, considering in particular the difference between bound and unbound species. As reported by Castner et al.,⁶⁵ there is a sort of hierarchical displacement in the position of the S(2p_3/2) core-level binding energy (CLBE), which follows this general trend: unbound thiol or disulfide (164–163 eV), bound thiol or thiyl in hollow site (162 eV) and thiyl in low-coordination site (<162 eV). Zubragel et al.⁶⁶ have also deeply studied the presence of different sulfur species in SAMs on Au and Ag, but they attribute the chemical shift at 161.8 eV to threefold bound thiols, and the shift at 163.1 eV the bound thiyl in lower coordination sites, in contrast with the work in ref. 65. More recent works have tried to describe more accurately the chemical species that can be found on a Au thin film, by comparing DFT simulations with surface experimental analysis.^67–69 In particular, Jia et al.⁶⁹ have recognized four different chemical shifts due to the interaction of sulfur species on the Au layer. A first component at low binding energy (161.2 eV) is assigned to the thiyl in a metastable site rather than atomic sulfur, as previously reported,⁶⁷ a second one (162.0 eV) to bound thiyl, a third one (163.0 eV) to unbound or free –SH, and a final one at binding energy higher than 163.5 eV, is assigned to physisorbed –SH on a second layer on SAM.

Thus we have checked the MMC powder, which provides the reference value for unbound thiol, and the MMC SAM on Au thin film sample. MMC powder survey spectrum (not reported) has shown the presence of C(1s), O(1s) and S(2p) peaks, as expected, while the MMC on Au sample has shown in addition the presence of Au(4f) doublet. In Fig. 4, high resolution S(2p) core level spectra have been reported for the two analyzed samples, along with the corresponding deconvolution curves.

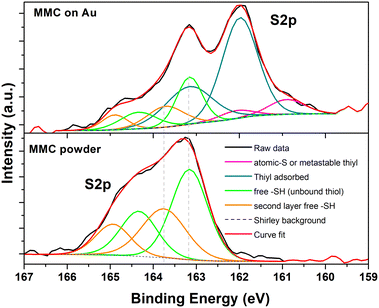Fig. 4 XPS S(2p) core level spectra for MMC precursor powder (bottom) and MMC SAM on Au (top). Deconvolution curves have been reported in both graphs.

For the MMC powder (Fig. 4, bottom) we identify two components, each one made by a doublet due to S(2p_3/2) and S(2p_1/2) spin–orbit splitting, at 163.1 eV (53.9%) and at 163.7 eV (46.1%). For the MMC SAM on Au (Fig. 4, top) the doublets rise to 4: at 161.0 eV (8.6%), at 162.0 eV (58.9%), at 163.1 eV (19.9%) and at 163.7 eV (12.6%).

In agreement with Jia et al. assignments,⁶⁹ the components detected in the MMC powder are attributed to free –SH or mutually interacting thiols (referred to as “second layer” in the figure caption). Passing to MMC SAM, two new, intense peaks arise at lower CLBE: most authors attribute the signals in this region to thiyls chemisorbed on the Au surface (often referred to in the literature as “thiolate”, as noted above), though the possibility of physisorbed thiols is not definitely excluded. Interestingly, the peaks due to free –SH above 163 eV are still present in the SAM photoemission spectra, even if weaker than the lower energy components, suggesting the presence of undissociated thiols also, either inside the SAM or in the second layer mentioned above.

Comparison of experimental and theoretical results

As seen above, the MD analysis of denser and denser SAMs allows to put an upper bound to the number of thiol or thiyl units that can be assembled on a flat, unreconstructed (111) gold surface: we found that the highest dynamically stable densities are 3.7 nm⁻² for thiols, and 4.8 nm⁻² for thiyls.

The calculation of SAM chemical potentials with MD thermodynamic integration leads to a refinement of the previous conclusion: with this approach, the maximum density of thiol SAMs is confirmed at 3.7 nm⁻² while for thiyl SAMs it results not higher than 4.4 nm⁻².

The SAM density obtained from the GIXRF experiments is (4.5 ± 0.7) molecules per nm². This value is comparable within the error bars with the theoretical prediction of the SAM density for thiyls, while the thiol theoretical density lies just below the interval given by the experimental uncertainty.

The XPS measurements performed on the same SAM allowed to probe the chemical bond at the SAM interface, and to postulate the sulfur oxidation state. Two signals have been assigned to adsorbed radicals: the more intense one (58.9%) to thiyl group and the second one (8.6%) to metastable thiyl in alternative adsorption sites. Two weaker components have been ascribed to free or physisorbed thiol species, either at the Au surface or in a second layer above the MMC SAM.

In conclusion, both the comparison of theoretical and experimental densities and the XPS analysis indicate a marked prevalence of thiyl radicals in the SAM, though the presence of a minor component of undissociated thiols is also compatible with XPS results.

Author contributions

D. M., A. Z. and M. Co. performed theoretical calculations; E. C., F. F. L., P. H., Y. K. and B. B. performed GIXRF experiments; M. Ca. performed XPS experiments; P. K. performed AFM surface area measurement; M. L. and M. Co. supervised; M. Co., E. C. and M. Ca. wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. M., A. Z., M. L. and M. Co. acknowledge the financial support by Università del Piemonte Orientale (through the FAR-2019 funding program). E. C., F. F. L., P. H., Y. K. and B. B. acknowledge the project 19ENV05 AEROMET II. The project 19ENV05 AEROMET II has received funding from the EMPIR programme co-financed by the Participating States and from the European Unions Horizon 2020 research and innovation programme.

References

1. R. G. Nuzzo and D. L. Allara, J. Am. Chem. Soc., 1983, 105, 4481–4483.
2. C. Vericat, M. Vela, G. Benitez, P. Carro and R. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834.
3. H. Häkkinen, Nat. Chem., 2012, 4, 443–455.
4. A. Laroussi, M. Kot, J. Flege, N. Raouafi and V. Mirsky, Appl. Surf. Sci., 2020, 513, 145827.
5. D. Rovati, B. Albini, P. Galinetto, P. Grisoli, B. Bassi, P. Pallavicini, G. Dacarro and A. Taglietti, Nanomaterials, 2019, 9, 1288.
6. Y.-S. Wang, S. Yau, L.-K. Chau, A. Mohamed and C.-J. Huang, Langmuir, 2019, 35, 1652–1661.
7. P. Pengo and L. Pasquato, J. Fluorine Chem., 2015, 177, 2–10.
8. T. Lawton, J. Uzarski and S. Filocamo, Chem. – Eur. J., 2016, 22, 12068–12073.
9. M. Bhuvana and V. Dharuman, Sens. Actuators, B, 2016, 223, 157–165.
10. D. Demirkol, H. Yildiz, S. Sayin and M. Yilmaz, RSC Adv., 2014, 4, 19900–19907.
11. C. Crudden, J. Horton, I. Ebralidze, O. Zenkina, A. McLean, B. Drevniok, Z. She, H.-B. Kraatz, N. Mosey, T. Seki, E. Keske, J. Leake, A. Rousina-Webb and G. Wu, Nat. Chem., 2014, 6, 409–414.
12. D. Valley, M. Onstott, S. Malyk and A. Benderskii, Langmuir, 2013, 29, 11623–11631.
13. L. Newton, T. Slater, N. Clark and A. Vijayaraghavan, J. Mater. Chem. C, 2013, 1, 376–393.
14. M. Reik, M. Calabro, S. Griesemer, E. Barry, W. Bu, B. Lin and S. Rice, Soft Matter, 2019, 15, 8800–8807.
15. W. Azzam, P. Cyganik, G. Witte, M. Buck and C. Wöll, Langmuir, 2003, 19, 8262–8270.
16. K. Heister, D. L. Allara, K. Bahnck, S. Frey, M. Zharnikov and M. Grunze, Langmuir, 1999, 15, 5440–5443.
17. R. Gerlach, G. Polanski and H.-G. Rubahn, Thin Solid Films, 1998, 318, 270–272.
18. C. M. Whelan, C. J. Barnes, C. G. Walker and N. M. Brown, Surf. Sci., 1999, 425, 195–211.
19. I. Tirotta, A. Calloni, C. Pigliacelli, A. Brambilla, G. Bussetti, L. Duò, P. Metrangolo and F. Baldelli Bombelli, J. Fluorine Chem., 2018, 206, 99–107.
20. A. Pick and G. Witte, Langmuir, 2016, 32, 8019–8028.
21. F. Pak, K. Meral, R. AltundaÅŸ and D. Ekinci, J. Electroanal. Chem., 2011, 654, 20–28.
22. P. A. Lewis, Z. J. Donhauser, B. A. Mantooth, R. K. Smith, L. A. Bumm, K. F. Kelly and P. S. Weiss, Nanotechnology, 2001, 12, 231–237.
23. Y. Tai, A. Shaporenko, W. Eck, M. Grunze and M. Zharnikov, Langmuir, 2004, 20, 7166–7170.
24. C. Vericat, M. E. Vela, G. A. Benitez, J. A. M. Gago, X. Torrelles and R. C. Salvarezza, J. Phys.: Condens. Matter, 2006, 18, R867–R900.
25. N. Mhlanga and T. Ntho, Mater. Today Commun., 2021, 26, 101698.
26. R. Chadha, A. Das, S. Kapoor and N. Maiti, J. Mol. Liq., 2021, 322, 114536.
27. C. Engelbrekt, R. Nazmutdinov, T. Zinkicheva, D. Glukhov, J. Yan, B. Mao, J. Ulstrup and J. Zhang, Nanoscale, 2019, 11, 17235–17251.
28. J. Roy, E. Vasquez, H. Pinto, S. Kumari, K. Walters and J. Leszczynski, Phys. Chem. Chem. Phys., 2019, 21, 23320–23328.
29. S. Herrera, F. Tasca, F. Williams, E. Calvo, P. Carro and R. Salvarezza, Langmuir, 2017, 33, 9565–9572.
30. H. Guesmi, N. Luque, E. Santos and F. Tielens, Chem. – Eur. J., 2017, 23, 1402–1408.
31. L. Peiretti, P. Quaino and F. Tielens, J. Phys. Chem. C, 2016, 120, 25462–25472.
32. E. Bedford, V. Humblot, C. Méthivier, C.-M. Pradier, F. Gu, F. Tielens and S. Boujday, Chem. – Eur. J., 2015, 21, 14555–14561.
33. J. First and L. Webb, J. Phys. Chem. B, 2019, 123, 4512–4526.
34. X. Liu, P. Lu, H. Zhai and Y. Wu, Mater. Res. Express, 2018, 5, 035001.
35. D. Sridhar, R. Gupta and B. Rai, Phys. Chem. Chem. Phys., 2018, 20, 25883–25891.
36. S. Meena, C. Goldmann, D. Nassoko, M. Seydou, T. Marchandier, S. Moldovan, O. Ersen, F. Ribot, C. Chanéac, C. Sanchez, D. Portehault, F. Tielens and M. Sulpizi, ACS Nano, 2017, 11, 7371–7381.
37. J. Devi, J. Mol. Graphics Modell., 2017, 74, 359–365.
38. M. Rodríguez González, P. Carro, E. Pensa, C. Vericat, R. Salvarezza and A. Hernández Creus, Chem. Phys. Chem., 2017, 18, 804–811.
39. N. B. Luque, E. Santos, J. Andres and F. Tielens, Langmuir, 2011, 27, 14514–14521.
40. F. Tielens and E. Santos, J. Phys. Chem. C, 2010, 114, 9444–9452.
41. L. L. Rouhana, M. D. Moussallem and J. B. Schlenoff, J. Am. Chem. Soc., 2011, 133, 16080–16091.
42. L. Kankate, A. Turchanin and A. Gölzhäuser, Langmuir, 2009, 25, 10435–10438.
43. M. Inkpen, Z. Liu, H. Li, L. Campos, J. Neaton and L. Venkataraman, Nat. Chem., 2019, 11, 351–358.
44. I. I. Rzeźnicka, J. Lee, P. Maksymovych and J. T. Yates, J. Phys. Chem. B, 2005, 109, 15992–15996.
45. M. Hasan, D. Bethell and M. Brust, J. Am. Chem. Soc., 2002, 124, 1132–1133.
46. R. G. Nuzzo, B. R. Zegarski and L. H. Dubois, J. Am. Chem. Soc., 1987, 109, 733–740.
47. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25.
48. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
49. A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037.
50. V. Khanna, J. I. Monroe, M. F. Doherty and B. Peters, J. Comput.-Aided Mol. Des., 2020, 34, 641–646.
51. C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268.
52. J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1170.
53. P. Hönicke, B. Detlefs, E. Nolot, Y. Kayser, U. Mühle, B. Pollakowski and B. Beckhoff, J. Vac. Sci. Technol., A, 2019, 37, 041502.
54. M. Müller, P. Hönicke, B. Detlefs and C. Fleischmann, Materials, 2014, 7, 3147–3159.
55. J. Sherman, Spectrochim. Acta, 1955, 7, 283–306.
56. B. Beckhoff, J. Anal. At. Spectrom., 2008, 23, 845–853.
57. V. Soltwisch, P. Hönicke, Y. Kayser, J. Eilbracht, J. Probst, F. Scholze and B. Beckhoff, Nanoscale, 2018, 10, 6177–6185.
58. P. Maksymovych, O. Voznyy, D. Dougherty, D. Sorescu and J. Yates Jr., Prog. Surf. Sci., 2010, 85, 206–240.
59. V. Ravi, J. M. Binz and R. M. Rioux, Nano Lett., 2013, 13, 4442–4448.
60. L. S. Jung and C. T. Campbell, J. Phys. Chem. B, 2000, 104, 11168–11178.
61. A. Królikowska, A. Kudelski, A. Michota and J. Bukowska, Surf. Sci., 2003, 532-535, 227–232.
62. G. E. Poirier and E. D. Pylant, Science, 1996, 272, 1145–1148.
63. M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 307–327.
64. T. Schoonjans, A. Brunetti, B. Golosio, M. S. del Rio, V. A. Solé, C. Ferrero and L. Vincze, Spectrochim. Acta, Part B, 2011, 66, 776–784.
65. D. G. Castner, K. Hinds and D. W. Grainger, Langmuir, 1996, 12, 5083–5086.
66. C. Zubrägel, C. Deuper, F. Schneider, M. Neumann, M. Grunze, A. Schertel and C. Wöll, Chem. Phys. Lett., 1995, 238, 308–312.
67. T. Ishida, N. Choi, W. Mizutani, H. Tokumoto, I. Kojima, H. Azehara, H. Hokari, U. Akiba and M. Fujihira, Langmuir, 1999, 15, 6799–6806.
68. F. Dufour, B. Fresch, O. Durupthy, C. Chanéac and F. Remacle, J. Phys. Chem. C, 2014, 118, 4362–4376.
69. J. Jia, A. Kara, L. Pasquali, A. Bendounan, F. Sirotti and V. A. Esaulov, J. Chem. Phys., 2015, 143, 104702.

---

Footnote

† Electronic supplementary information (ESI) available: Details on the FF parameterization, BAR method, surface area measurement, GIXRF measurements and XPS signal analysis, picture of high densiy thiyl SAM. See DOI: https://doi.org/10.1039/d2cp03103e

---