Why does solvent treatment increase the conductivity of PEDOT : PSS? Insight from molecular dynamics simulations

Abstract

Poly(3,4-ethylenedioxythiophene) : polystyrene sulfonate (PEDOT : PSS) is one of the most important conducting polymers. In its pristine form its electrical conductivity is low, but it can be enhanced by several orders of magnitude by solvent treatment, e.g. dimethyl sulfoxide (DMSO). There are various (and often conflicting) explanations of this effect suggested in the experimental literature, but its theoretical understanding based on simulation and modelling accounting for the complex realistic morphology of PEDOT : PSS is missing. Here, we report Martini coarse-grained molecular dynamics simulation for the DMSO solvent treatment of the PEDOT : PSS film. We show that during solvent treatment a part of the deprotonated PSS chains are dissolved in the electrolyte. After the solvent treatment and subsequent drying, the PEDOT-rich regions become closer to each other, with a part of the PEDOT chains penetrating into the PSS-rich regions. This leads to an efficient coupling between PEDOT-rich regions, leading to the enhancement of the conductivity. Another factor leading to the conductivity improvement is the π–π stacking enhancement resulting in more π–π stacks in the film and in the increased average size of PEDOT crystallites. Our results demonstrate that course-grained molecular dynamics simulations of a realistic system represent a powerful tool enabling theoretical understanding of important morphological features of conducting polymers, which, in turn, represents a prerequisite for materials design and improvement.

---

I. Introduction

In the past decades, conducting polymers have attracted tremendous attention for application in devices utilizing mixed electron–ion conductivity such as sensors, organic electronic ion pumps, electrochemical transistors, and supercapacitors.¹ Among different conducting polymers, poly(3,4-ethylenedioxythiophene) : polystyrene sulfonate (best known as PEDOT : PSS) is widely used due to its excellent optical, mechanical and electronic properties, stability and well-established low-cost synthesis process.^2–4

The morphology of PEDOT : PSS thin films is complex and depends on the synthesis process. One of the common features of its morphology is the formation of 20–30 nm size PEDOT- and PSS-rich regions.⁵ Pristine PEDOT : PSS is not a good conducting material, and this feature can be related to microscopic phase separation between PEDOT- and PSS-rich regions. However, its electrical conductivity can be enhanced by different chemical treatments, with one of the most used methods being the treatment with different high boiling point polar solvents (e.g. dimethyl sulfoxide (DMSO) and ethylene glycol) or ionic liquids.⁶ The conductivity enhancement by DMSO depends on the details of the experiment (e.g. type of solvent, solvent concentration and treatment method). However, the common observation in most experiments is the enhancement of the conductivity of PEDOT : PSS by 3 orders of magnitude, independent of the experimental details.^7–23Fig. 1 presents some of the models proposed in experimental papers to explain the conductivity enhancement in DMSO-treated PEDOT : PSS films. This includes the formation of coil-like PSS and PEDOT-PSS phase separation²³ (Fig. 1(a)), re-clustering of PEDOT^8,15,19 (Fig. 1(c and d)), DMSO covering of PEDOT¹¹ (Fig. 1(b)), changing PEDOT chains from a coil form into a linear structure²⁰ (Fig. 1(e)), barrier size reduction between PEDOT¹⁸ (Fig. 1(f)), removing free PSS¹⁴ (Fig. 1(g)) and the change of PEDOT : PSS from a coil structure into an ellipsoidal form⁷ (Fig. 1(f and h)). Even though the common feature in the above models is the re-shaping of the PEDOT-rich region and change of the PEDOT/PSS ratio, the different models offer very different explanations for the observed enhancement. Hence, a satisfactory understanding of this phenomenon is not achieved yet, and its interpretation still remains controversial.

Fig. 1 Graphical review of different models suggested for the explanation of PEDOT : PSS conductivity enhancement due to DMSO treatment. (a) Sketched based on Rwei et al.,²³ reproduced with permission from (b) Yan et al.,¹¹ (c) Thomas et al.,⁸ (d) Dhar et al.,¹⁵ (e) Wang et al.,²⁰ (f) Mahato et al.,¹⁸ (g) Kim et al.,¹⁴ (h) Gasiorowski et al.,⁷ and (i) Yildimir et al.²⁴

It should be noted that most of the above-mentioned models were suggested based purely on experimental observations, and not corroborated by theoretical simulation and modelling that are able to provide a microscopic insight into PEDOT : PSS morphology and its changes during solvent treatment. In recent years, molecular dynamics (MD) simulations became a powerful tool in studies of conducting polymers providing information on materials morphology that is not available by conventional means and that is in a position to quantitatively explain/predict experiments. This includes, for example, atomic resolution of the active layer of a bulk heterojunction in polymeric solar cells,²⁵ understanding the formation of the granular structure and the origin of swelling in PEDOT : PSS,⁵ the effect of the nature and length of side chains on electrochemically induced volume changes,^26,27 and the role of the substrate in structural phase transitions in a conducting polymer during ion injection and water intake under cyclic voltammetry.²⁸

Recently, density functional theory (DFT) calculations were performed for the pairwise interaction between PEDOT, PSS, PSSH (protonated PSS), DMSO, and water.²⁴ The authors also performed atomistic MD simulations for a small model system consisting of two PEDOT and two PSS chains, suggesting the phase separation between PEDOT and PSS as illustrated in Fig. 1i as the mechanism of the conductivity enhancement. It is noteworthy that related DFT and MD simulations addressing the conductivity enhancement of PEDOT : PSS after treatment by ionic liquids were reported by de Izarra et al.^29–31

As conjectured in the above-mentioned experimental studies, changing the morphology of PEDOT- and PSS-rich regions after the solvent treatment may represent the key to the conductivity enhancement. Therefore, an accurate and reliable MD modelling that is in the position to explain the experimental observation necessitates an accurate description of the PEDOT : PSS morphology, in particular accounting for the presence of PEDOT- and PSS-rich regions. Such a description requires coarse-grained MD simulations because all-atomistic MD simulations are computationally too expensive to reach the required length scale and system size (10 nm and above, with many hundreds of PEDOT and PSS chains).

In the present study we perform coarse-grained MD simulations of PEDOT : PSS treatment by a polar solvent, DMSO. In our simulations, we are able to reach the scale of realistic films with PEDOT- and PSS-rich regions, which is the prerequisite for the reliable modelling of the system at hand. The simulations provide a direct microscopic insight into the change in the configuration, morphology and arrangement of PEDOT and PSS chains by solvent treatment. Finally, the changes in the conductivity of the PEDOT : PSS film after the treatment are related to the changes in morphology.

II. Model and computational details

We adopt the Martini coarse-grained (CG) force field to investigate the morphology of PEDOT : PSS after solvent treatment.³² Our simulations mimic the post-treatment by immersing the PEDOT : PSS film into the solvent bath. In the Martini force field, each 3–4 atoms are grouped into a representative CG bead. The Martini CG beads are categorized into four main groups: polar (P), nonpolar (N), apolar (C) and charged (Q) beads. There are also subgroups for fine-tuning of non-bonded interactions between beads. Here by adopting the Martini coarse grained force field, we can simulate a large enough system to capture the nanoscale morphology of PEDOT- and PSS-rich regions.

The Martini CG models for PEDOT,³³ PSS,³⁴ PSSH,³⁵ and polarizable water³⁶ were adopted from previous works; see Fig. S1 (ESI†) showing beads representing all parts of the system. It should be noted that, despite the success of the Martini model for the description of various systems in biology and materials science,³² this model has some inherent limitations as recently discussed by Alessandri et al.³⁷ The ultimate validation of the model and force fields can be based on the agreement between the experimental results and corresponding simulations. In this respect it can be mentioned that MD simulations of PEDOT : PSS and a closely related system based on the developed MARTINI force field demonstrated quantitative agreement with a number of experimental observations. This includes the size of crystallites in PEDOT : TOS and PEDOT : PSS,^5,33 the degree of swelling of PEDOT : PSS when immersed in water,⁵ the z-potential of PEDOT : PSS particles in suspension,³⁸ and the mass change in PEDOT : TOS during voltammetry cycles.³⁹ It is noteworthy that atomistic modeling of PEDOT : PSS complexes and new all-atom force field parametrization were recently reported in ref. 40 and 41.

As mentioned in the Introduction, the enhancement of the conductivity of PEDOT : PSS is not limited specifically to DMSO, but represents a generic phenomenon that is observed for many different solvents. Therefore, to model DMSO we choose P5 which is the most polarizable bead from the Martini forcefield. Thus, this choice of the polarizable bead is representative of other polar solvents that are used in PEDOT : PSS treatment. It is noteworthy that, in order to investigate solvent-specific changes in the morphology caused by different solvents, the coarse-grained Martini calculations can be further refined by backmapping into atomic representation for specific solvents using different backmapping techniques reported in the literature.^25,42,43

The PEDOT chain length was considered as 12 monomer units which is consistent with recent experimental and theoretical works (see ref. 44 and references therein). The PEDOT oxidation level is set to 33%,⁴⁵ which is modeled by equal charge distribution in the virtual backbone atoms. The PSS and PSSH degree of polymerization is 50 which is longer than the persistent length.

For the simulation of solvent treatment, we first prepare the PEDOT : PSS film from an initial suspension of PEDOT : PSS particles, which mimics a typical experimental procedure (note that the present model for PEDOT : PSS solution and the dried film is based on the model and the corresponding computational procedure developed in our previous work⁵). The weight ratio between PEDOT and (PSS + PSSH) is 1 : 2.5, which corresponds to a typical experimental situation. We start with a PEDOT : PSS particle in water; its core represents the PEDOT-rich region which is composed of 500 PEDOT and 63 PSS chains. 2/3 of the sulphonate groups in PSS chains belonging to the PEDOT-rich region are deprotonated (i.e. negatively charged) to compensate PEDOT positive charge and keep charge neutrality in the system (the total number of charges is +2000e on PEDOT and −2000e on PSS in the PEDOT-rich region). The PEDOT core is surrounded by a PSS-rich region made of 217 PSSH chains (it should be noted that, in the initial aqueous solution, the sulfonate groups in the PSS-rich region are deprotonated, such that PSS gradually converts into PSSH as water evaporates. However, to speed up the calculation we use the model with already protonated PSSH chains in the initial solution because we showed previously that this model leads to practically the same morphology as the one when sulphonate groups are gradually protonated during evaporation⁵). The composition of the computational box for the preparation of the initial dry film is shown in Table S1 (ESI†).

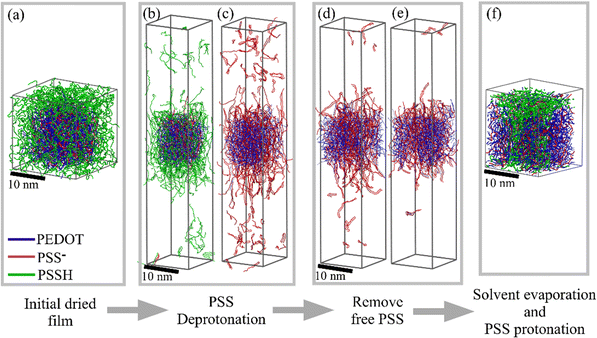
We perform the NPT equilibration for 50 ns and production run for 250 ns. The periodic boundary conditions for the box are used in all MD simulations. During the equilibration polymer chains are restrained and water molecules are allowed to move. Then, water is evaporated in successive steps, where in each step 1.25% of the remaining water is removed and the simulation box is equilibrated for 4 ns, followed by an 8 ns production run (note that the 8 ns production run is sufficient to reach the energy equilibrium; see Fig. S3 (ESI†) showing the evolution of the total energy during water evaporation). After evaporation we obtain the dry film as illustrated in Fig. 2a. The content of the computational box during preparation of the thin film is shown in Table S2 (ESI†).

Fig. 2 (a) Initial dry PEDOT : PSS film before immersing in the solvent. PEDOT : PSS film inside the solvent box at (b) 40% and (c) 100% deprotonation levels. Releasing PSS into the solvent after the (d) first and (e) third step. (f) The final dried film after solvent evaporation and PSS protonation.

Having prepared the dry film, we proceed with solvent treatment (the content of the computational box during solvent treatment is shown in Table S3, ESI†). First, the dried film is immersed into the DMSO solvent bath (with nearly 120 000 DMSO molecules) and all PSSH monomers are deprotonated in five steps. At each deprotonation step, 20% of randomly chosen PSSH units are converted to PSS⁻ units; the solvent is equilibrated for 50 ns and the production run lasts for 150 ns. Fig. S4 (ESI†) shows the evolution of the total energy during deprotonation. It is noteworthy that in our previous study we demonstrated that the details of the evaporation/solvation protocols (number of steps and equilibration time) practically do not affect the resulting morphology.⁵ During each deprotonation step the Na⁺ ions are added to compensate additional negative charge from PSS⁻ (in total, 12 000 Na⁺ ions are added). Note that the added Na⁺ ions in the Martini model can be also considered as hydronium ions.⁵ It should be mentioned that a reliable experimental report of the logarithmic dissociation constant (pK_a) of PSS in water is not available (see the discussion in ref. 46); the theoretical value of the logarithmic dissociation constant (pK_a) of PSS in water is 2.9,⁴⁷ which indicates the complete deprotonation of PSS acid in water. In general, the pK_a of acids in DMSO is larger than that in water.⁴⁸ Note however that in our modelling we immerse PEDOT : PSS into DMSO, whereas experimentally DMSO–water solution is used (typically ∼5 wt%). Therefore, it is expected that PSS experimentally is fully deprotonated, which we model in our simulations.

Some PSS chains that are not strongly bound to the polymer matrix are released into the solvent. We perform three step PSS removal with 50 ns solvent equilibration and 150 ns production run. Experimentally, the amount of solvent is much larger than that of the PEDOT : PSS film. As a result, the released PSS chains are dissolved in the bulk of the solvent. To mimic the experimental condition, we remove the released PSS chains from the simulation box, where we set 5 nm as a critical distance between the film surface and a chain to be removed from the system (note that a similar way to model released tosylate (TOS) counterions from the PEDOT:TOS films during cyclic voltammetry was adopted in ref. 39). The solvent is evaporated by removing 1.25% of DMSO molecules at each step; at each step the equilibration of the box for 4 ns is performed, followed by an 8 ns production run. The whole simulation time for the evaporation process is nearly 700 ns. Finally, the deprotonated PSS⁻ chains are again protonated in the dried film in one step. We protonate only those PSS chains that were initially protonated in the dry film in the PSS-rich region before the treatment. The PSS chains inside the PEDOT-rich region remain deprotonated to compensate a positive charge on PEDOT. It is noteworthy that the comparison of the initial films (before immersing into the solvent) and the final dried film after the treatment (and before de-protonation) shows that parts of the chains originally belonging to PEDOT- and PSS-rich regions stay in the respective regions after the treatment and do not diffuse into different regions. All molecular dynamics calculations are performed within the NPT (fixed number of particles, pressure and temperature) ensemble under ambient conditions (T = 300 K and P = 1 atm). For all MD simulations, the long-range Coulomb electrostatic interactions are calculated by using the smooth particle mesh Ewald method with a cutoff of 1.2 nm.⁴⁹ The MD simulations are performed by using the GROMACS package^50,51 and visualization of final morphologies is done by using VMD.⁵² A set of input files for the initial PEDOT : PSS solution are provided in the ESI† (see also Table S4 for file description).

III. Results and discussion

We start from preparation of a dried PEDOT : PSS film from the initial water solution as described in the Model section⁵ (see Fig. S2, ESI†). Fig. 2a shows the resulting pristine PEDOT : PSS dry film (note that because of the periodic boundary conditions used in the calculations the resulting film represents a periodic array as illustrated in Fig. 3a). As discussed in our previous study,⁵ the PEDOT-rich region (central core in Fig. 2a) is composed of PEDOT and PSS chains, whereas the PSS-rich region (i.e. the region surrounding the central core) is composed of primarily PSSH chains. The PSS-rich region forms a nanometer-scale insulating layer which prevents connections between conducting PEDOT-rich regions, and therefore limits electronic conductivity.

Fig. 3 (a) The schematic representation of a periodic boundary condition and a schematic drawing illustrating the inter core PEDOT distance. (b) The statistical analysis of the minimum distance between PEDOT chains belonging to two different cores. (c) The radial distribution function between PEDOT chains before and after solvent treatment in units of the π–π stacking distance between PEDOT chains r_π–π = 4.7 Å. The interface between PEDOT-rich regions (d) before and (e) after solvent treatment. For clarity, PSS chains in the PSS-rich region are not shown and substituted by a green background.

The dried PEDOT : PSS film is immersed into a solvent bath and PSS chains are gradually deprotonated. It should be stressed that the deprotonation of PSSH is an important process which should be accounted for in realistic modelling of PEDOT : PSS morphology. For example, it was shown that deprotonation of PSS is the reason for swelling of PEDOT : PSS films when immersed in water.⁵Fig. 2b and c show the PEDOT : PSS film inside the solvent box at 40% and 100% deprotonation levels. As the deprotonation level increases, some PSS chains that are not strongly bonded to the PEDOT matrix are released from the polymer region and float inside the solvent. This apparently reduces the PEDOT/PSS ratio. As described in the Model section, to mimic the experimental condition, we remove dissolved PSS from the box in three steps. Fig. 2d and e illustrate, respectively, the first and third steps of the PSS removal. It is important to stress that, for the case when the PEDOT : PSS film is immersed into water, PSS chains are not dissolved in the water from the polymer matrix (see Fig. 4 in ref. 5 where no PSS chains in water are visible). It is tempting to relate the ability of DMSO (as opposed to water) to dissolve PSS from the polymer matrix to the difference in the interaction strength between PSS and DMSO, and PSS and water. However, the DFT calculations showed that the pairwise interaction between PSS and DMSO is in fact weaker than that between PSS and water.²⁴ Therefore, the difference in the pairwise interaction cannot be the reason for the PSS dissolution, as it would lead to the opposite effect. Note that in ref. 24 the interaction energy was calculated for two molecules in the optimized geometry. However, in the film, each oligomer is surrounded by many other molecules affecting the resulting configuration, and therefore the optimized geometry of two oligomers is of very little relevance. Moreover, removal of PSS chains from the polymer matrix to the bulk of the solvent requires overcoming potential barriers created by the surroundings (PEDOT and PSS chains, and DMSO molecules), which is more relevant to the efficiency of the dissolution as opposed to the pairwise interaction between one oligomer and one solvent molecule. Further studies are needed in order to shed light on the factors that facilitate the removal of deprotonated PSS chains from the film. Driving forces leading to dissociation/association of polyanionic polymers in aqueous solutions have been recently a subject of intense debate, where the focus has been on the role of entropic, enthalpic, hydrophobic and electrostatic contributions.^53–55 In this respect, it would be interesting to relate the solvation of PSS chains to the changes of the entropy of the system during solvent treatment. We plan to address this question in our future works.

After dissolution and removal of PSS chains, the film is gradually dried and PSS chains outside the PEDOT-rich regions are protonated back to PSSH. The PEDOT : PSS film retains the original morphological features where PEDOT-rich regions are surrounded by PSS-rich regions. However, a visual inspection of the resulting morphology shows that PEDOT-rich regions become closer to each other and better connected via PEDOT-chains penetrating into the PSS-rich region. In order to quantify the change in the morphology, we calculated the minimum distance between PEDOT chains in the neighboring regions before and after solvent treatment (see Fig. 3b). Before the solvent treatment the system practically does not contain the chains situated at a distance smaller than 10 Å. After the treatment, the number of chains with a minimal distance <10 Å greatly increases.

The observed changes in the morphology where the PSS-rich shell becomes thinner and PEDOT-rich cores become close to each other with better connection between PEDOT chains can be attributed to several reasons. Most importantly, a part of the PSS chains are dissolved and thus removed from the film. This reduces the PEDOT/PSS ratio as discussed above and apparently leads to a decrease in the size of the PSS-rich regions. Second, during deprotonation, PSSH turns into negatively charged PSS chains, which leads to an enhanced interaction between PEDOT in the core and PSS in the shell. This enhanced interaction facilitates the penetration of PEDOT chains into the PSS-rich regions. It is interesting to note that the minimum distance between PEDOT chains decreases gradually during the solvent treatment when the film is placed in the DMSO solvent and then dried out (see Fig. S5, ESI†). However, the most pronounced changes in the minimum distance, especially for distances smaller than 10 Å (i.e. those important for the mobility enhancement), occur during the final stages of the treatment, i.e. during solvent evaporation. During this stage, the solvent (most of which is situated in the PSS-rich region) is removed, which leads to the shrinkage of the PSS-rich regions, and therefore to the decrease of the minimum distance between PEDOT chains.

Let us now discuss how the change in the morphology outlined above affects the charge mobility of the film. It is well established experimentally,^56,57 and confirmed via multi-scale electron transport calculations,^58,59 that the efficient charge transport in conductive polymers including PEDOT does not require good crystallinity and long-range order. Instead, the good conductivity is achieved via efficient short-range connections between crystallites or local aggregates via “tie” polymeric chains bridging these local conducting domains and thus giving rise to percolative paths extending through the entire film. Note that percolative paths comprise both polymer backbones as well as π–π stacking, with the latter being a prerequisite for the efficient coupling between neighboring chains.^58,60 As mentioned before, the system before the treatment does not contain the chains in the neighboring regions with a distance smaller than 10 Å. This distance is significantly larger than the π–π stacking distance between the PEDOT chains (≈4.7 Å, see the discussion below), which means that the coupling between the neighboring regions is exponentially suppressed, and the mobility is vanishingly small (note that for the case of hopping transport in conducting polymers the hopping probability ν(r) between two states exponentially depends on the separation distance r, ν(r) ∼ ν₀ exp(−r/a), where ν₀ is a constant and a describes the extension of the localized state).^58–61 As discussed above, after the treatment chains in the neighboring regions get close to each other, and the number of chains with the minimal distance before the treatment (10 Å) greatly increases (see Fig. 3b). Thus, the coupling (hopping probability) between chains is expected to increase exponentially, leading to an exponential increase of the conductivity.

In addition to the decrease of the minimum distances between PEDOT chains, the solvent treatment leads to the improvement of the π–π stacking. Fig. 3c presents the radial distribution function (RDF) between PEDOT chains, defining the probability to find PEDOT chains separated by the distance r. The RDF exhibits peaks at the integer multiple of the distance r = r_π–π (=4.7 Å). This periodicity in the arrangements of PEDOT chains corresponds to the formation of small crystallites, where the number of chains in the crystallite, N_chains, is apparently related to the number of peaks, N_peaks, as N_chains= N_peaks + 1, and the distance between the chains in the crystallites (i.e. the π–π stacking distance) is r_π–π. Before the treatment, the RDF exhibits peaks at r = r_π–π and 2r_π–π, which correspond to the formation of crystallites composed, on average, of 3 chains. After the treatment, the peak heights significantly increase and a peak at r = 3r_π–π also becomes discernible. The increase of the peak heights corresponds to the π–π stacking enhancement (i.e. more π–π stacks in the film), whereas the increase of the number of peaks in the RDF corresponds to an increased average size of crystallites (from 3 to 4 chains). Both these factors apparently contribute to the enhancement of the mobility. Our findings concerning the π–π stacking enhancement are consistent with the experimental observations of the improvement of the crystallinity after the solvent treatment in PEDOT : PSS.^17,21 It should be noted that, in our Martini calculations, the π–π stacking distance was found to be r_π–π = 4.7 Å. This is larger than the experimental value (and the theoretical value obtained from the all-atomistic calculations), i.e. r_π–π ≈ 3.5 Å.^5,33 The origin of this discrepancy is well understood and is related to the fact that the size of the Martini beads is larger than the distance between PEDOT chains.^25,37 However, it was demonstrated that this discrepancy does not affect the nanomorphological features of the polymer film.²⁵ It is noteworthy that, by performing the backmapping of the coarse-grained Martini calculations into the atomistic geometry, the correct π–π stacking distance is recovered.^25,43

It is worth noting that our conclusions are qualitatively different from previous MD simulations of Yildimir et al.²⁴ who attributed the conductivity enhancement to the increased phase separation between PEDOT and PSS (see Fig. 1i). As discussed above, our calculations instead show that PEDOT chains penetrate into the PSS-rich region improving the connection between the PEDOT-rich regions. This outlines the importance of utilization of coarse-grained MD simulations (including thousands of polymer chains) enabling simulation of the realistic PEDOT : PSS morphology accounting for the presence of the PEDOT- and PSS-rich regions, as opposed to the all-atomistic MD modelling in ref. 24 where a tiny model system containing just two PEDOT chains was considered.

Finally, we note that in the present study we focus on the morphological changes in the film, and based on the obtained morphological results we provide a qualitative conclusion on the effect of these changes on conductivity as discussed above. We believe that these estimations are fully sufficient to outline the reasons for the conductivity enhancement. The quantitative estimations of the changes in the conductivity (not relying on the phenomenological parameters of the theory) would require multi-scale transport calculations^58–62 for a system even larger than the one treated here (containing at least two PEDOT-rich regions), including back-mapping from the coarse-grained calculations to the atomistic ones^25,42,43 to perform the mobility calculations. This is however beyond the scope of the present paper and can be a subject of a separate study.

IV. Conclusion

Using a realistic model of a PEDOT : PSS thin film accounting for the presence of PEDOT- and PSS-rich regions, we performed coarse-grained molecular dynamics simulations to unravel the changes in the morphology of PEDOT : PSS induced by polar solvent treatment. A schematic diagram summarizing the mechanism of the conductivity enhancement is presented in Fig. 4. Before the treatment, the PEDOT-rich regions (primarily consisting of positively charged PEDOT chains counterbalanced by negatively charged PSS chains) are well separated by PSS-rich regions (consisting primarily of PSSH chains). Under solvent treatment PSSH is deprotonated, and a part of the deprotonated PSS chains are dissolved in the electrolyte. After the solvent treatment and subsequent drying, the PEDOT-rich regions become closer to each other, with a part of the PEDOT chains penetrating into the PSS-rich regions. As a result, the minimum distance between PEDOT chains belonging to different PEDOT-rich regions decreases, leading to an increased coupling between the chains, and therefore to the enhancement of the conductivity. Another factor leading to the conductivity improvement is the π–π stacking enhancement resulting in more π–π stacks in the film and in an increased average size of crystallites.

Fig. 4 A schematic diagram illustrating the PEDOT : PSS conductivity enhancement due to treatment with a polar solvent (see the “Conclusion” section for details).

Our results demonstrate that course-grained molecular dynamics simulations of a realistic system represent a powerful tool enabling theoretical understanding of important morphological features of conducting polymers, which, in turn, represents a prerequisite for materials design and improvement.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by the Swedish Research Council (Projects 2016-05990 and 2017-04474) and Åforsk. The computations were performed using the resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC and HPC2N.

References

1. S. T. Keene, V. Gueskine, M. Berggren, G. G. Malliaras, K. Tybrandt and I. Zozoulenko, Exploiting mixed conducting polymers in organic and bioelectronic devices, Phys. Chem. Chem. Phys., 2022, 24, 19144–19163.
2. M. Berggren, X. Crispin, S. Fabiano, M. P. Jonsson, D. T. Simon, E. Stavrinidou, K. Tybrandt and I. Zozoulenko, Ion Electron–Coupled Functionality in Materials and Devices Based on Conjugated Polymers, Adv. Mater., 2019, 31, 1805813.
3. I. Petsagkourakis, N. Kim, K. Tybrandt, I. Zozoulenko and X. Crispin, Poly(3,4-ethylenedioxythiophene): Chemical Synthesis, Transport Properties, and Thermoelectric Devices, Adv. Electron. Mater., 2019, 5, 1800918.
4. I. Zozoulenko, J. F. Franco-Gonzalez, V. Gueskine, A. Mehandzhiyski, M. Modarresi, N. Rolland and K. Tybrandt, Electronic, Optical, Morphological, Transport, and Electrochemical Properties of PEDOT: A Theoretical Perspective, Macromolecules, 2021, 54, 5915–5934.
5. M. Modarresi, A. Mehandzhiyski, M. Fahlman, K. Tybrandt and I. Zozoulenko, Microscopic Understanding of the Granular Structure and the Swelling of PEDOT:PSS, Macromolecules, 2020, 53, 6267–6278.
6. S. Kee, N. Kim, B. S. Kim, S. Park, Y. H. Jang, S. H. Lee, J. Kim, J. Kim, S. Kwon and K. Lee, Controlling Molecular Ordering in Aqueous Conducting Polymers Using Ionic Liquids, Adv. Mater., 2016, 28, 8625–8631.
7. J. Gasiorowski, R. Menon, K. Hingerl, M. Dachev and N. S. Sariciftci, Surface morphology, optical properties and conductivity changes of poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) by using additives, Thin Solid Films, 2013, 536, 211–215.
8. J. P. Thomas, L. Zhao, D. McGillivray and K. T. Leung, High-efficiency hybrid solar cells by nanostructural modification in PEDOT:PSS with co-solvent addition, J. Mater. Chem. A, 2014, 2, 2383.
9. T.-R. Chou, S.-H. Chen, Y.-T. Chiang, Y.-T. Lin and C.-Y. Chao, Highly conductive PEDOT:PSS films by post-treatment with dimethyl sulfoxide for ITO-free liquid crystal display, J. Mater. Chem. C, 2015, 3, 3760–3766.
10. C. Deetuam, D. Weise, C. Samthong, P. Praserthdam, R. R. Baumann and A. Somwangthanaroj, Electrical conductivity enhancement of spin-coated PEDOT:PSS thin film via dipping method in low concentration aqueous DMSO, J. Appl. Polym. Sci., 2015, 132, 42108.
11. F. Yan, E. P. J. Parrott, B. S.-Y. Ung and E. Pickwell-MacPherson, Solvent Doping of PEDOT/PSS: Effect on Terahertz Optoelectronic Properties and Utilization in Terahertz Devices, J. Phys. Chem. C, 2015, 119, 6813–6818.
12. S. Zhang, P. Kumar, A. S. Nouas, L. Fontaine, H. Tang and F. Cicoira, Solvent-induced changes in PEDOT:PSS films for organic electrochemical transistors, APL Mater., 2015, 3, 014911.
13. I. Lee, G. W. Kim, M. Yang and T.-S. Kim, Simultaneously Enhancing the Cohesion and Electrical Conductivity of PEDOT:PSS Conductive Polymer Films using DMSO Additives, ACS Appl. Mater. Interfaces, 2016, 8, 302–310.
14. S.-K. Kim, J.-H. Mo, J.-Y. Kim and K.-S. Jang, Improving the thermoelectric power factor of PEDOT:PSS films by a simple two-step post-treatment method, E-Polym., 2017, 17, 501–506.
15. S. Dhar, T. Majumder, P. Chakraborty and S. P. Mondal, DMSO modified PEDOT:PSS polymer/ZnO nanorods Schottky junction ultraviolet photodetector: Photoresponse, external quantum efficiency, detectivity, and responsivity augmentation using N doped graphene quantum dots, Org. Electron., 2018, 53, 101–110.
16. L. V. Lingstedt, M. Ghittorelli, H. Lu, D. A. Koutsouras, T. Marszalek, F. Torricelli, N. I. Crăciun, P. Gkoupidenis and P. W. M. Blom, Effect of DMSO Solvent Treatments on the Performance of PEDOT:PSS Based Organic Electrochemical Transistors, Adv. Electron. Mater., 2019, 1800804.
17. J. Dong and G. Portale, Role of the Processing Solvent on the Electrical Conductivity of PEDOT:PSS, Adv. Mater. Interfaces, 2020, 7, 2000641.
18. S. Mahato, J. Puigdollers, C. Voz, M. Mukhopadhyay, M. Mukherjee and S. Hazra, Near 5% DMSO is the best: A structural investigation of PEDOT: PSS thin films with strong emphasis on surface and interface for hybrid solar cell, Appl. Surf. Sci., 2020, 499, 143967.
19. R. M. Vedovatte, M. C. Saccardo, E. L. Costa and C. E. Cava, PEDOT:PSS post-treated by DMSO using spin coating, roll-to-roll and immersion: a comparative study, J. Mater. Sci.: Mater. Electron., 2020, 31, 317–323.
20. W.-C. Wang, Y.-T. Cheng and B. Estroff, Electrostatic Self-Assembly of Composite Nanofiber Yarn, Polymers, 2020, 13, 12.
21. M. Cassinelli, W.-T. Park, Y. Kim, J.-H. Kim, Y.-Y. Noh and M. Caironi, Rationalizing the enhancement of the thermoelectric properties of PEDOT:PSS by secondary doping, Appl. Phys. Lett., 2021, 119, 033301.
22. X. Li, Z. Liu, Z. Zhou, H. Gao, G. Liang, D. Rauber, C. W. M. Kay and P. Zhang, Effects of Cationic Species in Salts on the Electrical Conductivity of Doped PEDOT:PSS Films, ACS Appl. Polym. Mater., 2021, 3, 98–103.
23. S.-P. Rwei, Y.-H. Lee, J.-W. Shiu, R. Sasikumar and U.-T. Shyr, Characterization of Solvent-Treated PEDOT:PSS Thin Films with Enhanced Conductivities, Polymers, 2019, 11, 134.
24. E. Yildirim, G. Wu, X. Yong, T. L. Tan, Q. Zhu, J. Xu, J. Ouyang, J.-S. Wang and S.-W. Yang, A theoretical mechanistic study on electrical conductivity enhancement of DMSO treated PEDOT:PSS, J. Mater. Chem. C, 2018, 6, 5122–5131.
25. R. Alessandri, J. J. Uusitalo, A. H. de Vries, R. W. A. Havenith and S. J. Marrink, Bulk Heterojunction Morphologies with Atomistic Resolution from Coarse-Grain Solvent Evaporation Simulations, J. Am. Chem. Soc., 2017, 139, 3697–3705.
26. M. Moser, J. Gladisch, S. Ghosh, T. C. Hidalgo, J. F. Ponder, R. Sheelamanthula, Q. Thiburce, N. Gasparini, A. Wadsworth, A. Salleo, S. Inal, M. Berggren, I. Zozoulenko, E. Stavrinidou and I. McCulloch, Controlling Electrochemically Induced Volume Changes in Conjugated Polymers by Chemical Design: from Theory to Devices, Adv. Funct. Mater., 2021, 31, 2100723.
27. J. Gladisch, E. Stavrinidou, S. Ghosh, A. Giovannitti, M. Moser, I. Zozoulenko, I. McCulloch and M. Berggren, Reversible Electronic Solid–Gel Switching of a Conjugated Polymer, Adv. Sci., 2020, 7, 1901144.
28. S. Ghosh and I. Zozoulenko, Effect of Substrate on Structural Phase Transition in a Conducting Polymer during Ion Injection and Water Intake: A View from a Computational Microscope, ACS Appl. Electron. Mater., 2020, 2, 4034–4041.
29. A. de Izarra, C. Choi, Y. H. Jang and Y. Lansac, Ionic Liquid for PEDOT:PSS Treatment. Ion Binding Free Energy in Water Revealing the Importance of Anion Hydrophobicity, J. Phys. Chem. B, 2021, 125, 1916–1923.
30. A. de Izarra, C. Choi, Y. H. Jang and Y. Lansac, Molecular Dynamics of PEDOT:PSS Treated with Ionic Liquids. Origin of Anion Dependence Leading to Cation Design Principles, J. Phys. Chem. B, 2021, 125, 8601–8611.
31. A. de Izarra, S. Park, J. Lee, Y. Lansac and Y. H. Jang, Ionic Liquid Designed for PEDOT:PSS Conductivity Enhancement, J. Am. Chem. Soc., 2018, 140, 5375–5384.
32. R. Alessandri, F. Grünewald and S. J. Marrink, The Martini Model in Materials Science, Adv. Mater., 2021, 33, 2008635.
33. M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Morphology and ion diffusion in PEDOT:Tos. A coarse grained molecular dynamics simulation, Phys. Chem. Chem. Phys., 2018, 20, 17188–17198.
34. M. Vögele, C. Holm and J. Smiatek, Coarse-grained simulations of polyelectrolyte complexes: MARTINI models for poly(styrene sulfonate) and poly(diallyldimethylammonium), J. Chem. Phys., 2015, 143, 243151.
35. M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Computational microscopy study of the granular structure and pH dependence of PEDOT:PSS, Phys. Chem. Chem. Phys., 2019, 21, 6699–6711.
36. S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, Polarizable Water Model for the Coarse-Grained MARTINI Force Field, PLoS Comput. Biol., 2010, 6, e1000810.
37. R. Alessandri, P. C. T. Souza, S. Thallmair, M. N. Melo, A. H. de Vries and S. J. Marrink, Pitfalls of the Martini Model, J. Chem. Theory Comput., 2019, 15, 5448–5460.
38. K. Jain, A. Y. Mehandzhiyski, I. Zozoulenko and L. Wågberg, PEDOT:PSS nano-particles in aqueous media: A comparative experimental and molecular dynamics study of particle size, morphology and z-potential, J. Colloid Interface Sci., 2021, 584, 57–66.
39. N. Delavari, J. Gladisch, I. Petsagkourakis, X. Liu, M. Modarresi, M. Fahlman, E. Stavrinidou, M. Linares and I. Zozoulenko, Water Intake and Ion Exchange in PEDOT:Tos Films upon Cyclic Voltammetry: Experimental and Molecular Dynamics Investigation, Macromolecules, 2021, 54, 6552–6562.
40. W. Michaels, Y. Zhao and J. Qin, Atomistic Modeling of PEDOT:PSS Complexes I: DFT Benchmarking, Macromolecules, 2021, 54, 3634–3646.
41. W. Michaels, Y. Zhao and J. Qin, Atomistic Modeling of PEDOT:PSS Complexes II: Force Field Parameterization, Macromolecules, 2021, 54, 5354–5365.
42. M. L. Jones and E. Jankowski, Computationally connecting organic photovoltaic performance to atomistic arrangements and bulk morphology, Mol. Simul., 2017, 43, 756–773.
43. N. Rolland, M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Large scale mobility calculations in PEDOT (Poly(3,4-ethylenedioxythiophene)): Backmapping the coarse-grained MARTINI morphology, Comput. Mater. Sci., 2020, 179, 109678.
44. D. Kim, J. F. Franco-Gonzalez and I. Zozoulenko, How Long are Polymer Chains in Poly(3,4-ethylenedioxythiophene):Tosylate Films? An Insight from Molecular Dynamics Simulations, J. Phys. Chem. B, 2021, 125, 10324–10334.
45. D. Kim and I. Zozoulenko, Why Is Pristine PEDOT Oxidized to 33%? A Density Functional Theory Study of Oxidative Polymerization Mechanism, J. Phys. Chem. B, 2019, 123, 5160–5167.
46. B. N. Dickhaus and R. Priefer, Determination of polyelectrolyte pK_a values using surface-to-air tension measurements, Colloids Surf., A, 2016, 488, 15–19.
47. H. Dong, H. Du, S. R. Wickramasinghe and X. Qian, The Effects of Chemical Substitution and Polymerization on the pK_a Values of Sulfonic Acids, J. Phys. Chem. B, 2009, 113, 14094–14101.
48. S. T. Heller and T. P. Silverstein, pK_a values in the undergraduate curriculum: introducing pK_a values measured in DMSO to illustrate solvent effects, ChemTexts, 2020, 6, 15.
49. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103, 8577–8593.
50. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25.
51. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447.
52. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38.
53. J. Fu and J. B. Schlenoff, Driving Forces for Oppositely Charged Polyion Association in Aqueous Solutions: Enthalpic, Entropic, but Not Electrostatic, J. Am. Chem. Soc., 2016, 138, 980–990.
54. M. Ghasemi, S. Friedowitz and R. G. Larson, Overcharging of polyelectrolyte complexes: an entropic phenomenon, Soft Matter, 2020, 16, 10640–10656.
55. S. Kishani, T. Benselfelt, L. Wågberg and J. Wohlert, Entropy drives the adsorption of xyloglucan to cellulose surfaces – A molecular dynamics study, J. Colloid Interface Sci., 2021, 588, 485–493.
56. R. Noriega, J. Rivnay, K. Vandewal, F. P. V. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, A general relationship between disorder, aggregation and charge transport in conjugated polymers, Nat. Mater., 2013, 12, 1038–1044.
57. X. Zhang, H. Bronstein, A. J. Kronemeijer, J. Smith, Y. Kim, R. J. Kline, L. J. Richter, T. D. Anthopoulos, H. Sirringhaus, K. Song, M. Heeney, W. Zhang, I. McCulloch and D. M. DeLongchamp, Molecular origin of high field-effect mobility in an indacenodithiophene–benzothiadiazole copolymer, Nat. Commun., 2013, 4, 2238.
58. N. Rolland, J. F. Franco-Gonzalez, R. Volpi, M. Linares and I. V. Zozoulenko, Understanding morphology-mobility dependence in PEDOT:Tos, Phys. Rev. Mater., 2018, 2, 045605.
59. V. Rühle, J. Kirkpatrick and D. Andrienko, A multiscale description of charge transport in conjugated oligomers, J. Chem. Phys., 2010, 132, 134103.
60. E. Miller, M. Jones and E. Jankowski, Tying Together Multiscale Calculations for Charge Transport in P3HT: Structural Descriptors, Morphology, and Tie-Chains, Polymers, 2018, 10, 1358.
61. A. Khot and B. M. Savoie, How SIDE-CHAIN hydrophilicity modulates morphology and charge transport in mixed conducting polymers, J. Polym. Sci., 2022, 60, 610–620.
62. J. Nelson, J. J. Kwiatkowski, J. Kirkpatrick and J. M. Frost, Modeling Charge Transport in Organic Photovoltaic Materials, Acc. Chem. Res., 2009, 42, 1768–1778.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02655d

---