Stable excited dication: trapping on the S1 state of formaldehyde dication after strong field ionization†
Vaibhav
Singh
a,
Chuan
Cheng
 b,
Thomas
Weinacht
b and
Spiridoula
Matsika
b,
Thomas
Weinacht
b and
Spiridoula
Matsika
 *a
*a
aDepartment of Chemistry, Temple University, Philadelphia, PA 19122, USA. E-mail: smatsika@temple.edu
bDepartment of Physics, Stony Brook University, Stony Brook, NY 11790, USA
First published on 20th July 2022
Abstract
Combined theoretical and experimental work examines the dynamics of dication formaldehyde produced by strong field ionization. Trajectory surface hopping dynamics on the first several singlet electronic states of the formaldehyde dication are used to examine the relaxation pathways and dissociation channels, while kinetic energy distributions after strong field ionization of formaldehyde and deuterated formaldehyde are used to confirm the theoretical predictions. We find that the first excited state of the formaldehyde dication is stable, neither decays to the ground state nor dissociates, even though the ground state and higher lying states are directly dissociative. The stability of the first excited state is explained by its symmetry which does not allow for radiative or nonradiative transitions to the ground state and by large barriers to dissociate on the excited state surface.
1 Introduction
Excited state dynamics in closed shell, neutral organic molecules drive organic photochemistry, and thus have been studied extensively.1,2 When excitation occurs on higher excited states, Kasha's rule3 is expected to be followed, i.e. relaxation to the lowest excited state occurs rapidly while a slower decay (radiative or radiationless) occurs from the first excited state, S1, to the ground state. This is because the energetic gap between the closed shell ground state and the first excited state is usually large, while the gap between excited states is much smaller. So, a cascade of nonadiabatic transitions can easily relax the excited population to the S1 state. In radical cations, however, the situation is different, since it is more likely that the spacing between the ground and first excited state is comparable to the gap between excited states. So, in that case rapid radiationless relaxation to the ground state is expected, and it is often observed.4–8 Dications should be similar to monocations where the density of electronic states is high. There is however the possibility that the ground state of the dication is also closed shell if both electrons are ejected from the same orbital. In that case, the gap between the ground state and excited state may be larger than what one would intuitively expect.9,10 Nevertheless, the gaps are still smaller than for neutral molecules, and a long-lived excited state is not intuitively expected.In general, multiply charged cations in their excited state created by ionization are usually unstable, and they dissociate fast to create various fragments.11–13 In most cases the fragmentation process occurs very fast, although there have been cases where delayed fragmentation from excited dications after ionization has been observed. In ethylene and acetylene, for example, dications with lifetimes ranging from hundreds of nanoseconds to microseconds were observed.14 The delayed fragmentation process in ethylene is believed to occur on the electronically excited state, while in acetylene it occurs after intersystem crossing to the ground state.14 Another example of long-lived excited state in dications has been observed in CO22+, where the singly excited state is bound while the ground state is dissociative.15,16 Metastable excited states have also been found in the diatomic dication Ne22+ leading to excimers. The first clear evidence for the existence of metastable Ne22+ has been established by Ben-Itzhak et al.17 It was shown later that while the ground state is unstable, excited states are responsible for the observed dication.18
Metastable molecules in their excited states can be important intermediates where the stored electronic energy can be used to facilitate other reactions.10,19 For example, in atmospheric chemistry or intergalactic chemistry, the long lifetime of excited metastable states enables the initiation of reactions through collision with other species.20 Metastable excited states can also be used for population inversion, which is important for lasing. For this reason, the presence of long-lived excited states in charged ions is an important observation that should be studied in detail.
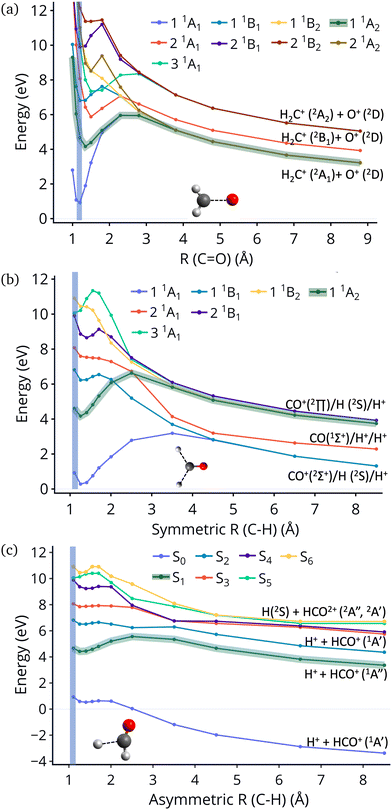
In this work we examine relaxation and fragmentation pathways in formaldehyde dication formed by strong field ionization. Based on the dissociation limits shown in Fig. 1 most dissociation channels are highly exothermic, and it is expected that dissociation will occur very fast. Theoretical calculations however show that dissociation from the first excited state is rare, and this is verified by experimentally observing the dication. Furthermore, the first excited state is predicted to be stable from relaxation to the ground state, having a much longer lifetime than what would be conventionally expected. We show that this surprising stability of the first excited state is due to the existence of barriers on the excited state preventing direct dissociation, and symmetry, which prohibits decay to the ground state.
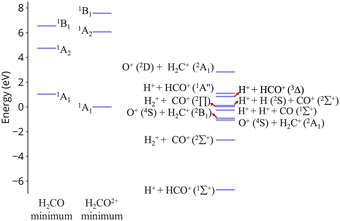 | ||
| Fig. 1 Excitation energies of CH2O2+ and dissociation energies of the fragments which are possible. Results are obtained at the CCSD/cc-pVQZ level of theory. Excitation energies are shown at two geometries, the minimum of neutral formaldehyde (corresponding to vertical ionization) and the minimum of the ground state of the dication. These geometries are shown in Fig. S1 (ESI†). | ||
2 Methods
2.1 Computational methods
The geometries of formaldehyde and its dication were optimized using the B3LYP21–24 functional of Density Functional Theory25,26 and the cc-pV5Z27 basis set. The appearance energies of the fragments that could be formed possibly from dissociation of CH2O2+ were calculated using coupled cluster singles and doubles (CCSD)28 with the cc-pVQZ27 basis set. The appearance energies of HCO+, H2C+ in their first excited states were calculated using equation of motion-for excited energies-CCSD (EOM-EE-CCSD) with cc-pVQZ, whereas, the excited states of CO+ were calculated using EOM- for ionization potential- CCSD (EOM-IP-CCSD) with cc-pVQZ starting from neutral CO.In order to obtain potential energy surfaces along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch, the single C–H (asymmetric C–H) stretch and the double C–H (symmetric C–H) stretch of CH2O2+, energies of the ground and excited states were plotted at the geometries produced with scans along each internal coordinate starting from the geometry of the neutral minimum of formaldehyde and stretching the corresponding bonds, while all the other degrees of freedom remain frozen at their initial value. The scans along asymmetric C–H were done using a state average of 10 states complete active space self consistent field with an active space of 8 electrons in 9 orbitals (10SA-CASSCF(8,9)) and the cc-pVDZ basis set. The scans along symmetric C–H and C
O stretch, the single C–H (asymmetric C–H) stretch and the double C–H (symmetric C–H) stretch of CH2O2+, energies of the ground and excited states were plotted at the geometries produced with scans along each internal coordinate starting from the geometry of the neutral minimum of formaldehyde and stretching the corresponding bonds, while all the other degrees of freedom remain frozen at their initial value. The scans along asymmetric C–H were done using a state average of 10 states complete active space self consistent field with an active space of 8 electrons in 9 orbitals (10SA-CASSCF(8,9)) and the cc-pVDZ basis set. The scans along symmetric C–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O were done at the CASSCF(8,9)/cc-pVDZ level of theory averaged over 4 A1, 2 B1, 2 B2 and 2 A2 states. Constrained optimizations along one C–H bond optimizing the S1 state were done using a two-state average CASSCF (2SA-CASSCF(8,9)), since the optimizations were not converging when more states were included in the average, and a two-state average will give better description of S1. The CASSCF(8,9)/cc-pVDZ calculations using the various averaging schemes were benchmarked by comparison to EOM-EE-CCSD with two larger basis sets, cc-pVTZ and cc-pVQZ. The energies are shown in ESI,† Tables S1 and S2, and confirm that this CASSCF approach is reasonable.
O were done at the CASSCF(8,9)/cc-pVDZ level of theory averaged over 4 A1, 2 B1, 2 B2 and 2 A2 states. Constrained optimizations along one C–H bond optimizing the S1 state were done using a two-state average CASSCF (2SA-CASSCF(8,9)), since the optimizations were not converging when more states were included in the average, and a two-state average will give better description of S1. The CASSCF(8,9)/cc-pVDZ calculations using the various averaging schemes were benchmarked by comparison to EOM-EE-CCSD with two larger basis sets, cc-pVTZ and cc-pVQZ. The energies are shown in ESI,† Tables S1 and S2, and confirm that this CASSCF approach is reasonable.
The B3LYP optimizations of formaldehyde geometries were done using the Gaussian0929 suite of packages. All CCSD calculations were done with the Q-Chem30 suite of packages. The CASSCF calculations were performed using COLUMBUS.31–33
Electronic state-resolved fragmentation of CH2O2+ and the kinetic energy releases (KERs) for the different products are calculated with the help of the semi-classical molecular dynamics approach, trajectory surface hopping (TSH).34,35 200 initial conditions were generated using the harmonic oscillator Wigner distribution of the S0 minimum of neutral CH2O, with frequencies at the B3LYP/cc-pV5Z level of theory. The Wigner distribution code implemented in Newton-X36 was used. The evolution of the classical trajectories was then studied separately for 6 singlet states of the dication, in order to get the dynamics and dissociation assuming ionization to each one of these states. The gradients along which the trajectories evolved, their electronic energies and non-adiabatic couplings at each time step, were calculated on-the-fly, with the help of quantum principles by applying 6SA-CASSCF(8,9)/cc-pVDZ level of theory. However, the nuclear motions were treated classically by applying the velocity-Verlet algorithm with a time step of 0.5 fs. The hopping probabilities between non-adiabatic states were dealt with the 'Fewest Switches Surface Hopping (FSSH)' algorithm,37 as implemented in Newton-X.38 The re-scaling of momentum after a hop was done along the derivative coupling vector in order to conserve the total energy. To deal with frustrated hops, i.e. when a trajectory does not have enough energy for a hop to occur, the momentum was left unaltered along the direction it was already moving. The decoherence correction of Persico and Grannuci39 was used with a factor of 0.1 Hartree.40
70 of the 200 trajectories for each state were ran for 400 fs, but since the dynamics are practically done by 100 fs, the remaining 130 trajectories were run for 135 fs only. Many trajectories fail by the time they reach 100 fs. The number of trajectories that survived after 100 fs are 29, 28, and 35, for S0, S1 and S2, respectively, while the numbers for S3, S4 and S5 are even less, 14, 5, and 1 trajectories, respectively. This small number of trajectories complicates the statistics when calculating the population on each state, so we only show those up to 100 fs.
2.2 Experimental methods
The experimental setup has been described in detail in previous work.41,42 Briefly, the output from a commercial amplified Ti:sapphire laser system (KM Labs, 1 mJ, 780 nm, 1 kHz, 30 fs) is sent into the vacuum chamber and is focused by a concave spherical silver mirror (f = 5 cm) to peak intensities between 40 and 240 TW cm-2 inside a Velocity Map Imaging (VMI) spectrometer. The VMI has a switchable three plate electrostatic lens stack, Microchannel Plates (MCP), phosphor screen, and camera (Tpx3Cam). The 1 ns resolution of the Tpx3Cam can resolve the 3D-vector momenta of ions, or 2-D electron momenta projected on the plane of the detector. The focused laser intensity is calibrated using the VMI to measure the classical 2Up cut-off for electrons arising from strong field ionization of argon.43The vacuum system consists of source and spectrometer chambers. The sample, deuterated formaldehyde, obtained by sublimation of paraformaldehyde-d2 (purity 98%, Sigma-Aldrich), is heated to 50–60 °C. A skimmed molecular beam of the target D2O molecules intersects the laser in the interaction region of the VMI.41 The deuterated version of the molecule is chosen to avoid potential contamination with low mass atomic ions like H+.
3 Results and discussion
3.1 Dynamics on the S1 surface
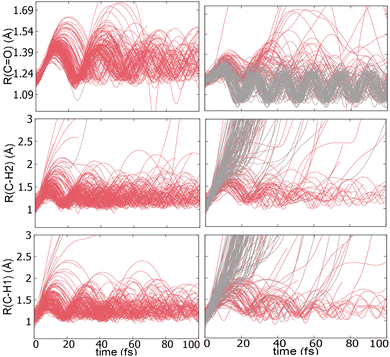
TSH dynamics were run starting from the ground and first five singlet excited states of the dication. Results of how the populations evolve in time for states S1 and S2 are shown in Fig. 2 while populations for the remaining states are shown in ESI.† When the dynamics are initiated on the S1 state, the population remains on that state for more than 100 fs. After 150 fs only one trajectory has decayed to the ground state. So, there are practically no nonadiabatic transitions occurring. When the population is initially on the S2 and higher states, population decays to lower states, as one would expect. Fig. 2 shows the populations for S2 where decay to S1 and eventually S0 occurs rapidly. After 100 fs about 60% of the population has decayed to the lower states, with 40% being on S1 and about 20% on the ground state. This pattern is similar for the other states.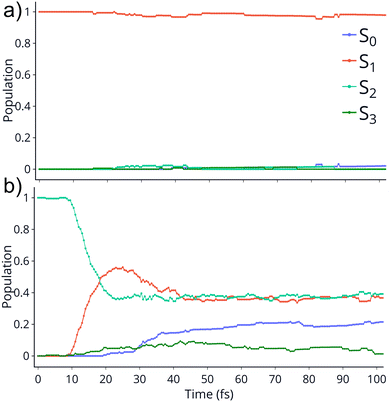 | ||
| Fig. 2 Populations of 4 singlet states vs time for the trajectories initiated at S1 (top) and S2 (bottom). The populations on S4 and S5 are not shown since they remain zero for the whole dynamics. | ||
An additional interesting observation when initiating dynamics on S1 is that most of the trajectories show no dissociation. Only 16/200 trajectories fragment to CHO+ and H+ (see Table S3 in ESI†). On the other hand, half of the trajectories on S2 dissociate to a three body channel CO+ + H+ + H. Plots of internal coordinates as a function of time in Fig. 3 show the dissociation patterns for the two states. Trajectories on the S1 surface do not show any breaking of the C–O bond, while there is a small number of trajectories that break the C–H bonds. On the contrary, trajectories on the S2 surface show a very fast dissociation along the C–H bonds. As shown in Fig. 3 C–H dissociation occurs within the first period of their oscillation, and the majority is symmetric. According to Fig. 1 all dissociation channels are exothermic with respect to the S2 surface, and five of them are exothermic when exciting to the S1 surface. Given the results of the dynamics, it is obvious that exothermicity alone cannot predict the dissociation patterns. In the case of S1 specifically, it is intriguing that despite so many channels being energetically accessible minimal dissociation is observed. A more detailed investigation into what determines the dynamics is needed.
3.2 Symmetry prevents nonadiabatic transitions from S1 to S0
Many of the observations seen in the TSH calculations can be explained by symmetry. Formaldehyde and its dication have C2v symmetry at their equilibrium geometries, and the electronic states belong to the corresponding irreducible representations. Fig. S9 in ESI† shows the configurations for the electronic states. The ground state of the dication is created by removing two electrons from the 2b1 orbital leading to a closed shell configuration with A1 symmetry. The S1 state is created by exciting an electron from 1b2 → 2b1, leading to an A2 symmetry. S2 is created by an excitation 5a1 → 2b1, leading to B1 overall symmetry, while the symmetries of the other states at vertical ionization are A1, B1, A1 for S3, S4, and S5, respectively.A 2 has unique properties compared to the other irreducible representations in C2v symmetry. Since the symmetries of S1 and S0 are A2 and A1, respectively, the nonadiabatic coupling between them should have a2 symmetry, which means that an a2 vibration is needed to couple the two. But an a2 vibration does not exist in formaldehyde. So, there is no nuclear motion that can lead to a coupling between the two states while C2v symmetry is preserved. This has profound consequences, as we see in the dynamics. Furthermore, the radiative transitions between A2 and the A1 ground state are also forbidden by symmetry. This creates the conditions for a trapped state, both radiatively and nonradiatively.
Fig. 4 show the dissociation pathways in formaldehyde dication that retain C2v symmetry. These are either C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O breaking or C–H symmetric stretch. Along C
O breaking or C–H symmetric stretch. Along C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching, S1 and S0 actually become degenerate at large nuclear separations. If the degeneracy could facilitate nonadiabatic transitions, then the S1 population could transfer to S0 and possibly lead to further dissociation along other coordinates. But no such hoppings are observed due to symmetry! Along the C–H symmetric stretch the S1 state crosses S2 and S3 and is diabatically correlated with an excited channel leading to CO(2Π) + H + H+. Again there are no transitions with any other state.
O stretching, S1 and S0 actually become degenerate at large nuclear separations. If the degeneracy could facilitate nonadiabatic transitions, then the S1 population could transfer to S0 and possibly lead to further dissociation along other coordinates. But no such hoppings are observed due to symmetry! Along the C–H symmetric stretch the S1 state crosses S2 and S3 and is diabatically correlated with an excited channel leading to CO(2Π) + H + H+. Again there are no transitions with any other state.
Finally, along the C–H asymmetric stretch coupling with the ground state could occur because the C2v symmetry is broken. However S1 remains more than 5 eV separated from S0 everywhere along the path, so again the coupling will be very small, because of the energy gap this time.
There is the possibility however that geometries deviating from these rigid scans can be accessed, where for example the C–O bond is stretched while at the same time symmetry is broken by asymmetric stretch of the C–H bonds. This motion however does not seem important in the dynamics. By examining the trajectories we see that when the C–O bond is stretched the asymmetry between the two C–H bonds remains very small, so even when the molecule does not have strictly C2v symmetry, it remains close to that symmetry and the nonadiabatic coupling remains small. More details of this analysis can be found in ESI† (Fig. S10).
3.3 No fragmentation on excited state surface
Although no transitions to the ground state occur, fragmentation could proceed along the excited state surface without need for decay to the ground state. However, Fig. 4 shows that the barriers for dissociation on the S1 surface are very high (more than 2 eV) along C–O and symmetric C–H. The barrier along the asymmetric C–H breaking as shown in Fig. 4(c) is lower, so there is some possibility to break one C–H bond to produce the H+ + HCO+ in its excited state. Since the paths in this figure are based on rigid scans, the barriers are upper bounds to true barriers. In order to have a better estimate of the actual barrier along the asymmetric C–H path we performed constrained optimizations with one C–H bond constrained, while the other degrees of freedom were optimized. This path is shown in ESI† (Fig. S2), and leads to a barrier along the C–H bond of 0.8 eV. This explains why the only products seen for 16 out of 200 trajectories are along this pathway and lead to HCO+ + H+.The non-dissociating trajectories on S1 show some coherent oscillations along all 3 coordinates as shown in Fig. 3, although the C–O vibrations lose coherence rapidly after a few oscillations due to coupling between modes.
The dissociation of CH2O2+ on the ground state surface forms HCO+ (1Σ+) with linear geometry and H+. However, the geometry of HCO+ on its S1 minimum is not linear with the H–C–O angle of 125°. The same has been seen by Weis and Yamashita.44 Hence, when dissociation occurs on the first excited state it will lead to a nonlinear HCO+ with a symmetry of 1A′′ instead of 1Σ−. Similarly, the degenerate second and third excited states of HCO+ (1Δ in linear symmetry) split into 1A′ and 1A′′ states at the nonlinear S1 minimum. This further suggests that the produced HCO+ will be vibrationally excited along the bending mode.
3.4 Dynamics on the other singlet states
It is interesting to contrast the dynamics occurring on the S1 surface with that of the S2 and higher states. Fig. 2 shows that when the population is initially on the S2 electronically excited state there is substantial decay to S1 and S0 within 100 fs. Specifically, about 40% of the population remains on S2 while 40% decays to S1 and 20% has reached the ground state after 100 fs. Fig. S8 in ESI† shows the populations for the other states. All the excited states lose more than 50% of their population within 20 fs. The statistics are not reliable for the higher states beyond 50 fs so we cannot predict the final distribution, but it is clear that radiationless decay is very fast. It should also be noted that when exciting to higher states the population does not get trapped on S1 but it decays further to the ground state, for the most part. This is because all these nonadiabatic transitions break the symmetry, so S1 is not an A2 state anymore.There is also substantial fragmentation observed in the dynamics of higher states. Table S3 in ESI† shows all the fragmentation products for each state. When starting on the S2 state most of the population dissociates via a three-body dissociation to produce CO+ + H + H+ or CO + H+ + H+, regardless of the state on which fragmentation occurs. This is obvious in Fig. 3 which shows that both of the CH bonds break symmetrically. Fig. 4b shows that S2 is strongly exothermic along the symmetric CH stretch coordinate, so that explains why this is the preferred dissociation mechanism. The data indicate that even when there is a nonadiabatic transition from S2 to S1, diabatically the population remains on the B1 surface. The B1 state dissociates via three body dissociation, while the A2 state is bound along that coordinate. Fig. 3 shows that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O continues to vibrate coherently (significantly longer than in S1) after the loss of the hydrogens. We note that it is with a higher frequency, as one would expect since the bond is stronger for CO+. The dominant channel for states S3, S4 and S5 is dissociation along the C
O continues to vibrate coherently (significantly longer than in S1) after the loss of the hydrogens. We note that it is with a higher frequency, as one would expect since the bond is stronger for CO+. The dominant channel for states S3, S4 and S5 is dissociation along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond leading to CH2+ + O+, with O+ being produced on its excited 2D state rather than the ground 4S state because of spin restrictions.
O bond leading to CH2+ + O+, with O+ being produced on its excited 2D state rather than the ground 4S state because of spin restrictions.
Dynamics on the ground state also predict fast dissociation. Almost all of the trajectories that have not failed lead to HCO+ + H+, since this pathway is more than 6 eV exothermic with a very small barrier on the ground state. Overall, a very small number of trajectories have not dissociated after 100 fs when starting from any other state except S1.
3.5 Experimental observation of CD2O2+
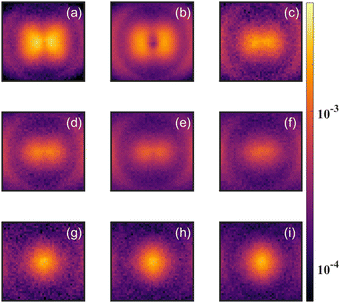
As a test of the theoretical predictions, we carried out measurements on CH2O as well as CD2O. Both measurements showed evidence for the parent dication (CH2O2+ or CD2O2+) in the time of flight mass spectrum. However, the signal for CH2O2+ suffered from contamination by high energy O+ and CH2+ fragments, and for CD2O2+ the signal was also complicated by the detection of O+/CD2+ fragments, which have the same time of flight (TOF) due to their common mass over charge. In order to clarify the evidence for the formation of a stable dication, we carried out detailed momentum resolved measurements of the fragment ions, which allowed us to distinguish O+ and CD2+ from CD2O2+.Fig. 5 shows the angular distribution for the ions having TOF corresponding to these fragments with different laser intensities. The variation of the angular distribution with laser intensity reveals multiple contributions to the yield. At low intensities, one can see a clear variation in the yield with angle, which is consistent with O+ and CD2+ fragments formed from dissociative single ionization. However, for higher laser intensities (bottom three panels of Fig. 5), the yield does not vary with angle, which is consistent with non-dissociative double ionization.
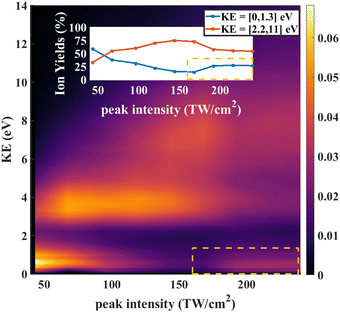
In strong field ionization, single ionization is generally dominant at low intensities. As the intensity increases, higher order ionization becomes more prominent.42,45–49 Thus it makes sense that the O+/CD2+/CD2O2+ signal for low intensities is dominated by fragments arising from dissociative single ionization, with Kinetic Energy Release (KER) between 0 and 1.3 eV, while the O+/CD2+/CD2O2+ signal for high intensities is dominated by the dication formed by double ionization, with KER between 1 and 5 eV.
As further evidence for the formation of the stable dication, we consider the KER for fragment ions at the position of the parent dication in the TOFMS. The expectation is that the dication parent should show very low KER since there is no dissociation involved. The KER distribution as a function of laser intensity is shown in Fig. 6. For low intensities (0 to 75 TW cm−2), dissociative single ionization dominates, producing relatively low energy O+ or CD2+ fragments. As the intensity goes higher (75 to 150 TW cm−2), the production of energetic fragments (2 to 5 eV) from dissociative single or double ionization dominates. Finally, for the highest intensities, we see very high energy fragments (greater than 5 eV) being formed, in addition to an increase in very low KER ions. The very high energy fragments can be associated with dissociative double and triple ionization, while the low energy fragments point to the formation of CD2O2+, which is consistent with the angular distributions at high intensity discussed above.
We note that strong field ionization leads to the population of multiple states of the dication, not only S1. However, given that the calculations indicate that only S1 is stable, and that our measurements agree with the calculations quantitatively regarding the dissociation energies from other states of the dication,50 we believe that our measurements of the dication come from molecules in the S1 state of the dication.
4 Conclusions
In conclusion, we have shown that the first excited state of the formaldehyde dication is stable both from decay to the ground state and from dissociation, even though the ground state and higher lying states are directly dissociative. This is a rather unexpected result because in general double ionization of closed shell molecules creates rather unstable species. Furthermore, when these dications are electronically excited they are expected to be even more unstable because of all the extra available energy. A stable excited state when the ground state is dissociative is possible here because of the high symmetry of formaldehyde which restricts the types of vibrations that can couple the different states. One may imagine that other molecules with high symmetry can be found that show similar dynamics. A bound excited state combined with a dissociative ground state can be useful in laser action. Excimer lasers create population inversion because they have a bound excited state, but a dissociative ground state. Emission is not possible in the current system since the S1 state has a zero transition dipole moment with the ground state by symmetry. The pair S0 (A1 symmetry)–S1 (A2 symmetry) in formaldehyde dication has both a zero radiative coupling (through the transition dipole moment operator) and radiationless coupling (through the nonadiabatic coupling operator). Since however these two operators are different a system that has zero nonadiabatic coupling but nonzero radiative coupling could create population inversion.The calculations described here motivate the measurement of dynamics in the stable dication. The analysis of the trajectories in Fig. 3 shows coherent C–O oscillations in S1, which could be detected by covariance pump probe measurements of the fragment ion yields. A pump pulse could launch a vibrational wave packet on the S1 state of the dication, which could be probed via further ionization to the trication, followed by momentum resolved measurements of the fragment ions in covariance.51
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the Department of Energy (DOE, Award no. DE-FG02-08ER15983 for V. S. and S. M. and DOE, Award no. DE-FG02-08ER15984 for C. C. and T. W.) for funding. Part of the computational work was performed using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant no. ACI-1548562.Notes and references
- M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, VCH Publishers, Inc., New York, 1995 Search PubMed.
- W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections: Theory, Computation and Experiment, World Scientific, Singapore, 2011 Search PubMed.
- M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19 RSC.
- M. Assmann, T. Weinacht and S. Matsika, J. Chem. Phys., 2016, 144, 034301 CrossRef PubMed.
- H. Koppel, M. Doscher, I. Baldea, H. Meyer and P. Szalay, J. Chem. Phys., 2002, 117, 2657–2671 CrossRef CAS.
- H. Tao, L. Shen, M. H. Kim, A. G. Suits and T. J. Martinez, J. Chem. Phys., 2011, 134, 054313 CrossRef PubMed.
- B. Joalland, T. Mori, T. J. Martinez and A. G. Suits, J. Phys. Chem. Lett., 2014, 5, 1467–1471 CrossRef CAS PubMed.
- K. Munkerup, D. Romanov, T. Bohinski, A. B. Stephansen, R. J. Levis and T. I. Solling, J. Phys. Chem. A, 2017, 121, 8642–8651 CrossRef CAS PubMed.
- A. Zhao, P. Sańdor, V. Tagliamonti, S. Matsika and T. Weinacht, J. Phys. Chem. A, 2016, 120, 3233–3240 CrossRef CAS PubMed.
- S. Banhatti, J. Palotás, P. Jusko, B. Redlich, J. Oomens, S. Schlemmer and S. Brünken, Astron. Astrophys., 2021, 648, A61 CrossRef CAS.
- T. Osipov, T. N. Rescigno, T. Weber, S. Miyabe, T. Jahnke, A. S. Alnaser, M. P. Hertlein, O. Jagutzki, L. P. H. Schmidt, M. Schöffler, L. Foucar, S. Schössler, T. Havermeier, M. Odenweller, S. Voss, B. Feinberg, A. L. Landers, M. H. Prior, R. Dörner, C. L. Cocke and A. Belkacem, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 091001 CrossRef.
- X. Zhou, P. Ranitovic, C. Hogle, J. H. D. Eland, H. C. Kapteyn and M. M. Murnane, Nat. Phys., 2012, 8, 232–237 Search PubMed.
- G. Basnayake, P. Hoerner, B. Mignolet, M. K. Lee, Y. F. Lin, A. H. Winney, D. A. Debrah, L. Popaj, X. Shi, S. K. Lee, H. B. Schlegel, F. Remacle and W. Li, Phys. Chem. Chem. Phys., 2021, 23, 23537–23543 RSC.
- S. Larimian, S. Erattupuzha, E. Lotstedt, T. Szidarovszky, R. Maurer, S. Roither, M. Schoeffler, D. Kartashov, A. Baltuska, K. Yamanouchi, M. Kitzler and X. Xie, Phys. Rev. A, 2016, 93, 053405 CrossRef.
- M. Alagia, P. Candori, S. Falcinelli, M. Lavollée, F. Pirani, R. Richter, S. Stranges and F. Vecchiocattivi, J. Phys. Chem. A, 2009, 113, 14755–14759 CrossRef CAS PubMed.
- S. Falcinelli, Acta Phys. Pol., 2017, 131, 112–116 CrossRef CAS.
- I. Ben-Itzhak, I. Gertner, D. Bortman and D. Zajfman, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 6548 CrossRef CAS PubMed.
- J. Ackermann and H. Hogreve, Phys. Chem. Chem. Phys., 2017, 19, 32433–32442 RSC.
- P. Tosi, R. Correale, W. Lu, S. Falcinelli and D. Bassi, Phys. Rev. Lett., 1999, 82, 450–452 CrossRef CAS.
- M. Torr and D. Torr, Rev. Geophys., 1982, 20, 91–144 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- T. Ziegler, Chem. Rev., 1991, 91, 651–667 CrossRef CAS.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem. A, 1996, 100, 12974–12980 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, G. A. P. V. Barone, H. Nakatsuji, X. Li, M. Caricato, J. B. A. Marenich, B. G. Janesko, B. M. R. Gomperts, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. P. Jr., F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, J. N. R. Kobayashi, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, C. A. M. Klene, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02,Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr., H. Dop, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. ONeill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Molecular Physics, 2015, 113, 184–215 CrossRef CAS.
- H. Lischka, R. Shepard, R. M. Pitzer, I. Shavitt, M. Dallos, T. Müller, P. G. Szalay, M. Seth, G. S. Kedziora, S. Yabushita and Z. Zhang, Phys. Chem. Chem. Phys., 2001, 3, 664–673 RSC.
- H. Lischka, R. Shepard, I. Shavitt, R. M. Pitzer, M. Dallos, T. Müller, P. G. Szalay, F. B. Brown, R. Ahlrichs, H. J. Böhm, A. Chang, D. C. Comeau, R. Gdanitz, H. Dachsel, C. Ehrhardt, M. Ernzerhof, P. Höchtl, S. Irle, G. Kedziora, T. Kovar, V. Parasuk, M. J. M. Pepper, P. Scharf, H. Schiffer, M. Schindler, M. Schüler, M. Seth, E. A. Stahlberg, J.-G. Zhao, S. Yabushita, Z. Zhang, M. Barbatti, S. Matsika, M. Schuurmann, D. R. Yarkony, S. R. Brozell, E. V. Beck, J.-P. Blaudeau, M. Ruckenbauer, B. Sellner, F. Plasser, J. J. Szymczak, R. F. K. Spada and A. Das, COLUMBUS, an ab initio electronic structure program, release 7.0, 2017.
- H. Lischka, R. Shepard, T. Müller, P. G. Szalay, R. M. Pitzer, A. J. A. Aquino, M. M. Araújo do Nascimento, M. Barbatti, L. T. Belcher, J.-P. Blaudeau, I. Borges, S. R. Brozell, E. A. Carter, A. Das, G. Gidofalvi, L. González, W. L. Hase, G. Kedziora, M. Kertesz, F. Kossoski, F. B. C. Machado, S. Matsika, S. A. do Monte, D. Nachtigallová, R. Nieman, M. Oppel, C. A. Parish, F. Plasser, R. F. K. Spada, E. A. Stahlberg, E. Ventura, D. R. Yarkony and Z. Zhang, J. Chem. Phys., 2020, 152, 134110 CrossRef CAS PubMed.
- M. Barbatti, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633 CAS.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- M. Barbatti, G. Granucci, M. Ruckenbauer, F. Plasser, R. Crespo-Otero, J. Pittner, M. Persico and H. Lischka, NEWTON-X: a package for Newtonian dynamics close to the crossing seam, Version 2.2, 2019.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33 CAS.
- G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114 CrossRef PubMed.
- C. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2004, 121, 7658–7670 CrossRef CAS PubMed.
- A. Zhao, M. van Beuzekom, B. Bouwens, D. Byelov, I. Chakaberia, C. Cheng, E. Maddox, A. Nomerotski, P. Svihra and J. Visser, et al. , Rev. Sci. Instrum., 2017, 88, 113104 CrossRef PubMed.
- C. Cheng, P. Vindel-Zandbergen, S. Matsika and T. Weinacht, Phys. Rev. A, 2019, 100, 053405 CrossRef CAS.
- P. B. Corkum, Phys. Rev. Lett., 1993, 71, 1994 CrossRef CAS PubMed.
- B. Weis and K. Yamashita, J. Chem. Phys., 1993, 99, 9512–9520 CrossRef CAS.
- T. Zuo and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, R2511 CrossRef CAS PubMed.
- D. N. Fittinghoff, P. R. Bolton, B. Chang and K. C. Kulander, Phys. Rev. Lett., 1992, 69, 2642 CrossRef CAS PubMed.
- C. Guo, M. Li, J. P. Nibarger and G. N. Gibson, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 033413 CrossRef.
- X.-M. Tong, Z. Zhao and C.-D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 033402 CrossRef.
- M. Kübel, C. Burger, N. G. Kling, T. Pischke, L. Beaufore, I. Ben-Itzhak, G. G. Paulus, J. Ullrich, T. Pfeifer and R. Moshammer, et al. , Phys. Rev. A, 2016, 93, 053422 CrossRef.
- C. Cheng, V. Singh, S. Matsika and T. Weinacht, submitted.
- F. Allum, C. Cheng, A. J. Howard, P. H. Bucksbaum, M. Brouard, T. Weinacht and R. Forbes, J. Phys. Chem. Lett., 2021, 12, 8302–8308 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information on dynamics results and excited state benchmarking. See DOI: https://doi.org/10.1039/d2cp02604j |
| This journal is © the Owner Societies 2022 |