Oxygen deficiency in Sr₂FeO_4−x: electrochemical control and impact on magnetic properties

Abstract

The oxygen-deficient system Sr₂FeO_4−x was explored by heating the stoichiometric Fe⁴⁺ oxide Sr₂FeO₄ in well-defined oxygen partial pressures which were controlled electrochemically by solid-state electrolyte coulometry. Samples with x up to about 0.2 were obtained by this route. X-ray diffraction analysis reveals that the K₂NiF₄-type crystal structure (space group I4/mmm) of the parent compound is retained. The lattice parameter a slightly decreases while the c-parameter increases with increasing x, which is in contrast to the Ruddlesden–Popper system Sr₃Fe₂O_7−x and suggests removal of oxygen atoms from FeO₂ lattice planes. The magnetic properties were studied by magnetization, ⁵⁷Fe Mössbauer, and powder neutron diffraction experiments. The results suggest that extraction of oxygen atoms from the lattice progressively changes the elliptical spiral spin ordering of the parent compound to an inhomogeneous magnetic state with coexistence of long-range ordered regions adopting a circular spin spiral and smaller magnetic clusters.

---

1. Introduction

Perovskite-related ferrates with iron in the high oxidation state +4 constitute an interesting class of transition metal (TM) oxides due to their peculiar electronic, magnetic, and structural properties. Formally, the electronic structure of Fe⁴⁺ oxides can be discussed starting from the t³_2ge¹_g (S = 2) ligand field configuration of 3d⁴ ions, where the high oxidation state of the TM ion gives rise to strong covalency of Fe–O bonding and in turn to strong hybridization between Fe 3d and O 2p orbitals. In the framework of configuration interaction models the iron(IV) oxides, along with Cu³⁺ and Ni³⁺ oxides,^1–4 belong to the class of negative-charge-transfer energy (negative-Δ) compounds, where the electronic ground state is rather dominated by holes in the oxygen bands (L⁻ⁿ, n = 1, 2), i.e. by a d⁵L⁻¹ electron configuration instead of an ionic d⁴ configuration.⁵ Remarkable properties which are related to the negative-Δ situation are the metallic behavior of SrFeO₃,⁶ a charge-disproportionation (CD) process which may be written as 2d⁵L⁻¹ → d⁵ + d⁵L⁻² or 2t³_2ge¹_g → t³_2ge²_g + t³_2g in CaFeO₃,^7,8 Sr₃Fe₂O₇,^7,9–12 CaCu₃Fe₄O₁₂,¹³ and Ca₂FeMnO₆,¹⁴ pressure-induced insulator-to-metal and/or high-spin to low-spin transitions in CaFeO₃,¹⁵ Sr₃Fe₂O₇,¹⁶ and CaCu₃Fe₄O₁₂,¹⁷ as well as antiferromagnetic ordering with different types of helical spin structures in SrFeO₃,¹⁸ CaFeO₃,⁸ cubic BaFeO₃,¹⁹ and Sr₃Fe₂O₇.²⁰ In particular, SrFeO₃ features a sensitive response of the helical spin structure to temperature and magnetic fields,^21,22 which makes this system an interesting model case for topological spin textures in the absence of Dzyaloshinskii–Moriya interactions.²³

Convenient ways for tuning the electronic and magnetic properties of TM oxides are cationic substitutions or variation of the oxygen content. In case of perovskite-related ferrates the great flexibility of the perovskite structure has allowed to vary the oxygen content in a wide range and thus to realize Fe in oxidation states between +2 and +4. For the SrFeO_3−x system several structurally and magnetically distinct phases have been described,^24,25 namely metallic and helimagnetic SrFeO₃, Sr₈Fe₈O₂₃ (SrFeO_2.875) which reveals a charge-ordering transition,^26,27 partially frustrated Sr₄Fe₄O₁₂ (SrFeO_2.75) where only the Fe³⁺ fraction orders magnetically, the antiferromagnetic Brownmillerite Sr₂Fe₂O₅, and finally the Fe²⁺ oxide SrFeO₂ with infinite FeO₂ layers in the crystal structure.²⁸ Similarly, in the bilayer Ruddlesden-Popper system Sr₃Fe₂O_7−x the iron oxidation state could be tuned between +4 and +2, but in contrast to the SrFeO_3−x system no well-defined vacancy-ordered phases were found.²⁹ The end members of the former homogeneity range are Sr₃Fe₂O₇ (Fe⁴⁺)^30,31 and Sr₃Fe₂O₅ (Fe²⁺).³² As changes in the oxygen content lead to changes in the oxidation states and coordination of the iron ions, also the magnetic properties are substantially affected. Oxygen-deficient perovskite-related ferrates are not only of interest as potential magnetic materials but also as mixed anionic conductors for applications in solid oxide fuel cells³³ and in oxygen-separating membranes³⁴ or as oxygen sources for NO oxidation.³⁵

A less studied Fe⁴⁺ oxide is the K₂NiF₄-type phase Sr₂FeO₄ which was first reported by Scholder et al.³⁶ and has an insulating ground state, but in contrast to Sr₃Fe₂O₇ does not feature a CD of Fe⁴⁺.^9,37 An unexpected oxygen-related phonon band in Raman spectra of Sr₂FeO₄ may indicate that the insulating ground state is associated with a tiny structural distortion which, however, has remained elusive so far.³⁸ Recently, we have shown that Sr₂FeO₄ adopts an elliptical spiral spin structure which shows a spin-flop-type reorientation in external magnetic field of about 5 T.³⁹ Sr₂FeO₄ can be considered as a negative-Δ insulator, which is supported by its high-pressure properties showing the disappearance of the additional Raman band near 6 GPa³⁸ and a concomitant change from a spiral to a ferromagnetic spin structure.^39,40 An insulator-to-metal transition near 18 GPa was attributed to the closure of the p–p-type excitation gap.⁴⁰ Only few substituted phases based on Sr₂FeO₄ were reported so far,^41–43 and to the best of our knowledge oxygen deficiency in the Sr₂FeO_4−x system has not been studied in detail. However, similar as for the 113 and 327 systems also for 214 a layered compound with Fe²⁺ in square planar coordination, Sr₂FeO₃, was synthesized.⁴⁴

In the present study we have explored the oxygen-deficient system Sr₂FeO_4−x by heating fully oxidized Sr₂FeO₄ at increasing temperatures and a well-defined oxygen partial pressure. The oxygen contents were controlled and analyzed electrochemically using solid-state electrolyte coulometry. Sr₂FeO_4−x samples with oxygen deficiencies 0 < x ≤ 0.2 could be prepared by this route. Attempts to increase the oxygen deficiency further required heating at temperatures above 700 °C where decomposition into Sr₃Fe₂O_7−x and SrO occurs. The impact of oxygen deficiency on the magnetic properties in Sr₂FeO_4−x was studied by magnetization, ⁵⁷Fe Mössbauer spectroscopy, and powder neutron diffraction experiments.

2. Experimental details

2.1. Synthesis of Sr₂FeO₄

Sr₂FeO₄ was prepared by solid state reaction of home-made SrO and Fe₂O₃ while applying elevated oxygen pressure. For the synthesis of SrO, 50 g SrCO₃ (Sigma-Aldrich, >99.99% metal basis) was mixed with 100 ml of H₂O, and HNO₃ (65% strength) was added with stirring until no gas evolution was evident. The solution was evaporated and the resulting Sr(NO₃)₂ was decomposed to SrO at 550 °C in dynamic vacuum in a Schlenk line. The purity of the product was verified by powder X-ray diffraction. For storage, the SrO was sealed in glass ampoules. Fe₂O₃ was synthesized by decomposition of FeC₂O₄·2H₂O (Alfa Aesar, Puratronic, 99.999% metal basis) in a tube furnace under a slow flow of oxygen at 350 °C and prior to use stored in an argon-filled glove box.

A mixture of SrO and Fe₂O₃ with a slight excess of SrO (molar ratio of 4.02/1.00) was finely ground in an agate mortar in a glove box under argon atmosphere. The mixture was placed in a corundum finger crucible, covered with a thin layer of SrO and a gold lid on top. High oxygen pressure synthesis was performed in a specifically designed, scale-resistant steel autoclave described earlier.⁴⁵ The charged crucible was placed in the autoclave, which was closed, loaded with 10 ml of liquid O₂ and subsequently heated at a rate of 20 K h⁻¹ to 773 K, which generates an O₂ pressure of 2.5 kbar (free volume ∼15 ml). This temperature was kept for 72 hours, next the heating source was switched off and the autoclave was allowed to cool to room temperature with a rate of about 300 K h⁻¹. The reaction product as obtained was reground, and annealed along the same procedure as described, once again. Samples with enrichment of the isotope ⁵⁷Fe to 10 or 20% for high-pressure synchrotron Mössbauer studies³⁹ were obtained by using isotopically enriched Fe₂O₃ as starting material.

2.2. Characterization methods

Powder X-ray diffraction (PXRD) was performed using a Huber G670 camera (Guinier technique, Co Kα₁ radiation, λ = 1.788965 Å, diffraction range 10° ≤ 2θ ≤ 100° in steps of 0.005°). Rietveld refinement⁴⁶ of the PXRD data of Sr₂FeO₄ was performed with the program WinCSD.⁴⁷

Thermogravimetric (TGA) analysis of Sr₂FeO₄ was carried out on a Netzsch STA 449 F3 thermoanalyzer. About 30 mg of the sample was placed in a corundum crucible, which was heated at a rate of 5 K min⁻¹ in the range of 300–1073 K under dynamic argon flow. The sample was kept at 1073 K (800 °C) for 4 hours where no further weight loss was observed. Finally, the sample was cooled down again.

Magnetization measurements of Sr₂FeO_4−x were recorded on samples sealed in Suprasil quartz tubes under He using an MPMS3 (Quantum Design) magnetometer in the temperature range of 1.8 to 400 K, in zero-field cooling (zfc) and field-cooling (fc) modes in applied fields up to 7 T. Isothermic magnetization measurements were performed after zero-field cooling by field ramping between 0 and 7 T.

⁵⁷Fe Mössbauer spectra were collected at various temperatures using a standard WissEl spectrometer operated in the constant acceleration mode (⁵⁷Co/Rh source) and a Janis SHI 850-5 closed cycle refrigerator. Powder samples of Sr₂FeO_4−x containing about 10 mg Fe cm⁻² were homogeneously distributed in an acrylic glass sample container with an inner diameter of 13 mm. In some cases the samples were diluted with BN to ensure homogeneous distribution. All isomer shifts are given relative to α-iron. The data were evaluated with the MossWinn program⁴⁸ using the thin absorber approximation. To model the shape of the spectra in the magnetically ordered phases hyperfine field distributions were either derived by the Hesse–Rübartsch method implemented in MossWinn or Gaussian hyperfine field distributions were assumed.

Magnetic structures were analyzed by powder neutron diffraction (PND) on two Sr₂FeO_4−x samples with x = 0.133(3) and x = 0.158(6). About 3 grams of material were placed in a vanadium sample container. Data were collected using the diffractometer E2 at the BER II reactor of the Helmholtz-Zentrum Berlin. This instrument is equipped with a pyrolytic graphite (PG) monochromator selecting the neutron wavelength λ = 2.380 Å. PND patterns were recorded at 1.8 and 80 K, well below and above the magnetic ordering temperatures, respectively. Additional PND patterns were measured within this temperature range to determine the temperature dependence of the lattice parameters and of the magnetic order parameters. The powder patterns were collected in the range of diffraction angles from 3.7° to 79.4°. Rietveld refinements of the PND data were carried out with the program FullProf,⁴⁹ using the nuclear scattering lengths b(O) = 5.805 fm, b(Fe) = 9.54 fm, and b(Sr) = 7.02 fm.⁵⁰ The magnetic form factors of the Fe atoms were taken from ref. 51.

2.3. Solid-state electrolyte coulometry

Solid-state electrolyte coulometry (SEC) was employed to analyze and adjust the oxygen content of Sr₂FeO_4−x, and to establish the corresponding p_O2-T-x-diagram. The basic principle of the technique and an overview on its applications has been detailed in ref. 52–54. The setup used for the studies presented here is sketched in Fig. 1. The system operates in a carrier gas mode and consists of two identical solid-state electrolyte (SE) SGM5EL ZIROX cells (doped zirconium oxide, ZIROX-Sensoren und Elektronik GmbH, 17489 Greifswald). Each cell has two electrode systems for potentiometric measurement of the chemical potential of oxygen and coulometric dosing or pumping of oxygen, respectively. The cells are positioned upstream (cell 1) and downstream (cell 2) of a quartz-tube reactor containing the sample whose change in oxygen content in course of the solid-gas interaction is to be studied as a function of temperature. In this setup the space containing the specimen to be equilibrated is thermally decoupled from the SE cells, thus the latter may operate constantly at such a temperature which is optimal for the solid electrolyte (∼750 °C for doped zirconium oxide). This measure taken admits to conveniently optimize the parameters of the gas-solid interaction (temperature program, geometry and material of the reactor) appropriate to the sample under investigation.⁵⁵ Current I, voltage U, O₂ concentration, and temperature of each SE cell, as well as the temperature of the sample were recorded using a customized computer program based on LabVIEW.

Fig. 1 Solid state electrolyte coulometry. Sketch of the experimental set up.

As carrier gases Ar, or gas mixtures Ar–H₂ and Ar–H₂–H₂O, respectively, were used. The range of partial pressures of oxygen realizable in Ar/O₂ is 10⁻⁶ to 10⁻³ bar and for Ar–H₂–H₂O mixtures 10⁻³² to 10⁻⁹ bar. For the latter, the oxygen partial pressures evolving as function of temperature for selected H₂/H₂O ratios are documented in Fig. S1 and Table S1 (ESI†). The actual oxygen chemical potential in the carrier gas was controlled in the upstream cell, whereas the uptake or loss of oxygen of the sample during the gas–solid equilibration was monitored in the downstream cell.

The mass of oxygen exchanged during solid-gas equilibration, Δm_O2, is obtained from Faraday's law,

where I₀ is the constant basic oxygen dosing current, I_t is the current registered in the downstream cell at time t, M_O2 is the molecular mass of oxygen, F the Faraday constant, and z = 4 the number of electrons transferred. The change Δx in oxygen stoichiometry for a sample with mass m and molecular weight M_s is obtained as

Δx = Δm_O2 × M_s/(m − Δm_O2)M_O2. (2)

The actual stoichiometry of the reduced specimen can be derived if the gas-solid reaction starts from a material with a well-defined oxygen content or if it leads to a well-defined final product. The samples of Sr₂FeO₄ used as starting materials were saturated with respect to oxygen content by annealing under elevated oxygen pressure.

The present experiments were carried out under the following conditions: depending on the size of the sample, the reaction chamber (quartz tube) had a diameter of approx. 18 mm outside and 16 mm inside, or alternatively 25/23 mm. A section of ∼17 cm of the total length of the reaction chamber (22 cm) was heated by a tube furnace. The sample was located in a quartz boat in the middle of the furnace. A thermocouple was attached close to the reaction site in a “quartz nose”, in order to enable a correct and continuous temperature registration at the reaction location.

In an exemplary run, an Ar gas flow of 5 l h⁻¹ with about 3 × 10⁻⁶ bar O₂ is used as carrier gas, the Sr₂FeO₄ samples are heated at a rate of 7 °C min⁻¹ and held at the targeted temperatures for 8 h. The O₂ activity is fine-tuned via the dosing current I₀ (∼10 mA) of the upstream cell.

3. Results and discussion

3.1. Synthesis and characterization of Sr₂FeO₄

The synthesis of Sr₂FeO₄ is challenging because of the fact that the compound decomposes above 700 °C into the Ruddlesden-Popper phase Sr₃Fe₂O_7−x and SrO. In previous work Sr₂FeO₄ was prepared either by heating of SrCO₃ and Fe₂O₃ at 1300 °C and subsequent conversion of the two-phase primary product Sr₃Fe₂O_7−x/SrO to Sr₂FeO₄ in a flow of high-pressure oxygen (200 bar) at 750 °C,⁵⁶ or by direct reaction from SrO and Fe₂O₃ at 650 °C in flowing O₂ atmosphere at ambient pressure.³⁷ The latter samples always contained a certain amount of unreacted Fe₂O₃. Here, we have successfully prepared phase-pure Sr₂FeO₄ by reaction of SrO and Fe₂O₃ in an autoclave at an oxygen pressure of 2500 bar at a moderate temperature of 500 °C. A Rietveld profile analysis (Fig. 2(a)) underlines the absence of any impurity phase, and has resulted in crystal structure data (cf. Table S2, ESI†) fully complying with those from previous studies.⁵⁶ Thermogravimetic analysis of a sample of Sr₂FeO₄ at 800 °C in an argon flow resulted in the composition Sr₂FeO_4.00(2) if decomposition of the sample to stoichiometric Sr₃Fe₂O₆ and SrO is assumed.

Fig. 2 Characterization of Sr₂FeO₄ obtained by high-pressure synthesis. (a) Rietveld analysis of the powder X-ray diffraction pattern. Dots correspond to the experimental data, red solid lines to the calculated pattern, blue solid lines to the difference pattern, and the tick bars to the peak positions. (b) Mössbauer spectrum at 290 K. The spectrum was fitted with a single quadrupole doublet with isomer shift IS = −0.014(1) mm s⁻¹ and quadrupole splitting QS = 0.444(1) mm s⁻¹ confirming the Fe⁴⁺ oxidation state. (c) Mössbauer spectrum at 5 K. The red arrows indicate a tiny Fe³⁺ fraction of ∼1% with B_hf ∼ 42 T which is seen in addition to the complex Fe⁴⁺ hyperfine pattern here approximated by 8 sextets.

Any oxygen deficiency in Sr₂FeO₄ can also be estimated using ⁵⁷Fe Mössbauer spectra. At room temperature (see Fig. 2(b)) the spectrum consists of a simple quadrupole doublet, assuring the absence of any Fe₂O₃ impurity and confirming that virtually all iron ions exist in the +4-oxidation state. Even more sensitive to small Fe³⁺ components is the Mössbauer spectrum in the magnetically ordered phase at 5 K which is shown Fig. 2(c). The spectrum is characterized by a complex hyperfine field (B_hf) distribution which reflects the elliptical spiral spin structure of Sr₂FeO₄ and was approximated by a superposition of eight hyperfine sextets having a typical Fe⁴⁺ isomer shift IS = 0.07 mm s⁻¹.³⁹ Detailed inspection of the spectrum reveals a tiny additional hyperfine component with an enlarged B_hf of ∼42 T and an intensity contribution of about 1% (marked by arrows in Fig. 2(c)) which is attributed to Fe³⁺. In different preparation runs the intensity fraction of this component slightly varied but was always ≤2%. Thus, using the Mössbauer spectra we estimate the oxygen deficiency in the high-pressure synthesized samples as ≤0.01. The good agreement with the results from the TGA reduction experiment at 800 °C in argon atmosphere indicates that under these conditions indeed reduction to the stoichiometric Fe³⁺ phase Sr₃Fe₂O₆ was achieved.

3.2. Investigation of the oxygen homogeneity range in Sr₂FeO_4−x by SEC

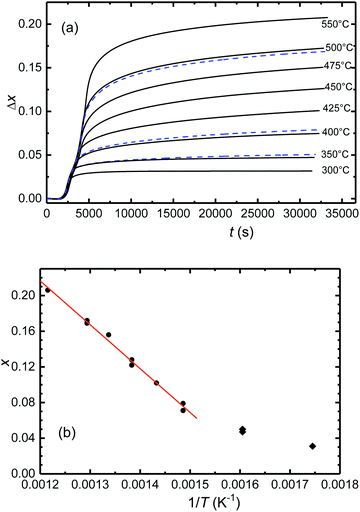
In exploring the homogeneity range of Sr₂FeO_4−x, pristine samples of Sr₂FeO₄ were equilibrated at constant temperatures and in argon carrier gas flows of defined oxygen partial pressure. The release of oxygen during solid/gas equilibration of the sample was compensated and monitored in the downstream cell, see section Experimental details.

A representative plot of the reduction process as function of time for target temperatures up to 500 °C is displayed in Fig. 3(a). Here, and in all other respective experiments two steps of reduction are apparent. The desorption of oxygen starts at about 150 °C with the maximum occurring at 300 °C. A second peak is apparent for temperatures ≥400 °C and represents further oxygen desorption in the Sr₂FeO_4−x phase. Integration of the temperature programmed oxygen desorption (TPOD) reaction curves yields the change in oxygen content Δx according to eqn (1) and (2) (Fig. 4(a)). Since during temperature rise the sample and gas phase are not always in equilibrium, details of the shape of the TPOD curve depend on the experimental conditions applied, as sample mass, gas flow and temperature gradient. Using this method oxygen-deficiency in Sr₂FeO_4−x with x up to about ∼0.20 was realized, which corresponds to Fe³⁺ fractions up to about 40%. Between 400 and 550 °C (673 and 823 K) a linear relation between x and inverse temperature was observed (Fig. 4(b)).

Fig. 3 Temperature programmed desorption curves for Sr₂FeO_4−x obtained by heating to the indicated temperatures. (a) Final temperature 300 to 500 °C, (b) final temperature 808 °C. The titration current I is represented as a function of time t. The temperature profiles for heating to 500 °C and to 808 °C are also shown. Typical sample masses were about 100 mg and the oxygen partial pressure was 3 × 10⁻⁶ bar.

Fig. 4 (a) Change of oxygen deficiency x in Sr₂FeO_4−x during the reaction in argon (p_O2 = 3 × 10⁻⁶ bar) with different final temperatures. If the initial phase is assumed to be stoichiometric Sr₂FeO₄, then Δx = x. (b) Oxygen deficiency as a function of inverse temperature. A linear relation is found between 400 °C (673 K) and 550 °C (823 K). The dashed blue lines correspond to a second independent experiment at the respective temperature.

Running the experiments at even higher temperatures of up to 800 °C leads to further reduction steps (Fig. 3(b)) which according to PXRD characterization (see Fig. 5) is accompanied by decomposition of Sr₂FeO_4−x finally leading to the formation of Sr₃Fe₂O₆ according to

2Sr₂FeO₄ → Sr₃Fe₂O₆ + SrO + ½O₂.

Fig. 5 Powder X-ray diffraction patterns of nominal Sr₂FeO_4−x samples with increasing oxygen deficiency x. The analysis of the PND pattern of the sample with x = 0.496 revealed complete decomposition to Sr₃Fe₂O₆ and SrO, where the peaks corresponding to SrO are marked by an asterisk.

At the same time this decomposition reaction demarcates the limit of oxygen deficiency in Sr₂FeO_4−x which can be achieved with this method. The change Δx = 0.496 in oxygen content obtained by reduction at 800 °C suggests a full reduction of Fe⁴⁺ in stoichiometric Sr₂FeO₄ to Fe³⁺ in Sr₃Fe₂O₆ which compares well with the TGA result.

Samples of Sr₂FeO_4−x with different values of x were synthesized by choosing different target temperatures and subsequent cooling. The samples were characterized by PXRD, a representative set of patterns is displayed in Fig. 5. Up to x ∼ 0.2 (heating up to 550 °C) the patterns still exhibit only reflections which are typical for the tetragonal K₂NiF₄-type crystal structure (space group I4/mmm) adopted by stoichiometric Sr₂FeO₄. Line broadening which increases with x may reflect strain effects owing to the oxygen desorption process, stacking faults,³⁹ and a certain inhomogeneity in x. For a sample with even higher x = 0.22 obtained by annealing at 600 °C a broad pattern was observed (not shown), which still shows the main reflections of the K₂NiF₄-type structure but also additional broad peaks. Further increase of temperature leads to degradation into Sr₃Fe₂O_7−x (space group I4/mmm) and SrO. These results suggest that Sr₂FeO_4−x samples with x up to ∼0.2 can be prepared by the present route, but decomposition occurs for larger x requiring higher reaction temperatures. In Fig. 6 the lattice parameters a and c as well as the cell volume V are shown for all samples prepared within this study and where the parent structure was retained. It is evident that the c parameter and V increase with increasing x whereas a slightly decreases. The variation of a with x in the Sr₂FeO_4−x system is in sharp contrast to the behavior of a in the Sr₃Fe₂O_7−x system,³¹ which contains double layers of FeO_m polyhedra (m = 5, 6) and is the n = 2 member of the Sr_n+1Fe_nO_3n+1 Ruddlesden-Popper series. For Sr₃Fe₂O_7−x the lattice parameter a increases linearly with increasing x, i.e. with increasing Fe³⁺ fraction, whereas the lattice parameter c shows a non-monotonic variation. This can be related to the fact that in Sr₃Fe₂O_7−x the oxygen defects are created in the c direction, namely the oxygen atoms which connect the FeO₆ octahedra of the double layers via corner-sharing in stoichiometric Sr₃Fe₂O₇ are removed. Finally, this leads to square pyramidal coordination of Fe³⁺ in Sr₃Fe₂O₆.³¹ The different behavior of a in Sr₂FeO_4−x suggests that mainly O atoms are removed from the FeO₂ layers in the ab plane. Then two opposing trends occur: on the one hand, the smaller Fe⁴⁺ ions are replaced by larger Fe³⁺ ions which should lead to an increase in a but on the other hand, the removal of O atoms from the layers leads to a collapse in a such that the overall variation of a with x is quite small. The increase in c mainly reflects the larger size of Fe³⁺ ions compared to Fe⁴⁺ ions. These considerations are in agreement with the different hydride reduction mechanisms proposed for Sr₃Fe₂O₇ and Sr₂FeO₄.^32,44 While for the former the reduction to Sr₃Fe₂O₅ proceeds via Sr₃Fe₂O₆ as intermediate phase, the latter was suggested to be reduced directly to Sr₂FeO₃ without intermediate phases.⁴⁴

Fig. 6 Lattice parameters and volume per formula unit for Sr₂FeO_4−x as function of x as determined from XRD patterns at room temperature. The different colors correspond to different sample preparation series. The solid lines are linear fits to all data sets.

3.3. Magnetic properties of Sr₂FeO_4−x

The peculiar electronic situation in strongly covalent Fe(IV) oxides, which is characterized by a negative charge-transfer energy,⁵ frequently gives rise to antiferromagnetic ordering with helical spin structures. Recently it was demonstrated that Sr₂FeO₄ adopts an elliptical spin spiral mainly oriented in the ab plane which undergoes a spin-flop transition in external magnetic fields of about 5 T.³⁹ To study the impact of oxygen deficiency, the magnetic properties of Sr₂FeO_4−x samples with x = 0.13 and 0.16 were investigated by magnetization, powder neutron diffraction, and ⁵⁷Fe Mössbauer measurements.

Magnetization measurements. In Fig. 7 we compare the magnetic susceptibilities χ(T) and inverse susceptibilities χ⁻¹(T) of oxygen-deficient Sr₂FeO_3.87 with those of the parent compound Sr₂FeO₄. The χ(T) curves of Sr₂FeO₄ (Fig. 7(a)) exhibit a maximum near 60 K which is the signature of antiferromagnetic order. According to specific heat data the Néel temperature is 55.8 K.³⁹ The field dependence of the χ(T) data for temperatures below the maximum reflects the spin-flop transition in Sr₂FeO₄ which also gives rise to a non-linearity in the magnetization curves M(H) (Fig. 8). A further weak cusp is seen in low-field zfc data of Sr₂FeO₄ while fc data only reveal an inflection. As the strength of this low-temperature feature varies in different samples and it shows some frequency dependence in ac susceptibility data³⁹ it is probably related to disorder effects owing to residual oxygen defects. A similar but now very pronounced cusp at 9 K is observed in the low-field zfc susceptibility data of Sr₂FeO_3.87 which is suppressed in larger magnetic fields (Fig. 7(b)). The irreversibility between zfc and fc data at low field suggests that the magnetic order is perturbed by the oxygen vacancies and glassy components contribute to the magnetism. Nevertheless, a cusp near 57 K which occurs under zfc as well as fc protocol and is independent of the magnetic field, suggests that Sr₂FeO_3.87 still exhibits long-range antiferromagnetic ordering with a similar T_N as in Sr₂FeO₄. An additional feature near 150 K seen in the fc data of Sr₂FeO_3.87 at 0.1 T is probably not intrinsic to the main phase. In contrast to Sr₂FeO₄ the χ(T) data at low temperatures and higher fields are essentially independent of the field and in fact, the M(H) curves of Sr₂FeO_3.87 at 1.8 K shown in Fig. 8 are linear between 1 and 7 T. These results suggest that the spin-flop transition of the parent compound is suppressed in the oxygen-deficient material. A non-linearity in M(H) below 1 T and a small remanent magnetic moment indicate a tiny ferromagnetic signal. Similar results were obtained for a sample with slightly higher oxygen deficiency (Sr₂FeO_3.84, see Fig. S2, ESI†).

Fig. 7 Comparison of the magnetic susceptibilities χ [(a), (b)] and inverse susceptibilities χ⁻¹ [(c), (d)] as a function of temperature of Sr₂FeO₄ and Sr₂FeO_3.87.

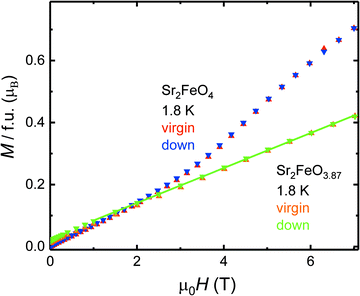Fig. 8 Comparison of the field dependence of the magnetic moments M(H) at T = 1.8 K of Sr₂FeO₄ and Sr₂FeO_3.87.

For Sr₂FeO_3.87 a Curie–Weiss (CW) analysis in the paramagnetic regime using the linear region in the χ⁻¹(T) data collected at 7 T (200–300 K) results in an effective magnetic moment μ_eff of 4.92 μ_B which is somewhat smaller than the spin-only value expected for a mixed-valence Fe⁴⁺/Fe³⁺ system with Fe⁴⁺ moments of 4.9 μ_B and Fe³⁺ moments of 5.9 μ_B. The corresponding θ_CW-parameter of +7 K in the CW law [χ(T) = C/(T − θ_CW), C is the Curie constant] suggests the presence of competing exchange interactions, where compared to Sr₂FeO₄ the relative strength of ferromagnetic interactions is reduced with respect to antiferromagnetic interactions. In the χ⁻¹(T) data of Sr₂FeO₄ no well-defined linear region can be identified up to 350 K but the data indicate strong ferromagnetic correlations.

Mössbauer spectroscopy. To study the evolution of the magnetic structure with oxygen deficiency we have measured Mössbauer spectra of Sr₂FeO_4−x samples with different x. The spectra of the parent compound Sr₂FeO₄ at low temperatures exhibit a peculiar asymmetric shape,^9,37 which can be considered as the signature of the elliptical spiral spin structure giving rise to a characteristic distribution of hyperfine magnetic fields B_hf and an associated modulation of the quadrupole interaction parameter 2ε.³⁹ The latter depends on the orientation angle between B_hf and the principal axis V_ZZ of the electric field gradient tensor. The shape of the Mössbauer spectrum at 5 K of a sample with composition Sr₂FeO_3.92 shown in Fig. 9(a) is still reminiscent of that of the parent phase but additional components with enhanced hyperfine fields are apparent. The latter can be attributed to Fe³⁺ sites which are created owing to the oxygen deficiency. The essential shape of the spectrum could be reproduced with a Fe⁴⁺ component having an isomer shift IS = 0.08 mm s⁻¹ and a B_hf distribution (〈B_hf〉 = 28.5 T) which was obtained according to the Hesse-Rübartsch method and two Fe³⁺ components (IS = 0.40 mm s⁻¹) differing in their B_hf values (〈B_hf〉 of 47.4 and 38.8 T, respectively). Similar as for Sr₂FeO₄, a linear correlation between B_hf and 2ε was assumed for the Fe⁴⁺ distribution. The extracted B_hf distribution (Fig. S3, ESI†) still reveals characteristic features of an elliptical spin spiral but the distribution is more complex which reflects modifications caused by the Fe³⁺ sites. Remarkably, the spectrum at 50 K reveals already about 30% of paramagnetic phase which indicates that in several domains of the Sr₂FeO_3.92 sample the magnetic ordering temperature is reduced. In the paramagnetic phase at 60 K the spectrum is well described by a superposition of two quadrupole doublets corresponding to Fe⁴⁺ and Fe³⁺, respectively.

Fig. 9 Mössbauer spectra of oxygen-deficient Sr₂FeO_3.92 (a) and Sr₂FeO_3.87 samples (b) measured at the indicated temperatures. Dots correspond to the experimental data, solid lines to the best fits. The subspectra are shown as colored lines (blue and cyan correspond to magnetically ordered and paramagnetic Fe⁴⁺, red and green to magnetically ordered Fe³⁺, and pink to paramagnetic Fe³⁺ sites, respectively). The sample of Sr₂FeO_3.87 was part of the batch investigated by PND.

As expected, the Mössbauer spectra of a sample with composition Sr₂FeO_3.87 exhibit an enhanced fraction of Fe³⁺ sites (Fig. 9(b)). For fitting the complex shape of the spectrum at 5 K we extracted B_hf distributions for the Fe⁴⁺ component (IS = 0.07 mm s⁻¹, 〈B_hf〉 = 25 T) and for the broad major Fe³⁺ contribution (〈B_hf〉 = 37 T) using the Hesse-Rübartsch method, while a smaller and less broad component with larger B_hf values (〈B_hf〉 = 47.5 T) was described by a Gaussian B_hf distribution. For the Fe⁴⁺ component still a linear correlation between B_hf and 2ε was assumed, for the Fe³⁺ components a single 2ε and equal IS = 0.39 mm s⁻¹ were used. The shape of the B_hf distribution of Fe⁴⁺ (Fig. S3, ESI†) differs from that of the parent phase which suggests that the spin structure is modified. The strong disturbance of the spin structure by the oxygen deficiency is also apparent from the presence of about 50% paramagnetic phase even at 30 K which is well below the T_N determined by neutron diffraction (see below). Similar spectra were obtained for a Sr₂FeO_3.84 sample but the fraction of magnetically ordered sites at 30 K is even smaller than in the Sr₂FeO_3.87 sample (see Fig. S4, ESI†).

The low-temperature spectra of all Sr₂FeO_4−x samples studied in this work revealed two different Fe³⁺ components, one with larger and one with smaller B_hf values. We have observed that samples from different reduction runs but with comparable oxygen deficiencies x resulted in different ratios of the two Fe³⁺ components. For instance, in the 5 K Mössbauer spectrum of a sample of Sr₂FeO_3.88 the area fraction of the Fe³⁺ component with larger B_hf (16%, Fig. S5, ESI†), is considerably enhanced compared to that (6%) in the spectrum of the Sr₂FeO_3.87 sample shown in Fig. 9(b). Remarkably, also the fraction of magnetically ordered sites at 30 K in the Sr₂FeO_3.88 sample is enhanced. The coexistence of magnetically ordered and collapsed phase below T_N suggests that the statistical extraction of oxygen atoms from Sr₂FeO₄ leads to fragmentation of the magnetic exchange network which results in magnetically ordered regions differing in size and ordering or freezing temperatures. It may be anticipated that removal of apical oxygen atoms has a less drastic effect for the magnetic exchange than the removal of oxygen atoms from the FeO₂ layers. A different ratio between apical and layer oxygen defects could be the reason for the differences in the low-temperature Mössbauer spectra of samples from different reduction runs. If we assign the Fe³⁺ component with larger B_hf to Fe³⁺ sites from regions where an apical O atom has been removed, it appears reasonable that at a given temperature a larger fraction of magnetically ordered regions persists in samples where the large B_hf-component dominates. Then the Fe³⁺ signal with smaller B_hf corresponds to regions where O atoms were removed from the layers, and thus for samples where this type of Fe³⁺ sites dominate, the fraction of magnetically ordered sites at a given temperature is smaller. It cannot be readily decided whether the oxygen vacancies occur around Fe³⁺ or Fe⁴⁺ sites. In the oxygen deficient SrFeO_3−x system the formation of square-pyramidal Fe⁴⁺O₅ units is known,²⁴ whereas in the Sr₃Fe₂O_7−x system Fe³⁺O₅ units occur.³¹ Our observations suggest that in different sample reduction runs somewhat different microstructures leading to differences in the local Fe³⁺ environment were produced. Unfortunately, attempts to control the microstructure by varying the reduction conditions were not conclusive.

Powder neutron diffraction studies. To clarify the influence of oxygen deficiency on the magnetic structure of Sr₂FeO_4−x, PND patterns of two samples with x = 0.133(3) and x = 0.158(6) were collected at 1.8 and 80 K, i.e. well in the magnetically ordered and in the paramagnetic state, respectively. For obtaining sufficient amount of material for the PND studies samples from different SEC reduction runs with comparable values of x were combined. In Fig. 10 the PND patterns of Sr₂FeO_3.87 and Sr₂FeO_3.84 are compared with those of the stoichiometric sample Sr₂FeO₄ which was investigated in our previous study.³⁹ The nuclear structures were refined in the tetragonal space group I4/mmm, and the results of the refinements are summarized in Table 1. Because of the limited range of diffraction angles 2θ, and the relatively large neutron wavelength of 2.380 Å it was not possible to determine the oxygen occupancies with good accuracy, but initial refinements of the oxygen occupancies indicated that oxygen atoms are mainly removed from the FeO₂ layers. Therefore, in the final refinements we have assumed full occupancy of the O1 atoms at the Wyckoff position 4e(0,0,z), while the occupancy of the O2 atoms at the Wyckoff position 4c(0,½,0) was fixed to the values calculated from the oxygen deficiency according to the SEC data. On the other hand, the structural parameters of Sr₂FeO₄, Sr₂FeO_3.87 and Sr₂FeO_3.84 could be reasonably well determined (see Table 1) although a certain deviation between calculated and observed lineshapes may indicate strain effects, lattice faults, and/or inhomogeneity in x, in agreement with the XRD study. The parameters of Sr₂FeO₄ obtained from neutron data at 80 K agree well with those from synchrotron data collected at 100 K.³⁹ A major goal of these refinements was to determine the overall scale factor with good accuracy which is needed to determine precisely the magnetic order parameters. In contrast to the refinement of the crystal structure it was possible to investigate in detail the magnetic structures since all magnetic reflections appear in the measured 2θ range. It is apparent from Fig. 10 that the strongest magnetic satellites [indexed as (000)^± or (τ, τ, 0)] of stoichiometric Sr₂FeO₄ and the two oxygen-deficient compounds appear practically at the same scattering angle of 2θ = 6.9°. Thus, the spin structures of the three compounds can be described by a propagation vector k = (τ, τ, 0) with τ = 0.137. Recently, we have shown that stoichiometric Sr₂FeO₄ adopts a cycloidal elliptical spin spiral with a pronounced modulation of the magnetic moments between μ_min = 1.9 μ_B and μ_max = 3.5 μ_B, although a certain out-of-plane tilting of the ellipse of about 27° (or a tilting angle to the c axis of about 63°) cannot be excluded.³⁹ According to Model II of ref. 39 the ellipse turns around the axis [11̄0] which keeps μ_max parallel to this axis. Thus, the component μ_min may partially turn out of the ab plane in the direction to the c axis.

Fig. 10 Powder neutron diffraction patterns of Sr₂FeO₄, Sr₂FeO_3.867 and Sr₂FeO_3.842, collected on the instrument E2 at 1.8 and 80 K. The observed magnetic reflections at 1.8 K are generated with the rule (hkl)_M = (hkl)_N ± k, where the incommensurate propagation vector is found to be k = (τ, τ, 0) with τ = 0.137(1). The calculated patterns (red solid lines) are compared with the observations (black-filled circles). The positions of the nuclear (N) and generated magnetic (M) reflections (black bars) as well as the difference patterns (I_obs − I_cal) (blue solid lines) are also shown.

Table 1 Results of the Rietveld refinements of the powder neutron diffraction data of Sr₂FeO_4−x collected at 1.8 and 80 K. The residuals of the crystal and magnetic structure refinements are defined as R_F = (∑||F_obs| − |F_calc||/∑|F_obs|) and R_M = (∑||I_obs| − |I_calc||/∑|I_obs), respectively. The crystal structure was refined in the tetragonal space group I4/mmm, where the Sr and O1 atoms are located at the Wyckoff position 4e(0,0,z), and the Fe and O2 atoms at the positions 2a(0,0,0) and 4c(0,½,0), respectively. Sr₂FeO₄ adopts an elliptical cycloidal spin structure and the two O deficient samples a circular helix. Using Model II of ref. 39 the spin ellipse turns slightly out of the ab plane around the axis along [11̄0]. Listed are the minor and major moments μ_min and μ_max, the averaged moment μ_av, the tilting angle β of the ellipse or circle to the c axis and the component τ of the propagation vector k = (τ, τ, 0). Also shown are the estimated correlation lengths ξ, the measured and calculated half widths at half maximum (HWHM) of the satellite (000)^± labeled as Δθ_obs and Δθ_sam, respectively

Sample	Sr2FeO4		Sr2FeO3.867		Sr2FeO3.847
T [K]	1.8	80	1.8	80	1.8	80
a From ref. 39, where the magnetic structure was analyzed based on the intensities of magnetic Bragg reflections, while here we performed Rietveld refinements using model II of ref. 39.
a [Å]	3.8459(3)	3.8457(4)	3.8409(3)	3.8414(4)	3.8473(3)	3.8480(4)
c [Å]	12.374(2)	12.370(2)	12.431(2)	12.432(3)	12.475(2)	12.474(2)
V [Å^3]	183.97(6)	183.89(7)	183.38(6)	183.47(8)	184.64(6)	184.71(7)
z(Sr)	0.3567(3)	0.3554(3)	0.3564(3)	0.3566(4)	0.3578(3)	0.3576(4)
z(O1)	0.1589(4)	0.1596(4)	0.1567(4)	0.1569(5)	0.1551(3)	0.1553(4)
d ap(Fe–O1) [Å]	1.967(5)	1.975(6)	1.947(5)	1.948(6)	1.934(5)	1.937(6)
d eq(Fe–O2) [Å]	1.9279(2)	1.9278(2)	1.9204(2)	1.9208(2)	1.9236(2)	1.9240(2)
R F	0.021	0.027	0.021	0.025	0.018	0.024
μ min(Fe) [μB]	2.1(2)/1.9(2)^a	—	1.27(17)	—	1.23(5)	—
μ max(Fe) [μB]	3.31(8)/3.46(5)^a	—	1.46(15)	—	1.23	—
μ av(Fe) [μB]	2.65(6)	—	1.33(3)	—	1.23(5)	—
β (°)	−65(7)/−63(16)^a	—	0	—	0	—
τ	0.13696(14)	—	0.1372(4)	—	0.1371(10)	—
R M	0.030	—	0.069	—	0.131	—
Δθobs [°]	0.446	—	0.475	—	0.731	—
Δθsam [°]	0	—	0.162	—	0.579	—
ξ [Å]	—	—	67	—	19	—

---

Rietveld refinement of the pattern of Sr₂FeO_3.87 at 1.8 K resulted in comparable moment components μ_min = 1.27(17) μ_B and μ_max = 1.46(15) μ_B which suggests that the anisotropy in the moments is much reduced compared to Sr₂FeO₄. The averaged magnetic moment μ_av = 1.33(3) μ_B is reduced by a factor of 2 compared to μ_av = 2.65(6) μ_B of the parent compound. The refinement of the tilting angle to the c axis leads to a value of 20(15)° which is not significantly different from zero, suggesting that one of the magnetic components is probably oriented parallel to the c axis. Thus, in the final refinement we assumed the presence of a circular helix, where the two components of the moment are aligned now parallel to the directions [11̄0] and [001]. A somewhat increased oxygen deficiency in Sr₂FeO_3.84 leads to further reduction of the magnetic moment reaching the smaller value μ_av = 1.23(5) μ_B. The results of the refinements are summarized in Table 1.

In Fig. 11(a–c) the thermal variation of the averaged magnetic moments μ_av, the component τ of the propagation vector k = (τ, τ, 0), as well as the shapes of the magnetic (000)^± peaks are shown. Most remarkably, only the magnetic moments and peak shapes are strongly changed in the oxygen-deficient samples, whereas the vector component τ and the Néel temperature T_N remain nearly the same as for Sr₂FeO₄. The vector component τ slightly decreases with increasing temperature for each sample as well as with increasing O deficiency. Our results suggest that oxygen deficiency mainly changes the shape and orientation of the spiral spin configuration while the propagation vector and therefore the rotation angle between adjacent spins remains the same. The spin structures of stoichiometric Sr₂FeO₄ and Sr₂FeO_3.87 are illustrated in Fig. 12.

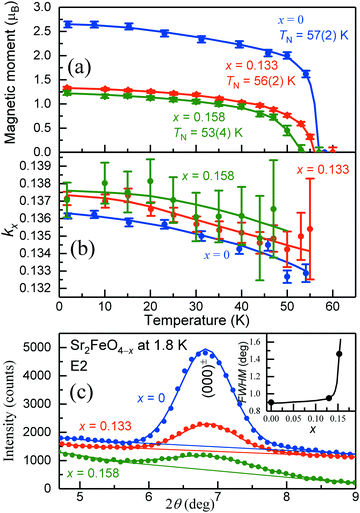Fig. 11 Results of the neutron diffraction study of samples of Sr₂FeO_4−x with x = 0, 0.133 and 0.158. (a and b) Temperature dependence of the total magnetic moments and vector components k_x of Sr₂FeO_4−x. The averaged moments of Sr₂FeO₄ were determined from the components μ_min and μ_max of the ellipse taken from ref. 39. For the two oxygen-deficient samples the magnitudes of μ_min and μ_max were found to be similar indicating the presence of circular spiral. The solid lines are guides for the eye. (c) Change of the peak shape and intensity of the strongest magnetic satellite (000)^± at 1.8 K with increasing oxygen deficiency. The insert shows the variation of the observed full widths at half maximum (FWHM).

Fig. 12 Incommensurate magnetic ordering in Sr₂FeO_4−x with the propagation vector k = (τ, τ, 0). The magnetic moments of the Fe atoms form ferromagnetic layers perpendicular to the propagation vector k pointing along the [110] direction. Stoichiometric Sr₂FeO₄ adopts a cycloidal elliptical spin spiral, where the magnetic moments are aligned within the tetragonal ab plane. Nevertheless, a small out-of-plane tilting of the ellipse cannot be excluded, where the moments are tilted away from the c axis by an angle β ∼ 70°.³⁹ The magnetic ordering of the oxygen-deficient compound shows the same k vector, but the tilting angle is decreased to 0° which changes the spin structure to an almost circular spiral.

To compare directly the magnetic intensity and peak shapes of the satellites (000)^± the overall scale factors are normalized for all three samples in Fig. 11(c). To analyze the degree of peak broadening of the O-deficient samples more quantitatively we used the profile function parameters determined for the stoichiometric Sr₂FeO₄ sample. For Sr₂FeO₄ we assumed a perfect long-range magnetic order. Thus, its half width at half maximum HWHM (HWHM = FWHM/2, where FWHM is the full width at half maximum) represents the instrumental resolution (labeled as Δθ_instr). While the difference between the moments of the two O-deficient samples is small, the peak width is strongly increased for Sr₂FeO_3.84 as shown in the insert of Fig. 11(c). For the estimation of the magnetic correlation lengths, defined as ξ = 1/q, the q-values (in units of Å⁻¹) are determined using q = 4π/λ × sin(Δθ_sam). The intrinsic HWHMs of Sr₂FeO_4−x (labeled as Δθ_sam) are calculated according to Δθ_sam = √(Δθ_obs² − Δθ_instr²), where Δθ_obs is the observed HWHM of the satellite (000)^±. The estimated correlation lengths of Sr₂FeO_3.87 and Sr₂FeO_3.84 are ξ = 67 Å and 19 Å, respectively. Further details are given in Table 1. The data suggest that increasing oxygen deficiency successively changes the spin arrangement from long-range order to a glassy state.

Such a scenario is supported by the Mössbauer spectra. The spectrum of Sr₂FeO_3.87 at 5 K indicates complete magnetic ordering or freezing of all iron moments (Fig. 9(b)). In particular, there is no drastic reduction in magnetic hyperfine fields which would be expected for a drastic reduction of the magnetic moments in the oxygen-deficient samples as suggested by the PND results. On the other hand, neutron diffraction yields average magnetic moments and only magnetically ordered regions with sufficiently large correlation length give rise to magnetic Bragg reflections. Thus, only larger-sized magnetically ordered regions are monitored in the PND experiment, whereas also the moments of smaller clusters not contributing to the neutron pattern are completely frozen at the lowest temperatures and seen by the local Mössbauer probe. This explains why the apparent magnetic moments of the iron ions appear to be reduced although Mössbauer spectra still reveal large hyperfine fields. A comparison of the magnetic moments of Sr₂FeO_3.87 and Sr₂FeO₄ suggests that only about 50% of the sample volume in the former shows long-range magnetic order detectable in PND experiments. This compares well with the area fraction of about 45% magnetically ordered phase in the 30 K Mössbauer spectrum of Sr₂FeO_3.87, whereas the other part is already paramagnetic. This fraction can be assigned to smaller magnetic clusters which do not contribute to magnetic Bragg reflections in the PND pattern. In Sr₂FeO_3.84 the coherence length is reduced and in fact the Mössbauer spectra of a sample at 30 K (Fig. S4, ESI†) show a decreased fraction of magnetically ordered sites which suggests a larger fraction of small magnetic clusters.

It is reasonable to attribute the long-range ordered magnetic regions detectable by powder neutron diffraction to regions where the exchange network is intact enough to maintain a spiral spin structure while the smaller clusters correspond to more disturbed regions. The varying magnetic properties may be related to some inhomogeneity in oxygen deficiency x but it is not clear whether there is a real phase separation which would imply vacancy clustering or ordering. It is known that the magnetic properties of perovskites featuring partial cation order at the transition metal site indeed depend much on the local composition and structure which is not readily apparent from diffraction studies but requires additional microstructural investigations.⁵⁷ Our Mössbauer studies described above and the spectra depicted in Fig. S5 (ESI†) indicate possible variations in the microstructure in Sr₂FeO_4−x materials from different synthesis runs.

4. Conclusions

In this work we have explored the K₂NiF₄-type oxygen-deficient system Sr₂FeO_4−x by heating stoichiometric Sr₂FeO₄ in well-defined oxygen partial pressures which were controlled by solid state electrolyte coulometry. Heating to temperatures up to 550 °C allows to prepare samples with x up to about 0.2, while annealing at higher temperatures leads to decomposition into SrO and Sr₃Fe₂O_7−x. The change of lattice parameters with increasing x suggests that oxygen atoms are mainly removed from the FeO₂ planes, which has drastic consequences for the magnetic properties. Our magnetization, Mössbauer, and powder neutron diffraction studies on Sr₂FeO_4−x samples with x = 0.13 and x = 0.16 suggest fragmentation of the magnetic exchange network owing to the oxygen defects and the creation of Fe³⁺ sites. This leads to the coexistence of larger domains which are long-range ordered and possibly adopt a circular helical spin structure and smaller magnetic clusters with reduced ordering or freezing temperatures. Further studies on Sr₂FeO_4−x and related cation substituted phases including transport measurements may be of interest with respect to a potential relevance of the system for applications as mixed anionic conductors below 700 °C and in catalysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Ralf Koban for help with magnetization measurements and Marcus Schmidt and Susann Scharsach for performing the TGA measurement.

Open Access funding provided by the Max Planck Society.

Notes and references

1. T. Mizokawa, H. Namatame, A. Fujimori, K. Akeyama, H. Kondoh, H. Kuroda and N. Kosugi, Origin of the band gap in the negative charge-transfer-energy compound NaCuO₂, Phys. Rev. Lett., 1991, 67, 1638.
2. T. Mizokawa, D. I. Khomskii and G. A. Sawatzky, Spin and charge ordering in self-doped Mott insulators, Phys. Rev. Lett., 2000, 61, 11263.
3. S. Johnston, A. Mukherjee, I. Elfimov, M. Berciu and G. A. Sawatzky, Charge disproportionation without charge transfer in the rare-earth-element nickelates as a possible mechanism for the metal–insulator transition, Phys. Rev. Lett., 2014, 112, 106404.
4. R. J. Green, M. W. Haverkort and G. A. Sawatzky, Bond disproportionation and dynamical charge fluctuations in the perovskite rare-earth nickelates, Phys. Rev. B, 2016, 94, 195127.
5. A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda and M. Takano, Electronic structure of SrFe⁴⁺O₃ and related Fe perovskites, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1561.
6. J. B. MacChesney, R. C. Sherwood and J. F. Potter, Electrical and magnetic properties of the strontium ferrates, J. Chem. Phys., 1965, 43, 1907.
7. M. Takano, N. Nakanishi, Y. Takeda, S. Naka and T. Takada, Charge disproportionation in CaFeO₃ studied with the Mössbauer effect, Mater. Res. Bull., 1977, 12, 923.
8. P. M. Woodward, D. E. Cox, E. Moshopoulou, A. W. Sleight and S. Morimoto, Structural studies of charge disproportionation and magnetic order in CaFeO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 844.
9. S. E. Dann, M. T. Weller, D. B. Currie, M. F. Thomas and A. D. Al-Rawwas, Structure and magnetic properties of Sr₂FeO₄ and Sr₃Fe₂O₇ studied by powder neutron diffraction and Mössbauer spectroscopy, J. Mater. Chem., 1993, 3, 1231.
10. P. Adler, Electronic state, magnetism, and electrical transport behavior of Sr₃A_xFe₂O₇ (x ≤ 0.4, A = Ba, La), J. Solid State Chem., 1997, 130, 129.
11. K. Kuzushita, S. Morimoto, S. Nasu and S. Nakamura, Charge disproportionation and antiferromagnetic order of Sr₃Fe₂O₇, J. Phys. Soc. Jpn., 2000, 69, 2767.
12. J.-H. Kim, D. C. Peets, M. Reehuis, P. Adler, A. Maljuk, T. Ritschel, M. C. Allison, J. Geck, J. R. L. Mardegan, P. J. Bereciartua Perez, S. Francoual, A. C. Walters, T. Keller, P. M. Abdala, P. Pattison, P. Dosanjh and B. Keimer, Hidden charge order in an iron oxide square-lattice compound, Phys. Rev. Lett., 2021, 127, 097203.
13. I. Yamada, K. Takata, N. Hayashi, S. Shimokura, M. Azuma, S. Mori, S. Muramaka, Y. Shimakawa and M. Takano, A perovskite containing quadrivalent iron as a charge-disproportionated ferrimagnet, Angew. Chem., Int. Ed., 2008, 47, 7032.
14. Y. Hosaka, N. Ichikawa, T. Saitoh, P. Manuel, D. Khalyavin, J. P. Attfield and Y. Shimakawa, Two-dimensional charge disproportionation of the unusual valence state Fe⁴⁺ in a layered double perovskite, J. Am. Chem. Soc., 2015, 137, 7468.
15. M. Takano, S. Nasu, T. Abe, K. Yamamoto, S. Endo, Y. Takeda and J. B. Goodenough, Pressure-induced high-spin to low-spin transition in CaFeO₃, Phys. Rev. Lett., 1991, 67, 3267.
16. P. Adler, U. Schwarz, K. Syassen, G. K. Rozenberg, G. Yu. Machiavariani, A. P. Milner, M. P. Pasternak and M. Hanfland, Collapse of the charge disproportionation and covalency-driven insulator-metal transition in Sr₃Fe₂O₇ under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 4609.
17. T. Kawakami, Y. Sekiya, A. Mimura, K. Kobayashi, K. Tokumichi, I. Yamada, M. Mizukami, N. Kawamura, Y. Shimakawa, Y. Ohishi, N. Hirao, N. Ishimatsu, N. Hayashi and M. Takano, Two-step suppression of charge disproportionation in CaCu₃Fe₄O₁₂ under pressure, J. Phys. Soc. Jpn., 2016, 85, 034716.
18. T. Takeda, Y. Yamaguchi and H. Watanabe, Magnetic structure of SrFeO₃, J. Phys. Soc. Jpn., 1972, 33, 967.
19. N. Hayashi, T. Yamamoto, H. Kageyama, M. Nishi, Y. Watanabe, T. Kawakami, Y. Matsushita, A. Fujimori and M. Takano, BaFeO₃: a ferromagnetic iron oxide, Angew. Chem., Int. Ed., 2011, 50, 12547.
20. J.-H. Kim, A. Jain, M. Reehuis, D. C. Peets, C. Ulrich, J. T. Park, E. Faulhaber, A. Hoser, H. C. Walker, D. T. Adroja, A. C. Walters, D. S. Inosov, A. Maljuk and B. Keimer, Competing exchange interactions at the verge of a metal-insulator transition in the two-dimensional spiral magnet Sr₃Fe₂O₇, Phys. Rev. Lett., 2014, 113, 147206.
21. S. Ishiwata, M. Tokunaga, Y. Kaneko, D. Okuyama, S. Wakimoto, K. Kakurai, T. Arima, Y. Taguchi and Y. Tokura, Versatile helimagnetic phases under magnetic fields in cubic perovskite SrFeO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 05447.
22. S. Chakraverty, T. Matsuda, H. Wadati, J. Okamoto, Y. Yamasaki, H. Nakao, Y. Murakami, S. Ishiwata, M. Kawasaki, Y. Taguchi, Y. Tokura and H. Y. Hwang, Multiple helimagnetic phases and topological Hall effect in epitaxial thin films of pristine and Co-doped SrFeO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 220405(R).
23. S. Ishiwata, T. Nakajima, J. H. Kim, D. S. Inosov, N. Kanazawa, J. S. White, J. L. Gavilano, R. Geogii, K. Seemann, G. Brandl, P. Manuel, D. D. Khalyavin, S. Seki, Y. Tokunaga, M. Kinoshita, Y. W. Long, Y. Kaneko, Y. Taguchi, T. Arima, B. Keimer and Y. Tokura, Emergent topological spin structures in the centrosymmetric cubic perovskite SrFeO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 134406.
24. J. P. Hodges, S. Short, J. D. Jorgensen, X. Xiong, B. Dabrowski, S. M. Mini and C. W. Kimball, Evolution of the oxygen-vacancy ordered crystal structures in the perovskite series Sr_nFe_nO_3n+1 (n = 2, 4, 8, and ∞), and the relationship to electronic and magnetic properties, J. Solid State Chem., 2006, 151, 190.
25. M. Reehuis, C. Ulrich, A. Maljuk, Ch Niedermeyer, B. Ouladdiaf, A. Hoser, T. Hofmann and B. Keimer, Neutron diffraction study of spin and charge ordering in SrFeO_3−δ, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184109.
26. A. Lebon, P. Adler, C. Bernhard, A. V. Boris, A. V. Pimenov, A. Maljuk, C. T. Lin, C. Ulrich and B. Keimer, Magnetism, charge order, and giant magnetoresistance in SrFeO_3−δ single crystals, Phys. Rev. Lett., 2004, 92, 037202.
27. P. Adler, A. Lebon, V. Damljanović, C. Ulrich, C. Bernhard, A. V. Boris, A. Maljuk, C. T. Lin and B. Keimer, Magnetoresistance effects in SrFeO_3−δ: dependence on phase composition and relation to magnetic and charge order, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094451.
28. Y. Tsujimoto, C. Tassel, N. Hayashi, T. Watanabe, H. Kageyama, K. Yoshimura, M. Takano, M. Ceretti, C. Ritter and W. Paulus, Infinite-layer iron oxide with a square-planar coordination, Nature, 2007, 450, 1062.
29. D. C. Peets, J.-H. Kim, P. Dosanjh, M. Reehuis, A. Maljuk, N. Aliouone, C. Ulrich and B. Keimer, Magnetic phase diagram of Sr₃Fe₂O_7−δ, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214410.
30. P. K. Gallagher, J. B. MacChesney and D. N. E. Buchanan, Mössbauer effect in the system Sr₃Fe₂O_6–7, J. Chem. Phys., 1966, 45, 2466.
31. S. E. Dann, M. T. Weller and D. B. Currie, Structure and oxygen stoichiometry in Sr₃Fe₂O_7−y, 0 ≤ y ≤ 1.0, J. Solid State Chem., 1992, 97, 179.
32. H. Kageyama, T. Watanabe, Y. Tsujimoto, A. Kitada, Y. Samida, K. Kanamori, K. Yoshimura, N. Hayashi, S. Muranaka, M. Takano, M. Ceretti, W. Paulus, C. Ritter and G. André, Spin-ladder iron oxide: Sr₃Fe₂O₅, Angew. Chem., Int. Ed., 2008, 47, 5740.
33. B. Li, S. He, J. Li, X. Yue, J. T. S. Irvine, D. Xie, J. Ni and C. Ni, A Ce/Ru codoped SrFeO_3−δ perovskite for a coke-resistant anode of a symmetrical solid oxide fuel cell, ACS Catal., 2020, 10, 14398.
34. K. Wiik, S. Aasland, H. L. Hansen, I. L. Tangen and R. Ødegård, Oxygen permeation in the system SrFeO_3−x–SrCoO_3−y, Solid State Ionics, 2002, 152–153, 675.
35. K. Tamai, S. Hosokawa, K. Kato, H. Asakura, K. Teramura and T. Tanaka, Low-temperaure NO oxidation using lattice oxygen in Fe-site substituted SrFeO_3−δ, Phys. Chem. Chem. Phys., 2020, 22, 24181.
36. R. Scholder, H. v Bunsen and W. Zeiss, Über Orthoferrate, Z. Anorg. Allg. Chem., 1956, 283, 330.
37. P. Adler, Properties of K₂NiF₄-type oxides Sr₂FeO_∼4, J. Solid State Chem., 1994, 108, 275.
38. P. Adler, A. F. Goncharov, K. Syassen and E. Schönherr, Optical reflectivity and Raman spectra of Sr₂FeO₄ under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11396.
39. P. Adler, M. Reehuis, N. Stüßer, S. A. Medvedev, M. Nicklas, D. C. Peets, J. Bertinshaw, C. K. Christensen, M. Etter, A. Hoser, L. Schröder, P. Merz, W. Schnelle, A. Schulz, Q. Mu, D. Bessas, A. Chumakov, M. Jansen and C. Felser, Spiral magnetism, spin flop, and pressure-induced ferromagnetism in the negative charge-transfer-gap insulator Sr₂FeO₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 105, 054417.
40. G. K. Rozenberg, A. P. Milner, M. P. Pasternak, G. R. Hearne and R. D. Taylor, Experimental confirmation of a p–p intraband gap in Sr₂FeO₄, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 10283.
41. Y. Takeda, K. Imayoshi, N. Imanishi, O. Yamamoto and M. Takano, Preparation and characterization of Sr_2−xLa_xFeO₄ (0 ≤ x ≤ 1), J. Mater. Chem., 1994, 4, 19.
42. T. Omata, K. Ueda, H. Hosono, M. Katada, N. Ueda and H. Kawazoe, Electrical and magnetic properties of hole-doped Sr_1+xLa_1−xFeO₄, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 10194.
43. Q. Zhao, M. D. Smith and H.-C. zur Loye, Crystal growth and structure determination of the mixed-valent iron(III/IV) oxides Sr_2−xLn_xFeO₄ (Ln = Nd, Sm, Eu), J. Chem. Crystallogr., 2011, 41, 674.
44. C. Tassel, L. Seinberg, N. Hayashi, S. Ganesanpotti, Y. Ajiro, Y. Kobayashi and H. Kageyama, Sr₂FeO₃ with stacked infinite chains of FeO₄ square planes, Inorg. Chem., 2013, 52, 6096.
45. C. Linke and M. Jansen, Über Ag₂SnO₃, das erste Silberstannat, Z. Anorg. Allg. Chem., 1997, 623, 1441.
46. H. M. Rietveld, A profile refinement method for nuclear and magnetic structures, J. Appl. Crystallogr., 1969, 2, 65.
47. L. Akselrud and Y. Grin, WinCSD: software package for crystallographic calculations (Version 4), J. Appl. Crystallogr., 2014, 47, 803.
48. Z. Klencsár, E. Kuzmann and A. Vértes, User-friendly software for Mössbauer spectrum analysis, J. Radioanal. Nucl. Chem., 1996, 210, 105.
49. J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192, 55.
50. V. F. Sears, in International Tables for Crystallography, ed. A. J. C. Wilson, Kluwer Academic Publishers, Dordrecht/Boston/London, 1995, vol. C, p. 383.
51. P. J. Brown, in International Tables for Crystallography, ed. A. J. C. Wilson, Kluwer Academic Publishers, Dordrecht/Boston/London, 1995, vol. C, p. 391.
52. K. Teske, H. Oppermann and G. Stöver, Zur Bestimmung der Phasenbreite von Zinkoxid, Z. Anorg. Allg. Chem., 1984, 511, 72.
53. M. Bode, K. Teske and H. Ullmann, Fest-Elektrolyt-Coulometrie (FEC). Eine vielseitige Methode zur Untersuchung von Gas-Festkörper-Wechselwirkungen, GIT-Fachz. Lab, 1994, 38, 495.
54. K. Teske, H. Ullmann and N. Trofimenko, Thermal analysis of transition metal and rare earth oxide system-gas interactions by a solid electrolyte-based coulometric technique, J. Thermal Anal., 1997, 49, 1211.
55. V. Vashook, J. Zosel and U. Guth, Oxygen solid electrolyte coulometry (SEC), J. Solid State Electrochem., 2012, 16, 3401.
56. S. E. Dann, M. T. Weller and D. B. Currie, Synthesis and structure of Sr₂FeO₄, J. Solid State Chem., 1991, 92, 237.
57. M. Hendrickx, Y. Tang, E. C. Hunter, P. D. Battle and J. Hadermann, Structural and magnetic properties of the perovskites A₂LaFe₂SbO₉ (A = Ca, Sr, Ba), J. Solid State Chem., 2021, 295, 121914.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02156k

---