Effect of alkali metal cations on network rearrangement in polyisoprene ionomers†
Yohei
Miwa
 *ab,
Koki
Hasegawa
a,
Taro
Udagawa
*ab,
Koki
Hasegawa
a,
Taro
Udagawa
 a,
Yu
Shinke
c and
Shoichi
Kutsumizu
a,
Yu
Shinke
c and
Shoichi
Kutsumizu
 *a
*a
aDepartment of Chemistry and Biomolecular Science, Faculty of Engineering, Gifu University, Yanagido, Gifu 501-1193, Japan. E-mail: y_miwa@gifu-u.ac.jp; kutsu@gifu-u.ac.jp
bPRESTO, Japan Science and Technology Agency, Japan
cThe Yokohama Rubber Co., Ltd, Hiratsuka, 254-8601, Japan
First published on 7th July 2022
Abstract
The effects of cations, Li+, Na+, and Cs+, on the structure of ionic aggregates and network rearrangement in carboxylated polyisoprene (PI) ionomers were studied. We found that network rearrangement via interaggregate hopping of metal carboxylates is improved with a decrease in cation size, even though density functional theory (DFT) calculation indicated the increase in the attractive interaction between metal carboxylates. At the same time, we also found that as the size of the cation decreases, the inclusion of the PI segment in the ionic aggregate increases. The DFT calculation suggested the cation–π interaction between the cation and double bonds in the PI segment as the cause for the inclusion. The inclusion of the PI segment with a low glass transition temperature (Tg) plasticizes the ionic aggregate and would sterically hinder the attractive interaction between metal carboxylates. In fact, the electron spin resonance measurement revealed a decrease in the Tg of the ionic aggregate with a decrease in cation size. Based on our findings, we proposed that the inclusion of PI segments in the ionic aggregate is the possible cause for the enhancement of network rearrangement in the carboxylated PI ionomers with a decrease in the cation size.
Introduction
Since ionic groups covalently attached to hydrophobic polymer chains aggregate and serve as physical crosslinks, they significantly alter the material's rheological and mechanical properties. This type of ionic polymer is an ionomer.1–3 The reversible nature of the ionic crosslinks in ionomers has attracted interest from various fields, including theoretical and experimental studies. For example, advanced ionomers with self-healing4–11 and shape-memory12–14 properties have recently been developed using the network's dynamic nature.Recently, the authors have developed novel ionomers composed of sodium-neutralized carboxylated polyisoprene (PI)8,10,11 and carboxylated poly(dimethylsiloxane) (PDMS).9 These ionomers exhibit the “ion-hopping”,15–17 in which ionic groups hop between ionic aggregates along with attached polymer chains, below room temperature. In other words, the networks in these ionomers autonomously rearrange at room temperature. Because of the network rearrangement, these ionomers exhibit unique properties, such as autonomous self-healing at room temperature.8–11 The mechanical and self-healing properties of these ionomers strongly depend on the rate of the network rearrangement. For example, an ionomer with fast network rearrangement at room temperature exhibits relatively weak mechanical properties while the self-healing effects occur quickly. Therefore, controlling the network rearrangement speed is crucial in such ionomers to tune the material's performances. Network rearrangement is accelerated by decreasing the neutralization degree of the carboxy group because unneutralized carboxy groups plasticize the ionic interactions in the ionic aggregates.17 That is, the lifetime of the reversible crosslinks in ionomers can be easily tuned by varying the neutralization degree, in contrast to other supramolecular systems with dynamic covalent bonds,18–22 π–π interactions,23 hydrogen bonding,24–27etc. In fact, the authors showed that the rate of the network rearrangement in the PI and PDMS ionomers can be widely varied via neutralization degree.8,9
In this work, we studied the effects of alkali metal cations, Li+, Na+, and Cs+, on the network rearrangement in carboxylated PI ionomers. We found that network rearrangement is accelerated by decreasing cation radius. To understand this phenomenon, the composition of the ionic aggregate and the interactions between the alkali metal cation and the double bonds in the PI segments have been experimentally and theoretically studied in detail.
Experiments
Materials
Isoprene (>99%, Tokyo Chemical Industry) was purified using molecular sieves (3A 1/16, Nacalai Tesque) and aluminum oxide (activated, Kanto Chemical) before use. N,N,N′,N′-tetramethylethylenediamine (>98%, Tokyo Chemical Industry) was dried using molecular sieves. sec-Butyllithium (sec-BuLi, 1 mol L−1 in cyclohexane (95%) and n-hexane (5%), Kanto Chemical), n-hexane (>96.0%, Kanto Chemical), cyclohexane (>99.5%, Kanto Chemical), tetrahydrofuran (THF, >99.5%, Kanto Chemical), methanol (>99.8%, Kanto Chemical), hydrochloric acid (35%, Nacalai Tesque), CDCl3 (99.8%, Nacalai Tesque), 2,6-di-tert-butyl-p-cresol (BHT, >98%, Kanto Chemical), lithium hydroxide anhydrous (LiOH, 98%, Kishida Chemicals), sodium hydroxide (NaOH, 97%, Nakalai Tesque), cesium hydroxide monohydrate (CsOH, >95%, Nakalai Tesque), 4-carboxy-2,2,6,6-tetramethylpiperidine 1-oxyl (4-carboxy-TEMPO, >97%, Tokyo Chemical Industry), and 5-DOXYL-stearic acid (5DSA, Aldrich Chemical Co., Ltd) were used without further purification.Preparation of PI ionomer
PI ionomers were synthesized using our previously reported procedure.8,10 A monodisperse PI was prepared via the anionic polymerization using sec-BuLi as an initiator. The weight average molecular weight (Mw) and polydispersity index (Mw/Mn) of the obtained PI determined by gel permeation chromatography (GPC) calibrated with standard PI (Scientific Polymer Products) samples were 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 and 1.07, respectively. 1H-nuclear magnetic resonance (NMR) and 13C-NMR spectra of the PI are shown in Fig. S3 in the ESI.† The microstructures of the PI determined using 13C-NMR are cis-1,4 (80%), trans-1,4 (15%), and 3,4 microstructure units (5%). Carboxy groups were randomly added along the main chain of PI via the reaction with sec-BuLi and carbon dioxide gas in cyclohexane solution.8,10 The carboxy group concentration in the repeat isoprene units was 2.0 mol%, as calculated by neutralization titration. LiOH, NaOH, and CsOH were used to fully neutralize the carboxy groups in the carboxylic PI (PI–COOH). These ionomers are noted as PI-M, where M is Li, Na, or Cs; the chemical structure of PI-M is shown in Fig. 1. Fourier transform infrared (FT–IR) spectra for PI, PI–COOH, and PI-M are shown in Fig. S4 (ESI†). A stretching vibration for the carbonyl of COOH was observed at 1708 cm−1, whereas it was absent for PI-M owning to the complete neutralization. Alternatively, an asymmetric stretching vibration for the metal carboxylate appears at ∼1580 cm−1 in PI-M. PI-M and 0.1 wt% of BHT were dissolved in THF/methanol (9
800 and 1.07, respectively. 1H-nuclear magnetic resonance (NMR) and 13C-NMR spectra of the PI are shown in Fig. S3 in the ESI.† The microstructures of the PI determined using 13C-NMR are cis-1,4 (80%), trans-1,4 (15%), and 3,4 microstructure units (5%). Carboxy groups were randomly added along the main chain of PI via the reaction with sec-BuLi and carbon dioxide gas in cyclohexane solution.8,10 The carboxy group concentration in the repeat isoprene units was 2.0 mol%, as calculated by neutralization titration. LiOH, NaOH, and CsOH were used to fully neutralize the carboxy groups in the carboxylic PI (PI–COOH). These ionomers are noted as PI-M, where M is Li, Na, or Cs; the chemical structure of PI-M is shown in Fig. 1. Fourier transform infrared (FT–IR) spectra for PI, PI–COOH, and PI-M are shown in Fig. S4 (ESI†). A stretching vibration for the carbonyl of COOH was observed at 1708 cm−1, whereas it was absent for PI-M owning to the complete neutralization. Alternatively, an asymmetric stretching vibration for the metal carboxylate appears at ∼1580 cm−1 in PI-M. PI-M and 0.1 wt% of BHT were dissolved in THF/methanol (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v)), and the solution was slowly evaporated in a Teflon dish at 35 °C. Then, cast sheets (0.5 mm tick) were vacuum-dried using a rotary pump at 35 °C for more than 2 days. The dried sample sheets were quickly packed into an aluminum laminated package with molecular sieves and oxygen absorbent to prevent oxidation and moisture absorption of the samples. The package was stored in a freezer. The sample sheets were further vacuum-dried using a rotary pump at 35 °C for more than 3 days before measurement. Complete drying was confirmed with no hydroxy stretching vibration at 3430 cm−1 in the FT-IR spectra (Fig. S5, ESI†). No weight loss from water desorption in thermogravimetric (TG) measurements further supports evidence of complete sample drying (Fig. S6, ESI†).
1 (v/v)), and the solution was slowly evaporated in a Teflon dish at 35 °C. Then, cast sheets (0.5 mm tick) were vacuum-dried using a rotary pump at 35 °C for more than 2 days. The dried sample sheets were quickly packed into an aluminum laminated package with molecular sieves and oxygen absorbent to prevent oxidation and moisture absorption of the samples. The package was stored in a freezer. The sample sheets were further vacuum-dried using a rotary pump at 35 °C for more than 3 days before measurement. Complete drying was confirmed with no hydroxy stretching vibration at 3430 cm−1 in the FT-IR spectra (Fig. S5, ESI†). No weight loss from water desorption in thermogravimetric (TG) measurements further supports evidence of complete sample drying (Fig. S6, ESI†).
Measurements
Typical measurements performed in this work have been described in our previous papers.8–111H-NMR and 13C-NMR measurements were conducted for samples dissolved in CDCl3 containing TMS as an internal standard using a 400 MHz JEOL-ECS400 spectrometer. GPC was performed on an HLC-8020 system (Tosoh Co., Ltd) using THF as eluent. FT–IR spectra were obtained using a Spectrum400 spectrometer (PerkinElmer) equipped with a DTGS detector. Differential scanning calorimetry (DSC) was performed on a DSC7020 (SII). Samples were loaded into aluminum pans and measured at a rate of 10 K min−1 between −120 °C and 100 °C until the third heating cycle. TG was measured from a room temperature to 500 °C at a heating rate of 5 K min−1 under N2 flow on a STA200 (HITACHI). Synchrotron small angle X-ray scattering (SAXS) measurements were performed using the BL-6A beamline at the Photon Factory of High Energy Accelerator Research Organization (KEK) in Tsukuba, Japan. The irradiated X-ray has a wavelength (λ) of 1.5 Å. The sample sheets were further dried at 35 °C in a vacuum for 3 days and packed into an aluminum laminated package with molecular sieves and oxygen absorbent. The package was opened just before the SAXS measurement, and the sample sheets were measured as soon as possible to prevent moisture absorption. The rheological data were obtained by a parallel-plate rheometer (AR-G2, TA instruments) with 8 mm diameter plates. A temperature sweep test was performed in the range −100 °C to 110 °C at 1 Hz and a heating rate of 3 K min−1. PI with Mn = 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 was used for the rheology measurement. Before measuring the rheology, the sample sheets were further dried at 35 °C in a vacuum for more than 3 days and set into the rheometer as soon as possible. The set sample sheet was additionally dried under dry nitrogen flow for more than 3 hours to remove any absorbed moisture. Electron spin resonance (ESR) measurements were conducted on JEOL X-band (∼9 GHz) FA100 spectrometer. The PI-Ms were spin-probed with 4-carboxy-TEMPO at a concentration of 6 × 10−8 mol g−1. The sample was encapsulated into a 5 mm o.d. quartz tube and sealed under a vacuum. The glass transition temperature of the spin-probed sample was measured by the microwave power saturation method that was developed by the author.28–33
900 was used for the rheology measurement. Before measuring the rheology, the sample sheets were further dried at 35 °C in a vacuum for more than 3 days and set into the rheometer as soon as possible. The set sample sheet was additionally dried under dry nitrogen flow for more than 3 hours to remove any absorbed moisture. Electron spin resonance (ESR) measurements were conducted on JEOL X-band (∼9 GHz) FA100 spectrometer. The PI-Ms were spin-probed with 4-carboxy-TEMPO at a concentration of 6 × 10−8 mol g−1. The sample was encapsulated into a 5 mm o.d. quartz tube and sealed under a vacuum. The glass transition temperature of the spin-probed sample was measured by the microwave power saturation method that was developed by the author.28–33
DFT calculations
The interaction energy between the metal carboxylates was calculated by the density functional theory (DFT) method with the GAUSSIAN09 Revision B.01 program package by following procedures.10 Since there are numerous possible conformations for the metal carboxylate pair, we used the anharmonic downward distortion following (ADDF)34 calculation to narrow down the conformations for those with lower electronic energies. First, we applied the ADDF calculation to an isoprene model trimer having one carboxy group. The initial geometry for the ADDF calculation was obtained by PM635 semi-empirical calculation. The ADDF calculation was also performed at PM6 level with a large anharmonic downward distortion (LADD) = 3, NLowest = 20 and EQOnly keywords. The bond condition keyword was also adopted to prevent covalent bonds in the given initial geometry from breaking. The ADDF calculation was performed in gas phase to produce 82 equilibrium geometries. The 10 lowest-energy monomer conformations were used to build 55 initial geometries for the DFT geometry optimization of a combination of the model isoprene trimers. The initial geometries for the DFT calculation of –COOLi⋯LiOOC–, –COONa⋯NaOOC–, and –COOCs⋯CsOOC– were obtained by replacing the H atoms in COOH groups in the 10 lowest-energy combinations with Li, Na, and Cs atoms, respectively. The interaction energies of –COOLi⋯LiOOC–, –COONa⋯NaOOC–, and –COOCs⋯CsOOC– were then calculated as the average interaction energy of the 10 lowest-energy combinations. The M0636 exchange-correlation functional and 6-31G(d,p)37,38 basis set were used for the DFT calculation. The LanL2DZ39–41 effective core potential was adopted for the Cs atom.DFT calculations were also used to measure the cation–π interaction energy between the metal carboxylate and the double bond in the PI segment. The multi-component artificial force induced reaction (MC-AFIR)42 calculation with PM6 semi-empirical method was performed with nsample = 30 and gamma = 50 kJ mol−1 keywords to obtain the initial geometries for DFT calculation. The M06 exchange-correlation functional, 6-31G(d,p) basis set, and LanL2DZ effective core potential were also used for these DFT calculations. We have checked that the M06/6-31G(d,p)+LanL2DZ method is accurate enough for calculating the cation–π interaction energy (see, ESI†). Using these procedures, we calculated the coordination between segmented PI-Li and PI units and between segmented PI-Cs and PI units as illustrated in Fig. S7 (ESI†). In the case of PI-Li, from one to four PI units were coordinated to the PI-Li (the coordination is denoted as PI-Li + nPI (n = 1–4)), while from one to five PI units were coordinated to the PI-Cs (denoted as PI-Cs + nPI (n = 1–5)). As a result, we obtained 30 one-PI-coordinated, 29 two-PI-coordinated, 7 three-PI-coordinated, and 0 four-PI-coordinated structures for PI-Li + nPI, and 30 one-PI-coordinated, 30 two-PI-coordinated, 28 three-PI-coordinated, 22 four-PI-coordinated, and 7 five-PI-coordinated structures for PI-Cs + nPI. The cation–π interaction energy of PI-M + nPI was calculated as the average of the interaction energies of n-PI-coordinated structures.
Results and discussion
Effect of cations on the structure of ionic aggregates
SAXS was used to investigate the morphology of the PI ionomers. As shown in Fig. 2, experimental SAXS patterns for the neutralized samples at room temperature show a broad scattering peak at a scattering vector q of approximately 1.2 nm−1, where q is defined as (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ with 2θ as the scattering angle. The broad scattering peak, known as the “ionomer peak,” is caused by the interference between the ionic aggregates. With an increase in the cation's electron density, the peak intensity increases. The experimental SAXS patterns were simulated using the Yarusso–Cooper (Y–C) model.43 This model assumes that spherical ionic aggregates randomly arrange in the hydrophobic polymer matrix with the closest approach limitation. As shown in previous works, the Y–C model gives good simulations for experimental SAXS patterns for the PI ionomers.8–11 In this model, a radius of the ionic aggregate R1, the radius of the closest approach limitation between the ionic aggregates RCA, the sample volume per ionic aggregate Vp, and the scattering peak intensity parameter K are used as fitting parameters. For the PI-Li, a Lorentz function was combined with the Y–C fitting as previously treated because an upturn in the low q side overlaps the ionomer peak.9,11 The R1, RCA, and Vp used for each sample are listed in Table 1. In addition, the number density of the ionic aggregate per 1000 nm3 (ND) was calculated from Vp and listed in Table 1.
θ with 2θ as the scattering angle. The broad scattering peak, known as the “ionomer peak,” is caused by the interference between the ionic aggregates. With an increase in the cation's electron density, the peak intensity increases. The experimental SAXS patterns were simulated using the Yarusso–Cooper (Y–C) model.43 This model assumes that spherical ionic aggregates randomly arrange in the hydrophobic polymer matrix with the closest approach limitation. As shown in previous works, the Y–C model gives good simulations for experimental SAXS patterns for the PI ionomers.8–11 In this model, a radius of the ionic aggregate R1, the radius of the closest approach limitation between the ionic aggregates RCA, the sample volume per ionic aggregate Vp, and the scattering peak intensity parameter K are used as fitting parameters. For the PI-Li, a Lorentz function was combined with the Y–C fitting as previously treated because an upturn in the low q side overlaps the ionomer peak.9,11 The R1, RCA, and Vp used for each sample are listed in Table 1. In addition, the number density of the ionic aggregate per 1000 nm3 (ND) was calculated from Vp and listed in Table 1.
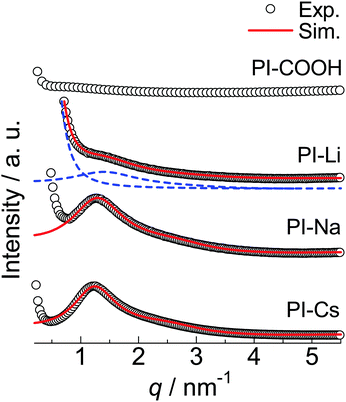 | ||
| Fig. 2 Experimental and simulated SAXS patterns for the indicated samples shown as the plot and red line, respectively. For PI-Li, simulation components for the Yarusso–Cooper model43 and Lorentz function are shown with blue broken lines. The blue broken lines are shifted lower to avoid overlapping. | ||
| Sample | R 1/nm | R CA/nm | V p/nm3 | ND/(10 nm)−3 |
|---|---|---|---|---|
| PI-Li | 0.95 | 1.82 | 106 | 9.4 |
| PI-Na | 0.95 | 2.09 | 119 | 8.4 |
| PI-Cs | 0.96 | 2.21 | 112 | 8.9 |
The R1 and ND are almost independent of the cations even though the size of ionic groups significantly increases in the order PI-Li < PI-Na < PI-Cs. The sizes of ionic metal carboxylate groups for the PI-Li, PI-Na, and PI-Cs approximated from the individual metal acetates are 87.0 × 10−3, 95.2 × 10−3, and 132 × 10−3 nm3, respectively. Moreover, the R1s of PI-M, ∼0.95 nm, are much larger than the size of metal carboxylate groups. For example, the average one-dimensional size of the ionic group is 0.457 nm ((95.2 × 10−3 nm3)0.33) for PI-Na. The difference in these sizes clearly indicates that the ionic aggregates in PI-M are not constructed with only ionic groups, where some polymer segments must be included in the ionic aggregates. The inclusion of polymer segments in the ionic aggregate has been reported for many other ionomers, such as poly(ethylene-co-methacrylic acid) (EMAA),44,45 poly(styrene-ran-methacrylic acid),46 and sulfonated polystyrene (SPS) ionomers.47–49
In this work, we calculated the occupancy ratio of an ionic group in the ionic aggregate to estimate the inclusion of polymer segments in the ionic aggregate.44,48 In this method, the number of ionic groups in an ionic aggregate is calculated using two procedures. In the first procedure, the spherical ionic aggregate volume calculated using R1 was divided by the volume of one ionic group (Vion), and the number of ionic groups per aggregate Nagg(R1) was determined as follows:
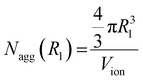 | (1) |
In the second procedure, the number of the ionic groups per aggregate Nagg(Vp) is determined using the Vp and the entire composition of ionomer as follows:
| Nagg(Vp) = ϕionVpnion | (2) |
The Nagg(R1), Nagg(Vp), and occupancy ratio of the PI-M are listed in Table 2, where the occupancy ratio is calculated by dividing Nagg(Vp) by Nagg(R1). The Nagg(R1) decreases with an increase in the radius of alkali metal cations, whereas the Nagg(Vp) is almost constant. An occupancy ratio of unity indicates that the ionic aggregate includes only ionic groups. The occupancy ratios of all samples are less than unity, meaning some polymer segments are included in the ionic aggregate as well as other ionomers.44,45,47–49 The occupancy ratio decreases with decreasing radius of alkali metal cations. The expected reason for this tendency will be discussed below.
| Sample | N agg(R1) | N agg(Vp) | N agg(Vp)/Nagg(R1) |
|---|---|---|---|
| PI-Li | 41 | 16 | 0.39 |
| PI-Na | 38 | 18 | 0.47 |
| PI-Cs | 28 | 17 | 0.61 |
Effect of cations on the rearrangement of ionic networks.
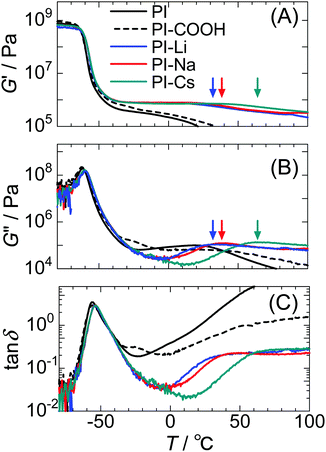
Fig. 3 shows the storage modulus (G′), loss modulus (G′′), and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (G′′ G′−1) for the samples measured at 1 Hz against temperature. The significant decrease in the G′ at ∼−60 °C is attributed to the glass transition of the PI matrix region. The Tg of PI was almost unchanged by ionization. This indicates that the PI matrix and ionic groups are strongly phase separated, and the isolated ionic groups are limited in the matrix region. Further, DSC measurements demonstrate similar Tg values for these samples (Fig. S8, ESI†). The ionized samples exhibit a plateau region in G′ toward high temperatures due to the formation of ionic aggregates that act as physical crosslinks.
δ (G′′ G′−1) for the samples measured at 1 Hz against temperature. The significant decrease in the G′ at ∼−60 °C is attributed to the glass transition of the PI matrix region. The Tg of PI was almost unchanged by ionization. This indicates that the PI matrix and ionic groups are strongly phase separated, and the isolated ionic groups are limited in the matrix region. Further, DSC measurements demonstrate similar Tg values for these samples (Fig. S8, ESI†). The ionized samples exhibit a plateau region in G′ toward high temperatures due to the formation of ionic aggregates that act as physical crosslinks.
An additional relaxation attributed to the interaggregate hopping motion of the ionic groups was observed for the PI-M samples at 20 °C–70 °C.8,10 This motion is generally called “ion-hopping.”15–17 In this motion, the network structure in the ionomer rearranges because ionic groups hop between neighboring ionic aggregates together with the linked polymer chain segments. The ionomer's unique viscoelastic behaviors via transient crosslinking with the ion-hopping have been theoretically and experimentally studied.50–54
As shown in our previous work,8,10 since free carboxy groups plasticize the ionic aggregates and weaken the restriction on the ionic aggregates to the polymer's segmental motion, the relaxation temperature in the PI-Na decreases with decreasing degree of neutralization. This mechanism was first revealed by Tierney and Register for EMAA ionomers.17 Further, we used the DFT method to calculate the interaction energies for the combinations of two isoprene model trimers containing a sodium carboxylate or a carboxy group.10 This calculation demonstrated that the combination between –COONa⋯NaOOC– is more attractive than that between –COONa⋯HOOC–. Furthermore, the relaxation temperature assigned to ion-hopping significantly decreases with moisture absorption because the water molecules plasticize the ionic aggregates (Fig. S9, ESI†). Therefore, we have carefully dried the samples.
The relaxation temperature for the network rearrangement, defined as the G′′ peak, for PI-Li, PI-Na, and PI-Cs were 33 °C, 38 °C, and 64 °C, respectively. Thus, the network rearrangement with respect to ion-hopping is restricted in the order PI-Cs > PI-Na > PI-Li. This result is somewhat contrary to other ionomers neutralized with alkali metal cations. For example, Weiss et al. found that the lifetime of the ion-hopping in SPS ionomers increases with decreasing the radius of the alkali metal cations, although the Li-neutralized ionomer exhibited a shorter lifetime than the Na-neutralized one.52,53,55 Jérôme et al. demonstrated that ion-hopping in carboxylated telechelic PB ionomers typically slows with decreasing ionic radius of alkali metal cations from Cs+ to Na+, but the result for Li-neutralization largely deviates from this trend.56 These results indicate that the ion-hopping relaxations in these ionomers are primarily restricted by the alkali metal cations with a smaller radius even though some exceptions of for Li+ were frequently observed.
To confirm the strength of interaction between the ionic groups with different cations, we calculated the interaction energies for the combinations between two model isoprene trimers containing lithium, sodium, and cesium carboxylate.10 We calculated the average interaction energy from the 10 lowest-energy combinations of different conformations. The obtained average interaction energies for –COOLi⋯LiOOC–, –COONa⋯NaOOC–, and –COOCs⋯CsOOC– were −205, −184, and −148 kJ mol−1, respectively. The DFT calculation predicts that ion-hopping should be restricted in the order PI-Li > PI-Na > PI-Cs if the ionic aggregates consist of only ionic groups.
However, as shown in the above, the ionic aggregates in PI-M include some PI segments, and the inclusion of PI segments increases with decreasing cation size. The inclusion of PI segments in the ionic aggregate is expected to weaken the interactions between ionic groups due to the steric hindrance. Moreover, the ionic aggregate would be plasticized due to flexible PI segments (Tg ∼ −60 °C). The plasticization of the ionic aggregate is expected to be significant in the order PI-Li > PI-Na > PI-Cs because the inclusion of PI segment in the ionic aggregate increases in this order (see Table 2). We speculate that the network rearrangement with ion-hopping is enhanced by the plasticization of the ionic aggregate via the inclusion of the PI segment.
To evaluate the effect of the plasticization of included PI segments on the ionic aggregate, the Tg of the ionic aggregate was measured using the ESR spin probe method. This technique allows us to selectively measure the Tg of the ionic aggregate in ionomers when a probe molecule that localizes in the ionic aggregate is used. Using this technique, the Tgs of the ionic aggregates in EMAA,31 PI,8 and PDMS9 ionomers were evaluated. If there was no plasticization of PI segments on the ionic aggregates, the Tg of the ionic aggregates would be in the order PI-Li > PI-Na > PI-Cs because the interaction between ionic groups increases in the same order. In fact, the Tgs of poly(sodium acrylate), poly(potassium acrylate), and poly(cesium acrylate) are 251 °C, 195 °C, and 174 °C, respectively.57
In Fig. 4, the temperature dependence of a saturation factor (S) determined by ESR measurement is compared among the three samples. S is a parameter proportional to the motional correlation time of the probe molecules.28 The inflection temperature in the plot is defined as Tg,ESR. The Tg,ESRs for the PI-Li, PI-Na, and PI-Cs are −48 °C, −47 °C, and −45 °C, respectively. The apparent difference is only slight, however, Tg,ESR increases with increasing ionic radius of alkali metal cation. From this result, we conclude that the included PI segments plasticize the ionic aggregate and this effect is more significant for PI-Li because of the inclusion of more PI segments in the ionic aggregate.
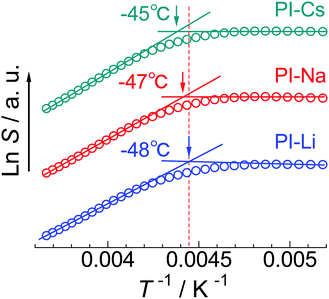 | ||
| Fig. 4 Temperature dependence of saturation factor, S, for indicated samples. Tg,ESR of each sample is indicated with arrow. Each plot is vertically shifted to avoid overlapping. | ||
Here, one may consider the perturbation of the probe molecules on the measurement of Tg,ESR of ionic aggregate. To confirm this, we measured the Tg,ESR of PI-Na at lower 4-carboxy-TEMPO concentration (4 × 10−8 mol g−1) and using different probe molecule, 5DSA, at 6 × 10−8 mol g−1 (Fig. S10, ESI†). Even in these cases, the same Tg,ESR value, −47 °C, was obtained. Therefore, we conclude that the perturbation of the probe molecules on the Tg,ESR value is little.
Estimation of cation–π interaction between the alkali metal cation and double bonds in the PI segment
Why does the inclusion of the PI segment in the ionic aggregate increase with decreasing radius of the alkali metal cation? To understand this phenomenon, we estimated the interaction energies between PI units and a lithium and a cesium cation using DFT calculations. In the calculation, we found that some PI units stably coordinate to alkali metal cation via cation–π interaction. The detailed geometrical arrangements for those coordinations composed of the PI units and counter-cation with the lowest interaction energy are presented in Fig. S7 in the ESI.† These calculations revealed that more than four PI units cannot coordinate to a lithium carboxylate because of its smaller cation size. On the other hand, even five PI units can coordinate to a cesium carboxylate due to the larger ionic size of Cs+. In Fig. 5, the average interaction energy per one double bond for each coordinate is plotted against the total number of coordinated double bonds. For both Li+ and Cs+, the average interaction energy decreases with an increase in the coordinated PI units because of the steric hindrance between PI units. In any coordination numbers, the Li+ exhibits more attractive interaction with the PI units than the case of the Cs+. Here, the occupancy ratios of PI-Li and PI-Cs are 0.39 and 0.64, respectively. Therefore, the average coordinate numbers of PI unit to a lithium carboxylate and a cesium carboxylate in the ionic aggregate are roughly estimated to be 1 and 0.6, respectively, taking into account the volume of a PI unit, ∼130 × 10−3 nm3. Namely, the cation–π interaction energy for the coordination with one PI unit is important in this study; the value for Li+ is almost the double of that for Cs+. As a possible explanation for the increase in the inclusion of PI segment in the ionic aggregate with decreasing the radius of alkali metal cation, we propose that the cation–π interaction is the driving force for that.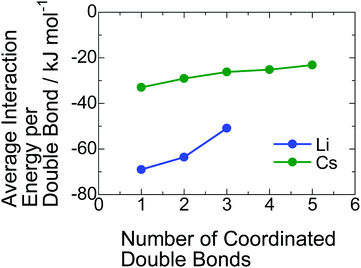 | ||
| Fig. 5 Average interaction energies between the double bond in the PI segment and a lithium or a cesium cation. | ||
Conclusions
In this study, we examined the effects of alkali metal cations, Li+, Na+, and Cs+, on the internal structures of ionic aggregates and ionic group dynamics in carboxylated PI ionomers. The alkali metal carboxylates attached to the PI backbone formed nanosized spherical aggregates, which acted as physical crosslinks. Based on the Y–C model fitted of the SAXS pattern, it was determined that the cation radius has a negligible effect on radius of ionic aggregate. In contrast to numerous previously reported ionomers, the network rearrangement with interaggregate hopping of metal carboxylates enhanced with decreasing cation radius, despite the DFT calculation indicating an increase in the attractive interaction between metal carboxylate units. To examine the unexpected behavior of the network rearrangement, we proposed the inclusion of PI segments in the ionic aggregate. It was found that the inclusion of PI segments in ionic aggregates increase with a decreasing cation radius. Notably, this tendency was the most prominent for Li+ cations. We speculated that the presence of PI segments with low Tg would plasticize the ionic aggregates and sterically hinder the attractive interactions between metal carboxylates. A marginal decrease in Tg values of the ionic aggregates with decreasing cation radius was demonstrated via ESR measurement. On the basis of the DFT calculation results, we proposed that the cation-π interactions between double bonds in PI and alkali metal cations are responsible for the increased inclusion of the PI component in ionic aggregates. As a conclusion, we proposed that the inclusion of the polymer components in the ionic aggregates would lead to enhanced network rearrangement, even though the attractive interactions between ionic groups dominate this behavior.Author contributions
Y. M. planned and directed the project, Y. M., K. H., and T. U. conducted the experiments and calculations. Y. M., K. H., Y. S., S. K., and T. U. analyzed and discussed about the data; Y. M., S. K., and T. U. wrote the paper.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Beam time at PF-KEK provided by Programs 2016G627, 2017G562, 2019G116, and 2020G610 is acknowledged herein. Portion of these computations was performed at Research Center for Computational Science (RCCS), Okazaki. This research was financially supported by the JSPS KAKENHI Grant Numbers JP19K05612 (YM) and JP20H05739 (TU); JST, PRESTO Grant Number JPMJPR199B (YM), Japan.Notes and references
- S. Schlick, Ionomers: Characterization, Theory, and Applications, CRC Press, Boca Raton, FL, 1996 Search PubMed.
- M. R. Tant, K. A. Mauritz and G. L. Wilkes, Ionomers: Synthesis, Structure, Properties and Applications, Blackie Academic and Professional, London, 1997 Search PubMed.
- A. Eisenberg and J.-S. Kim, Introduction to Ionomers, A Wiely-Interscience Publication, Toronto, 1998 Search PubMed.
- S. J. Kalista, J. R. Pflug and R. J. Varley, Polym. Chem., 2013, 4, 4910–4926 RSC.
- N. Hohlbein, A. Shaaban, A. R. Bras, W. Pyckhout-Hintzen and A. M. Schmidt, Phys. Chem. Chem. Phys., 2015, 17, 21005–21017 RSC.
- A. Das, A. Sallat, F. Böhme, M. Suckow, D. Basu, S. Wießner, K. W. Stöckelhuber, B. Voit and G. Heinrich, ACS Appl. Mater. Interfaces, 2015, 7, 20623–20630 CrossRef CAS PubMed.
- C. Xu, L. Cao, B. Lin, X. Liang and Y. Chen, ACS Appl. Mater. Interfaces, 2016, 8, 17728–17737 CrossRef CAS PubMed.
- Y. Miwa, J. Kurachi, Y. Kohbara and S. Kutsumizu, Commun. Chem., 2018, 1, 5 CrossRef.
- Y. Miwa, K. Taira, J. Kurachi, T. Udagawa and S. Kutsumizu, Nat. Commun., 2019, 10, 1828 CrossRef PubMed.
- Y. Miwa, J. Kurachi, Y. Sugino, T. Udagawa and S. Kutsumizu, Soft Matter, 2020, 16, 3384–3394 RSC.
- Y. Miwa, M. Yamada, Y. Shinke and S. Kutsumizu, Polym. Chem., 2020, 11, 6549–6558 RSC.
- R. Dolog and R. A. Weiss, Macromolecules, 2013, 46, 7845–7852 CrossRef CAS.
- T. Tsujimoto, K. Toshimitsu, H. Uyama, S. Takeno and Y. Nakazawa, Polymer, 2014, 55, 6488–6493 CrossRef CAS.
- A. González-Jiménez, M. A. Malmierca, P. Bernal-Ortega, P. Posadas, R. Pérez-Aparicio, Á. Marcos-Fernández, P. T. Mather and J. L. Valentín, Soft Matter, 2017, 13, 2983–2994 RSC.
- J. G. Van Alsten, Macromolecules, 1996, 29, 2163–2168 CrossRef CAS.
- N. K. Tierney and R. A. Register, Macromolecules, 2002, 35, 2358–2364 CrossRef CAS.
- N. K. Tierney and R. A. Register, Macromolecules, 2002, 35, 6284–6290 CrossRef CAS.
- X. Chen, M. A. Dam, K. Ono, A. Mal, H. Shen, S. R. Nutt, K. Sheran and F. Wudl, Science, 2002, 295, 1698–1702 CrossRef CAS PubMed.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- Y. Amamoto, J. Kamada, H. Otsuka, A. Takahara and K. Matyjaszewski, Angew. Chem., Int. Ed., 2011, 50, 1660–1663 CrossRef CAS PubMed.
- C. Zeng, H. Seino, J. Ren, K. Hatanaka and N. Yoshie, Macromolecules, 2013, 46, 1794–1802 CrossRef CAS.
- H. Ying, Y. Zhang and J. Cheng, Nat. Commun., 2014, 5, 3218 CrossRef PubMed.
- S. Burattini, B. W. Greenland, D. H. Merino, W. Weng, J. Seppala, H. M. Colquhoun, W. Mayes, M. E. Mackay, I. W. Hamely and S. J. Rowan, J. Am. Chem. Soc., 2010, 132, 12051–12058 CrossRef CAS PubMed.
- P. Cordier, F. Tournilhac, C. Soulie-Ziakovic and L. Leibler, Nature, 2008, 451, 977–980 CrossRef CAS PubMed.
- Y. Chen, A. M. Kushner, G. A. Williams and Z. Guan, Nat. Chem., 2012, 4, 467–472 CrossRef CAS PubMed.
- Y. Yanagisawa, Y. Nan, K. Okuro and T. Aida, Science, 2018, 359, 72–76 CrossRef CAS PubMed.
- R. Tamate, K. Hashimoto, T. Horii, M. Hirasawa, X. Li, M. Shibayama and M. Watanabe, Adv. Mater., 2018, 20, 1802792 CrossRef PubMed.
- Y. Miwa, Macromolecules, 2009, 42, 6141–6146 CrossRef CAS.
- Y. Miwa, O. Urakawa, A. Doi, K. Yamamoto and S. Nobukawa, J. Phys. Chem. B, 2012, 116, 1282–1288 CrossRef CAS PubMed.
- Y. Miwa and K. Yamamoto, J. Phys. Chem. B, 2012, 116, 9277–9284 CrossRef CAS PubMed.
- Y. Miwa, T. Kondo and S. Kutsumizu, Macromolecules, 2012, 116, 9277–9284 CAS.
- Y. Miwa, Y. Kohbara, H. Furukawa and S. Kutsumizu, Polymer, 2018, 148, 303–309 CrossRef CAS.
- Y. Miwa, M. Koike, Y. Kohbara and S. Kutsumizu, Polymer, 2020, 197, 122495 CrossRef CAS.
- S. Maeda, T. Taketsugu, K. Morokuma and K. Ohno, Bull. Chem. Soc. Jpn., 2014, 87, 1315–1334 CrossRef.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299 CrossRef CAS.
- S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki, T. Ichino, Y. Sumiya, K. Sugiyama and Y. Ono, J. Comput. Chem., 2018, 39, 233–251 CrossRef CAS PubMed.
- D. J. Yarusso and S. L. Cooper, Polymer, 1985, 26, 371–378 CrossRef CAS.
- S. Kutsumizu, K. Tadano, Y. Matsuda, M. Goto, H. Tachino, H. Hara, E. Hirasawa, H. Tagawa, Y. Muroga and S. Yano, Macromolecules, 2000, 33, 9044–9053 CrossRef CAS.
- S. Kutsumizu, M. Goto, S. Yano and S. Schlick, Macromolecules, 2002, 35, 6298–6305 CrossRef CAS.
- N. C. Zhou, C. D. Chan and K. I. Winey, Macromolecules, 2008, 41, 6134–6140 CrossRef CAS.
- J. S. Enokida, W. Hu, H. Fang, B. F. Morgan, F. L. Beyer, H. H. Winter and E. B. Coughlin, Macromolecules, 2020, 53, 1767–1776 CrossRef CAS.
- N. C. Zhou, C. D. Chan and K. I. Winey, Macromolecules, 2008, 41, 6134–6140 CrossRef CAS.
- A. M. Castagna, W. Wang, K. I. Winey and J. Runt, Macromolecules, 2011, 44, 2791–2798 CrossRef CAS.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707 CrossRef CAS.
- R. H. Colby, X. Zheng, M. H. Rafailovich, J. Sokonov, D. G. Peiffer, S. A. Schwarz, Y. Strzhemechny and D. Nguyen, Phys. Rev. Lett., 1998, 18, 3876–3879 CrossRef.
- Q. Chen, C. Huang, R. A. Weiss and R. H. Colby, Macromolecules, 2015, 48, 1221–1230 CrossRef CAS.
- C. Huang, C. Wang, Q. Chen, R. H. Colby and R. A. Weiss, Macromolecules, 2016, 49, 3936–3947 CrossRef CAS.
- X. Cao, X. Yu, J. Qin and Q. Chen, Macromolecules, 2019, 52, 8771–8780 CrossRef CAS.
- R. A. Weiss and H. Zhao, J. Rheol., 2009, 53, 191–213 CrossRef CAS.
- J. Horrion, R. Jérôme, P. Teyssié, C. Macro and C. E. Williams, Polymer, 1988, 29, 1203–1210 CrossRef CAS.
- A. Eisenberg, H. Matsuda and T. Yokoyama, J. Polym. Sci., Part A-2, 1971, 9, 2131–2135 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: NMR, FT-IR, DSC, TG, and DFT calculation results of materials (PDF). See DOI: https://doi.org/10.1039/d2cp01159j |
| This journal is © the Owner Societies 2022 |