A powder XRD, solid state NMR and calorimetric study of the phase evolution in mechanochemically synthesized dual cation (Cs_x(CH₃NH₃)_1−x)PbX₃ lead halide perovskite systems

Abstract

Methylammonium (MA⁺) lead halide perovskites (MAPbX₃) have been widely investigated for photovoltaic applications, with the addition of Cs improving structural and thermal stability. This study reports the complete A site miscibility of Cs⁺ and MA⁺ cations in the lead chloride and lead bromide perovskites with nominal stoichiometric formulae (Cs_xMA_1−x)Pb(Cl/Br)₃ (x = 0, 0.13, 0.25, 0.37, 0.50, 0.63, 0.75, 0.87, 1). These suites of materials were synthesized mechanochemically as a simple, cost-effective synthesis technique to produce highly ordered, single phase particles. In contrast to previous studies using conventional synthetic routes that have reported significant solubility gaps, this solvent-free approach induces complete miscibility within the dual cation Cs⁺/MA⁺ system, with the resultant structures exhibiting high short-range and long-range atomic ordering across the entire compositional range that are devoid of solvent inclusions and disorder. The subtle structural evolution from cubic to orthorhombic symmetry reflecting PbX₆ octahedral tilting was studied using complementary high resolution TEM, powder XRD, multinuclear ¹³³Cs/²⁰⁷Pb/¹H MAS NMR, DSC, XPS and UV/vis approaches. The phase purity and exceptional structural order were reflected in the very high resolution HRTEM images presented from particles with crystallite sizes in the ∼80–170 nm range, and the stability and long lifetimes of the Br series (10–20 min) and the Cl series (∼30 s–1 min) under the 200 kV/146 μA e⁻ beam. Rietveld refinements associated with the room temperature PXRD study demonstrated that each system converged towards single phase compositions that were very close to the intended target stoichiometries, thus indicating the complete miscibility within these dual cation Cs⁺/MA⁺ solid solution systems. The multinuclear MAS NMR data showed a distinct sensitivity to the changing solid solution compositions across the MAPbX₃–CsPbX₃ partition. In particular, the ¹³³Cs shifts demonstrated a sensitivity to the cubic–orthorhombic phase transition while the ¹³³Cs T₁s exhibited a pronounced sensitivity to the variable Cs⁺ cation mobility across the compositional range. Variable temperature PXRD studies facilitated the production of phase diagrams mapping the Cs⁺/MA⁺ compositional space for the (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ solid solution series, while Tauc plots of the UV/vis data exhibited reducing bandgaps with increasing MA⁺ incorporation through ranges of cubic phases where octahedral tilting was absent.

---

Introduction

Organic–inorganic hybrid Lead Halide Perovskites (LHPs) have been widely investigated for photovoltaic applications resulting in solar cells with a record power conversion efficiency (PCE) of >25%,^1,2 and light emitting diodes (LEDs) with an external quantum efficiency (EQE) reaching 23.4%.³ The prototype material for solar cells is methyl ammonium lead iodide (CH₃NH₃PbI₃). The key advantages of this class of materials are solution processability, inexpensive starting materials, good hole and electron conductivity and a high tolerance to defects.⁴ Apart from solar cells and light emitting diodes LEDs, LHPs show promise as semiconductor lasers with an ultra-low threshold as lasing media.⁵ Moisture and thermal sensitivity remain major challenges to the lifetime of perovskite photovoltaic devices and have delayed widespread adoption. Multiple strategies such as encapsulation, polymer coatings, fluoride additives and the incorporation of hydrophobic cations can inhibit moisture sensitivity.^6–8 Saliba et al. were the first to report the advantages of a Cs additive in solar cell materials by using CsI to enhance the structural and thermal stability of photovoltaic devices; this produced smoother and more reproducible films and superior phase stability and moisture resistance.⁹ The presence of Cs⁺ cation incorporation in perovskite films was indirectly observed via changes in the X-ray diffraction (XRD) data (and the measured lattice parameters) and increases in the material band gap, however the short-range nature of Cs⁺ and Rb⁺ incorporation in lead halide perovskite powders was unambiguously identified using solid state MAS NMR techniques.^10,11

LHP nanoparticles have been successfully employed to fabricate the active layer in LEDs and are widely investigated for better efficiency and stability of these devices.¹² This class of materials show excellent tunability of emission properties when prepared from facile, yet robust, synthetic methods employing ultrasonic mixing, hot injection and anti-solvent addition for low cost photovoltaics. Organic salts such as methylammonium (MA) and formamidinium (FA) are hygroscopic and have poor thermal stability as they decompose above 180 °C. Partial replacement of organic cations with Cs⁺ improves both moisture and thermal stability. Zhang et al. reported the then brightest and most efficient LEDs (EQE ∼ 10.4%) having an active layer composition of Cs_0.87MA_0.13PbBr₃ demonstrating that the mixed cation varieties have better optoelectronic properties than single A site ion equivalents.¹³ Although the reported composition is precise, it was indirectly estimated from the valence band edge shift. Alternatively, others have assumed the precursor ratio as the nominal and actual composition.¹⁴ Without direct analysis of the phase purity and composition, sample reproducibility based on target nominal compositions alone can be difficult as experimental conditions can vary subtly between syntheses. This study demonstrates that the solid state NMR technique is a reliable, non-destructive method of analysis to ensure the targeted composition was obtained and verifying phase purity.

Optimising precipitation parameters including precursor ratios realized composition-tunable and morphology-controlled nanoparticles with high photoluminescence quantum yield (PLQY) of >90%.¹³ The feasibility of targeted compositions can be limited by the relative solubility of precursors, especially that of Cs salts in the common solvents dimethylformamide (DMF) or dimethylsulfoxide (DMSO). The low solubility of Cs salts in DMF restricts the quantities that can be added to the precursor solution, limiting the final Cs content to ∼16 atom%. Alternatively, thermal annealing has successfully synthesised many inorganic halide perovskites with large grain size and precise compositions, including those of mixed halide compositions.¹⁵ This involved heating the precursor salts to high temperatures in a sealed ampoule, followed by a slow cooling. The temperatures needed to achieve homogeneity are close to the melting points of the precursor salts (>400 °C); consequently, this approach is unsuitable for organic–inorganic hybrid perovskite systems containing MA⁺ and FA⁺ cations that decompose above 200 °C. Hence, low temperature, solvent-free approaches are far more advantageous for these syntheses. Karmakar et al. explored the mechanochemical fabrication of limited suites hybrid lead and tin halide perovskite systems to achieve better compositional control.^16–19 Other studies by Mozur et al. attempted hand grinding followed by thermal annealing for 5 days at 150 °C for the synthesis of mixed cation hybrid perovskites; however, this was only partially successful as Cs⁺ cation incorporation levels of >40 mol% could not be achieved.²⁰

This study demonstrates that mechanochemical synthesis techniques represent a simple, cost-effective approach for the production of wide-ranging compositional suites of dual-cation lead halide perovskites of nominal stoichiometry (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ (x = 0.13, 0.25, 0.37, 0.5, 0.63, 0.75, 0.87). Mechanochemical synthesis routes avoid the use of organic solvents (thus representing a more environmentally compatible option) and facilitate ultra-clean reactions that proceed to completeness subsequently rendering homogeneous and highly-ordered products.^21–24 Mechanochemical reaction syntheses can be achieved using hand grinding methods (using mortar and pestle),^21–24 however more recent studies have reported that improvements in reaction efficiency and time can be achieved using ball milling techniques.^16–19 Ball milling efficiently combines the effects of mixing and thermal annealing by exploiting the conversion of kinetic energy to heat at the precise point of reaction, thus leading to extremely high yields and homogeneity.^21–24 Through the use of characterisation techniques such as powder XRD, high resolution TEM (HRTEM) and multinuclear ¹³³Cs/²⁰⁷Pb/¹H MAS NMR, this study aims to demonstrate the success of mechanochemical ‘alloying’ to achieve complete miscibility within these hybrid perovskites series. The exceptional quality, single phase reaction products permit the unambiguous observation of the phase evolution from cubic MA-lead halides to lower symmetry hettotypes to be demonstrated.

Experimental

Synthesis

A site endmembers. The MAPbCl₃ and MAPbBr₃ endmembers were derived from halide salt precursors using the inverse temperature crystallization method following the protocol of Saidaminov et al.^25,26 MAPbBr₃ was prepared from 1 M MABr and PbBr₂ solutions in DMF while the chloride analogue was made in DMSO–DMF (1 : 1) mixture. CsPbCl₃ and CsPbBr₃ were prepared from 0.5 M precursor salt solution in DMSO. The perovskite solutions passed through a 0.2 μm PVDF filter and heated to 80 °C. The crystalline precipitates were washed with diethyl ether and dried at 60 °C for 20 minutes then powdered prior to synthesis of mixed cation samples.

A site cation solid solutions. The (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ (x = 0.13, 0.25, 0.37, 0.5, 0.63, 0.75, 0.87) series of solid solution, dual cation lead halide perovskites were prepared mechanochemically from stoichiometric combinations of CsPbX₃ and MAPbX₃. The perovskite solids (300 mg) were ball milled in hardened steel vials with matching steel balls. The sample-to-grinding media weight ratio was kept constant (1 part perovskite: 15 parts grinding media) and the milling time was optimized (2 h) to obtain optimally reacted and highly ordered products. The crystallinity and homogeneity were analysed by powder XRD and solid state NMR to follow the reaction progress (see Fig. 1). The mechanochemically derived perovskites exhibit a single ¹³³Cs and ²⁰⁷Pb MAS NMR resonances confirming complete homogeneity and phase purity. Furthermore, each powder XRD confirmed a solid solution without an observable amorphous component. The reaction time was limited to 2 hours to avoid thermal degradation and amorphization.

Fig. 1 A comparison of the hand grinding (HG) and ball milling (BM) mechanochemical grinding procedures for the Cs_0.5MA_0.5PbCl₃ sample preparation analysed by (a) ²⁰⁷Pb MAS NMR, (b) ¹³³Cs MAS NMR, and (c) powder XRD techniques. These comparisons demonstrate that the ball milling route achieves complete solid solution character without the presence of impurity phases in approximately half the time that the hand grinding technique achieves.

Laboratory source and synchrotron powder X-ray diffraction

High resolution laboratory source powder XRD (PXRD) data were measured at room temperature for the (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ series using a Bruker D8 Advance diffractometer fitted with a Cu Kα X-ray tube (λ = 1.54187 Å) operating at 40 kV and 40 mA. Each sample was mounted in a silicon single crystal zero background sample holder which was rotated at 40 rpm in the beam. The data was measured over the 10°–100° 2θ range using a 0.02° step size and a time duration of 1.5 s per step. Experimental fitting of the data was performed using TOPAS 6 employing a fundamental parameter approach with a simple axial model. The background was modelled by a third order Chebyshev function. The MA⁺ cation is known to be dynamically disordered in MAPbCl₃ and MAPbBr₃ over the Wyckoff position 24m.^27–29 For Rietveld refinement of the powder XRD data, MA⁺ was modelled as a sphere with the same atomic scattering factor as isoelectronic K⁺ ion. The thermal parameters of all atoms were fixed to 1 as high angle data above 100° were not measured. Only the variable atomic fractional coordinates were refined. Average crystallite sizes were estimated by the Scherrer equation using the Lorentzian component of the diffraction peaks (see Table 3). This was implemented using the ‘crystallite size Lorentzian’ function in TOPAS 6, and it is noted that these values are semi-quantitative as microstrain contributions have not been deconvoluted.

Variable temperature, high resolution laboratory source PXRD data were acquired for the (Cs_xMA_1−x)PbCl₃ series using a Rigaku Synergy S diffractometer fitted with a Cu Kα X-ray tube (λ = 1.54187 Å) and a large area Hypix-6000E detector. All samples were finely ground and packed in 0.3 mm sealed Mark tubes, rotated in the beam at 40 rpm during data acquisition, and cooled using an Oxford Cryostream Cobra Plus system with each measurement being undertaken over 5 °C intervals. The acquired images were integrated over 4°–66° 2θ range. As the sample absorption correction function was insufficient to account for significant absorption, Pawley refinement of all experimental data was performed using TOPAS 6 utilising pseudo-Voigt peakshapes, with peak and instrumental factors fixed using a LaB₆ standard. Sequential batch refinements starting with the lowest temperature measurements, followed by successive higher temperatures, was adopted.

Variable temperature, high resolution synchrotron PXRD data were measured for the corresponding (Cs_xMA_1−x)PbBr₃ series at the I11 beamline at Diamond Light Source, UK using a wavelength of 0.82646 Å. A wide-angle Mythen microstrip position sensitive detector (PSD) was used to acquire the data in transmission geometry. All data was measured over the 2°–92° 2θ range with a resolution of 0.004° and an exposure time of 20 s per step. All samples were finely ground and packed in 0.3 mm sealed Mark tubes and rotated in the beam at 40 rpm during the data acquisition. The sample temperature was regulated using an Oxford Cryostream which enabled a heating/cooling rate of 6 °C min⁻¹. For these variable temperature studies, the range of temperatures was limited to ±25 °C around the phase transition temperature as identified by DSC. All Rietveld refinement was undertaken using TOPAS 6 employing pseudo-Voigt peakshapes, with peak and instrumental factors fixed using a Si standard.

High resolution transmission electron microscopy (HRTEM)

Selected (Cs_xMA_1−x)PbX₃ specimens were prepared by ultrasonically dispersing a small quantity of powder in absolute acetone and placing a drop of suspension on a holey carbon-coated copper grid. These preparations were air dried. High-resolution transmission electron microscopy (HRTEM) was performed using a JEOL 2100F TEM with a field-emission gun operating at 200 kV and beam current of 146 μA. Samples were orientated with a double tilting holder and the selected area electron diffraction (SAD) patterns recorded. Observation times were limited to a few minutes due to electron amorphization, especially when a more converged beam was used for imaging.

Solid state magic-angle-spinning NMR (MAS NMR)

Multinuclear solid state MAS NMR data were acquired at 14.1 T using a Bruker Avance 600WB Avance III spectrometer operating at ¹H, ¹³³Cs and ²⁰⁷Pb Larmor frequencies (ν_o) of 600.13, 78.7 and 125.5 MHz, respectively. Single pulse ¹³³Cs MAS NMR data were obtained a using a Bruker 4 mm HX probe enabling a MAS rate (ν_r) of 12 kHz for all data acquisition. A CsNO₃ 0.1 M aqueous solution was used for pulse calibration and referencing. A non-selective (‘solution’) π/2 pulse duration of 6.0 μs was calibrated on solid CsCl, with a selective (‘solids’) π/2 pulse time 1.5 μs being used for acquisition of the I = 7/2 nucleus. A recycle delay of 300 s was used for all ¹³³Cs measurements in the Cs_xMA_1−xPbCl₃ and Cs_xMA_1−xPbBr₃ (where x = 0.0, 0.13, 0.25, 0.37, 0.5, 0.63, 0.75, 0.87, 1.0) series which represented 5 × T₁ to ensure complete relaxation, as determined on the slowest relaxing (CsPbCl₃) system. The ¹³³Cs T₁ values were determined using a saturation-recovery experiment which implemented 100 pulses in the saturation pulse train with a 50 ms delay between pulses. All ¹³³Cs chemical shifts were calibrated to the IUPAC recommended 0.1 M CsNO₃ (in D₂O) reference (δ 0.0 ppm) via a secondary solid CsCl reference (δ_iso 223.2 ppm) (representing a frequency ratio (Ξ) of ¹³³Cs = 13.116142% to the ¹H signal from 1% TMS in CDCl₃).³⁰ The corresponding ²⁰⁷Pb MAS NMR data were measured using a rotor-synchronized Hahn echo (90°–τ–180°) experiment on a Bruker 4 mm HX probe enabling MAS rate (ν_r) of 12 kHz. A π/2 pulse with a pulse width of 4 μs was calibrated using solid PbNO₃ from which a π/2/π pulse pair of 4 μs/8 μs was used for all measurements. A recycle delay of 30 s was used for all ²⁰⁷Pb experiments in both series which represented 5 × T₁ to ensure complete relaxation, as determined on the slowest relaxing (CsPbBr₃) system. In similar fashion to the ¹³³Cs measurements, the ²⁰⁷Pb T₁ values were determined using a saturation-recovery experiment which implemented 100 pulses in the saturation pulse train with a 50 ms delay between pulses. All ²⁰⁷Pb chemical shifts were calibrated to the IUPAC recommended PbMe₄ (neat) reference (δ 0.0 ppm) via a secondary solid PbNO₃ reference (δ −3490 ppm) (representing a frequency ratio (Ξ) of ²⁰⁷Pb = 20.920599% to the ¹H signal from 1% TMS in CDCl₃).³⁰ The ¹H MAS NMR data were acquired using single pulse methods using a Bruker 4 mm HX probe enabling MAS rate (ν_r) of 12 kHz. A π/2 pulse length of 4.0 μs duration was calibrated solid using adamantane and π/4 pulse excitation pulses of 2 μs were sued throughout. A recycle delay of 120 s was used for all ¹H measurements within both series which represented 5 × T₁ to ensure complete relaxation, as determined on the slowest relaxing (MAPbBr₃) system. In similar fashion to the ¹³³Cs and ²⁰⁷Pb measurements above, the ²⁰⁷Pb T₁ values were determined using a saturation-recovery experiment which implemented 100 pulses in the saturation pulse train with a 50 ms delay between pulses. All ¹H chemical shifts were calibrated to the IUPAC recommended TMS (δ 0.0 ppm) reference via a secondary solid adamantane reference (δ 1.82 ppm).³⁰

X-ray photoelectron spectroscopy

X-ray photoelectron spectroscopy (XPS) was performed using a Kratos AXIS Supra spectrometer with a monochromatic Al K-alpha source (15 mA, 15 kV) on solid powder samples pressed onto carbon tape. A 3.1 V bias was applied to neutralise surface charge. Individual core levels were measured with a pass energy of 20 eV.

Differential scanning calorimetry

Differential Scanning Calorimetry (DSC) was performed using a Mettler Toledo DSC 1 Star^e system. Standard aluminium pans with 40 μl volume were used to load the samples. The ramp rate for both the cooling and heating segments was maintained at 10 °C min⁻¹.

UV/Vis spectroscopy

The UV/Vis absorption data were measured on a PerkinElmer Lambda 850 spectrometer equipped with an integrating sphere. The acquired data is presented as Tauc plots with change in absorption coefficient as a function of photon energy. The band gap is estimated by extrapolating the linear change in absorption coefficient.

Results and discussion

Mechanochemically prepared sample integrity, high resolution transition electron microscopy (HRTEM)

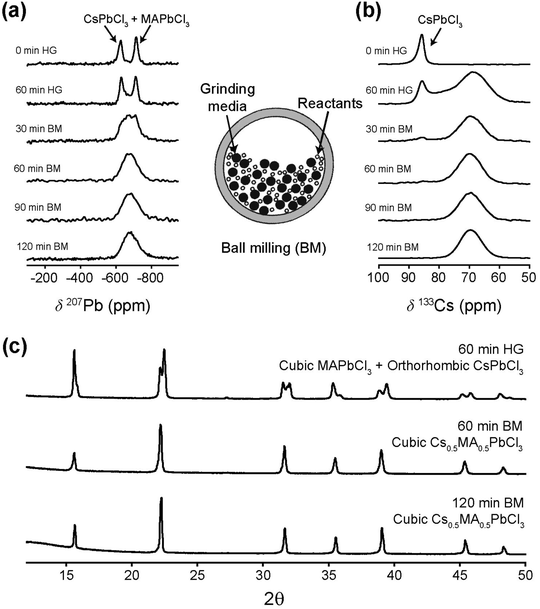
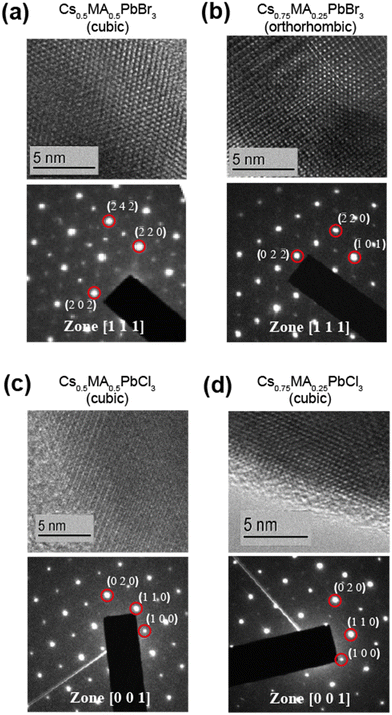
Ball milling involves a continuous process of particle fracturing, re-forming and annealing during collisions with the milling media. The average particle size reduces gradually to a limit where any further milling can induce amorphization. The presence of these amorphous phases and their compositions cannot be ascertained directly by PXRD, however the high resolution transmission electron microscopy (HRTEM) and solid state NMR techniques provide descriptions of the short range chemical environment about each atomic position rather than descriptions of averaged long range order. HRTEM data presented in Fig. 2 and Fig. S1 (ESI‡) depict very high resolution images of a number of the mechanochemically prepared dual cation lead halide perovskites comprising the (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ (x = 0.0, 0.13, 0.25, 0.37, 0.5, 0.63, 0.75, 0.87, 1.0) suites of samples. Previous attempts at HRTEM of MAPbBr₃ only exhibited lattice fringe structure, with no evidence of atomic positions on the particle surface.^31,32 This contrasts with the near-atomic resolution imaging demonstrated in Fig. 2 as measured from the (Cs_0.50MA_0.50)PbBr₃, (Cs_0.75MA_0.25)PbBr₃, (Cs_0.5MA_0.5)PbCl₃ and (Cs_0.75MA_0.25)PbCl₃ systems prepared under mechanochemical conditions. The incorporation of the Cs⁺ cation into the structure coupled with the high purity/high short range order products and the lack of solvent inclusions increases the stability under the electron beam facilitating near atomic resolution information. The (Cs_0.5MA_0.5)PbBr₃ image in Fig. 2a shows equidistant (220) and (202) planes as expected from a [111]_cubic zone axis. The Br series exhibits high electron beam stability of up to 10–20 minutes, whereas the analogous Cl series demonstrated a reduced persistence and degrades over a period of ∼30 s–1 min under the beam. In addition, an increased Cs⁺ cation content reduces the e-beam sensitivity as evidenced by comparisons of Fig. 2a and b (i.e. (Cs_0.50MA_0.50)PbBr₃ and (Cs_0.75MA_0.25)PbBr₃)), and comparisons of Fig. 2c and d (i.e. (Cs_0.50MA_0.50)PbCl₃ and (Cs_0.75MA_0.25)PbCl₃). High e⁻ beam stability of the dual cation Cs⁺/Ma⁺ systems in comparison to pure MA⁺ analogues suggests that these materials may be more stable under high electric fields, which is critical for LED applications where the active layer experiences electric fields on the order of 2000 kV m⁻¹.

Fig. 2 HRTEM images and selected area electron diffraction (SAD) patterns of powder samples prepared from mechanochemical synthesis. The indexed reflections confirm the lattice symmetry of Cs_0.75MA_0.25PbBr₃ sample to be orthorhombic while the others are cubic. These images also indicate the exceptional stability of Cs–MA hybrid perovskite samples under an electron beam in high vacuum conditions.

PXRD and solid state MAS NMR studies of the as-synthesized mechanochemically derived products

The perovskite ABX₃ aristotype is cubic Pm3̄m (space group no. 221) where A occupies the 1a Wyckoff position, B the 1b site and X the 3c site, permitting the crystallochemical formula to be expressed as [A][B][X₃] with one formula unit per unit cell (Z = 1). MAPbCl₃ and MAPbBr₃ satisfy Pm3̄m symmetry; however, because MA⁺ is a non-centrosymmetric cation it is necessarily disordered over the 24m Wyckoff position (rather than occupying the 1a position) to maintain O_h symmetry.²⁹ The structural topology of perovskites consists of [BX₆]⁴⁻ octahedra that extends three dimensional connectivity by corner sharing such that the aristotype creates A-centred cuboctahedral interstices. As the octahedra are hinged, symmetry is readily modified by cooperative BX₆ octahedral tilting that is mediated through varying temperature, pressure or composition. In addition, the ionic radius of MA⁺ cation (2.17 Å) is significantly larger than that of the Cs⁺ cation (1.88 Å).^33,34

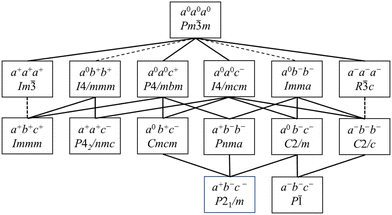
Hettotypes arise when the A cation is too small to reside in an undistorted cuboctahedron, thus requiring a reduction of the coordination number from 12. To satisfy the bond valence criteria, the BX₆ octahedra (to a first approximation considered as rigid bodies) tilt about the pseudocubic 100, 010 and 001 axes. Glazer proposed the commonly used notation to describe perovskite tilt systems using the rotation of octahedra in successive layers about each of the orthogonal Cartesian axis.³⁵ In this nomenclature a, b and c represent rotations about the x, y and z axes, respectively, with the sense of rotation denoted by using 0/+/− superscripts. The aristotype in which the octahedra are not tilted is represented as a⁰a⁰a⁰, while in-phase tilts are denoted + and the out-of-phase tilts are denoted −. This approach was reanalysed by Howard et al.; Scheme 1 below illustrates the octahedral tilt systems and resultant lowering of symmetry in accordance with the group–subgroup relationships from their analysis.³⁶ Tilt angles can be calculated from the Rietveld refinement of diffraction data yielding atomic fractional coordinates, bond angles, cell dimensions and polyhedral volumes, although complications can arise when the octahedra distort.^37,38 In this respect, it is advantageous to use synchrotron X-ray or neutron diffraction when acquiring data to enhance the observation of weak superlattice peaks, especially as the X-ray scattering is dominated by the Pb atoms. Typical peak splitting observed in CsPbCl₃ and CsPbBr₃ are provided in Table 1. At room temperature, CsPbCl₃ was found to be orthorhombic (Pnma), but upon heating above 37 °C it transforms into a tetragonal (P4/mbm) phase which upon further heating >47 °C, transforms into a cubic (Pm3̄m) structure.^39,40 From Scheme 1 and Table 1 these transformations are characterized by octahedral tilting as described by a⁺b⁻b⁻ (orthorhombic) and a⁰a⁰c⁺ (tetragonal) tilt systems, respectively.

Scheme 1 Schematic representation of octahedral tilting modes and their group–subgroup relationships. The cubic aristotype (Pm3̄m) transforms into tetragonal P4/mbm or I4/mcm with tilting in one direction while tilts in more than one direction give rise to lower symmetry space group settings. This schematic relationship shows that P4/mbm is an intermediate pathway between Pnma and Pm3̄m. This relationship allows second order phase transformations according to Landau theory. At low temperatures MAPbCl₃ transforms into P4/mmm which doesn’t occur in the above relationship confirming that it occurs via octahedral distortion rather than tilting.

Table 1 Peak splitting patterns of perovskite hettotypes based on octahedral tilting³⁶

Cubic Pm3̄m	Tetragonal P4/mbm	Tetragonal I4/mcm	Orthorhombic Cmcm	Pseudo-orthorhombic Pnma
a a is cubic unit cell length.
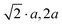
a			2a, 2a, 2a
a ^0 a ^0 a ^0	a ^0 a ^0 c ^+	a ^0 a ^0 c ^−	a ^0 b ^+ c ^−	a ^+ b ^− b ^−
100	001	002	020	110
	110	110	002	002
			200
110	200	200	022	020
	111	112	200	112
				200
111	201	202	222	202
				022
200	002	004	040	220
	220	220	004	004
			400

---

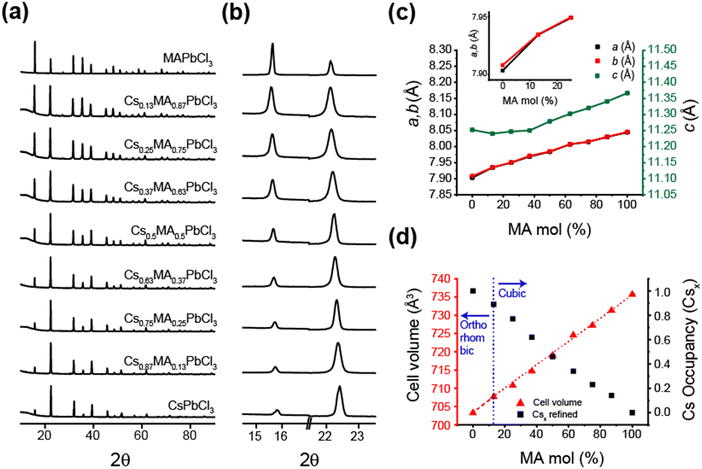
Fig. 3 and 4 illustrate the evolution of crystallographic parameters obtained from Rietveld refinement of laboratory PXRD data (see Fig. S3, S4, ESI,‡ and Tables 2, 3) measured from (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ series measured at room temperature. From Table 3 the estimated average crystallite sizes of the samples in these series resulting from mechanochemical synthesis fall within the ∼80–170 nm range. The a and b lattice parameters of CsPbCl₃ sample differ from each other by <0.005 Å indicating that the room temperature structure is close to a phase transition. While in the PbCl₆ octahedra displacements of the Cl would be characteristic of octahedral tilting, the relatively weak scattering of Cl⁻ compared to Pb²⁺ weakens the sensitivity to superlattice peak asymmetry and splitting. However, lattice dilation through chemical substitution of Cs⁺ cations with MA⁺ is unequivocal and a transition to cubic symmetry, as indicated by the converging a and b lattice parameters (see Fig. 3c) in Cs_0.87MA_0.13PbCl₃. Although (Cs_xMA_1−x)PbCl₃ compositions in the range x ≤ 0.87 exist in a cubic structure, the orthorhombic equivalent cell was used for comparison with CsPbCl₃. Substitution of Cs⁺ with the larger MA⁺ cation causes a predictable monotonic change in the size of the unit cell and cell volume as seen in Fig. 3d. The difference in the X-ray scattering factors of Cs and MA ions causes a monotonic change in the relative intensity of 100 reflection at 15.9° and 110 reflection at 22.2° and permits a compositional refinement of Cs content that shows excellent agreement with the nominal composition (Fig. 2d). These results validate the viability of the mechanochemical synthesis in obtaining homogenous products with targeted compositions.

Fig. 3 High resolution laboratory source PXRD data and structural analyses from the (Cs_xMA_1−x)PbCl₃ (x = 0–1) solid solution series highlighting, (a) the measured PXRD data, (b) an expansion of the ∼15–23° 2θ region showing monotonic intensity changes intensity due to different scattering factors of the Cs⁺ and MA⁺ cations, (c) variation in the (Cs_xMA_1−x)PbCl₃ (x = 0–1) series lattice parameters obtained from Rietveld refinement using an orthorhombic lattice demonstrating that the lattice parameters gradually converge indicating an increase in symmetry, and (d) cell volume and Cs⁺ occupancy from the Rietveld refinements showing excellent agreement between the targeted (red line) and experimentally obtained compositions produced under mechanochemical conditions.

Fig. 4 High resolution synchrotron PXRD data and structural analyses from the (Cs_xMA_1−x)PbBr₃ (x = 0–1) solid solution series highlighting, (a) the measured PXRD data, (b) an expansion of the ∼14–22° 2θ region showing monotonic intensity changes intensity due to different scattering factors of the Cs⁺ and MA⁺ cations, (c) variation in the (Cs_xMA_1−x)PbCl₃ (x = 0–1) series lattice parameters obtained from Rietveld refinement using an orthorhombic lattice demonstrating that the lattice parameters that gradually converge indicating an increase in symmetry from Cs_0.25MAPbBr₃ to Cs_0.37MA_0.63PbBr₃, and (d) cell volume and Cs⁺ occupancy from the Rietveld refinements showing excellent agreement between the targeted (red line) and experimentally obtained compositions produced under mechanochemical conditions.

Table 2 Atomic site parameters used for Rietveld refinement of the powder XRD data from the Cs_0.87MA_0.13PbBr₃ system measured at room temperature

Space group	Pnma	a = 8.236(4) Å	b = 8.254(5) Å	c = 11.776(8) Å	R Bragg = 3.2	B eq
Site	Multiplicity	x	y	z	Occupancy
Cs1	4	0.990	0.971	0.25	0.89	1
MA2	4	0.990	0.971	0.25	0.11	1
Pb3	4	0.5	0.0	0.0	1	1
Br4	4	0.046	0.505	0.25	1	1
Br5	8	0.793	0.205	0.025	1	1

---

Table 3 Refined lattice parameters from Rietveld refinement of the room temperature powder XRD data of the mechanochemically prepared (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ (x = 0.0, 0.13, 0.25, 0.37, 0.5, 0.63, 0.75, 0.87, 1.0) solid solution series. The cubic and orthorhombic refinements were fitted using the Pm3̄m and Pnma space groups, respectively

Nominal composition	Lattice symmetry	R Bragg	a, b, c (Å)	Refined Cs occupancy (±0.03)	Cell volume	Bond length Pb–X^a (Å)	Bond length Cs/MA–X^b (Å)	Crystallite size L (nm)	Measured tilt angles
a Average bond lengths from the PbX6 octahedra (CN = 6). b Average bond lengths from the cuboctahedral Cs^+ or MA^+ cation containing interstices (CN = 12).
(CsxMA1−x)PbBr3 series
MAPbBr3	Cubic	6.7	5.9325(7)	0	208.79(9)	2.966(2)	5.137(6)	17(2)
Cs0.13MA0.87	Cubic	4.0	5.9193(3)	0.11	207.40(4)	2.959(6)	5.126(1)	13(9)
Cs0.25MA0.75	Cubic	4.1	5.9052(9)	0.22	205.93(2)	2.952(6)	5.114(0)	8(3)
Cs0.37MA0.63	Cubic	6.6	5.8946(7)	0.37	204.82(9)	2.947(3)	5.104(8)	11(5)
Cs0.50MA0.50	Cubic	4.9	5.8838(5)	0.52	203.69(8)	2.941(9)	5.095(4)	16(1)
Cs0.63MA0.37	Cubic	5.9	5.8747(2)	0.65	202.75(1)	2.937(3)	5.087(5)	15(4)
Cs0.75MA0.25	Orthorhombic	3.7	8.261(6)	0.75	805.79(9)	Equatorial 2.965(7) axial 2.970(0)	Average 4.14(7)	12(0)	In-phase 159.5° out-of-phase 169.2°
			8.272(1)
			11.790(9)
Cs0.87MA0.13	Orthorhombic	3.5	8.236(4)	0.89	800.67(3)	Equatorial 2.959(5) axial 2.960(6)	Average 4.15(3)	9(6)	In-phase 158.4° out-of-phase 167.8°
			8.254(5)
			11.776(8)
CsPbBr3	Orthorhombic		8.207(3)	1	796.73(3)	Equatorial 2.952(4) axial 2.960(6)	Average 4.08(3)	9(1)	In-phase 157.2° out-of-phase 165.9°
			8.255(9)
			11.758(4)
(CsxMA1−x)PbCl3 series
MAPbCl3	Cubic	12.2	5.6849(0)	0	183.72(5)	2.842(4)	4.923(1)	12(9)
Cs0.13MA0.87	Cubic	6.8	5.6761(9)	0.14	182.88(1)	2.838(1)	4.915(6)	9(5)
Cs0.25MA0.75	Cubic	4.6	5.6597(6)	0.23	181.29(8)	2.829(9)	4.901(4)	9(6)
Cs0.37MA0.63	Cubic	4.9	5.6529(1)	0.34	180.64(0)	2.826(4)	4.895(4)	8(4)
Cs0.50MA0.50	Cubic	6.9	5.6393(3)	0.46	179.34(2)	2.819(7)	4.883(6)	11(6)
Cs0.63MA0.37	Cubic	8.2	5.6258(6)	0.62	178.06(0)	2.812(9)	4.872(0)	11(5)
Cs0.75MA0.25	Cubic	7.5	5.6172(0)	0.77	177.23(9)	2.808(6)	4.864(4)	11(8)
Cs0.87MA0.13	Cubic	5.3	5.6090(7)	0.89	176.47(0)	2.804(5)	4.857(4)	9(4)
CsPbCl3	Orthorhombic	6.5	7.903(2)	1	703.25(1)	Equatorial 2.812(8)	Average 3.97(8)	11(7)
			7.908(0)			Axial
			11.252(3)			2.833(5)

---

The room temperature laboratory XRD data is presented in Fig. 4a and b. As evident from Fig. 4c, CsPbBr₃ is orthorhombic (Pnma) with the a and b lattice parameters differing by >0.05 Å. This larger difference in comparison to that of CsPbCl₃ indicates that the CsPbBr₃ structure is further removed from the cubic phase transition. This is also supported by the fact that CsPbBr₃ transforms into a cubic phase above 130 °C, which is ∼105 °C above room temperature in comparison to ∼23 °C above room temperature for CsPbCl₃.⁴¹ The superlattice peaks in the bromide samples show a higher intensity and are easily detected as Br has a higher electron density than Cl. The emergence of these peaks is observed for the bromide series of samples with <25% MA⁺ composition as the incorporated Cs⁺ destabilizes the cubic perovskite structure thus tilting the octahedra. From Fig. 4b and Table 1 the CsPbBr₃ data exhibits clear peak splitting with the (100) reflection at 15° splitting into (110) and (002) in the orthorhombic setting, and these progressively converging when the composition evolves from Cs_0.25MA_0.75PbBr₃ to Cs_0.37MA_0.63PbBr₃ indicating an additional orthorhombic to cubic phase transition (see Fig. 4c and d). It can be inferred that PbBr₆ octahedral tilting is also eliminated to satisfy the change in symmetry. Following the hierarchy of space groups proposed by Howard et al. (see Scheme 1 and Table 1) it can be inferred that during thermal expansion of the orthorhombic CsPbBr₃ lattice the formation of a tetragonal intermediate at >88 °C occur; i.e. before transformation into the cubic aristotype. While not explicitly detected as a discrete tetragonal phase transition, this phase may exist over a narrow temperature and compositional range as indicated by the discontinuity in cell volume and lattice parameter variation in Fig. 4c and d, respectively.

Solid state MAS NMR analysis

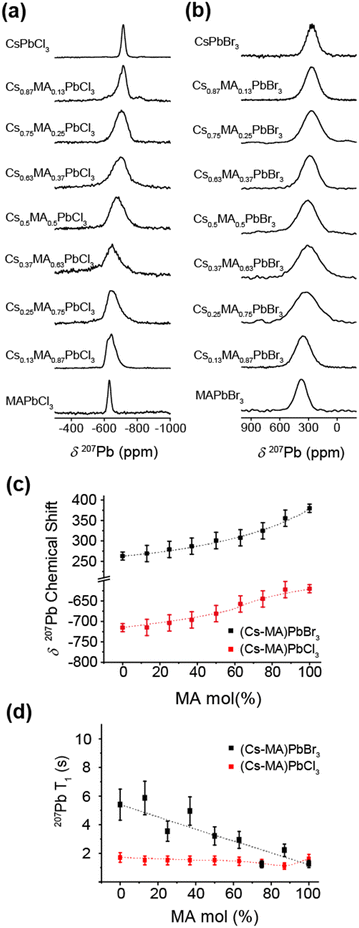
The ¹³³Cs and ²⁰⁷Pb MAS NMR data measured from the mechanochemically prepared (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ series (x = 0.0, 0.13, 0.25, 0.37, 0.5, 0.63, 0.75, 0.87, 1.0) shown in Fig. 5 and 6. They illustrate the acquired ¹³³Cs MAS NMR and ²⁰⁷Pb MAS NMR spectra (see Fig. 5a and b, and Fig. 6a and b, respectively), the observed ¹³³Cs and ²⁰⁷Pb chemical shift trends (see Fig. 5c and 6c, respectively), and the variation in the characteristic T₁ relaxation times (see Fig. 5d and 6d, respectively) as function of composition for each series.

Fig. 5 The ¹³³Cs MAS NMR study showing, (a) the ¹³³Cs data for the (Cs_xMA_1−x)PbCl₃ series, (b) the ¹³³Cs data for the (Cs_xMA_1−x)PbBr₃ series, (c) the variation in the ¹³³Cs apparent chemical shifts with MA⁺ incorporation and their sensitivity to the orthorhombic–cubic phase transition, and (d) the sensitivity of the ¹³³Cs T₁s to MA⁺ incorporation and the pronounced T₁ minimum exhibited at the orthorhombic–cubic phase transition.

Fig. 6 The ²⁰⁷Pb MAS NMR study showing, (a) the ²⁰⁷Pb data for the (Cs_xMA_1−x)PbCl₃ series, (b) the ²⁰⁷Pb data for the (Cs_xMA_1−x)PbBr₃ series, (c) the variation in the ²⁰⁷Pb isotropic chemical shifts with MA⁺ incorporation and their insensitivity to the orthorhombic–cubic phase transition, and (d) the minimal decrease in the ²⁰⁷Pb T₁s with increasing MA⁺ incorporation associated with increasing Pb–X bond lengths and cell volumes rather than sensitivity to the orthorhombic–cubic phase transition.

The ¹³³Cs MAS NMR spectra shown in Fig. 5a and b exhibit one resonance highlighting the phase purity of the mechanochemically prepared dual cation Cs⁺/MA⁺ solid solutions. This result corroborates the high quality HRTEM data presented in Fig. 2. As evidenced by the PXRD data of Fig. 3c and 4c, the lattice parameter (and hence the cubic phase bond length) increases proportionally with increasing mol% MA⁺ content, which is consistent with the larger ionic radius of the MA⁺ cation in comparison to that of its Cs⁺ counterpart. The expanding PbBr₆ and PbCl₆ frameworks reduce the electronic/covalent contact with the Cs⁺ positions, subsequently contracting the electron rich Cs⁺ cation valence electron clouds inducing a comparatively more ionic position with higher electron density. As a consequence, shifts trending to higher shielding (i.e. to lower ppm) are observed (see Fig. 5c). It is interesting to note that the ¹³³Cs chemical shift is linearly proportional to mol% MA⁺ concentration within the same compositional range. As indicated in Fig. 5c, the cubic–orthorhombic phase transition can be observed as an inflection point in the gradient characterizing the rate of change of the ¹³³Cs chemical shift with mol% MA⁺ incorporation. This linear δ(¹³³Cs)/mol% MA⁺ trend can be used to predict the achieved nominal compositions and phase transition regions across these compositional series.

Similarly, the ²⁰⁷Pb MAS NMR spectra shown in Fig. 6a and b also exhibit one resonance mirroring the phase purity indicated by the ¹³³Cs MAS NMR and HRTEM data. In contrast to the ¹³³Cs MAS NMR data, the ²⁰⁷Pb chemical shift variation trends monotonically to higher deshielding (i.e. to higher ppm) with increasing mol% MA⁺ incorporation (see Fig. 6c). As reflected in Table 3, this behaviour is influenced by the increasing average 〈Pb–Cl〉 and 〈Pb–Br〉 bond distances comprising the PbCl₆ and PbBr₆ frameworks, respectively, as they accommodate the increasing proportions of the MA⁺ cation which possesses a larger ionic radius. Furthermore, to within the resolution afforded by the ²⁰⁷Pb linewidths (∼7–16 kHz) these data are insensitive to the cubic–orthorhombic phase transition suggesting that Cs⁺ cation positions are more responsive to the octahedral tilting defining this phase transition. As reported in previous ²⁰⁷Pb MAS NMR studies on the CsPbBr₃ system, a heteronuclear ¹J(Pb, Br) coupling has been observed and measured, although the ability to observe this phenomenon is intrinsically associated with the sample quality and the integrity of the short range order.^42–44 From simulation of the ²⁰⁷Pb MAS NMR data from the CsPbBr₃ endmember shown in Fig. 6b and Fig. S2a (ESI‡) ¹J(Pb, Br) coupling constant of 2360 ± 50 Hz has been measured. Although this is consistent with previous studies, it is not detected in subsequent data reflecting increasing MA⁺ incorporation as the substitutional and positional Cs⁺/MA⁺ cation disorder influencing the PbBr₆ octahedra precludes observation of this fine structure.^42–44

From Fig. 5d and 6d it can be observed that the ¹³³Cs and ²⁰⁷Pb T₁ values measured across the mechanochemically synthesized (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ compositional series exhibit contrasting behavioral trends. Although the ¹³³Cs nucleus (I = 7/2) is a quadrupolar nucleus it possesses a very small quadrupole moment (Q ∼ −0.343 × 10⁻³⁰ m²), and coupled with the high point symmetry of the cuboctahedral Cs⁺ cation environment which induces small or zero electric field gradients, the overall ¹³³Cs quadrupole coupling interaction within these systems is negligible. Hence, contributions from the quadrupole interaction to the ¹³³Cs T₁ relaxation rates/times will be small, and they will be thus dominated by a dipolar relaxation mechanism. Variation in the in dipolar-dominated ¹³³Cs T₁s have been previously used as diagnostic probes of mobility, dynamics and phase transitions in halide perovskite materials.^18,43–46 The measured reduction in ¹³³Cs spin-lattice relaxation rates have been correlated to phase transitions and associated increase in electrical conductivity due to increase in halide mobility.^44,47Fig. 5d indicates marked variation in the ¹³³Cs T₁ with respect to sample composition. For the (Cs_xMA_1−x)PbCl₃ series the T₁ decreases from 51 s in the CsPbCl₃ end member to a T₁ minimum of 8 s for (Cs_0.87MA_0.13)PbCl₃ which represents an orthorhombic–cubic phase transition. As the mol% of the MA⁺ cation increases past this point the T₁ increases to 44 s in the final dual cation (Cs_0.13MA_0.87)PbCl₃ composition. Similarly for the (Cs_xMA_1−x)PbBr₃ series, the T₁ decreases from 54 s in the CsPbBr₃ end member to a T₁ minimum of 17 s for the (Cs_0.75MA_0.25)PbBr₃ system which also represents an orthorhombic–cubic phase transition for this series; this monotonically increases to 47 s for the final (Cs_0.13MA_0.87)PbBr₃ dual cation composition.

The ¹³³Cs T₁ minima corresponding to the orthorhombic–cubic phase transition for each series represent compositions where the local (or short range) disorder is maximized, thus facilitating optimal conditions for Cs⁺ cation and halide anion mobility. As observed in Fig. 5d, these minima are represented by pronounced reductions in T₁ by factors of ∼6–7 for the (Cs_xMA_1−x)PbCl₃ series and ∼3 for the (Cs_xMA_1−x)PbBr₃ series at this transition point. However, the subsequent increase in T₁s back to values approaching the starting (orthorhombic) CsPbCl₃ and CsPbBr₃ endmembers occurs throughout cubic compositions where no change in lattice symmetry is observed. This phenomenon suggests that these T₁ increases can be attributed primarily to Cs⁺ cation and halide anion mobility. Indeed, other studies of similar lead iodide perovskite analogues have shown that the electrical conductivity is dominated by halide mobility rather than cation mobility in these materials.^48–50 Notably, the compositions associated with these phase transitions in Fig. 5d are coincident with the points on inflection (i.e. change in the slopes) of the δ(¹³³Cs)/mol% MA⁺ trends for each system in Fig. 5c, indicating that the ¹³³Cs T₁ relaxation times and chemical shifts δ data are both sensitive to the precise compositions where phase transitions occur within the dual cation (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ series. Sensitivity to the orthorhombic–cubic phase transition is not mirrored by the accompanying ²⁰⁷Pb and ¹H chemical shift δ and T₁ data of Fig. 6a–d and 7a–c, respectively. Fig. 6a–d show that an increasing MA⁺ content induces an increase in the ²⁰⁷Pb chemical shifts δ that are correlated with the increasing average 〈Pb–X〉 bond lengths, while the ²⁰⁷Pb T₁ data exhibit small monotonic decreases which correlate with increasing average octahedral 〈Pb–X〉 bond lengths, average cuboctahedral 〈Cs/MA–X〉 distances and cell volumes (see Table 3). In contrast, Fig. 7a–c show that the ¹H chemical shifts δ are completely invariant with composition, while the associated T₁ data also exhibits a similar invariance except for those compositions approaching (and including) the MAPbCl₃ endmembers. This phenomenon is attributed to the local disorder introduced throughout the solid solution part of the series; however, an abrupt increase in T₁ is observed for the ordered MAPbCl₃ endmembers where optimal structural order is coupled with the maximised cell volume.

Fig. 7 The ¹H MAS NMR data exhibiting methyl and ammonium resonances at δ ∼3 ppm and δ ∼6.5 ppm, respectively, for (a) the (Cs_xMA_1−x)PbCl₃ series, (b) the (Cs_xMA_1−x)PbBr₃ series, together with (c) the largely invariant ¹H T₁ data across the Cs⁺/MA⁺ compositional range (except for the MAPbX₃ endmembers), indicating that the MA⁺ dynamics are relatively unaffected by the orthorhombic–cubic phase transition.

PXRD and thermal analyses of the temperature induced phase transitions

Room temperature TEM, PXRD and solid state NMR studies of the as-synthesized mechanochemically derived (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ (x = 0.0, 0.13, 0.25, 0.37, 0.5, 0.63, 0.75, 0.87, 1.0) solid solution series all demonstrate the superior homogeneity, and long and short range structural order that emanates from this preparative method. These properties can be exploited to accurately map the more extensive temperature induced phase transitions enabling phase diagrams for these entire solid solution compositional ranges to be constructed.

The CsPbCl₃ and MAPbCl₃ systems have been extensively studied. For CsPbCl₃ the low temperature orthorhombic (Pnma, a⁻b⁺a⁻) phase transforms at 310 K to a tetragonal (P4/mbm, a⁰a⁰c⁺) variant through the elimination of out-of-phase PbCl₆ octahedral tilting,³⁹ with conversion to a cubic (Pm3̄m, a⁰a⁰a⁰) phase following closely above 320 K as a second order transformation.^15,40 Poglish et al. determined that cubic MAPbCl₃ transforms into a pseudo-cubic tetragonal (P4/mmm, a⁰a⁰c⁰) structure below 177 K with disordered methylammonium ions,⁵¹ while Songvilay et al. established that phase transitions from orthorhombic to tetragonal and cubic forms are driven by thermally activated framework vibrations.⁵² The tetragonal P4/mmm polymorph possesses non-tilted BX₆ octahedra similar to the cubic Pm3̄m aristotype, but the PbCl₆ octahedra are elongated to accommodate the rigid methylammonium ions leading to a reduction in symmetry, and consequently is not captured in Scheme 1. Kawamura et al. reported that the MA⁺ cations are incommensurately modulated along the c-axis of the tetragonal cell,⁵³ with the tetragonal to cubic transition occurring at 177–178 K appearing second order in nature.⁵⁴ Despite the large body of work that exists characterising the CsPbCl₃ and MAPbCl₃ systems, no study has attempted to map the phase transitions characterising Cs⁺/MA⁺ solid solution compositional series linking these endmembers.

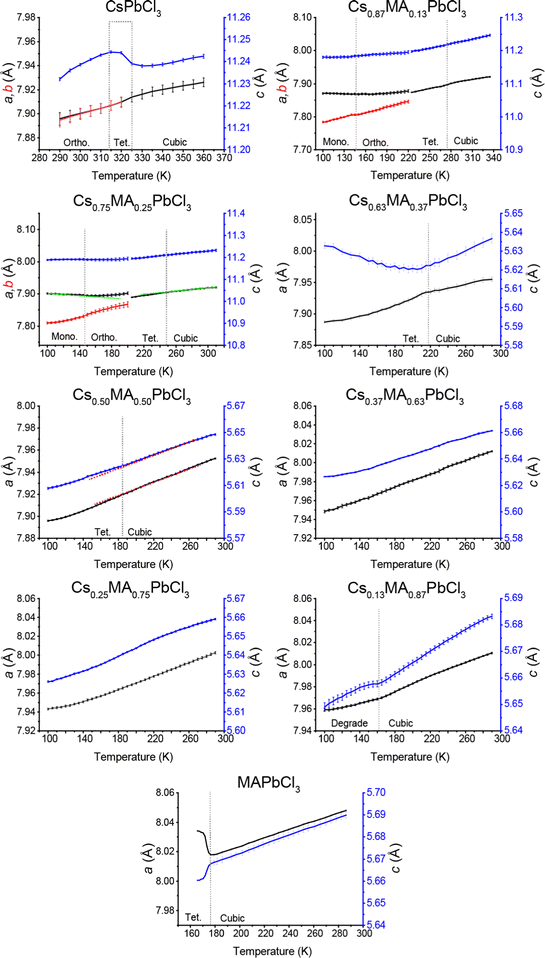
The lattice parameter evolution from the Pawley refinement of the variable temperature laboratory PXRD data from the (Cs_xMA_1−x)PbCl₃ series, and the variable temperature synchrotron PXRD data from the (Cs_xMA_1−x)PbBr₃ series, are given in Fig. 8 and 9, respectively. All phase transitions detected using diffraction techniques are corroborated by DSC measurements shown in Fig. S5 and S6 (ESI‡), with the overall mapping of the temperature induced phase transitions determined from both techniques summarised in the phase diagrams of Fig. 10a and b. From Fig. 8, 10a and Fig. S5 (ESI‡) the tetragonal (P4/mbm)–cubic (Pm3̄m) transition for the pure CsPbCl₃ endmember measured at 320 K closely corroborates previous reports.^40,55 The subsequent increase in MA⁺ content monotonically depresses the cubic–tetragonal transition temperature from 320 K in CsPbCl₃ to 220 K in Cs_0.63MA_0.37PbCl₃. Although the phase transitions for CsPbCl₃ and Cs_0.87MA_0.13PbCl₃ are closely mirrored by the DSC data of Fig. S5 (ESI‡), compositions from Cs_0.63MA_0.37PbCl₃ to Cs_0.13MA_0.87PbCl₃ undergo a slow and irreversible disproportionation or phase segregation below 210 K yielding the 2D layered CsPb₂Cl₅ structure and highly disordered MA⁺-containing MA/Cs/Pb/Cl phases of mixed compositions. At these reduced temperatures the solid solution enthalpy of formation (or activation) is not satisfied, and a more entropic state appears to be supported. However, pure MAPbCl₃ alters to tetragonal (P4/mmm) perovskite below 177 K in agreement with earlier reports.⁵³ In summary, the (Cs_xMA_1−x)PbCl₃ solid solution series demonstrates that the phase transition temperature can be tuned by replacing the smaller A site Cs⁺ cation with larger MA⁺ so that the cubic phase persists at room temperature.

Fig. 8 Refined lattice parameter evolution (pseudocubic axes a black, c blue) elucidated from Pawley refinement of laboratory XRD data collected on the (Cs_xMA_1−x)PbCl₃ solid solution series. The cubic (Pm3̄m) to tetragonal (P4/mbm) phase transformations in Cs⁺-rich end of the series are dominated by second order effects.

Fig. 9 Refined lattice parameter evolution (pseudocubic axes a black, c blue) elucidated from Rietveld refinement of synchrotron XRD data collected on the (Cs_xMA_1−x)PbBr₃ solid solution series. The cubic (Pm3̄m) to tetragonal (P4/mbm) phase transformations in Cs⁺-rich end of the series are dominated by second order effects. The second order effects gradually reduce in the MA⁺-rich compositions with MAPbBr₃ resembling first order behavior.

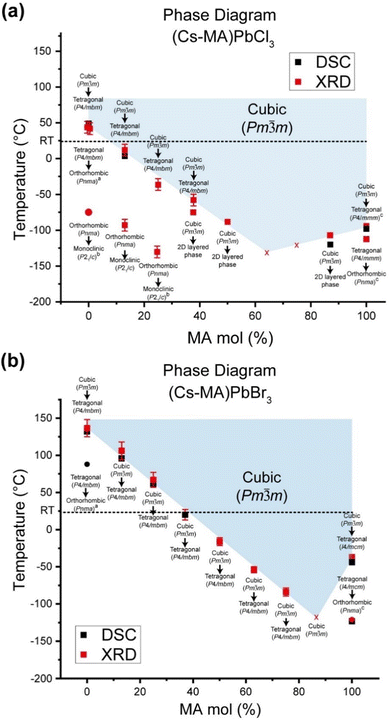Fig. 10 Variable temperature phase diagrams for, (a) the (Cs_xMA_1−x)PbCl₃, and (b) the (Cs_xMA_1−x)PbBr₃ solid solution series highlighting the cubic–tetragonal transitions as determined by the combined DSC/laboratory source PXRD study (for the (Cs_xMA_1−x)PbCl₃ series) and the DSC/synchrotron source PXRD study (for the (Cs_xMA_1−x)PbBr₃ series). The additional lower symmetry phase transitions denoted with superscripts a, b and c corroborate previous reports in ref. 38, 39 and 59, respectively. The room temperature PXRD and solid state NMR studies correspond to the phase transitions indicated by the dotted lines in each series.

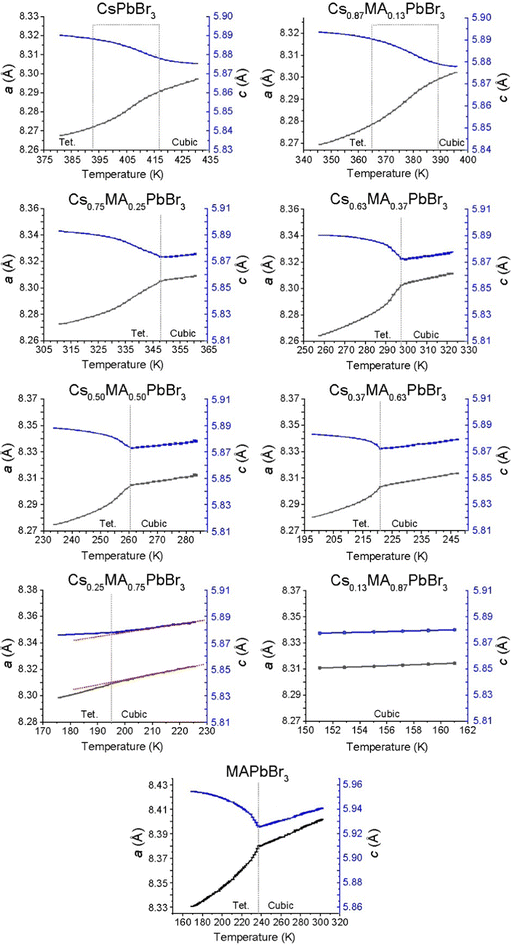
The corresponding phase diagram generated from the diffraction and DSC data for the (Cs_xMA_1−x)PbBr₃ solid solution series (see Fig. 10b) exhibits a more homogeneous and less complex response to MA⁺ incorporation. As observed from Fig. 9, 10b and Fig. S6 (ESI‡) the tetragonal (P4/mbm)–cubic (Pm3̄m) transition for the pure CsPbBr₃ endmember identified at 403 K (130 °C) is consistent with previous studies,⁴¹ while the increasing MA⁺ content depresses the phase transition temperature monotonically to 195 K for the Cs_0.25MA_0.75PbBr₃ composition. Thereafter, the Cs_0.13MA_0.87PbBr₃ system represents an unusually stable cubic phase down to <150 K which is considerably lower than the adjacent MAPbBr₃ and Cs_0.25MA_0.75PbBr₃ phase transition temperatures at 177 and 195 K, respectively. Identifying this composition with exceptional phase stability could have potential implications for the fine tuning of photovoltaic device efficiency and stability. Furthermore, the PXRD data of Fig. 9 reveals that this monotonic behaviour is mirrored by a gradual change in the nature of the tetragonal–cubic phase transition. For CsPbBr₃ this phase transition is distinctly second order and spread over a ∼20 K temperature range (∼395–415 K); however, this narrows and assumes greater first order character with increasing MA⁺ incorporation with MAPbBr₃ exhibiting a completely first order phase transition with a temperature range of ∼3 K (∼236–239 K). As shown in Fig. 10b, the phase transitions detected from the DSC and PXRD measurements (see Fig. S6, ESI‡ and Fig. 9, respectively) are in excellent agreement.

In contrast to MAPbCl₃ (P4/mbm), cubic MAPbBr₃ cools into a tetragonal (I4/mcm) structure described by the tilt system a⁰a⁰c⁻.⁵⁴ Tetragonal MAPbBr₃ has been found to be incommensurately modulated similar to the chloride analogue,^56,57 with the disorder of the MA⁺ cations in the tetragonal phase being previously characterised using neutron diffraction.⁵⁸ The intrinsic structural difference between the tetragonal CsPbBr₃ and MAPbBr₃ structures centres around the octahedral tilting which is in-phase in the former system and out-of-phase in the latter. Since the PXRD data of Fig. S3 and S4 (ESI‡) alone cannot distinguish in-phase and out-of-phase tilts, reflections from space groups such and P4/mbm and I4/mcm cannot be resolved. While changes in the lattice parameters indicate variation in lattice symmetry, the lack of phase information from the reflections determines that precise space group information cannot be elucidated for the intermediate solid solution compositions. Hence, the reported tetragonal space groups shown in Fig. 10a and b are assumed directly from the parent endmembers.

The cubic polymorph stability can be displayed by plotting the minimum unit cell size determined by the PXRD data below which the tetragonal phase becomes measurable (see Fig. 11). These observations are supplemented by DSC measurements to assess the latent heat capacity near these transition temperatures (see Fig. S5 and S6, ESI‡) which are collated in the phase diagrams of Fig. 10a and b. All endmembers (i.e. CsPbCl₃, CsPbBr₃, MAPbCl₃, MAPbBr₃) show sharp, well-defined transitions, while only some intermediate compositions exhibit detectable changes in latent heat capacity. From the (Cs_xMA_1−x)PbBr₃ series the Cs_0.87MA_0.13PbBr₃, Cs_0.75MA_0.25PbBr₃ and Cs_0.63MA_0.37PbBr₃ compositions the DSC data of Fig. S6 (ESI‡) demonstrate heat capacities corresponding to successively smaller changes in the unit cell volumes upon increasing MA⁺ content.

Fig. 11 Correlated structural, bandgap and XPS data from the mechanochemically prepared (Cs_xMA_1−x)PbX₃ (x = 0–1, X = Cs, Br) solid solution series highlighting, (a) refined lattice parameters immediately prior to the cubic (Pm3̄m)–tetragonal (P4/mbm) phase transition, (b) estimation of the bandgap using Tauc plots based on the UV/vis absorption spectra shown in Fig. S7 and S8 (ESI‡), respectively, (c–f) XPS data of the Cl 2p, Br 3d, Pb 4f and Cs 4d electronic states, respectively.

In addition to the detected cubic–tetragonal phase transitions characterising the (Cs_xMA_1−x)PbCl₃ solid solution series, Fig. 10a also indicates lower temperature transformations to reduced symmetry. In agreement with Linaberg et al.,³⁹ the CsPbCl₃ endmember shows a tetragonal–orthorhombic transition at ∼315 K close to its cubic–tetragonal counterpart, although the lower temperature orthorhombic-monoclinic transition previously reported by Hirotsu at ∼200 K was not detected under these experimental conditions.⁴⁰ From Fig. 8 and 10a additional orthorhombic-monoclinic transitions can be observed for the Cs_0.87MA_0.13PbCl₃ and Cs_0.75MA_0.25PbCl₃ compositions at lower temperatures of ∼150 K with increasing MA⁺ incorporation, mirroring the cubic–tetragonal trend. As indicated above, compositions with higher MA content are unstable below 210 K, phase segregating to CsPb₂Cl₅ and other MA/Cs/Pb/Cl-containing phases. The room temperature XRD data (see Fig. 3 and 4) represent a slice of the phase diagram as marked with a dashed line in Fig. 10. When viewed along this line, the transition from orthorhombic to cubic is apparent as a crossover for compositions with MA⁺ contents of more than Cs_0.87MA_0.13PbCl₃ and Cs_0.63MA_0.37PbBr₃.

Octahedral tilting influence on the bandgap

The solid state NMR and diffraction data from the highly ordered dual cation (Cs_xMA_1−x)PbX₃ (x = 0–1, X = Cs, Br) solid solution series formed under mechanochemical conditions demonstrate that complete miscibility exists across the entire mixed A site cation compositional range. This contrasts with other mixed A site cation systems such as Cs⁺-formamidinium (FA⁺) which exhibits a pronounced miscibility gap. Some conjecture surrounds the size of this Cs⁺–FA⁺ miscibility gap as different studies by Ralf et al.⁶⁰ and Prasanna et al.⁶¹ reported miscibility gaps of 15–100 mol% Cs⁺ and 33–100 mol% Cs⁺, respectively. The latter study employed materials modelling and DFT calculations to examine the band gap evolution with respect to lattice contraction for low-intermediate compositions, concluding that lattice contraction in Cs⁺-rich compositions correlated with smaller band gaps that were attributed to octahedral tilting. However, the study by Prasanna et al. did not consider the scenario of lattice contraction without tilting.⁶¹ While focusing on well-formed mechanochemically synthesized (Cs_xMA_1−x)PbX₃ (x = 0–1, X = Cs, Br) solid solution products, this study presents an opportunity to accurately test this hypothesis relating electronic structure and band gap size to the impact of bond length contraction and octahedral titling.

As established in Table 3 and Fig. 3, 4, 8–10, this work shows that high proportions of the Cs⁺ cation can be introduced into the A site of the cubic phase at room temperature without any change in bond angle or octahedral tilting. This compositional range can be extended to higher Cs⁺ cation incorporation with increasing temperature (especially for the (Cs_xMA_1−x)PbBr₃ series). Fig. 11a emphasizes the uniformity of refined lattice parameters of cubic (Cs_xMA_1−x)PbBr₃ and (Cs_xMA_1−x)PbCl₃ solid solution series immediately prior to the cubic (Pm3̄m)–tetragonal (P4/mbm) phase transition. For the Br series the PbBr₆ octahedra are consistently compressed to assume unit cell dimensions of ∼5.872 Å, either through compositional (A site) or temperature variation, beyond which the PbBr₆ octahedra tilt to avoid further bond length reduction. Similarly, for the Cl series the PbCl₆ octahedra are consistently compressed to unit cell dimensions of ∼5.620 Å. The Tauc plots of the UV/vis absorption data of Fig. 11b and Fig. S7, S8 (ESI‡) display a gradual reduction in bandgap with increasing MA⁺ content, although the errors are large due to the nature of the measurement. Importantly, this bandgap trend exists over MA⁺ incorporation ranges (x = 0–0.87 for the Cl series, x = 0–0.63 for the Br series) where only cubic phases exist (i.e. phases not supporting octahedral tilting), suggesting that octahedral tilting exerts a comparatively smaller perturbation on the bandgap in comparison to other factors (i.e. A site cation size, unit cell size, Pb–X bond length) in this class of materials.

Further XPS data shown in Fig. 11c–f demonstrates that both series exhibit correlated trends of strengthening Cs 4d, Br 3d, Pb 4f and Cl 2p binding energies with increasing MA⁺ content despite the increasing unit cell sizes and bond lengths reported above (see Fig. 3d, 4d and 6c). These results emphasize that change of the A site cation size influences the Pb–X bond length and bond strength in the absence of octahedral tilting. Conventional electronic band structure modelling of metal halide perovskites is normally dominated by the electronic spin-orbit coupling and bonding hybridization schemes between the lead and halide positions.⁶¹ The increasing MA⁺ content through each solid solution series induces structural change and variable disorder that correlates empirically with these electronic factors and the resultant bandgap variation; however, the specific mechanisms are not well understood. This evidence highlights the need for further theoretical investigations of the structural influences on bandgaps in these materials, and presents implications and factors for the materials modelling of these systems that cannot be neglected.

Conclusion

Mechanochemical synthesis is demonstrated to be a viable method for the preparation of dual cation hybrid perovskites of the nominal stoichiometric form (Cs_xMA_1−x)Pb(Cl/Br)₃ (x = 0, 0.13, 0.25, 0.37, 0.50, 0.63, 0.75, 0.87, 1). The continuous compositional variation demonstrates that Cs⁺ and MA⁺ are completely miscible which allows the formation of homogeneous and high purity solid solution products. The phase purity was studied using HRTEM, XRD and solid state NMR techniques which established that room temperature cubic–orthorhombic phase transitions exists in the region of 0.63 < x < 0.75 for (Cs_xMA_1−x)PbBr₃ system, and in the region of 0.87 < x < 1 (Cs_xMA_1−x)PbCl₃ system. HRTEM studies showed the Br series exhibits higher electron beam stability of up to ∼10–20 min, whereas the analogous Cl series demonstrated a reduced persistence with degradation occurring over a period of ∼30 s–1 min under the beam, although lattice fringes were still able to be observed. High e⁻ beam stability of the dual cation Cs⁺/Ma⁺ systems in comparison to pure MA⁺ analogues suggests that these materials may be more stable under high electric fields, which is critical for LED applications where the active layer experiences electric fields on the order of 2000 kV m⁻¹.

The ²⁰⁷Pb NMR chemical shift exhibits sensitivity to changes in the first coordination sphere of Pb²⁺ position promoted by Pb–X bond length variation upon A site compositional variation, and the halide composition. In contrast, the ¹³³Cs resonance is sensitive to the Pb–X bond length change (upon A site compositional change and halide composition), and the phase transitions induced throughout the compositional range. Synchrotron and laboratory source PXRD data exhibit good agreement with the ¹³³Cs MAS NMR study in identifying the phase transitions, indicating that the local (short range) structural changes observed from NMR are accurately reflected in the periodic (long range) structural transformation observed with XRD.

Phase diagrams mapping the Cs⁺/MA⁺ compositional space for the (Cs_xMA_1−x)PbCl₃ and (Cs_xMA_1−x)PbBr₃ solid solution series were undertaken using variable temperature PXRD. While the cubic polymorph in most compositions exhibited a stability range from 403–195 K, the Cs_0.13MA_0.87PbBr₃ composition displayed an exceptionally wide stability field for the cubic polymorph that extended below <150 K. This unique phase stability has promising potential for photovoltaic devices as the phase stability minimises thermal degradation and phase segregation. The Cl series also shows increasing cubic phase stability down to 210 K, below which solid solution formation no longer occurs and phase segregation (or disproportionation) into a 2D layered CsPb₂Cl₅ and other disordered MA/Cs/Pb/Cl phases of mixed compositions are thermodynamically favoured. Tauc plots of the UV/vis data highlighted the occurrence of a bandgap reduction observed for increasing MA⁺ incorporation throughout the range of cubic phases where octahedral tilting was absent.

Author contributions

SSHD, TW and JVH designed the initial experiments relating to the mechanochemical synthesis of these materials. SSHD performed the materials syntheses, while SSHD, DW and YF undertook the initial PXRD/crystallographic analyses, TEM, UV/vis, XPS and DSC characterization. SSHD and JVH designed and performed all solid state NMR measurements, while SSHD and TAB performed the synchrotron PXRD/crystallographic analysis. SSHD and JVH wrote the manuscript with all authors viewing and contributing to its content.

Conflicts of interest

The authors declare that there are no conflicts of interest.

Acknowledgements

JVH and TJW gratefully acknowledge the Diamond Light Source at the Rutherford Appleton Laboratories for access to the I11 beamline through the Diamond Light Source Block Allocation Group award “Oxford/Warwick Solid State Chemistry BAG to Probe Composition–Structure–Property Relationships in Solids” (STFC grants EE18786 and CY25166). The authors thank Assoc Prof. Mark Senn and Dr Anna Herlihy for assistance in running the I11 beamline, acquisition of the diffraction data, and for data handling. JVH and DW thank the Diffraction Research Technology Platform at the University of Warwick for access to the laboratory source PXRD instrumentation. TJW, JVH and SSHD acknowledges financial support from the Singapore National Research Foundation, Prime Minister's Office, through the Competitive Research Program (CRP Award No. NRF-CRP14-2014-03). JVH and TJW thank Center of High Field NMR Spectroscopy and Imaging at NTU for access to the solid state MAS NMR capability.

References

1. H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. Il, Seok, Nature, 2021, 598, 444–450.
2. Best Research Cell Efficiency, 2021, https://www.nrel.gov/pv/cell-efficiency.html.
3. Y.-H. Kim, S. Kim, A. Kakekhani, J. Park, J. Park, Y.-H. Lee, H. Xu, S. Nagane, R. B. Wexler, D.-H. Kim, S. H. Jo, L. Martínez-Sarti, P. Tan, A. Sadhanala, G.-S. Park, Y.-W. Kim, B. Hu, H. J. Bolink, S. Yoo, R. H. Friend, A. M. Rappe and T.-W. Lee, Nat. Photonics, 2021, 15, 148–155.
4. M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647.
5. H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Nat. Mater., 2015, 14, 636–642.
6. F. Bella, G. Griffini, J.-P. Correa-Baena, G. Saracco, M. Grätzel, A. Hagfeldt, S. Turri and C. Gerbaldi, Science, 2016, 354, 203.
7. H. Tsai, W. Nie, J.-C. Blancon, C. C. Stoumpos, R. Asadpour, B. Harutyunyan, A. J. Neukirch, R. Verduzco, J. J. Crochet, S. Tretiak, L. Pedesseau, J. Even, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, Nature, 2016, 536, 312.
8. D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 7843–7850.
9. M. Saliba, T. Matsui, J. Y. Seo, K. Domanski, J. P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Gratzel, Energy Environ. Sci., 2016, 9, 1989–1997.
10. D. J. Kubicki, D. Prochowicz, A. Hofstetter, S. M. Zakeeruddin, M. Gratzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 14173–14180.
11. D. J. Kubicki, D. Prochowicz, A. Hofstetter, S. M. Zakeeruddin, M. Gratzel and L. Emsley, J. Am. Chem. Soc., 2018, 140, 7232–7238.
12. Y. H. Kim, H. Cho, J. H. Heo, T. S. Kim, N. Myoung, C. L. Lee, S. H. Im and T. W. Lee, Adv. Mater., 2015, 27, 1248–1254.
13. L. Zhang, X. Yang, Q. Jiang, P. Wang, Z. Yin, X. Zhang, H. Tan, Y. M. Yang, M. Wei and B. R. Sutherland, Nat. Commun., 2017, 8, 15640.
14. M.-H. Park, S.-H. Jeong, H.-K. Seo, C. Wolf, Y.-H. Kim, H. Kim, J. Byun, J. S. Kim, H. Cho and T.-W. Lee, Nano Energy, 2017, 42, 157–165.
15. S. Hirotsu and S. Sawada, Phys. Lett. A, 1969, 28, 762–763.
16. A. Karmakar, A. M. Askar, G. M. Bernard, V. V. Terskikh, M. Ha, S. Patel, K. Shankar and V. K. Michaelis, Chem. Mater., 2018, 30, 2309–2321.
17. A. M. Askar, A. Karmakar, G. M. Bernard, M. Ha, V. V. Terskikh, B. D. Wiltshire, S. Patel, J. Fleet, K. Shankar and V. K. Michaelis, J. Phys. Chem. Lett., 2018, 9, 2671–2677.
18. A. Karmakar, A. Bhattacharya, D. Sarkar, G. M. Bernard, A. Mar and V. K. Michaelis, Chem. Sci., 2021, 12, 3253–3263.
19. A. Karmakar, A. Bhattacharya, G. M. Bernard, A. Mar and V. K. Michaelis, ACS Mater. Lett., 2021, 3, 261–267.
20. E. M. Mozur, A. E. Maughan, Y. Cheng, A. Huq, N. Jalarvo, L. L. Daemen and J. R. Neilson, Chem. Mater., 2017, 29, 10168–10177.
21. G. A. Bowmaker, Effendy, J. V. Hanna, P. C. Healy, S. P. King, C. Pettinari, B. W. Skelton and A. H. White, Dalton Trans., 2011, 40, 7210–7218.
22. G. A. Bowmaker, J. V. Hanna, R. D. Hart, B. W. Skelton and A. H. White, Dalton Trans., 2008, 5290–5292,  10.1039/B810659M.
23. G. A. Bowmaker, J. V. Hanna, B. W. Skelton and A. H. White, Chem. Commun., 2009, 2168–2170,  10.1039/B822370J.
24. G. A. Bowmaker, J. V. Hanna, R. D. Hart, P. C. Healy, S. P. King, F. Marchetti, C. Pettinari, B. W. Skelton, A. Tabacaru and A. H. White, Dalton Trans., 2012, 41, 7513–7525.
25. G. Maculan, A. D. Sheikh, A. L. Abdelhady, M. I. Saidaminov, M. A. Haque, B. Murali, E. Alarousu, O. F. Mohammed, T. Wu and O. M. Bakr, J. Phys. Chem. Lett., 2015, 6, 3781–3786.
26. M. I. Saidaminov, A. L. Abdelhady, B. Murali, E. Alarousu, V. M. Burlakov, W. Peng, I. Dursun, L. Wang, Y. He and G. Maculan, Nat. Commun., 2015, 6, 7586.
27. D. Weber, Z. Naturforsch. B, 1978, 33, 1443–1445.
28. D. Weber, Z. Naturforsch. B, 1978, 33, 862–865.
29. T. Baikie, Y. N. Fang, J. M. Kadro, M. Schreyer, F. X. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641.
30. R. K. Harris, E. D. Becker, S. M. C. De Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795–1818.
31. S. S. Mali, C. S. Shim and C. K. Hong, NPG Asia Mater., 2015, 7, e208.
32. V. Malgras, J. Henzie, T. Takei and Y. Yamauchi, Chem. Commun., 2017, 53, 2359–2362.
33. C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr. B, 2008, 64, 702–707.
34. H. A. Maddah, V. Berry and S. K. Behura, Comput. Mater. Sci., 2020, 173, 109415.
35. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Sci., 1972, 28, 3384–3392.
36. C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789.
37. Y. S. Zhao, D. J. Weidner, J. B. Parise and D. E. Cox, Phys. Earth Planet. Inter., 1993, 76, 1–16.
38. N. W. Thomas and A. Beitollahi, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 549–560.
39. M. R. Linaburg, E. T. McClure, J. D. Majher and P. M. Woodward, Chem. Mater., 2017, 29, 3507–3514.
40. S. Hirotsu, J. Phys. Soc. Jpn., 1971, 31, 552–560.
41. S. Hirotsu, J. Harada, M. Iizumi and K. Gesi, J. Phys. Soc. Jpn., 1974, 37, 1393–1398.
42. M. Aebli, L. Piveteau, O. Nazarenko, B. M. Benin, F. Krieg, R. Verel and M. V. Kovalenko, Sci. Rep., 2020, 10, 1–9.
43. L. Piveteau, V. Morad and M. V. Kovalenko, J. Am. Chem. Soc., 2020, 142, 19413–19437.
44. P. Vashishtha, S. A. Veldhuis, S. S. Dintakurti, N. L. Kelly, B. E. Griffith, A. A. Brown, M. S. Ansari, A. Bruno, N. Mathews, Y. Fang, T. J. White, S. G. Mhaisalkar and J. V. Hanna, J. Mater. Chem. C, 2020, 8, 11805–11821.
45. P. Vashishtha, B. E. Griffith, A. A. M. Brown, T. J. N. Hooper, Y. Fang, M. S. Ansari, A. Bruno, S. H. Pu, S. G. Mhaisalkar, T. White and J. V. Hanna, ACS Appl. Electron. Materials, 2020, 2, 4002–4011.
46. P. Vashishtha, B. E. Griffith, Y. Fang, A. Jaiswal, G. V. Nutan, A. P. Bartók, T. J. White and J. V. Hanna, J. Mater. Chem. A, 2022, 10, 3562–3578.
47. K. Yamada, Y. Kuranaga, K. Ueda, S. Goto, T. Okuda and Y. Furukawa, Bull. Chem. Soc. Jpn., 1998, 71, 127–134.
48. W. M. J. Franssen, S. G. D. van Es, R. Dervişoğlu, G. A. de Wijs and A. P. M. Kentgens, J. Phys. Chem. Lett., 2017, 8, 61–66.
49. A. Osherov, Y. Feldman, I. Kaplan-Ashiri, D. Cahen and G. Hodes, Chem. Mater., 2020, 32, 4223–4231.
50. W. Peng, C. Aranda, O. M. Bakr, G. Garcia-Belmonte, J. Bisquert and A. Guerrero, ACS Energy Lett., 2018, 3, 1477–1481.
51. A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378.
52. M. Songvilay, Z. Wang, V. G. Sakai, T. Guidi, M. Bari, Z. G. Ye, G. Xu, K. L. Brown, P. M. Gehring and C. Stock, Phys. Rev. Mater., 2019, 3, 125406.
53. Y. Kawamura and H. Mashiyama, J. Korean Phys. Soc., 1999, 35, S1437–S1440.
54. H. Mashiyama, Y. Kawamura, E. Magome and Y. Kubota, J. Korean Phys. Soc., 2003, 42, S1026–1029.
55. M. Hidaka, Y. Okamoto and Y. Zikumaru, Phys. Status Solidi A, 1983, 79, 263–269.
56. D. Wiedemann, J. Breternitz, D. W. Paley and S. Schorr, J. Phys. Chem. Lett., 2021, 12, 2358–2362.
57. Y. Guo, O. Yaffe, D. W. Paley, A. N. Beecher, T. D. Hull, G. Szpak, J. S. Owen, L. E. Brus and M. A. Pimenta, Phys. Rev. Mater., 2017, 1, 042401.
58. C. A. López, M. C. Álvarez-Galván, M. V. Martínez-Huerta, M. T. Fernández-Díaz and J. A. Alonso, Chem. – Eur. J., 2019, 25, 4496–4500.
59. N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395.
60. R. G. Niemann, L. Gouda, J. G. Hu, S. Tirosh, R. Gottesman, P. J. Cameron and A. Zaban, J. Mater. Chem. A, 2016, 4, 17819–17827.
61. R. Prasanna, A. Gold-Parker, T. Leijtens, B. Conings, A. Babayigit, H.-G. Boyen, M. F. Toney and M. D. McGehee, J. Am. Chem. Soc., 2017, 139, 11117–11124.

---

Footnotes

† The experimental data for this study are provided as a supporting dataset from WRAP, the Warwick Research Archive Portal at https://wrap.warwick.ac.uk/160750/.

‡ Electronic supplementary information (ESI) available: Supporting experimental and materials characterization including HRTEM, ²⁰⁷Pb MAS NMR data, high resolution laboratory source powder XRD data for the Cl series and Br series, DSC data, UV/vis data with Tauc plots, in addition to tables summarising the ¹³³Cs, ²⁰⁷Pb and ¹H T₁ (spin-lattice) relaxation times and the variable temperature evolution of refined lattice parameters for each system. See DOI: https://doi.org/10.1039/d2cp02131e

---