Dissipative particle dynamics simulation study on ATRP-brush modification of variably shaped surfaces and biopolymer adsorption

Abstract

We present a dissipative particle dynamics (DPD) simulation study on the surface modification of initiator embedded microparticles (MPs) of different shapes via atom transfer radical polymerization (ATRP) brush growth. The surface-initiated ATRP-brush growth leads to the formation of a more globular MP shape. We perform the comparative analysis of ATRP-brush growth on three different forms of particle surfaces: cup surface, spherical surface, and flat surface (rectangular/disk-shaped). First, we establish the chemical kinetics of the brush growth: the monomer conversion and the reaction rates. Next, we discuss the structural changes (shape-modification) of brush-modified surfaces by computing the radial distribution function, spatial density distribution, radius of gyration, hydrodynamic radius, and shape factor. The polymer brush-modified particles are well known as the carrier materials for enzyme immobilization. Finally, we study the biopolymer adsorption on ATRP-brush modified particles in a compatible solution. In particular, we explore the effect of ATRP-brush length, biopolymer chain length, and concentration on the adsorption process. Our results illustrate the enhanced biopolymer adsorption with increased brush length, initiator concentration, and biopolymer concentration. Most importantly, when adsorption reaches saturation, the flat surface loads more biopolymers than the other two surfaces. The experimental results verified the same, considering the disk-shaped flat surface particles, cup-shaped particles, and spherical particles.

---

1. Introduction

The structural modification of MPs is gaining immense attention in the biomedical field (mainly in targeted drug/cell delivery, self-assembly, and diagnostics)^1–4 due to its enormous applications. Recent studies show that MP's structure, shape, and size significantly influence the biological performances^5,6 and physiological interactions such as margination, circular half-life, and opsonization.^7–10 Apart from the extensively used spherical MPs, a noticeable rise has also been observed in MPs of various other shapes such as cup, disc, rod, tube, and ellipsoid as an emerging controlled drug delivery system.^5,6,11,12 For example, hemispherical-shaped particles have been shown to exhibit higher cellular uptake compared to spheres because of a higher contact area of the former at the affected sites.^7,13 On the other hand, hemispherical particles showed higher margination ability in the microvasculature compared with spheres.⁷ Among other anisotropic shapes, rod-like particles and flattened/disc-shaped particles also exhibited higher adhesion to the microvascular network than spherical particles because of their high binding affinity. In addition, the binding affinity of rods and discs is high due to their high aspect ratio and flat surface area.^14,15 Therefore, a controlled surface modification of the particles could be crucial to several biomedical applications.^16–20 There are numerous reports demonstrating the importance of surface modification of MPs such as polymeric cup-shaped particles using various techniques such as solvent evaporation,¹³ vapor deposition,²¹ mini-emulsion,^22,23 and microfluidics.²⁴

Among the numerous applications of surface-modified particles, the immobilization of biopolymers (e.g., enzymes) has been getting enormous attention in the last decade due to its use in biocatalysts, food processing, drug delivery, textile manufacturing, biosensors, and so on.^25–27 This inspired researchers to find a better solution to utilize biopolymers more efficiently to expand their applications.^19,28–31 Further, the immobilization of biopolymers on insoluble solid particles has enhanced the rapid arrest and controlled quenching of reaction kinetics. This is because of a comparatively more straightforward extraction of solid surface-bound biopolymers from the solution.^19,28–36 Thus, this immobilization process improves the stability and reusability of biopolymers against the change in pH, solvent, and temperature over successive chemical reactions.^37–39 The immobilization of biopolymers on solid surfaces has significant medical and industrial applications.³⁷ Additionally, surface-modified solid particles with polyelectrolyte ATRP-brush (e.g., poly(DMAEMA)) can immobilize a considerable amount of biopolymers through electrostatic adsorption in their brush morphology due to the high charge density.^39–41 Thus, brush-modified surfaces proved fascinating in immobilizing biopolymers due to their unique structures.^38,39

Ifra and co-workers have recently illustrated differently shaped MP modifications using the electrojetting technique.^17–19 In particular, different MPs are prepared from a blend of polylactide (PLA) and poly[methylmethacrylate-co-2-(2-bromopropionyloxy)ethyl methacrylate] (poly(MMA-co-BEMA)) in 3 : 1 ratio.¹⁷ To fabricate the surface, poly(DMAEMA) brushes are synthesized via the grafting from approach at the initiator (BEMA molecule) embedded surfaces via atom transfer radical polymerization (ATRP)^17–19 with DMAEMA monomers in water (pH ∼ 7). The brush grafting density is regulated by altering the initiator concentration on the surfaces. Different polymerization time periods yield ATRP brushes of different lengths and thus the surface charge at the fabricated surface can be controlled. Thus, the efficiency of electrostatic adsorption of biopolymers (α-glucosidase) onto the surface of a brush-modified particle gets enhanced.^19,38,39

To understand the experimental findings by Ifra and co-workers,¹⁹ we present a DPD simulation study to gain further insights into the underlying physical phenomena at the atomic level. In DPD, the system evolution follows Newton's equation of motion.^42–45 The advantage of using the DPD technique is that it preserves the hydrodynamic behavior of modeled polymeric solutions, melts, and biopolymers in crowded and confined environments, which is crucial to estimating the system's dynamic behavior.^46,47 Hence, it is proved to be a very effective particle (DPD bead) simulation technique.^42,43 DPD is used extensively to model various types of free radical polymerization processes and the effect of shape and size on the dynamics of complex soft materials.^44,45

This contribution presents a generic DPD model focusing on surface fabrication via surface-initiated ATRP-brush growth at differently shaped MP (such as cup, sphere, and rectangular) surfaces and biopolymer adsorption occurring at these modified surfaces. Our simulation demonstrates a comparative study by varying the percentage of initiator concentration and polymerization time to vary the brush density and length and their effect on biopolymer adsorption. Further, we correlate them with the experimental findings.^18,19 The biopolymer is modeled as a linear free-rotating chain of soft beads connected by harmonic bonds.^44,45

We organize this paper as follows. First, in Section 2, we describe the Computational model details and simulation parameters of the system. Then, Section 3.1 discusses the Results obtained for brush growth from the initiators implanted at the three different surfaces via surface-initiated ATRP in the solvent. Further, we discuss the biopolymer adsorption at the brush-modified cup surface (CS), spherical surface (SS), and flat rectangular surface (RS) particles for various biopolymer concentrations in the solution. Next, Section 3.2 presents the Experimental results of CS, SS, and disk surface modification, and biopolymer adsorption. Finally, in Section 4, we conclude the paper with a Summary.

2. Methodology and model parameters

2.1. Dissipative particle dynamics

DPD is a coarse-grained molecular dynamics (MD) approach where a bead symbolizes a molecule or a cluster of particles.^42,43 The beads interact through a soft-core potential, making DPD a more appropriate technique to simulate a system over a more considerable length and time scale than conventional MD simulations. Typically, DPD is utilized to simulate a system up to 100 nm in the linear dimension and tens of microseconds for the time scale.^45,48–50 We briefly outline the key features of the DPD approach below. Moreover, a detailed description can be found in some original and latest publications.^42,49–52

The equation of motion of each bead is governed by integrating Newton's second law:^42,43

where r⃑_i, v⃑_i, m_i, and p⃑_i = m_iv⃑_i denote the position, velocity, mass, and momentum related to the ith bead. The total force acting on the ith bead due to all other j beads within an interaction distance r_c consists of three pairwise additive forces, where F⃑^C_ij, F⃑^D_ij, and F⃑^R_ij represent the conservative, dissipative and random force. The force symmetry F⃑_ij = −F⃑_ji ensures the momentum conservation. The cutoff distance r_c is considered as an intrinsic length scale in the DPD model.^42,43,51 Each bead in the system has equal mass, i.e., m_i = m. The typical conservative force considered in DPD is⁴²

F⃑^C_ij = a_ijω_C(r_ij)r̂_ij, (2)

where ω_C(r_ij) = (1 − r_ij/r_c) is the weight function that belongs to a soft repulsive interaction which enables a more considerable length and time scale in DPD; a_ij denotes the maximum repulsion parameter between i and j beads; r_ij = |r⃑_ij|, r̂_ij = r⃑_ij/|r⃑_ij|, and r⃑_ij = r⃑_i − r⃑_j.

The dissipative force, which represents the effects of viscosity, and the random force, which denotes the impact of thermal fluctuations, are described by^42,43

F⃑^D_ij = −γω_D(r_ij)(r̂_ij·v⃑_ij)r̂_ij, (3)

andHere, γ and σ denote the strength of dissipative and random forces, v⃑_ij = v⃑_i − v⃑_j. Δt is the simulation time step. The noise amplitude ξ_ij in eqn (4) signifies a Gaussian random distribution with zero-mean, 〈ξ_ij(t)〉 = 0, and unit variance:^42,43 〈ξ_ij(t)ξ_kl(t′)〉 = (δ_ikδ_jl + δ_ilδ_jk)δ(t − t′). The symmetry relation ξ_ij = ξ_ji and the forces F⃑^D_ij and F⃑^R_ij act along the line of bead centers, ensuring momentum conservation. For a correct canonical equilibrium state, the dissipative and random forces are coupled with the following relations:^42,43σ² = 2γk_BT and ω_D(r_ij) = ω_R(r_ij)² = (1 − r_ij/r_c)^s for r_ij < r_c, where k_B is the Boltzmann constant and T is the equilibrium temperature of the system. Here, we took the traditional weight function exponent s = 2. However, other choices are also allowed if the above two conditions are fulfilled.^51,53 Overall, the notable advantage of the DPD approach is that the pairwise forces shown in eqn (2)–(4) conserve the momentum locally, thus upholding the correct hydrodynamic⁵⁴ behavior with only a few hundred particles.^42,43

We set the interaction parameter between the compatible beads, a_ij = 25 (in reduced DPD units). This choice is based on the compressibility of water by coarse-graining ten water molecules into one bead.⁴² In general, for any two incompatible beads, we set a_ij = 60.⁴⁵ We provide the other a_ij values in a short while. The parameters r_c, m, and T are set to 1.0 and γ = 4.5 in reduced DPD units. The typical energy scale of the model is set by k_BT.^42,55 We use the modified velocity-verlet algorithm to integrate the equations of motion.^42,56 The simulation time step is set to Δt = 0.02τ, where τ = (mr_c²/k_BT)^1/2 is defined as the characteristic time scale. The total bead number density in the simulation box is set to ρ = 3, which is a reasonable choice for DPD simulation of liquids.^42,43 The above choices of coarse-graining yield the dimensional values of length r_c ≈ 0.97 nm and time τ ≈ 8.3 ps.^57,58

We simulate the polymer chains as a bead-spring model⁵⁸ where the harmonic bond potential E_b = 1/2k_b(r − r₀)² connects neighboring DPD beads of the chain. Here k_b = 128 is the elastic bond strength and r₀ = 0.5 is the equilibrium bond distance.⁵⁹ The angle potential E_a = 1/2k_a(cos θ − cos θ₀)² provides the polymer chain stiffness. We set the potential strength k_a = 5 and the equilibrium angle θ₀ = 180 degrees;^58–60θ denotes the angle between two successive bonds along a polymer chain.

2.2. Modeling the microparticles

In the framework of DPD simulation, we model the differently shaped MPs (CS, SS, and RS) as rigid bodies. Therefore, the forces and torques acting on rigid MPs are computed as the sum of all the forces and torques on constituent DPD beads. The particles are made of PLA blended with poly(MMA-co-BEMA) in a 3 : 1 ratio, as described in the experiments.¹⁹ The poly(BEMA) compound acts as an initiator to instigate the ATRP process with DMAEMA monomers available in the solution to fabricate the surface. The cup (half-sphere) and spherical-shaped MPs are composed of double-layered DPD beads arranged on the vertices of a geodesic grid generated by subdividing an icosahedron.⁶¹ The inner and outer radii are set to R_in = 7.7r_c and R_o = 8.0r_c. The cup-shaped MP contains N_cs = 1962 beads (ϕ_cs = 5.23 × 10⁻³) and the spherical-shaped MP comprises N_ss = 3924 beads (ϕ_ss = 1.04 × 10⁻²). The rectangle-shaped MP surface is also modeled as a double-layered flat structure with N_Rs = 1960 beads (ϕ_rs = 5.23 × 10⁻³) arranged in a regular lattice structure with a lattice constant of 0.5r_c. Each layer contains an equal number of beads. The rectangular MP size is 17.5r_c × 14r_c (in reduced DPD units) with dz = 0.5r_c dimensionless unit in thickness. The number density of beads is kept sufficiently high (ρ_m ∼ 11) in each layer of CS, SS, and RS to prevent the penetration of ATRP-brush and other beads.

The experimental studies^17–19 illustrated that only a fraction of poly(BEMA) molecules on the MP's surface act as initiators in the solution. Our simulation models this experimental observation by considering a certain fraction of MP beads as the initiator beads. Furthermore, we chose the initiator beads randomly at either particle surface for CS and RS, whereas for SS, they are selected only on the outer surface. Note that the flat surface is a disk-shaped particle in the experiment, whereas we model it as a rectangular-shaped particle in the simulation. We considered three initiator values: N_i = 20, 50, and 100, i.e., 1%, 2.5%, and 5% of MP beads, respectively; the corresponding volume fractions are ϕ_i = 5.3 × 10⁻⁵, 1.33 × 10⁻⁴, and 2.66 × 10⁻⁴. Thus, polymer brushes (B) will grow from the surface during polymerization. Since MPs are insoluble in the solvent (s),¹⁹ we set their interaction with the solvent a_ms = 45. To model the fact that the interaction between MP bead (m) and monomer bead (M) is slightly incompatible, we set a_mM = 35, and the interaction of the MP bead with the polymer brush is set as a_mB = 35.

2.3. Surface fabrication of microparticles via ATRP-brush

To simulate ATRP-brush growth, we exploit the recently developed DPD approach⁴⁵ for living controlled radical polymerization (CRP), where a set of relevant elemental reactions model the ATRP processes.^45,62 The DPD polymerization approach is similar to the earlier modeled CRP via coarse-grained MC^63–65 and MD simulations. The DPD model⁴⁵ is validated by the prior experimental^63,64 and modeling studies.^63–65 The previous simulation results^63–65 are obtained using the dynamic lattice liquid (DLL)^63,64 approach (an alternative to MC simulations of living free radical polymerization) and MD approach.⁶⁵ Similar to these simulations,^63–65 the DPD approach^{45,62,66–69} considers the polymer geometry and the spatial distribution of active groups. Specifically, the spatial distribution and long-range diffusion of active radicals in the macromolecules are essentially hindered due to topological constraints and reactions between macromolecules to form even larger molecules or clusters.^63–65 The same framework was further utilized to develop the first simulation approach for modeling iniferter-based photo-CRP within polymer networks.^{45,62,66–69} This examined the relative effects of the photo-initiation systematically due to bond breaking, propagation with monomers and crosslinkers, and termination reactions in forming nanocomposite gels⁴⁴ and self-healing gels,^66,68 and hence, enabled greater insight into the polymerization process.

The elements involved in ATRP are the initiator and monomer; all are modeled as DPD beads. The main reaction steps are the initiation and propagation of monomers in the explicitly considered solvent beads. Herein, we picked the monomer volume fraction, ϕ_M = 1.0 × 10⁻¹ (N_M = 37 500), to grow up the polymer brush. We randomly selected initiator beads to begin the ATRP reactions. In each reaction step, we randomly select monomer beads within the interaction radius r_i = 0.7r_c of each initiator bead.^44,45 The selected bead pair will form a covalent bond with the polymerization probability 0 < P^x_r < 1, where the superscript x stands for the type of chemical reaction; x = i for the initiation and x = pM for the propagation with monomers.^66–68 Next, we draw a random number n_r ∈ (0, 1) from a uniform distribution and compare it with the reaction probability P^x_r. The covalent bond formation reaction step is accepted when n_r < P^x_r, otherwise rejected. Thus, each successful reaction step yields an irreversible covalent bond represented by the harmonic bond potential with k_b = 128, k_a = 5, and θ₀ = 180 (in reduced DPD units).

In our simulation, we set the initiation probability Pⁱ_r = 0.5 and the chain propagation probability P^pM_r = 0.05.^44,66,67 The respective reaction rate constants can be adjusted efficiently by selecting different values of P^x_r. Nevertheless, lower P^x_r values are chosen to ensure kinetically controlled polymerization. The stated value of r_i is chosen to reproduce the expected linear first-order kinetics for living radical polymerization. Any smaller values delay the brush growth, and higher values significantly deviate from the linear first-order kinetics.⁴⁵ We exclude the degenerative chain transfer and the termination reaction of active radicals to dormant species in ATRP due to the characteristics of living polymerization.^70,71 The details of bead types involved in the primary reaction steps are summarized via a schematic shown in Fig. 1. Since the characteristic simulation time step is set to Δt = 0.02τ and the reaction time interval between any two successive reaction steps is selected to be τ_r = 0.2τ,^44,69 the reactions are performed every ten simulation time steps.⁴⁴

Fig. 1 Schematic diagram illustrating the atom transfer radical polymerization (ATRP) process from the initiators embedded at the nanoparticle surface.

The monomer and ATRP-brush beads are considered hydrophilic (compatible) with solvent beads; hence, their interaction parameters are set to a_Ms = a_Bs = 25 (in DPD units). Similarly, for monomer and brush (polymerized monomer) bead interaction, a_MB = 25. The experimental results^17,18 suggest that in a pure solvent (water at pH ≈ 7), poly(DMAEMA) brushes are positively charged due to protonated amino groups present in the brush, and they are well dispersed in the solvent due to the long-range electrostatic repulsion. In other words, the electrostatic repulsion avoids their aggregation in the solvent. Due to brush–biopolymer affinity, we aim to probe the biopolymer adsorption within the brush matrix. However, solving electrostatic interactions explicitly in the DPD framework^72–75 is computationally very expensive for large systems,⁷⁶ even with the recent parallel Poisson solver.^74,76 Therefore, the explicit use of charge distribution in the DPD simulation approach of biological systems is rare.^76–79 Thus, to phenomenologically prevent their aggregation, we set the DPD interaction parameter between brush beads to a_BB = 27.

2.4. Biopolymer adsorption at the fabricated microparticle surface

We modeled the biopolymer (α-glucosidase enzyme) in the same way as the brush chain – a linear chain of N_b DPD beads, connected by harmonic bonds with an elastic constant k_b = 128 and equilibrium bond distance r₀ = 0.5.⁸⁰ The angle potential coefficient between two consecutive bonds along with the biopolymer chain k_a = 5, and θ₀ = 180 is an equilibrium angle between the successive bonds. The mass of each biopolymer bead is set to 1.0 in the reduced DPD unit. We study biopolymer adsorption for three different concentrations: c_b = 2%N (ϕ_b = 2.0 × 10⁻²), 4%N (ϕ_b = 4.0 × 10⁻²), and 8%N (ϕ_b = 8.0 × 10⁻²). The corresponding number of DPD beads are N_b = 7500, 15 000, and 30 000, respectively. To study the effect of biopolymer length (l_b) on the adsorption at fabricated surfaces, we choose l_b = 25, 10, and 1.

The biopolymer (α-glucosidase¹⁹) is chemically compatible with the solvent and negatively charged molecules. Like the brush case, we set the effective DPD interaction parameters between biopolymer beads, a_bb = 27, to prevent their aggregation phenomenologically. The positively charged brush beads will attract the negatively charged biopolymers. Thus, to incorporate this favorable interaction, we set the interaction parameters between these beads, a_Bb = 15. Compared with the short-range effective DPD interactions, we expect that explicit modeling of long-range electrostatic interactions will further promote brush dispersion in the solvent. Therefore, direct electrostatic interactions could make the biopolymer adsorption more prominent, but this study's conclusions will not be altered.

We consider a simulation box of size 50r_c × 50r_c × 50r_c. The total number density in the box is fixed at ρ = 3r_c⁻³ (i.e., N = 375 000 beads).^42–45 The periodic boundary conditions are applied in the x- and y-directions. In contrast, the simulation box in the transverse z-direction is bounded by amorphous solid walls.⁴⁴ The height of both walls is fixed to h = 1, and bead density is set to ρ_w = 3 (volume fraction, ϕ_w = 4.0 × 10⁻²). In addition, we apply bounce-back boundary conditions at the fluid–wall interface⁸¹ to inhibit the penetration of solvent, moieties, and polymer brush beads into the walls.⁸² We consider repulsive interaction (a_wj = 60) between wall beads and other beads in the system. The solvent volume fraction in our simulation box is fixed to ϕ_s ≈ 8.3 × 10⁻¹ (for ϕ_b = 2.0 × 10⁻²), 8.1 × 10⁻¹ (for ϕ_b = 4.0 × 10⁻²), and 7.7 × 10⁻¹ (for ϕ_b = 8.0 × 10⁻²). The interaction parameters for all DPD beads are summarized in Table 1.

Table 1 The interaction parameter a_ij used in the simulation for different DPD beads

a ij	w	s	m	M	B	b
Wall (w)	25	60	60	60	60	60
Solvent (s)		25	45	25	25	25
Microparticle (m)			25	35	35	20
Monomer (M)				25	25	25
Brush (B)					27	15
Biopolymer (b)						27

---

To start the DPD simulation, we place the microparticle in a simulation box and generate the initial configuration of the monomer and solvent by randomly placing them in the box. Then, we equilibrate the system for t = 1 × 10⁵ simulation time steps, and allow the polymerization reactions to begin. First, we let the ATRP brush grow up to three different time steps, t_BG = 400, 800, and 1500, to get the fabricated MP surface with varying brush lengths. Next, we introduce the biopolymers in the solution containing fabricated MPs and observe the biopolymer adsorption up to t_bA = 3000 simulation time steps.

3. Results and discussion

3.1. Simulation study

We utilize the DPD simulation approach to study the biopolymer adsorption at ATRP-brush modified different-shaped MPs such as cup, spherical, and rectangular surfaces. To begin with, first, we study the surface modification of a cup particle where initiators are equally distributed at the inner and outer surfaces. Three initiator percentages c_i = 1%, 2.5%, and 5% of N_cs are considered to differentiate the initiator concentration effect on surface fabrication. We allow the atom transfer radical polymerization (ATRP) reaction to begin with monomers in the solution. To analyze the polymerization kinetics, we plot the monomer conversion (Conv_M = [M]_rt/[M]₀) and the reaction rate, log([M]₀/[M]_ut), as a function of time (t_BG) in Fig. 2, where [M]₀ denotes the initial monomer concentration, and [M]_rt and [M]_ut indicate the reacted and unreacted monomer concentration, respectively, at t_BG. The polymerization is allowed up to t_BG = 1500 for all three initiator concentrations. Fig. 2(a) illustrates that the monomer conversion rate increases with an increase in c_i. We obtained nearly 6% conversion for c_i = 1% (black curve), 13% conversion for c_i = 2.5% (red curve), and 21% conversion for c_i = 5% (green curve) within the given simulation time – the amount of monomer conversion up to t_BG = 1500 suggests an early time conversion. Thus, we observe a linear monomer conversion in ATRP at early times (as in Fig. 2(a)), which converges towards one (Conv_M → 1.0) at late times (shown in Fig. S1(a), ESI†).

Fig. 2 (a) Monomer conversion (Conv_M) as a function of time (t_BG) for different initiator concentrations: c_i = 1.0% (black curve), 2.5% (red curve), and 5.0% (green curve) presented at CS. (b) Temporal change in the monomer conversion rate, log([M]₀/[M]_ut), for the reaction kinetics corresponding to data in (a). (c–e) The ATRP brush modified cup surfaces at different c_i for the monomer conversion up to t_BG = 1500. (f–h) Crosssection (xy-plane) plots at l_z = 25 corresponding to the brush modified CS in (c), (d), and (e), respectively, indicating the brush density variation around CS. The color bar is at the extreme right.

The nearly linear dependence of log([M]₀/[M]_ut) versus time for all c_i values illustrated in Fig. 2(b) for early times and in Fig. S1(b) (ESI†) at late times shows that our model accurately reproduces the pseudo-first-order kinetics, a typical characteristic of living radical polymerization.^44,66,67Fig. 2(c–e) show the snapshots of the fabricated CS for the ATRP-brush growth till t_BG = 1500 at different initiator concentrations. Fig. 2(f–h) display brush density variation around CS in the xy-plane at l_z = 25 corresponding to Fig. 2(c–e). The yellow circle shows the cross section of CS, and the red region displays the ATRP-brush density. These snapshots clarify that the brush density is higher for higher monomer conversion (∼21%) for c_i = 5.0% at CS. The presence of the red region within CS (yellow circle) also confirms the initiators’ presence at the inner surface of CS.

The two most frequently used physical parameters that characterize the size of a macromolecule are the radius of gyration (R_g) and hydrodynamic radius (R_h). Both R_g and R_h use different ways to compute the size of a macromolecule and arrive at a similar conclusion. We calculate the radius of gyration^83,84 as a function of time t_BG for c_i = 1.0%, 2.5%, and 5.0%, as displayed by the black, red, and green curves in Fig. 3(a). Here N denotes the total number of CS and brush beads, and r_i represents the distance of the ith bead from the center of mass of CS and brush beads. The angular brackets signify the averaging over five ensembles. The plots in Fig. 3(a) show that brush fabricated cup particle size increases with time as the degree of polymerization (Conv_M) increases for all c_i. However, Conv_M is more for higher c_i (= 5.0%) at a set duration of polymerization. Hence, the larger values of R_g are observed as a function of time (see the curves in Fig. 3(a)).

Fig. 3 Variation in the radius of gyration (R_g) (a), the hydrodynamic radius (R_h) (b), and the shape factor (ρ_sf = R_g/R_h) (c) against ATRP brush growth time t_BG for CS. The black, red, and green curves illustrate R_g for the initiator concentration, c_i = 1.0%, 2.5%, and 5.0%, respectively, embedded at CS.

Note that in ATRP, one monomer adds up at a time to a growing chain (i.e., the propagation rate is the same for each initiator). Consequently, the growing chains are nearly monodispersed.^64,67,70,71 Therefore, at a given monomer concentration, the individual chain length (degree of polymerization) is longer for a low initiator concentration for any given time during the polymerization. Thus, from the results shown in Fig. 2, the estimated individual brush length is l_B ≃ n_Br₀, where n_B ≃ 115, 100, and 86 are the average number of polymerized beads per brush chain for c_i = 1.0%, 2.5%, and 5.0%, respectively, at t_BG = 1500. The averaging is done over five ensembles. Given the fact that polymer brushes are repulsive with CS (a_mB = 35) and also with themselves (a_BB = 27) due to positively charged DPD beads, the ATRP-brushes are more swollen and thus relatively more extended in the solvent for c_i = 5.0% than for c_i = 1.0%, and hence, higher R_g is observed.

We compute R_h to gain further insight into the brush-modified particle size. R_h imitates the size of a solvated molecule more closely. Therefore, it is a more appropriate biological parameter to determine the size of a molecule in the context of its environment. Thus, R_h of a modified particle is measured by assuming that the brush embedded on its surface moves through the solution and is resisted by the solvent viscosity. The hydrodynamic radius formulation is ,^83–86 where r_ij is the distance between i and j beads of the polymer brush and CS(N); the angular brackets denote the averaging over five ensembles. Like R_g in Fig. 3(a), R_h also increases linearly with time as the brush density increases at CS, having almost the same order of magnitude. The brush swells more with higher initiator concentration, thus explaining a higher R_h for c_i = 5.0%.

The ratio of R_g and R_h, ρ_sf = R_g/R_h (also known as the shape factor), characterizes the shape of a macromolecule. The shape factor for a globular polymer structure is approximately ρ_sf ∼ 0.775.^83,84 However, for any departure from the globular to nonglobular (or elongated) shape, R_g/R_h attains higher values as R_g turns out to be larger than R_h. For a hollow sphere, ρ_sf ∼ 1.0. At early times, the brush growth is minimal; hence, the shape factor for the modified CS at this stage is estimated as ρ_sf ∈ (1.05–1.065) for all c_i values as displayed in Fig. 3(c). However, ATRP-brush modified CS tends toward attaining a relatively more globular shape with time; thus, ρ_sf decreases. At late times, the shape factor is smaller (ρ_sf ≃ 0.985) for c_i = 5.0% than for the other two c_i values (see Fig. 3(c)). Nevertheless, when we allow the brush growth for a much longer time at which Conv_M → 90%, the fabricated MP attains the shape factor ρ_sf ≃ 0.94 (this result is not displayed here due to brevity).

Next, we compute the radial distribution function (RDF), g(r) = ρ_lB/ρ_B, of brush beads at a radial distance, r = (|dx|² + |dy|² + |dz|²)^1/2, from the CS beads. Here, ρ_lB(r) = n_lB(r)/V_sh denotes the local brush density and ρ_B = N_B/V indicates the total brush density. n_lB(r) is the local number of brush beads (displayed in blue and green colors) in a shell of volume V_sh at a distance r from the microparticle bead (displayed in orange color), N_B represents the total brush beads, and V is the total volume of the box. The plots in Fig. 4(a) show the variation in RDF for three different c_i values as denoted by the black, red, and green symbols. As expected, the larger peak width and height shown by the green curve validate that brush beads are more tightly bound around CS at c_i = 5.0% due to higher monomer conversion than at c_i = 1.0% and 2.5%. The plot of number density ρ(z) of brush beads along the transverse (z)-direction is displayed in Fig. 4(b). The curves at different c_i further certify that more brush beads are localized around CS (10 < z < 30) at c_i = 5.0% than at c_i = 1.0% (black curve) and c_i = 2.5% (red curves). Overall, an increase in the initiator concentration yields noticeable brush swelling, which could facilitate the biopolymer diffusion into the brush matrix, thereby enabling immobilization.

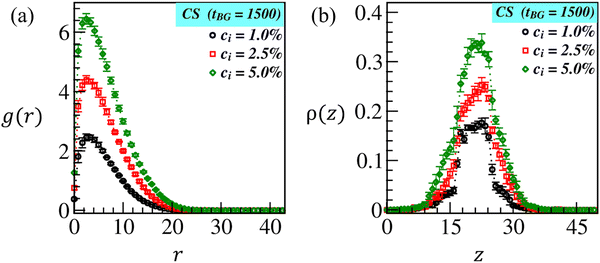Fig. 4 (a) Radial distribution function (RDF): g(r) against radial distance r, and (b) density distribution: ρ(z) along the z-direction of the grown ATRP-brushes at t_BG = 1500 at CS for different initiator concentrations c_i = 1.0% (black symbols), 2.5% (red symbols) and 5.0% (green symbols) corresponding to the snapshots shown in Fig. 2(c–e).

Next, we consider SS and RS to study the surface modification due to ATRP-brush growth and its influence on biopolymer adsorption. However, first, we compare the corresponding physical properties related to the structural change of SS and RS with CS, as discussed above. Then, since the brush-modified CS is highly swollen for the brush growth up to t_BG = 1500 at c_i = 5.0%, we compare the SS and RS fabrication with CS by considering the polymerization up to the same simulation time steps for c_i = 5.0%.

In Fig. 5, we plot Conv_M and log([M]₀/[M]_ut) as a function of time for SS and RS and compare them with the results obtained for CS. The initiators are evenly distributed at both the surfaces of RS and only at the outer surface of SS. The surface fabrication is led by growing the ATRP brushes up to t_BG = 1500. We observe that Conv_M for SS (red curve) is slightly higher than that for RS (green curve) and CS (black curve) at early times (t_BG ⪅ 350). On the other hand, the gap is enhanced over time, as displayed in Fig. 5(a) and (b), due to higher monomer accessibility to active radicals tethered at a larger outer surface of SS compared to the case of CS and RS. The propagation reaction (Conv_M) for RS is also growing at almost the same rate as CS at early times (t_BG ⪅ 1000). However, a slightly higher conversion is obtained for RS beyond this time. For RS, the monomers are equally accessible to initiators at both surfaces. Thus, initiators/active radicals have equal accessibility to monomers. The brush growth at the outer CS can occur at the same rate for the SS; however, the monomers are less accessible to initiators at the inner concave surface of CS. Thus, the effective rate of chain propagation at CS is balanced by yielding less monomer conversion than on RS and SS. Overall, Fig. 5(b) illustrates that the propagation reaction rate (log([M]₀/[M]_ut)) at different surfaces varies linearly with time (t_BG), thus exhibiting the expected first-order reaction kinetics.

Fig. 5 Comparison of temporal variation of Conv_M (a) and log([M]₀/[M]_ut) (b) at the cup surface (CS, black curve), spherical surface (SS, red curve), and rectangular surface (RS, green curve) for c_i = 5.0% embedded on their surfaces.

We illustrate the morphology of fabricated CS, SS, and RS due to ATRP-brush growth up to different polymerization times, t_BG = 400 (Fig. 6(a–c)), 800 (Fig. 6(d–f)), and 1500 (Fig. 6(g–i)) at c_i = 5.0%. The Conv_M at CS, SS, and RS for t_BG = 1500 are ∼23%, ∼26%, and ∼24%, respectively, as illustrated in Fig. 5(a). The corresponding estimated brush length is l_B ≃ n_Br₀, where n_B ≃ 79, 97, and 86 are the number of polymerized beads per brush chain bounded at CS, SS, and RS, respectively. At t_BG = 400, the monomer conversion is almost the same at all surfaces; hence, nearly the same brush length, l_B ≃ 21r₀ for CS and RS, and l_B ≃ 26r₀ for SS, is assessed. However, l_B increases with time and the brush lengths are slightly different from each other at different surfaces due to diverse monomer conversion, as seen in Fig. 5. For the polymerization up to t_BG = 800, the approximate brush lengths are l_B ≃ 41r₀, 53r₀, and 43r₀ at CS, SS, and RS where Conv_M ≃ 11%, 14%, and 12%, respectively. Fig. 6(j–l) show the brush density variation around MP surfaces in the xy-plane at l_z = 25, corresponding to Fig. 6(g–i). The yellow color represents the cross section of various MPs, and the red region displays the ATRP-brush density.

Fig. 6 ATRP brush modified CS, SS, and RS for c_i = 5.0% and for the brush growth (polymerization) time up to t_BG = 400 (a–c), 800 (d–f), and 1500 (g–i). (j–l) The brush density variation in the xy cross-section at l_z = 25 corresponding to the snapshots in (g–i).

The shape and size of ATRP-brush modified differently shaped particles are compared at c_i = 5.0%. First, we plot R_g as a function of t_BG in Fig. 7(a). The differences in R_g values are due to different MP structures; R_g for SS is higher than that for CS and RS. However, the latter two surfaces maintained similar growth in R_g against time with a tiny advancement for RS at late times due to higher Conv_M (shown in Fig. 5). With a considerable Conv_M at SS (as discussed in Fig. 5), the initial surge in R_g is maintained till late times. Similar to R_g, the hydrodynamic radius (R_h) for the modified surfaces varies linearly with time, as presented in Fig. 7(b). In Fig. 7(c), we plot the shape factor (ρ_sf) to characterize and compare the temporal variation in the shape of modified MPs. At early times, when Conv_M is small, ρ_sf is highest for RS and lowest for SS due to their different unmodified shapes. However, ρ_sf for CS and RS approaches a similar value as the polymerization increases with time. However, ρ_sf for SS remains the lowest for the entire polymerization period considered here.

Fig. 7 Comparison of (a) radius of gyration (R_g), (b) hydrodynamic radius (R_h), and (c) size factor (ρ_sf) against the polymerization time t_BG for the brush modified CS (black curve), SS (red curve), and RS (green curve), respectively, at c_i = 5%.

We compare g(r) versus r for the ATRP brushes around CS in Fig. 8(a), SS in Fig. 8(b), and RS in Fig. 8(c) at c_i = 5.0% for three different brush lengths assessed at t_BG = 400, 800, and 1500. The corresponding brush lengths at each surface were estimated and discussed a short while ago. Fig. 8 demonstrates that the peak height increases with brush length, and its position moves to higher r for the modified particles. This suggests an increase in the local brush density (ρ_lB). Thus, the brushes are more closely bound to MP surfaces. The rise in RDF width with r validates the spreading of growing brush chains. The local brush density becomes negligible with r → ∞ and hence g(r) → 0. Following the previous observations as depicted in Fig. 5–7, the variation of g(r) is very similar for both CS and RS; nevertheless, g(r) for RS has a slight edge (in Fig. 8(c)) over CS (in Fig. 8(a)). Fig. 8(b) shows that the peak of g(r) for SS is lower than that for CS and RS. The reason for this could be the lower n_lB per shell because of the hollow core of the spherical MP and higher N_ss (= 2 × N_cs or 2 × N_Rs), which reduces ρ_lB(r). Since SS has a hollow core, and no other beads, including the brush beads, can penetrate it, we also see a sudden jump at r ≈ 2R₀.

Fig. 8 Comparison of RDF (g(r)) of ATRP brushes around (a) CS, (b) SS, and (c) RS at different brush lengths observed at different polymerization times for c_i = 5%.

Recall that the brush grafting density increases with the polymerization, which causes an increase in the surface charges. Thus, the brushes get stretched out and swollen due to the incompatible interaction between the brush beads (a_BB = 27). Furthermore, the negatively charged biopolymers (a_bb = 27) pave the way to enter into the brush region and get adsorbed due to the much favorable interaction (a_Bb = 15) between the swollen brush and biopolymers.

We introduce the equilibrated biopolymer chains of length l_b = 25 in the solution, and analyze the adsorption at different brush-modified surfaces for a period t_bA = 3000. In Fig. 9(a–c), we compare the fraction of biopolymers adsorbed (ϕ_bA) with time on fabricated CS (black curve), SS (red curve), and RS (green curve) in the presence of various fractions of biopolymers, ϕ_b = 2 × 10⁻², 4 × 10⁻², and 8 × 10⁻², respectively. We found that the biopolymers are getting adsorbed within the brush region at nearly the same rate on different brush-modified surfaces for some initial period (t_bA ⪅ 300). However, as time progresses, ϕ_bA for SS is growing faster than that for CS and RS for up to t_bA ⪅ 900. This observation is consistent with all the biopolymer concentrations used in the simulation. Furthermore, it seems pretty evident as the brush length (l_B) and the radius of gyration (R_g) are prominent for SS due to higher monomer conversion than for CS and RS.

Fig. 9 The estimated fraction of adsorbed biopolymers (ϕ_bA) on the brush modified CS (black symbols), SS (red symbols), and RS (green symbols) in the presence of a different fraction of biopolymers, (a) ϕ_b = 2 × 10⁻², (b) ϕ_b = 4 × 10⁻² and (c) ϕ_b = 8 × 10⁻², respectively, in the solution for c_i = 5%. The adsorption process is monitored for a period t_bA = 3000.

To compute ϕ_bA, we count the number of biopolymer beads within R_g of modified MPs and then scale it with the total number of beads (N) in the system. Interestingly, for t_bA > 900, we find a gradual crossover in ϕ_bA curves for RS to its corresponding noticeable higher value (see the green curves in Fig. 9) than for the other two surfaces at all the biopolymer concentrations (ϕ_b). The crossover becomes more prominent with increasing values of ϕ_b as depicted in Fig. 9(b and c). On the other hand, ϕ_bA data for SS (red curve) and CS (black curve) converge to nearly the same lower value (steady-state value) for a given ϕ_b at late times. However, the red curve (ϕ_bA for SS) approaches the steady state faster than the black curve (for CS) at a relatively high ϕ_b. At late times, the reason for a lower ϕ_bA at SS could be a relatively high volume of the swollen brush region due to a more considerable brush length (l_B) caused by higher monomer conversion at SS. The larger volume implies a more porous brush region around SS. The biopolymers more easily diffuse into the brush matrix due to a favorable interaction (a_Bb = 15) between the brush and biopolymer beads. Note that biopolymers are negatively charged molecules. Therefore, some biopolymers can easily diffuse out of the brush region after relatively quick initial adsorption due to the unfavorable interaction (a_bb = 27) between the biopolymer beads. Therefore, the number of trapped biopolymers within fabricated SS is relatively small than in the case of RS.

Let us understand the biopolymer adsorption at different modified surfaces in terms of thermodynamic terminology. At early times, the brush density is low, so the biopolymer adsorption is mainly enthalpy driven due to the favorable brush–biopolymer interaction. The entropic contribution to the Gibbs free energy is minimal (dG = dH − TdS). The biopolymer adsorption follows a similar trend (see Fig. 9) to the monomer conversion up to t_bA ≈ 900 (see Fig. 5(a)). With the increase in monomer conversion, more free space is created for the brush to move around, suggesting a gradual rise in brush entropy, which would apparently be higher for the spherical particle. The entropy gain is usually accompanied by an enthalpic penalty (positive enthalpy change).⁸⁷ The biopolymers that diffuse into the grown brush region also contribute to the enthalpic penalty over time due to slightly unfavorable brush–brush and biopolymer–biopolymer interactions. Thus, the binding affinity reduces over time, and the biopolymer adsorption saturates at late times for all three surfaces. Therefore, a flat surface, even with a relatively low surface area and slightly lower monomer conversion compared to the other two surfaces (see the green curve in Fig. 5), illustrates more enzyme adsorption than the spherical surface due to its lower entropy gain (or higher binding affinity). See the green curve in Fig. 9 which gradually crosses over to a higher saturation value at late times.

To demonstrate the effect of brush length on biopolymer adsorption, we consider the surface-initiated ATRP brushes grown up to t_BG = 400, 800, and 1500 at each surface considered here for c_i = 5% and ϕ_b = 8 × 10⁻². The corresponding brush lengths are l_B ≈ 21, 41, and 79 for CS, l_B ≈ 26, 53, and 97 for SS, and l_B ≈ 21, 43, and 86 for RS (brush lengths are measured in the units of r₀). To analyze the biopolymer adsorption at different brush lengths, we first plot g(r) versus r in Fig. 10 at t_bA = 3000, mainly to show the radial distribution of biopolymers within the brush region. Here, we take the biopolymer chain length l_b = 25. In the ascending order, the black, red, and green curves exhibit g(r) data for different brush lengths. Fig. 10(a) displays a gain in the g(r) curve's peak strength, position, and width with increasing l_B for CS. This implies that a more fraction of biopolymers have uniformly diffused into the brush region for a longer brush length; a similar behavior is observed for SS and RS, as shown in Fig. 10(b and c). A sudden jump in g(r) is observed for SS at r ≈ 2R₀ due to the absence of biopolymer molecules within the hollow SS, as explained earlier in Fig. 8(b). We plot ϕ_bAversus t_bA in Fig. 10(d–f), which displays that biopolymer adsorption increases with l_B as shown by the black, red, and green curves. Similar to the results in Fig. 9, the fraction of biopolymers adsorbed is relatively more for RS as in Fig. 10(f) than for CS and SS as in Fig. 10(d and e). After an initial growth in ϕ_bA, the data saturate to a specific value for each brush length at late times; this behavior remains the same for all the modified surfaces. The adsorption is relatively small for the shorter brushes, and the corresponding data saturate early.

Fig. 10 Comparison of the biopolymer adsorption for different brush lengths grown up to t_BG = 400, 800, and 1500 on CS, SS, and RS, respectively. The corresponding brush lengths are displayed in the legend. For each brush length, the adsorption is considered till t_bA = 3000. (a–c) g(r) versus r for the biopolymers around CS, SS, and RS beads, respectively. (d–f) The temporal variation in the adsorbed fraction of biopolymers (ϕ_bA).

The biopolymer length (l_b) significantly influences the amount of adsorption on brush-modified surfaces, as illustrated in Fig. 11. To characterize this, we consider biopolymers of three different chain lengths l_b = 1, 10, and 25, and monitor their adsorption up to t_bA = 3000 at ϕ_b = 8 × 10⁻². The plots of g(r) versus r, and ϕ_bAversus t_bA are displayed in Fig. 11 with black, red, and green symbols. They exhibit the biopolymer distribution and the fraction adsorbed within the ATRP-brush matrix on CS, SS, and RS. The brushes are allowed to grow on these surfaces till t_BG = 1500 for c_i = 5%. These plots explain that the adsorption is more for the longer biopolymer chains, independent of the modified surface type. Notice the RDF curves in Fig. 11(a–c); the higher peak strength at lower r certifies that biopolymers are more closely packed around the modified surfaces for l_b = 25 and 10 (see the green and red curves). However, the black g(r) curves show that when we coarse-grain the biopolymer with a single bead (l_b = 1), they are loosely bound around the modified surfaces and uniformly distributed in a wide range of r from the surface beads.

Fig. 11 Assessment of biopolymer adsorption of different chain lengths: l_b = 1 (black curve), l_b = 10 (red curve), and l_b = 25 (green curve) on the brush-modified surfaces: CS, SS, and RS. The adsorption is allowed to continue for t_bA = 3000. (a–c) RDF plot (g(r) versus r) and (d–f) the temporal variation of the adsorbed fraction of biopolymers (ϕ_bA).

The curves in Fig. 11(d–f) demonstrate that ϕ_bA saturates to a finite value, i.e., the biopolymer adsorption attains a steady-state value, for all the cases studied here within the adsorption time t_bA = 3000. Similar to the results obtained for l_b = 25 (see Fig. 9 and 10), ϕ_bA is higher at RS (ϕ_bA ≈ 11.6 × 10⁻³) than at CS and SS with ϕ_bA ≈ 10.6 × 10⁻³ for l_b = 10. It is interesting to note that ϕ_bA reaches its steady-state (constant) value sooner with decreasing biomolecule size l_b. The gap in ϕ_bA values at different modified surfaces is also getting insignificant. Therefore, for l_b = 1, ϕ_bA ≈ 6.0 × 10⁻³ for all the modified surfaces (see the black curves in Fig. 11(d–f)). This could be attributed to a quick diffusion of smaller molecules into and out of the brush region as the diffusion coefficient D ∼ N_b⁻¹, where N_b is the number of beads in a biopolymer chain. Since the diffusion of longer biopolymer chains is slow, their saturation takes more time than smaller chains. However, when longer biopolymer chains are diffused into the brush matrix due to strong favorable interactions, they mostly remain trapped due to structural constraints.

3.2. Experimental study

Further, we performed an additional experimental study to verify the simulation results. We focus on biopolymer adsorption at differently shaped brush-modified surfaces such as cups, spheres, and disc surfaces; recall that we have considered the rectangular surface in our simulation instead of the disc-shaped surface. Nevertheless, we presumed that both the flat surfaces (rectangular or disc) would yield the same result within the statistical error. The details of the experimental setup are briefly provided in ESI.† However, we can find a more detailed design and explanation in some recent publications.^17,19

In the experimental study, we synthesize poly(DMAEMA) brush-modified particles of various shapes such as spheres, cups, and discs following our previous publications^17,19 to study the effect of particles’ shape on enzyme immobilization efficiency. To serve the purpose, first, we copolymerize the acrylate monomers, i.e., methyl methacrylate (MMA) and 2-hydroxy ethyl methacrylate (HEMA), and modify the hydroxyl groups of HEMA moieties via reacting with bromopropionyl bromide (poly(MMA-co-BEMA)) as discussed in our previous study.^17,19 The bromo functional moiety of the copolymer is then utilized as an ATRP initiator to grow polymer brushes from the surface of the particles consisting of the copolymer, poly(MMA-co-BEMA). The particles with different shapes are made by electrojetting a blend of polylactide (75%) and poly(MMA-co-BEMA) (25%) under various conditions, as stated in Table S1 (ESI†).^17,19

During the electrojetting process, the polymer droplets are thought to be attracted to the collector at a low solution concentration. The polymer droplet starts bending depending upon the process parameters, resulting in the cup-shaped particle formation. However, in the case of high concentrations (3% w/v and 4.5% w/v), this bending is restricted because of enough viscous forces acting on the droplet. At 3% w/v, the viscosity is not very high, so there is fast solvent evaporation from the polymer droplet's outer shell, leading to polymer skin formation outside the droplet. When solvent from the internal core of this droplet gets evaporated, it leads to the collapsing of the polymer droplet, and disc-shaped particles are formed.^17,19 However, at 4.5% w/v, the concentration gradient from the skin to the core is comparatively high. In this case, relatively more uniform solvent evaporation occurs from the shell to the core of the jetted droplet leading to the formation of spheres. In the next step, surface-initiated ATRP (SIATRP) is carried out for one hour to grow poly(DMAEMA) brushes from the surface of the spherical, cup, and disc-shaped particles.¹⁷ Brightfield images and confocal laser scanning microscope (CLSM) images for brush modified and ‘as jetted’ spheres, cup-shaped particles, and disc-shaped particles are shown in Fig. 12 and 13, respectively.^17,19

Fig. 12 Brightfield images of poly(DMAEMA) brush unmodified (a) spheres (average size – 4.9 μm ± 1.1), (b) cups (average size – 5.9 μm ± 1.6), and (c) discs (average size – 8.4 μm ± 1.0), and poly(DMAEMA) brush modified (d) spheres (average size – 16.2 μm ± 3.2), (e) cup-shaped particles (average size – 9.2 μm ± 1.8) and (f) disc-shaped particles (average size – 18.4 μm ± 2.9).

Fig. 13 Confocal laser scanning microscopic (CLSM) images of poly(DMAEMA) brush modified (a) spheres (average size – 17.1 μm ± 3.6), (b) cup-shaped particles (average size – 8.9 μm ± 1.4) and (c) disc-shaped particles (average size – 19.2 μm ± 3.9).

Later the α-glucosidase enzyme is allowed to adsorb onto the surface of these brush-modified particles of various shapes via electrostatic interactions.¹⁹ It is found that brush-modified disc-shaped particles exhibit the highest enzyme loading capacity (58 900 U g⁻¹ or 589 mg g⁻¹ of particles), as displayed in Fig. 14. This is in excellent agreement with the simulation results (shown in Fig. 9–11). The brush-modified spherical particles demonstrate the lowest enzyme immobilization capacity (41 000 U g⁻¹ or 410 mg g⁻¹ of particles) (black curve). On the other hand, the brush-modified cup-shaped particles adsorbed (red curve) in between spheres and discs (44 100 U g⁻¹ or 441 mg g⁻¹ of particles) (blue curve in Fig. 14).¹⁹ The cup-shaped particles adsorb slightly more enzyme than spheres (within the error bar), as observed by other researchers also.¹³ However, their enzyme adsorption capacity was still less than that of brush-modified disc-shaped particles. This may be due to the difference in the availability of surface area of these particles for polymer brush growth. Cup-shaped particles have the probability of growing polymer brushes from inside and outside surfaces. However, the grafting density of polymer brushes will be less inside the cup due to the less accessibility of the monomer (DMAEMA) inside the cup surface. Hence, polymer chain growth will be restricted to the confined concave surface. In contrast, the disc surface should be equally available, leading to enhanced grafting density and maximum enzyme immobilization efficiency.¹⁹ The excellent qualitative agreement of the experimental and simulation results further justifies our simulation model.

Fig. 14 Immobilized enzyme (mg) per g of particles: (A) spheres, (B) cup-shaped particles and (C) disc-shaped particles.

4. Conclusions

In conclusion, we have utilized the DPD approach to present a generic and robust simulation model for surface fabrication of different-shaped microparticles with surface-initiated ATRP brush grafting. In particular, we have considered the initiator embedded cup, sphere, and flat (rectangular/disc-shaped) surfaces for the modification. We then performed a comparative study of biopolymer adsorption on these brush-modified surfaces to appreciate the critical chemical and physical processes happening at the microscopic level.

Independent of the shape of microparticles, the monomer conversion is enhanced with the increase of initiator concentration for a fixed period of ATRP; thus, for any given surface, we marked an increase in the radius of gyration and hydrodynamic radius under the same conditions. The reaction rate kinetics depicted a linear brush growth, as expected for any typical living radical polymerization process, thus validating the chemical kinetics of our simulation model. We found that polymerization reduced the shape factor for all the fabricated surfaces at a fixed initiator concentration. However, we noted a more significant change for the rectangular surface due to its initial structural constraint that advanced to form a more globular shape with polymerization. As illustrated by the radial distribution function, we found uniform distribution of ATRP brushes near the surface for all the initiator concentrations. Still, they were denser at higher initiator concentrations. The brush density smoothly reduced when moving away from the surface, confirming the brush swelling in the solvent.

Further, we have studied biopolymer adsorption on brush-modified surfaces. We have noticed enhanced biopolymer adsorption with the increase of (i) brush length at a given surface with fixed initiator concentration; (ii) initiator concentration, which triggered the brush-modified surfaces with higher grafting density and hence, a more swelled brush morphology, and (iii) biopolymer concentration. In addition, we observed biopolymer adsorption for an extended period, allowing the amount of adsorbed biopolymers to reach a steady-state (saturation point) value for most cases studied here. Most importantly, when adsorption reached a saturation point at late times, the flat surface (rectangular/disc-shaped) could adsorb (load) more biopolymers than the other two surfaces having nearly the same adsorption. The experimental results verified the same, considering disk-shaped flat surface particles, cups, and spherical particles.

Finally, we have demonstrated a significantly high biopolymer loading for a longer biopolymer chain length for all the surfaces. Nevertheless, the modified flat surface had maximum adsorption when biopolymers were modeled as linear chain molecules. When the small biopolymer molecules were coarse-grained as a single bead, we observed a significantly low and nearly similar loading for all the modified surfaces. Overall, our simulation data appeared to agree with the experimental results. These results could lead to a different way of regulating the shape of complex soft materials crucial to diverse applications in the biomedical field. For example, the shape and surface chemistry are deciding factors in advanced drug delivery and the development of biomedical devices using cell–material interactions.

Author contributions

Conceptualization, A. S., S. Saha, S. S., and Ifra; methodology, S. S. and Ifra; validation, S. S., Ifra, A. S., and S. Saha; formal analysis and investigation, S. S., Ifra, A. S., and S. Saha; resources, A. S. and S. Saha; data curation, S. S. and Ifra; writing – original draft preparation, S. S. and Ifra; writing – review and editing, A. S. and S. Saha; visualization, S. S. and Ifra; supervision, A. S. and S. Saha; funding acquisition, A.S. and S. Saha. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

S. S. thanks IIT (BHU) for financial support. A. S. acknowledges the Science and Engineering Research Board (SERB) (Grant No. ECR/2017/002529), and S. S. acknowledges the Indian Council of Medical Research (ICMR) (Grant No. ICMR/2020-5642) for funding.

References

1. J. W. Yoo, D. J. Irvine, D. E. Discher and S. Mitragotri, Nat. Rev. Drug Discovery, 2011, 10, 521–535.
2. S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96–102.
3. S. Saha, D. Copic, S. Bhaskar, N. Clay, A. Donini, A. J. Hart and J. Lahann, Chemically Controlled Bending of Compositionally Anisotropic Microcylinders, Angew. Chem., Int. Ed., 2012, 51, 660–665.
4. S. Rahmani, S. Saha, H. Durmaz, A. Donini, A. C. Misra, J. Yoon and J. Lahann, Chemically Orthogonal Three-Patch Microparticles, Angew. Chem., Int. Ed., 2014, 53, 2332–2338.
5. I. Mirza and S. Saha, Biocompatible Anisotropic Polymeric Particles: Synthesis, Characterization, and Biomedical Applications, ACS Appl. Bio Mater., 2020, 3, 8241–8270.
6. R. A. Meyer, M. P. Mathew, E. Ben-Akiva, J. C. Sunshine, R. B. Shmueli, Q. Ren, K. J. Yarema and J. J. Green, Anisotropic biodegradable lipid coated particles for spatially dynamic protein presentation, Acta Biomater., 2018, 72, 228–238.
7. P. Decuzzi, B. Godin, T. Tanaka, S. Y. Lee, C. Chiappini, X. Liu and M. Ferrari, Size and shape effects in the biodistribution of intravascularly injected particles, J. Controlled Release, 2010, 141, 320–327.
8. A. B. Jindal, The effect of particle shape on cellular interaction and drug delivery applications of micro- and nanoparticles, Int. J. Pharm., 2017, 532, 450–465.
9. B. R. Smith, P. Kempen, D. Bouley, A. Xu, Z. Liu, N. Melosh, H. Dai, R. Sinclair and S. S. Gambhir, Shape matters: Intravital microscopy reveals surprising geometrical dependence for nanoparticles in tumor models of extravasation, Nano Lett., 2012, 12, 3369–3377.
10. V. P. Chauhan, Z. Popović, O. Chen, J. Cui, D. Fukumura, M. G. Bawendi and R. K. Jain, Fluorescent Nanorods and Nanospheres for Real-Time In Vivo Probing of Nanoparticle Shape-Dependent Tumor Penetration, Angew. Chem., Int. Ed., 2011, 50, 11417–11420.
11. W. Li, T. Suzuki and H. Minami, The interface adsorption behavior in a Pickering emulsion stabilized by cylindrical polystyrene particles, J. Colloid Interface Sci., 2019, 552, 230–235.
12. B. Heidarshenas, H. Wei, Z. A. Moghimi Moghimi, G. Hussain, F. Baniasadi and G. Naghieh, Nanowires in magnetic drug targeting, Mater. Sci. Eng. Int. J., 2019, 3, 3–9.
13. J. Chen, V. Kozlovskaya, A. Goins, J. Campos-Gomez, M. Saeed and E. Kharlampieva, Biocompatible Shaped Particles from Dried Multilayer Polymer Capsules, Biomacromolecules, 2013, 14, 3830–3841.
14. N. Doshi, B. Prabhakarpandian, A. Rea-Ramsey, K. Pant, S. Sundaram and S. Mitragotri, Flow and adhesion of drug carriers in blood vessels depend on their shape: A study using model synthetic microvascular networks, J. Controlled Release, 2010, 146, 196–200.
15. S. Shah, Y. Liu, W. Hu and J. Gao, Modeling particle shape-dependent dynamics in nanomedicine, J. Nanosci. Nanotechnol., 2011, 11, 919–928.
16. M. Alvarez-Paino, M. H. Amer, A. Nasir, V. Cuzzucoli Crucitti, J. Thorpe, L. Burroughs, D. Needham, C. Denning, M. R. Alexander, C. Alexander and F. R. A. J. Rose, Polymer Microparticles with Defined Surface Chemistry and Topography Mediate the Formation of Stem Cell Aggregates and Cardiomyocyte Function, ACS Appl. Mater. Interfaces, 2019, 11, 34560–34574.
17. Ifra and S. Saha, Fabrication of topologically anisotropic microparticles and their surface modification with pH responsive polymer brush, Mater. Sci. Eng., 2019, 104, 109894.
18. Ifra, A. Singh and S. Saha, Shape Shifting of Cup Shaped Particles on Growing poly (2-hydroxy ethyl methacrylate) Brushes by “Grafting From” Approach and Dissipative Particle Dynamics Simulation, ChemistrySelect, 2020, 5, 4685–4694.
19. Ifra, A. Singh and S. Saha, High Adsorption of α-Glucosidase on Polymer Brush-Modified Anisotropic Particles Acquired by Electrospraying – A Combined Experimental and Simulation Study, ACS Appl. Bio Mater., 2021, 4, 7431–7444.
20. S. S. Pradhan and S. Saha, Advances in design and applications of polymer brush modified anisotropic particles, Adv. Colloid Interface Sci., 2022, 300, 102580.
21. H. Kim, H. Terazono, H. Takei and K. Yasuda, Cup-Shaped Superparamagnetic Hemispheres for Size-Selective Cell Filtration, Sci. Rep., 2014, 4, 1–6.
22. Z. Tong and Y. Deng, Synthesis of polystyrene encapsulated nanosaponite composite latex via miniemulsion polymerization, Polymer, 2007, 48, 4337–4343.
23. S. Jairam, Z. Tong, L. Wang and B. Welt, Encapsulation of a Biobased Lignin–Saponite Nanohybrid into Polystyrene Co-Butyl Acrylate (PSBA) Latex via Miniemulsion Polymerization, ACS Sustainable Chem. Eng., 2013, 1, 1630–1637.
24. L. Wang, Y. Liu, J. He, M. J. Hourwitz, Y. Yang, J. T. Fourkas, X. Han, Z. Nie, L. Wang, Y. Liu, J. He, M. J. Hourwitz, Y. Yang, Z. Nie, X. Han and J. T. Fourkas, Continuous Microfluidic Self-Assembly of Hybrid Janus-Like Vesicular Motors: Autonomous Propulsion and Controlled Release, Small, 2015, 11, 3762–3767.
25. S. Li, X. Yang, S. Yang, M. Zhu and X. Wang, Technology Prospecting on Enzymes: Application, Marketing and Engineering, Comput. Struct. Biotechnol. J., 2012, 2, e201209017.
26. S. Raveendran, B. Parameswaran, S. B. Ummalyma, A. Abraham, A. K. Mathew, A. Madhavan, S. Rebello and A. Pandey, Applications of Microbial Enzymes in Food Industry, Food Technol. Biotechnol., 2018, 56, 16–30.
27. S. Bhatia, Introduction to Pharmaceutical Biotechnology, IOP Publishing, 2018, vol. 2.
28. D. Wang and W. Jiang, Preparation of chitosan-based nanoparticles for enzyme immobilization, Int. J. Biol. Macromol., 2019, 126, 1125–1132.
29. D. M. Liu, J. Chen and Y. P. Shi, α-Glucosidase immobilization on chitosan-modified cellulose filter paper: Preparation, property and application, Int. J. Biol. Macromol., 2019, 122, 298–305.
30. Y. K. Cen, Y. X. Liu, Y. P. Xue and Y. G. Zheng, Immobilization of Enzymes in/on Membranes and their Applications, Adv. Synth. Catal., 2019, 361, 5500–5515.
31. A. T. Thodikayil, S. Sharma and S. Saha, Engineering Carbohydrate-Based Particles for Biomedical Applications: Strategies to Construct and Modify, ACS Appl. Bio Mater., 2021, 4, 2907–2940.
32. N. R. Mohamad, N. H. C. Marzuki, N. A. Buang, F. Huyop and R. A. Wahab, An overview of technologies for immobilization of enzymes and surface analysis techniques for immobilized enzymes, Agriculture and Environmental, J. Biotechnol., 2015, 29, 205–220.
33. G. F. D. del Castillo, M. Koenig, M. Müller, K. J. Eichhorn, M. Stamm, P. Uhlmann and A. Dahlin, Enzyme Immobilization in Polyelectrolyte Brushes: High Loading and Enhanced Activity Compared to Monolayers, Langmuir, 2019, 35, 3479–3489.
34. B. Haupt, T. Neumann, A. Wittemann and M. Ballauff, Activity of Enzymes Immobilized in Colloidal Spherical Polyelectrolyte Brushes, Biomacromolecules, 2005, 6, 948–955.
35. J. Zdarta, A. S. Meyer, T. Jesionowski and M. Pinelo, A General Overview of Support Materials for Enzyme Immobilization: Characteristics, Properties, Practical Utility, Catalysts, 2018, 8, 92.
36. B. Krajewska, Application of chitin- and chitosan-based materials for enzyme immobilizations: a review, Enzyme Microb. Technol., 2004, 35, 126–139.
37. R. Li, M. Hoarau, S. Badieyan, E. Neil and G. Marsh, Immobilized enzymes: understanding enzyme – surface interactions at the molecular level, Org. Biomol. Chem., 2017, 15, 9539–9551.
38. C. Marschelke, I. Raguzin, A. Matura, A. Fery and A. Synytska, Controlled and tunable design of polymer interface for immobilization of enzymes: does curvature matter?, Soft Matter, 2017, 13, 1074–1084.
39. C. Marschelke, M. Müller, D. Köpke, A. Matura, M. Sallat and A. Synytska, Hairy Particles with Immobilized Enzymes: Impact of Particle Topology on the Catalytic Activity, ACS Appl. Mater. Interfaces, 2019, 11, 1645–1654.
40. A. Kusumo, L. Bombalski, Q. Lin, K. Matyjaszewski, J. W. Schneider and R. D. Tilton, High Capacity, Charge-Selective Protein Uptake by Polyelectrolyte Brushes, Langmuir, 2007, 23, 4448–4454.
41. P. Jain, J. Dai, S. Grajales, S. Saha, G. L. Baker and M. L. Bruening, Completely aqueous procedure for the growth of polymer brushes on polymeric substrates, Langmuir, 2007, 23, 11360–11365.
42. R. D. Groot and P. B. Warren, Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation, J. Chem. Phys., 1997, 107, 4423–4435.
43. P. Espanol and P. Warren, Statistical-Mechanics of Dissipative Particle Dynamics, Europhys. Lett., 1995, 30, 191–196.
44. A. Singh, O. Kuksenok, J. A. Johnson and A. C. Balazs, Tailoring the structure of polymer networks with iniferter-mediated photo-growth, Polym. Chem., 2016, 7, 2955–2964.
45. X. Yong, O. Kuksenok, K. Matyjaszewski and A. C. Balazs, Harnessing interfacially-active nanorods to regenerate severed polymer gels, Nano Lett., 2013, 13, 6269–6274.
46. A. G. Schlijper, P. J. Hoogerbrugge and C. W. Manke, Computer simulation of dilute polymer solutions with the dissipative particle dynamics method, J. Rheol., 1998, 39, 567.
47. N. A. Spenley, Scaling laws for polymers in dissipative particle dynamics, Europhys. Lett., 2000, 49, 534.
48. M. B. Liu, G. R. Liu, L. W. Zhou and J. Z. Chang, Dissipative Particle Dynamics (DPD): An Overview and Recent Developments, Arch. Comput. Methods Eng., 2014, 22, 529–556.
49. Y. H. Feng, Y. H. Feng, X. P. Zhang, X. P. Zhang, Z. Q. Zhao, Z. Q. Zhao, X. D. Guo and X. D. Guo, Dissipative Particle Dynamics Aided Design of Drug Delivery Systems: A Review, Mol. Pharm., 2020, 17, 1778–1799.
50. J. Wang, Y. Han, Z. Xu, X. Yang, S. Ramakrishna and Y. Liu, Dissipative Particle Dynamics Simulation: A Review on Investigating Mesoscale Properties of Polymer Systems, Macromol. Mater. Eng., 2021, 306, 2000724.
51. P. Espanol and P. B. Warren, J. Chem. Phys., 2017, 146, 150901.
52. M. B. Liu, G. R. Liu, L. W. Zhou and J. Z. Chang, Dissipative Particle Dynamics (DPD): An Overview and Recent Developments, Arch. Comput. Methods Eng., 2015, 22, 529–556.
53. P. Nikunen, M. Karttunen and I. Vattulainen, How would you integrate the equations of motion in dissipative particle dynamics simulations?, Comput. Phys. Commun., 2003, 153, 407–423.
54. R. D. Groot and A. Local, Galilean Invariant Thermostat, J. Chem. Theory Comput., 2006, 2, 568–574.
55. P. J. Hoogerbrugge and J. M. V. A. Koelman, Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics, Europhys. Lett., 1992, 19, 155–160.
56. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular-Dynamics, J. Comput. Phys., 1995, 117, 1–19.
57. V. Symeonidis, G. E. Karniadakis and B. Caswell, Schmidt number effects in dissipative particle dynamics simulation of polymers, The, J. Chem. Phys., 2006, 125, 184902.
58. C. Junghans, M. Praprotnik and K. Kremer, Transport properties controlled by a thermostat: An extended dissipative particle dynamics thermostat, Soft Matter, 2008, 4, 156–161.
59. A. K. Singh, A. Chauhan, S. Puri and A. Singh, Photo-induced bond breaking during phase separation kinetics of block copolymer melts: a dissipative particle dynamics study, Soft Matter, 2021, 17, 1802–1813.
60. H.-P. Hsu and K. Kremer, Static and dynamic properties of large polymer melts in equilibrium, J. Chem. Phys., 2016, 144, 154907.
61. Y. Liu, O. Kuksenok, X. He, M. Aizenberg, J. Aizenberg and A. C. Balazs, Harnessing Cooperative Interactions between Thermoresponsive Aptamers and Gels to Trap and Release Nanoparticles, ACS Appl. Mater. Interfaces, 2016, 8, 30475–30483.
62. X. Yong, O. Kuksenok and A. C. Balazs, Modeling free radical polymerization using dissipative particle dynamics, Polymer, 2015, 72, 217–225.
63. J. Genzer, In silico polymerization: Computer simulation of controlled radical polymerization in bulk and on flat surfaces, Macromolecules, 2006, 39, 7157–7169.
64. H. F. Gao, K. Min and K. Matyjaszewski, Gelation in ATRP Using Structurally Different Branching Reagents: Comparison of Inimer, Divinyl and Trivinyl Cross-Linkers, Macromolecules, 2009, 42, 8039–8043.
65. R. L. C. Akkermans, S. Toxvaerd and W. J. Briels, Molecular dynamics of polymer growth, J. Chem. Phys., 1998, 109, 2929–2940.
66. A. Singh, O. Kuksenok, J. A. Johnson and A. C. Balazs, Photo-regeneration of severed gel with iniferter-mediated photo-growth, Soft Matter, 2017, 13, 1978–1987.
67. S. Biswas, A. Singh, A. Beziau, T. Kowalewski, K. Matyjaszewski and A. C. Balazs, Modeling the formation of layered, amphiphilic gels, Polymer, 2017, 111, 214–221.
68. M. Chen, Y. Gu, A. Singh, M. Zhong, A. M. Jordan, S. Biswas, L. T. J. Korley, A. C. Balazs and J. A. Johnson, Living Additive Manufacturing: Transformation of Parent Gels into Diversely Functionalized Daughter Gels Made Possible by Visible Light Photoredox Catalysis, ACS Cent. Sci., 2017, 3, 124–134.
69. A. Beziau, A. Singh, R. N. L. de Menezes, H. Ding, A. Simakova, O. Kuksenok, A. Balazs, T. Kowalewski and K. Matyjaszewski, Miktoarm star copolymers as interfacial connectors for stackable amphiphilic gels, Polymer, 2016, 101, 406–414.
70. K. Matyjaszewski and J. H. Xia, Atom transfer radical polymerization, Chem. Rev., 2001, 101, 2921–2990.
71. J. S. Wang and K. Matyjaszewski, Controlled Living Radical Polymerization - Atom-Transfer Radical Polymerization in the Presence of Transition-Metal Complexes, J. Am. Chem. Soc., 1995, 117, 5614–5615.
72. K. Procházka, Z. Limpouchová, M. Štěpánek, K. Šindelka and M. Lísal, DPD Modelling of the Self- and Co-Assembly of Polymers and Polyelectrolytes in Aqueous Media: Impact on Polymer Science, Polymers, 2022, 14, 404.
73. M. Lísal, Z. Limpouchová and K. Procházka, The self-assembly of copolymers with one hydrophobic and one polyelectrolyte block in aqueous media: a dissipative particle dynamics study, Phys. Chem. Chem. Phys., 2016, 18, 16127–16136.
74. R. D. Groot, Electrostatic interactions in dissipative particle dynamics—simulation of polyelectrolytes and anionic surfactants, The, J. Chem. Phys., 2003, 118, 11265.
75. M. González-Melchor, E. Mayoral, M. E. Velázquez and J. Alejandre, Electrostatic interactions in dissipative particle dynamics using the Ewald sums, The, J. Chem. Phys., 2006, 125, 224107.
76. S. Chen and X. Yong, Janus Nanoparticles Enable Entropy-Driven Mixing of Bicomponent Hydrogels, Langmuir, 2019, 35, 14840–14848.
77. F. J. M. de Meyer, M. Venturoli and B. Smit, Molecular Simulations of Lipid-Mediated Protein-Protein Interactions, Biophys. J., 2008, 95, 1851–1865.
78. R. D. Groot and K. L. Rabone, Mesoscopic Simulation of Cell Membrane Damage, Morphology Change and Rupture by Nonionic Surfactants, Biophys. J., 2001, 81, 725–736.
79. Y. L. Wang, Z. Y. Lu and A. Laaksonen, Specific binding structures of dendrimers on lipid bilayer membranes, Phys. Chem. Chem. Phys., 2012, 14, 8348–8359.
80. A. Vishnyakov, D. S. Talaga and A. V. Neimark, DPD simulation of protein conformations: From α-helices to β-structures, J. Phys. Chem. Lett., 2012, 3, 3081–3087.
81. A. C. C. Esteves, K. Lyakhova, L. G. J. van der Ven, R. A. T. M. van Benthem and G. de With, Surface Segregation of Low Surface Energy Polymeric Dangling Chains in a Cross-Linked Polymer Network Investigated by a Combined Experimental-Simulation Approach, Macromolecules, 2013, 46, 1993–2002.
82. Y. Liu, G. T. McFarlin, X. Yong, O. Kuksenok and A. C. Balazs, Designing Composite Coatings That Provide a Dual Defense against Fouling, Langmuir, 2015, 31, 7524–7532.
83. B. M. Tande, N. J. Wagner, M. E. Mackay, C. J. Hawker and M. Jeong, Viscosimetric, Hydrodynamic, and Conformational Properties of Dendrimers and Dendrons, Macromolecules, 2001, 34, 8580–8585.
84. M. Baalousha, F. V. D. Kammer, M. Motelica-Heino, H. S. Hilal and P. le Coustumer, Size fractionation and characterization of natural colloids by flow-field flow fractionation coupled to multi-angle laser light scattering, J. Chromatogr. A, 2006, 1104, 272–281.
85. M. Schmidt and W. Burchard, Translational diffusion and hydrodynamic radius of unperturbed flexible chains, Macromolecules, 2002, 14, 210–211.
86. W. Burchard, Solution Properties of Branched Macromolecules, Adv. Polym. Sci., 1999, 143, 113–194.
87. E. Freire, Do enthalpy and entropy distinguish first in class from best in class?, Drug Discovery Today, 2008, 13, 869–874.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01749k

---