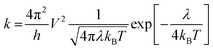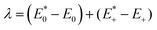Electronic structure and interfacial features of triphenylamine- and phenothiazine-based hole transport materials for methylammonium lead iodide perovskite solar cells

Abstract

Recently, great research efforts have been devoted to perovskite solar cells (PSCs) leading to sunlight-to-power conversion efficiencies above 25%. However, several barriers still hinder the full deployment of these devices. Critical issues are related to PCE stability and device lifetimes, which could be improved by targeted engineering of the hole transport material (HTM). Indeed, the HTM is not only responsible for transporting holes and preventing direct contact between the photo-active perovskite and the charge collector layer, but it plays important structural and protective roles too. As alternatives to the widely used yet expensive and unstable Spiro-OMeTAD, organic HTMs based on triphenylamine (TPA) and phenothiazine (PTZ) moieties have been proposed. However, their performances in PSC devices, and in particular their interfacial properties with the most popular methylammonium lead iodide perovskite (MAPI) still need investigations to be fully determined. In this framework, here we report a first-principles study on the structural and the electronic properties of a recently designed TPA and PTZ-based HTM (HTM1) and its interface with the MAPI (001) surface, considering both the PbI₂- and the MAI-terminations. We also addressed already known HTM molecular systems to allow for a direct comparison with the recently proposed HTM1: we characterized the molecular parameters and the MAPI/HTM interfacial properties for Spiro-OMeTAD, PTZ1, and PTZ2. Our results suggest that good adhesion properties do not ensure effective and efficient MAPI-HTM hole injection. Despite the theoretical good alignment between HTM1 HOMO and MAPI valence band edge, our results for the mutually polarized interface point out the lack of a sufficient driving force for hole transport. While the hole mobility of HTM1 outperforms those of the other HTM molecules, for this HTM molecule, our findings suggest the application of lead halide perovskite compositions other than MAPI, with substituents that lower its valence band maximum potential value.

---

Introduction

The photovoltaic community is devoting unprecedented efforts to perovskite solar cells (PSCs), which have rapidly increased their sunlight-to-power conversion efficiency (PCE) from 3.8% in 2009 to 25.5% in 2021.^1,2 The prototypical organic–inorganic lead halide-based perovskite is CH₃NH₃PbI₃, commonly known as MAPI, which possesses a direct band gap, strong absorption and good ambipolar charge carrier mobility, all factors enhancing the PCE.³ The working principle of a PSC starts from the photoexcitation of the perovskite material, which leads to the formation of electron–hole pairs. The electrons are then injected into the electron transport material (ETM), while the holes are injected into the hole transport material (HTM), which are in contact with the transparent conductive oxide (TCO) and with the metal electrode, respectively, in the normal (n–i–p) device configuration.^4,5 PSC components can also be arranged in an inverted (p–i–n) device configuration, which can guarantee higher intrinsic stability.⁶ The lack of long-term stability is actually the main issue that is hampering large-scale PSC production and it can be mainly ascribed to the degradation of PSC components. In particular, it has been proven that PSC stability largely depends on the HTMs because they are responsible for the charge extraction and transfer at the interfaces while blocking charge recombination, and also act as physical barriers by preventing the contact of the active perovskite layer with the metal electrode and by blocking moisture and oxygen penetration.⁷ For these reasons, the development of more efficient HTMs and the optimization of their interface with the perovskite material are the key steps in the further development of PSC devices.⁸Spiro-OMeTAD (2,2′,7,7′-tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene) is hitherto the most popularly employed HTM in n–i–p devices. Its energy levels are well aligned with the valence band maximum (VBM) and conduction band minimum (CBM) of the MAPI perovskite (−5.4 eV and −3.9 eV, respectively) and the methoxybenzene of arylamines moieties acts as good binding sites to the perovskite surface.⁹ Still, Spiro-OMeTAD presents a series of fundamental flaws. It has intrinsic low hole mobility and low conductivity, and the addition of dopants (e.g. lithium bis(trifluoromethane)sulfonimide (Li-TFSI) and 4-tert-butylpyridine (tBP)) to improve such parameters not only is detrimental for the stability, reproducibility and device performances but also promotes undesired recombination phenomena.^3,10,11 None of the deposition methods of Spiro-OMeTAD on the perovskite layer proposed so far has delivered a completely optimal interfacial contact. Moreover, Spiro-OMeTAD does not represent an efficient barrier for the ionic migration from dopants, electrodes, and other PSC components.^12,13

To overcome the drawbacks of Spiro-OMeTAD, a wide library of novel doped or dopant-free organic HTMs has been proposed and developed.^13,14 In particular, HTMs based on triphenylamines (TPA) and phenothiazine (PTZ) moieties (Scheme S1, ESI†) have attracted great research interest. The TPA moieties feature a non-planar geometry that confers unique hole transport properties, while the PTZ unit has an electron-donating butterfly structure, suitable for several kinds of functionalization, which allows the formation of stable radical cations.^14–26 HTMs designed from a combination of TPA and PTZ moieties, e.g.PTZ2 reported by Grisorio et al.,²⁶ have shown efficiencies comparable to those obtained with Spiro-OMeTAD. With this aim, we recently designed in silico four novel TPA and PTZ-based HTMs, HTM1-4, and investigated their electronic properties by means of density functional theory (DFT) and time dependent density functional theory (TDDFT) methods; the results obtained for these novel HTMs were comparable to those obtained for Spiro-OMeTAD and PTZ2.²⁷ Among them, HTM1 showed the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) positions at −4.88 eV and −1.35 eV, respectively, hence higher in energy than the VBM and CBM of MAPI, respectively. Moreover, the wavefunction plot analysis revealed the HOMO of neutral HTM1, as well as the singly occupied molecular orbital (SOMO) of (HTM1)˙⁺, are fully delocalized over the molecule, while the LUMO is confined on its central core. Such correct energy levels alignment and the slight HOMO LUMO overlap suggest that HTM1 could possess good intermolecular hole-transport ability.²⁵ Moreover, the calculated absorption maximum of neutral HTM1 was found to be 337 nm (3.68 eV), which minimizes competition with the perovskite absorption in the visible range, and it has shown good chemical hardness, higher than that of Spiro-OMeTAD.²⁷ Further synthesis and spectroscopic characterization ratified HTM1 (also named BPT-1) as a valid HTM in PSCs.²⁸

Although the design process of highly efficient PSCs largely benefits from physicochemical studies on isolated HTMs, it is also crucial to investigate their physicochemical interactions with the perovskite, as they strongly influence the ultimate performance of the devices.¹³ Nevertheless, due to the large size of state-of-the-art HTMs, perovskite/organic HTM interfaces have been rarely studied from the computational point of view, and, thus, HTM adsorption features and interface electronic properties at the microscopic level are yet to be fully understood. To the best of our knowledge, the few computational studies available have explored the interfacial behavior of Spiro-OMeTAD on different MAPI surfaces.^29–32 The early work by Torres et al.³⁰ investigated the binding modes of methoxybenzene, i.e.Spiro-OMeTAD anchoring groups, on the MAPI (001) surface to clarify the HTM/perovskite attachment mechanism. They found that interaction mainly occurs when methoxy groups occupy MA⁺ sites, while a repulsive behavior is observed with the surface iodine atoms.³⁰ Saliba et al.,²⁹ instead, theoretically investigated the whole Spiro-OMeTAD/MAPI interface. They focused on the interaction between the perovskite and the molecule and confirmed that it does not involve the core of the molecule but only the protruding methoxy groups.²⁹ The entire Spiro-OMeTAD/MAPI system has also been studied by Yin and co-workers.³¹ This work points out the importance of the perovskite exposed facet in promoting the hole transfer. The most recent work devoted to a full Spiro-OMeTAD/MAPI interface by Wang et al.,³² explores the role of interface termination, namely PbI₂ and MAI, in determining both the strength of the interaction with the MAPI (110) surface and the ability to ensure the charge transfer across the interface.³² Besides the ones with Spiro-OMeTAD, other interfaces of the MAPI with TPA-based molecules have been theoretically investigated, both in terms of the interaction and driving force for the hole injection.^33–36 Motivated by the inspiring preliminary results obtained for isolated HTM1,²⁷ in this work we aim to assess the potential of the TPA and PTZ-based HTM1 molecule as HTM in PSCs involving MAPI as an absorber by first-principles DFT-calculations. We first evaluate key electronic properties of isolated HTM1 (Scheme 1(a)) related to the hole mobility and band alignment with the perovskite, such as the reorganization energies and redox potentials. In order to assess perovskite/HTM mutual polarization effects, we then investigate MAPI/HTM1 interfaces, with HTM1 in contact with either the PbI₂- or MAI-terminated MAPI (001) surface. Binding energies are rationalized in terms of structural modifications and bond formation, which are the main features leading to new channels for charge transport. We also assess how the mutual perovskite-HTM1 polarization affects the HOMO-VBM alignment, providing results that contradict the results of isolated molecules, but allow us to understand available experimental outcomes, with direct implications on the final device performances. To allow a direct comparison with state-of-the-art and well-known TPA and PTZ-based HTMs, we extend our interfacial study to Spiro-OMeTAD (Scheme 1(b)), PTZ1 (Scheme 1(c)) and PTZ2 (Scheme 1(d)).²⁶

Scheme 1 Molecular structure drawings of molecules investigated in this work: (a) HTM1 (b) Spiro-OMeTAD (c) PTZ1 and (d) PTZ2.

Results and discussion

HTM molecular properties

The hole transport behaviour of HTMs is strongly influenced by the reorganization energy λ, i.e. the energy required to reorganize nuclei positions on a given oxidation state. The smaller the λ, the faster could be the hole transport,^37–39 indeed, the charge hopping rate (k) in our case can be defined by Marcus theory⁴⁰ as follows:
where h is the Planck's constant, V is the electronic coupling between adjacent molecules in the structure, λ is the reorganization energy, k_B is the Boltzmann constant and T is the temperature. The reported hopping rate is a special case of the more general Marcus formula that stands for the self-exchange reaction involving an electron exchange between two adjacent HTM molecules in which the free Gibbs energy change of the reaction is null. λ can be divided into inner-sphere reorganization energy (λ_in) and external reorganization energy (λ_ext). Considering that the latter accounts for the effect of the polarized medium on the charge transfer and that in organic solids is usually small, it is often neglected.^37,38 For this reason, only the contribution from the internal reorganization energy is considered here (λ ≅ λ_in). Once the structures of the two electronic states involved in the hole transport event are known, λ can be obtained by the adiabatic potential energy surface method as follows:^37,38
where represents the total energy of the neutral molecule at the cation geometry, E₀ is the total energy of the neutral molecule, represents the total energy of the cation at the neutral molecule geometry and E₊ is the total energy of the cation. We must note that a full characterization of charge-transfer kinetic parameters (k, V) is beyond the purpose of this study, and it can be the object of future works. However, the comparison among the reorganization energies, which are intrinsic molecular properties, can provide insights into the different charge-transfer properties of these HTM molecules, as it has been already very helpful in rationalizing the behavior of different components in solar cells.^41–44 Inner-sphere reorganization energies of compounds HTM1, Spiro-OMeTAD, PTZ1 and PTZ2 computed in this way in vacuum are listed in Table 1.

Table 1 Inner-sphere reorganization energies (λ) and oxidation potentials (G_ox) of HTM1, Spiro-OMeTAD, PTZ1 and PTZ2. All quantities are calculated in vacuum at both PBE/6-31G(d,p) and B3LYP/6-31G(d,p) levels of theory

MOLECULE	METHODS	λ (eV)	G ox (eV)
HTM1	PBE/6-31G(d,p)	0.064	−4.48
	B3LYP/6-31G(d,p)	0.092	−4.99
Spiro-OMeTAD	PBE/6-31G(d,p)	0.087	−4.61
	B3LYP/6-31G(d,p)	0.132	−5.00
PTZ1	PBE/6-31G(d,p)	0.233	−4.66
	B3LYP/6-31G(d,p)	0.381	−4.95
PTZ2	PBE/6-31G(d,p)	0.139	−4.71
	B3LYP/6-31G(d,p)	0.217	−5.10

---

The reorganization energy values present the trend HTM1 < Spiro-OMeTAD < PTZ2 < PTZ1, at both levels of theory, with the λ of Spiro-OMeTAD in accordance with the B3LYP results of Chi et al. in dichloromethane (0.131 eV).⁴⁵ This outcome reports that the TPA and PTZ-based dimeric HTM1 has a lower reorganization energy than those of the monomeric PTZ1 and PTZ2. Additionally, it also has lower reorganization energy than that of Spiro-OMeTAD, hence we predicted good hole mobility and potentially minor need for further additive upon device assembly. The higher reorganization energies of Spiro-OMeTAD, PTZ2 and PTZ1 could be among the reasons behind the need for p-type doping, as reported in the literature.^26,46

The low reorganization energy for HTM1 can be associated with a slightly more rigid structure than those of the other molecules. Indeed, moving from its neutral to its oxidized form, we observed only a little average decrease of ∼0.01 Å along main bond lengths (C–C) and ∼3.1° in main dihedral angles (C–C–C–C) among the PTZ and the TPA moieties. Similarly, upon oxidation, the average bond lengths (C–N) and dihedral angles (C–C–N–C) among the 9,9′-spirobifluorene core and the arylamine moieties in Spiro-OMeTAD decreased by ∼0.01 Å and ∼4.6°, respectively. On the other hand, the decrease in the main bond lengths and dihedral angles among the PTZ and the TPA moieties is ∼0.2 Å (C–C) and ∼7° (C–C–C–C) moving from neutral to oxidized PTZ2 and of ∼0.2 Å (C–N) and ∼12.7° (C–C–N–C) moving from neutral to oxidized PTZ1. Hence, by a difference of ca. 3.9°, in PTZ2 the torsional freedom of the C–C–C–C dihedral angles among the PTZ and the TPA moieties is higher than that observed for HTM1, while the C–C–N–C dihedral angles of PTZ1 have a torsional freedom higher than that of PTZ2 of ca 5.7°. These increased values correspond to higher reorganization energy values with respect to those of HTM1.

Oxidation potentials (G_ox) have been calculated as the difference between the free energies of the neutral and the oxidized states of each molecule (G⁰ and G⁺, respectively), i.e. G_ox = G⁰ − G⁺, and are listed in Table 1. The computed G_ox values follow the expected trend for both DFT functionals. Indeed, a recent article by Wang et al.⁴⁷ reports oxidation potentials of 50 compounds, theoretically determined employing different exchange correlation functionals and compared with experimental values: pure functionals as PBE underestimate G_ox, while the presence of Hartree–Fock-like exchange in hybrid functionals increases the G_ox values.⁴⁷ In particular, the calculated G_ox for Spiro-OMeTAD with B3LYP/6-31G(d,p) in this work (−5.00 eV) is in good agreement with the one reported by Wang et al. at B3LYP/6-31G* (−4.98 eV) and with Spiro-OMeTAD experimental oxidation potential in CH₂Cl₂ (-5.09 eV).³² Calculated G_ox of PTZ1 (-4.95 eV) and PTZ2 (-5.10 eV) are in fair agreement with the experimental oxidation potentials obtained at −4.77 eV and −5.15 eV by Grisorio et al.,²⁶ respectively. All lying in a narrow range, the G_ox of HTM1 calculated and reported here for the first time is very similar to those of the other three analysed HTMs and it is higher in energy than the experimental value of the MAPI VBM potential (∼−5.4 eV).^9,38

HTMs/MAPI interfaces: structures and energetics

MAPI features temperature-dependent structural phases: cubic, stable at high temperatures (T > 330 K), tetragonal at 160 < T < 330 K and orthorhombic at low temperatures (T < 160 K).⁴⁸ By single-crystal X-ray diffraction analysis, the cubic structure (belonging to the Pm3m group) has been reported to be the most stable under operating conditions,⁴⁹ hence it has been adopted here to model MAPI interactions with HTM1, Spiro-OMeTAD, PTZ1, and PTZ2. The theoretically determined lattice constant for the MAPI bulk unit cell (Fig. S1(a), ESI†) at the PBE level, a = 6.256 Å, results in very good agreement with the experimental one (a = 6.276 Å).⁴⁹ From this bulk, two symmetric (non-stochiometric) five-layer slabs of the MAPI (001) surface have been constructed in order to simulate the two possible MAPI terminations, i.e., PbI₂- and MAI-exposing facets, here identified as MAPI:PbI₂ (Fig. S1(b), ESI†) and MAPI:MAI (Fig. S1(c), ESI†). Among all surfaces, the (001) termination has been chosen since it has been reported as one of the most stable surfaces of the MAPI cubic and tetragonal phases.^30,35 The slabs composed of 5 crystal planes perpendicular to the c axis (plus a vacuum slab of 12 Å) are a good compromise between accuracy and computational costs from a surface energy convergence test made on 5, 7 and 9 crystal planes slabs (see the Slab convergence tests section in the ESI†).

A slab supercell with different periodicity within the xy plane has been considered for each termination and each HTM, according to their size, i.e. 7 × 7 for HTM1, 4 × 4 for Spiro-OMeTAD and PTZ1 and 6 × 6 for PTZ2. In order to account for the molecule's complex structure and to obtain reliable energy minima for each termination, different adsorption modes of HTM1 have been considered. HTM1 has been placed on the MAPI surface either exposing the PTZ or the TPA moieties, which have been labeled as down and up orientations, respectively (Fig. S2, ESI†). The same strategy and labeling have been adopted also for PTZ1 and PTZ2 (Fig. S3 and S4, respectively, ESI†). In the case of Spiro-OMeTAD, it has been previously reported that it interacts with the MAPI surface exposing the methoxybenzene of the arylamine moieties,^29–32 thus the up and down orientations refer to the methoxybenzene of the two different facets of the 9,9′-spirobifluorene core. The minimum-energy interfaces from preliminary rigid scans have been allowed to relax without symmetry constraints. After relaxation, HTMs/MAPI:PbI₂ and HTMs/MAPI:MAI interface binding energies have been computed as follows:

E_bind = E_interface − E_MAPI − E_molecule

where E_interface is the energy of the HTMs/MAPI system, E_MAPI is the energy of the isolated MAPI slabs and E_molecule is the energy of the isolated HTMs. All the minimum-energy interfaces and their relative binding energies are shown in Fig. S2–S5 (ESI†), while the most stable interfaces of the considered HTMs/MAPI:PbI₂ and HTMs/MAPI:MAI systems are shown in Fig. 1 and 2, respectively, together with their binding energies. In particular, the most stable configurations of HTM1/MAPI, PTZ1/MAPI and Spiro-OMeTAD/MAPI have binding energies in the −1.49/−2.83 eV range for MAPI:PbI₂ and −2.14/−5.01 eV range for MAPI:MAI. On the other hand, the preferred PTZ2/MAPI interfaces are the most stable with a binding energy of −7.30 eV in the case of MAPI:PbI₂ and −6.08 eV for MAPI:MAI.

Fig. 1 Most stable interfaces and corresponding binding energies (E_bind) of (a): HTM1/MAPI:PbI₂, (b) PTZ2/MAPI:PbI₂, (c) PTZ1/MAPI:PbI₂, and (d) Spiro-OMeTAD/MAPI:PbI₂ systems. Color code: Pb-dark gray; I-violet; C-light grey; N-blue; H-white; O-red; S-yellow.

Fig. 2 Most stable interfaces and corresponding binding energies (E_bind) of (a): HTM1/MAPI:MAI, (b) PTZ2/MAPI:MAI, (c) PTZ1/MAPI:MAI, and (d) Spiro-OMeTAD/MAPI:MAI. Color code: Pb-dark gray; I-violet; C-light grey; N-blue; H-white; O-red; S-yellow.

HTM1 preferably adopts the up orientation on both PbI₂ and MAI terminations, which causes some distortions in the overall surfaces (Fig. 1(a) and 2(a)) due to the interaction of methoxybenzene of the TPA moieties with the MAPI. In particular, HTM1/MAPI:MAI interaction is stronger than that calculated for HTM1/MAPI:PbI₂, due to the formation of some hydrogen bonds between the oxygen atoms of HTM1 methoxybenzene groups and the hydrogen atoms of MAPI methylammonium cations. Differently, when HTM1 adopts the down orientation on both MAPI:PbI₂ and MAPI:MAI, the resultant interaction with the MAPI (001) surface is just a localized event, which is initiated by the sulfur atoms of the PTZ moieties (Fig. S2, ESI†).

Despite the molecular similarities between HTM1 and PTZ2, the latter gets stabilized by adopting the down orientation on both MAPI (001) terminations (Fig. 1(b) and 2(b)). In these cases, PTZ2 interacts with MAPI by exposing the sulfur atom of the PTZ moiety and additional interactions occur through the methoxybenzene of the TPA moieties and from the methoxybenzene directly linked to the PTZ nitrogen. These additional interactions are unlikely to occur in HTM1, since the benzene ring linking the two PTZ moieties has limited rotational freedom and the molecule is overall more rigid, which limits the interactions between the TPA moieties and the MAPI in the down orientation (Fig. S6, ESI†). Regarding PTZ1/MAPI, the up orientations are preferred, where the HTM exposes the metoxybenzene of arylamine moieties. More convenient binding energies for PTZ1/MAPI:MAI than for PTZ1/MAPI:PbI₂ can be attributed to the formation of hydrogen bonds between the oxygen of methoxybenzene and the hydrogens of methylammonium cations (Fig. 1(c) and 2(c)), as it also occurs for HTM1/MAPI:MAI (up). Indeed, differently from PTZ2, when PTZ1 adopts the down orientation, the sulfur atom of the PTZ moiety is less involved in the interaction with MAPI, because of a more pronounced torsion of the methoxybenzene directly linked to the PTZ nitrogen, which has an almost parallel position during the interaction in PTZ2 instead (Fig. S7, ESI†). As for Spiro-OMeTAD, our calculations are in close agreement with previous results^29–32 reporting the down orientation as the preferred one on MAPI surfaces (Fig. 1(d) and 2(d)). Spiro-OMeTAD, indeed, interacts with the MAPI through the methoxybenzene of arylamine moieties. In particular, when Spiro-OMeTAD adopts the down orientation, methoxybenzene has a preferential arrangement with respect to the MAPI surface, which allows a closer interaction between the molecule and the surface, thus contributing to stabilizing the binding energy values. Hence, in the case of Spiro-OMeTAD/MAPI:PbI₂ the oxygens of methoxybenzene interact with the Pb atoms of the MAPI (Fig. 1(d)), while in the case of Spiro-OMeTAD/MAPI:MAI the oxygens of methoxybenzene interact with the hydrogens of methylammonium cations (Fig. 2(d)). While in the first case the interaction is stronger than those of HTM1/MAPI:PbI₂ and PTZ1/MAPI:PbI₂, Spiro-OMeTAD/MAPI:MAI has lower binding energy with respect to HTM1/MAPI:MAI and PTZ1/MAPI:MAI, which are more stabilized thanks to the formation of hydrogen bonds between the molecules and the MAPI surface. Indeed, while in HTM1/MAPI:MAI and PTZ1/MAPI:MAI the distances among the oxygen atoms of the methoxybenzene and some hydrogen atoms of the methylammonium cations recall the typical distances of an intermolecular hydrogen bond (e.g. dO₇–H₈₂₈ = 1.74 Å in HTM1/MAPI, dO₁–H₂₇₅ = 1.73Å in PTZ1/MAPI), major distances are found in Spiro-OMeTAD/MAPI (e.g. dO₂–H₁₄₃ = 2.17 Å).

HTMs/MAPI interfaces: electronic features

The electronic properties of the investigated HTMs/MAPI systems have also been analyzed in terms of their projected density of states (pDOS). The pDOS plots of the most stable interfaces of HTMs/MAPI:PbI₂ and HTMs/MAPI:MAI systems are depicted in Fig. 3 and 4, respectively. Close-up views near the Fermi level are reported in Fig. S8 and S9 (ESI†).

Fig. 3 pDOS plots of (a) HTM1/MAPI:PbI₂ (up), (b) PTZ2/MAPI:PbI₂ (down), (c) PTZ1/MAPI:PbI₂ (up) and (d) Spiro-OMeTAD/MAPI:PbI₂ (down), computed at GGA-PBE, including D3BJ dispersion forces.

Fig. 4 pDOS plots of (a) HTM1/MAPI:MAI (up), (b) PTZ2/MAPI:MAI (down), (c) PTZ1/MAPI:MAI (up) and (d) Spiro-OMeTAD/MAPI:MAI (down) computed at GGA-PBE, including D3BJ dispersion forces.

Regarding PbI₂-terminated surfaces (Fig. 3), the pDOS reveal that the VBM of MAPI slightly lies at a higher energy than the HOMO level of HTM1 and PTZ2 (Fig. 3(a and b)). Thus for the standard MAPI perovskite, there is no adequate driving force for the hole-injection process and undesired charge-recombination events can occur. Differently, in the cases of Spiro-OMeTAD and PTZ1, the pDOS highlight a slight but convenient driving force for the hole injection at the MAPI:PbI₂ interfaces (see also the zoom-in of the pDOS in Fig. S8 in the ESI†). Indeed, the HOMO levels of Spiro-OMeTAD and PTZ1 are slightly higher in energy than the MAPI VB edge, thus granting a convenient extraction of the hole from the photo-excited MAPI.

As for HTMs/MAPI:MAI interfaces (Fig. 4), the VBM of MAPI is higher in energy than the HOMO levels of all HTMs considered. Thus, these interfaces, although energetically very stable, do not provide a sufficient driving force for the holes to be injected into the HTMs.

Considering these results, the prototypical MAPI perovskite has resulted in an inefficient charge transport process when combined with TPA and PTZ-based molecules. For this reason, if it is to be adopted for the construction of PSC devices, the chemical doping of HTM1 could be considered as a valid approach to increase its HOMO energy level. Still, since isolated HTM1 possesses optimal properties to be used as a dopant-free HTM and it is well known that the doping could lead to perovskite degradation,^{3,4,9,13–15} an alternative and valid strategy could consist in the exploration of different kinds of perovskite compositions to understand the potential of this molecule in PSC devices. As a matter of fact, the properties of dopant-free HTM1 (also named BPT-1) have been recently investigated in a methylammonium-free p–i–n PSC, adopting Cs_0.17FA_0.83Pb(I_0.9Br_0.1)₃ as the perovskite and achieving 17.26% PCE, while that obtained employing the standard PTAA in the same experimental conditions is found to be 17.96%.²⁸ This result further corroborates the suitability of HTM1 as HTM, as well as the influence of the perovskite formulation on the hole transport process. Additionally, the promising performances of PSC devices built with PTZ2 as HTM have been reported together with the use of dopants but most of all considering the employment of the mixed halide (bromine and iodine) and cations (methylammonium, formamidinium and cesium) perovskite.²⁶ Hence, this is an additional proof that the interaction between the HTMs and the perovskite is not the only parameter influencing the charge transport process. Indeed, a good binding motif does not always provide sufficient driving force for the hole injection/extraction, but also the perovskite composition plays a fundamental role in determining an effective charge transport process.

Conclusions

In this work, DFT methods have been employed to study the electronic properties of a novel triphenylamine and phenothiazine-based molecule, HTM1, in its isolated form and when it interacts with the MAPI (001), considering the two possible MAPI terminations, PbI₂ and MAI. The results have been compared with those obtained for well-known hole transport materials already present in the literature, such as Spiro-OMeTAD, PTZ1, and PTZ2, to investigate the potential applicability of HTM1 in MAPI-based perovskite solar cells, and to provide new insights into the hole transport behavior at the interface between MAPI and TPA and PTZ-based molecules.

The calculations revealed that HTM1 has the lowest reorganization energy, hence it could possess good hole mobility, while its G_ox is well aligned with those of Spiro-OMeTAD, PTZ1, and PTZ2, which would allow its application as HTM in common PSCs. The investigation of the structural and electronic properties of HTM1/MAPI has shown that HTM1 has a good interaction with both MAPI:PbI₂ and MAPI:MAI, when it exposes the methoxybenzene of TPA moieties. In particular, the interaction with MAPI:MAI results in a more stabilized binding energy, due to the formation of hydrogen bonds between the oxygen atoms of methoxybenzene and the hydrogen atoms of methylammonium cations. Nevertheless, from the pDOS plots it has been found that the HOMO level of HTM1 has lower energy than the VBM of MAPI, thus we found that sufficient driving force is not available for the hole injection process to occur. An inadequate driving force for the hole injection/extraction has also been found for PTZ2/MAPI, even if the latter presents the most stabilized binding energies thanks to the presence of additional interactions. In the end, Spiro-OMeTAD and PTZ1 have shown a convenient but low driving force for the hole extraction from the MAPI:PbI₂ configuration. Hence, from this study, it emerged that the intrinsic HTM properties and the binding motif are not the only parameters influencing the charge transport process, while the perovskite composition can also strongly affect it. Besides MAPI perovskite is often taken as a reference for the investigation of electronic properties at the interface with HTMs, it has resulted to be inadequate for TPA and PTZ-based molecules. This finding supports the limited employment of MAPI for the real fabrication of devices. For this reason and to shed further light on interfacial processes, additional computational studies involving a different kind of perovskite composition should be performed. Moreover, more TPA and PTZ-based HTM conformations on MAPI surface could be explored to further analyze the dynamics of the charge transport processes.

Methods and computational details

Geometry optimizations of neutral and oxidized HTM1, Spiro-OMeTAD, PTZ1 and PTZ2 have been performed via density functional theory (DFT)^50,51 at the B3LYP/6-31G(d,p)^52,53 and PBE/6-31G(d,p)^54,55 levels of theory in vacuo, using Gaussian 16, Revision C.01 suite of programs.⁵⁶ Dispersion forces have been included within the Grimme's D3 framework⁵⁷ using the damping scheme by Becke and Johnson (D3BJ).^58,59 Frequency calculations have been performed to check that stationary points were true energy minima.

HTMs reorganization energies in vacuo of compounds HTM1, Spiro-OMeTAD, PTZ1 and PTZ2 have been calculated at the PBE/6-31G(d,p) and B3LYP/6-31G(d,p) levels of theory, on the lowest energy neutral and oxidized geometries optimized at the PBE/6-31G(d,p) and B3LYP/6-31G(d,p) levels of theory, respectively.

To investigate HTMs/MAPI structural and electronic properties, the cubic structure of the MAPI bulk and the four considered compounds have been optimized with Periodic Boundary Conditions (PBC) via DFT at PBE-GGA, using the DZP basis set, including 5d¹⁰ semicore electrons for Pb atoms,⁶⁰ along with Troullier–Martins norm-conserving pseudopotentials,^61,62 as implemented in the SIESTA 4.1 program package.⁶³ A mesh cutoff of 400 Ry and 8 × 8 × 8 and 1 × 1 × 1 Γ-centered Monkhorst–Pack k-point grid for sampling the Brillouin zone have been considered respectively for the optimization of the MAPI bulk and for the optimization of HTM1, Spiro-OMeTAD, PTZ1 and PTZ2.

In the same way, the HTMs/MAPI energy minima have been optimized at PBE-GGA, using the DZP basis set, including 5d¹⁰ semicore electrons for Pb atoms, along with Troullier–Martins norm-conserving pseudopotentials. A mesh cutoff of 400 Ry and a 1 × 1 × 1 Γ-centered Monkhorst–Pack k-point grid have been considered. SCF energy threshold and total force threshold have been set at 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively, for each geometry optimization. The binding energies have been determined through single point calculations on the optimized systems at 8 × 8 × 1 Γ-centered Monkhorst–Pack k-point grid. The energies of all investigated systems have been corrected including the dispersion force calculated by the D3BJ damping scheme. We must note that more accurate quantitative predictions of the electronic properties would require a perturbative approach (e.g. GW) and inclusion of the spin orbit coupling (SOC) effects, which influence both the optical and electronic properties of compounds involving heavy atoms such as Pb. However, such an approach is more computationally expensive than DFT and would not be feasible for our interface systems. On the other hand, the combination of DFT+SOC predicts bandgaps very different from experiments. In particular, SOC addition affects to a larger extent the conduction band (made of Pb, p states) while retaining the position of the iodine (p) states forming the valence band. This results in a strong underestimation of the experimental bandgap.¹¹ Moreover, we expect that the SOC would equally affect all the considered interfaces, so neglecting it in all calculations does not prevent us to make a qualitative comparison of the different HTMs, that is the purpose of this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The computing resources and the related technical support used for this work have been provided by the CRESCO/ENEAGRID High Performance Computing Infrastructure and its staff.⁶⁴ CRESCO/ENEAGRID High Performance Computing Infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European research programmes, see https://www.cresco.enea.it/english for information. C. C. and A. S. also acknowledge the Department of Biotechnology, Chemistry and Pharmacy, Department of Excellence 2018–2022 and the hpc@dbcf for providing computational resources.

References

1. J. Jeong, M. Kim, J. Seo, H. Lu, P. Ahlawat, A. Mishra, Y. Yang, M. A. Hope, F. T. Eickemeyer, M. Kim, Y. J. Yoon, I. W. Choi, B. P. Darwich, S. J. Choi, Y. Jo, J. H. Lee, B. Walker, S. M. Zakeeruddin, L. Emsley, U. Rothlisberger, A. Hagfeldt, D. S. Kim, M. Grätzel and J. Y. Kim, Nature, 2021, 592, 381–385.
2. NREL. Best Research-Cell Efficiency Chart, https://www.nrel.gov/pv/cell-efficiency.html, (Accessed November 2021).
3. J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, Chem. Rev., 2020, 120, 7867–7918.
4. S. A. Olaleru, J. K. Kirui, D. Wamwangi, K. T. Roro and B. Mwakikunga, Sol. Energy, 2020, 196, 295–309.
5. D. Zhou, T. Zhou, Y. Tian, X. Zhu and Y. Tu, J. Nanomater., 2018, 2018, 8148072.
6. L. A. Castriotta, R. F. Pineda, V. Babu, P. Spinelli, B. Taheri, F. Matteocci, F. Brunetti, K. Wojciechowski and A. Di Carlo, ACS Appl. Mater. Interfaces, 2021, 13, 29576–29584.
7. M. Vasilopoulou, A. Fakharuddin, A. G. Coutsolelos, P. Falaras, P. Argitis, A. R.-B. M. Yusoffd and M. K. Nazeeruddin, Chem. Soc. Rev., 2020, 49, 4496–4526.
8. R. Singh, P. K. Singh, B. Bhattacharya and H.-W. Rhee, Appl. Mater. Today, 2019, 14, 175–200.
9. J. Urieta-Mora, I. García-Benito, A. Molina-Ontoria and N. Martín, Chem. Soc. Rev., 2018, 47, 8541–8571.
10. G. Ren, W. Han, Y. Deng, W. Wu, Z. Li, J. Guo, H. Bao, C. Liu and W. Guo, J. Mater. Chem. A, 2021, 9, 4589–4625.
11. A. Pecoraro, A. De Maria, P. Delli Veneri, M. Pavone and A. B. Muñoz-García, Phys. Chem. Chem. Phys., 2020, 22, 28401–28413.
12. H. Taherianfard, G.-W. Kim, F. Ebadi, T. Abzieher, K. Choi, U. W. Paetzold, B. S. Richards, A. A. Eliwi, F. Tajabadi, N. Taghavinia and M. M. Byranvand, ACS Appl. Mater. Interfaces, 2019, 11, 44802–44810.
13. F. M. Rombach, S. A. Haque and T. J. Macdonald, Energy Environ. Sci., 2021, 14, 5161–5190.
14. H. D. Pham, T. C. J. Yang, S. M. Jain, G. J. Wilson and P. Sonar, Adv. Energy Mater., 2020, 10, 1903326.
15. E. Sheibani, L. Yang and J. Zhang, Sol. RRL., 2020, 4, 1–16.
16. R. Hussain, M. Y. Mehboob, M. U. Khan, M. Khalid, Z. Irshad, R. Fatima, A. Anwar, S. Nawab and M. Adnan, J. Mater. Sci., 2021, 56, 5113–5131.
17. M. Li, S. Ma, M. Mateen, X. Liu, Y. Ding, J. Gao, Y. Yang, X. Zhang, Y. Wu and S. Dai, Sol. Energy, 2020, 195, 618–625.
18. M. R.-S. A. Janjua, Chem. – Eur. J., 2021, 27, 4197–4210.
19. S. A. Siddique, M. B. A. Siddique, R. Hussain, X. Liu, M. Y. Mehboob, Z. Irshad and M. Adnan, Comput. Theor. Chem., 2020, 1191, 113045.
20. X. Liu, X. Tan, Q. Chen, H. Shan, C. Liu, J. Xu, Z. K. Chen, W. Huang and Z. X. Xu, RSC Adv., 2017, 7, 53604–53610.
21. C. Lu, M. Paramasivam, K. Park, C. H. Kim and H. K. Kim, ACS Appl. Mater. Interfaces, 2019, 11, 14011–14022.
22. S. Revoju, A. Matuhina, L. Canil, H. Salonen, A. Hiltunen, A. Abate and P. Vivo, J. Mater. Chem. C, 2020, 8, 15486–15506.
23. J. Salunke, X. Guo, M. Liu, Z. Lin, N. R. Candeias, A. Priimagi, J. Chang and P. Vivo, ACS Omega, 2020, 5, 23334–23342.
24. S. Thokala and S. P. Singh, ACS Omega, 2020, 5, 5608–5619.
25. F. Zhang, S. Wang, H. Zhu, X. Liu, H. Liu, X. Li, Y. Xiao, S. M. Zakeeruddin and M. Grätzel, ACS Energy Lett., 2018, 3, 1145–1152.
26. R. Grisorio, B. Roose, S. Colella, A. Listorti, G. P. Suranna and A. Abate, ACS Energy Lett., 2017, 2, 1029–1034.
27. C. Coppola, R. Infantino, A. Dessì, L. Zani, M. L. Parisi, A. Mordini, G. Reginato, R. Basosi and A. Sinicropi, Mater. Chem. Phys., 2022, 278, 125603.
28. L. A. Castriotta, R. Infantino, L. Vesce, M. Stefanelli, A. Dessì, C. Coppola, M. Calamante, G. Reginato, A. Mordini, A. Sinicropi, A. Di Carlo and L. Zani, submitted manuscript.
29. M. Saliba, S. Orlandi, T. Matsui, S. Aghazada, M. Cavazzini, J.-P. Correa-Baena, P. Gao, R. Scopelliti, E. Mosconi, K.-H. Dahmen, F. De Angelis, A. Abate, A. Hagfeldt, G. Pozzi, M. Graetzel and M. K. Nazeeruddin, Nat. Energy, 2016, 1, 15017.
30. A. Torres and L. G.-C. Rego, J. Phys. Chem. C, 2014, 118, 26947–26954.
31. J. Yin, D. Cortecchia, A. Krishna, S. Chen, N. Mathews, A. C. Grimsdale and C. Soc, J. Phys. Chem. Lett., 2015, 6, 1396–1402.
32. Q. Wang, E. Mosconi, C. Wolff, J. Li, D. Neher, F. De Angelis, G. P. Suranna, R. Grisorio and A. Abate, Adv. Energy Mater., 2019, 9, 1900990.
33. Y. Zhang, P. Heng, H. Su, J. Li, J. Guo, P. Ning, W. Wu, T. Ren, L. Wang and J. Zhang, Chem. Rec., 2018, 18, 1–10.
34. Y. Zhang, J. Guo, H. Su, J. Li, W. Wu and L. Wang, Dyes Pigm., 2018, 154, 275–281.
35. Y. Li, Y. Zhang, J. Zhang, J. Li, W. Wu and L. Wang, Org. Electron., 2018, 62, 591–597.
36. Y. Li, Y. Zhang, P. Heng, R. Shao, Y. Liu, W. Qiao, L. Wanga and J. Zhang, Org. Electron., 2018, 54, 14–20.
37. Z. Zhang and R. He, Comput. Theor. Chem., 2019, 1161, 10–17.
38. J. Deng, W. Hu, W. Shen, M. Li and R. He, Phys. Chem. Chem. Phys., 2019, 21, 1235–1241.
39. J. Simokaitiene, M. Cekaviciute, K. Baucyte, D. Volyniuk, R. Durgaryan, D. Molina, B. Yang, J. Suo, Y. J. Kim, D. A. da Silva Filho, A. Hagfeldt, G. Sini and J. V. Grazulevicius, ACS Appl. Mater. Interfaces, 2021, 13, 21320–21330.
40. R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610.
41. Y. Saygili, M. Söderberg, N. Pellet, F. Giordano, Y. Cao, A. B. Muñoz-García, S. M. Zakeeruddin, N. Vlachopoulos, M. Pavone, G. Boschloo, L. Kavan, J.-E. Moser, M. Grätzel, A. Hagfeldt and M. Freitag, J. Am. Chem. Soc., 2016, 138, 15087–15096.
42. Y. Saygili, M. Stojanovic, H. Michaels, J. Tiepelt, J. Teuscher, A. Massaro, M. Pavone, F. Giordano, S. M. Zakeeruddin, G. Boschloo, J.-E. Moser, M. Grätzel, A. B. Muñoz-García, A. Hagfeldt and M. Freitag, ACS Appl. Energy Mater., 2018, 1, 4950–4962.
43. Y. Saygili, M. Stojanovic, N. Flores-Díaz, S. M. Zakeeruddin, N. Vlachopoulos, M. Grätzel and A. Hagfeldt, Inorganics, 2018, 7, 30.
44. A. B. Muñoz-García, I. Benesperi, G. Boschloo, J. J. Concepcion, J. H. Delcamp, E. A. Gibson, G. J. Meyer, M. Pavone, H. Pettersson, A. Hagfeldt and M. Freitag, Chem. Soc. Rev., 2021, 50, 12450–12550.
45. W.-J. Chi, Q.-S. Li and Z.-S. Li, Nanoscale, 2016, 8, 6146–6154.
46. Y. Li, H. Li, C. Zhong, G. Sini and J.-L. Brédas, npj Flex Electron, 2017, 1, 1–8.
47. D. Wang, S. Huang, C. Wang, Y. Yue and Q. Zhang, Org. Electron., 2019, 64, 216–222.
48. C. T. Crespo, J. Phys. Chem. Solids, 2021, 152, 109958.
49. F. F. Targhi, Y. S. Jalili and F. Kanjouri, Results Phys., 2018, 10, 616–627.
50. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
51. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1134–A1138.
52. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
53. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
54. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
55. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision C.01), Gaussian, Inc., Wallingford CT, 2016.
57. S. Grimme, J. Antony, S. Ehrlic and S. Krieg, J. Chem. Phys., 2010, 132, 154104.
58. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
59. A. D. Becke and E. R.-J. Johnson, Chem. Phys., 2005, 122, 154101.
60. J. Junquera, Ó. Paz, D. Sánchez-Portal and E. Artacho, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235111.
61. N. Troullier and J. L. Martins, Solid State Commun., 1990, 74, 613–616.
62. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 43, 1993–2006.
63. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
64. F. Iannone, F. Ambrosino, G. Bracco, M. De Rosa, A. Funel, G. Guarnieri, S. Migliori, P. Palombi, G. Ponti, G. Santomauro and P. Procacci, International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland, 2019, pp. 1051–1052.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01270g

---