Anion⋯anion interaction within Ch(CH₃)X₄⁻ (Ch = S, Se, Te; X = Cl, Br, I) dimers stabilized by chalcogen bonds

Abstract

In a crystal, a pair of homoanions (Te(C₆H₅)Cl₄⁻) are arranged in a parallel manner, close enough to interact with each other. Quantum chemical analysis indicates the existence of two strong noncovalent chalcogen bonds engaging the σ-hole of the chalcogen atoms from one unit and electron density accumulated on the Cl atom of the neighboring unit. In a solid, chalcogen bonds are supported by a multitude of HBs between interacting (Te(C₆H₅)Cl₄⁻) anions and the C₅H₅NBr⁺ counterions. These studies are extended to the model homodimers [(Ch(CH₃)X₄)⁻]₂, where Ch represents an atom of group 16 (S, Se, and Te) while X = Cl, Br, and I. In these model systems, the aromatic ring was replaced by a methyl group and the counterions were not included. The consequence of this is a different noncovalent bond network in comparison to the system in a solid (the absence of intermolecular HBs and the presence of dihalogen bonds). The tendency for more exoenergetic complexation increases in the Cl < Br < I series. The chalcogen size effect is much smaller. However, critical to the stability of this system is overcoming the Coulomb repulsion between the two monoanions. This is possible because of the polarizable environment that exists in the crystal due to the presence of counter ions.

---

Introduction

Noncovalent interactions are attracting increasing research attention, which is understandable because of their role in biology and medicine as well as their usefulness in technology and industry. The most intensively studied bond of this type and also historically the earliest described is the hydrogen bond.^1,2 However, many studies have shown that the acceptor–donor mechanism is available for elements of many groups of the periodic table. The anisotropy of electron density and the resulting presence of electron-poor regions make molecules more sensitive to nucleophilic attack. The concept of σ-hole^3–5 and π-hole^6–8 distinguishes electron-deficient regions into those lying at the extension of the bond (the former) or perpendicular to the plane of the molecule (the latter). The measure of this deficit is the value of the electrostatic potential at its maximum.^9–11 Typically, a decrease in electron density results in a positive value of the maximum (V_s,max) at the electrostatic potential surface. However, it has recently been shown that for an isolated Lewis acid, the sign of the potential at its maximum alone is not critical in assessing the acceptor capacity of the acid. The Lewis base approaching the acid can overcome the shielding effect of electrons at the acceptor site. In a study of neutral systems stabilized by a chalcogen bond, it was shown that the electrostatic potential calculated at the Ch⋯N bond distance is positive.¹² However, donor–acceptor systems between anionic Lewis acids and anionic Lewis bases have recently gained much interest. The maxima on the surface of the electrostatic acid potential had a negative sign in the cases of MCl₃⁻ ions where M = Ca, Sr, and Ba, to give an example.¹³ Taking the value of interaction energy as an indicator of stability, it was shown that in the gas phase such combinations can be stable or have a metastable character.^13,14 In any case, immersion of anionic systems in a polar medium results in a significant increase in dimer stability. Evidence for interactions between monoanions is also provided by crystal structures deposited with the CSD base.¹⁵ The HgCl₃⁻ monomers form polymeric structures in the solid state in which the structural distinctness of the trichloromercurate(II) subunits is preserved and quantum calculations performed for tetramers in the solid state geometry and optimized HgCl₃⁻ dimers immersed in water indicated the attractive nature of the interaction between monomers.^16,17 Zierkiewicz et al. showed that attractive interactions are also possible between dinuclear anions. PdCl₄²⁻ monomers interact with each other using the electron depleted region (π-hole) above the Pd atom as a nucleophilic attack site for the chlorine atom of the neighboring tetrachloropalladate(II).¹⁸ In both of the above cases, an important and even critical role is played by counterions present in the crystal network. Anion interactions supported in the solid state by the presence of counterions were the inspiration for the analysis of such interactions among elements of the 16th group of the periodic table.

Overall, the Cambridge Structural Database (CSD) identifies thirteen systems involving five valent tetrahalogenated group 16 elements in subunits with formal charge −1 linked to each other by an intermolecular contact distance less than the sum of the corresponding vdW radii. Only the tellurium atom meets these criteria, and in each of them, the Te atom is involved in unusual Te⋯X (X = F, Cl, Br, and I) interactions. Among these thirteen systems, two contain fluorine,^19,20 five chlorine,^21–25 two bromine,^23,26 and four iodine^23,27,28 atoms as ligands (Fig. S1, ESI†). The intermolecular distance of Te⋯Cl and Te⋯I within the chloride or iodine complexes ranges from 3.241 to 3.619 Å (X = Cl) and from 3.827 to 3.957 Å (X = I).

In the structure of WUTJOK refcode^15,25 the two mononuclear Te(C₆H₅)Cl₄⁻ are arranged in a way suggesting an attractive interaction stabilized by a double chalcogen bond. To the best of our knowledge, the current work discusses for the first time the experimental and theoretical aspects of an attractive interaction between two anions involving pentacoordinate chalcogen atoms.

Methods

Full optimization of Ch(CH₃)X₄⁻ dimers (Ch = S, Se, Te; X = Cl, Br, I), as well as the isolated Ch(CH₃)X₄⁻ monomers, were carried out in MP2/aug-cc-pVDZ.^29–31 The pseudopotential aug-cc-pVDZ-PP basis set was used for thallium and iodine atoms to account for relativistic effects.^32,33 The energy accuracy was related to calculations at a higher level, CCSD(T)/aug-cc-pVDZ(-PP).^30,34–37 These calculations were performed as single-point calculations for systems of geometry optimized with MP2/aug-cc-pVDZ. Harmonic frequency analysis confirmed that the optimized geometries represent true minima on the potential energy surfaces without any imaginary frequencies. Calculations were performed in the gas phase and in water (ε = 78.4). The aqueous solvent was simulated with a polarizable continuum model (PCM).³⁸ The interaction energy (E_int) of each complex was calculated as the difference between the total electron energy of the fully optimized complex and the energies of the monomers in the geometries adopted in the complex, while for the binding energy (E_bin) the difference between the energy of the complex and the doubling of the total electron energy for the corresponding monomer in its fully optimized isolated state. The basis set superposition error (BSSE) was corrected using the counterpoise procedure introduced by Boys and Bernardi.³⁹ Because the Gaussian package does not allow calculation of BSSE corrections using the solvent model, corrections were derived from gas-phase calculations for systems in their solvent geometry. Calculations were performed using Gaussian code 16, Rev. C.01.⁴⁰ The magnitude of the MEP (molecular electrostatic potential) was estimated from its extrema value at an isodensity surface of 0.001 a.u. In addition, NCI (noncovalent index)⁴¹ analysis of the reduced electron density gradient was performed using the MultiWFN program.^42,43 MEP maps and NCI diagrams were visualized using the VMD program.⁴⁴ The atoms-in-molecules (AIM) method was used to determine bond paths and their topological properties using the AIMAll program.⁴⁵ Decomposition of interaction energies was performed using the LMOEDA⁴⁶ protocol implemented in GAMESS-US software (version 2020-R2)⁴⁷ with a Morokuma–Ziegler scheme⁴⁶ (embedded in the ADF software).^48–50 Energy barriers were found quantitatively using the QST2 method from the Synchronous Quasi-Newton (STQN) program.⁵¹ The Cambridge Structural Database (CSD)¹⁵ supported the current study by providing X-ray structures against which the systems analyzed in this work were modeled.

CSD sample

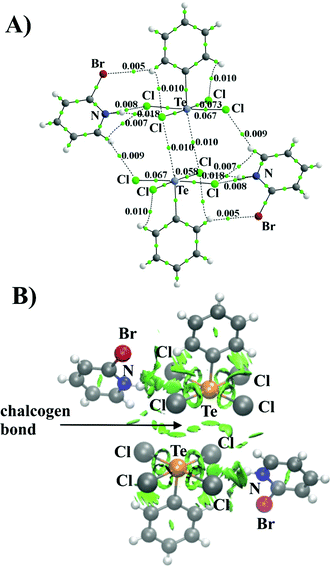
Cambridge Structural Database was screened for the presence of a structural motif wherein two anionic, pentacoordinated chalcogen atom subunits are close enough to each other so they can interact. Fig. 1 presents the alignment of Te(C₆H₅)Cl₄⁻ anions in the crystal structure (WUTJOK, ref. code). One chlorine atom of each subunit lies almost directly above the tellurium atom of the other monomer and the Te⋯Cl distance of 3.597 Å represents 94% of the sum of the vdW radii (3.81 Å). Analysis of the electrostatic potential distribution (MEP) around an isolated molecule can provide insight into the nature of the interaction between these subunits. Calculated for the bare isolated monomer, the maximum of this potential located over the Te atom is −62.5 kcal mol⁻¹ which is understandable as the monomer is an anion (Fig. 2A). A clear increase in the V_s,max value is seen when the counterion (C₅H₅NBr⁺) is included. Then, for solid state geometry, the value of V_s,max at the same point increases to −0.42 kcal mol⁻¹ (Fig. 2B).

Fig. 1 Arrangement of Te(C₆H₅)Cl₄⁻ and C₅H₅NBr⁺ ions in the crystal state (WUTJOK, ref. code).

Fig. 2 MEP of the [Te(C₆H₅)Cl₄]⁻ monomer (A) and [Te(C₆H₅)Cl₄]⁻⋯C₅H₅NBr⁺ pair (B) on the 0.001 au isodensity surface. Black dot indicates V_s,max on the Te atom (σ-hole).

Insight into the energy aspects provides not only general information about the stability of the system but also, more importantly, allows estimating the importance of the individual factors defining a given interaction. The interaction energy between a pair of Te(C₆H₅)Cl₄⁻ units, for geometrical parameters taken from the crystal, was estimated to be +46.97 kcal mol⁻¹. This positive value reflects the Coulombic repulsion between the two monoanions. The situation is diametrically different if one considers the counterions present in the crystal lattice. Then the calculated value of E_int changes drops to −22.84 kcal mol⁻¹, thus the energetic benefit amounts to about 70 kcal mol⁻¹. These quantitative changes are confirmed by the interaction energy decomposition for both systems which is presented in Table 1. The interaction energy components show a significant change in the term related to the electrostatic interaction, whose character changes from repulsive to attractive when the counterions are included. Additionally, this effect is enhanced by the increase in the stabilizing role of the dispersion and orbital interaction components. The change like the electrostatic interaction from repulsive to attractive can be attributed to the weakening of the charge on Te(C₆H₅)Cl₄⁻ monoanions. This is manifested by an increase in V_s,max to near zero, in the location corresponding to the σ-hole, which makes this region more sensitive to nucleophilic attack.

Table 1 EDA/BLYP-D3/ZORA/TZ2P decomposition of the interaction energy of complexes into Pauli repulsion (E_Pauli), electrostatic (E_elec), orbital interaction (E_oi) and dispersion (E_disp) components. All energies in kcal mol⁻¹

	E Pauli	E elec	E oi	E disp	E int
(C6H5)TeCl4^−	12.89	49.47	−7.57	−7.48	47.32
(C5H5NBr^+)(C6H5)TeCl4^−	19.72	−19.61	−10.24	−12.54	−22.67

---

The AIM method, introduced by Bader, provides a formal definition of a chemical bond. Within this formulation, bond classification is based on the values of electron density, Laplacian of electron density, energy density, and ellipticity calculated at the bond critical point (BCP), namely, the electron density saddle point with directionality (3,−1). As can be seen, the AIM method indicates the presence of two Te⋯Cl bonds between Te(C₆H₅)Cl₄⁻ anions supported by a hydrogen bond system formed by C₅H₅NBr⁺ with both Te(C₆H₅)Cl₄⁻ monomers. The topology of the electron density distribution of the Te(C₆H₅)Cl₄⁻ dimer with the presence of counterions is shown in Fig. 3A. The value of electron density for the Te⋯Cl bond is 0.010 au. In conjunction with a small value of ∇²ρ and H close to zero, it creates the picture typical for noncovalent interactions according to AIM methodology.^52–54

Fig. 3 AIM diagram (A) of the [Te(C₆H₅)Cl₄]⁻⋯C₅H₅NBr⁺ dimer, small green dots represent bond critical points (BCPs) and the numbers are ρ values in au and NCI isosurfaces (B) (green spheres represent noncovalent interaction regions) at the RDG 0.5 a.u. isovalue.

The Te⋯Cl bonds are not the only factor responsible for the total interaction energy between the anionic subunits. There are several specific noncovalent contacts formed by the counterions present in the solid. For example, the CH and NH groups of the C₅H₅NBr⁺ counterions form H-bonds with the Cl atoms of the [Te(C₆H₅)Cl₄]⁻ ion and each phenyl ring forms two internal CH⋯Cl bonds. The noncovalent bond energy was estimated using the relationship ½V,⁵⁵ where V represents the potential energy density at the bond critical point. Relying on this correlation both bonds Te⋯Cl (ρ = 0.009 a.u.) and CH⋯Cl (ρ = 0.010 a.u.) between (Te(C₆H₅)Cl₄⁻)(C₅H₅NBr⁺) pairs are characterized by the similar strength: −1.51 kcal mol⁻¹. While the NH⋯Cl (ρ = 0.018 a.u.) is the strongest (−3.45 kcal mol⁻¹) among the internal interactions in the (Te(C₆H₅)Cl₄⁻)(C₅H₅NBr⁺) pair. The AIM protocol was complemented by the NCI approach, which depicts noncovalent interactions using a color scheme. The green disks in Fig. 3B are a clear picture of the main Te⋯Cl interaction, and the smaller spots correspond to the mentioned interactions involving counterions.

Theoretical models

Monomers

Each Ch(CH₃)X₄⁻ (Ch = S, Se, Te; X = Cl, Br, I) unit adopts a tetragonal pyramid type geometry as shown in Fig. 4A, where the CH₃ group occupies the axial positions and the four halogen atoms are in one plane with the chalcogen atom. As noted in Table 2, two of the four X atoms are nearly opposite to each other, with θ(X–Ch–X) close to 180°. The bond distance r(Ch–X) increases with the size of the Ch atom. The geometries optimized in the aqueous phase do not differ from the vacuum structures.

Fig. 4 Structure of Ch(CH₃)X₄⁻ monomers (A) and its dimers (B) (Ch = S, Se, and Te; X = Cl, Br, and I).

Table 2 Geometrical parameters (distances in angstroms, angles in degrees) of Ch(CH₃)X₄⁻ (Ch = S, Se, Te; X = Cl, Br, I) monomers calculated at the MP2/aug-cc-pVDZ level of theory

Isolated molecule	R(Ch–X)^a	∑Cov%	R(Ch–C)	θ(X–Ch–X)	∑θ(X–Ch–X)^b
a In the case of complexes in solvents the M–X distance values are averages of four different Ch–X distances. b Sum of the four angles XChX around the Ch atom.
Vacuum
S(CH3)Cl4^−	2.353	88	1.838	90.0/179.0	360
Se(CH3)Cl4^−	2.427	91	1.950	90.0/177.5	360
Te(CH3)Cl4^−	2.556	94	2.125	89.8/172.8	359
S(CH3)Br4^−	2.529	89	1.843	90.0/177.8	360
Se(CH3)Br4^−	2.597	92	1.957	90.0/178.6	360
Te(CH3)Br4^−	2.721	95	2.131	89.8/173.5	359
S(CH3)I4^−	2.773	88	1.853	89.9/176.4	357
Se(CH3)I4^−	2.837	91	1.966	90.0/179.2	360
Te(CH3)I4^−	2.960	94	2.141	89.9/174.7	360
Water
S(CH3)Cl4^−	2.352	88	1.839	90.0/177.8	360
Se(CH3)Cl4^−	2.462	90	1.951	90.0/178.6	360
Te(CH3)Cl4^−	2.559	94	2.124	89.8/173.5	359
S(CH3)Br4^−	2.523	89	1.845	90.0/176.5	360
Se(CH3)Br4^−	2.594	93	1.957	90.0/179.3	360
Te(CH3)Br4^−	2.722	95	2.131	89.9/174.2	359
S(CH3)I4^−	2.766	88	1.853	89.9/175.1	360
Se(CH3)I4^−	2.833	91	1.967	90/178.2	360
Te(CH3)I4^−	2.959	94	2.141	89.9/175.4	359

---

The MEP of each Ch(CH₃)X₄⁻ anion is characterized as containing a strongly negative region surrounding each halogen atom. The region of depleted electron density lying at the extension of the Te–C bond (green, Fig. 1A) has been designated as σ-hole. For all Ch(CH₃)X₄⁻ monomers, this MEP scheme coincides with that shown in Fig. 1A. The numerical values of the MEP at maxima, V_s,max, for each anion, are collected in Table 3. They range from −77 kcal mol⁻¹ for S(CH₃)Cl₄⁻ to −51 kcal mol⁻¹ for Te(CH₃)I₄⁻ and increase as the Ch atom is changed from S to Te. The values calculated for monomers immersed in an aqueous solution are generally slightly more negative (up to 7 kcal mol⁻¹).

Table 3 Maxima in the MEP (kcal mol⁻¹) of Ch(CH₃)X₄⁻ (Ch = S, Se, Te; X = Cl, Br, I) monomers calculated at the MP2/aug-cc-pVDZ level of theory

Isolated molecule	V s,max (σ-hole, Ch atom)
	Vacuum	Water
S(CH3)Cl4^−	−76.57	−82.86
Se(CH3)Cl4^−	−68.77	−72.66
Te(CH3)Cl4^−	−60.33	−59.07
S(CH3)Br4^−	−72.00	−78.63
Se(CH3)Br4^−	−64.50	−68.80
Te(CH3)Br4^−	−55.93	−55.24
S(CH3)I4^−	−66.56	−73.70
Se(CH3)I4^−	−59.55	−64.69
Te(CH3)I4^−	−51.06	−51.32

---

Dimers

The structure of Ch(CH₃)X₄⁻ (Ch = S, Se, Te; X = Cl, Br, I) dimers presented in Fig. 4B was fully optimized in a vacuum and a water solvent. All dimers immersed in water gain an energy advantage of 126 to 150 kcal mol⁻¹. This decreases with an increase in both chalcogen and halogen atom size (Table S1, ESI†).

The data summarized in Table 4 indicate only slight (not exceeding 0.07 Å) changes in the intramolecular Ch–X bond lengths in the complex relative to the isolated monomer. In gas, the distances between the units (Ch⋯X) are much larger than the intramolecular Ch–X distances (from 0.6 to 1.1 Å).

Table 4 Structural parameter distances (Å), angles (deg.) in Ch(CH₃)X₄⁻ (Ch = S, Se, Te; X = Cl, Br, I) dimers calculated at the MP2/aug-cc-pVDZ level of theory

	M–Xa	M–Xb	M–Xc	M⋯Xb	∑vdW %	θ(Ch–Xb⋯Ch)	θ(Ch–Xb⋯Ch–Xb)
Vacuum
S(CH3)Cl4^−	—	—	—	—	—	—	—
Se(CH3)Cl4^−	2.430	2.391	2.485	3.477	96	104.6	0.08
Te(CH3)Cl4^−	2.561	2.540	2.597	3.645	96	104.3	0.00
S(CH3)Br4^−	2.531	2.496	2.573	3.376	90	98.3	0.01
Se(CH3)Br4^−	2.598	2.568	2.640	3.411	71	98.0	0.04
Te(CH3)Br4^−	2.725	2.708	2.759	3.611	94	100.1	0.03
S(CH3)I4^−	2.776	2.761	2.791	3.450	74	92.9	0.00
Se(CH3)I4^−	2.838	2.817	2.864	3.485	90	91.7	0.01
Te(CH3)I4^−	2.961	2.950	2.986	3.661	91	91.2	0.02
Water
S(CH3)Cl4^−	2.352	2.350	2.359	3.325	90	92.4	0.01
Se(CH3)Cl4^−	2.426	2.442	2.417	3.330	91	87.6	0.01
Te(CH3)Cl4^−	2.552	2.562	2.553	3.761	99	70.6	0.04
S(CH3)Br4^−	2.526	2.517	2.533	3.363	90	92.2	0.00
Se(CH3)Br4^−	2.596	2.600	2.592	3.374	92	88.5	0.01
Te(CH3)Br4^−	2.723	2.750	2.703	3.586	93	78.7	0.02
S(CH3)I4^−	2.770	2.768	2.771	3.487	89	92.1	0.02
Se(CH3)I4^−	2.835	2.830	2.836	3.505	91	89.3	0.02
Te(CH3)I4^−	2.958	2.975	2.949	3.657	91	82.1	0.00

---

When the dimers are immersed in water the trend for the intermolecular Ch⋯X bond lengths is preserved. The dihedral angle θ(Ch–X_b⋯Ch–X_b) values presented in the last column of Table 4 are close to zero, indicating that the two monomers are parallel to each other. Table 5 collects the calculated values of interaction energy (E_int) and binding energy (E_bin). The former is calculated as the difference between the energy of the optimized complex and the energies of the monomers in the geometry they adopt in the complex. E_bin represents the difference between the energy of the dimer and the sum of the energies of the isolated monomers in their geometry. Thus, the difference between the two represents the energy cost associated with the structural deformation of the subunits necessary to adjust for the dimer geometry. In the gas phase, all E_int and E_bin values are endothermic, indicating the metastable nature of the systems formed. The numerical values of E_int and E_bin become less positive as the halogen size increases and both are less sensitive to the chalcogen atom size.

Table 5 Interaction and binding energies (E_int, E_b in kcal mol⁻¹) of Ch(CH₃)X₄⁻ (Ch = S, Se, Te; X = Cl, Br, I) dimers calculated at the MP2/aug-cc-pVDZ and CCSD(T)/aug-cc-pVDZ level of theory

	E int		E bin
	MP2	CCSD(T)	MP2	CCSD(T)
a For water solvent, in parenthesis are given BSSE corrections calculated with the counterpoise procedure for dimers in their vacuum geometry.
Vacuum
S(CH3)Cl4^−	—	—	—	—
Se(CH3)Cl4^−	44.55 (48.09)^a	46.07 (49.92)	45.35 (48.90)	46.58 (50.43)
Te(CH3)Cl4^−	40.04 (43.47)	41.20 (44.92)	40.71 (44.14)	41.57 (45.29)
S(CH3)Br4^−	41.56 (47.61)	45.28 (51.72)	41.96 (47.99)	45.44 (51.88)
Se(CH3)Br4^−	38.49 (45.41)	41.81 (49.16)	38.92 (45.83)	42.00 (49.35)
Te(CH3)Br4^−	35.01 (41.18)	37.31 (43.87)	35.43 (41.61)	37.43 (43.99)
S(CH3)I4^−	32.76 (41.05)	40.12 (49.03)	32.92 (41.21)	40.11 (49.02)
Se(CH3)I4^−	30.72 (39.56)	37.13 (46.62)	30.91 (39.75)	37.16 (46.64)
Te(CH3)I4^−	28.89 (37.04)	33.42 (42.19)	29.06 (37.21)	33.34 (42.11)
Water
S(CH3)Cl4^−	−8.84 (−5.14)	−6.50 (−2.42)	−8.77 (−5.07)	−6.52 (−2.44)
Se(CH3)Cl4^−	−10.54 (−5.21)	−8.25 (−2.46)	−10.45 (−5.12)	−8.26 (−2.47)
Te(CH3)Cl4^−	−10.69 (−4.13)	−8.37 (−1.27)	−10.54 (−3.98)	−8.19 (−1.09)
S(CH3)Br4^−	−13.41 (−6.77)	−9.18 (−2.12)	−13.28 (−6.64)	−9.14 (−2.07)
Se(CH3)Br4^−	−14.99 (−6.95)	−11.06 (−2.50)	−14.86 (−6.81)	−11.00 (−2.45)
Te(CH3)Br4^−	−14.44 (−5.95)	−11.33 (−2.29)	−14.28 (−5.78)	−11.23 (−2.19)
S(CH3)I4^−	−18.03 (−9.83)	−10.78 (−1.97)	−17.69 (−9.48)	−10.53 (−1.73)
Se(CH3)I4^−	−19.11 (−10.40)	−12.58 (−2.86)	−18.91 (−9.85)	−12.46 (−2.73)
Te(CH3)I4^−	−18.65 (−9.26)	−13.54 (−3.44)	−18.52 (−9.13)	−13.50 (−3.40)

---

The nature of inter- and intra-molecular interactions was evaluated by AIM analysis. The properties of the critical points of the studied dimers are given in Table S3 (ESI†). For intermolecular Ch⋯X interactions, the electron density value is in the range of 0.01 to 0.02 a.u. Which, in the context of Laplacian values of density varying from 0.02 to 0.04 a.u. signposts the presence of noncovalent interactions of moderate strength between the subunits. The same analysis for complexes immersed in water showed that these values remain almost unchanged.

In our previous work¹⁴ where we considered anion-anion interactions in systems containing an atom of group 12 of the periodic table and the corresponding BCP parameters of the BCPs in aqueous solvent took similar values.

Replacement of the benzene ring with a CH₃ group in model systems results in the appearance of X⋯X dihalogen bonds, as indicated by both AIM and NCI diagrams (Fig. 5). In a vacuum, the ρ(X⋯X) value in BCPs decreases slightly with Ch size and increases with the size of X. Immersion of the systems in water results in an increase in the value of ρ(X⋯X). For X = Br, I the X⋯X interaction strength, expressed by the magnitude of the electron density potential energy (V) in BCP, is several times (3.5 to 7, Table S3, ESI†) smaller than the Ch⋯X bonds. The AIM diagram for Te(CH₃)Cl₄⁻ (water) is somewhat more complex. In addition to the two Cl⋯Cl bonds (ρ = 0.006 a.u.), the four Ch⋯Cl bonds (ρ = 0.008 a.u.) are present, and also the Te⋯Te dichalcogen contact (ρ = 0.009 a.u.) is indicated. For both of the latter two, the V value is 0.004 a.u.

Fig. 5 AIM diagram (A) of the Se(CH₃)Br₄⁻ dimer, small green dots represent bond critical points (BCPs) and the numbers are ρ values in au, and NCI isosurfaces (B) (green spheres represent noncovalent interaction regions) at the RDG 0.5 a.u. isovalue.

The interaction energy distribution of each complex illustrates the mixture of different forces, the resultant of which leads to bond formation. As can be seen in Tables 6 and 7 in the gas phase, the electrostatic component is positive and thus has a destabilizing effect on the complexes. This is understandable since each interacting monomer has a formal negative charge. As the size of the substituted halogen increases, the value of Coulomb repulsion decreases, and the effect of Pauli repulsion on reducing the stability of the system increases. There is no change in the proportions of the stabilizing term of the system, the dispersion and polarization forces, which are about 70% and 30% of total attractive interaction, respectively. The ADF-EDA scheme used for Se(CH₃)X₄⁻ dimers (X = Cl, Br, I) in the gas phase estimates almost equal contributions of the dispersion and orbital interaction terms. The decomposition of interaction energy components is completely different when the systems are immersed in a water solvent. The destabilizing effect of the electrostatic component increases about three times, while the value of the Pauli repulsion practically remains unchanged. As shown in Table 6, placing the dimer in water causes a sharp increase in the polarization on the stability of the systems and a relatively small increase of the dispersion contribution. The polarization term accounts for about 90% of the sum of E_pol and E_disp, suggesting that it plays a key role in overcoming the Coulomb repulsion, which allows E_int to reach exoenergetic values. The NBO methodology offers a useful means to analyze the interaction between orbitals. The sums of the second-order interaction energies E(2) of the interactions between the lone electron pair of nitrogen atoms LP(X) (X = Cl, Br, I) and the σ*(Ch–C) as well as σ*(Ch–X) anti-bonding orbitals are collected in Table 8. One can observe similarities between the NBO quantities and the interaction energies in Table 5. First, for the (CH₃)SeX₄⁻ domains, the NBO parameters reflect an energy ordering I > Br > Cl consistent with changes in E_int. NBO data are also parallel with the interaction energies for dimers immersed in water (Fig. 6).

Table 6 LMOEDA/MP2/aug-cc-pVDZ decomposition of the interaction energy of complexes into electrostatic (E_es), repulsion (E_Pauli), polarization (E_pol) and dispersion (E_disp) components. All quantities in kcal mol⁻¹

	E es	E Pauli	E pol	%^b	E disp	%	E int
a E Pauli = ∑(Eex + Erep). b Percentage contribution to total attractive interactions (Epol + Edisp).
Vacuum
Se(CH3)Cl4^−	51.98	9.40	−4.44	33	−8.91	67	48.02
Se(CH3)Br4^−	47.54	18.43	−6.15	30	−14.36	70	45.46
Se(CH3)I4^−	40.62	30.20	−8.54	27	−22.53	73	39.75
Water
Se(CH3)Cl4^−	161.44	14.94	−170.10	93	−12.53	7	−6.26
Se(CH3)Br4^−	148.31	21.19	−160.87	91	−16.61	9	−7.97
Se(CH3)I4^−	131.34	28.93	−148.46	87	−22.67	13	−10.87

---

Table 7 EDA/BLYP-D3/ZORA/TZ2P decomposition of the interaction energy of complexes into Pauli repulsion (E_Pauli), electrostatic (E_elec), orbital interaction (E_oi) and dispersion (E_disp) components. All energies in kcal mol⁻¹

	E Pauli	E elec	E oi	%^a	E disp	%	E int
a Percentage contribution to total attractive interactions (Eoi + Edisp).
Se(CH3)Cl4^−	10.13	51.31	−6.05	50	−6.05	50	49.34
Se(CH3)Br4^−	19.29	46.45	−9.90	51	−9.62	49	46.22
Se(CH3)I4^−	33.35	37.46	−13.12	47	−15.07	53	42.62

---

Table 8 NBO results, the second-order energies (E²) values of interacted orbital in kcal mol⁻¹

	LP (X) → σ*(Se–C)	LP (Cl) → σ*(Se–X)	Σ
Vacuum
Se(CH3)Cl4^−	7.08	0.36	7.44
Se(CH3)Br4^−	13.90	0.64	14.54
Se(CH3)I4^−	19.45	1.68	21.13
Water
Se(CH3)Cl4^−	11.00	0.74	11.74
Se(CH3)Br4^−	15.24	1.10	16.34
Se(CH3)I4^−	18.46	1.46	19.92

---

Fig. 6 The isosurface (on the 0.001 isovalue) of two of the interacting orbitals [LP(Br) → σ*(Se–C)] for the Se(CH₃)Br₄⁻ dimer; (blue, LP(Br) orbital; orange, σ*(Se–C)).

Discussion

The conventional concept of σ- and π-holes associated with electron density anisotropy around the molecule is in many cases sufficient for qualitative and quantitative description of forming systems stabilized by noncovalent bonding. It works well for neutral monomers, where the reduction of electron density in the hole regions is so large that the maxima on the electrostatic potential isosurface take positive values (V_s,max > 0). Sometimes, however, despite the negative value of V_s,max (shallow hole) stable bonds are also formed. This is possible when the nucleophile can overcome the shielding effect of the valence electrons of the Lewis acid. In this case, bond formation occurs at a distance where an attractive interaction is already possible and explainable based on the electrostatic concept of holes. The calculated value of the maximum of the electrostatic potential at a particular distance from the electrophile nucleus then has a positive value.¹²

The situation becomes more complex in the case of anion⋯anion interactions. In negatively charged monomers, the electron density anisotropy rarely results in a positive V_s,max in isolated LA.¹³ It is also shown that the sign of the MEP maximum in LA can change due to deformation of its geometry occurring during complexation.

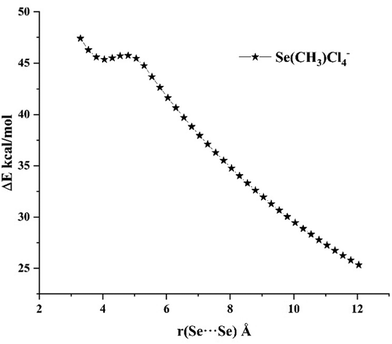
A typical feature of all previously studied systems is their metastability in the gas phase. This is worth emphasizing, even when the Coulomb interaction has an attractive character. Systems of this type are characterized by the presence of a dissociation barrier.^13,14,56 It was shown that this barrier for CN-⋯M (M = Zn, Cd, Hg) systems is about 25 kcal mol⁻¹, slightly higher than the barrier of 20 kcal mol⁻¹ for M as the atoms of the 2nd group. As it seems, this barrier is mainly related to the geometrical deformation of the subunits. For the systems presented in this work, in the absence of deformation, the barrier is very small 0.1 kcal mol⁻¹ (Se(CH₃)Cl₄⁻ dimer, Fig. 7).

Fig. 7 Dissociation profile of the Se(CH₃)Cl₄⁻ dimer in a vacuum.

The results presented in this paper demonstrate the metastability of chalcogen complexes in the gas phase. When immersed in an aqueous medium, the interaction energies and binding energies adopt exoenergic values thus there is no barrier to dissociation for them. Similar results were also obtained at the CCSD(T)/aug-cc-pVDZ level (Table 5).

The results obtained for the model systems are qualitatively consistent with the values obtained for the dimer in the crystal geometry. For the bare dimer, the E_int calculated in the gas phase is endoenergetic. Electrostatics is an element that hinders the stabilization of the complex. When one considers the counterions present in the crystal lattice it results in a change of interaction character. The performed decomposition of the interaction energy shows the reversal of the role of the Coulomb interaction from repulsive to attractive, which is mainly due to the compensation of the charge of the anion Te(C₆H₅)Cl₄⁻ by C₅H₅NBr⁺. Thus, the role of the counterion can be dualistic: it compensates charge and locks the anionic subunits.

Interactions of anions in the solid have recently been indicated for monoanions¹⁶ (HgCl₃⁻) and also for dianions¹⁸ (PdCl₄²⁻). In the solid, the interaction of anionic subunits is stabilized by an additional network of secondary hydrogen bonds. The observations were also supported by quantum chemical calculations in the gas phase and polar solvents. The use of water as a polar medium for the model systems studied does not provide charge compensation. However, the polar medium facilitates electron density polarization by enhancing the ion interaction, which in the case of monoanions is associated with an increase in electrostatic repulsion and finally results in the increased stability of the systems studied.

Similar results were obtained for other ionic pairs, both cationic and anionic, that were identified in the gas phase.⁵⁷ In subsequent studies, it was found that immersion of such systems in a polar medium resulted in a marked boost in their stability.^58,59

There are also many reports in the literature regarding possible anion-anion interactions in the context of hydrogen bonding. Metastable dication and dianion complexes stabilized by HBs have been identified.⁶⁰ HB anion–anion bonding has been documented in the crystal structure,⁶¹ and CSD⁶² analysis has identified protonated pyridine–boronic acid dimers in the solid phase. Quantum chemical calculations showed that the metastable complex gains stability when placed in a dielectric medium.

For the cationic systems, it was shown that increasing the size of the cation makes it easier for them to disperse the positive charge causing them to be more stable than the separated⁶³ monomers. Studies of a number of cationic complexes supported by HB bonds show the importance of the environment for the stability of such systems.⁶⁴

Conclusions

The current work provides clear crystallographic and theoretical evidence for an attractive interaction between two monoanions of pentacoordinate chalcogen atoms. The main cause of this attraction is the σ-hole bond involving charge transfer from lone pairs of halogens to an atom of the 16th group of the periodic table in the context of the monoanion pair Ch(C₆H₅)X₄⁻ (Ch = S, Se, and Te; X = Cl, Br, and I). Tandem with counterions in the crystal lattice results in a stable system with a reversal of the role of electrostatics from repulsive to attractive.

In dimer model studies, it was shown that Ch(CH₃)X₄⁻ ions can interact with each other despite their strong Coulomb repulsion. Each Ch(CH₃)X₄⁻ monomer retains its structural distinctness and the system is stabilized by a pair of noncovalent Ch⋯X chalcogen bonds. The structure arranged in this manner does not represent a stable minimum, in the gas phase, but forms a metastable system. However, the interaction energies are consistently exothermic in aqueous solution. There is a tendency towards more exothermic complexation for larger halogen atoms, and the effect of the size of chalcogen atoms is less. The interactions in the gas phase have a positive electrostatic component. The dispersion and polarization terms also play a stabilizing role. On the other hand, polarization is the dominant factor in the solvent, where the electrostatic interaction is still repulsive.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financed in part by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology. A generous allotment of computer time from the Wroclaw Supercomputer and Networking Center is acknowledged.

References

1. S. Scheiner, Struct. Chem., 2019, 30, 1119–1128.
2. S. Scheiner, J. Indian I Sci., 2020, 100, 61–76.
3. P. Politzer and J. S. Murray, J. Comput. Chem., 2018, 39, 464–471.
4. A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517.
5. T. Clark, J. S. Murray and P. Politzer, ChemPhysChem, 2018, 19, 3044–3049.
6. P. Politzer, P. Lane, M. C. Concha, Y. G. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311.
7. J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2007, 107, 2286–2292.
8. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2021, 23, 16458–16468.
9. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
10. J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 153–163.
11. J. S. Murray, P. Lane and P. Politzer, J. Mol. Model., 2009, 15, 723–729.
12. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, Molecules, 2021, 26, 6394–6411.
13. W. Zierkiewicz, R. Wysokinski, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 870–877.
14. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 1119–1125.
15. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
16. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2021, 22, 818–821.
17. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 13853–13861.
18. W. Zierkiewicz, M. Michalczyk, T. Maris, R. Wysokinski and S. Scheiner, Chem. Commun., 2021, 57, 13305–13308.
19. A. R. Mahjoub, D. Leopold and K. Seppelt, Z. Anorg. Allg. Chem., 1992, 618, 83–88.
20. A. Haas and M. Pryka, J. Chem. Soc., Chem. Commun., 1993, 993–994,  10.1039/c39930000993.
21. M. A. James, O. Knop and T. S. Cameron, Can. J. Chem., 1992, 70, 1795–1821.
22. J. Bergman, J. Siden and K. Maartmannmoe, Tetrahedron, 1984, 40, 1607–1610.
23. S. S. Dos Santos, E. S. Lang and G. M. de Oliveira, J. Organomet. Chem., 2007, 692, 3081–3088.
24. R. K. Chadha, J. E. Drake and M. A. Khan, Can. J. Chem., 1984, 62, 32–35.
25. E. S. Lang, R. M. Fernandes, C. Peppe, R. A. Burrow and E. M. Vazquez-Lopez, Z. Anorg. Allg. Chem., 2003, 629, 215–218.
26. G. A. Casagrande, C. Raminelli, E. S. Lang and S. D. Lemos, Inorg. Chim. Acta, 2011, 365, 492–495.
27. F. Einstein, J. Trotter and C. Williston, J. Chem. Soc. A, 1967, 2018–2023.
28. E. Faoro, G. M. de Oliveira, E. S. Lang and C. B. Pereira, J. Organomet. Chem., 2011, 696, 807–812.
29. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
30. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
31. A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667–7676.
32. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
33. K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883.
34. K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296.
35. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244.
36. J. A. Pople, M. Headgordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
37. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Headgordon, Chem. Phys. Lett., 1989, 157, 479–483.
38. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
39. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, 2016.
41. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
42. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
43. T. Lu and F. W. Chen, J. Mol. Graph. Model., 2012, 38, 314–323.
44. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph. Model., 1996, 14, 33–38.
45. T. A. Keith in AIMAll (Version 19.10.12) TK Gristmill Software, Overland Park KS, USA, 2019 (aim.tkgristmill.com).
46. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
47. G. M.-J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102.
48. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J.-A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
49. O. A. Stasyuk, R. Sedlak, C. F. Guerra and P. Hobza, J. Chem. Theory Comput., 2018, 14, 3440–3450.
50. ADF2014, SCM, Theoretical Chemistry, Amsterdam, The Netherlands, 2014.
51. C. Y. Peng and H. B. Schlegel, Isr. J. Chem., 1993, 33, 449–454.
52. R. Bader, Atoms In Molecules, A Quantum Theory, Clarendon Press, Oxford, 1990.
53. R. F.-W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
54. F. Cortes-Guzman and R. F.-W. Bader, Coord. Chem. Rev., 2005, 249, 633–662.
55. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
56. S. Scheiner, R. Wysokinski, M. Michalczyk and W. Zierkiewicz, J. Phys. Chem. A, 2020, 124, 4998–5006.
57. F. Weinhold and R. A. Klein, Angew. Chem., Int. Ed., 2014, 53, 11214–11217.
58. I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Phys. Chem. A, 2015, 119, 183–194.
59. Y. Yang, Z. Xu, Z. Zhang, Z. Yang, Y. Liu, J. Wang, T. Cai, S. Li, K. Chen, J. Shi and W. Zhu, J. Phys. Chem. B, 2015, 119, 11988–11997.
60. I. Alkorta, I. Mata, E. Molins and E. Espinosa, Chem. – Eur. J., 2016, 22, 9226–9234.
61. R. Barbas, R. Prohens, A. Bauza, A. Franconetti and A. Frontera, Chem. Commun., 2019, 55, 115–118.
62. I. Iribarren, M. M. Montero-Campillo, I. Alkorta, J. Elguero and D. Quinonero, Phys. Chem. Chem. Phys., 2019, 21, 5796–5802.
63. T. Niemann, A. Strate, R. Ludwig, H. J. Zeng, F. S. Menges and M. A. Johnson, Phys. Chem. Chem. Phys., 2019, 21, 18092–18098.
64. S. G. Dash and T. S. Thakur, Phys. Chem. Chem. Phys., 2019, 21, 20647–20660.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00271j

---