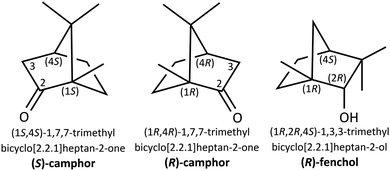
Sniffing out camphor: the fine balance between hydrogen bonding and London dispersion in the chirality recognition with α-fenchol

Abstract

Binary complexes between the chiral monoterpenoids camphor and α-fenchol were explored with vibrational and rotational jet spectroscopy as well as density functional theory in order to explore how chirality can influence the binding preferences in gas-phase complexes. The global minimum structures of the two diastereomers were assigned. It is found that chirality recognition leads to different compromises in the fine balance between intermolecular interactions. While one isomer features a stronger hydrogen bond, the other one is more tightly arranged and stabilized by larger London dispersion interactions. These new spectroscopic results help understand the influence of chirality in molecular aggregation and unveil the kind of interactions involved between a chiral alcohol and a chiral ketone with large dispersion contributions.

---

1 Introduction

Chirality recognition manifests itself perhaps most intuitively in the different smells of the enantiomers of certain compounds, mediated by chiral olfactory receptors in noses trained by evolution. Among molecular examples readily discriminated by most or all of the tested animals, including us humans,¹ are the monoterpenes carvone, limonene, and α-pinene.² But for the enantiomers of camphor, most tested species, including humans,¹ fail this challenge, only Asian elephants² and mice³ were confirmed so far to succeed.

We explore here a technological alternative for the identification of the absolute configuration of camphor vapor. This is pursued by mixing camphor with the vapor of a second chiral compound with a known absolute configuration, here (+)-α-fenchol, as well as an excess of carrier gas. In this chiral tagging approach,⁴ the dilute gas mixture is expanded in a supersonic jet into vacuum, providing low internal and translational temperatures, so that a complex between the two chiral compounds is formed through collisions. Dictated by the relative handedness of the interaction partners, diastereomeric isomers result, which can be distinguished in principle by spectroscopy. However, two previous attempts with this chiral tag spectroscopy approach failed to achieve a direct spectral differentiation for combinations of camphor with a chiral hydrogen bond donor, using electronic⁵ or vibrational spectroscopy.⁶ However, differences in the fluorescence decay or collision-induced dissociation rates were observed. In the present article, we investigate which differences in molecular interactions facilitate spectral chirality recognition^7,8 of camphor by characterizing the complexes with a combination of vibrational and rotational spectroscopy as well as density functional theory.

Chiral tag rotational spectroscopy was recently advanced to not only allow qualitative identification of chemical species from the positions of spectral lines, but to also use their relative intensities for the accurate determination of the enantiomeric excess of the sample. This technique got significantly enhanced by the broadband chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy technique.^9–12 Another complementary approach is microwave three-wave mixing, which also relies on rotational spectroscopy combined with jet expansion.^11,12 For a recent minireview and comparison of these two techniques, see ref. 11.

Here, we are less interested in the determination of the enantiomeric excess of the camphor samples, but more in better understanding the involved intermolecular interactions and current limits of the chiral tag approach, both on the experimental and theoretical side. Camphor and α-fenchol are bicyclic monoterpenoids; their structural formulas and systematic names are given in Fig. 1. Both molecules are rather large – at least according to the standards of gas-phase spectroscopy and theoretical chemistry – with eleven heavy, non-hydrogen atoms, and feature low volatilities with normal boiling points in excess of 200 °C, posing a challenge to detection sensitivity. On the one hand, their shared bicyclic framework limits the intramolecular conformational flexibility of the respective monomers, compared to monocyclic¹³ and especially acyclic monoterpenes.¹⁴ On the other hand, this also leads to shapes and mass distributions in these molecules that are roughly spherical. This is expected to reduce the dependence of the rotational constants of the complex on the relative orientation of its constituents and thus to complicate the assignment of the observed species (along with a challenge for chiral discrimination). The polar hydroxy and carbonyl functional groups introduce substantial permanent electric dipole moments – the precondition for rotational spectroscopy – and enable the formation of a hydrogen bond as a directional primary intermolecular interaction. This puts some constraints on the relevant intermolecular conformational space, which can be explored with electronic structure methods to identify and assign the most stable isomers. In addition, the hydrogen bond formed between the two molecules upon complex formation allows to take advantage of the OH stretching chromophore with vibrational spectroscopy as a complementary detection technique.

Fig. 1 Structural formulas, systematic names, and common names of the employed compounds.

In the picture of sp² hybridization, the carbonyl group of camphor offers two free electron pairs for coordination, which can be non-equivalent depending on the symmetry of the ketone. This often energetically subtle isomerism for complexation can be used as an experimental benchmark for the predicted energy difference of electronic structure methods and can be tuned by modification of the donor or the acceptor molecule.^15–17 Here, we will also explore whether the preference might be influenced by simple mirroring of either interaction partner. Unlike chemical modifications, this does not change the intrinsic hydrogen bond acceptor or donor quality of the docking sites, therefore exposing geometric consequences from secondary interactions.

In the case of camphor, hydrogen bond donors can either approach the free electron pair adjacent to the quaternary bridgehead carbon atom C1 or the pair near the secondary carbon atom C3 (Fig. 1). Hydrogen bonded binary complexes of camphor were structurally analyzed before for water,¹⁸ phenol,¹⁹ methanol,²⁰ ethanol,²⁰ protonated alanine,⁶ chloroform,¹⁹ and cytochrome P-450cam.²¹ In all of these systems, a preferred coordination of the lone pair on the side of the secondary C3 of camphor was concluded, while also the presence of a minor conformer on the quaternary C1 side was established for the first five systems. The comparison with the results obtained for chiral and bulky fenchol as binding partner will be useful to further disentangle the different interaction contributions – an important task on the way to get a detailed understanding of how molecules dock.

2 Computational and experimental methods

2.1 Computational methods

(R)-fenchol refers to (+)-(1R,2R,4S)-α-fenchol (also known as (+)-(1R,2R,4S)-endo-fenchyl alcohol) throughout the manuscript. (S)-fenchol was not used in our calculations or experiments because it was not commercially available and is not expected to provide additional information as only relative, not absolute, chirality is of importance in this study. The conformational landscapes of the (R)-camphor – (R)-fenchol and (S)-camphor – (R)-fenchol complexes were explored with four strategies. First, the program ABCluster was used to identify suitable complex structures.²² This program uses the so-called “artificial bee colony” (ABC) algorithm. Using this algorithm, the monomer structures are constrained preventing any structural rearrangements due to intermolecular interactions, which needs to be considered when treating molecules with flexible groups. Second, the simulated annealing conformational search implemented in the GFN-xTB program was performed (option –siman).^23,24 For these two approaches, we used the three different fenchol conformations²⁵ A, B, and C as inputs in the different conformational searches (as shown in Fig. 2). Third, the GFN-xTB program was used again, this time with its driver program CREST (Conformer–Rotamer Ensemble Sampling Tool, option –nci recommended for non-covalently bound complexes).²⁶ The isomers resulting from these three automated conformational searches were further optimized using the DFT hybrid functional B3LYP^27–29 with Grimme's dispersion correction D3³⁰ and Becke–Johnson damping (B3LYP-D3(BJ)) and the def2-TZVP³¹ basis set. The energy values presented herein are zero-point vibrational energy corrected relative energies. In parallel, a manual conformational search was performed at this level based on chemical intuition and systematic variation of fenchol conformers, plausible binding sites, and orientations in the input structures. More details are provided in the ESI.‡ Structure optimizations and frequency calculations were performed within the double-harmonic approximation using Gaussian09 (Revision E.01)³² for B3LYP-D3(BJ)/def2-TZVP calculations and the ORCA package^33,34 for selected isomers using B97-3c^35–37 (a revised version of the well-established B97-D functional with Grimme's D3 dispersion scheme) and the def2-TZVP basis set (see Section 3.3).

Fig. 2 Possible conformations of the (R)-fenchol monomer.

We used non-covalent interaction (NCI)³⁸ plots to characterize the non-covalent interactions present in the complexes and the symmetry-adapted perturbation theory (SAPT)³⁹ approach to gain insight into the different binding contributions (see Section 3.4). The structures optimized at the B3LYP-D3(BJ)/def2-TZVP level of theory were used as inputs for the SAPT(0)/jun-cc-pVDZ computations using the Psi4 package⁴⁰ and the non-covalent interaction (NCI) plots using the Multiwfn⁴¹ and Chimera⁴² software.

2.2 FTIR spectroscopy

In two separate saturators, a helium atmosphere of 1.6 bar was enriched with the vapor pressure of fenchol and camphor at 23 °C, estimated as 0.0002 bar and 0.0005 bar, respectively, from extrapolation of reported Antoine parameters.⁴³ Samples of (+)-(R)-α-fenchol (Aldrich, 98.5%) and either (+)-(R)-camphor (Alfa Aesar, 98.1%), (−)-(S)-camphor (Aldrich, 99.1%) or racemic camphor (Alfa Aesar, 96.5%) were used. A reservoir was filled with 0.75 bar of the gas from either a single saturator or from both saturators with a 1 : 1 mixing ratio. A pulsed (2 min⁻¹) adiabatic expansion through a (600 × 0.2) mm² slit nozzle was probed by a synchronized FTIR scan. Between 300 and 450 repetitions were averaged for each spectrum with a 3900–2600 cm⁻¹ range and a 2 cm⁻¹ resolution. More information on the setup is available in ref. 44.

2.3 Chirped-pulse Fourier-transform microwave (CP-FTMW) spectroscopy

The broadband rotational spectra of mixtures of (R)-camphor and (R)-fenchol as well as (S)-camphor and (R)-fenchol were recorded with the broadband chirped-pulse Fourier-transform microwave (CP-FTMW) spectrometer COMPACT in the frequency range 2–8 GHz.⁴⁵ The experimental setup is described in detail in ref. 45. Equimolar amounts of (R)-camphor and (R)-fenchol (RR complex) as well as (S)-camphor and (R)-fenchol (SR complex) were mixed in two different flasks and used for separate experiments. Custom-made sample reservoirs located close to the valve orifice were used. The samples were heated to 50 °C to generate sufficient vapor pressure. Neon was used as the carrier gas, with a backing pressure of 3 bar, and flowed through the heated reservoir containing the mixture of camphor and fenchol. The pulsed valve (General valve Series 9) was operated at 9 Hz and used to supersonically expand the molecules seeded in the carrier gas into the vacuum chamber, where they were polarized by a microwave chirp spanning the 2–8 GHz frequency range within 4 μs. The microwave chirps were created by an arbitrary waveform generator (AWG), amplified with a 300 W traveling wave tube amplifier and then broadcast into the vacuum chamber using a horn antenna where they interacted with the molecular ensemble. After the microwave excitation pulse was stopped, the molecular signal was collected in the time domain as a free-induction decay (FID) and amplified with a low-noise amplifier. Fast Fourier transformation of the FID from the time domain into the frequency domain resulted in the rotational spectrum. The “fast frame” option of the digital oscilloscope was used for these experiments.⁴⁶ Eight back-to-back excitation chirps were performed per gas pulse, and the subsequent eight FID acquisitions were co-added and averaged. In this way, the measurement time and sample consumption were decreased, resulting in an effective repetition rate of 72 Hz for the experiment. The FID was recorded for 40 μs, which generated a frequency resolution of 25 kHz in our Fourier transformed microwave spectrum. The number of FIDs that were co-added to obtain the final spectra was 5 million and 7.5 million for the SR and RR complexes, respectively.

The initial assignment of the observed experimental lines to rotational transitions was performed through fits based on an asymmetric rigid rotor Hamiltonian, using the JB95⁴⁷ program package. Refined fits were obtained using the AABS^48–50 program suite and a standard Watson-type Hamiltonian (A-reduction and I^r representation) by using the nonlinear least-squares fit program SPFIT developed by Pickett.⁵¹

3 Results

3.1 Theoretical results

The camphor monomer is conformationally rigid; only one conformer was observed in previous rotational spectroscopy studies in the gas phase.^18,52 For the fenchol monomer, the hydroxy hydrogen atom can adopt three different local minimum energy positions, resulting in the expected conformers A, B, and C (Fig. 2). Only a single species, assigned to fenchol A, has been detected in previous studies using rotational spectroscopy and the cold conditions of a supersonic jet with neon as a carrier gas.^10,25 Subsequent investigation employing FTIR and Raman jet spectroscopy and helium as carrier gas revealed the second and third conformer.⁵³ However, it was concluded that the hydroxy hydrogen atom is highly delocalized between positions A and B through a tunnelling interaction facilitated by an energetic near-degeneracy as well as a low and narrow interconversion barrier. The difference between the two lowest torsional states was determined as 0.19(1) kJ mol⁻¹, which represents an upper bound for the difference between the calculated hypothetical localized conformers A and B due to the also contributing tunnelling splitting. At the here employed B3LYP-D3(BJ)/def2-TZVP level, conformer A is calculated to be the lowest in energy trailed by fenchol B and C with relative energies of 0.5 and 1.0 kJ mol⁻¹, respectively. This means this level of theory somewhat overestimates the E(B)–E(A) difference, as other tested DFT methods do.⁵³ In the complex with camphor, the tunnelling is expected to be quenched.

The exploration of the shallow potential energy surface for RR and SR complexes using the four conformational searches (as described in Section 2.1) rendered a total of 18 and 15 isomers, respectively, with relative energies within 5 kJ mol⁻¹. The nomenclature of the camphor-fenchol complexes throughout this manuscript will follow the example “RR-A-a-(I)”, where “RR” refers to (R)-camphor – (R)-fenchol, “A” refers to the fenchol conformer, “a” refers to the binding site of camphor (Fig. 3), and (I) is related to the corresponding relative energy ordering (Table 1). The four qualitatively different binding sites (a–d) result from the non-equivalence of the two lone pairs of the carbonyl oxygen of camphor and pronounced preferences for out-of-carbonyl-plane coordination, represented by the four quadrants of the τ(C3–C2=O⋯H) dihedral angle.

Fig. 3 Schematic representation of the preferred binding sites for (R)- and (S)-camphor.

Table 1 Computational results at the B3LYP-D3(BJ)/def2-TZVP level of theory for the lower-energy RR and SR complexes with relative energies within 3.0 kJ mol⁻¹

	RR-A-a-(I)	RR-A-c-(II)	RR-A-b-(III)	RR-B-b-(IV)	RR-B-a-(V)	RR-B-a-(VI)	RR-A-d-(VII)
a ΔE is the calculated zero-point corrected energy difference to the global minimum isomer within each diastereomeric dimer in kJ mol^−1. b ω(OH) is the harmonic OH stretching wavenumber in cm^−1. c I(OH) is the calculated integrated IR band strength of the OH stretching fundamental in km mol^−1 in the double-harmonic approximation. d A, B and C are the rotational constants in MHz. e B–C is the difference between the rotational constants B and C in MHz. f κ is Ray's asymmetry parameter: . g μ α (α = a, b or c) are the absolute values of the electric dipole moment components in D.
ΔE^a	0.0	0.7	1.3	2.0	2.4	2.8	3.0
ω(OH)^b	3631	3655	3606	3640	3625	3692	3647
I(OH)^c	483	473	746	419	594	263	723
A/B/C	581.1/156.1/149.5	597.6/155.4/147.8	629.9/135.2/132.6	593.9/160.4/151.0	598.3/145.2/141.2	560.4/160.5/155.4	625.0/135.3/132.4
B–C^e	6.6	7.6	2.6	9.4	4.0	5.1	2.9
κ	−0.97	−0.97	−0.99	−0.96	−0.98	−0.97	−0.99
μ a/μb/μc^g	4.0/0.8/1.8	4.3/0.2/2.4	3.6/1.1/1.1	3.5/1.3/2.1	3.3/1.0/1.1	2.4/0.7/0.9	4.7/1.2/0.1

---

	SR-A-b-(I)	SR-A-d-(II)	SR-A-a-(III)	SR-B-b-(IV)	SR-A-a-(V)	SR-B-a-(VI)	SR-A-c-(VII)
ΔE^a	0.0	1.4	1.8	2.6	2.6	2.6	2.6
ω(OH)^b	3648	3680	3598	3652	3684	3624	3661
I(OH)^c	363	385	779	429	348	539	463
A/B/C	598.5/161.5/152.0	581.1/163.2/153.9	600.8/135.8/131.7	615.7/148.9/146.9	562.6/153.2/148.7	575.1/154.2/146.7	590.5/149.0/143.8
B–C^e	9.5	9.3	4.1	2.0	4.5	7.6	5.3
κ	−0.96	−0.96	−0.98	−0.99	−0.98	−0.96	−0.98
μ a/μb/μc^g	3.5/1.1/1.9	4.3/0.5/2.2	3.7/0.5/1.1	2.8/0.5/1.8	2.4/0.6/1.0	3.8/1.3/1.6	3.8/1.3/1.6

---

The theoretical spectroscopic parameters and relative energies for the isomers with relative energies below 3 kJ mol⁻¹ are listed in Table 1, and their structures are shown in Fig. 4 (see the ESI‡ for a complete list of isomers with relative energies up to 5 kJ mol⁻¹). The SR global minimum is 0.4 kJ mol⁻¹ lower in energy than the lowest-energy RR complex. In all of the energetically relevant RR and SR camphor-fenchol complexes, camphor and fenchol interact via an O–H⋯O hydrogen bond and non-covalent C–H⋯O and C–H⋯H–C interactions (see NCI analysis Section for further explanations and Fig. S1, ESI‡). Isomers without an O–H⋯O hydrogen bond are predicted to be at least 15 kJ mol⁻¹ less stable than the global minimum structures.

Fig. 4 Molecular structures and zero point corrected relative energies (ΔE, kJ mol⁻¹) of the most stable RR and SR isomers calculated at the B3LYP-D3(BJ)/def2-TZVP computational level.

The lowest-energy structures of the RR and SR complexes involve the fenchol conformer A interacting with either (S)- or (R)-camphor, respectively. Fenchol B appears in camphor–fenchol complexes not lower than 2.0 (RR) and 2.6 kJ mol⁻¹ (SR), and fenchol C is involved in isomers with relative energies of at least 3.1 (RR) and 3.7 kJ mol⁻¹ (SR) (see Fig. 4 and Table 1, and the ESI‡). This amplification of the energy ordering relative to the fenchol monomer is further discussed at the end of Section 4.1.

3.2 FTIR spectroscopy

In the top trace of Fig. 5, an FTIR jet spectrum of (R)-fenchol seeded in helium is shown. Two bands at 3675 and 3666 cm⁻¹ were assigned to monomer transitions from the vibrational ground state to different torsional levels of the OH stretch excited state.⁵³ An intense signal downshifted at 3499 cm⁻¹ was attributed to the most stable dimer consisting of two (R)-fenchol molecules with conformer A as the donor and C as the acceptor for the hydrogen bond.⁵³ These three fenchol absorption bands remain visible when camphor is added. The admixture of (S)-camphor results in an additional signal at 3517 cm⁻¹, while in contrast the addition of (R)-camphor leads to a band at 3504 cm⁻¹, with signal-to-noise ratios of about 4 : 1 for both. Confirming the achieved enantiodifferentiation, the two resolved signals are present with similar intensities when using racemic camphor. This is a result of the widely statistical formation of SR and RR complexes, which cannot interconvert into each other. Signal intensities between different experiments cannot be straightforwardly compared due to challenges in reproducibly reaching the full vapor pressures. This can be attributed to the dependence of the evaporation rate on the changing surface area of solid compounds, which applies to both camphor and fenchol. In addition, a control spectrum of racemic camphor without fenchol was recorded, which was found to be free of any detectable absorption in the OH stretching region (not shown).

Fig. 5 FTIR jet spectra of (+)-(R)-fenchol in helium without and with admixtures of camphor in different enantiomeric compositions.

A direct comparison of the observed fundamental wavenumbers with the calculated harmonic predictions of mixed fenchol–camphor dimers is not possible due to anharmonicity. However, as applied to alcohol monomers,⁵⁴ one can assume that the OH stretching oscillators are again in similar enough environments that the anharmonic contributions are alike and therefore widely cancel when analyzing spectral differences. This proved to be a successful assumption for predicting the extent to which different alcohols, including fenchol, show spectral chirality recognition with α-pinene, also using B3LYP-D3(BJ).⁵⁵ Accordingly, the observed downshift of 13 cm⁻¹ upon switching from (S)- to (R)-camphor is in good agreement with the predicted one of 17 cm⁻¹ between the global minimum structures SR-A-b-(I) and RR-A-a-(I) (Table 1). Considerably less likely, but not entirely unreasonable, would be alternative assignments to the two second lowest-energy isomers SR-A-d-(II) and RR-A-c-(II) (with an energetic disadvantage of 1.4 and 0.7 kJ mol⁻¹, respectively) with a calculated downshift of 25 cm⁻¹ between them. This alternative assignment can be ruled out with microwave spectroscopy (vide infra).

3.3 Chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy

The top traces of Fig. 6(a–d) show several sections of the experimental broadband rotational spectra of the (R)-camphor – (R)-fenchol (RR) (Fig. 6a and b) and (S)-camphor – (R)-fenchol (SR) complexes (Fig. 6c and d) recorded in the 2–8 GHz region. The bottom traces correspond to simulations based on an asymmetric-top Hamiltonian using the experimentally determined rotational constants for the complexes. In Table 2, these experimental rotational constants are summarized, whereas those computed at the B3LYP-D3(BJ)/def2-TZVP level of theory are given in Table 1 for the lowest-energy isomers (≤3 kJ mol⁻¹).

Fig. 6 Sections of the broadband rotational spectra of RR (a and b) and SR (c and d) camphor-fenchol complexes. The upper traces depict the experimental spectra, while the lower traces are simulations of the experimentally identified complexes based on fitted rotational parameters (Table 2) using the corresponding rotational partition functions at 1.0 K. Some intense monomer transitions have been removed for the sake of clarity.

Table 2 Comparison between experimental and theoretical (B3LYP-D3(BJ)) spectroscopic constants of the assigned RR and SR complexes

	Exp. RR	Theor. RR-A-a-(I)	Exp. SR	Theor. SR-A-b-(I)
a A, B, and C are the rotational constants; ΔJ, ΔJK, ΔK and δJ are the quartic centrifugal distortion constants. b κ is Ray's asymmetry parameter: . c a, b, and c are the type of transitions observed. d N is the number of fitted transitions. e σ is the root-mean square deviation of the fit. f 1σ standard error in parentheses in units of the last digit.
A (MHz)^a	580.77281(19)^f	581.1	597.58944(23)	598.5
B (MHz)	153.464146(55)	156.1	159.011164(60)	161.5
C (MHz)	146.840175(55)	149.5	149.704572(60)	152.0
B–C (MHz)	6.623971(55)	6.6	9.306592(60)	9.5
κ	−0.97	−0.97	−0.96	−0.96
ΔJ (kHz)	0.008025(55)	0.006800	0.007228(61)	0.006593
ΔJK (kHz)	0.03078(89)	0.016765	0.0113(15)	0.004353
ΔK (kHz)	−0.0208(20)	−0.007785	-	0.000385
δ J (kHz)	−0.000259(43)	0.000180	0.000314(46)	0.000368
a/b/c	131/108/155	-	132/63/101	-
N	394	-	296	-
σ (kHz)^e	7.1	-	7.8	-

---

Only one isomer for each RR and SR complex was identified under the cold conditions of the supersonic expansion using neon as a carrier gas. Their spectra are quite weak, with signal-to-noise ratios of around 11 : 1 (RR) and 13 : 1 (SR) for the most intense transitions. Consequently, we could not observe rotational transitions corresponding to singly substituted ¹³C isotopologs of these complexes in natural abundance, which would have provided us with the experimental structures of the complexes. Instead, our structures were identified through comparison of the rotational parameters with the results from quantum–chemical calculations. The different relative orientations of camphor and fenchol cause only small changes in the mass distribution of the complexes due to their roughly spherical shapes. For this reason, the predicted rotational constants for the different RR and SR isomers are quite similar (Table 1). This complicates an assignment based on the rotational constants alone. However, their electric charge distributions change with the different arrangements within the complexes (see Table 1), resulting in differences in the permanent electric dipole-moment components. In all the predicted complexes, μ_a is the largest dipole moment component, whereas the μ_b : μ_c ratio varies, which can be used as a guide for the assignment.

In the CP-FTMW experiment, the intensities of rotational transitions depend on the square of the respective dipole-moment components.⁵⁶ The experimentally determined RR and SR complexes showed a-, b-, and c-type rotational transitions, with their experimental relative intensities leading to an ordering of the magnitudes of the dipole-moment components of μ_a > μ_c > μ_b for both diastereomers. Additionally, the μ_b value is approximately half of the μ_c value for both RR and SR (Fig. 6a and c). This ratio was obtained using the following procedure with the PGOPHER⁵⁷ and SPCAT programs, based on the experimental rotational constants: We systematically introduced different μ_b and μ_c values in these programs, resulting in simulated rotational spectra with different intensities for the b- and c-type rotational transitions. These simulated intensities were then compared with those of the experimental rotational spectra (see Fig. 6a and c), and the best correspondence was a μ_b : μ_c ratio of 1 : 2 in both RR and SR complexes. The simulations of the rotational spectra were made using the corresponding rotational partition functions at 1.0 K (see below), which resulted to be the temperature that best resembled the overall intensity patterns.

The comparison of the predicted and experimentally observed transition intensities for the RR complex indicates that either RR-A-a-(I), RR-B-b-(IV) or RR-B-d-(XVI) could be the isomer present in our experiment. The agreement between the experimental and calculated (B3LYP-D3(BJ)/def2-TZVP) rotational constants is better for RR-A-a-(I) and RR-B-d-(XVI) than for RR-B-b-(IV). Relative values, such as the differences between the B–C rotational constants, are often predicted better by quantum-chemical computations than absolute values. The B–C difference for the RR-A-a-(I) isomer (6.6 MHz), which is calculated to be the global minimum, agrees up to the first decimal digit with the experimental value. In contrast, those calculated for RR-B-b-(IV) and RR-B-d-(XVI) are 9.4 MHz and 10.7 MHz, respectively. All these observations, together with the predicted higher relative energy (4.5 kJ mol⁻¹) for RR-B-d-(XVI), point to the presence of RR-A-a-(I) in our experiment. We also performed a re-optimization of the four lowest-energy isomers (<2 kJ mol⁻¹) and RR-B-d-(XVI) at the B97-3c/def2-TZVP level to evaluate the robustness of the relative energy values. The B97-3c approach is also a recommended functional to treat non-covalent interactions.^37,58 The calculations using B97-3c/def2-TZVP gave similar results as using B3LYP-D3(BJ) in terms of the relative energies and dipole moment components. RR-B-d-(XVI) is predicted to be even higher in energy (5.7 kJ mol⁻¹) by B97-3c than by B3LYP-D3(BJ) (4.5 kJ mol⁻¹), thereby further strengthening our assignment to RR-A-a-(I).

The assignment of the SR complex is more straightforward. The molecular parameters of SR-A-b-(I), the calculated global minimum, agree the best with the parameters of the experimentally observed SR diastereomer in terms of rotational constants, B–C difference, and the observed transition intensities. Note that also other isomers of somewhat higher relative energy agree quite well with the experimental values, such as SR-A-c-(VII). It shows good agreement with the experimental isomer in terms of the dipole-moment components, but its B–C difference is only 5.3 MHz compared to the experimental B–C value (9.3 MHz) and 9.5 MHz for SR-A-b-(I). SR-B-a-(VI) shows a predicted ordering of μ_a > μ_c > μ_b, but their calculated rotational constants agree less with the experimental ones than those of SR-A-b-(I). SR-B-a-(VI) and SR-A-c-(VII) are 2.6 kJ mol⁻¹ higher in energy than SR-A-b-(I). Like in the RR case, we also reoptimized these three isomers at the B97-3c/def2-TZVP level of theory, and SR-B-a-(VI) and SR-A-c-(VII) turned out to be 3.4 kJ mol⁻¹ higher in energy than SR-A-b-(I) at that level of theory.

As mentioned above, the simulations of the rotational spectra were made using the corresponding rotational partition functions at 1.0 K. Using the predicted dipole moment components for RR and SR (Table 1), the agreement between the simulated and experimental rotational spectra is acceptable considering that the intensities are also affected by the nonlinear response of the microwave electronics, especially the high-power amplifiers. The largest disagreements appeared for the a-type transitions (Fig. 6, panels b and d). This can be rationalized considering that these discrepancies might be caused by the large magnitude of μ_a. This has most likely led to an overdriving of the a-type transitions through the population transfer phenomenon that affects the intensities. In the work on benzonitrile,⁴⁵ it was demonstrated that this effect takes place for a molecule with a 4 D dipole moment. Altogether, it can be concluded that the experimental intensities are satisfactorily reproduced by the simulations.

4 Discussion

4.1 Isomerism

Strikingly, the global minima were only identified by two of the four employed conformational search procedures, namely by the manual approach and by the GFN-xTB program with its CREST driver. This highlights the importance to check and rationalize the results of automatic procedures. Otherwise, one risks misassignments for isomers with similar spectroscopic properties, such as the ones investigated here. Automatic search algorithms can be considered at this time as a valuable supplement but not yet a reliable substitute for the chemist's intuition in combination with a systematic conformational evaluation. Structure generation from experimental data of rare isotopologs^59–62 or using isotopic enrichment^18,59,61,62 is a powerful alternative to solve difficult cases.⁶³ However, for weakly bound complexes consisting of larger molecules, as presented in the present work, the signal-to-noise ratios of the corresponding rotational transitions are often not sufficient to detect rare isotopologs in natural abundance, and isotopically enriched samples can be expensive or not available.

In the two most stable RR and SR complexes, independently assigned with vibrational and rotational spectroscopy, camphor is coordinated on the free electron pair on the secondary C3 side. This resembles previous findings with other hydrogen bond donors. However, it is notable that (R)-fenchol shows a binding preference to two different camphor sites depending on camphor's absolute handedness (a for RR and b for SR). For both enantiomer combinations, the second most stable isomer is predicted to feature a coordination with the alternative free electron pair with an energy disadvantage of 0.7 (RR) and 1.4 kJ mol⁻¹ (SR), indicating some impact of relative chirality on this balance. A more pronounced analogous effect in the camphor complex with protonated alanine was used to explain the observed difference in the fragmentation rate.⁶ Due to the limited low signal-to-noise ratios, we can only assess rough lower bounds for these energy differences in camphor – fenchol. Based on the signal-to-noise ratios in the FTIR spectra, calculated IR activities and an assumed conformational Boltzmann temperature of 60 K (as a typical value for a low-barrier situation in a helium expansion)^64,65 we estimate an energy difference of at least 0.7 kJ mol⁻¹ for both RR and SR. The predictions are therefore compatible with the non-observation of these isomers. If one instead assumes that the relaxation was hindered, i.e., a conformational freezing temperature of more than 100 K, one would expect more than one isomer to be detectable (or none at all in the case of mostly statistical formation with associated intensity dilution). The observation of only a single structure each suggests that even two rather large molecules can efficiently obtain their preferred docking orientation in a supersonic jet.

In both global minima, fenchol adopts the A conformation. This result resembles the one of an FTIR spectroscopy study on the fenchol – α-pinene complex,⁵⁵ in which fenchol was also found in the A arrangement for all three assigned isomers. Fenchol C is less energetically stable in these complexes because its hydroxy group points towards the hydrogen atoms of the bicyclic methylene groups, which apparently hinders its approach to a hydrogen bond acceptor (Fig. 2). It is interesting that when fenchol interacts with water,⁶⁶ in contrast only the C conformer was observed experimentally. Here, water acts as the hydrogen bond donor, whereas fenchol is instead the hydrogen bond acceptor. This preference was attributed to the orientation of the hydroxy group in fenchol C, which grants the formation of two intermolecular interactions between water and the two geminal methyl groups of fenchol. These two interactions cannot be formed for fenchol A interacting with water, since the OH points towards these geminal methyl groups. However, we note that this reasoning does not explain the preference of fenchol C over B, which permits equivalent interactions.

4.2 Non-covalent interactions and energy decomposition analyses

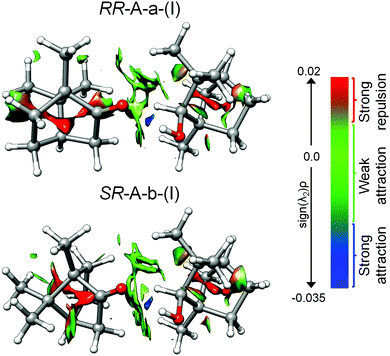
The non-covalent interaction (NCI) analysis provides a visualization and characterization of the different interactions present in the camphor-fenchol complexes as hydrogen bonds (strong attraction, blue color), van der Waals (weak attraction, green color), and steric (strong repulsion, red color) interactions (Fig. 7). The NCI plots of the camphor–fenchol complexes below 2 kJ mol⁻¹ are quite similar. In Fig. 7 we show the results for the two global minima (RR and SR) as representative examples (see ESI‡ for more complexes). In order to facilitate the following discussion, the naming scheme of RR-A-a-(I) and SR-A-b-(I) is reduced to RR and SR, respectively. Camphor and fenchol are linked via an O_camphor⋯H–O_fenchol (1.91 Å for RR and 1.94 Å for SR) hydrogen bond, as stated before, and also through two O_camphor⋯H–C_fenchol (2.87 Å for RR and 2.95 Å for SR), one C–H_camphor⋯O_fenchol (2.88 Å for RR and 2.65 Å for SR), and multiple C–H_camphor⋯H–C_fenchol (2.21–3.12 Å for RR and 2.42–2.97 Å for SR) contacts (Fig. S1, ESI‡). The monomers are further stabilized by intramolecular O⋯H–C and C–H⋯H–C interactions. Despite the difference that (R)-fenchol links to (R)- or (S)-camphor via the respective “a” or “b” arrangement, the interactions that they establish appear qualitatively similar. As pointed out in Section 3.1, the energy difference between the RR and SR global minima is just 0.4 kJ mol⁻¹, which can be assumed to be isoenergetic considering the uncertainties of the quantum-chemical calculations. Because the interconversion between SR and RR isomers is not feasible, their energy sequence is not plumbable with our experimental techniques, but could in principle be investigated by the measurement and comparison of their dissociation energies.⁶⁷ However, the small difference and the lack of a UV chromophore pose challenges.

Fig. 7 Non-covalent interaction (NCI) representations for the lowest-energy RR and SR complexes. Blue color shows strong attractive interactions, green represents weak attractive interactions such as dispersion, and red indicates repulsive interactions.

Symmetry-adapted perturbation theory (SAPT) computations were performed for quantitative insight into the different binding contributions to the dissociation energies. In Table 3, the results of SAPT(0)/jun-cc-pVDZ calculations are summarized for the camphor-fenchol complexes below 2 kJ mol⁻¹. RR-A-a-(I) and SR-A-b-(I) present the highest total interaction energy values, which further supports – together with the statements made in Sections 3.2. and 3.3. – their assignments as the experimentally observed isomers.

Table 3 SAPT(0) energies for the RR and SR complexes below 2.0 kJ mol⁻¹ and comparison with the SAPT(0) energies for related complexes.^18,20 The energies are given in kJ mol⁻¹

	ΔEelect	ΔEind	ΔEdisp	ΔEexch	ΔEtot
RR-A-a-(I)	−47.8	−16.3	−32.5	56.5	−40.1
RR-A-c-(II)	−47.6	−15.9	−33.3	57.3	−39.4
RR-A-b-(III)	−51.8	−17.0	−27.5	56.8	−39.4
RR-B-b-(IV)	−44.2	−15.2	−34.3	56.1	−37.6
SR-A-b-(I)	−46.8	−15.0	−35.1	56.5	−40.4
SR-A-d-(II)	−43.9	−14.2	−34.7	53.3	−39.6
SR-A-a-(III)	−52.4	−17.2	−26.1	56.3	−39.3
Camphor–H2O	−49.2	−14.6	−11.6	43.6	−31.8
Camphor–MeOH-I	−45.8	−14.1	−14.3	44.2	−30.0
Camphor–EtOH-I	−47.4	−14.3	−18.6	47.2	−33.1

---

Some interesting differences in the composition of the interactions between isomers are revealed. SR-A-b-(I) draws its energetic advantage mainly from the overall highest dispersion interaction, while the electrostatic and inductive contributions are only of medium size when compared to other isomers such as RR-A-b-(III) and SR-A-a-(III). In contrast, the dispersion contribution for RR-A-a-(I) is slightly smaller than that for SR-A-b-(I), which correlates with its three rotational constants being smaller than those of SR-A-b-(I), reflecting a less compact mass distribution. In return, RR-A-a-(I) has slightly larger electrostatic and inductive contributions than SR-A-b-(I), which could indicate a stronger hydrogen bond than in SR-A-b-(I). This is supported by the sequences of the calculated and observed OH stretching wavenumbers as well as of the calculated infrared activities (Table 1). The achieved enantiodifferentiation with vibrational spectroscopy in the OH stretching region is ultimately enabled by this difference in hydrogen bond strength. It can be also rationalized on structural terms. Geometric parameters, which were found to correlate with differences in OH stretching wavenumbers between isomers of alcohol-ketone complexes, are the hydrogen bond donor attack angle to the carbonyl group α(C2=O⋯H) and the out-of-carbonyl-plane dihedral angle τ(C3–C2=O⋯H).^15–17 One might amend this with the hydrogen bond linearity angle β(O⋯H–O).⁶⁸ In RR-A-a-(I), the values of all three angles are closer to their assumed respective optima (α = 120°, τ = 0°/180°, β = 180°) than in SR-A-b-(I). The stronger hydrogen bond is also reflected by a shorter O⋯H interaction distance and a longer H–O covalent bond in RR-A-a-(I). Details are given in Table S4 in the ESI.‡

Two isomers, for which the hydrogen bond strength is maximized, are RR-A-b-(III) and SR-A-a-(III). Their respective hydroxy hydrogen atom is close to the carbonyl plane, and their hydrogen bond angles are not far from linearity. This arrangement closely resembles the main isomer of the camphor–water complex.¹⁸ However, this geometry increases the distance between the hydrocarbon frameworks of the two molecules. This is of little concern for water, but strongly reduces the dispersion interaction for alcohols, so that a better compromise structure is realized already for the smallest alcohol methanol.²⁰ One isomer on the other end of such a trade-off is SR-A-d-(II) with an especially weak hydrogen bond but strong dispersion attraction and low exchange repulsion. Interestingly, the latter is very uniform for the other low-energy isomers.

An interesting comparison can be made with the series of camphor–H₂O,¹⁸ -methanol (MeOH)²⁰ and -ethanol (EtOH)²⁰ complexes, whose SAPT energies were also computed at the SAPT(0)/jun-cc-pVDZ level. Camphor–fenchol shows the highest total interaction energies, followed by the other complexes, i.e., camphor–EtOH, –MeOH, and –H₂O, which have comparable values. This is primarily due to the additional dispersion interactions (O⋯H–C and C–H⋯H–C) that further stabilize the structures of the camphor–fenchol complexes. It can be observed how the share of the dispersion contributions progressively increases with the size of the alcohol partner (see Table 3). This finding also ensued in a recent study on diadamantyl ether (DAE)-alcohol aggregates with increasing side-chain length.⁶⁹

5 Conclusions

We presented a vibrational and rotational spectroscopic study of mixed dimers between either of the two enantiomers of camphor with (R)-fenchol, supported by quantum-chemical calculations. The global minimum of each stereoisomer was experimentally identified under the cold conditions of supersonic jets. Both (R)-camphor and (S)-camphor coordinate to (R)-fenchol via the free electron pair on the secondary C3 side, while (R)-fenchol shows a binding preference to two different camphor sites depending on camphor's absolute handedness. In both complexes, the two monoterpenoids interact via an O–H⋯O hydrogen bond and non-covalent C–H⋯O and C–H⋯H–C interactions. Non-hydrogen bonded clusters are not observed and are predicted to have much higher relative energies. The SR isomer features larger London dispersion contributions than RR, which correlates with a more compact structure and larger rotational constants. In contrast, the RR isomer has slightly larger electrostatic and inductive contributions than SR; this difference in the hydrogen bond strength and thus OH stretching fundamental wavenumber allowed the discrimination of the camphor enantiomers in the complex with fenchol by vibrational spectroscopy. This work illustrates how chirality can dictate binding preferences in the gas phase and could contribute to the understanding of its influence in molecular aggregation. It may also help to understand at least qualitatively why olfactory discrimination of camphor enantiomers has been challenging for evolution. Or perhaps there was simply no important driving force.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Deutsche Forschungsgemeinschaft (SCHN1280/4-2 project number 271359857 and Su 121/5-2 project number 271107160) in the context of the priority program SPP 1807 “Control of London dispersion interactions in molecular chemistry”. We acknowledge the use of the GWDG computer cluster. M.M.Q.M. thanks Fundación Alfonso Martín Escudero for a postdoctoral grant and Ministerio de Ciencia, Innovación y Universidades for a Juan de la Cierva formación contract (fellowship FJC2018-035709-I funded by MCIN/AEI/10.13039/501100011033). Helpful discussions with M. A. Suhm are acknowledged.

Notes and references

1. M. Laska and P. Teubner, Chem. Senses, 1999, 24, 161.
2. L. Rizvanovic, M. Amundin and M. Laska, Chem. Senses, 2013, 38, 107.
3. M. Laska and G. M. Shepherd, Neuroscience, 2007, 144, 295.
4. A. R. Al-Rabaa, E. Bréhéret, F. Lahmani and A. Zehnacker, Chem. Phys. Lett., 1995, 237, 480.
5. F. Lahmani, K. Le Barbu and A. Zehnacker-Rentien, J. Phys. Chem. A, 1999, 103, 1991.
6. A. Sen, K. Le Barbu-Debus, D. Scuderi and A. Zehnacker-Rentien, Chirality, 2013, 25, 436.
7. K. Le Barbu, V. Brenner, P. H. Millié, F. Lahmani and A. Zehnacker-Rentien, J. Phys. Chem. A, 1998, 102, 128.
8. A. Zehnacker and M. A. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970.
9. L. Evangelisti, W. Caminati, D. Patterson, J. Thomas, Y. Xu, C. West and B. Pate, The 72nd International Symposium on Molecular Spectroscopy, Talk RG03, Urbana-Champaign, IL, 2017.
10. B. H. Pate, L. Evangelisti, W. Caminati, Y. Xu, J. Thomas, D. Patterson, C. Pérez and M. Schnell, in Chiral Analysis: Advances in Spectroscopy, Chromatography and Emerging Methods, Quantitative Chiral Analysis by Molecular Rotational Spectroscopy, ed. P. L. Polavarapu, Elsevier, Amsterdam, 2018, ch. 17, pp. 679–730.
11. S. R. Domingos, C. Pérez, M. D. Marshall, H. O. Leung and M. Schnell, Chem. Sci., 2020, 11, 10863.
12. J. L. Neill, A. V. Mikhonin, T. Chen, R. E. Sonstrom and B. H. Pate, J. Pharm. Biomed., 2020, 189, 113474.
13. J. R.-A. Moreno, T. R. Huet and J. J.-L. González, Struct. Chem., 2013, 24, 1163.
14. S. R. Domingos, C. Pérez, C. Medcraft, P. Pinacho and M. Schnell, Phys. Chem. Chem. Phys., 2016, 18, 16682.
15. C. Zimmermann, H. C. Gottschalk and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 2870.
16. C. Zimmermann, T. L. Fischer and M. A. Suhm, Molecules, 2020, 25, 5095.
17. C. Zimmermann, M. Lange and M. A. Suhm, Molecules, 2021, 26, 4883.
18. C. Pérez, A. Krin, A. L. Steber, J. C. López, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 154.
19. P. Banerjee, P. Pandey and B. Bandyopadhyay, Spectrochim. Acta, Part A, 2019, 209, 186.
20. M. Fatima, C. Pérez and M. Schnell, Manuscript in preparation. Side chain length inducing dispersion interaction in camphor-alcohol complexes.
21. I. Schlichting, C. Jung and H. Schulze, FEBS Lett., 1997, 415, 253.
22. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173.
23. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989.
24. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652.
25. E. M. Neeman and T. R. Huet, Phys. Chem. Chem. Phys., 2018, 20, 24708.
26. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169.
27. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
28. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
29. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
30. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
31. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision E.01), Gaussian Inc., Wallingford CT, 2009.
33. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73.
34. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
35. A. D. Becke, J. Chem. Phys., 1997, 107, 8554.
36. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
37. J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104.
38. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498.
39. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887.
40. R. M. Parrish, L. A. Burns, D. G.-A. Smith, A. C. Simmonett, A. Eugene DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. D. Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185.
41. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.
42. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin., J. Comput. Chem., 2004, 25, 1605.
43. J. Dykyj, H. Landolt, R. Börnstein and W. Martienssen, Numerical data and functional relationships in science and technology: new series. Group 4 Vol. 20 Subvol. b: Physical chemistry Vapor pressure of chemicals Vapor pressure and Antoine constants for oxygen containing organic compounds, ed. K. R. Hall, O. Madelung, Springer, Berlin, 2000.
44. M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702.
45. D. Schmitz, V. Alvin Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77.
46. C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1.
47. D. Plusquellic, JB95, available at https://www.nist.gov/pml/electromagnetics/grp05/jb95.cfm.
48. Z. Kisiel in Assignment and Analysis of Complex Rotational Spectra. In Spectroscopy from Space, ed. Demaison J.et al., Kluwer Academic Publishers, Dordrecht, 2001, pp. 91–106.
49. Z. Kisiel, L. Pszczółkowski, I. R. Medvedev, M. Winnewisser, F. C. De Lucia and E. Herbst, J. Mol. Spectrosc., 2005, 233, 231.
50. Z. Kisiel, L. Pszczółkowski, B. J. Drouin, C. S. Brauer, S. Yu, J. C. Pearson, I. R. Medvedev, S. Fortman and C. Neese, J. Mol. Spectrosc., 2012, 280, 134.
51. H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371.
52. Z. Kisiel, O. Desyatnyk, E. Białkowska-Jaworska and L. Pszczjłkowski, Phys. Chem. Chem. Phys., 2003, 5, 820.
53. R. Medel, J. R. Springborn, D. L. Crittenden and M. A. Suhm, Molecules, 2022, 27, 101.
54. R. Medel and M. A. Suhm, Phys. Chem. Chem. Phys., 2021, 23, 5629.
55. R. Medel, C. Stelbrink and M. A. Suhm, Angew. Chem., Int. Ed., 2019, 58, 8177.
56. G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103.
57. C. M. Western, PGOPHER, a Program for Simulating Rotational, Vibrational and Electronic Structure, https://pgopher.chm.bris.ac.uk.
58. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184.
59. C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Science, 2012, 336, 897.
60. N. A. Seifert, D. P. Zaleski, C. Pérez, J. L. Neill, B. H. Pate, M. Vallejo-López, A. Lesarri, E. J. Cocinero, F. Castaño and I. Kleiner, Angew. Chem., 2014, 126, 3274.
61. J. A. Smith, K. B. Wilson, R. E. Sonstrom, P. J. Kelleher, K. D. Welch, E. K. Pert, K. S. Westendorff, D. A. Dickie, X. Wang, B. H. Pate and W. D. Harman, Nature, 2020, 581, 288.
62. H. S.-P. Müller, M. Ananya Brahmi, J.-C. Guillemin, F. Lewen and S. Schlemmer, Astron. Astrophys., 2021, 647, A179.
63. F. Xie, M. Fusè, A. S. Hazrah, W. Jäger, V. Barone and Y. Xu, Angew. Chem., Int. Ed., 2020, 59, 22427.
64. R. Medel and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 25538.
65. T. N. Wassermann and M. A. Suhm, J. Phys. Chem. A, 2010, 114, 8223.
66. E. M. Neeman and T. R. Huet, Phys. Chem. Chem. Phys., 2021, 23, 2179.
67. J. A. Frey, C. Holzer, W. Klopper and S. Leutwyler, Chem. Rev., 2016, 116, 5614.
68. J. Kroon and J. A. Kanters, Nature, 1974, 248, 667.
69. M. M. Quesada-Moreno, P. Pinacho, C. Pérez, M. Šekutor, P. R. Schreiner and M. Schnell, Chem. – Eur. J., 2020, 26, 10817.

---

Footnotes

† Dedicated to the memory of Markus Gerhards.

‡ Electronic supplementary information (ESI) available: RR-A-a-(I) and SR-A-b-(I) structures highlighting the main interactions, NCI plots and scatter graphs, computed rotational parameters, experimental vibrational fundamental transitions and assignments, computed structural hydrogen bond parameters for camphor complexes, SAPT(0) energies for the RR and SR complexes and comparison with those from other works, line lists with all fitted rotational transitions, Gaussian input and optimized coordinates, and number of isomers found with each conformational search. See DOI: https://doi.org/10.1039/d2cp00308b

§ These authors contributed equally to this work.

---