Open Access Article
Open Access ArticleMultipole-moment effects in ion–molecule reactions at low temperatures: part III – the He+ + CH4 and He+ + CD4 reactions at low collision energies and the effect of the charge-octupole interaction
Valentina
Zhelyazkova
 ,
Fernanda B. V.
Martins
,
Fernanda B. V.
Martins
 and
Frédéric
Merkt
and
Frédéric
Merkt
 *
*
ETH Zurich, Zurich, Switzerland. E-mail: merkt@phys.chem.ethz.ch
First published on 8th June 2022
Abstract
We present experimental and theoretical studies of the He+ + CH4 and He+ + CD4 reactions at collision energies in the kB·(0–10) K range. Helium atoms in a supersonic beam are excited to a low-field-seeking Rydberg–Stark state and merged with a supersonic beam of CH4 or CD4 using a curved surface-electrode deflector. The ion–molecule reactions are studied within the orbit of the helium Rydberg [He(n)] electron, which suppresses stray-electric-fields-induced heating and makes it possible to reach very low collision energies. The collision energy is varied by adjusting the velocity of the He(n) atoms with the surface deflector, keeping the velocity of the methane beam constant. The reaction product ions (C(H/D)p+ with p∈ {1,2,3}) are collected in a time-of-flight mass spectrometer and monitored as a function of the collision energy. No significant energy-dependence of the total reaction yields of either reactions is observed. The measured relative reaction rate coefficient for the He+ + CH4 reaction is approximately twice higher than the one for the He+ + CD4 reaction. The CH+, CH2+ and CH3+ (CD+, CD2+ and CD3+) ions were detected in ratios 0.28(±0.04)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.00(±0.11)
1.00(±0.11)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.11(±0.04) [0.35(±0.07)
0.11(±0.04) [0.35(±0.07)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.00(±0.16):0.04+0.09−0.04]. We also present calculations of the capture rate coefficients for the two reactions, in which the interaction between the charge of the helium ion and the octupole moment of the methane molecule is included. The rotational-state-specific capture rate coefficients are calculated for states with J = (0–3) at collision energies below kB·15 K. After averaging over the rotational states of methane populated at the rotational temperature of the supersonic beam, the calculations only predict extremely weak enhancements (in the order of ∼0.4%) of the rate coefficients compared to the Langevin rate constant kL over the collision-energy range considered.
1.00(±0.16):0.04+0.09−0.04]. We also present calculations of the capture rate coefficients for the two reactions, in which the interaction between the charge of the helium ion and the octupole moment of the methane molecule is included. The rotational-state-specific capture rate coefficients are calculated for states with J = (0–3) at collision energies below kB·15 K. After averaging over the rotational states of methane populated at the rotational temperature of the supersonic beam, the calculations only predict extremely weak enhancements (in the order of ∼0.4%) of the rate coefficients compared to the Langevin rate constant kL over the collision-energy range considered.
1 Introduction
Numerous ion–molecule reactions are barrierless and exothermic and proceed with high rate coefficients even at very low temperatures. These reactions play an important role in the chemistry of the tenuous (with number density <106 cm−3)1 and cold (10–150 K) environment of interstellar clouds.2 Precise knowledge of the absolute reaction rate coefficients and the branching ratios for different product channels is necessary as input parameters for kinetics models of the relevant chemical processes.1,3–5 Ion–molecule reactions at and above room temperature have been experimentally studied since the 1960s in drift-tube,6 flowing-afterglow,7 selected ion-flow tube8 and ion-cyclotron-resonance9 setups. The introduction of the uniform-supersonic-flow method to study ion–molecule reactions in the 1980s made it possible to reach temperatures down to ≈10 K.10 Such low temperatures can also be reached in experiments with sympathetically cooled ions in ion traps and guided ion beams.11–13 In recent years, techniques relying on the combination of trapped ions in Coulomb crystals and slow beams of molecules have been developed to study low-temperature ion–molecule chemistry.14,15In most experiments, stray electric fields in the reaction volume accelerate the ions, which prevents investigations below ∼10 K. This limitation is unfortunate, because it is precisely below 10 K that strong variations of the rate coefficients with the temperature or the collision energy are expected.16–24 Replacing the ion with an atom or molecule in a Rydberg state and merging the Rydberg sample with a supersonic beam containing the molecule of interest suppresses the heating of the ion core by stray electric fields and enables one to reach very low collision energies, down to ∼kB·100 mK,25–30 when studying the reactions within the Rydberg-electron orbit.
This article is the third in a series of three articles exploring the effect of the molecular electric multipole moments on ion–molecule reaction rate coefficients at low collision energies. The article series is dedicated to studies of the interactions between the He+ ion and molecules possessing either a dipole, a quadrupole or an octupole moment. In the series, we also develop and test the theoretical framework necessary for treating the ion-multipole-moment interactions and calculating the rotational-state-dependent capture rate coefficients at low collision energies. Experimentally, we reach collision energies close to 0 K in a merged-beam approach by replacing the He+ ion with a helium atom in a Rydberg state (referred to as He(n) henceforth). We vary the energy of the collision by varying the velocity of the He(n) atoms using a surface-electrode Rydberg–Stark deflector,27,29–31 and keeping the velocity of the molecular beam fixed.
In the first article of this series (Article I),29 the reaction between He+ and ammonia (both NH3 and ND3) was investigated in the kB·(0–40) K collision-energy range to characterise the effect of the charge–dipole interaction. A significant increase of the total reaction yield at the lowest collision energies was observed and attributed to the interaction between the dipole of the ammonia molecule and the He+-ion charge. In the second article (Article II),32 the He+ + N2 reaction was studied in the range of collision energies between 0 and kB·10 K and a suppression of ∼30% of the reaction yield was observed at the lowest collision energies compared to the reaction yield at Ecoll/kB≈10 K. This suppression was attributed to the interaction between the negative quadrupole moment (Qzz) of the N2 molecule and the He+ ion charge. In the current article, we extend these studies to reactions involving molecules that do not have a permanent dipole or quadrupole moment and present results on the He+ + CH4 and He+ + CD4 reactions in the kB·(0–10) K collision-energy range.
The lowest nonvanishing electric moment of methane is the octupole moment (ΩCH4 = 3.12 ea03).33 Interactions between oriented (in the case of the dipole) and aligned (in the case of the quadrupole) molecules and ions scale with the ion–molecule separation R as R−2 and R−3, respectively. In the case of the octupole moment the interaction scales as R−4. Because of the small value of ΩCH4 and the R−4− dependence of the charge-octupole-moment interaction, the reaction between methane and the helium ion is expected to be well described by the Langevin capture model down to very low collision energies. Our experiments are carried out to test this expectation. To complement the experimental observations, we present theoretical calculations of the rotational-state-dependent capture rate coefficients for the He+ + CH4 and He+ + CD4 reactions.
The current paper is organised as follows. After a short introduction to the He+ + CH4 reaction in the remainder of this introductory section, we briefly recapitulate the main aspects of the experimental setup and method in Section 2. The experimental results are then reported in Section 3. In Section 4, we present calculations of the rotational-state-dependent reaction rate coefficients for the rotational states of methane that are populated at the 6 K rotational temperature of the supersonic source (J≤2). Finally, we present the conclusions for this article and the three-article series in Section 5.
The reactions between He+ and methane at low temperatures and densities have relevance for the chemistry of the interstellar medium (ISM). Methane has been detected both in the gas phase and as ice in several interstellar molecular clouds,34 with an abundance estimated to be ∼10−3 that of carbon monoxide, the second most abundant molecule in the ISM after H2.35 Helium is the second most abundant species in the ISM, corresponding to about 25% of the primordial baryonic mass of the universe,36 and it can be ionised by cosmic rays to form He+.2 The ionisation energy of 4He (24.5874 eV)37 is higher than that of all neutral atomic and molecular species, and in particular much higher than the adiabatic ionization energy of CH4 (12.615 eV),38 and even higher than the dissociative ionisation energy of CH4.39
The reaction between methane and He+ has been studied at ∼300 K and ∼700 K in the 1970s and 1980s in drift-tube (DT),40 ion-cyclotron-resonance (ICR),41,42 selected-ion-flow-tube (SIFT)43 and flowing-afterglow (FA)44 experiments, and in the 2000s at higher collision energies in the 4–4000 e V range.45 The main reaction channels observed in several of the experiments conducted at 300 and 700 K are:
He+ + CH4 → H++ CH3+ He + 6.51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV eV | (R1) |
→ CH++ H2+ H + He + 4.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV eV | (R2) |
→ CH2++ H2+ He + 9.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV eV | (R3) |
→ CH3++ H + He + 10.26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV eV | (R4) |
→ CH4++ He + 11.97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV, eV, | (R5) |
2 Experimental setup
The experimental setup has been described in detail in Article I of the current series (see also ref. 27). Here we outline the details relevant to the study of the He(n) + CH4 and He(n) + CD4 reactions.The merged-beam apparatus consists of two supersonic beams produced by home-built short-pulse valves (pulse duration ∼20 μs, repetition rate 25 Hz) – one for the He and one for the ground-state (GS) methane beams. The two beams propagate along axes initially separated by a 5° angle. An electric discharge at the He valve orifice populates the metastable (1s)(2s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3S1 state of helium (referred to as He* below). After passing through two skimmers, the He* beam is crossed at right angles by a UV laser beam and is photoexcited in a dc electric field to a low-field-seeking Rydberg–Stark state [(n, k, m) = (30, 21, 0), referred to as He(n) below]. After excitation, the He(n) atoms are loaded into electric quadrupole traps formed above the surface of the 50-electrode Rydberg–Stark decelerator and deflected and merged with the GS supersonic beam. After the He(n) atoms are merged with the GS beam, they enter a Wiley–McLaren-type46 time-of-flight mass spectrometer (TOF-MS), where the reaction product ions are extracted toward a microchannel plate (MCP) detector in a direction perpendicular to the merged-beam propagation axis (see Fig. 1 of Article I). In the experiments described here, the helium valve is temperature-stabilised to 100.0 ± 0.1 K, resulting in a supersonic beam with a mean forward velocity of about 1000 m s−1. By setting the appropriate time-dependent potentials to the electrodes of the surface deflector, the trapped He(n) atoms can also be accelerated or decelerated to selected final velocities, vRyd, in the 750–1200 m s−1 range.
3S1 state of helium (referred to as He* below). After passing through two skimmers, the He* beam is crossed at right angles by a UV laser beam and is photoexcited in a dc electric field to a low-field-seeking Rydberg–Stark state [(n, k, m) = (30, 21, 0), referred to as He(n) below]. After excitation, the He(n) atoms are loaded into electric quadrupole traps formed above the surface of the 50-electrode Rydberg–Stark decelerator and deflected and merged with the GS supersonic beam. After the He(n) atoms are merged with the GS beam, they enter a Wiley–McLaren-type46 time-of-flight mass spectrometer (TOF-MS), where the reaction product ions are extracted toward a microchannel plate (MCP) detector in a direction perpendicular to the merged-beam propagation axis (see Fig. 1 of Article I). In the experiments described here, the helium valve is temperature-stabilised to 100.0 ± 0.1 K, resulting in a supersonic beam with a mean forward velocity of about 1000 m s−1. By setting the appropriate time-dependent potentials to the electrodes of the surface deflector, the trapped He(n) atoms can also be accelerated or decelerated to selected final velocities, vRyd, in the 750–1200 m s−1 range.
The GS-beam valve has an orifice diameter of ∼0.5 mm. It is operated with one of the following gases: (i) pure 12CH4, (ii) pure 12CD4, and (iii) a mixture of 13CH4 and 12CD4, corresponding to molar fractions of x (13CH4) = 0.479 and x (12CD4) = 0.521, determined from the weight of the gas cylinder before and after filling it with CH4 and CD4. For the measurements recorded with gas samples (i) and (ii), the valve was temperature-stabilised to 273 K and the gas was kept at a stagnation pressure of 2.5 bar. The measurements recorded with the 13CH4–12CD4 mixture were performed with the valve operated at room temperature and a stagnation pressure of 4 bar. Two fast ionisation gauges (FIGs) positioned after the TOF-MS were used to determine the velocity distribution of the GS beam. The central velocities, vGS, of the 12CH4, 12CD4 and 13CH4–12CD4 mixture beams were measured to be 1068 ± 5 m s−1, 960 ± 5 m s−1 and 1033 ± 5 m s−1, respectively. The reaction product ions were collected by applying a potential of 1 kV (0.5 kV) to electrode E1 (E2) [see Fig. 1 of Article I]. A prepulse of 125 V applied to E1 was used to define a reaction-observation time Δtr of 7 μs, as explained in Article I.
3 Results
3.1 Ion-product mass spectra and integrated signals
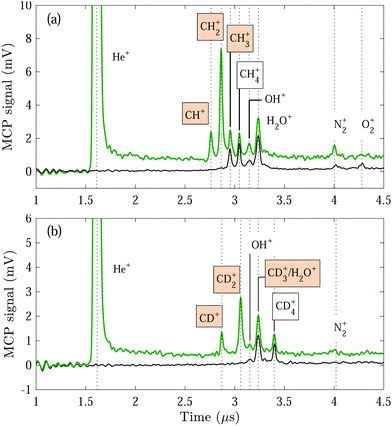
Displayed in Fig. 1 are reaction-product TOF mass spectra measured following reactions between the He(n) atoms and a GS beam containing pure CH4 (a) and pure CD4 (b) gas. The spectra were recorded with the He(n) atoms guided by the surface deflector at a constant velocity of vRyd = 1040 m s−1, corresponding to collision energies of Ecoll/kB = 0.2 K (a) and 1.2 K (b). When the Rydberg-excitation laser is turned on [green traces in Fig. 1(a) and (b)], a prominent peak is visible at ∼1.6 μs, corresponding to field-ionised helium Rydberg atoms.In addition, several peaks appear in the TOF mass spectra. These peaks can be assigned to (i) the GS-beam-specific reaction products from reactions (R2), (R3) and (R4), i.e., CHp∈{1,2,3}+ (a) and CDp∈{1,2,3}+ (b) ions, (ii) ions produced from the Penning-ionisation reactions
| He* + CH4 → He + CH3+ + H | (R6) |
| → He + CH4+, | (R7) |
To distinguish the ion products formed in the He(n) + CH4/CD4 reactions from ions formed in the Penning-ionisation reactions (R6) and (R7), we also recorded mass spectra with the Rydberg-excitation laser turned off [black traces in 1(a) and (b)]. When the GS beam is CH4, we can identify the He* + CH4 reaction products to be CH3+ and CH4+, in addition to the products originating from reactions with the H2O, N2 and O2 molecules in the reaction chamber. The Penning-ionisation products from the He* +CD4 reaction are analogous to the ones from the He* + CH4 reaction, however, the H2O+ and CD3+ ions both have a mass of ∼18 u and are not resolved in the mass spectra.
We did not observe the H+ or D+ product ions in our experiments. For all other product ions, no significant losses are expected to take place during the reaction–observation time. Moreover, the detection efficiency can be assumed to be identical for all reaction product ions because of their similar masses.
A considerable He+ signal is detected even when the GS beam is on, indicating that only a small fraction (about 1%) of the He(n) atoms takes part in the chemical reaction, as already observed for the other reactions discussed in Articles I and II. Because the particle number density of the GS beam is much greater than that of the Rydberg atoms, the reaction can be described with pseudo-first-order kinetics. From the experimental conditions under which the supersonic expansion is produced, we estimate that the density of the GS-beam particles in the interaction region is ρGS ≈ 3 × 1017 m−3 using standard expressions for the isentropic expansion of gases in vacuum.47 The estimated effective reaction rate coefficient is keff = kLρGS ≈ 6 × 102 s−1, corresponding to a reaction probability per He(n) atom of only 0.004 during the 7 μs-long reaction–observation time. Typically, less than one reaction product ion is detected on average during each experimental cycle.
We measure the dependence of the product-ion yields of the He+ + CH4 and He+ + CD4 reactions on the collision energy Ecoll = ½μvrel2 = ½μ(vRyd – vGS)2 (μ is the reduced mass) by varying vRyd and keeping vGS constant. The integrated product-ion signals, 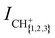 and
and 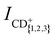 , were corrected for (i) the different amount of He(n) atoms and (ii) the different overlap with the GS beam dependent on vRyd, as explained in part I. Time-of-flight spectra recorded with the excitation laser turned off are subtracted from each recorded reaction time-of-flight mass spectrum prior to integration. The measured product-ion branching ratios, excluding the contributions from channels releasing H+/D+, for the two reaction systems are summarised in Table 2 in Section 3.2.
, were corrected for (i) the different amount of He(n) atoms and (ii) the different overlap with the GS beam dependent on vRyd, as explained in part I. Time-of-flight spectra recorded with the excitation laser turned off are subtracted from each recorded reaction time-of-flight mass spectrum prior to integration. The measured product-ion branching ratios, excluding the contributions from channels releasing H+/D+, for the two reaction systems are summarised in Table 2 in Section 3.2.
3.2 Reaction-product yields as a function of the reaction collision energy
Fig. 2(a) and (b) display the integrated product-ion signals ICH+, ICH2+ and ICH3+ (ICD+, ICD2+ and ICD3+) measured for the He+ + CH4 and He+ + CD4 reactions, respectively. The error bars correspond to the standard deviation of five consecutive measurements, each averaged over 500 experimental cycles. Examples of the measured ion signals, after subtraction of the TOF mass spectra recorded without the Rydberg excitation laser, but prior to the correction for the vRyd-dependent amounts of He(n) atoms that make it to the reaction region, are displayed for vRyd = 840 and 1050 m s−1 in the insets of Fig. 2. The coloured rectangles in the insets indicate the integration windows used for the three product ions.We do not observe a significant dependence of  and
and 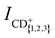 on vRyd in the range of He(n) velocities probed. The product branching ratios, determined from the mean value and standard deviations of
on vRyd in the range of He(n) velocities probed. The product branching ratios, determined from the mean value and standard deviations of  as a function of vRyd are summarised in Table 2 and compared to the relative branching ratios reported in ref. 40–43 (excluding the contributions from H+ and D+ ions, which were not detected in our experiments, and CH4+ and CD4+, for which we estimate a branching ratio of ≤3%).
as a function of vRyd are summarised in Table 2 and compared to the relative branching ratios reported in ref. 40–43 (excluding the contributions from H+ and D+ ions, which were not detected in our experiments, and CH4+ and CD4+, for which we estimate a branching ratio of ≤3%).
The measured product branching ratios for all product ions in the current work are consistent with those measured in previous work, within the experimental uncertainty.
The He+ + CH4 and He+ + CD4 data sets presented in Fig. 2 were obtained under near-identical experimental conditions (e.g., GS-beam stagnation pressure, valve temperature), so that the product yields for the two reactions can be directly compared. In Fig. 2, the detected product-ion signals for the He+ + CH4 reaction are almost twice higher than those for the He+ + CD4 reaction. This result is unexpected because the Langevin rate constant of the former reaction, 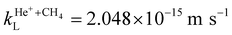 is only 2.1% higher than the one of the latter,
is only 2.1% higher than the one of the latter,  . To explain this discrepancy, we first considered the possibility that the CD4 gas, because of its higher mass of 20.067 u, undergoes different expansion dynamics compared to the CH4 gas (mass 16.043 u) leading to a lower CD4 density in the supersonic beam. To test this hypothesis, we repeated the experiment with a GS supersonic beam composed of a ≈1
. To explain this discrepancy, we first considered the possibility that the CD4 gas, because of its higher mass of 20.067 u, undergoes different expansion dynamics compared to the CH4 gas (mass 16.043 u) leading to a lower CD4 density in the supersonic beam. To test this hypothesis, we repeated the experiment with a GS supersonic beam composed of a ≈1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 13CH4 (17.035 u) and 12CD4 (20.067 u). The use of a mixture of both gases in the supersonic expansion is expected to reduce the differences in the expansion dynamics of the two species. The choice of 13CH4 in this experiment ensures that the dominant product ion of each reaction, namely 13CH2+ and 12CD2+, is less contaminated with product ions from other ion–molecule and Penning-ionisation reactions.
1 mixture of 13CH4 (17.035 u) and 12CD4 (20.067 u). The use of a mixture of both gases in the supersonic expansion is expected to reduce the differences in the expansion dynamics of the two species. The choice of 13CH4 in this experiment ensures that the dominant product ion of each reaction, namely 13CH2+ and 12CD2+, is less contaminated with product ions from other ion–molecule and Penning-ionisation reactions.
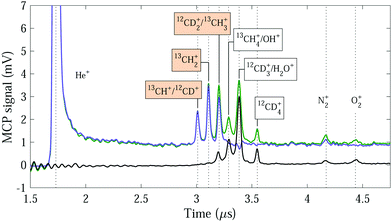
Typical TOF mass spectra recorded with the GS beam containing the 13CH4–12CD4 gas mixture are displayed in Fig. 3. When the Rydberg-excitation laser is turned on (green trace), many peaks are observed. Because there is usually more than one molecular ion corresponding to a given mass, most of the peaks cannot be unambiguously assigned to a particular molecular ion. The detected peaks in order of increasing time of flight are assigned to: He+, 13CH+ and 12CD+, 13CH2+, 12CD2+ and 13CH3+, 13CH4+ and OH+, 12CD3+ and H2O+, 12CD4+, N2+, and O2+. By subtracting the background spectra recorded with the laser turned off [black trace in Fig. 3], we obtain a time-of-flight spectrum which only contains the ion–molecule reaction products from the two reaction systems [blue trace in Fig. 3]. If the H+/D+ product channel is disregarded, the main products of the He+ + 13CH4 and He+ + 12CD4 reactions are 13CH+ and 13CH2+, and 12CD+ and 12CD2+, respectively. The 13CH+ and 12CD+ products have the same mass number (14) and we cannot determine the individual contributions to the measured signal. The heavier and more dominant reaction product of the He+ + 13CH4 reaction, 13CH2+, is not contaminated by any other product-ion contributions. The corresponding product ion of the He+ + 12CD4 reaction, 12CD2+, only coincides in mass with the minor 13CH3+ product of the He+ + 13CH4 reaction. From our measurements using the pure CH4 and CD4 beams, this contribution was determined to be ∼11% of the 13CH2+ peak intensity (see Table 2) and can be subtracted to derive the 12CD2+ signal.
The integrated product-ion signals corresponding to the CH2+:CD2+ product-ion ratio, measured with GS beams of pure 12CH4 and 12CD4 gas in separate experiments and the 13CH4–12CD4 mixture, and vRyd = 1040 m s−1, are 0.66 ± 0.04 and 0.72 ± 0.06, respectively. These ratios are identical within the experimental uncertainties, which suggests that the expansion effects do not significantly affect the CH4/CD4 densities in the reaction volume. The He+ + CH4 reaction thus appears to have a larger rate coefficient (by about 40%) at low collision energies than the He+ + CD4 reaction. This difference is significantly larger than predicted from the Langevin rate coefficients (about 2.1%).
The collision-energy dependence of the total measured product-ion yield (Itot) of the He(n) +CH4 (purple) and He(n) +CD4 (green) reactions is displayed in Fig. 4. The triangles and circles indicate measurements with vRyd < vGS and vRyd > vGS, respectively. The dashed horizontal lines and coloured rectangles represent the mean and standard deviation of the experimentally measured values for Itot. The product yields of these reactions do not exhibit a significant dependence on the collision energy in the kB·(0–10) K collision-energy range studied experimentally.
In our experiments, there is a very large excess of the ground-state molecules (density ρGS in the order of 1010 cm−3 compared to a density ρRg of about 106 cm−3 of the Rydberg atoms). Consequently, the density of the ground-state molecules remains unchanged during the reaction, which corresponds to pseudo-first-order kinetics. In addition, the conditions are such that less than 1% of the Rydberg atoms react during the duration Δt of the reaction–observation window. Their concentration therefore also does not significantly change during the reaction and the product yields are proportional to the rate coefficients. Fig. 4 thus indicates that the rate coefficients do not depend on the collision energy, as expected for Langevin-capture reactions. This observation suggests that the charge-octupole interaction between He+ and CH4 (CD4) does not affect the rate coefficients. This aspect is now examined in more detail from a theoretical point of view.
4 The effect of the octupole moment on the rate coefficients of ion–molecule reactions
Because of its tetrahedral symmetry, the methane molecule does not have a permanent electric dipole nor a quadrupole moment. Its first non-vanishing permanent electric moment is the octupole moment. The interaction between the charge of the He+ ion and the octupole moment can lead to a modification of the R− and rotational-state-dependent ion–molecule interaction potentials and capture rate coefficients (R is the distance between the ion and the molecule). In this section, we present a theoretical analysis of this interaction.We consider methane molecules in their ground electronic (![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A1) and vibrational state (v1,2,3,4 = 0). The interaction between the electric field generated by the ion and the octupole moment of the methane molecule results in a mixing of the |JKM〉 rotational levels and induces a small energy shift from the Stark effect, ΔEJKM, of the rotational energy levels which depends on the distance between the methane molecule and the ion. The total ion–molecule interaction potential, consisting of the pure Langevin term, VL (R), and the state-dependent Stark shift, ΔEJKM, as described in Article I, is used to calculate the state-dependent capture rate coefficients.
1A1) and vibrational state (v1,2,3,4 = 0). The interaction between the electric field generated by the ion and the octupole moment of the methane molecule results in a mixing of the |JKM〉 rotational levels and induces a small energy shift from the Stark effect, ΔEJKM, of the rotational energy levels which depends on the distance between the methane molecule and the ion. The total ion–molecule interaction potential, consisting of the pure Langevin term, VL (R), and the state-dependent Stark shift, ΔEJKM, as described in Article I, is used to calculate the state-dependent capture rate coefficients.
4.1 Nuclear-spin statistics of methane in the Td (M) group and rotational-state population in the supersonic beam
The methane molecule has a tetrahedral structure and, if tunnelling effects are ignored, its states can be labelled by the irreducible representations A1, A2, E, F1 and F2 of the molecular symmetry group Td (M). The total wavefunction (including the electronic, nuclear-spin and rovibrational components) must have either A1 or A2 symmetry, both for CH4 and CD4. CH4 (CD4) has three nuclear-spin isomers with total nuclear spin I = 2, 1, 0 (I = 4, 2, 0). The nuclear spin of 1/2 (1) of the protons (deuterons) in CH4 (CD4) leads to 16 (81) nuclear spin wavefunctions, which span the total irreducible representations:48–50 | (1) |
 | (2) |
The allowed rovibronic states span the irreducible representations:
 | (3) |
 | (4) |
The symmetries of the rotational wavefunctions of methane and the nuclear-spin-statistical weights of the rovibronic states determined from the allowed combinations of nuclear-spin and rovibronic wavefunctions are presented in Tables 3 and 4, respectively.
| CH4 | CD4 | Degeneracy | Total nuclear spin I(CH4; CD4) |
|---|---|---|---|
| A1(5) | A1(15) | 1 | {2; 4 |
| A2(5) | A2(15) | 1 | |
| E(2) | E(12) | 2 | 0 |
| F1(3) | F1(18) | 3 | {1; 2 |
| F2(3) | F2(18) | 3 |
The octupole-allowed transitions in the Td (M) group are:51
| A1↔A2, |
F1↔F2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| E ↔ E, |
| A1 → A1++ A2−, |
| A2 → A2++ A1−, |
| E → E++ E−, |
| F1 → F1++ F2−, |
| F2 → F2++ F1−. |
The selection rules arising from the conservation of the total angular momentum (see eqn (8) in the following section) and of the nuclear-spin symmetry of the rotational wavefunctions of methane in the Td (M) group are:
 | (5) |
| ΔK = 0, | (6) |
| ΔM = 0. | (7) |
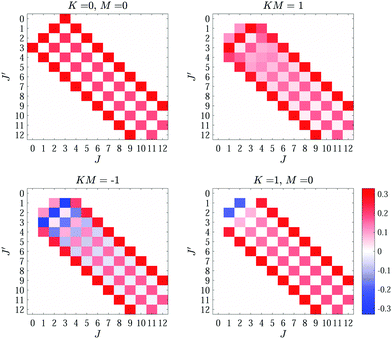
To illustrate these selection rules, the calculated R−independent matrix elements [without the factor of eΩ/(4πε0R4)] of the Stark Hamiltonian in eqn (8) for J = 0–12 and KM values of 0 and ±1 are presented in Fig. 5.
States with J = 1 (rovibrational symmetry F1) and the E component of the J = 2 states are metastable because they cannot decay to a lower rotational state without changing the nuclear-spin symmetry (see Table 3). The lowest rotational state that can decay to J = 0 is the J = 3 state. The ground states of the three nuclear-spin isomers are thus the J = 0 (A1 character), J = 1 (F1 character) and J = 2 (E character) states, respectively.
In supersonic expansions of CH4 and CD4, states of different nuclear-spin symmetry do not interconvert.53,54 Because of the relatively large ground-state rotational constant in CH4 (BCH4 = 5.241 cm−1), only the J = 0, 1 and 2 states, and thus only the ground state of each nuclear-spin isomer, are significantly populated at the rotational temperature Trot = 6 K of our supersonic beam (the fraction of molecules in states with J > 2 is <10−5). The fraction pJ of CH4 molecules in state J, including the K and M degeneracies and the nuclear-spin statistical weights, is 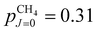 ,
,  and
and 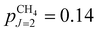 . The rotational constant of CD4 is smaller (BCD4 = 2.591 cm−1), but the nuclear spin isomers of A and E symmetry still mostly occupy their respective J = 0 and J = 2 ground states (97.25% and 99.95% of the molecules belonging to the nuclear-spin isomers of A and E symmetry, respectively, are in their respective ground state). The distribution of the nuclear-spin isomer of F symmetry among its three lowest energy states is ∼80.5% (J = 1), ∼18.6% (J = 2) and ∼0.9% (J = 3). The fractions of molecules in specific J states in CD4 in our supersonic beam (Trot ≈ 6 K) are:
. The rotational constant of CD4 is smaller (BCD4 = 2.591 cm−1), but the nuclear spin isomers of A and E symmetry still mostly occupy their respective J = 0 and J = 2 ground states (97.25% and 99.95% of the molecules belonging to the nuclear-spin isomers of A and E symmetry, respectively, are in their respective ground state). The distribution of the nuclear-spin isomer of F symmetry among its three lowest energy states is ∼80.5% (J = 1), ∼18.6% (J = 2) and ∼0.9% (J = 3). The fractions of molecules in specific J states in CD4 in our supersonic beam (Trot ≈ 6 K) are:  ,
, 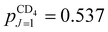 and
and  , with ∼1% of the molecules in states with J ≥ 3.
, with ∼1% of the molecules in states with J ≥ 3.
4.2 The interaction potentials between the He+ ion and the methane molecule
In the absence of electric dipole and quadrupole moments, the matrix elements of the Stark Hamiltonian in the basis of the symmetric-top rotational wavefunctions, are given by:55–57 | (8) |
The He+ + CH4(JKM) and He+ + CD4(JKM) interaction potentials
 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e a03.33 Convergence was achieved by including all rotational states with J ≤ 7.
e a03.33 Convergence was achieved by including all rotational states with J ≤ 7.
The solid black (dashed black) and solid coloured (transparent coloured) lines in Fig. 6 indicate the Langevin ion–molecule interaction potential [V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )L(R)] and the total interaction potentials including the charge-octupole interaction [V(
)L(R)] and the total interaction potentials including the charge-octupole interaction [V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,JKM)int(R)] for
,JKM)int(R)] for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 (
= 0 (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 10), respectively. For all states, the deviation of V(
= 10), respectively. For all states, the deviation of V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,JKM)int(R) from V(
,JKM)int(R) from V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )L(R) is very small, particularly for the states of the J = 0 and J = 1 manifolds. The effect of the octupole moment becomes stronger as J increases from 0 to 2. For states with J = 0 and 1, the effect of the charge-octupole interaction is more pronounced in CD4 than in CH4 because the rotational constant of CD4 is half that of CH4, leading to stronger mixing of the different J levels in the electric field of the He+ ion, as explained below. At an internuclear separation of R ≃ 19 Å, which corresponds to the Langevin radius at a collision energy of ∼kB·6.3 K, the (JKM) = (000) state is shifted from the value of V(
)L(R) is very small, particularly for the states of the J = 0 and J = 1 manifolds. The effect of the octupole moment becomes stronger as J increases from 0 to 2. For states with J = 0 and 1, the effect of the charge-octupole interaction is more pronounced in CD4 than in CH4 because the rotational constant of CD4 is half that of CH4, leading to stronger mixing of the different J levels in the electric field of the He+ ion, as explained below. At an internuclear separation of R ≃ 19 Å, which corresponds to the Langevin radius at a collision energy of ∼kB·6.3 K, the (JKM) = (000) state is shifted from the value of V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =0)L by ∼−0.0005 cm−1 (∼−0.001 cm−1) in CH4 (CD4) [insets of Fig. 6(a) and (b)]. In the J = 1 manifold, the potential-energy curves for all (JKM) states are also shifted to lower energies compared to V(
=0)L by ∼−0.0005 cm−1 (∼−0.001 cm−1) in CH4 (CD4) [insets of Fig. 6(a) and (b)]. In the J = 1 manifold, the potential-energy curves for all (JKM) states are also shifted to lower energies compared to V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =0)L(R). The change in energy is largest for the (100) state of the J = 1 manifold and is ∼0.001 cm−1 (∼0.002 cm−1) in CH4 (CD4) [insets of Fig. 6(c) and (d)]. This energy shift is twice as large as for the (000) state. In the J = 2 manifold of states, the different (JKM) states are shifted to both higher and lower energies compared to V(
=0)L(R). The change in energy is largest for the (100) state of the J = 1 manifold and is ∼0.001 cm−1 (∼0.002 cm−1) in CH4 (CD4) [insets of Fig. 6(c) and (d)]. This energy shift is twice as large as for the (000) state. In the J = 2 manifold of states, the different (JKM) states are shifted to both higher and lower energies compared to V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =0)L(R) [insets of Fig. 6(e) and (f)]. These shifts are in the order of ±0.15 cm−1 in both CH4 and CD4. Their larger values come from the fact that these states are closer in energy to states of the J = 3 manifold than states with J = 0 and 1 and that J = 3 states are the lowest rotational levels that can support an octupole moment. In addition, there are more (and stronger) coupling matrix elements to states of the J = 3 manifold compared to states with J = 0 and J = 1, as can be seen by evaluating the relevant Wigner 3 − j symbols in eqn (8), see also Fig. 5.
=0)L(R) [insets of Fig. 6(e) and (f)]. These shifts are in the order of ±0.15 cm−1 in both CH4 and CD4. Their larger values come from the fact that these states are closer in energy to states of the J = 3 manifold than states with J = 0 and 1 and that J = 3 states are the lowest rotational levels that can support an octupole moment. In addition, there are more (and stronger) coupling matrix elements to states of the J = 3 manifold compared to states with J = 0 and J = 1, as can be seen by evaluating the relevant Wigner 3 − j symbols in eqn (8), see also Fig. 5.
In general, the Stark shifts of all rotational states of CH4 and CD4 are several orders of magnitude smaller than the Stark shifts encountered in polar molecules, such as NH329 and CH3F27 (see, e.g., Fig. 6(a) and (b) of Article I) and more than an order of magnitude smaller than the shifts in quadrupolar molecules, such as N232 and H221,32,60 (see, e.g., Fig. 4 and 7 of Article II), as expected.
4.3 The rotational-state-dependent capture rate coefficients
We calculate the state-dependent capture rate coefficients as a function of the collision energy (Ecoll) by finding the highest classically-allowed partial wave,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) max, which results in a capture, for each selected value of Ecoll. The value of
max, which results in a capture, for each selected value of Ecoll. The value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) max is then used to calculate the maximal impact parameter
max is then used to calculate the maximal impact parameter | (10) |
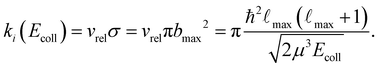 | (11) |
 | (12) |
The results of the calculations for the ki(Ecoll) rate coefficients for the two reactions and rotational states of the J = 0, 1 and 2 manifolds are presented in Fig. 7. The calculations were performed in the range of collision energies Ecoll/kB between 0.25 and 15 K, in steps of 0.25 K. For states experiencing a total interaction potential that is more (less) attractive than the Langevin potential, the centrifugal potential-energy barrier for a given value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is lowered (raised) compared to V(
is lowered (raised) compared to V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )L(R), leading to values of ki(Ecoll) that are larger (smaller) than the Langevin rate kL. The exact dependence of ki on the collision energy is determined by the Stark shift and the shape of the interaction potential in state i, Vi=(
)L(R), leading to values of ki(Ecoll) that are larger (smaller) than the Langevin rate kL. The exact dependence of ki on the collision energy is determined by the Stark shift and the shape of the interaction potential in state i, Vi=(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,JKM)int(R). We can classify the states in three categories as types I, II and III depending on whether the deviation of ki(Ecoll) from kL is small (≲1%), intermediate (∼1–5%) or large (≳5%), respectively, keeping in mind that what we call large here is still small compared to the deviations observed in polar and quadrupolar molecules.
,JKM)int(R). We can classify the states in three categories as types I, II and III depending on whether the deviation of ki(Ecoll) from kL is small (≲1%), intermediate (∼1–5%) or large (≳5%), respectively, keeping in mind that what we call large here is still small compared to the deviations observed in polar and quadrupolar molecules.
States of type I include all the states from the J = 0 and J = 1 manifolds [Fig. 6(a)–(d)], the |M| = 0, 1, 2 states of the (J = 2, K = 0) manifold [see lower insets of Fig. 6(e) and (f)] and the (J, |K|, M) = (2, 2, 0) states. At the lowest collision energies, Ecoll ≃ kB·(0.25–5) K for the He+ + CH4 reaction and Ecoll ≃ kB·(0.25–2.5) K for the He+ + CD4 reaction, the rate coefficients of these states are very close to the Langevin rate constant, k(I)i(Ecoll) ≃ kL. At higher collision energies, the rate coefficients of the type-I states increase (decrease) for interaction potentials that are more (less) attractive than VL (R). The deviation from kL in type-I states is more pronounced for CD4 [see Fig. 7(b), (d) and (f)].
States of type II comprise the |K| = 2, |M| = 1, 2 states from the J = 2 manifold. These states experience deviations from V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =0)L at R ≈ 19 Å of ∼0.03–0.06 cm−1 [upper insets in Fig. 6(e) and (f)]. The rate coefficients of these states all gradually increase with increasing Ecoll. The deviation of the rate coefficients k(II)i(Ecoll) from kL is relatively insensitive to the collision energy in the considered range, particularly for the states with |M| = 1.
=0)L at R ≈ 19 Å of ∼0.03–0.06 cm−1 [upper insets in Fig. 6(e) and (f)]. The rate coefficients of these states all gradually increase with increasing Ecoll. The deviation of the rate coefficients k(II)i(Ecoll) from kL is relatively insensitive to the collision energy in the considered range, particularly for the states with |M| = 1.
States of type III exhibit the largest deviation from kL (≳5%), but their rate coefficients almost do not depend on the collision energy. States of type III are the MK = ±1 states of the J = 2 manifold, which are shifted by approximately ±0.15 cm−1 from V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) =0)L(R) at R≈19 Å, in both CH4 and CD4. These states exhibit the largest deviation from VL (R) [see upper insets in Fig. 6 (e) and (f)] and kL and have rate coefficients of ∼0.94kL for the KM = 1 states and ∼1.05kL for the KM = −1 states, in both CH4 and CD4 [see Fig. 7(e) and (f)].
=0)L(R) at R≈19 Å, in both CH4 and CD4. These states exhibit the largest deviation from VL (R) [see upper insets in Fig. 6 (e) and (f)] and kL and have rate coefficients of ∼0.94kL for the KM = 1 states and ∼1.05kL for the KM = −1 states, in both CH4 and CD4 [see Fig. 7(e) and (f)].
The calculated rate coefficients averaged over all (K, M) sublevels of the J = 0, 1 and 2 manifolds are displayed in Fig. 7(g) and (h). They are almost equal to ∼kL at the lowest collision energy and grow with increasing Ecoll value. This increase is more pronounced for the J = 0 and 1 states. The J = 2 manifold consists primarily of states of type II and III. Although the deviations of the interaction potentials from VL(R) for type-II and III states are the most pronounced, approximately half of the states in this manifold experiences a positive energy shift while the other half experiences a negative energy shift relative to VL(R). Consequently, the overall effect on the rate coefficient cancels out.
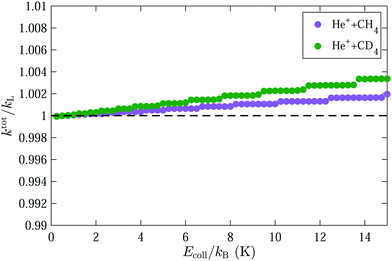
The total capture rate coefficients for the He+ + CH4 and He+ + CD4 reactions obtained after averaging over the rotational-state population of our supersonic beam are displayed in Fig. 8. The weighting factors of each (JKM) sublevel were determined assuming a rotational temperature of the supersonic beam of Trot = 6 K and including the nuclear-spin statistical weights. A small increase, of ∼0.2% and ∼0.4% for CH4 and CD4, respectively, compared to the Langevin rate is predicted in the range of collision energies between 0 and kB·15 K. The overall effect of the octupole moment on the total capture rate coefficients arises from states with negative Stark shifts, i.e., mostly from states with J = 0 and J = 1. The effect is more pronounced in CD4 than in CH4 because of the smaller rotational constant of CD4.
The effect of the octupole moment on the total rate constant is expected to be larger in molecules with larger values of Ω and smaller rotational constants, such as CCl4.61 The results presented in Fig. 8 imply that the capture rate coefficients of the He+ + CH4 and He+ + CD4 reactions do not significantly depend on the collision energy in the range between 0 and kB·15 K. This finding is in accord with the experimental observations presented in Fig. 2 and 4, which did not reveal any significant change of the rate coefficient over the range of collision energies probed in the experiment.
5 Conclusions
We have presented measurements of the relative rate coefficients of the reactions between He+ ions and methane molecules (CH4 and CD4) in the collision-energy range between 0 and ∼kB·10 K. The reactions were studied in a merged Rydberg-He-neutral beam setup, within the orbit of the helium Rydberg electron. We did not observe any dependence of the total product ion yield of either reaction on the collision energy in this range.The measured product ion yield of the He+ + CH4 reaction was found to be approximately twice as large as the one of the He+ + CD4 reaction. This result is unexpected because the Langevin capture rate coefficients of the two reactions are almost identical. Only a very small part of this discrepancy can be explained with the different expansion dynamics affecting the CH4 and CD4 supersonic beams, as demonstrated in measurements using a supersonic beam consisting of a ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 13CH4
1 mixture of 13CH4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12CD4. Most likely, the bias towards the product-ion formation in the He+ + CH4 reaction compared to the He+ + CD4 reaction arises because of non-adiabatic coupling effects, which are expected to be more pronounced in CH4 because the protons are lighter than the deuterons.
12CD4. Most likely, the bias towards the product-ion formation in the He+ + CH4 reaction compared to the He+ + CD4 reaction arises because of non-adiabatic coupling effects, which are expected to be more pronounced in CH4 because the protons are lighter than the deuterons.
We have also presented calculations of the rotational-state-dependent capture rate coefficients, which include the effect of the interaction between the charge of the He+ ion and the octupole moment of the methane molecule. These calculations confirmed that the charge-octupole interaction does not significantly affect the rate coefficients of ion–molecule reactions in the range of collision energies investigated in our studies (i.e., between kB·100 mK and kB·10 K). Nevertheless, the calculations revealed small differences, on the order of 5% or less, in the rate coefficients of reactions involving CH4 and CD4 in specific rotational states. The effect of these differences might become observable in experiments achieving a higher sensitivity than the present ones or using samples prepared in selected rotational states. The absence of electric dipole and quadrupole moments in CH4 makes the He+ + CH4 reaction an attractive system to observe the factor-of-two quantum enhancement of the rate coefficient that has been predicted theoretically for Langevin-type ion–molecule reactions at very low collision energies.21,62,63 In most other systems, deviations from the Langevin rate constant caused by long-range interactions are dominant and effectively mask the pure quantum enhancement.
This article concludes the three-part series investigating the effects of the molecular multipole moments on the capture rate coefficients of fast, barrierless ion–molecule reactions. In each article, we have presented experimental data on a reaction involving the He+ ion and a molecule possessing either a permanent dipole, a quadrupole or an octupole moment, and compared the experimental results with calculations of the molecular-rotational-state- and collision-energy-dependent capture rate coefficients. The results overall demonstrate the rapid convergence of the capture rate coefficients to the Langevin rate constant, kL, as the lowest non-vanishing molecular multipole moment (nmp = 2λ) increases in the sequence dipole (λ = 1), quadrupole (λ = 2) and octupole (λ = 3).
In Article I, we presented experimental results and calculations showing the molecular-dipole-moment-induced enhancement of the total reaction rate coefficients of the He+ + NH3 and He+ + ND3 reactions, kHe++NH3 and kHe++ND3, with decreasing collision energy (the ammonia molecule has a dipole moment of 1.47 D).69 At the lowest experimentally resolvable collision energy of ∼kB·200 mK, the calculated capture rate coefficients of the two reactions were estimated to be kHe++NH3 ≳ 17kL and kHe++ND3 ≳ 22kL.
In Article II, we treated the case of the charge–quadrupole-moment interaction with the example of the He+ + N2 reaction, demonstrating a suppression of the total reaction rate coefficient, kHe++N2, at the lowest collision energies, and an increase of the reaction rate coefficient with increasing energy, reaching a value of ∼1.3kL at Ecoll/kB ≈ 10 K. This suppression at the lowest collision energies was shown to arise from the negative sign of the quadrupole moment of N2 .70
.70
In the He+ + NH3/ND3 and He+ + N2 reaction systems, the rate coefficients strongly depend on the rotational level of the molecule. The results we obtained are for jet-cooled samples in which the occupation of rotational levels is approximately described by a rotational temperature of ∼6–7 K. The pronounced deviations we observed at low collision energies are thus the results of the average behaviour of molecules in different rotational states. Much stronger effects could be observed if fully state-selected samples are generated, and if the molecules are aligned or oriented.
The good agreement between the experimentally observed and the calculated state-averaged rate coefficients indicates that the adiabatic capture treatment we used in our calculations, which was developed more than 30 years ago,17,18 is adequate to describe the energy dependence of the rate coefficients from ∼50 K down to ≈0.1 K, which covers the entire temperature and collision-energy ranges relevant for chemical processes in interstellar clouds.
Capture models do not provide information on the branching ratios for different reaction channels. Moreover, they only provide the absolute values of the capture rate coefficients, whereas our experiments probe the relative rate coefficients for reactive collisions. However, we can use our calculations together with the experimentally measured absolute thermal rate coefficients in previous experiments in order to estimate the absolute thermal coefficients for the studied reactions at temperatures below ∼100 K, which is the temperature regime relevant for astrophysics.
The thermal rate coefficients calculated using our framework and the experimentally measured absolute rate coefficients at the lowest temperatures available in the literature are listed in Table 5 for the reactions studied in the current series, together with key parameters describing each reaction. For all reactions considered, the calculated thermal rates are higher than the experimentally measured ones, implying that only a fraction of the collisions are reactive. In the case of the reaction between He+ and ammonia, the calculated and experimentally measured thermal rate coefficients at 27 K and 68 K are larger than the Langevin rate kL by factors of ∼6 and ∼4 (assuming nuclear-spin conservation),29 and ∼2.4 and ∼1.6, respectively. The enhancement of the He+ + NH3 thermal reaction rates with decreasing temperature originates from the interaction between the charge of the He+ ion and the dipole moment of the ammonia molecule, as described in Article I. We infer that the fraction of reactive collisions for the He+ + NH3 reaction is ∼40%. Moreover, our results indicate that the rate coefficient exceeds ∼5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kL at 3 K.
kL at 3 K.
| NH3 | ND3 | N2 | CH4 | CD4 | |||
|---|---|---|---|---|---|---|---|
| a Experimental uncertainty of ±30%. b Assuming nuclear-spin conservation. c Current article. d Assuming nuclear-spin relaxation. | |||||||
| k L (10−15 m3 s−1) | 1.887 | 1.860 | 1.637 | 2.048 | 2.006 | ||
| k obs (10−15 m3 s−1) | 4.5 (T = 27 K)64 3.0 (T = 68 K)64 | — | 1.2a (T = 8 K)10 1.3a (T = 20 K)10 | 1.26 (T = 300 K)41 | — | ||
| k calc (10−15 m3 s−1) | 11.3 (T = 27 K)b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 7.39 (T = 68 K)b 29 7.39 (T = 68 K)b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 29 |
— | 2.06 (T = 8 K)32 1.98 (T = 20 K)32 | 2.048 (all![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T)c T)c |
2.006 (all![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T)c T)c |
||
| k est (10−15 m3 s−1) | 9.38 (0.16) (T = 3 K)b 6.67 (0.12) (T = 10 K)b | — | 1.28(0.10) (T = 3, 10 K) | 1.25 (all![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T) T) |
0.762 (all![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T) T) |
||
| 9.83 (0.17) (T = 3 K)d 7.76 (0.14) (T = 10 K)d | — | ||||||
| Estimated percentage of reactive collisions | 40% | 41% | — | 58 ± 17% | 66 ± 20% | 61% | 37% |
| Reduced mass μ (u) | 3.241 | 3.336 | 3.502 | 3.203 | 3.337 | ||
| Polarizability volume α′ (10−30 m3) | 2.103 (ref. 65) | 1.710 (ref. 65) | 2.448 (ref. 65) | ||||
| Rotational constants (cm−1) | 9.444 (ref. 66) | 5.143 (ref. 67) | 1.990 (ref. 68) | 5.241 (ref. 58) | 2.591 (ref. 59) | ||
| 6.196 (ref. 66) | 3.125 (ref. 67) | ||||||
| Leading multipole moment | Dipole | Quadrupole | Octupole | ||||
| 4.91 × 10−30 C m (ref. 69) | −4.65 × 10−40 C m2 (ref. 60) | 7.41 × 10−50 C m3 (ref. 33) | |||||
The calculated thermal capture rate coefficients for the reaction between He+ and N2 at 8 and 20 K are estimated to be ∼26% and ∼21% higher than kL. The enhancement over the value of kL of the He+ + N2 reaction thermal rate coefficient at low temperatures is caused by the interaction between the charge of the He+ ion and the quadrupole moment of N2, as described in Article II. As the temperature increases, the thermal capture rate coefficient of the He+ + N2 reaction is expected to converge to the value of kL. At 50 K and 100 K the thermal capture rate coefficient is 1.16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kL and 1.07kL, respectively. Using the experimentally measured reaction rate coefficients at 8 and 20 K,64 we estimate a reaction probability of ∼60% of the He+ + N2 system, with an uncertainty of ∼±20% resulting from the experimental uncertainty of the measurements.64
kL and 1.07kL, respectively. Using the experimentally measured reaction rate coefficients at 8 and 20 K,64 we estimate a reaction probability of ∼60% of the He+ + N2 system, with an uncertainty of ∼±20% resulting from the experimental uncertainty of the measurements.64
Because of the minimal effect of the methane octupole moment on the capture rate coefficients of both the He+ + CH4 and the He+ + CD4 reactions, the calculated thermal rate coefficients for these reactions already converge to the value of kL at 1 K. Using (a) the experimentally measured absolute rate coefficients of the He+ + CH4 reaction available in the literature for 300 K,41 and (b) the relative product yield of the He+ + CH4 and He+ + CD4 reactions measured in our experiments, we estimate that ∼60% and ∼40% of the collisions in the He+ + CH4 and He+ + CD4 systems, respectively, are reactive.
Taking the earlier measurements of absolute thermal rate coefficients at elevated temperatures into account and using our calculated capture rate coefficients and the corresponding percentage of reactive collisions, we determined values of the thermal reactive rate coefficients for all reactions in the temperature range relevant for the chemistry of interstellar clouds. Values of these reaction rate constants are given for T = 3 and 10 K in the row labelled kest in Table 5. These values correspond to the sum of the rates of the different reaction channels and the rates for specific channels can be obtained from the respective branching ratios, as given, e.g., in Tables 1 and 2. We recommend that these values be used in kinetic models of the chemical processes in these clouds.
The reactions between He+ and CH4, NH3 and N2 involve a charge transfer and thus more than one adiabatic potential-energy surface. These reactions are thus not simply “downhill” reactions on a single surface but involve nonadiabatic dynamics, which is likely to be the reason for the less-than-unity reaction probability. The smaller fraction of reactive collisions in the He+ + CD4 system compared to the He+ + CH4 system observed in our study may therefore reflect the fact that protons are lighter than deuterons and thus more likely to undergo nonadiabatic processes. Differences in the zero-point vibrational energies along the reaction paths may also play a role. Capture models do not provide information on the reaction mechanisms leading to different products, nor on the product branching ratios, nor on the percentage of reactive collisions. Nonadiabatic calculations for the reactions studied in this article series would be needed to reach a full understanding of the experimental observations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Josef A. Agner and Hansjürg Schmutz for their technical assistance, and Joel Jenny for help with the data acquisition during the initial stages of this project. This work is supported financially by the Swiss National Science Foundation (Grant No. 200020B-200478) and by the European Research Council through the ERC advanced grant no. 743121 under the European Union's Horizon 2020 research and innovation programme.References
- T. P. Snow and V. M. Bierbaum, Annu. Rev. Anal. Chem., 2008, 1, 229 CrossRef CAS PubMed.
- D. Smith, Chem. Rev., 1992, 92, 1473 CrossRef CAS.
- I. W. M. Smith, Annu. Rev. Astron. Astrophys., 2011, 49, 29–66 CrossRef CAS.
- V. Wakelam, I. W. M. Smith, E. Herbst, J. Troe, W. Geppert, H. Linnartz, K. Öberg, E. Roueff, M. Agúndez, P. Pernot, H. M. Cuppen, J. C. Loison and D. Talbi, Space Sci. Rev., 2010, 156, 13 CrossRef CAS.
- E. F. van Dishoeck, Proc. Int. Astron. Union, 2017, 13, 3–22 CrossRef.
- J. Heimerl, R. Johnsen and M. A. Biondi, J. Chem. Phys., 1969, 51, 5041–5048 CrossRef CAS.
- E. Ferguson, F. Fehsenfeld and A. Schmeltekopf, Adv. At. Mol. Phys., Academic Press, 1969, vol. 5, pp. 1–56 Search PubMed.
- D. Smith and N. G. Adams, Adv. At. Mol. Phys., Academic Press, 1988, vol. 24, pp. 1–49 Search PubMed.
- J. K. Kim and W. T. Huntress, Int. J. Mass Spectrom. Ion Phys., 1975, 16, 451–454 CrossRef CAS.
- B. Rowe, J. Marquette, G. Dupeyrat and E. Ferguson, Chem. Phys. Lett., 1985, 113, 403–406 CrossRef CAS.
- D. Gerlich, J. Chem. Soc., Faraday Trans., 1993, 89, 2199–2208 RSC.
- C. R. Markus, O. Asvany, T. Salomon, P. C. Schmid, S. Brünken, F. Lipparini, J. Gauss and S. Schlemmer, Phys. Rev. Lett., 2020, 124, 233401 CrossRef CAS PubMed.
- R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001 CrossRef.
- S. Willitsch, Adv. Chem. Phys., 2017, 162, 307–340 CrossRef CAS.
- B. R. Heazlewood and T. P. Softley, Nat. Rev. Chem., 2021, 5, 125–140 CrossRef CAS.
- D. C. Clary, Mol. Phys., 1985, 54, 605–618 CrossRef CAS.
- D. C. Clary, Annu. Rev. Phys. Chem., 1990, 41, 61–90 CrossRef CAS.
- J. Troe, Chem. Phys., 1987, 87, 2773–2780 CAS.
- J. Troe, J. Chem. Phys., 1996, 105, 6249–6262 CrossRef CAS.
- T. Stoecklin, D. C. Clary and A. Palma, J. Chem. Soc., Faraday Trans., 1992, 88, 901–908 RSC.
- E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2005, 122, 184311 CrossRef CAS PubMed.
- E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2016, 145, 244315 CrossRef CAS PubMed.
- M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 084311 CrossRef CAS PubMed.
- M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 144315 CrossRef CAS PubMed.
- P. Allmendinger, J. Deiglmayr, O. Schullian, K. Höveler, J. A. Agner, H. Schmutz and F. Merkt, ChemPhysChem, 2016, 17, 3596–3608 CrossRef CAS PubMed.
- P. Allmendinger, J. Deiglmayr, K. Höveler, O. Schullian and F. Merkt, J. Chem. Phys., 2016, 145, 244316 CrossRef PubMed.
- V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 125, 263401 CrossRef CAS PubMed.
- K. Höveler, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 2676–2685 RSC.
- V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 21606–21622 RSC.
- F. B. V. Martins, V. Zhelyazkova, Ch. Seiler and F. Merkt, New J. Phys., 2021, 23, 095011 CrossRef CAS.
- P. Allmendinger, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 043403 CrossRef.
- V. Zhelyazkova, F. B. V. Martins, M. Žeško and F. Merkt, Phys. Chem. Chem. Phys., 2022, 24, 2843–2858 RSC.
- G. Birnbaum and E. R. Cohen, J. Chem. Phys., 1975, 62, 3807 CrossRef CAS.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2018, 239, 17 CrossRef CAS.
- J. H. Lacy, J. S. Carr, N. J. Evans, F. Baas, J. M. Achtermann and J. F. Arens, Astrophys. J., 1991, 376, 556–560 CrossRef CAS.
- Y. I. Izotov and T. X. Thuan, Astrophys. J., 2010, 710, L67–L71 CAS.
- D. Z. Kandula, Ch. Gohle, T. J. Pinkert, W. Ubachs and K. S. E. Eikema, Phys. Rev. Lett., 2010, 105, 063001 CrossRef PubMed.
- W. A. Chupka and J. Berkowitz, J. Chem. Phys., 1971, 54, 4256–4259 CrossRef CAS.
- A. N. Zavilopulo, M. I. Mykyta, A. N. Mylymko and O. B. Shpenik, Tech. Phys., 2013, 58, 1251–1257 CrossRef CAS.
- H. Chatham, D. Hils, R. Robertson and A. C. Gallagher, J. Chem. Phys., 1983, 79, 1301–1311 CrossRef CAS.
- W. T. Huntress, J. B. Laudenslager and R. F. Pinizzotto, Int. J. Mass Spectrom. Ion Phys., 1974, 13, 331–341 CrossRef CAS.
- G. Mauclaire, R. Derai and R. Marx, Int. J. Mass Spectrom. Ion Phys., 1978, 26, 289–301 CrossRef CAS.
- N. G. Adams and D. Smith, J. Phys. B: At. Mol. Phys., 1976, 9, 1439–1451 CrossRef CAS.
- R. C. Bolden, R. S. Hemsworth, M. J. Shaw and N. D. Twiddy, J. Phys. B: At. Mol. Phys., 1970, 3, 45–60 CrossRef CAS.
- K. Motohashi and S. Tsurubuchi, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 5215–5224 CrossRef CAS.
- W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- M. D. Morse, Atomic, Molecular, and Optical Physics: Atoms and Molecules, Academic Press, 1996 Search PubMed.
- P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, Canada, 2006 Search PubMed.
- J. T. Hougen, Methane Symmetry Operations, https://www.nist.gov/pml/methane-symmetry-operations.
- Z. Bjelobrk, C. M. Tanner and M. Quack, Z. Phys. Chem., 2015, 229, 1575–1607 CrossRef CAS.
- M. Hepp, G. Winnewisser and K. M. Yamada, J. Mol. Spectrosc., 1991, 146, 181 CrossRef CAS.
- M. Quack, Fundamental Symmetries and Symmetry Violations from High Resolution Spectroscopy, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. I Search PubMed.
- H. J. Wörner, X. Qian and F. Merkt, J. Chem. Phys., 2007, 126, 144305 CrossRef PubMed.
- G. Wichmann, E. Miloglyadov, G. Seyfang and M. Quack, Mol. Phys., 2020, 118, e1752946 CrossRef.
- R. N. Zare, Angular momentum, John Wiley & Sons, New York, 1988 Search PubMed.
- S. S. M. Wong, Introductory Nuclear Physics, John Wiley & Sons, New York, 1998 Search PubMed.
- A. D. Buckingham, Q. Rev., Chem. Soc., 1959, 13, 183–214 RSC.
- G. Herzberg, Molecular spectra and molecular structure; Volume III – Electronic spectra and electronic structure of polyatomic molecules, Van Nostrand, New York, 1966 Search PubMed.
- H. M. Kaylor and A. H. Nielsen, J. Chem. Phys., 1955, 23, 2139 CrossRef CAS.
- E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2004, 120, 9989–9997 CrossRef CAS PubMed.
- S. Brode, C. Kölmel, H. Schiffer and R. Ahlrichs, Z. Phys. Chem., 1987, 155, 23–28 CrossRef CAS.
- E. Vogt and G. H. Wannier, Phys. Rev., 1954, 95, 1190–1198 CrossRef CAS.
- B. Gao, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 062712 CrossRef.
- J. B. Marquette, B. R. Rowe, G. Dupeyrat, G. Poissant and C. Rebrion, Chem. Phys. Lett., 1985, 122, 431–435 CrossRef CAS.
- T. N. Olney, N. M. Cann, G. Cooper and C. E. Brion, Chem. Phys., 1998, 223, 59–98 CrossRef.
- Š. Urban, R. D'Cunha, R. Romola, K. N. Rao and D. Papoušek, Can. J. Phys., 1984, 62, 1775–1791 CrossRef.
- F. Daniel, C. Rist, A. Faure, E. Roueff, M. Gérin, D. C. Lis, P. Hily-Blant, A. Bacmann and L. Wiesenfeld, Mon. Not. R. Astron. Soc., 2016, 457, 1535–1549 CrossRef CAS.
- K. P. Huber and G. G. Herzberg, Molecular spectra and molecular structure; Volume IV – Constants of diatomic molecules, Van Nostrand Reinhold Company, New York, 1979 Search PubMed.
- M. D. Marshall, K. C. Izgi and J. S. Muenter, J. Chem. Phys., 1997, 107, 1037–1044 CrossRef CAS.
- C. Graham, D. A. Imrie and R. E. Raab, Mol. Phys., 1998, 93, 49–56 CrossRef CAS.
| This journal is © the Owner Societies 2022 |