Open Access Article
Open Access ArticleEnhancement of phase stability and optoelectronic performance of BiFeO3 thin films via cation co-substitution†
Pamela
Machado
 a,
Ivan
Caño
a,
César
Menéndez
b,
Claudio
Cazorla
a,
Ivan
Caño
a,
César
Menéndez
b,
Claudio
Cazorla
 c,
Huan
Tan
a,
Ignasi
Fina
a,
Mariano
Campoy-Quiles
c,
Huan
Tan
a,
Ignasi
Fina
a,
Mariano
Campoy-Quiles
 a,
Carlos
Escudero
a,
Carlos
Escudero
 d,
Massimo
Tallarida
d,
Massimo
Tallarida
 d and
Mariona
Coll
d and
Mariona
Coll
 *a
*a
aICMAB-CSIC, Campus UAB, 08193 Bellaterra, Spain. E-mail: mcoll@icmab.es
bSchool of Chemical Engineering, UNSW Australia, Sydney, NSW 2052, Australia
cDepartament de Física, Universitat Politècnica de Catalunya, Campus Nord B4-B5, 08034 Barcelona, Spain
dALBA Synchrotron Light Source, 08290 Cerdanyola del Vallès, Barcelona, Spain
First published on 19th November 2020
Abstract
Compositional engineering of BiFeO3 can significantly boost its photovoltaic performance. Therefore, controlling site substitution and understanding how it affects the optical and electronic properties while achieving robust and stable phases is essential to continue progressing in this field. Here the influence of cation co-substitution in BiFeO3 on phase purity, optical and electronic properties is investigated by means of X-ray diffraction, spectroscopic ellipsometry and X-ray absorption spectroscopy, respectively. Piezoelectric force microscopy and ferroelectric characterization at room temperature has been carried out in co-doped BiFeO3 films. First-principles calculations are also performed and compared to the experimental observations. It is shown that the incorporation of La3+ in Bi(Fe,Co)O3 films improves phase purity and stability while preserving the reduced band gap achieved in metastable Bi(Fe,Co)O3. Moreover, it is suggested that the changes in the optoelectronic properties are mainly dictated by the hybridisation between unoccupied Co 3d and O 2p states along with the presence of Co3+/Co2+ species. This thorough study on (Bi,La)(Fe,Co)O3 thin films coupled with the use of a cost-effective and facile solution deposition synthesis increases the motivation to continue exploiting the potential of these perovskite materials.
1 Introduction
The use of ferroelectric oxide perovskites as a stable photoactive layer has opened up a ground-breaking new arena of research in the field of energy.1,2 They present an alternative mechanism for solar energy conversion that could potentially surpass the fundamental efficiency limits of conventional semiconductors.3,4 Unfortunately, most ferroelectric oxide perovskites have a relatively large band gap, i.e. 3–4 eV (being able to harvest only 8–20% of the solar spectrum), and present poor charge transport properties.5,6 Of the various oxide perovskite materials with general ABO3 structure, BiFeO3 (BFO) has generated much interest being ferroelectric at room temperature with a bandgap at 2.7 eV.7–9 The polarization in BFO arises in part from the 6s2 lone pair of Bi3+ cations occupying the A-site position, whereas the band gap is mostly affected by the chemical bonding between the Fe3+, in the B-site position, and the surrounding oxygen anions. As promising as it is, there are still drawbacks to overcome such as improving band gap towards the visible. In this regard, compositional substitution turned out to be effective to tune their structure and physical properties. It has already been shown that chemical substitution of Fe by Cr in the B-site of the perovskite BFO can tune the band gap from 2.7 eV to 1.9 eV reaching power conversion efficiencies of 8%.2 Notably, controlling site engineering in BFO is often complicated for the generation of secondary phases (such as Bi2Fe4O9 and Bi25FeO39)10 and charge defects (including Fe2+, Fe4+, bismuth and oxygen vacancies)11,12 which at the same time depend on the processing conditions, and will ultimately interfere with the film functionality.On the other hand, previous studies underlined the benefit of A-site doping with rare-earth cations like La, Nd and Gd, to improve film crystallinity, phase purity and decrease in leakage current.13–15 Since they are located far from the Fermi level, this substitution is expected to have little influence on the electronic band structure.16 Nonetheless, large substitution of A-site ions can trigger a ferroelectric to paraelectric phase transition.17,18
Solution-processing is an effective approach to prepare BFO19,20 films allowing to alter the cation composition by incorporating different stoichiometric amounts of the corresponding metalorganic precursors. Our recent work demonstrates that the optical gap of BFO can be reduced from 2.7 eV to 2.3 eV through cobalt doping while preserving a robust ferroelectricity.21 The valence configuration of this cobalt-doped system is found to be Fe3+ for iron and Co3+/Co2+ for cobalt.22 The presence of Co2+ is expected to alter the charge defect scenario such as the ubiquity of oxygen vacancies and thus the leakage currents.23 Additionally, phase stabilization still remains a challenge for cobalt loads ≥30%.24
Herein we investigate the effect of A-site substitution by La3+ in solution processed BiFe1−xCoxO3 (BFCO) thin films to gain insight on the influence of the defect chemistry on its structure, optical, electronic and ferroelectric properties while pursuing a single phase formation. La3+ is an attractive candidate to stimulate the formation of stable (Bi,La)(Fe,Co)O3 perovskite structure benefiting from the same valence state as Bi3+, similar ionic radii (ri(La3+) = 1.36 Å and ri(Bi3+) = 1.54 Å for coordination number of 12)25,26 and larger bond dissociation energy with oxygen (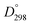 (La–O) = 798 kJ mol−1 and
(La–O) = 798 kJ mol−1 and 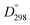 (Bi–O) = 337 kJ mol−1).27 In this work La-doping is kept at 10% to stay far from the concentrations in which structural phase transition occurs.18,28
(Bi–O) = 337 kJ mol−1).27 In this work La-doping is kept at 10% to stay far from the concentrations in which structural phase transition occurs.18,28
2 Experimental methods
Film preparation
The precursor solutions are prepared by weighting the chemical precursors (powder) according to the stoichiometric ratio of the final films. Following after, they are mixed in a solvent blend of 2-methoxyethanol and acetic acid in order to obtain a final concentration of 0.25 M respect to Bi. The precursors are: Bi(NO3)3·5H2O (98.0%), Fe(NO3)3·9H2O (98.0%), Co(NO3)2·6H2O (98.0–102.0%) and La(NO3)3·6H2O (99.999%). Since Ln precursors are difficult to dissolve in the solvents here mentioned, the solution is left 24 h under stirring and moderate temperature (∼55 °C) using a reflux condenser. The process of deposition itself is carried out using a spin-coater located in a dry chamber, with an atmosphere whose relative humidity is less than 10%. 17.5 μl of the 0.25 M BFO-based solution are taken with a syringe, deposited on the substrate and then spin-coated at 6000 rpm for 40 seconds. We have performed the deposition on 5 × 5 mm SrTiO3 (STO) substrates. For piezoelectric force microscopy and macroscopic ferroelectric characterization, films have been deposited on La0.7Sr0.3MnO3 (LSMO)-buffered (001) STO substrates. Following the deposition, a low-temperature treatment is performed in order to eliminate organic compounds.21 Finally, the sample is subjected to a high temperature thermal treatment at 600–700 °C for 30 min by which the phase crystallizes and grows on the substrate. This high-temperature process is carried out in a pre-heated tubular furnace to minimize the formation of Bi2Fe4O9 and Bi25FeO39,10 with an O2 flow of 0.6 l min−1. Then, the samples are fast cooled to room temperature to prevent perovskite decomposition. For the macroscopic ferroelectric characterization, this process has been repeated five times to obtain 100 nm thin films.Structural and surface morphology characterization
Routine studies of phase purity and film crystallinity were performed in a Siemens XRD Diffractometer D-5000 with Cu-Kαλ = 1.5418 Å. Additionally, a Bruker D8 Advance (GADDS) diffractometer equipped with a 2D detector was used for advanced characterization. Atomic Force Microscopy (AFM) was used to study the surface morphology and roughness of the samples. AFM topography measurements were performed with Keysight 5100 instrument in dynamic mode, acquiring images from 5 μm × 5 μm areas of the samples. Following after, the images were analyzed with MountainsMap Premium software.Optical characterization
Variable-angle spectroscopic ellipsometry (VASE) measurements were carried in reflection mode at ambient conditions using a SOPRALAB GES5E rotating polarized ellipsometer (Xe lamp as light source and charge-coupled device detector). The ellipsometric spectra (Ψ, Δ) were recorded within the spectral range 1.3 to 4.5 eV at a fixed analyzer angle of 20° varying the angle of incidence from 67.5°, 70° to 72.5° for each sample. Data sets were analyzed using WinElli II piece of software and fitted with the multi-layer model void/rough layer/BFO-based film/substrate. Rough layer assumes a medium consisting of air and film (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) that uses the Bruggeman approximation to model the effective dielectric function. Roughness values have been taken from the AFM analysis performed in these samples (Fig. S1, ESI†). The Tauc–Lorentz model was used to describe the optical properties of the BFO-based films as previously described.21 To study the optical absorption spectra, the Tauc relationship29 was employed:
1) that uses the Bruggeman approximation to model the effective dielectric function. Roughness values have been taken from the AFM analysis performed in these samples (Fig. S1, ESI†). The Tauc–Lorentz model was used to describe the optical properties of the BFO-based films as previously described.21 To study the optical absorption spectra, the Tauc relationship29 was employed:| αhν ∝ (hν − Eg)n |
Photoemission characterization
X-ray photoemission spectra (XPS) were recorded at the NAPP end station from CIRCE beamline at the ALBA Synchrotron Light Source30 using a PHOIBOS 150 NAP electron energy analyser (SPECS GmbH). The angle between the analyser axis and the incoming synchrotron radiation horizontal linear polarization vector was 54.7°, the magic angle, and the take-off angle was approximately 55°. The spectra were acquired with a 20 nm exit slit, and the X-ray spot was estimated to be in the order of 100–50 μm (H × V). Two different photon energies were used, 1032 and 525 eV, the former for the survey spectra with a pass energy of 20 eV and the latter for the high resolution scans with 10 eV pass energy. All the measurements were performed under high vacuum conditions. X-ray absorption spectra (XAS) have also been obtained at the NAPP end station in total electron yield mode upon measuring the drain current on the samples by an electrometer (ALBA Em current amplifier31) and corrected by the incoming photon flux as measured by a gold mesh just upstream the sample. The beam dimensions and sample orientation were the same as for the XPS measurements.Ferroelectric characterization
Top Pt electrodes (10 nm thick) were deposited by sputtering through a stencil mask on LSMO-buffered films, allowing to obtain arrays of contacts of 40 μm × 40 μm. Ferroelectric polarization loops were measured at room temperature in top-top configuration32 (two BFO capacitors were measured in series, contacting two top Pt electrodes and using the conducting LSMO buffer layer as common bottom electrode) by means of an AixACCT TFAnalyser2000 platform. Ferroelectrics loops were obtained by sweeping an electric field at a constant rate with a frequency of 1 kHz and measuring the current, using the dielectric leakage current compensation (DLCC) to minimize leakage current effects.33 Polarization has been obtained by displacive current integration through time and by its normalization to the electrodes area.PFM characterization
Piezoelectric Force Microscopy (PFM) measurements were performed with an MFP-3D ASYLUM RESEARCH microscope (Oxford Instrument Co.), using the AppNano silicon (n-type) cantilevers with Pt coating (ANSCM-PT-50). Scanned areas were 30 × 30 μm2 and the electrically written regions were 10 × 10 μm2. To achieve better sensitivity, the Dual-Frequency Resonance-Tracking (DART) mode was employed.34,35 PFM voltage hysteresis loops were always performed at remanence, using a dwell time of 100 ms. The quantification of the piezo coefficient using DART is difficult due to the simultaneous variation of measurement frequency and the variation of the maxima of the resonance amplitude while measuring; consequently arbitrary units (a.u.) are indicated in the amplitude of the piezoresponse.First-principles calculations
Spin-polarized density functional theory (DFT) calculations were performed with the generalized gradient approximation proposed by Perdew, Burke and Ernzerhof (PBE) as implemented in the VASP package.36,37 The “Hubbard-U” scheme derived by Dudarev et al. was employed for the description of Co and Fe 3d electrons by adopting a U value of 6 and 4 eV, respectively.38,39 The “projected augmented wave” method40 was used to represent the ionic cores by considering the following electronic states as valence: Co 4s13d8, Fe 3p64s13d7, Bi 6s25d106p3, La 6s25d15p65s2 and O 2s22p4. An energy cut-off of 800 eV and a Γ-centered k-point grid of 6 × 6 × 6 were employed for a 2 × 2 × 2 simulation cell containing 40 atoms, thus obtaining zero-temperature energies converged to within 0.5 meV per formula unit. Geometry relaxations were performed for an atomic force threshold of 0.005 eV Å−1.The effects of chemical disorder were addressed by generating all possible atomic Co–Fe and and Bi–La arrangements in the adopted 40-atoms supercell. The energetically most favorable magnetic ordering was determined for each configuration by considering the four possible magnetic spin arrangements compatible with our simulation cell (that is, ferromagnetic -FM- and antiferromagnetic -AFM- of type A, C, and G).38,39 Off-stoichiometric systems were generated by removing one oxygen atom from all possible apical and equatorial positions in the 40-atoms simulation cell,41 thus rendering the general chemical composition Bi1−yLayFe1−xCoxO2.875. In order to obtain accurate electronic band structure and band gap results, we performed range-separated hybrid DFT calculations with the HSE06 exchange–correlation functional42 on the equilibrium geometries determined previously with the PBE potential.
The electric polarization of stoichiometric Bi1−yLayFe1−xCoxO3 systems were estimated with the Born effective charges method.43,44 In this approach, the electric polarization is calculated with the formula:
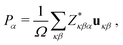 | (1) |
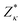 the Born effective charge tensor calculated for a non-polar reference state. It is worth noting that recently it has been shown that the estimation of electric polarization for BiFe1−xCoxO3 solid solutions with such a perturbative and computationally feasible method turns out to be very accurate.43
the Born effective charge tensor calculated for a non-polar reference state. It is worth noting that recently it has been shown that the estimation of electric polarization for BiFe1−xCoxO3 solid solutions with such a perturbative and computationally feasible method turns out to be very accurate.43
3 Results and discussion
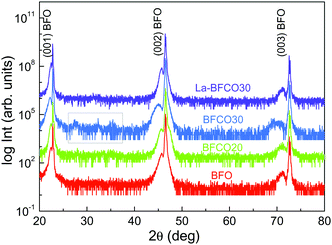
Four compositions have been selected for this study: BiFeO3 (BFO), BiFe0.8Co0.2O3 (BFCO20), BiFe0.7Co0.3O3 (BFCO30) and Bi0.9La0.1Fe0.7Co0.3O3 (La-BFCO30). In Fig. 1, XRD θ–2θ patterns of the thin films show the (00l) Bragg reflections of the BFO-based phase next to the intense (00l) reflections of the SrTiO3 (STO) substrate confirming epitaxial growth of the 20 nm-perovskite films indexed assuming a pseudocubic cell. For BFCO30 films, the (00l) reflections from the BFCO30 broaden and extra diffraction peaks appear between 2θ 25° and 40°, highlighted in a grey square in Fig. 1, which are attributed to bismuth and iron oxide rich phases. The presence of secondary phases in the BiFeO3–BiCoO3 system for cobalt concentrations up to 30% is attributed to the system instability, as previously reported in MOCVD samples.45,46 In fact, pure BiCoO3 is stable only at high pressure.24 With the incorporation of La in BFCO30, the presence of secondary phases is suppressed and the (00l) reflections from La-BFCO30 sharpened, indicating the formation of pure phase epitaxial films with improved crystallinity. The lattice parameter and unit cell volume for the chemically substituted BFO samples have been determined from the high resolution reciprocal space maps performed around the (103) STO reflection, showing minimal variations, see Table 1. These variations have been attributed to the subtle differences in the ionic radii of the cations forming the structure (Table S1, ESI†) along with in-plane compression strain (aSTO = 3.905 Å).| Composition | t | a (Å) | c (Å) | V (Å3) |
|---|---|---|---|---|
| BFO | 0.97 | 3.908 | 3.976 | 60.72 |
| BFCO20 | 0.97 | 3.908 | 3.997 | 61.04 |
| BFCO30 | 0.98 | 3.908 | 4.047 | 61.81 |
| La-BFCO30 | 0.97 | 3.909 | 3.992 | 61.00 |
On the basis of these results, altering the pristine BFO films with simultaneous La- and Co-site substitutions promotes the formation of pure phase and crystalline films and does not jeopardize the stability of the pseudocubic structure, in good agreement with the calculated Goldschmidt tolerance factor,47t, being 0.97 < t < 0.98. It is expected that the formation of this stable, pure-single crystalline phase could positively affect the good traits of BFO for PV by enhancing the abnormal photovoltaic effect while reducing the leakage current although this study would be beyond the scope of the present work.
The benefit of La incorporation in BFCO30 can also be observed from the smooth an homogeneous surface morphology from AFM analysis (Fig. S1, ESI†).
To investigate the effect of chemical doping in BFO on the optical properties, spectroscopic ellipsometry studies are performed. Fig. 2 shows the Tauc plots for direct (αhν)2 transitions where α is the absorption coefficient.48 For pristine BFO films it is shown a nearly linear dependence with photon energy in line with previous observations of spray deposited BFO.49 The extrapolation of the linear region of the plot to the X-axis intercept (α = 0) allows to obtain the Tauc gap, being 2.7 eV. Cobalt substitution barely modifies the shape of the direct transition except by introducing a red shift of the absorption edge.21 By incorporating La, the optical properties of BFCO30 are no further altered (Fig. S2, ESI†) preserving the red shift obtained in BFCO30, Fig. 2.
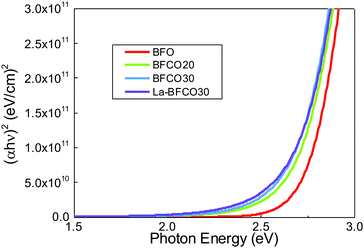 | ||
| Fig. 2 (αhν)2 Tauc plots for 20 nm BFO, BFCO20, BFCO30 and La-BFCO30 used to determine the direct transition energies of the films. | ||
In order to better understand the effect of gradual change in the chemical substitution on the electronic structure of BFO, X-ray Absorption Spectroscopy (XAS) of the Fe L2,3, Co L2,3 and O K-edges were carried out. The absorption at the Fe L2,3-edge corresponds to electron transitions from Fe 2p to Fe 3d orbitals and it is very sensitive to crystal-field interactions. In Fig. 3a it is shown the Fe L2,3 spectra of all samples studied here. It is observed that regardless of the A-site and B-site substitution there are negligible differences in the peak positions and the line shape of all spectra. A comparison of our results with the well known Fe L2,3 spectrum of both BiFeO3 and LaFeO3, which exhibits a high spin Fe3+ ground state,50,51 shows a good agreement. Therefore, Fe3+ is the dominant oxidation state for undoped and doped samples and the 3d occupancy of Fe barely changes with neither the Co nor La doping, being consistent with previous XAS studies of La1−xSrxFeO3 and La0.8Bi0.2Fe1−xMnxO3.52,53
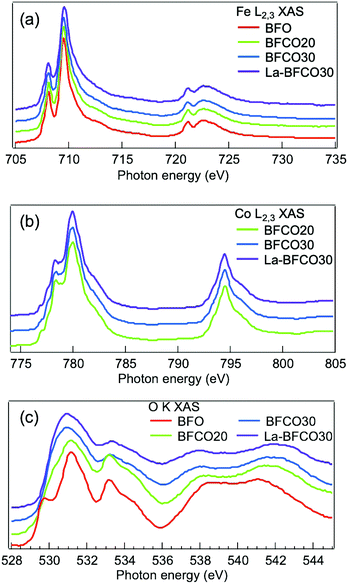 | ||
| Fig. 3 XAS spectra of the 20 nm BFO, BFCO and La-BFCO thin films on STO (a) at the Fe L2,3-edge, (b) Co L2,3-edge, (c) O K-edge. Spectra are vertically shifted for clarity. | ||
The shape of the absorption spectra at the Co L2,3-edge reveals the presence of a combination of Co2+ and Co3+ species54 with small variation of the Co2+/Co3+ ratio for the different cobalt concentrations (Fig. 3b), being about 0.7 in BFCO20 and about 0.5 in BFCO30 and La-BFCO30. Note that the oxidation state of cobalt is influenced by the preparation method and the processing conditions.55,56
The substitution of Bi by La, does not change this ratio significantly. Besides the XAS of the transition metal elements, it is also interesting to follow the behaviour of the oxygen K-edge for the various samples. In this case, the variations are more complex as they involve the density of oxygen-related unoccupied states which originate from the hybridisation between the O 2p and Fe/Co 3d (region 528–532 eV) states, as well as with the unoccupied Bi 6p (region 532–536 eV) states, and with the Fe/Co 4s4p (region 536–544 eV).50
In Fig. 3c it is observed that the feature near the onset undergoes a continuous transformation by the substitution of Fe by Co, i.e. the O 2p–Fe 3d hybridised states are substituted by O 2p–Co 3d hybridised states, while the La substitution does not bring any further change. Moreover, the integrated intensity of the spectra near the onset (528–532 eV) increases for increasing amount of Co doping. This trend can be related to the increase in d-electron number when Fe is substituted by Co and therefore the O 2p–Fe/Co 3d hybridised states increase concordantly. Similar behavior has been previously observed in LaBO3 samples (B = Cr, Mn, Fe, Co, Ni) under the claim that at fixed transition metal valence, going from left to right in the first row of the periodic table, the electronegativity of the transition metal increases (more covalent); as a consequence, the 3d orbitals may get closer to the O 2p thus leading to stronger hybridisation.57,58 This change in the number of d electrons and therefore hybridisation, has already been reported to modify the optical bandgap.57,59 Nonetheless, it is important to note that our samples contain Co3+ and Co2+ species, with a decreasing Co2+/Co3+ ratio with Co substitution (Fig. 3b). Based on that, the first feature of the O K-edge spectra indicates that the hybridisation increases for those samples with moderately higher content of Co3+. This behavior agrees with the study of Suntivich et al.58 carried out in a series of La–Ni–O compositions in which the hybridisation between Ni 3d orbitals and O 2p orbitals increased by increasing the oxidation state of Ni from Ni2+, Ni2.7+ to Ni3+. In this case, the increase in hybridisation is explained by lowering of the transition metal 3d level leading to smaller charge-transfer energy (Δ).57 Note that the effect of Co doping is also observed in the shape of the valence band showing an increase of the feature at valence band maximum (VBM) attributed to the O 2p–Co 3d occupied states (Fig. S3, ESI†). Therefore, it is very likely that the optical band gap reduction identified from spectroscopic ellipsometry upon cobalt substitution (Fig. 2) is due to an increase in the hybridisation between the transition metal 3d and O 2p orbital states, which is enabled by the presence of Co3+. Nevertheless, we anticipate that the first-principles calculations described below suggest that this hybridisation is mediated by the presence of both, Co3+ and Co2+ ions. Finally, we recall that low level of A-site substitution barely modified the O K-edge spectra and thus the hybridisation, being consistent with the reported less significant role of A-cation on the electronic structure.52,58
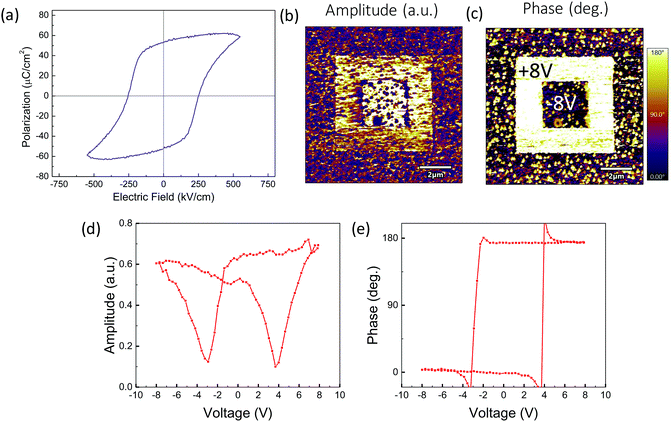
Ferroelectric characterization has been performed in 100 nm La-BFCO30 films on 10 nm-LSMO/STO substrates (Fig. 5a). It is obtained a remanent polarization of 53 μC cm−2, similar to that obtained for epitaxial BFCO films and slightly higher than pristine BFO films.21,60 Note that similar behavior is also identified in thicker (>300 nm) (La)BFO polycrystalline films but at significantly lower Co dopings (2–3%).61,62 Additionally, piezoelectric characterization has been performed in 20 nm La-BFCO30 films on LSMO/STO. In Fig. 4b and c, the amplitude and phase signal images collected after applying −8 and +8 V in the regions indicated in panel c are shown. In the outer regions no voltage was applied and, thus, it corresponds to the as-grown state. It can be observed that 180° phase contrast is obtained and that the amplitude signal at domain walls between domains written with opposite voltage is near zero. These results are indicative of the genuine ferroelectric nature of the observed contrast.63,64 Amplitude and phase signal loops (Fig. 4b and c) show butterfly and 180° hysteresis, respectively, also revealing the ferroelectric nature of the material. BFO, BFCO and BFCO30 LSMO-buffered 20 nm thick film (Fig. S4, ESI†) show similar results.
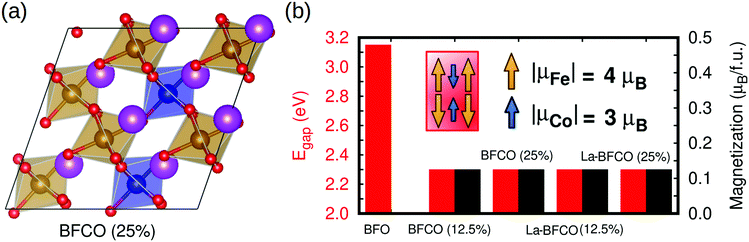
In order to characterize the synthesized materials also theoretically, we performed a first-principles study of BFCO and La-BFCO solid solutions at 12.5 and 25% Co and 12.5% La contents based on density functional theory (DFT). Albeit such concentrations of substitutional atoms are not identical to the experimental ones (due to the constraints imposed by the size of the adopted simulation cell, see Experimental section for technical details) and the limitations of DFT methods to predict exact energy band gaps are well known,65 we expect our theoretical results to be qualitatively meaningful and comparable to our experimental findings. Following previous experimental and theoretical works,66,67 we adopted a low-symmetry rhombohedral-like phase presenting large anti-phase O6 rotations along the three pseudo-Cartesian axes (i.e., similar to the BFO ground-state phase described by the space group R3c39 but with lower symmetry) to perform our DFT calculations and analysis. Our sampling of all possible Fe/Co B-site arrangements compatible with the adopted simulation cell indicates that Co atoms tend to disperse homogeneously in the solution (i.e., Co nearest neighbours are Fe ions, see Fig. 5a).
We estimated the energy band gap, Egap, and magnetic properties of several BFCO and La-BFCO solid solutions and compared them to those obtained for bulk BFO using analogous computational methods (Fig. 5b). Our DFT results are overall consistent with the experimental results explained above. In particular, the band gap of the system is reduced by a significant ∼30% with respect to that of pristine BFO as a consequence of Co substitution. Our DFT results do not depend appreciably on the concentration of cobalt when all the substitutional ions adopt the oxidation state Co3+ (see next paragraph). As it was expected, the introduction of La atoms does not have any noticeable impact on Egap because the corresponding 6s orbitals lie well below the Fermi energy level (Fig. 6a and b). We have found that the analysed solid solutions present a net magnetization of ∼0.1 μB per formula unit at low temperatures, which is consistent with recent magnetic hysteresis loop measurements reported by Gao et al.68 The origin of the estimated net magnetization is a magnetic spin imbalance between the Fe and Co sublattices (i.e., magnetic spins arrange antiferromagnetically but the individual Co magnetic moments are smaller than the Fe ones, Fig. 5b), a mechanism that is similar to what has been predicted recently for off-stoichiometric BiCoO3 thin films.69 Other authors reported that larger rare earth loads (i.e. 20%) could significantly alter the electronic, magnetic an optical properties of the BFCO system.70
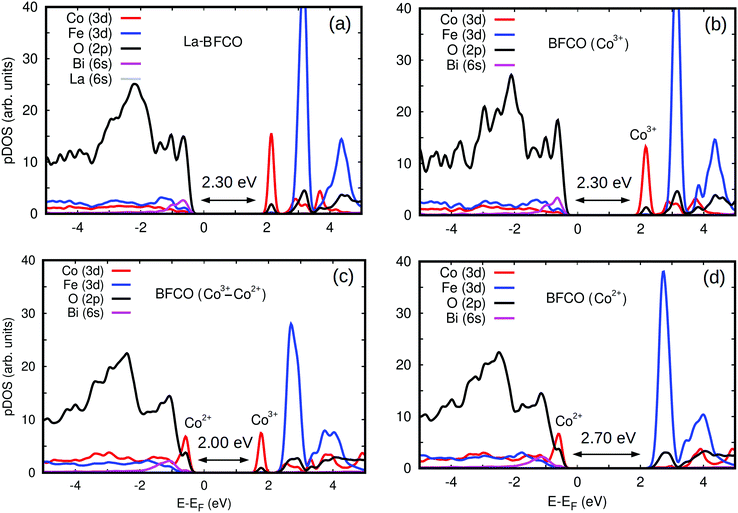
To gain further insight into the band gap reduction observed in BFCO and La-BFCO solid solutions, we analysed the partial density of electronic states (pDOS) around the Fermi energy level (Fig. 6). In our DFT simulations of pristine systems, the oxidation state of Co ions is consistently identified as 3+. Nevertheless, upon the introduction of oxygen vacancies the Co ions surrounding the point defects are reduced and consequently adopt the oxidation state 2+ (as shown by an increase in the amount of charge occupying d-orbitals and a decrease of ∼10% in the corresponding magnetic moments). The electronic properties of Fe ions are hardly affected by the introduction of oxygen vacancies, which agrees with our XAS observations. In the simulated pristine BFCO system (Fig. 6b), in which only Co3+ ions are present, we observe a strong Fe/Co d and O p orbitals hybridisation at the VBM and the appearance of a large pDOS peak corresponding to unoccupied Co d states at the minimum of the conduction band (CBM). When enough oxygen vacancies are introduced in the system so that all the cobalt ions are Co2+ (Fig. 6d), the energy band gap increases appreciably with respect to the pristine case due to an increase in the occupation of Co d electronic states at the VBM and the disappearance of the Co d pDOS peak at the CBM. Meanwhile, when both Co3+ and Co2+ ionic species coexist in the material (Fig. 6c) a significant energy band gap reduction follows from the simultaneous presence of Co d peaks at the VBM and CBM.
The qualitative discrepancy between XAS and DFT on whether the generation of Co2+ at the VBM or the existence of unoccupied Co3+ states are the origin of the band gap change could be due to having considered an oversimplified scenario on the local symmetry of the BFCO system due to the large spin variability of the cobalt ions. In particular, high-spin was systematically identified as the energetically most favorable state for Co in the DFT simulations, but it could be possible that other intermediate and/or low spin configurations existed also in the synthesized solid solutions.71,72 In addition, in this study it has been assumed that cobalt atoms exclusively replace Fe.67 Nonetheless, a recent publication on Co-substituted SrTiO3 has shown that cobalt in the divalent state could substitute the cation in the A-site.73 It will be interesting to clarify these important aspects on the magnetic properties of BFCO in future works.
Finally, we estimated the electric polarization, P, of BFO and BFCO and La-BFCO solid solutions with the first-principles methods explained in Section 2 to characterize the effects of chemical substitutions and disorder on their ferroelectric properties. For the ground-state of bulk BFO we obtained a P value of 69.87 μC cm−2, which is in good agreement with the reported experimental values of 50–90 μC cm−2 (recall that our DFT calculations are performed for “single crystal” configurations).74 It was found that the electric polarization of BFCO and La-BFCO solid solutions were practically identical among them and very similar to that estimated for bulk BFO. In particular, for BFCO (12.5%) and La-BFCO (12.5%) we obtained P = 73.63 and 72.41 μC cm−2, respectively, and for BFCO (25%) and La-BFCO (25%) 74.01 and 70.02 μC cm−2. These theoretical results are also in consistent agreement with our experimental ferroelectric characterization of La-BFCO (Fig. 4). Therefore, the incorporation of La ions in BFCO films does not affect negatively their polar features.
Overall, our first-principles results reproduce the experimentally observed influence of the relative population of Co2+/Co3+ ions on the optoelectronic properties of BFCO and La-BFCO solid solutions and rationalize their superior multifunctionality as compared to that of pristine BFO.21
4 Conclusions
In this work we presented a thorough study based on the double cation substitution in the ferroelectric perovskite BiFeO3 prepared by chemical solution deposition. We identified that the band gap shift is mostly attributed to the Co 3d hybridisation with O 2p and the coexistence of Co2+ and Co3+ species, while Fe 3d remains unchanged upon substitution, as supported by first-principles calculations. Importantly, the benefit of substituting Bi by La in BFCO30 is twofold, it helps stabilizing the metastable BFCO30 phase with no secondary phases promoting epitaxial growth and preserves the reduced optical band gap values and electric polarization obtained in Co-doped BiFeO3. Our work offers a stable composition to perform further systematic studies such as help unravelling the cross-coupling mechanism between light absorption and ferroelectricity in ferroelectric oxide perovskites. Additionally, the multiferroicity of BiFeO3 could be further explored in this new La-BFCO composition to go beyond simple photovoltaic devices envisaging new computing memories, optomechanical devices and detectors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Spanish Ministerio de Ciencia, Innovación y Universidades (“Severo Ochoa” Programme for Centres of Excellence in R&D CEX2019-000917-S, MAT2017-83169-R, RTI2018-093996-B-C32, PID2019-107727RB-I00 (AEI/FEDER, EU)). P. M. thanks financial support from FPI fellowship (PRE2018-084618). C. M. and C. C. acknowledge computational resources and technical assistance from the Australian Government and the Government of Western Australia through the National Computational Infrastructure (NCI) and Magnus under the National Computational Merit Allocation Scheme and The Pawsey Supercomputing Centre. The authors acknowledge Prof. J. Fontcuberta for providing access to his experimental facilities and the support of ALBA staff for the successful performance of the measurements at CIRCE beamline of the ALBA Synchrotron Light Source. I. F. and C. C. acknowledge support from the Spanish Ministry of Science, Innovation and Universities under the “Ramón y Cajal” fellowship RYC2017-226531 and RYC2018-024947-I, respectively. M. C and I. F acknowledge Beca Leonardo from fundación BBVA. H. T is financially supported by China Scholarship Council (CSC) with no. 201906050014. The work of P. M. and H. T have been done in the framework of the doctorate in Materials Science of the Autonomous University of Barcelona.References
- I. Grinberg, D. West, M. Torres, G. Gou, D. M. Stein, L. Wu, G. Chen, E. M. Gallo, A. R. Akbashev, P. K. Davies, J. Spanier and A. M. Rappe, Nature, 2013, 503, 509–512 CrossRef CAS.
- R. Nechache, C. Harnagea, S. Li, L. Cardenas, W. Huang, J. Chakrabartty and F. Rosei, Nat. Photonics, 2014, 9, 61–67 CrossRef.
- J. Spanier, V. Fridkin, A. M. Rappe, A. R. Akbashev, A. Polemi, Y. Qi, Z. Gu, S. Young, C. Hawley, D. Imbrenda, G. Xiao, A. Bennett-Jackson and C. L. Johnson, Nat. Photonics, 2016, 10, 611–616 CrossRef CAS.
- V. Fridkin, Crystallogr. Rep., 2001, 46, 654–658 CrossRef.
- P. Lopez-Varo, L. Bertoluzzi, J. Bisquert, M. Alexe, M. Coll, J. Huang, J. A. Jimenez-Tejada, T. Kirchartz, R. Nechache, F. Rosei and Y. Yuan, Phys. Rep., 2016, 653, 1–40 CrossRef CAS.
- C. Paillard, X. Bai, I. C. Infante, M. Guennou, G. Geneste, M. Alexe, J. Kreisel and B. Dkhil, Adv. Mater., 2016, 28, 5153–5168 CrossRef CAS.
- T. Choi, S. Lee, Y. J. Choi, V. Kiryukhin and S.-W. Cheong, Science, 2009, 324, 63–66 CrossRef CAS.
- M. Alexe and D. Hesse, Nat. Commun., 2011, 2, 256–261 CrossRef.
- A. Bhatnagar, A. R. Chaudhuri, Y. H. Kim, D. Hesse and M. Alexe, Nat. Commun., 2013, 4, 2835–2843 CrossRef.
- S. M. Selbach, M.-A. Einarsrud and T. Grande, Chem. Mater., 2009, 21, 169–173 CrossRef CAS.
- T. Rojac, A. Bencan, G. Drazic, N. Sakamoto, H. Ursic, B. Jancar, G. Tavcar, M. Makarovic, J. Walker and B. Malic, et al. , Nat. Mater., 2017, 16, 322–327 CrossRef CAS.
- M. Schrade, N. Masó, A. Perejón, L. A. Pérez-Maqueda and A. R. West, J. Mater. Chem. C, 2017, 5, 10077–10086 RSC.
- Z. X. Cheng, A. H. Li, X. L. Wang, S. X. Dou, K. Ozawa, H. Kimura, S. J. Zhang and T. R. Shrout, J. Appl. Phys., 2008, 103, 07E507 CrossRef.
- F. Huang, X. Lu, W. Lin, X. Wu, Y. Kan and J. Zhu, Appl. Phys. Lett., 2006, 89, 242914 CrossRef.
- S. R. Das, R. N. P. Choudhary, P. Bhattacharya, R. S. Katiyar, P. Dutta, A. Manivannan and M. S. Seehra, J. Appl. Phys., 2007, 101, 034104 CrossRef.
- C.-H. Yang, D. Kan, I. Takeuchi, V. Nagarajan and J. Seidel, Phys. Chem. Chem. Phys., 2012, 14, 15953–15962 RSC.
- D. Kan, L. Pálová, V. Anbusathaiah, C. J. Cheng, S. Fujino, V. Nagarajan, K. M. Rabe and I. Takeuchi, Adv. Funct. Mater., 2010, 20, 1108–1115 CrossRef CAS.
- L. You, F. Zheng, L. Fang, Y. Zhou, L. Z. Tan, Z. Zhang, G. Ma, D. Schmidt, A. Rusydi, L. Wang, L. Chang, A. M. Rappe and J. Wang, Sci. Adv., 2018, 4, 1–9 Search PubMed.
- C. De Dobbelaere, M. L. Calzada, R. Jiménez, J. Ricote, I. Bretos, J. Mullens, A. Hardy and M. K. Van Bael, J. Am. Chem. Soc., 2011, 133, 12922–12925 CrossRef CAS.
- Q. Zhang, N. Valanoor and O. Standard, J. Mater. Chem. C, 2015, 3, 582–595 RSC.
- P. Machado, M. Scigaj, J. Gazquez, E. Rueda, A. Sánchez-Diáz, I. Fina, M. Gibert-Roca, T. Puig, X. Obradors, M. Campoy-Quiles and M. Coll, Chem. Mater., 2019, 31, 947–954 CrossRef CAS.
- N. S. Bein, P. Machado, M. Coll, F. Chen, M. Makarovic, T. Rojac and A. Klein, J. Phys. Chem. Lett., 2019, 10, 7071–7076 CrossRef CAS.
- X. Qi, J. Dho, R. Tomov, M. G. Blamire and J. L. MacManus-Driscoll, Appl. Phys. Lett., 2005, 86, 062903 CrossRef.
- A. A. Belik, S. Iikubo, K. Kodama, N. Igawa, S.-I. Shamoto, S. Niitaka, M. Azuma, Y. Shimakawa, M. Takano, F. Izumi and E. Takayama-Muromachi, Chem. Mater., 2006, 18, 798–803 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. Gebhardt and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 125202 CrossRef CAS.
- Y.-R. Luo, Handbook of bond dissociation energies in organic compounds, CRC Press, 1st edn, 2002 Search PubMed.
- H. Uchida, R. Ueno, H. Funakubo and S. Koda, J. Appl. Phys., 2006, 100, 014106 CrossRef.
- J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637 CrossRef CAS.
- V. Pérez-Dieste, L. Aballe, S. Ferrer, J. Nicolàs, C. Escudero, A. Milán and E. Pellegrin, J. Phys.: Conf. Ser., 2013, 425, 072023 CrossRef.
- J. Lidon-Simon, D. Fernandez-Carreiras, J.-V. Gigante, J. Jan Jamroz, J. Klora and O. Matilla, Proceedings of ICALEPCS conference, 2011, vol. 361, pp. 1032–1035.
- F. Liu, I. Fina, R. Bertacco and J. Fontcuberta, Sci. Rep., 2016, 6, 25028 CrossRef CAS.
- I. Fina, L. Fàbrega, E. Langenberg, X. Mart, F. Sánchez, M. Varela and J. Fontcuberta, J. Appl. Phys., 2011, 109, 074105 CrossRef.
- B. J. Rodriguez, C. Callahan, S. V. Kalinin and R. Proksch, Nanotechnology, 2007, 18, 475504 CrossRef.
- S. V. Kalinin and A. Gruverman, Scanning probe microscopy of functional materials: nanoscale imaging and spectroscopy, Springer Science & Business Media, 2010 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- C. Cazorla, O. Diéguez and J. Íñiguez, Sci. Adv., 2017, 3, e1700288 CrossRef.
- C. Cazorla and J. Íñiguez, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214430 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- C. Cazorla, Phys. Rev. Appl., 2017, 7, 044025 CrossRef.
- B. G. Janesko, T. M. Henderson and G. E. Scuseria, Phys. Chem. Chem. Phys., 2009, 11, 443–454 RSC.
- C. Menéndez and C. Cazorla, Phys. Rev. Lett., 2020, 125, 117601 CrossRef.
- C. Cazorla and M. Stengel, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214108 CrossRef.
- S. Yasui, K. Nishida, H. Naganuma, S. Okamura, T. Iijima and H. Funakubo, Jpn. J. Appl. Phys., 2007, 46, 6948–6951 CrossRef CAS.
- S. Yasui, K. Yazawa, T. Yamada, K. Nishida, H. Uchida, M. Azuma and H. Funakubo, Jpn. J. Appl. Phys., 2010, 49, 09MB04 Search PubMed.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- J. Tauc, Mater. Res. Bull., 1968, 3, 37–46 CrossRef CAS.
- T. Gujar, V. Shinde and C. Lokhande, Mater. Chem. Phys., 2007, 103, 142–146 CrossRef CAS.
- J. Meng, K. Chen, Y. Mijiti, D. Chen, F. Choueikani, Z. Zou, L. Wang, G. Mu, W. Geng, Q. Kong, A. Jiang, X.-J. Ning and T.-C. Weng, Phys. Rev. Appl., 2019, 12, 044010 CrossRef CAS.
- H. Ikeno, I. Tanaka, T. Miyamae, T. Mishima, H. Adachi and K. Ogasawara, Mater. Trans., 2004, 45, 1414–1418 CrossRef CAS.
- M. Abbate, F. M. F. de Groot, J. C. Fuggle, A. Fujimori, O. Strebel, F. Lopez, M. Domke, G. Kaindl, G. A. Sawatzky, M. Takano, Y. Takeda, H. Eisaki and S. Uchida, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4511–4519 CrossRef CAS.
- G. Anjum, R. Kumar, S. Mollah, P. Thakur, S. Gautam and K. H. Chae, J. Phys. D: Appl. Phys., 2011, 44, 075403 CrossRef.
- M. W. Haverkort, Z. Hu, J. C. Cezar, T. Burnus, H. Hartmann, M. Reuther, C. Zobel, T. Lorenz, A. Tanaka, N. B. Brookes, H. H. Hsieh, H.-J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. Lett., 2006, 97, 176405 CrossRef CAS.
- L. Bi, H.-S. Kim, G. F. Dionne and C. A. Ross, New J. Phys., 2010, 12, 043044 CrossRef.
- W. Zhang, H.-P. Li and W. Pan, J. Mater. Sci., 2012, 47, 8216–8222 CrossRef CAS.
- T. Saitoh, A. E. Bocquet, T. Mizokawa and A. Fujimori, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 7934–7938 CrossRef CAS.
- J. Suntivich, W. T. Hong, Y.-L. Lee, J. M. Rondinelli, W. Yang, J. B. Goodenough, B. Dabrowski, J. W. Freeland and Y. Shao-Horn, J. Phys. Chem. C, 2014, 118, 1856–1863 CrossRef CAS.
- T. Arima, Y. Tokura and J. B. Torrance, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17006–17009 CrossRef CAS.
- S. Yasui, M. Nakajima, H. Naganuma, S. Okamura, K. Nishida, T. Yamamoto, T. Iijima, M. Azuma, H. Morioka, K. Saito, M. Ishikawa, T. Yamada and H. Funakubo, J. Appl. Phys., 2009, 105, 061620 CrossRef.
- S. Yasui, H. Naganuma, S. Okamura, K. Nishida, T. Yamamoto, T. Iijima, M. Azuma, H. Morioka, K. Saito, M. Ishikawa, T. Yamada and H. Funakubo, Jpn. J. Appl. Phys., 2008, 47, 7582–7585 CrossRef CAS.
- D. Do, J. W. Kim, S. S. Kim, T. K. Song and M. H. Kim, J. Korean Phys. Soc., 2012, 61, 1409–1412 CrossRef CAS.
- Z. Guan, Z.-Z. Jiang, B.-B. Tian, Y.-P. Zhu, P.-H. Xiang, N. Zhong, C.-G. Duan and J.-H. Chu, AIP Adv., 2017, 7, 095116 CrossRef.
- S. Kim, D. Seol, X. Lu, M. Alexe and Y. Kim, Sci. Rep., 2017, 7, 41657 CrossRef CAS.
- J. P. Perdew, W. Yang, K. Burke, Z. Yang, E. K. U. Gross, M. Scheffler, G. E. Scuseria, T. M. Henderson, I. Y. Zhang, A. Ruzsinszky, H. Peng, J. Sun, E. Trushin and A. Görling, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2801–2806 CrossRef CAS.
- H. Hojo, K. Oka, K. Shimizu, H. Yamamoto, R. Kawabe and M. Azuma, Adv. Mater., 2018, 30, 1705665 CrossRef.
- O. Diéguez and J. Íñiguez, Phys. Rev. Lett., 2011, 107, 057601 CrossRef.
- B. Gao, L. Lin, C. Chen, L. Wei, J. Wang, B. Xu, C. Li, J. Bian, S. Dong, J. Du and Q. Xu, Phys. Rev. Mater., 2018, 2, 084401 CrossRef CAS.
- C. Menéndez, D. Chu and C. Cazorla, npj Comput. Mater., 2020, 6, 76 CrossRef.
- N. Gao, W. Chen, R. Zhang, J. Zhang, Z. Wu, W. Mao, J. Yang, X. Li and W. Huang, Comput. Theor. Chem., 2016, 1084, 36–42 CrossRef CAS.
- C. F. Chang, Z. Hu, H. Wu, T. Burnus, N. Hollmann, M. Benomar, T. Lorenz, A. Tanaka, H.-J. Lin, H. H. Hsieh, C. T. Chen and L. H. Tjeng, Phys. Rev. Lett., 2009, 102, 116401 CrossRef CAS.
- J.-M. Chen, Y.-Y. Chin, M. Valldor, Z. Hu, J.-M. Lee, S.-C. Haw, N. Hiraoka, H. Ishii, C.-W. Pao, K.-D. Tsuei, J.-F. Lee, H.-J. Lin, L.-Y. Jang, A. Tanaka, C.-T. Chen and L. H. Tjeng, J. Am. Chem. Soc., 2014, 136, 1514–1519 CrossRef CAS.
- I. A. Sluchinskaya and A. I. Lebedev, J. Alloys Compd., 2020, 820, 153243 CrossRef CAS.
- J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, Science, 2003, 299, 1719–1722 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Ionic radius of cations in BFO composition, atomic force microscopy and piezoelectric force microsocopy of BFCO films, n, k optical constants for BFCO30 and La-BFCO30. Valence band spectra of BFO films with different dopings. See DOI: 10.1039/d0tc04304d |
| This journal is © The Royal Society of Chemistry 2021 |