Lamellar-to-MLV transformation in SDS/octanol/brine examined by microfluidic-SANS and polarised microscopy

Abstract

The lamellar-to-multilamellar vesicle (MLV) transformation in a model surfactant system, sodium dodecyl sulfate (SDS), octanol and brine, is investigated under continuous and oscillatory microfluidic contraction–expansion flows, employing polarised optical microscopy and small angle neutron scattering (SANS), with sample volume probed down to ≃20 nL. We determine the lamellar-to-MLV transition requirements at varying flow velocity, oscillation amplitude, frequency, and number of oscillatory cycles. The spatio-temporal evolution of the hierarchical fluid structure is elucidated: lamellar sheets initially align with flow direction upon entering a constriction and then perpendicularly upon exiting; the formation of MLVs at the nanoscale is first observed by SANS within a few (<5) oscillatory cycles, followed by the gradual appearance of a regular (albeit not crystalline) MLV arrangement, at the micronscale, by optical microscopy after tens of cycles, under the conditions investigated. Once MLVs form under flow, these remain metastable for several days.

---

1 Introduction

Surfactants in solution can self-assemble into ordered mesophases, known as lyotropic liquid crystalline phases,¹ which are generally responsive to flow, changing macro- and microscale properties upon application of shear. In the lamellar L_α phase, surfactant molecules assemble to form a bilayer structure with a thickness δ and interlayer distance d (Fig. 1a). Under shear flow, for instance in a Couette geometry, lamellar phases can be aligned along any of three principal directions termed neutral, velocity and velocity-gradient alignment.^2,3 Further, L_α lamellae can also be transformed into multilamellar vesicles (MLVs), or “onions”^4–6 which is the focus of this work. Vesicles find numerous applications, ranging from drug molecule carriers^7,8 and nano/microparticle encapsulants (“stuffed onions”)⁹ to microreactors¹⁰ and can be formed by electrolyte addition,^11,12via extrusion¹³ under shear,^3,4,6,14 or less commonly, spontaneously.¹⁵

Fig. 1 (a) SDS/octanol/brine lamellar system and illustration of the shear-induced lamellar to MLV transformation; (b) schematic of the high-pressure contraction–expansion microfluidic device platform coupled to SANS and cross-polarised optical microscopy. A SANS beam footprint of 175 × 420 μm² yields a scattering volume of 22 nL, and allows the mapping of the chip at different positions; (c) square-wave oscillatory shear profile imposed, shown by the red trace; (d) contraction–expansion microdevice dimensions.

The formation of vesicles under shear is particularly appealing for its size control and spatial ordering.^6,14 In the pioneering work of Roux and co-workers, over two decades ago, the formation of vesicles (“onion” phase in di(2-ethylhexyl) sulfosuccinate (AOT)/brine was established by polarised optical microscopy and small angle light scattering (SALS).¹⁶ A critical shear rate required for MLV formation ([small gamma, Greek, dot above]_c ∼ 10 s⁻¹) was identified, and the resulting vesicle radii R was found to depend on the applied shear rate [small gamma, Greek, dot above] as

Subsequent studies with Sodium Dodecyl Sulphate (SDS)/pentanol/dodecane/water proposed a ‘flow phase map’ with three distinct regions comprising defective L_α, packed MLVs and aligned L_α phases as a function of shear rate, established with the aid 2D small angle neutron scattering (SANS).¹⁴ Further, the MLV radius was found to be proportional to the square-root of lamellar d-spacing and square of the lamellar membrane fraction ϕ, following¹⁴

R ∝ d⁻² ∝ ϕ² (2)

Once formed, MLVs can undergo a further ordering transition, identified by Sierro and Roux⁶ using the SDS/octanol/brine (20 g L⁻¹ of NaCl in H₂O) L_α pseudoquaternary system. At higher shear rates ([small gamma, Greek, dot above] ≈ 80 s⁻¹) MLVs can form a hexagonally packed structure accompanied by jump in vesicle size (from ∼1 μm to ∼10 μm). The (dis)continuous nature of the transition appears, in part, to be controlled by temperature, with higher temperatures favouring continuous transitions from MLVs into a packed structure.⁶

Several mechanisms have been proposed to describe MLV formation under flow, generally in terms of a balance between the curvature energy and compression energy.¹⁷ Zilman and Granek¹⁸ consider that flow acts to reduce the membrane excess area via suppression of thermal membrane undulations; in turn, this induces buckling of the lamellar sheets and, above certain critical pressure (or shear rate), MLVs form. Theoretical predictions deviate considerably from experiment, which was rationalised as due to defects in lamellar phase which cause the ‘local’ shear rate to be higher than the imposed shear rate. A different model suggests that the undulations are introduced via non-uniformities in the applied shear.^5,19 Experimentally, the formation of MLVs has been described by the emergence of intermediate multilamellar cylinder (MLC) phase^20–22 in continuous shear flow or a direct emergence of MLVs with oscillatory flows.⁴

Numerous experimental reports have considered the effect of shear field, stress and rate, on various model systems (non-ionic,^4,21,23,24 cationic^25,26 and anionic^27,28), the effect of added co-surfactants^3,29 and salt,^30,31 and the effect of oscillatory shear flows.^4,28,32 Predominant analytical techniques include rheology,^33,34 scattering,^21,22,34,35 optical microscopy^35,36 and ²H NMR.^4,37–40

In this work, we consider tubular flow, in continuous and oscillatory modes, and both wall shear and extensional (viz. contraction–expansion) flows, motivated by their industrial relevance in complex fluid processing (e.g., through nozzles and continuous flow reactors) and academic importance. In order to precisely control flow type, magnitude and enable the spatiotemporal investigation of flow-induced transformations, we employ microfluidics, coupled with SANS and polarised optical microscopy (and ancillary characterisation approaches). Flow induced self-assembly in microfluidics has been employed to investigate, for example, the formation of wormlike micelles from micellar solutions under extensional flows^41–43 and the formation of non-spherical block copolymer nanostructure.⁴⁴ The coupling of microfluidics with a range of analytical techniques such as rheology,⁴⁵ SANS/SAXS^46–48 and NMR⁴⁹ has enabled the precise, in situ characterisation of minute (<0.1 μL) samples in exceptionally well defined environments. While the effect of microflow on L_α phases has been previously investigated by SANS/SAXS (and shown to undergo orientational flips upon exiting constrictions),^46,50,51 here we focus on the lamellar to MLV transformation in model microdevice geometries. We select the well-known SDS/octanol/brine system, illustrated in Fig. 1a, and employ a bespoke contraction–expansion microdevice, depicted in Fig. 1d, compatible with both crosspolarised optical microscopy and SANS (Fig. 1b), subjected to continuous and oscillatory shear flows, as illustrated in Fig. 1c. We demonstrate that a single contraction–expansion device can induce flow transformations on a short timescale, with lamellar phase reorientation orthogonal to the flow direction, and over longer time periods, achieve size control in an isotropic MLV phase.

2 Methods

2.1 SDS/octanol/brine solution sample preparation

Fresh samples were prepared prior to each series of measurements, as follows: 6.50 g (22.5 mM) of sodium dodecyl Sulphate, SDS (Sigma-Aldrich BioXtra, ≥99.0%) was dissolved in 85.6 g of brine solution made of 20% NaCl (ACS Reagent, ≥99.0%) in D₂O (Sigma-Aldrich, 99.9 atom% D). Dissolution was aided by heating to 30 °C until clear and allowed to cool to room temperature; then 7.90 g (60.7 mM) of 1-octanol (Sigma-Aldrich, anhydrous, ≥99%) was added to the SDS/brine mixture and stirred for 2 min at 1000 rpm until fully incorporated. The solution was then left to equilibrate for 48 h to relax inadvertent shear effects induced during sample preparation.

2.2 Sample characterisation in tubular geometry

Preliminary characterisation was carried out on samples loaded on 1 mL plastic syringe and sheared with a long (150 cm) capillary FEP tubing (inner diameter = 0.79 mm) assembly, subjected to oscillatory flow (1 mL sample volume displaced at a flow rate of 5 mL h⁻¹ with a Harvard 33 DDS pump in infuse/withdraw mode) for 5 h. The sample was then placed between glass coverslips with a 120 μm thick spacer and imaged by cross-polarised microscopy (Olympus BX41) with 50×/0.50 magnification MPlanFLN objective. Additionally, ²H NMR spectra were acquired before and after shear with a Jeol 400 MHz NMR spectrometer.

2.3 Microscopy-microfluidic set-up

A custom-designed, boron-free, crown glass contraction–expansion microfluidic device (fabricated by Dolomite Microfluidics) was fitted with 20 cm long inlet and outlet polytetrafluoroethylene (PTFE) tubing (inner diameter = 0.79 mm) and mounted on Linkam THMS600 temperature control stage set at 24.3 °C. The sample was slowly loaded on 20 mL plastic syringe, mounted on a LabVIEW-controlled Harvard PHD ULTRA 4400 pump, and connected to the device; the outlet was connected to a glass vessel containing unsheared sample. The sample was first infused at 0.5 mL h⁻¹ and allowed to stabilise for 10 min. Continuous and oscillatory shear experiments were then recorded with an Olympus BX41 reflection microscope equipped with a Basler acA2000-165um camera controlled with PylonViewer using 5×/0.10 MPlan, 10×/0.25 Ach and 50×/0.50 MPlanFLN Olympus objectives with cross-polarised filters (U-AN-2 analyser and U-PO3 polariser), and data were analysed with ImageJ. Volumetric velocities used in microscopy experiments ranged from 0.5 to 100 mL h⁻¹ corresponding to linear velocities between 0.5 to 90 mm s⁻¹ assuming plug flow and wall shear rates between 8.5 to 1700 s⁻¹ in the expansion and between 35 to 7000 s⁻¹ in the constriction. Wall shear rates estimated based on Son's⁵² approach [small gamma, Greek, dot above] = (6Q/WH²)(1 + H/W)f × (H/W), where Q is volumetric flow rate and f × H/W is a geometric function calculated based on aspect ratio between H (height) an dW (width). In this instance the f × H/W for expansion is 0.7297 and for the constriction 0.5928 (see Fig. S2 for shear rate as a function of flow rate linear plots, ESI†). The extension rate along the channel centreline was approximately between 2 to 430 s⁻¹ at the flow rates stated above.

2.4 Velocity flow profile

The flow velocity profile in the microchannel was measured by cross-polarised microscopy with a 10× objective and 10 ms frame rate with 2000 μs exposure time. Matlab based PIVLab software employed 20 consecutive images and ensemble correlation with 2 passes with 64 × 64 and 32 × 32 pixel by pixel interrogation window sizes (1 pixel = 1.54 μm), and selecting a Gauss 2 × 3-point sub-pixel estimator and ‘standard’ correlation quality. The velocity profiles largely followed plug flow, and thus the flow velocity in the wide and narrow sections of the channel could be approximated by 0.46, 4.55, 45.5 mm s⁻¹ and 1.49, 14.9, 149 mm s⁻¹ corresponding to the (representative) 0.5, 5, 50 mL h⁻¹ volumetric flow rates.

2.5 SANS-microfluidic set-up

SANS experiments were performed on the D22 spectrometer at the Institut Laue Langevin, Grenoble. For reference, static sample measurements were collected using ‘banjo’ Hellma cells (1 mm path length) with sample to detector distances of 2, 8 and 17.6 m and neutron wavelength of 6 Å. Microfluidic experiments were acquired at the mid-q (8 m) configuration. The microfluidic chip was mounted on a 3D printed frame (Fig. S1, ESI†) and the temperature was set to 24.3 °C. A neutron beam mask (or diaphragm) with dimensions of 420 μm by 175 μm was used to define the beam footprint, commensurate with microdevice dimensions, resulting in an scattering volume of only 22 nL (given the 300 μm sample pathlength, i.e. channel depth). The device was illuminated in the neutral flow direction (z in Fig. 1b), probing the xy plane. The channel was aligned with the neutron beam by iteratively scanning the empty chip and tracking the scattering and transmission signals along x and y directions until a microchannel map is resolved (this ‘battleship’ exercise requires spatial precision, and the microdevice assembly must be stable and drift-free, to ensure repeatability of the data over time). Continuous microfluidic flow spectra were collected for flow rates 0.5 and 5 mL h⁻¹ at the inlet, contraction and exit of the chip with acquisition time of 10 min. Oscillatory shear flow experiments were performed after at 0.5–50 mL h⁻¹ flow rates, and data acquired after cycles 1, 2, 3, 4, 10 and 30, for 10 min, at the outlet position, under stopped flow conditions (needed as the acquisition time exceeded the flow oscillation frequency). Microstructural stability was monitored by acquiring spectra for 10 min after complete cessation of shear at 0, 4 and 20 h. The data were reduced with GRASP software by taking into account the empty beam, sample transmission and blocked beam and calibrated with direct beam. Data fitting of the radially and sector-averaged spectra was performed with SasView 5.0.2, employing the random head–tail sheet with Caillé structure factor model.⁵³

3 Results

3.1 Fluid structure before and after shear in a tubular geometry

The system was first characterised by ²H NMR, optical microscopy and SANS, prior and following the application of shear in a long capillary to emulate the conditions of a microdevice, as shown in Fig. 2. The ‘quiescent’ sample was allowed to equilibrate for 48 h prior to measurement, to minimise effects of sample preparation. Upon application of shear lamellar sheets aligned with the flow based on crosspolarised optical microscopy (Fig. S3, ESI†). An average flow velocity of 4.55 mm s⁻¹ (estimated from the volumetric flow rate 5 mL h⁻¹ and cross-sectional area 0.495 mm²) and shear rate of 58.5 s⁻¹ is expected to be well above the critical shear rate for MLV formation.⁶ The ²H NMR (Fig. 2a) and cross-polarised microscopy data (Fig. 2b) show characteristic features of anisotropic (prior to shearing) and isotropic (after shearing for 5 h) lamellar structure. ²H NMR indicates a doublet indicative of an anisotropic lamellar phase and a broad singlet peak after shearing, expected for the isotropic phase with either non uniform distribution of MLVs or coexistence between lamellar sheets and MLV phase.^39,40,54 The transformation of doublet peak into singlet peak in ²H NMR indicates that the transformation is continuous rather than discontinuous³⁸ under these experimental conditions.

Fig. 2 SDS/octanol/brine sample characteristics measured by (a) ²H NMR of sample in bulk before and after shear (in a 3 m long, 1/32′′ diameter capillary, for 5 h and flow rate of 5 mL h⁻¹); (b) corresponding cross-polarised optical microscopy images and FFT inset; (c) 2D SANS scattering images and radially-averaged scattering profile (before shear) measured at detector distances 17.6, 8 and 2 m, and λ = 6 Å neutron wavelength with fitted with random head–tail sheet with Caillé structure factor model.

Similarly, cross-polarised optical microscopy indicates presence of disordered lamellar sheets before shear and an ordered isotropic phase indicated by the change in optical texture.^35,36 This is corroborated by fast Fourier transform (FFT) analysis after shearing, displaying the characteristic cloverleaf pattern indicative of formation of spherical objects.^4,34–36 The size of the vesicles was estimated to be 3 μm. Microscopy images recorded over the duration of the experiment indicate that the onset of cloverleaf pattern development is around 20 min into the experiment (Fig. S3, ESI†). The birefringence intensity along the channel cross-section drops in the middle of the channel likely due to shear being close to 0 and lamellar sheet alignment on both sides of the tubing being orthogonal to each other. The L_αd-spacing is measured to be 15.7 nm, in agreement with the previous literature for this sample composition⁵⁵ and with the octanol to SDS molar fraction ratio ∼2.7 and the membrane volume fraction ϕ around 0.15 this value close to pure SDS/octanol/water d-spacing value 15 nm.⁵⁶ Generally, the addition of long chain alcohol will aid the swelling of L_α since the phase boundary for L_α formation is lowered. Typical values for such systems are between 4 to 40 nm.^3,57 The SANS scattering profile is unchanged by flow, with d spacing remaining at ≃15.7 nm. 2D scattering orientational change reflects the expected lamellar (anisotropic) to MLV (isotropic) transformation, as shown in Fig. 2c. The scattering data could be well described by a random head–tail sheet with Caillé structure factor model (lamellar_hg_stack in SASView, as detailed in Fig. S4, ESI†).

3.2 Continuous microfluidic flow

Since one of the most effective ways to form MLVs is via extrusion we examine the effect of continuous flow over a short timescale (<72 s) and the impact of a single constriction on the fluid structure at the nano and mesoscale. Fig. 3 shows cross-polarised microscopy data for two representative flow rates (0.5 and 5 mL h⁻¹, Fig. 3a), with accompanying PIV map. The residence time of the fluid within the chip was 72 and 7.2 s for 0.5 and 5 mL h⁻¹ respectively. The linear flow rates in the expansion were 0.455 mm s⁻¹ and 4.55 mm s⁻¹ and 1.49 mm s⁻¹ and 14.9 mm s⁻¹ in the constriction for 0.5 and 5 mL h⁻¹ respectively with corresponding wall shear rate values roughly representative of shear rates below and above the MLV transformation region.⁶ Cross-polarised optical microscopy reveals a large scale orientation and qualitatively shows alignment along the flow before and upon entering the construction, and normal to the flow upon exiting. The birefringence intensity and the relative alignment with the flow is greater for 5 mL h⁻¹ (bottom image Fig. 3b) than for 0.5 mL h⁻¹ (top image Fig. 3b). PIV of fluid at 0.5 mL h⁻¹ volumetric flow rate shows plug-like flow for which the linear velocity component roughly corresponds to the estimated velocity obtained dividing volumetric flow rate by cross-sectional area, namely 0.43 mm s⁻¹ and 1.46 mm s⁻¹.

Fig. 3 Continuous flow. (a) Constant volumetric flow rate over time, illustrated here for 0.5 and 5 mL h⁻¹, corresponding to an average velocity within the constriction of ≃1.49 and 14.9 mm s⁻¹, respectively; (b) cross-polarised microscopy images of the fluid flow at the two flow rates with PIV for 0.5 mL h⁻¹ indicating plug-like flow.

SANS confirms that the lamellar sheets undergo an orientational 90° flip upon exiting the constriction, as shown in Fig. 4a (more detail in Fig. S5a and S6a, ESI†). Quantitative population analysis from the scattering intensity of the lamellar sheet orientation shown by the colours (blue, grey, orange) can be obtained from data fitting and azimuthal intensity I(q) analysis. Orientational lamellar phase flips are well documented in the literature for microfluidic constriction-expansion devices alongside with the decrease in the scattering intensity.^46,50,51 Further analysis of the continuous flow SANS images shows that the radially averaged structure factor profile does not change with the flow and the position along the channel (Fig. 4b and more detail in Fig. S5b, c and S6b, c, ESI†). However, the scattering intensity and orientation of the pattern does (Fig. 4c and more detail in Fig. S5d, e and S6d, e, ESI†), reflecting the number density of lamellar sheets contributing to the scattering orientation probed and the ratio of lamellar sheets as a function of direction subjected to the contraction–expansion flow. A drop in intensity could be caused by the sheets changing plane (aligning in the grey plane indicated in Fig. 4a) or by changing phase (e.g. entering a micellar phase). The latter is ruled out by the fact that S(q) does not show the characteristic micellar profile at low q, and thus the drop in intensity is ascribed to a change in orientation of polycrystalline grains of lamellar sheets or the formation of regular MLVs.

Fig. 4 Continuous flow SANS analysis. (a) Microfluidic SANS 2D scattering images of oscillatory shear cycles (measured at 8 m and λ = 6 Å); (b) radially-averaged 2D SANS intensity acquired at the entrance (in), constriction (c), and exit (out) of the contraction–expansion geometry, at flow rates of 0.5 and 5 mL h⁻¹; the dashed lines around the lamellar peak indicate the integration limit selected for the azimuthal average; (c) azimuthal average within 0.035 ≤ q ≤ 0.045 Å⁻¹ computed from the 2D data shown in panel (a), from where an orientation parameter ΔI is estimated from the difference between the maximum and minimum intensities as a function of azimuthal angle; (d) summary of the parameters extracted, ΔI (red), and I_max at 0° (blue) and 90° (green), at the constriction entrance (in), centre (c) and exit (out), measured at 0.5 mL h⁻¹. The x axis coordinate refers to the distance from the center of the channel.

From the azimuthal average of the SANS 2D spectra (within 0.035 ≤ q ≤ 0.045 Å⁻¹), we define an orientation parameter ΔI from the difference between the maximum and minimum intensity as a function of azimuthal angle. In addition, we also examine the maximum intensities at 0°, along the flow direction, and 90°, perpendicular to the flow direction, as shown in blue and green traces in Fig. 4. These are computed at three representative channel locations, namely at the constriction entrance (in), centre (c) and exit (out). The overall anisotropy is found to decrease as shown by ΔI (Fig. 4d) and the fact that I_max0 and I_max90 profiles are not mirrored upon the orientational flip (Fig. 4c and d) caused by the contraction–expansion. While a scaling relation might be expected between orientation parameters (e.g., ΔI) and flow descriptors (e.g., extension gradient or a particular derivative of the shear field, sampled over the illuminated scattering volume), the two flow rates and single contraction–expansion ratio investigated do not enable a sufficiently precise quantification. Nonetheless, given the reduction in anisotropy with one-pass constriction, we hypothesise that oscillatory microfluidic flow can be effective at inducing a lamellar-to-MLV transformation and seek to quantify its requirements.

3.3 Oscillatory flow: effects of flow rate, volume and time of oscillation

We thus investigate the effect of flow cycling to quantify the cumulative effect of sequential contraction expansion flows (Fig. 5). Here we select three different flow rates of 0.5, 5 and 50 mL h⁻¹ (Fig. 5a) with wall shear rates in the expansion ranging from 8.5 to 850 s⁻¹.⁵² The shear rates correspond to the literature values for the shear diagram regions of no MLV, disordered MLVs and hexagonally packed MLVs.⁶ We further choose to oscillate 20 and 50 μL volumes based on an iterative approach to ensure the reliability of the displaced volume by the syringe pump, given the compressibility and capacitance of the flow system.⁵⁸ The overall time of oscillation was kept constant (1 h). Crosspolarised optical microscopy images (Fig. 5b) taken after the constriction across the middle of the channel show increased long range ordering with increasing flow rates and oscillatory volumes with the emergence of cloverleaf pattern indicative of spherical objects.^4,34–36 This is further quantified by normalised intensity analysis (obtained by dividing each curve by its baseline intensity value) of FFTs as a function of azimuthal angle (Fig. 5d), which shows an increase in anisotropy over repeat oscillatory shear cycles. The FFTs indicated spherical object size of 2 μm for 5 mL h⁻¹ flow rate and 1.5 μm for 50 mL h⁻¹ (50 μL volume amplitude). The values were calculated by measuring the intensity profile across the microfluidic channel and further verified by measuring repeat distance from the center to one of the lobes of the cloverleaf in FFT. Empirically, the relationship between the shear rate and radius corresponds roughly to scaling law of −1/4. This follows the general trend of radius of MLVs decreasing with increase of [small gamma, Greek, dot above]. However, it deviates from the value of −1/2 reported by and Roux.⁶ Explanation for the difference could be down to applied shear rate deviating from the effective shear rate due to wall slip.⁵⁹

Fig. 5 Oscillatory shear amplitude volume (V) and volumetric flow rate (Q) effect on flow induced structure formation. (a) Schematic of applied oscillatory flow profiles for 0.5, 5 and 50 mL h⁻¹, for V = 20 μL (dashed) and V = 50 μL (solid); (b) cross-polarised optical microscopy images with corresponding FFT images for samples sheared at 0.5, 5 and 50 mL h⁻¹ and displaced volume V = 50 and 20 μL, sheared for 3600 s; (c) azimuthal average of FFT computed around the intensity maximum (0.12–0.18 μm⁻¹ for 5 mL h⁻¹ and 0.18–0.23 μm⁻¹ for 50 mL h⁻¹) normalised by dividing each curve by its minimum value; (d) morphology map indicating the sheared volume and flow rate conditions investigated; after 3600 s (1 h) the conditions marked with the box resulted in a regular MLV arrangement.

From this sparse flow phase map, we conclude that sufficient conditions for the formation of ordered structures from L_α phase include 50 μL amplitude and 5 and 50 mL h⁻¹. These are within the wall shear rate range previously reported for the formation of MLVs in SDS/octanol/brine system.⁶ We next investigate the development of the ordered structures under oscillatory shear with flow rates between 1 to 100 mL h⁻¹, corresponding to wall shear rate between 20 to 1700 s⁻¹.

To examine MLV formation, we monitor the polarised light intensity (integrated over the image size) as a function of oscillatory shear cycle and time. MLV dimensions were estimated from FFT of optical birefringence data, from the outer q value of the clover-leaf patterns, and validated using the intensity profile across several MLVs on the real-space optical images. Further, since the intensity is related to particle size, we associate a plateau in intensity with completion on the transition. We find that the formation of the vesicles is time-dependent rather than oscillatory shear cycle dependent (Fig. 6a). Except for lowest flow rate of 1 mL h⁻¹, possibly affected by finite compressibility an flow non-linearity, the light intensity starts leveling off after cycle 80. Evidently, different flow rates will reach cycle 80 at different time, and we thus extract the corresponding time dependence for vesicle formation. This can be rationalised in terms of a total shear γ required for the sample to undergo the transformation, computed from t × [small gamma, Greek, dot above], where the associated time is shown in Fig. 6b.

Fig. 6 Effect of flow rate on MLV formation. (a) Average light intensity of cross-polarised optical images as a function of oscillatory shear cycle (top) and time (bottom), at flow rates 1–100 mL h⁻¹ and V = 50 μL. The blue area (top) indicates the oscillatory shear cycle range at which the data reach a plateau, while the grey dotted line (bottom) indicates the completion time for MLV formation. Lines are fits to a logistic function; (b) cycle number and associated time for MLV formation as a function of flow rate, obtained from (a). Generally, MLVs form after the same approximate number of cycles, and thus the associated time decreases with increasing flow rate.

We next consider the effect of shear rate on vesicle size scanning from 1 to 100 mL h⁻¹ after fluid had been subjected to 80 cycles of shearing, as illustrated by the microscopy images and FFTs in Fig. 7. The vesicle size estimated by the light intensity profile variation (Fig. 7b shaded circles) and verified by the I_∞ intensity plateau (Fig. 7b hollow triangles) value. The optical textures and accompanying FFTs display a decrease in vesicle size with increasing shear rate (Fig. 7a). The increase in size above 200 s⁻¹ (corresponding to 20 mL h⁻¹ flow rate) did not show a size jump as observed by Roux.⁶ The size dependence of vesicles on shear rate followed a more gradual trend with the power law of 1/4 rather than 1/2 as previously reported⁶ until the wall shear rate reaches 200 s⁻¹ (20 mL h⁻¹). This could be due to overestimation of the actual shear rate experienced by the bulk fluid since we refer to the wall shear rate in this tubular geometry.

Fig. 7 MLV size dependence on flow rate. (a) Cross-polarised optical images and their corresponding FFTs at selected flow rates 1–50 mL h⁻¹. (b) Vesicle size (°) and the asymptotic average optical image intensity (Δ) dependence on flow rate. Data are generally described by a 1/4 power with wall shear rate; given the data scatter, the 1/2 power (observed by Roux⁶) can not be ruled out above 20 s⁻¹ shear rate.

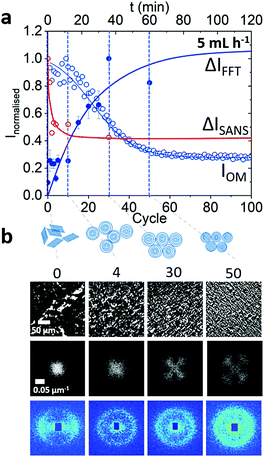
The emergence of the isotropic phase upon oscillatory shear cycles was examined at 5 h⁻¹ 50 μL amplitude condition. (We note that shear-induced effects on the optical texture at the wall and centre of the channel were indiscernible, (Fig. S7b and c, ESI†) for flow rate 5 mL h⁻¹.) This was further elucidated by the corresponding FFTs with the emergence of the characteristic cloverleaf pattern (Fig. 8a). The gradual evolution of peaks indicates that the transformation from lamellar to MLV phase is continuous under these experimental conditions. Further azimuthal analysis showed emergence of four peaks (Fig. 8b) whose intensity evolution was fitted to an exponential and leveled out around cycle 30 (Fig. S8, ESI†), earlier than the overall intensity drop had taken place (cycle 80).

Fig. 8 Effect of oscillatory flow at 5 mL h⁻¹ on L_α phase over multiples cycles from 0–50. (a) Morphology evolution observed by cross-polarised optical microscopy at the channel wall and corresponding FFTs, associated with MLV formation; (b) oscillatory shear cycle azimuthal average of FFTs (computed within 0.12–0.18 μm⁻¹).

This is likely due to the initial formation of vesicles and subsequent reduction in size since the FFT analysis is expected to capture the emergence of ordered structures, while overall light intensity correlates favourably with the size of the scattering objects. No further long range ordering as reported by Sierro and Roux⁶ was observed.

Since the formation of the isotropic phase appeared to be uniform across the channel (Fig. S7b and c, ESI†), SANS data were was acquired only at the centre of the channel after the constriction. 2D SANS indicated a formation of isotropic phase already after the second oscillatory cycle (Fig. 9a) in contrast to the formation of ordered phase observed by optical microscopy appeared to form around cycle 30. This is somewhat expected given the smaller lengthscales probed by SANS, compared to those of optical microscopy. Employing SANS, we probe the evolution of nanoscale orientation of the system (measured at the exit) subjected to 5 mL h⁻¹ flow rate and 50 μL amplitude. Upon a few cycles (∼5), the anisotropy decreases significantly shown by azimuthal intensity ΔI value decreasing (Fig. 9b), while the overall I(q) profile remains unchanged (Fig. S9a, ESI†). Simultaneously, 0° intensity drops and 90° increases until the pattern is (nearly) centrosymmetric (Fig. 8a). Finally, ΔI, , and all plateau around 5th cycle suggesting that the formation of an isotropic MLV phase takes place early on (Fig. S9b, ESI†). The timescales for MLV formations observed with microscopy were approximately the same as timescales observed by rheo-SALS in literature.³⁵

Fig. 9 Oscillatory flow SANS analysis. (a) Microfluidic SANS 2D scattering images of oscillatory shear cycles (measured at 8 m and λ = 6 Å); (b) azimuthal average for selected cycles 0, 1, 3 and 30 within 0.035 ≤ q ≤ 0.045 Å⁻¹ computed from the 2D data shown in panel (a), from where an orientation parameter ΔI is estimated from the difference between the maximum and minimum intensities as a function of azimuthal angle.

3.4 Stability of MLVs after the cessation of shear

Once MLVs have been formed they remain stable after cessation of shear (Fig. 10). In this experiment, we sheared the sample for consecutive 500 cycles with flow rate of 50 mL h⁻¹ and amplitude of 50 μL which corresponded to the plateau region where MLVs have been already formed. The resulting 2D SANS images showed emergence of isotropic phase that remained virtually unchanged for 20 h (Fig. 10b and c). This was further corroborated by ²H NMR showing the stability of isotropic MLV phase to extend over a period of few (2 days). After 5 days, the appearance of two shoulder peaks at the position and distance (150 Hz) can be observed pointing to re-emergence of lamellar phase. These stability timescales correspond to the values often reported in literature, where MLVs would stay stable over period of several days.⁶

Fig. 10 MLV stability after shearing. (a) Oscillatory shear profile with flow rate of 50 mL h⁻¹ and 50 μL volume amplitude applied for 500 cycles; (b) 2D SANS scattering images collected before and 0, 4 and 20 h after cessation of shear; (c) azimuthal average within 0.035 ≤ q ≤ 0.045 Å⁻¹ computed from the 2D data shown in panel (b). (d) ²H NMR relaxation over several days. Vesicles remain stable for up to 2 days.

4 Conclusions

In this work, we investigate a flow-responsive surfactant model system, namely SDS/octanol/brine in the lamellar L_α phase, subjected to microfluidic contraction–expansion flows by a combination of SANS, optical and NMR experiments. While the shear induced L_α to MLV transformation of SDS/octanol/brine has been previously documented,^5,6 herewith we focus on tubular microflow, the role of frequency and amplitude of oscillation (analogous to LAOS), and both wall shear and extensional flow. This system exhibits low membrane bending rigidity (near 1, based on the Caillé model fit) and is thus prone to forming vesicles. Owing to its highly scattering nature and large SANS beam flux, sample volumes down to ∼nL could be interrogated (with ∼min acquisition times) enabling the spatiotemporal mapping by SANS, employing a custom designed, high-transmission microdevice capable of withstanding considerable pressures (∼100 mbar), and demonstrated here with fluid velocities up to ∼0.3 m s⁻¹.

Under continuous flow, we observe orientation of lamellae along the flow direction upon entering a constriction, and in the normal orientation upon exiting, although the short residence time of the fluid within the microchip (typically, a few to tens of seconds) was not found to induce MLV formation. However, a reduction in anisotropy and overall scattering intensity is observed following one single constriction pass, leading us to examine their cumulative effect in oscillatory flow, thus extending the fluid residence time up to multiple hours.

Under oscillatory flow, the lamellar L_α to MLV transformation is readily observed, and Fig. 11 illustrates our findings for a specific flow condition (5 mL h⁻¹ volumetric flow rate with 50 μL displaced volume, or ‘amplitude’). Optical microscopy shows progressively finer textures and an oriented morphology upon cycling, corroborated by the FFT; this contrasts with the decrease in orientation observed by SANS. Within a few cycles (∼5 in this case) MLVs form, as shown by SANS, and upon further cycling, these arrange over 10s of micron lengthscales into progressively ordered arrays. Under the conditions studied, we did not however observe long range order.⁶

Fig. 11 Overview of MLV formation under oscillatory shear flow. (a) Normalised azimuthal intensities of cross-polarised microscopy images and SANS for flow rate of 5 mL h⁻¹. A drop in SANS intensity ΔI_SANS around cycle 4 indicates MLV formation (isotropic) while the drop in optical intensity I_OM and increase in azimuthal optical parameter ΔI_FFT, plateau at cycle ∼60, indicates the progressive ordering of packed vesicles. (b) corresponding SANS and microscopy images.

The onset of MLV formation is found to be dependent on the total shear applied, with higher flow rates form the MLVs faster, requiring an approximately similar number of cycles. As expected, MLV size decreases with flow, and thus shear rate, but with following a α ≃ 1/4 power law (although the shear rate estimate may not be sufficiently precise). Once MLVs form, they remain stable for several hours to days as indicated by SANS 2D and ²H NMR data, in line with the reported metastability of various systems.

Our findings and reported methodology are relevant for the industrial processing of complex fluid formulations, often carried out in tubular reactors and continuous flows, and employing a combination of extensional and shear flows.

Data availability

Data are available at DOI: 10.5291/ILL-DATA.LTP9-6.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Institut Laue Langevin (Grenoble) for beamtime (LTP-9-6), EPSRC and the Imperial College London for a PhD studentship for LD, and the Royal Academy of Engineering (RAEng, UK) for funding a Research chair for JTC.

Notes and references

1. R. A. L. Jones, Soft Condensed Matter, OUP, Oxford, 2002.
2. C. R. Safinya, E. B. Sirota, R. F. Bruinsma, C. Jeppesen, R. J. Plano and L. J. Wenzel, Science, 1993, 261, 588–591.
3. C. R. Safinya, D. Roux, G. S. Smith, S. K. Sinha, P. Dimon, N. A. Clark and A. M. Bellocq, Phys. Rev. Lett., 1986, 57, 2718–2721.
4. S. Kuczera, L. Gentile, T. I. Brox, U. Olsson, C. Schmidt and P. Galvosas, Langmuir, 2018, 34, 8314–8325.
5. D. Roux, F. Nallet and O. Diat, Europhys. Lett., 1993, 24, 53–58.
6. P. Sierro and D. Roux, Phys. Rev. Lett., 1997, 78, 1496–1499.
7. S. K. Jain, R. K. Jain, M. K. Chourasia, A. K. Jain, K. B. Chalasani, V. Soni and A. Jain, AAPS PharmSciTech, 2005, 6, E35–E41.
8. A. D. Sezer, J. Akbuğa and A. L. Baş, Drug Delivery, 2007, 14, 47–53.
9. J. Arrault, C. Grand, W. C. Poon and M. E. Cates, Europhys. Lett., 1997, 38, 625–630.
10. D. W. Kim, S. G. Oh, S. C. Yi, S. Y. Bae and S. K. Moon, Chem. Mater., 2000, 12, 996–1002.
11. A. Sein and J. B. F. N. Engberts, Langmuir, 1995, 11, 455–465.
12. M. S. Liaw, M. R. Mackley, J. Bridgwater, G. D. Moggridge and A. E. Bayly, AIChE J., 2003, 49, 2966–2973.
13. B. J. Frisken, C. Asman and P. J. Patty, Langmuir, 2000, 16, 928–933.
14. O. Diat, D. Roux and F. Nallet, J. Phys. II, 1993, 3, 1427–1452.
15. S. Khodaparast, W. Sharratt, H. Wang, E. S. Robles, R. Dalgliesh and J. T. Cabral, J. Colloid Interface Sci., 2019, 546, 221–230.
16. O. Diat and D. Roux, J. Phys. II, 1993, 3, 9–14.
17. D. Roux, in Soft and Fragile Matter: Nonequilibrium Dynamics, Metastability and Flow, ed. M. E. Cates and M. R. Evans, SUSSP Publications, 2000, pp. 185–204.
18. A. Zilman and R. Granek, Eur. Phys. J. B, 1999, 11, 593–608.
19. P. Oswald and S. Ben-Abraham, J. Phys., 1982, 43, 1193–1197.
20. L. Gentile, M. A. Behrens, L. Porcar, P. Butler, N. J. Wagner and U. Olsson, Langmuir, 2014, 30, 8316–8325.
21. L. Gentile, M. A. Behrens, S. Balog, K. Mortensen, G. A. Ranieri and U. Olsson, J. Phys. Chem. B, 2014, 118, 3622–3629.
22. F. Nettesheim, J. Zipfel, U. Olsson, F. Renth, P. Lindner and W. Richtering, Langmuir, 2003, 19, 3603–3618.
23. Y. Kosaka, M. Ito, Y. Kawabata and T. Kato, Langmuir, 2010, 26, 3835–3842.
24. T. Kato, K. Miyazaki, Y. Kawabata, S. Komura, M. Fujii and M. Imai, J. Phys.: Condens. Matter, 2005, 17, S2923–S2928.
25. Z. Yuan, S. Dong, W. Liu and J. Hao, Langmuir, 2009, 25, 8974–8981.
26. C. Liu and J. Hao, J. Phys. Chem. B, 2011, 115, 980–989.
27. L. Coppola, L. Gentile, I. Nicotera, C. O. Rossi and G. A. Ranieri, Langmuir, 2010, 26, 19060–19065.
28. A. S. Wunenburger, A. Colin, J. Leng, A. Arnéodo and D. Roux, Phys. Rev. Lett., 2001, 86, 1374–1377.
29. H. Egger, G. H. Findenegg, O. Holderer, R. Biehl, M. Monkenbusch and T. Hellweg, Soft Matter, 2014, 10, 6926–6930.
30. Y. Kawabata, R. Bradbury, S. Kugizaki, K. Weigandt, Y. B. Melnichenko, K. Sadakane, N. L. Yamada, H. Endo, M. Nagao and H. Seto, J. Chem. Phys., 2017, 147, 034905.
31. J. U. De Mel, S. Gupta, R. M. Perera, L. Ngo, P. Zolnierczuk, M. Bleuel, S. V. Pingali and G. J. Schneider, Langmuir, 2020, 36, 9356–9367.
32. F. Nettesheim, U. Olsson, P. Lindner and W. Richtering, J. Phys. Chem. B, 2004, 108, 6328–6335.
33. G. M. Wilkins and P. D. Olmsted, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 21, 133–143.
34. L. Gentile, C. Oliviero Rossi and U. Olsson, J. Colloid Interface Sci., 2012, 367, 537–539.
35. S. Großkopf, B. Tiersch, J. Koetz, A. Mix and T. Hellweg, Langmuir, 2019, 35, 3048–3057.
36. S. Fujii and Y. Yamamoto, Soft Matter, 2015, 11, 9330–9341.
37. L. Gentile, L. Coppola, S. Balog, K. Mortensen, G. A. Ranieri and U. Olsson, ChemPhysChem, 2015, 16, 2459–2465.
38. B. Medronho, J. Brown, M. G. Miguel, C. Schmidt, U. Olsson and P. Galvosas, Soft Matter, 2011, 7, 4938–4947.
39. B. Medronho, C. Schmidt, U. Olsson and M. G. Miguel, Langmuir, 2010, 26, 1477–1481.
40. D. Bernin, V. Koch, M. Nydén and D. Topgaard, PLoS One, 2014, 9, 1–11.
41. Y. Shen, J. Hao, H. Hoffmann and Z. Wu, Soft Matter, 2008, 4, 805–810.
42. Y. Zhao, A. Q. Shen and S. J. Haward, Soft Matter, 2016, 12, 8666–8681.
43. J. J. Cardiel, A. C. Dohnalkova, N. Dubash, Y. Zhao, P. Cheung and A. Q. Shen, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1653–1660.
44. C. W. Wang, D. Sinton and M. G. Moffitt, J. Am. Chem. Soc., 2011, 133, 18853–18864.
45. C. J. Pipe and G. H. McKinley, Mech. Res. Commun., 2009, 36, 110–120.
46. C. G. Lopez, T. Watanabe, A. Martel, L. Porcar and J. T. Cabral, Sci. Rep., 2015, 5, 1–7.
47. M. Adamo, A. S. Poulos, R. M. Miller, C. G. Lopez, A. Martel, L. Porcar and J. T. Cabral, Lab Chip, 2017, 17, 1559–1569.
48. P. T. Corona, N. Ruocco, K. M. Weigandt, L. G. Leal and M. E. Helgeson, Sci. Rep., 2018, 8, 1–18.
49. A. J. Oosthoek-De Vries, J. Bart, R. M. Tiggelaar, J. W. Janssen, P. J. M. Van Bentum, H. J. Gardeniers and A. P. Kentgens, Anal. Chem., 2017, 89, 2296–2303.
50. A. S. Poulos, M. Nania, P. Lapham, R. M. Miller, A. J. Smith, H. Tantawy, J. Caragay, J. Gummel, O. Ces, E. S. Robles and J. T. Cabral, Langmuir, 2016, 32, 5852–5861.
51. H. P. Martin, N. J. Brooks, J. M. Seddon, P. F. Luckham, N. J. Terrill, A. J. Kowalski and J. T. Cabral, Soft Matter, 2016, 12, 1750–1758.
52. Y. Son, Polymer, 2007, 48, 632–637.
53. F. Nallet, R. Laversanne and D. Roux, J. Phys. II, 1993, 3, 487–502.
54. R. Dong, Z. Zhong and J. Hao, Soft Matter, 2012, 8, 7812–7821.
55. J. Leng, F. Nallet and D. Roux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 77–83.
56. M.-F. Ficheux, A.-M. Bellocq and F. Nallet, J. Phys. II, 1995, 5, 823–834.
57. P. Panizza, A. Colin, C. Coulon and D. Roux, Eur. Phys. J. B, 1998, 4, 65–74.
58. J. T. Cabral and S. D. Hudson, Lab Chip, 2006, 6, 427–436.
59. A. Lutti and P. T. Callaghan, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 24, 129–137.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01215k

‡ School of Mechanical Engineering, University of Leeds, Leeds LS2 9JT, UK.

---