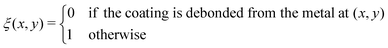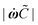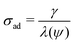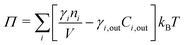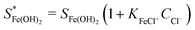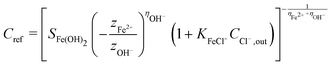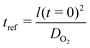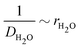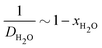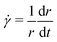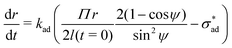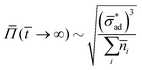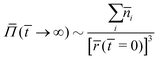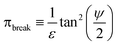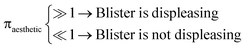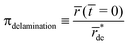Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Blistering failure of elastic coatings with applications to corrosion resistance†
Surya
Effendy
 a,
Tingtao
Zhou
a,
Tingtao
Zhou
 b,
Henry
Eichman
c,
Michael
Petr
b,
Henry
Eichman
c,
Michael
Petr
 d and
Martin Z.
Bazant
d and
Martin Z.
Bazant
 *ae
*ae
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02138, USA. E-mail: bazant@mit.edu
bDivision of Engineering and Applied Sciences, California Institute of Technology, 1200 E. California Blvd., Pasadena, CA91125, USA
cDow Coating Materials, 400 Arcola Road, Collegeville, PA19426, USA
dDow Wire and Cable, 400 Arcola Road, Collegeville, PA19426, USA
eDepartment of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02138, USA
First published on 28th September 2021
Abstract
A variety of polymeric surfaces, such as anti-corrosion coatings and polymer-modified asphalts, are prone to blistering when exposed to moisture and air. As water and oxygen diffuse through the material, dissolved species are produced, which generate osmotic pressure that deforms and debonds the coating. These mechanisms are experimentally well-supported; however, comprehensive macroscopic models capable of predicting the formation osmotic blisters, without extensive data-fitting, is scant. Here, we develop a general mathematical theory of blistering and apply it to the failure of anti-corrosion coatings on carbon steel. The model is able to predict the irreversible, nonlinear blister growth dynamics, which eventually reaches a stable state, ruptures, or undergoes runaway delamination, depending on the mechanical and adhesion properties of the coating. For runaway delamination, the theory predicts a critical delamination length, beyond which unstable corrosion-driven growth occurs. The model is able to fit multiple sets of blister growth data with no fitting parameters. Corrosion experiments are also performed to observe undercoat rusting on carbon steel, which yielded trends comparable with model predictions. The theory is used to define three dimensionless numbers which can be used for engineering design of elastic coatings capable of resisting visible deformation, rupture, and delamination.
1 Introduction
The global cost of corrosion in 2019 is approximately 3 trillion USD, of which between 15% to 35% is preventable.1,2 For this reason, there have been concerted political efforts for a more rigorous implementation of corrosion prevention technology in civilian, military, and industrial contexts.3,4 Such technology includes, but is not limited to, manipulation of surface5,6 and bulk geometry,7–9 design of corrosion-resistant alloys,9,10 elimination of oxidative environments, application of corrosion inhibitors,11,12 anodic protection,13 cathodic protection via sacrificial anode14 or impressed current systems,15 and application of organic16,17 and inorganic coatings.18,19Of the existing corrosion prevention technology, aside from metallurgical modifications, protective coatings remain the most widely used. Various failure mechanisms have been discussed in the literature, ranging from loss of adhesion due to particulate inclusions6 or chemical reactions,20–22 salt or solvent entrapment,23–27 microstructural defects,6,16,24,28 solvent absorption,23 decreased plasticity due to polymer degradation29,30 or loss of plasticizers,31,32 and miscellaneous environmental stresses (e.g., accidental scratches).33,34 These mechanisms are well-supported by experimental and field observations;25,35 however, continuum models capable of predicting failure of protective coatings, without extensive data-fitting, is scarce. This limits the pace of coating development, which is presently reliant on time- and resource-intensive field tests.36–38
In the present work, we focus on osmotic blistering as the primitive form of the failure mechanisms listed above, taking considerable inspiration from the macroscopic delamination physics of van der Meer-Lerk and Heertjes in ref. 35. Van der Meer-Lerk and Heertjes presented some of the earliest works on osmotic blistering on coated metallic surfaces. For example, they successfully predicted the volume of a blister as a function of time using a setup consisting of salt crystals trapped underneath polymeric coatings on steel immersed in deionized water.25 However, their transport model relied on measured blister area as a function of time, which precludes its use for a priori model prediction. The aforementioned macroscopic delamination physics also lacks key dependencies on contact angle; as a consequence, van der Meer-Lerk and Heertjes were only able to use the pressure chamber data collected in35 to correlate equilibrium adhesion parameters, versus the kinetic and equilibrium parameters obtained using the same data sets in Section 3.1 of the present work.
More recent theoretical works on osmotic blistering has been largely and exclusively focused on either the chemical or mechanical components of blistering, the latter usually investigated on a mesoscopic scale. On the chemical side, Li, Lo, and Chang6 considered osmotic pressure arising from dissolved soluble components as the primary cause of osmotic blistering, while the work of Leng, Streckel, and Stratmann21 hints at cathodic delamination as the primary cause of the phenomenon. The more comprehensive review works of Funke23 and Hare24 likewise treats the coating as an inert elastic substance that acts largely as a source of soluble components, if any.
On the mechanical side, Castaing, Lemoine, and Gourdenne39 treated blistering as a bulk deformation phenomenon caused by swelling and models it as a circular clamped membrane. We note that the model is developed for polyester laminates with gelcoats, which typically contain considerable amounts of hygroscopic glycols.40 This accounts for the exclusive focus on swelling. However, the model can be easily and perhaps more accurately applied to osmotic blistering, as it assumes axisymmetry. Affixed, swollen coats are known to wrinkle and crease instead of forming a smooth spherical segment at high deformations.41 The approximate quartic solution discussed by Castaing, Lemoine, and Gourdenne more closely resembles the typical morphology of an osmotic blister (see Fig. 7(a)). Nazir, Khan, and Stokes42 developed a theory of interfacial fracture at the perimeter of a blister based on the work of Dundurs and Mura.43 While remarkably thorough and simple, i.e., consisting of only algebraic equations, the model makes a strong assumption that interfacial stress is caused solely by transport; the stretching of the coating as a consequence of blister formation is eliminated by the buckling of the interface. This is in contrast to experimental measurements21 suggesting that interface buckling does not happen, at least not at the length scale suggested by the authors.
More recent works on mechanical modelling of blisters rely on continuum viscoelastic models solved at the mesoscale using finite element method or some variant of it. Graczyk, Zbiciak, Michalczyk, and Kowalewski44 modelled the formation of blisters in between the isolation and subgrade layers of a waterproofed concrete, focusing on the viscoelastic properties of asphalt-aggregate mixtures. Hu, Zhang, He, Midson, and Zhu45 modelled the formation of blisters on and in thixocast solids; in this case, pressure is caused by entrapped air which expand upon heating. The study focuses on extent of entrapment as a function of viscoelastic behavior and casting speed. Both of the aforementioned studies provide detailed insights into stress distribution (for ref. 44) and air entrapment/velocity field (for ref. 45) profiles, but do not provide generalized insights into the nature of blistering, as a consequence of the complex nature of the model.
Clearly, there is a need for a macroscopic model which takes into account the chemical and mechanical components of osmotic blistering, especially if such a model can be validated with experimental data and possesses only a small number of parameters and key physics. The model can then provide generalized insights on osmotic blistering, or potentially blistering phenomenon as a whole, including effects caused by the interaction between the chemical and mechanical components of the model. The present work showcases one such model. In Section 2, we develop a general mathematical model capable of predicting the formation of blisters at a macroscopic scale, and simplify the formulation by assuming an axisymmetric blister overlaying carbon steel, a situation commonly encountered in field applications. In Section 3, we introduce the experimental data sets used to validate the model and the methodology used to analyze raw data sets taken from the literature. In Section 4, we show that the model is able to fit the experimental data sets, validating the hypothesis of an irreversible, nonlinear blister growth rate, and more generally, the growth and deformation of blisters under the influence of osmotic pressure. The model predicts a long-term behavior characterized by a stable, ruptured, or delaminated blister and outlines the initiation, propagation, and termination steps of the blistering process. We then use the theory to define three dimensionless numbers, each classified according to the source of osmotic pressure, which can be used for engineering design of polymeric coatings capable of resisting visible deformation, rupture, and delamination. In Section 5, we discuss the limitations of the model, as well the various other contexts within which the model may be applicable. In Section 6, we summarize the main findings of the work.
2 Mathematical model
Osmotic blisters are formed due to the tendency for water to move from regions of low solute activity to regions of high solute activity. When this transfer occurs across a semi-permeable membrane, i.e., a membrane permeable to water but not to solutes, pockets of soluble materials hydrate and expand, exerting an osmotic pressure on the surrounding matrix. If these pockets are trapped between a coating and a metal surface, the resulting osmotic pressure can push the two materials apart, leading to coating failure.The entrapped water-soluble components are often salts that are deliberately introduced to modify the properties of the coating or transferred to the metal surface during the coating application process.26,27 Small organic compounds have also been considered as possible water-soluble components, especially for poorly-formulated solvent-based paints.23 Blisters may then develop upon exposure to rain, fog, or other domestic and industrial water sources (e.g., bathroom and kitchen appliances, water tanks).
To illuminate the osmotic blistering mechanism, we will begin by presenting the general form of the model and then provide a more practical axisymmetric formulation.
2.1 Full Model
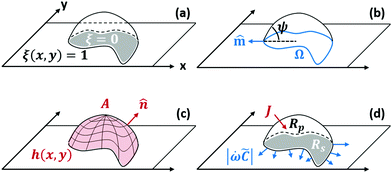
We treat the coated metal surface as an infinite two-dimensional surface with Cartesian coordinates x and y immersed in an infinite reservoir of water. The adhesion state is characterized by a binary variable ξ, illustrated in Fig. 1(a):With the implicit assumption that the debonded area is finite, the above formulation is equivalent to the set of perimeters {Ωi}, with each perimeter Ωi describing a distinct contiguous debonded area. With no loss of generality, we will assume a single contiguous debonded area with perimeter Ω (see Fig. 1(b)) satisfying the parametric equation ω(s) = (ωx(s),ωy(s)).
This perimeter is associated with a contiguous volume V containing blister fluid at pressure Π. Assuming elastic, isotropic, and sufficiently linear material properties, the coating deforms freely:
Π = γ∇·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) | (1) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) the unit vector normal to the deformed surface, illustrated in Fig. 1(c). Eqn (1) is solved with the boundary condition:
the unit vector normal to the deformed surface, illustrated in Fig. 1(c). Eqn (1) is solved with the boundary condition:| h(ωx(s),ωy(s)) = 0 |
Most coatings of practical interest are viscoelastic. However, their viscoelastic relaxation times (∼1 hour46,47) tend to be much shorter than the timescale associated with the formation of blisters and the attendant coating failure (∼1 day to 1 year). We thus treat the coating as an elastic material, which can be modelled as a Mooney–Rivlin solid:48,49
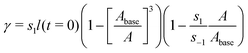 | (2) |
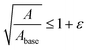 | (3) |
At the perimeter, the interface between the coating and the metal experiences an adhesion stress, which causes the coating to debond from the metal:
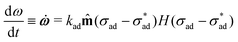 | (4) |
![[m with combining circumflex]](https://www.rsc.org/images/entities/b_char_006d_0302.gif) is the unit vector normal to the perimeter at ω on the (x,y) plane (see Fig. 1(b)), σad is the adhesion stress,
is the unit vector normal to the perimeter at ω on the (x,y) plane (see Fig. 1(b)), σad is the adhesion stress, 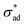 is the critical adhesion stress, and H(·) is the Heaviside function. The critical adhesion stress
is the critical adhesion stress, and H(·) is the Heaviside function. The critical adhesion stress 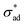 is an interfacial property which describes stickiness. The adhesion stress describes the magnitude of debonding force at the perimeter:
is an interfacial property which describes stickiness. The adhesion stress describes the magnitude of debonding force at the perimeter:Here ψ is the local contact angle, which is evaluated from:
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ = −∇h· ψ = −∇h·![[m with combining circumflex]](https://www.rsc.org/images/entities/b_char_006d_0302.gif) |
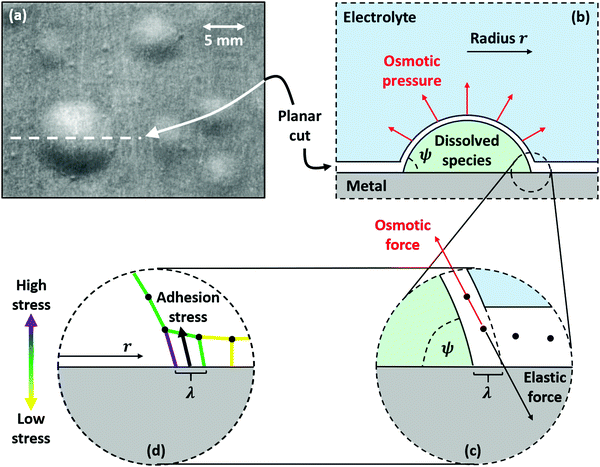 | ||
| Fig. 2 (a) Light microscopy image of circular blisters formed on epoxy-coated aluminum, taken from ref. 27. Further evidence of circular blisters formed on polymer-coated metals can be found in ref. 6, 23, 24 and 51. (b) Schematic of the blister along the planar cut shown in (a). Osmotic pressure generated by corrosion products and soluble inclusions stretches the coating into a sphere segment with contact angle ψ and base radius r assuming isotropic mechanical properties. (c) A close-up view of the perimeter of the coating shows the balance between osmotic force, obtained by integrating osmotic pressure across the surface of the blister, and the elastic restoring force, which occurs due to polymer stretching. (d) The elastic restoring force incurs a stress on the polymer near the perimeter of the blister. This is the adhesion stress, which must exceed the yield strength of the polymer-metal interface for the blister to grow. The elastic restoring force is spread over a characteristic length scale λ, which is assumed to be the projected thickness of the coating. | ||
The pressure Π can be effected by inertial, viscous, or body forces, but the present work focuses on osmotic pressure. We assume quasi-steady solute distribution within the blister, which holds for most cases of practical interest:
Here γi is the activity coefficient of species i, n the amount of soluble species, Cout the concentration in the bulk electrolyte, kB the Boltzmann constant, and T the temperature.
The amount of soluble species ni is tracked using mass balance, as illustrated in Fig. 1(d):
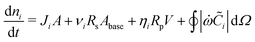 | (5) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) (x,y) is the surface concentration of soluble species along the metal/coating interface. The forms of Ji, Rs, Rp, and
(x,y) is the surface concentration of soluble species along the metal/coating interface. The forms of Ji, Rs, Rp, and ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) vary according to the choice of metal, coating, and coating application.
vary according to the choice of metal, coating, and coating application.
2.2 Axisymmetric blister
As illustrated in Fig. 2(a) and (b), most blisters of practical interest are approximately radially symmetric, and can be described by the contact angle ψ and the base radius r. With this geometry, eqn (1)–(3), which describe coating deformation and failure, are simplified to: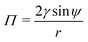 | (6) |
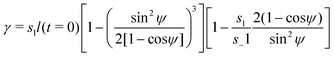 | (7) |
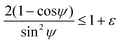 | (8) |
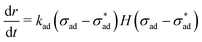 | (9) |
Evaluation of adhesion stress requires additional knowledge of material compressibility. Most coatings of practical interest are designed to be rubbery at room temperature and thus approximately incompressible,50 leading to the expression:
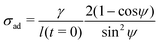 | (10) |
The osmotic pressure is evaluated assuming an ideal solution:
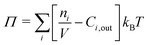 | (11) |
The mass balance, i.e., eqn (5) is evaluated assuming that all soluble contaminants are initially concentrated at a spot:
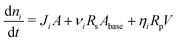 | (12) |
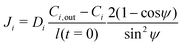 | (13) |
Eqn (6) through (13) complete the mechanical and transport components of the axisymmetric model, which is general with respect to the chemistry of the corrosion reaction. We now turn our attention to a specific realization of the corrosion chemistry.
2.3 Corrosion chemistry
To simplify the system under consideration, we will focus on polymer-coated iron, whose corrosion rate is known to be limited by the transport of oxygen:52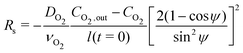 | (14) |
| 2Fe + 2H2O + O2 → 2Fe2+ + 4OH− |
The corrosion reaction results in accumulation of soluble species, which eventually exceeds its maximum solubility:
| Fe2+ + 2OH− → Fe(OH)2 |
| Fe2+ + Cl− ↔ FeCl+ | (15) |
Here
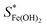 and SFe(OH)2 are the solubility limits in the presence and absence of chloride ions, respectively, and KFeCl+ is the equilibrium constant of eqn (15).
and SFe(OH)2 are the solubility limits in the presence and absence of chloride ions, respectively, and KFeCl+ is the equilibrium constant of eqn (15).
In the present work, we will assume a linear non-equilibrium expression for precipitation kinetics, driven by chemical potential difference:57
Rp = kp(−ηFe2+kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CFe2+ − ηOH−kBT CFe2+ − ηOH−kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) COH− − μ⊖) COH− − μ⊖) | (16) |
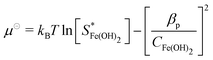 | (17) |
2.4 Nondimensionalization
We set the length scale of the problem to the initial thickness of the coating:| lref = l(t = 0) |
The time scale is set by the transport of oxygen through the coating:
The resulting nondimensionalized equations are summarized in the ESI.†
2.5 Numerical implementation
The model presented in Table S1 of the ESI,† is solved on MATLAB R2020a using the command ode15s. The model combines differential and algebraic equations, which necessitates the mass option. The code is sped up using the vectorized option. The absolute and relative tolerances are set to 10−8 and 10−6, respectively. Each simulation takes less than a second to complete.3 Experimental data and analysis
In this section, we briefly describe the key assumptions and consequences of the model, and describe the experiments which have been performed to validate those assumptions and the model in general. The data in Sections 3.1 and 3.2 is taken from the literature,25,35 while the data in Section 3.3 has been generated specifically for the present work.3.1 Irreversible, nonlinear growth rate
Eqn (4) predicts a linear relationship between growth rate and adhesion stress, but only if the adhesion stress exceeds a critical value.60 The bonds between the coating and the underlying metal may be thought of as elastic springs which fail irreversibly under excessive tensile stress (see Fig. 2(d)). This suggests the presence of a parameter which describes the failure stress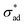 and a debonding rate which is driven by the tensile stress σad. Finally, we speculate, based on considerations of simplicity, that this rate is linear with respect to the driving force beyond
and a debonding rate which is driven by the tensile stress σad. Finally, we speculate, based on considerations of simplicity, that this rate is linear with respect to the driving force beyond 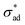 .
.
Anticipating potential confusion in word use, we note that the Heaviside function H(·) renders eqn (4) nonlinear, even if the equation is linear for both 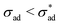 and
and 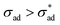 . We thus refer to the growth rate as irreversible and nonlinear.
. We thus refer to the growth rate as irreversible and nonlinear.
The data validating eqn (4) is taken from ref. 35. A simplified schematic of the experimental setup is shown in Fig. 3. In brief, the setup consists of an airtight deaerated vessel containing water. The top of the vessel is clamped shut with a coated metal substrate; the metal substrate possesses a pinhole defect of known size. By displacing a piston attached to the vessel, the pressure in the vessel is temporarily raised, causing the coating to deform and detach from the underlying substrate about the pinhole defect. Coating deformation and blister growth causes the pressure to relax, and the pressure of the vessel is tracked as a function of time using a pressure transducer. An optical device consisting of parallel planar light sources of known separation is used to track the height and the contact angle as a function of time.
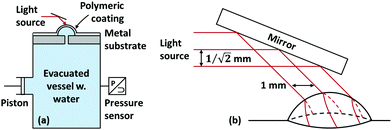 | ||
| Fig. 3 A simplified schematic of the experimental setup used by ref. 35. (a) The setup consists of an airtight deaerated vessel containing water. A piston, used to modify the pressure within the vessel, and a pressure transducer, used to track the pressure within the vessel as a function of time, are attached to the vessel. The top of the vessel is clamped shut with a coated metal substrate. The metal substrate possesses a pinhole defect of known size. Upon application of pressure, the blister deforms and detaches from the underlying substrate. (b) The curvature of the blister is tracked using an optical device consisting of parallel planar light sources of known separation. The pattern formed on the surface of the blister is recorded and processed assuming that the blister is a sphere segment. Van der Meer-Lerk and Heertjes recorded the average radius, the pressure, and the contact angle as a function of time. For a more complete discussion on the experimental setup, which includes vessel evacuation and substrate replacements/reuse, see ref. 35. | ||
The experiment was performed using stainless steel substrates. The coatings investigated were polyurethane, epoxy, alkyd, and chlorinated rubber, although van der Meer-Lerk and Heertjes (the authors of ref. 35) were only able to obtain meaningful quantitative polyurethane and alkyd data, the remainder breaking before a sufficiently large data set could be gathered. The stated intention of their work was to investigate a parameter describing the adhesion strength of coating/substrate pairs. In this regard, our aims overlap with theirs; however, our definition of critical adhesion stress 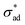 is more comprehensive, as it accounts for the effect of deformation at the perimeter of the blister. Furthermore, our theoretical approach differs considerably from that of van der Meer-Lerk and Heertjes, who employed a graphical method reliant on visual extrapolation to zero rate of change of blister area.
is more comprehensive, as it accounts for the effect of deformation at the perimeter of the blister. Furthermore, our theoretical approach differs considerably from that of van der Meer-Lerk and Heertjes, who employed a graphical method reliant on visual extrapolation to zero rate of change of blister area.
In the present work, we have re-processed the polyurethane and alkyd data using eqn (6) and (10). Combining these two equations together, we get:
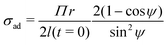 | (18) |
 and validate the form of eqn (4).
and validate the form of eqn (4).
3.2 Deformation under osmotic pressure
Our second validation data set is taken from an earlier work by the same pair of authors.25 In brief, droplets containing known amounts of magnesium acetate, potassium hydrogen sulfate, zinc sulfate, or sodium sulfite were deposited on top of polished, degreased stainless steel surfaces. These salts leave behind uniform deposits, which were subsequently coated over with polyurethane, epoxy, or chlorinated rubber. The coated substrates were then immersed in distilled water for 160 days. At irregular intervals, the coated substrates were removed from water, wiped dry, and analyzed using a light-section microscope. The maximum height and the size of the major and minor axes of the blisters were recorded. A summary of the experimental procedure is shown in Fig. 4.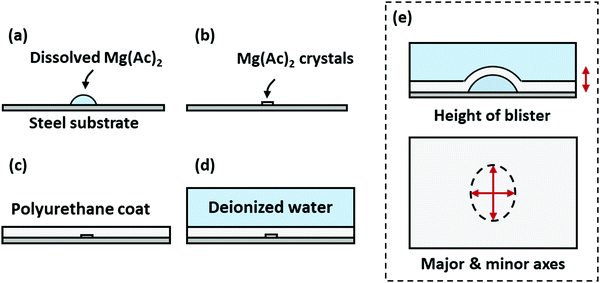 | ||
| Fig. 4 A summary of the experimental procedure in ref. 25. In chronological order, (a) a known amount of salt dissolved in water is deposited on top of a polished, degreased stainless steel substrate, (b) the solution is allowed to evaporate, leaving behind a uniform layer of salt, (c) a coating is cured on top of the salt, and (d) the coated substrate is immersed in distilled water. (e) The height and the size of the major and minor axes are recorded at irregular intervals using light-sectioning microscopy. Note that the authors have only reported quantitative blistering data sets for magnesium acetate/polyurethane pairs; this has been reflected in the figure. | ||
This data set differs from their later work in several respects. Osmotic pressure, effected through entrapped soluble salts, was used in place hydrostatic pressure, which provides a more direct validation of the present work. The accuracy of the measurement was also improved through the use of light-section microscopy, and the analysis allows for ellipsoidal segments, which retains more information concerning the surface area and volume of the blister.
However, the only blistering data sets which were reported quantitatively by van der Meer-Lerk and Heertjes (in Fig. 2 of ref. 25) are the blister volume versus time data for three different amounts of magnesium acetate. Our attempts to recover the remaining data sets are not successful, as the data from the laboratory is lost. We extract the blister volume versus time data from Fig. 2 of ref. 25 using the grabit toolbox,61 downloaded from MATLAB central. This data set has been included in the ESI,† for posterity; we recommend not repeating the data extraction procedure using the figures presented in our work, to avoid error accumulation.
The experimental procedures reported in Fig. 4 requires some modification on the basic model reported in Table S1 of the ESI† and some deductive work based on other data sets reported by van der Meer-Lerk and Heertjes. The model developed in Section 2 assumes that the transport of water is fast relative to the soluble species. This is needed to obtain a well-defined expression for osmotic pressure, which allows the curvature of the blister to be directly evaluated from eqn (6). However, the data sets presented by van der Meer-Lerk and Heertjes were obtained at timescales in which the transport of water dominates coating deformation, and osmotic pressure is not well-defined. We thus modify the basic model by eliminating eqn (6) and (11). The former is replaced by a mass balance for water, i.e., eqn (12) and the latter is replaced with a thermodynamic expression:
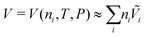 | (19) |
The diffusivity of water in the polyurethane coating, the Young's modulus of the coating, and the critical adhesion stress of the coating/substrate pair are the missing parameter values. These parameter values are expected to influence the accuracy of the model substantially, but are strong functions of the coating composition and surface preparation method, which are not comprehensively discussed in the authors' body of work. Since the authors are no longer contactable, we did the next best thing, which is to infer parameters values from the authors' other works. The diffusivity of water is obtained by fitting the steady-state permeation data reported in Fig. 5 of ref. 25 to the following expression:
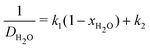 | (20) |
Eqn (20) is inspired by the Stokes–Einstein relation, wherein the diffusivity of the dilute soluble species is inversely proportional to size:
Finally, we acknowledge that the Stokes–Einstein relation only holds for dilute soluble species, whereas water is the dominant species of the blister fluid. In particular, it must have a finite self-diffusion coefficient within the coating, giving us the form of eqn (20). The fitting result for the diffusivity of water in polyurethane is shown in Fig. 5(a). The data used to fit the diffusivity of water in polyurethane is recorded for posterity in the ESI.†
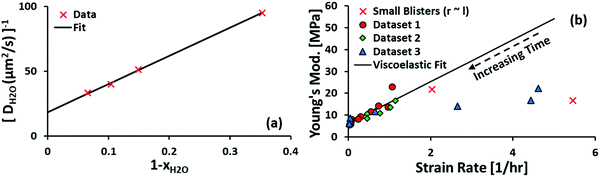 | ||
| Fig. 5 (a) The semi-empirical fit for the diffusivity of water in polyurethane. The equation of the semi-empirical fit is DH2O−1[s μm−2] = 216.7(1 − xH2O) + 18.4. The trend of increasing mobility with decreasing fraction of soluble components is consistent with observations made in the literature62–64 for a fairly broad range of solute–solvent pairs. (b) The Young's modulus of polyurethane is found to vary linearly with strain rate at low strain rates. In the present work, and in most cases of practical interest, the strain rate is low, which gives the limiting value E = 6.2 MPa. | ||
The Young's modulus is obtained by fitting data from van der Meer-Lerk and Heertjes' later work.35 In brief, we solve eqn (6) for each data point reported in Table 1 of ref. 35 assuming KMR = −s1/s−1 = 1.5.65 The Young's modulus is obtained from the limiting expression:
| E = 6s1(1 + KMR) |
The result is shown in Fig. 5(b). Linear regression is performed for strain rates ≤1.5 h−1; the dependence of Young's modulus on strain rate is a clear sign of viscoelastic behavior. For the timescale of practical interest (∼24 h), the strain rate is expected to be negligible, which validates the elastic assumption made in Section 2. We note that the data is heteroscedastic about the best-fit line, which arises because the strain rate is inhomogeneous along the surface of the coating. The smallest strain rates correspond to coatings which have relaxed for the longest duration, for which the heterogeneity is expected to have vanished.
The critical adhesion stress is obtained from the first validation data set discussed in Section 3.1. The set of parameter values used for comparison against the second validation data set is listed in Table 1.
| Symbol | Value | Unit | Note |
|---|---|---|---|
| C i,out | 0 | mol m−3 | |
| C H2O,out | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
mol m−3 | |
| D H2O −1 | 216.7(1 − xH2O) + 18.4 | s μm−2 | See Fig. 5(a) |
| E | 6.2 × 106 | Pa | See Fig. 5(b) |
| k ad | 2.07 × 10−12 | m s−1 Pa−1 | See Fig. 8(a) |
| K MR | 1.5 | See ref. 65 | |
| l(t = 0) | 80 | μm | See ref. 25 |
| n MgAc2(t = 0) | 8.81 × 10−9 | mol | Case 1,25 |
| 2.98 × 10−8 | Case 2,25 | ||
| 3.96 × 10−8 | Case 3,25 | ||
| r(t = 0) | 107 | μm | Case 1,25 |
| 161 | Case 2,25 | ||
| 177 | Case 3,25 | ||
| t span | 160 | days | See ref. 25 |
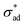
|
2.5 × 106 | Pa | See Fig. 8(a) |
| T | 298 | K |
3.3 Critical delamination length
Our third validation data set, generated specifically for the present work, is obtained in relation to three intertwined hypotheses. Combining eqn (9) and (18), and assuming that adhesion stress exceeds critical adhesion stress, we obtain:Ordinarily, the osmotic pressure Π is inversely proportional to volume (∼r3) and thus the blister growth stops. However, if the corroding surface can act as a source of soluble materials, then the osmotic pressure may not decrease with r3. Two possibilities arise here – if the solubility limit is not exceeded, then new soluble materials are produced at a rate proportional to the total surface area of the blister (∼r2). Then at
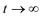 ,
,| r ∼ t2 |
r ∼ exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t t |
Assuming that osmotic pressure is set by the solubility limit, a critical length scale emerges:
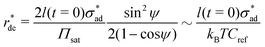 | (21) |
It is immediately evident to us that Fe(OH)3 cannot give rise to plausible critical delamination length values. The solubility product of Fe(OH)3 (∼10−38 M4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68) gives rise to mPa-range osmotic pressure and km-range critical delamination lengths. More probable results are obtained with Fe(OH)2, whose solubility product (∼10−15 M3
68) gives rise to mPa-range osmotic pressure and km-range critical delamination lengths. More probable results are obtained with Fe(OH)2, whose solubility product (∼10−15 M3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68) leads to Pa-range osmotic pressure and m-range critical delamination lengths.
68) leads to Pa-range osmotic pressure and m-range critical delamination lengths.
This is still large but is calculated assuming a critical adhesion stress of ∼1 MPa. There is a consensus within the organic coating literature that the critical adhesion stress of broad classes of polymeric coatings is lowered when corrosion occurs.21,23,24,69 This mechanism is termed coating saponification and occurs when ester bonds within the coating break in the high-pH environment of the blister:
| R1COOR2 + OH− → R1COO− + R2OH | (22) |
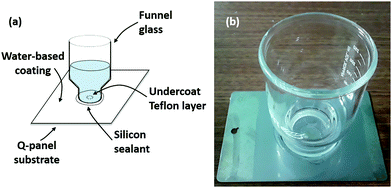
We thus have three hypotheses. First, corrosion-induced osmotic pressure can cause unstable delamination for blisters above a certain size. Second, Fe(OH)3 cannot be reasonably expected to cause unstable delamination in field applications – however, Fe(OH)2 can. Third, this event is made more probable if there is significant loss of adhesion due to saponification. Ultimately, we were only able to confirm the second hypothesis. However, it seems valuable to discuss our setup, if only to stimulate discussion of potential working variations. We wish to create blisters of known size; from there, we can study the rate of blister growth as a function of its initial size. Our setup consists of 4 by 6 in type-R Q-panels.70 On each panel, we apply a circular patch of DuPont non-stick dry film lubricant with Teflon.71 The circular patch is applied using a small (∼1 mm) cotton swab which has been immersed for 24 hours in excess DI water to remove water-soluble components and dried at room temperature and pressure for a further 24 hours. The lubricant evaporates almost immediately upon application, creating a thin but uneven layer of Teflon which is smooth to the touch. The average thickness of the Teflon layer is calculated from its mass, density, and surface area, and is found to be consistently in between 2 and 4 μm across all panels. At this thickness, the Teflon layer is not expected to provide significant mass-transfer resistance relative to the coating.
Afterwards, 200 μm (wet thickness) water-based coatings are applied using a BYK-Gardner steel drawdown bar. Two commercial acrylic latex anti-corrosion coating formulations (pigmented and non-pigmented), generously provided by Dow Chemical Company, are considered in the present work. The coatings are allowed to dry for 24 hours at room temperature and pressure. After the coatings dry, we affix a 300 mL VWR funnel glass centered at the circular patch of Teflon using Gorilla clear silicone sealant. The sealant is applied over the outer edge of the funnel glass and allowed to dry at room temperature under pressure (∼500 Pa above atmosphere). The funnel is then filled with 100 mL of DI water equilibrated with air. The top view of the blister is photographed using a Samsung Galaxy S5 at 3, 6, 12, 18, 24, and every 12 hours hence up to 10 days. Every 24 hours, 25 mL of DI water is siphoned off from each container, and the solution is topped up to 100 mL with equilibrated DI water to ameliorate oxygen and water depletion due to corrosion and evaporation, respectively. A schematic of the setup is shown in Fig. 6.
This setup is exploratory in nature, in line with our goal of creating blisters with known initial size. We also explore the effect of adding a pinhole defect at the center of the coating using a 25G medical syringe as a way to initiate blister formation.23 In all, a total of four factors are explored, namely (1) pigment versus no pigment, (2) Teflon versus no Teflon (i.e., control), (3) diameter of circular Teflon patch (∼0.5 cm versus ∼1.5 cm), and (4) defect versus no defect. For each experiment, we perform a replicate, resulting in a total of 24 panels. The list of experiments and a selection of experimental results are shown in the ESI.†
4 Model predictions and validation results
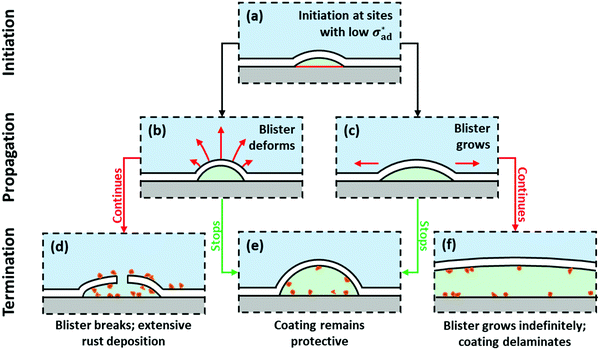
Our model predicts the qualitative behavior summarized in Fig. 7. At time t = 0, blisters initiate at sites exhibiting a combination of low critical adhesion stress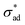 and high solute concentration. Localized loss of
and high solute concentration. Localized loss of 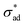 may occur due to interface contamination by oils, salts, solids, or other inclusions6 which prevent the coating from adhering to the surface. In particular, we note that uneven surfaces, in conjunction with low metal/coating surface energy, encourages entrapment of air bubbles, which behave like unprotected cavities. More generally, coating formulations with low metal/coating surface energy are expected to have low
may occur due to interface contamination by oils, salts, solids, or other inclusions6 which prevent the coating from adhering to the surface. In particular, we note that uneven surfaces, in conjunction with low metal/coating surface energy, encourages entrapment of air bubbles, which behave like unprotected cavities. More generally, coating formulations with low metal/coating surface energy are expected to have low 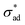 and blister with relative ease. Interface contamination by salts also introduces soluble components which can generate osmotic pressure which drives osmotic blistering. These explain the field observation that coatings tend to last longer when applied on polished, degreased surfaces.
and blister with relative ease. Interface contamination by salts also introduces soluble components which can generate osmotic pressure which drives osmotic blistering. These explain the field observation that coatings tend to last longer when applied on polished, degreased surfaces.
Blisters can propagate by deformation and/or growth, as shown in Fig. 7(b) and (c), respectively. Deformation occurs when adhesion is sufficiently strong to hold the perimeter in place – transport of water causes the blister to swell instead, and the contact angle increases. Growth occurs when adhesion stress exceeds its critical value, and the base radius increases. If deformation and growth stop, the coating remains protective (Fig. 7(e)); as discussed in Section 5, oxidation of Fe2+ to Fe3+ occurs and a protective oxide layer builds up. This reduces the rate of corrosion, and shifts the solution equilibrium to that of Fe2O3, which does not generate enough osmotic pressure to deform the blister. The blister then deflates. If deformation continues unabated, the maximum elongation of the coating is eventually exceeded (see eqn (3)), and the blister breaks (Fig. 7(d)). If growth continues unabated, the critical delamination length is eventually exceeded, and the coating grows in an unstable manner (Fig. 7(f)), assuming that the surface does not passivate.
4.1 Endpoint classification
The endpoints summarized in the last row of Fig. 7 can be more comprehensively classified by asking three questions:(1) Does deformation stop?
(2) Does growth stop?
(3) What is the source of osmotic pressure?
In what follows, we discuss each of these possible outcomes and the dimensionless numbers that govern them. The limitations of this classification are discussed in Sections 5.1 and 5.2.
Using these, and the third and fourth equations in Table S1 of the ESI,† we estimate the contact angle ψ.
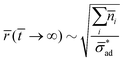
If the osmotic pressure arises from corrosion products, and assuming that the solubility limit of the corrosion products is exceeded, then the osmotic pressure is constant. This osmotic pressure is unlikely to cause critical delamination, due to the small initial size of the blister. We thus expect:
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ( (![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) → ∞) ∼ → ∞) ∼ ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ( (![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) → 0) → 0) |
As before, using these, as well as the third and fourth equations in Table S1 of the ESI,† we estimate ψ.
With ψ available, we calculate the dimensionless number:
 | (23) |
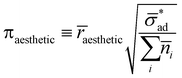
Let ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) aesthetic be the size of a blister which is visibly displeasing. Then, if osmotic pressure is generated by soluble components, we can evaluate the dimensionless number:
aesthetic be the size of a blister which is visibly displeasing. Then, if osmotic pressure is generated by soluble components, we can evaluate the dimensionless number:
On the other hand, if osmotic pressure is generated by corrosion products, then we encounter the case of critical delamination length, as described in Section 3.3 and in eqn (21). The following dimensionless number arises:
4.2 Model validation
The validation results corresponding to Sections 3.1 and 3.2 are summarized in Fig. 8(a), (b) and (c), (d), respectively. The fit in Fig. 8(a) is excellent, but there is a tendency to underestimate growth rate at low adhesion stress. We considered the possibility of a quadratic dependence on stress difference: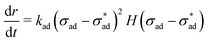 | (24) |
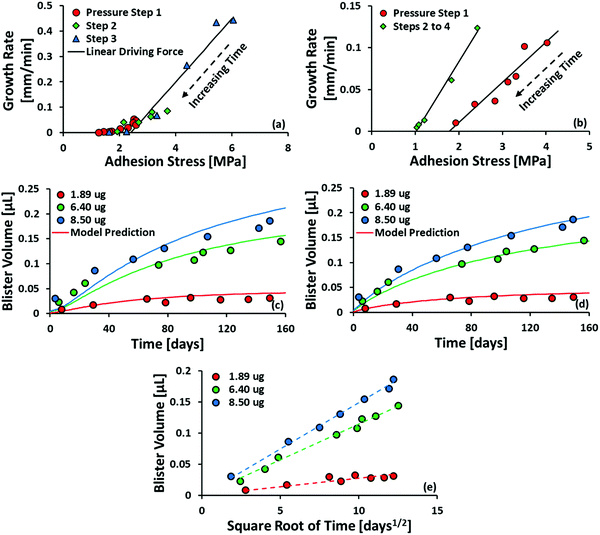 | ||
Fig. 8 (a and b) Plot of growth rate as a function of adhesion stress for steel/polyurethane and steel/alkyd, respectively. Adhesion stress is calculated using eqn (10) from the raw data published in ref. 35. Solid black lines are the fit from eqn (9). (c) Plot of blister volume as a function of time. Model prediction has no free parameters, i.e., no fitting is performed. Data is taken from ref. 25. (d) Same as the previous plot, but the diffusivity of water in the coating is assumed to be constant w.r.t. composition and fitted to the data set. The resulting diffusivity is 3.36 × 10−14 m2 s−1, equivalent to the diffusivity at xH2O ≈ 0.95 based on the correlation in Fig. 5(a). (e) Plot of blister volume as a function of 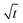 . The dotted lines are best-fit linear equations passing through (0,0). . The dotted lines are best-fit linear equations passing through (0,0). | ||
Equally good fits are obtained using the alkyd data set (Fig. 8(b)), but only if the data is split into the first pressure step and all subsequent pressure steps. We speculate that there is a considerable time gap between these two subsets of data, during which the interface changes considerably by wetting or corrosion, although this is difficult to verify, as the authors are no longer contactable.
The model prediction in Fig. 8(c) shows good agreement with the data, especially considering that the model prediction is made completely a priori, i.e., with no fitting parameters. For t ≲ 50 days, the model under-predicts blister volume and, otherwise, over-predicts it. We suspect that this is caused by an incorrect diffusion model. As shown in Fig. 8(e), the data set shows a linear dependence on 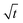 for most of the duration of the experiment. This suggests that the diffusivity is constant, in contrast to the result obtained from the Payne cup experiment. A greatly improved fit is observed when DH2O is used as a fitting parameter, as seen in Fig. 8(d).
for most of the duration of the experiment. This suggests that the diffusivity is constant, in contrast to the result obtained from the Payne cup experiment. A greatly improved fit is observed when DH2O is used as a fitting parameter, as seen in Fig. 8(d).
The fitted value of DH2O is found to be 3.36 × 10−14 m2 s−1, which corresponds to xH2O ≈ 0.95 using the correlation in Fig. 5(a). We speculate that the failure of the correlation is caused by the unsteady-state nature of the experimental setup in Fig. 4. At time t = 0, the coating immersed in DI water is dry; the salt is trapped underneath the coating, and there should be no salt within the coating. Water thus penetrates from the outside into the inside of the blister in its pure state. When the water front begins wetting the salt, the salt dissolves and goes into the coating. This logic suggests that, for most of the early part of the experiment, the average concentration of salt within the pore volume of the coating would be lower than the idealized value of ni/2V present in the steady-state Payne cup experiment. We believe that the correlation in Fig. 5(a) is valid, but the proper value of xH2O requires modelling of unsteady-state transport through a polymer matrix, which is beyond the scope of the present work.
As discussed in Section 3.3, we were ultimately unable to experimentally verify the existence of a critical delamination length. However, as shown in Fig. 9, there is a clear dark-green patina characteristic of mixed Fe2+/Fe3+ ions, with a tendency towards lighter green coloration near the delaminating edge of the blister indicating a higher proportion of Fe2+. This is in general agreement with the qualitative prediction of the model summarized in Fig. 7. As the blister progresses, corrosion produces Fe(OH)2, which appears as a green patina. A combination of osmotic pressure arising from corrosion products and saponification due to increased pH causes the coating to detach from the underlying metal substrate. The only aspect which has not been accounted for in the model is the tendency for Fe2+ to oxidize to Fe3+ near the center of the blister. We speculate on two possible explanations – rust precipitation at the center of the blister could create a protective oxide layer which reduces corrosion, thus increasing the availability of oxygen for oxidizing Fe2+. Alternatively, this could be a consequence of chemical kinetics, i.e., it takes time for Fe2+ to be oxidized to Fe3+. In either hypothesis, it makes sense for a metallic surface freshly exposed by the delamination process to show a lighter green coloration.
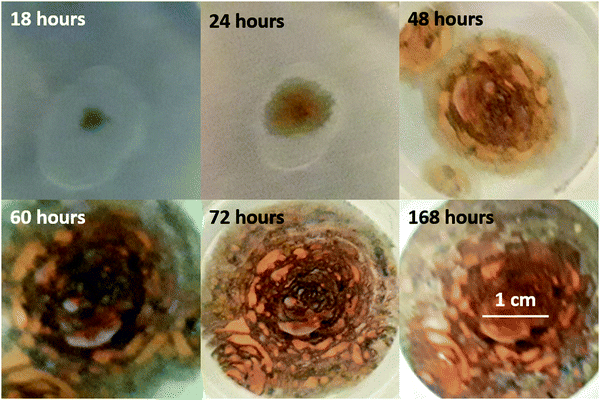 | ||
| Fig. 9 Development of undercoat blister and rust. This set of figures correspond to experiment 9 as listed in the ESI.† Dark-green coloration is observed at the edge of the blister at all points in time, at least until the blister edge meets the funnel glass. As the blister grows, small pocket-shaped patterns develop. By hour 168, the surface coloration has turned mostly brown. Similar observations were made for other experiments listed in the ESI;† for brevity, these images are placed in the ESI.† | ||
At first glance, the accelerating growth shown in Fig. 9 seems to support the critical delamination hypothesis, although it is difficult to distinguish whether r ∼ t2 or r ∼ exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t as t → ∞. However, as discussed in the ESI,† the Teflon layer seems to impart a significant degree of corrosion resistance. As a consequence, it is not obvious whether the accelerating growth is due to increasing osmotic force, which scales with the surface area, or due to the corroding area spreading beyond the Teflon patch.
t as t → ∞. However, as discussed in the ESI,† the Teflon layer seems to impart a significant degree of corrosion resistance. As a consequence, it is not obvious whether the accelerating growth is due to increasing osmotic force, which scales with the surface area, or due to the corroding area spreading beyond the Teflon patch.
The formation of pocket-shaped patterns radiating outward from the initial defect suggests that coating delamination occurs in batch. In context of the present work, as osmotic pressure builds up, the coating deforms, causing the contact angle to be more obtuse. Following eqn (18), the adhesion stress increases until it exceeds the local critical adhesion stress. If the critical adhesion stress is inhomogeneous, then the boundary slips and the contact angle drops. The process then repeats itself, resulting in the pattern observed in Fig. 9. We note that the pocket-shaped morphology and the batch delamination mechanism closely resemble those observed and proposed by Watson, Coleman, Williams, and McMurray72 for filiform corrosion. If our description is accurate, we can further deduce that the length scale of critical adhesion stress inhomogeneity for the metal/coating pair in Fig. 9 is ∼100 μm.
5 Discussion
In this section, we discuss the limitations and applications of the model within and beyond the field of corrosion.5.1 Effect of surface passivation on model prediction
As illustrated in Fig. 9, a considerable amount of Fe2O3 is precipitated at the center of the blister. To what degree does this rust layer protect against corrosion and how does that impact the model predictions?To our knowledge, even to present day, there is still uncertainty on the degree to which rust precipitation protects against corrosion. On the materials engineering side, the well-known Pilling–Bedworth theory73 predicts a porous unprotective oxide layer, if the oxide is Fe2O3, and a dense protective oxide layer, if the oxide is Fe3O4, provided that corrosion reaction is sufficiently rapid. Current studies suggest that, aside from the edge of the blister, the oxide produced by undercoat corrosion of iron contains mostly Fe2O3,23 a conclusion which is supported by the undercoat visualization results shown in Fig. 9 and more clearly in the photo-micrograph taken by Hare.24 However, other studies have suggested that underneath this layer of Fe2O3, there is a thin layer of Fe3O4.54
Furthermore, due to finite oxidation and precipitation kinetics,58 one would expect rust to precipitate away from the surface of the metal. This follows from the following sequence of events: Fe2+ ions are produced by corrosion, oxidizes in the bulk volume of the blister to Fe3+, and then precipitates on the exposed surface. One would then expect the rust layer to be porous regardless of the Pilling–Bedworth ratio, a conclusion which is supported by high-temperature iron corrosion experiments.74 However, the very same set of high-temperature iron corrosion experiments also show the formation of a thin, dense, protective oxide layer underneath a loose, porous one. This is attributed to the Arrhenius dependence of corrosion rate on temperature, which causes the formation of a large excess of Fe2+ and Fe3+ ions which then precipitate within the pore volume of the porous oxide layer.
The formation of a dense, protective oxide layer is likewise observed in electrochemical experiments. The existence of a passivation potential/regime for corroding steel in some electrolytes is well-known; in brief, as surface potential is increased, instead of an exponentially increasing corrosion rate, as expected from Butler–Volmer theory, the corrosion rate decreases when one goes above the passivation potential.52,75 This suggests that very fast corrosion produces excess Fe2+ and Fe3+ ions which precipitate as a dense, protective layer. However, this passivation regime can quickly vanish when a small amount of Br−, Cl−, S2O32−, etc. is added to the electrolyte.53–56 The mechanism for loss of passivation in the presence of these aggressive anions is still uncertain,59 as is the mechanism by which SO4−2 and NO3− reduce corrosion when added to electrolytes containing Cl− ions.76–78
Our model assumes that O2 is completely reduced and that osmotic pressure within the blister is set by the solubility limit of the metal salt. This condition is satisfied for reactive alloys with no or no protective oxide layers trapped underneath a semi-permeable membrane, as is the case of the porous oxide layer formed on the carbon steel in Fig. 9. If a dense, protective oxide layer is formed, the osmotic pressure can be instead set by the balance between heterogeneous reaction flux and flux of ions through the semi-permeable membrane. If this is the case, then additional experiments are needed to elucidate the degree to which the oxide layer protects the surface, which can then be incorporated into the model. The difficulty lies in the lack of prior knowledge on the effect of alloy composition and other thermodynamic variables on the protectiveness of the oxide layer.
5.2 Coating defects
The model we present assumes a smooth, isotropic coating. In practice, coatings almost always exhibit some form of defect, introduced during application or use, e.g., air bubbles during spraying, rugosity due to the bristles of the brush used, and scratches from daily use. These impact the blistering process by providing small open sites where corrosion can take place – the resulting saponification reactions, if applicable, then causes localized loss of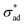 , thus initiating osmotic blistering. This phenomenon is clearly observed in Fig. 10, wherein a scratch deliberately introduced to a coating causes the formation of blisters near the scratch, possibly compounded by loss of adhesion due to mechanical damage. At the same time, the presence of such defects can act as locations where ions leak, removing the osmotic pressure needed to cause blistering, provided that the defects are not sealed by the corrosion products.23
, thus initiating osmotic blistering. This phenomenon is clearly observed in Fig. 10, wherein a scratch deliberately introduced to a coating causes the formation of blisters near the scratch, possibly compounded by loss of adhesion due to mechanical damage. At the same time, the presence of such defects can act as locations where ions leak, removing the osmotic pressure needed to cause blistering, provided that the defects are not sealed by the corrosion products.23
In short, there is considerable uncertainty regarding the protectiveness of oxide layers and the effect of coating defects. Given that most practical setups incorporate some amount of aggressive anions and operate at corrosion potential, there should be a lack of protective oxide layers in most field applications. If the surface does form a protective oxide layer, or if there is a large pinhole defect which allows the content of the blister to escape, then critical delamination does not occur; otherwise, the qualitative conclusions of the study is unchanged. However, as far as conservative design is concerned, critical delamination should be considered.
5.3 Filiform corrosion
The present work has been largely focused on osmotic blistering, but the ideas we present can also be used to explain or at least supplement existing explanations for other corrosion phenomena.Filiform corrosion refers to the formation of finger-like patterns on coated metals, typically aluminum, when exposed to an environment with high relative humidity. The pattern initiates at macroscopic defects contaminated with aggressive anions and grows in the direction of the liquid-filled “head” while leaving behind a porous oxide-filled “tail”.23,72 Due to the large mass-transfer resistance of the coating, the macroscopic defect and oxide tail act as the primary channel through which oxygen is transported to the head.79 The boundary between the oxide tail and the liquid-filled head is chevron-shaped due to the oxidation of Fe2+ to Fe3+ followed by rust precipitation near the relatively oxygen-rich fluid adjacent to the confining cylinder.80 We note that the chevron shape can also arise from preferential precipitation at existing surfaces. As the head propagates, precipitation at the tail/head boundary causes a localized decrease in concentration, which drives evaporation through the coating, i.e., loss of osmotic pressure. Non-volatile aggressive anions are concentrated by the evaporation process and diffuse towards the head, which increases the concentration at the head, attracts water from the surrounding, and begins the cycle anew.72
There are three major hypotheses explaining the directional nature of filiform corrosion. In the cathodic delamination hypothesis, relative enrichment of oxygen at the tip of the head, caused by the curvature, encourages O2 reduction, which increases the local pH, shift the saponification equilibrium (see reaction (22)), and delaminate the coating.21,81 In the anodic undermining hypothesis, the oxygen-rich tail/head boundary preferentially acts as the cathode, which induces the tip of the head to act as an anode. This undermines the tip of the head, causing the head to propagate over time.80 In the electro-osmotic hypothesis, diffusion and electromigration “pumps” the content of the head in the direction of the tip of the head, causing a mechanical force which separates the coating from the substrate.82,83 To our knowledge, there is no clear consensus on the “correct” model for the delamination process.
The present work can contribute to the understanding of filiform corrosion in three ways. One, the aforementioned mechanisms predict growth in a straight line, which is clearly not the case in real setups.72,80,84 We propose that sudden changes in filiform growth is attributable to inhomogeneity in critical adhesion stress. If this is the case, then we expect the length scale of the inhomogeneity to be the distance in between sudden changes in growth direction. Two, with some modifications, e.g., implementing kinetics of 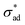 loss due to saponification (for the cathodic delamination hypothesis) or metal dissolution (for anodic undermining), changing the definition of osmotic pressure to incorporate electro-osmotic forces (for electro-osmotic hypothesis), and/or adding spatial refinement across the fingers, the model presented in Section 2.1 can be adapted to describe filiform corrosion. Finally, due to the similarity in underlying physics, provided that the proper estimates for
loss due to saponification (for the cathodic delamination hypothesis) or metal dissolution (for anodic undermining), changing the definition of osmotic pressure to incorporate electro-osmotic forces (for electro-osmotic hypothesis), and/or adding spatial refinement across the fingers, the model presented in Section 2.1 can be adapted to describe filiform corrosion. Finally, due to the similarity in underlying physics, provided that the proper estimates for 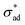 and Π are available, the classification introduced in Section 4.1 should remain applicable, thus allowing prediction of unstable growth, coating rupture, and filiform visibility.
and Π are available, the classification introduced in Section 4.1 should remain applicable, thus allowing prediction of unstable growth, coating rupture, and filiform visibility.
5.4 Other applications of the model
The particular use of metal/coating pairs is not intrinsic to the model. For example, with some modification to the expressions for surface tension (see eqn (2)) and pressure source (see eqn (11)), the model can be directly used to assess the risk associated with formation of hydrogen blisters in aluminum fusion reactors,85 or indeed any metal/metal oxide pairs.The present work focuses on anti-corrosion coatings, but is also applicable to osmotic blistering occurring on non-metallic or passive surfaces coated with other types of elastic coatings. For example, bituminous and polymer-modified bituminous roofings or coatings on concrete, as commonly observed on roads, bridges, buildings, and other infrastructures, often experience osmotic blistering.86 For bituminous coatings on concrete, this can enhance corrosion of reinforcement bars affixed within.87 In this case, a distinction needs to be made between waterproofed86,88 and non-waterproofed coatings.89 The former does not allow water to pass through the coating; instead, water passes from the concrete structure underneath, which acts as an inelastic, semi-permeable membrane. This modifies the form of the transport equation, i.e., eqn (5) considerably. Regardless of the direction from which water is transported into the blister, two further modifications are needed to adapt the present work for coated concrete: (1) the soluble components can arise from the concrete mixture90,91 and (2) the coating may exhibit orthotropic elasticity.88 Nevertheless, the generality of the present work is such that we still expect the conclusions in Section 4.1 to hold despite these mismatches in the exact statement on the model.
The current state of anti-corrosion and bituminous coating design incorporates a significant amount of empirical observation, as evidenced by the plethora of standardized tests for coating development published by the International Organization for Standardization (ISO), the National Association of Corrosion Engineers (NACE), etc. Some of these tests can be time- and resource-intensive (see ref. 36–38 and 86, among many others). Classification based on the dimensionless numbers introduced in 4.1 can provide an affordable theoretical alternative for coating development, although more experimental verification is needed.
Our model could also be applied in medical settings, e.g., formation of blisters on the skin upon exposure to heat sources92,93 or after excessive rubbing,94 the latter possibly exacerbated by hereditary illnesses, e.g., epidermolysis bullosa. In this context, the pressure source is the heart, from whence we make several predictions: (1) blistering should be more extensive when it occurs in the vicinity of arteries closer to the heart, (2) blistering should be more extensive in locations where the critical adhesion stress of neighboring pairs of skin layers is lower, (3) blisters exceeding a critical size undergo runaway growth – a situation which may assist in understanding the effect of extensive burns. We note that, in agreement with the prediction of the model, epidermolysis bullosa has been extensively linked to the inability to form functional structural proteins, which is expected to reduce critical adhesion stress.95–97 The model is also more generally applicable to biological sciences, e.g., to understand the mechanics of biofilm growth98 or deformation of dentin adhesives.99
6 Conclusion
The present work builds upon existing understanding of blister formation to arrive at a comprehensive macroscopic model of osmotic blistering. Blisters initiate at locations with low critical adhesion stress and/or high local solute concentration and propagate by growth and/or deformation. Irreversible blister growth occurs when adhesion stress exceeds the critical adhesion stress of the metal/coating pair, and deformation occurs when osmotic pressure exceeds the elastic stress of the coating. If the growth continues unabated, the coating eventually becomes delaminated, and if deformation continues unabated, the coating eventually ruptures. The present work distinguishes between osmotic pressure arising from entrapped solutes and osmotic pressure arising from corrosion products. In the former, blister growth eventually stops due to decaying osmotic pressure; however, depending on the kinetics of delamination and the critical adhesion stress, the maximum elongation of the coating may still be exceeded, causing rupture. In the latter, we predict the existence of a critical delamination length, beyond which unstable blister growth occurs.The model has been validated against blister growth data. We were able to confirm that blister growth is irreversibly driven by difference between adhesion stress and critical adhesion stress using two separate data sets employing polyurethane and alkyd coatings on steel. We were also able to predict the volume vs. time data of polyurethane coatings immersed in water with various amounts of undercoat magnesium acetate with no fitting parameters. We then use the model to develop three dimensionless numbers, each classified according to the source of osmotic pressure, which can be used for engineering design of polymeric coatings capable of resisting visible deformation, rupture, and delamination.
Author contributions
Surya Effendy and Tingtao Zhou conceptualized the idea of a quantitative macroscopic model for osmotic blistering. Surya Effendy conceptualized the idea for irreversible blister growth driven by difference between adhesion stress and critical adhesion stress (see Section 3.1). Surya Effendy conceptualized the idea of endpoint classification using dimensionless numbers (see Section 4.1).Surya Effendy investigated and curated the data published in ref. 25 and 35, specifically by extracting the data using an image analysis tool and reporting those data for posterity (see Tables S2 and S3 of the ESI†). The data were subsequently used, also by Surya Effendy, to validate components of the model. Henry Eichman investigated the formation of blisters about macroscopic defects, leading to Fig. 10.
Michael Petr and Martin Z. Bazant acquired the funding needed to perform this study through the University Partnership Initiative. Michael Petr represented Dow Chemical Company at the time this work was conceived. Martin Z. Bazant heads the Bazant Research Group, in which this work was performed, and provided the resources needed to validate the critical delamination length hypothesis.
Surya Effendy created almost all aspects of the model; however, it should be made clear that pieces of the model were already in the literature when the model was conceived. Tingtao Zhou pointed out the relevance of free volume problem, which became eqn (1). Surya Effendy also wrote the software encoding the model leading to the predictions/fits shown in Fig. 8.
Tingtao Zhou and Martin Z. Bazant supervised the work and provided advice leading to the publication of the manuscript. Surya Effendy visualized the data, model predictions/fits, and schematics, and wrote the original draft of the manuscript. Tingtao Zhou, Michael Petr, and Martin Z. Bazant contributed in various ways towards reviewing and editing the manuscript.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge support from Dow through the University Partnership Initiative and Colin Cwalina from Dow for providing guidance throughout this research project. We thank Dimitrios Fraggedakis and Hongbo Zhao for the insights they shared on this topic. We thank Ernie Latham-Brown and Yu Ren Zhou for the technical advice leading to the schematic in Fig. 6.References
- L. H. Bennett, J. Kruger, R. L. Parker, E. Passaglia, C. Reimann, A. W. Ruff and H. Yakowitz, Economic effects of metallic corrosion in the United states: a report to the congress, The National Bureau of Standards, 1978, vol. 1 Search PubMed.
- G. Koch, Cost of corrosion, Trends in Oil and Gas Corrosion Research and Technologies, Woodhead Publishing, 2017, pp. 3–30 Search PubMed.
- C. G. Munger and L. D. Vincent. Corrosion prevention by protective coatings, NACE International, 1999 Search PubMed.
- W. M. Solis, J. Prybyla, M. Spiers and A. Westheimer, Subject: defence management: observations on dod's fiscal year 2010 budget requests for corrosion prevention and control, US Government Accountability Office, 2009 Search PubMed.
- D. Dwivedi, K. Lepkova and T. Becker, Carbon steel corrosion: a review of key surface properties and characterization methods, RSC Adv., 2017, 7, 4580–4610 RSC.
- J. C. M. Li, K. H. Lo and B. T. A. Chang, Blister initiation mechanism of fbe coatings, NACE International Corrosion Conference Proceedings, 2019, pp. 1–11.
- P. K. Beatenbough, D. J. Twichell and L. G. Dey, Joint crevice corrosion inhibitor, US Pat., 4997035, 1991 Search PubMed.
- S. Karlsen, Cable with crevice corrosion protection, US Pat., 6973244, 2005 Search PubMed.
- R. W. Staehle and J. A. Gorman, Quantitative assessment of submodes of stress-corrosion cracking on the secondary side of steam generator tubing in pressurized water reactors: Part 1, Corrosion, 2003, 59(11), 931–994 CrossRef CAS.
- D. S. Bergstrom, J. M. Rakowski, C. P. Stinner, J. J. Dunn and J. F. Grubb, Corrosion resistant lean austenitic stainless steel, US Pat., 8877121, 2014 Search PubMed.
- I. Ahamad and M. A. Quraishi, Mebendazole: new and efficient corrosion inhibitor for mild steel in acid medium, Corros. Sci., 2010, 52(2), 651–656 CrossRef CAS.
- M. A. Amin, S. S. A. El-Rehim, E. E. F. El-Sherbini and R. S. Bayoumi, The inhibition of low carbon steel corrosion in hydrochloric acid solutions by succinic acid: part i. weight loss, polarization, eis, pzc, edx, and sem studies, Electrochim. Acta, 2007, 520(11), 3588–3600 CrossRef.
- H. Merle, O. L. Riggs Jr. and J. D. Sudbury, Anodic protection against corrosion, US Pat., 3208925, 1965 Search PubMed.
- I. R. Lasa, R. G. Powers and D. L. Leng, Jacketed sacrificial anode cathodic protection system, US Pat., 5714045, 1998 Search PubMed.
- C. Christodoulou, G. Glass, J. Webb, S. Austin and C. Goodier, Assessing the long-term benefits of impressed current cathodic protection, Corros. Sci., 2010, 520(8), 2671–2679 CrossRef.
- M.-Y. Jiang, L.-K. Wu, J.-M. Hu and J.-Q. Zhang, Silane-incorporated epoxy coatings on aluminum alloy (aa2024). part 1: improved corrosion performance, Corros. Sci., 2015, 92, 118–126 CrossRef CAS.
- Y. González-Garciá, S. González and R. M. Souto, Electrochemical and structural properties of a polyurethane coating on steel substrates for corrosion protection, Corros. Sci., 2007, 490(9), 3514–3526 CrossRef.
- A. Ghanbari and M. M. Attar, Surface free energy characterization and adhesion performance of mild steel treated based on zirconium conversion coating: a comparative study, Surf. Coat. Technol., 2014, 246, 26–33 CrossRef CAS.
- B. R. W. Hinton, D. R. Arnott and N. E. Ryan, Cerium conversion coatings for the corrosion protection of aluminum, Mater. Sci. Forum, 1986, 9(3), 162–173 CAS.
- V. V. Arslanov and W. Funke, The effect of water on the adhesion of organic coatings on aluminium, Prog. Org. Coat., 1988, 15(4), 355–363 CrossRef CAS.
- A. Leng, H. Streckel and M. Stratmann, The delamination of polymeric coatings from steel. part 1: calibration of the kelvinprobe and basic delamination mechanism, Corros. Sci., 1999, 41(3), 547–578 CrossRef CAS.
- S. Nešić, M. Nordsveen, R. Nyborg and A. Stangeland, A mechanistic model for carbon dioxide corrosion of mild steel in the presence of protective iron carbonate films-part 2: a numerical experiment, Corrosion, 2003, 59(6), 489–497 CrossRef.
- W. Funke, Blistering of paint films and filiform corrosion, Prog. Org. Coat., 1981, 9(1), 29–46 CrossRef CAS.
- C. H. Hare, Blistering of paint films on metal, part 1: osmotic blistering, J. Prot. Coat. Linings, 1998, 15, 45–63 Search PubMed.
- L. A. van der Meer-Lerk and P. M. Heertjes, Blistering of varnish films on substrates induced by salts, J. Oil Colour Chem. Assoc., 1975, 58(3), 79–84 CAS.
- J. Pommersheim and T. Nguyen, Prediction of blistering in coating systems, Organic coatings for corrosion control, ACS Publication, 1998 Search PubMed.
- Y. Tu and J. K. Spelt, Blistering as a form of degradation in adhesive joints, J. Adhes., 2000, 72(3–4), 359–372 CrossRef CAS.
- H. Luo, J. Zhu, E. Sahraei and Y. Xia, Adhesion strength of the cathode in lithium-ion batteries under combined tension/shear loadings, RSC Adv., 2018, 8(8), 3996–4005 RSC.
- C. Jin, P. A. Christensen, T. A. Egerton, E. J. Lawson and J. R. White, Rapid measurement of polymer photo-degradation by ftir spectrometry of evolved carbon dioxide, Polym. Degrad. Stab., 2006, 91(5), 1086–1096 CrossRef CAS.
- X. F. Yang, J. Li, S. G. Croll, D. E. Tallman and G. P. Bierwagen, Degradation of low gloss polyurethane aircraft coatings under uv and prohesion alternating exposures, Polym. Degrad. Stab., 2003, 80(1), 51–58 CrossRef CAS.
- H. C. Erythropel, M. Maric, J. A. Nicell, R. L. Leask and V. Yargeau, Leaching of the plasticizer di (2-ethylhexyl) phthalate (dehp) from plastic containers and the question of human exposure, Appl. Microbiol. Biotechnol., 2014, 98(24), 9967–9981 CrossRef CAS PubMed.
- M. Rahman and C. S. Brazel, The plasticizer market: an assessment of traditional plasticizers and research trends to meet new challenges, Prog. Polym. Sci., 2004, 29(12), 1223–1248 CrossRef CAS.
- C. Merlatti, F. X. Perrin, E. Aragon and A. Margaillan, Natural and artificial weathering characteristics of stabilized acrylic-urethane paints, Polym. Degrad. Stab., 2008, 93(5), 896–903 CrossRef CAS.
- M. S. Tirumkudulu and W. B. Russel, Cracking in drying latex films, Langmuir, 2005, 21(11), 4938–4948 CrossRef CAS PubMed.
- L. A. van der Meer-Lerk and P. M. Heertjes, The influence of pressure on blister growth, J. Oil Colour Chem. Assoc., 1981, 64(1), 30–38 CAS.
- Standard practice for operating salt spray (fog) apparatus. https://www.astm.org/Standards/B117, 2019. Accessed: 28th August 2021.
- Paints and varnishes – determination of resistance to cathodic disbonding of coatings exposed to sea water. https://www.iso.org/standard/28039.html, 2003. Accessed: 28th August 2021.
- Exterior protective coatings for seawater immersion service. https://store.nace.org/64d2a236-81c0-4b47-a727-144793b8238e, 2019. Accessed: 28th August 2021.
- P. Castaing, L. Lemoine and A. Gourdenne, Mechanical modelling of blisters in coated laminated i – theoretical aspects, Compos. Struct., 1995, 30(2), 217–222 CrossRef.
- A short guide to osmosis and its treatment. http://www.anchormarinesurveys.com/wp-content/uploads/2018/03/osmosis3v6.pdf, 2009. Accessed: 15th September 2021.
- F. Weiss, S. Cai, Y. Hu, M. K. Kang, R. Huang and Z. Sou, Creases and wrinkles on the surface of a swollen gel, J. Appl. Phys., 2013, 114(7), 073507 CrossRef.
- M. H. Nazir, Z. A. Khan and K. Stokes, A unified mathematical modelling and simulation for cathodic blistering mechanism incorporating diffusion and fracture mechanic concepts, J. Adhes. Sci. Technol., 2015, 29(12), 1200–1228 CrossRef CAS.
- J. Dundurs and T. Mura, Interaction between an edge dislocation and a circular inclusion, J. Mech. Phys. Solids, 1964, 12(3), 177–189 CrossRef.
- M. Graczyk, A. Zbiciak, R. Michalczyk and L. Kowalewski, Numerical modelling of bubbles formation in the bridge asphalt pavement under gas pressure impact, Transp. Res. Procedia, 2016, 14, 3925–3934 CrossRef.
- G. X. Hu, F. Zhang, Y. F. He, S. P. Midson and Q. Zhu, Experimental study and numerical simulation on the blistering defect during thixocasting, Solid State Phenomena, 2015, vol. 217, pp. 144–150 Search PubMed.
- T. Nicolai, H. Randrianantoandro, F. Prochazka and D. Durand, Viscoelastic relaxation of polyurethane at different stages of the gel formation. 2. sol- gel transition dynamics, Macromolecules, 1997, 30(19), 5897–5904 CrossRef CAS.
- K. Ueda, H. Kanai and T. Amari, Viscoelastic properties of paint films and formability in deep drawing of pre-painted steel sheets, Prog. Org. Coat., 2002, 45(1), 15–21 CrossRef CAS.
- M. Mooney, A theory of large elastic deformation, J. Appl. Phys., 1940, 11(9), 582–592 CrossRef.
- R. S. Rivlin, Large elastic deformations of isotropic materials iv. further developments of the general theory, Philos. Trans. R. Soc., A, 1948, 241(835), 379–397 CrossRef.
- P. J. Ludovice, Structure-property relationships – rubbery polymers, Mechanical Properties and Testing of Polymers, Springer, 1999, pp. 238–241 Search PubMed.
- J. Gao, C. Li, H.-X. Feng and X.-G. Li, In situ and dynamic observation of coating failure behavior, Prog. Org. Coat., 2020, 138, 105387 CrossRef CAS.
- D. Landolt, Corrosion and surface chemistry of metals, CRC Press, 2007 Search PubMed.
- S. Ahn, H. Kwon and D. D. Macdonald, Role of chloride ion in passivity breakdown on iron and nickel, J. Electrochem. Soc., 2005, 152(11), B482 CrossRef.
- H. Kaesche, Die korrosion der metalle: physikalisch-chemische Prinzipien und aktuelle Probleme, Springer-Verlag, 1990 Search PubMed.
- M. Naghizadeh, D. Nakhaie, M. Zakery and M. H. Moayed, Effect of thiosulfate on pitting corrosion of 316ss: I. critical pitting temperature and pit chemistry, J. Electrochem. Soc., 2014, 162(1), C71 CrossRef.
- H. H. Uhlig and R. W. Revie, Corrosion and corrosion control, John Wiley and Sons, 1985 Search PubMed.
- M. Z. Bazant, Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics, Acc. Chem. Res., 2013, 46(5), 3588–3600 CrossRef PubMed.
- T. Grundle and J. Delwiche, Kinetics of ferric oxyhydroxide precipitation, J. Contam. Hydrol., 1993, 14(1), 71–87 CrossRef.
- G. S. Frankel, Pitting corrosion of metals: a review of the critical factors, J. Electrochem. Soc., 1998, 145(6), 2186 CrossRef CAS.
- E. Memet, F. Hilitski, Z. Dogic and L. Mahadevan, Static adhesion hysteresis in elastic structures, Soft Matter, 2021, 17(10), 2704–2710 RSC.
- Grabit: extract data points off image files. https://www.mathworks.com/matlabcentral/fileexchange/7173-grabit, 2021. Accessed: 28th August 2021.
- J. Cui, T. Kobayashi, R. L. Sacci, R. A. Matsutomo, P. T. Cummings and M. Pruski, Diffusivity and structure of room temperature ionic liquid in various organic solvents, J. Phys. Chem. B, 2020, 124(44), 9931–9937 CrossRef CAS PubMed.
- E. S. Hamborg, W. P. M. van Swaaij and G. F. Versteeg, Diffusivities in aqueous solutions of the potassium salt of amino acids, J. Chem. Eng. Data, 2008, 53(5), 1141–1145 CrossRef CAS.
- R. Matsutomo, M. W. Thompson and P. T. Cummings, Ion pairing controls physical properties of ionic liquid-solvent mixtures, J. Phys. Chem. B, 2019, 123(46), 9944–9955 CrossRef PubMed.
- G. D. Spathis, Polyurethane elastomers studied by the mooney-rivlin equation for rubbers, J. Appl. Polym. Sci., 1991, 43(3), 613–620 CrossRef CAS.
- D. R. Lide, CRC handbook of chemistry and physics, CRC Press, 2004, vol. 85 Search PubMed.
- A. Martinez-Urrutia, P. F. de Arroiabe, M. Ramirez, M. Martinez-Agirre and M. M. Bou-Ali, Contact angle measurement for libr aqueous solutions on different surface materials used in absorption systems, Int. J. Refrig., 2018, 95, 182–188 CrossRef CAS.
- Solubility constant products. http://www.wiredchemist.com/chemistry/data/solubility-product-constants, 2021. Accessed: 28th August 2021.
- J. Pommersheim, T. Nguyen, Z. Zhang, C. Lin and J. Hubbard, A mathematical model of cathodic delamination and blistering processes in paint films on steel, National Institute of Standards and Technology, 1992 Search PubMed.
- Steel panels. https://www.q-lab.com/documents/public/db90baad-72b8-4ed1-bc61-49e0c46f090f.pdf, 2021. Accessed: 28th August 2021.
- Dupont non-stick dry film lubricant with Teflon fluoropolymer. http://www.performancelubricantsusa.com/files/DuP_InfoSheet_NON%20STICK_1511.pdf, 2015. Accessed: 28th August 2021.
- T. M. Watson, A. J. Coleman, G. Williams and H. N. McMurray, The effect of oxygen partial pressure on the filiform corrosion of organic coated iron, Corros. Sci., 2014, 89, 46–58 CrossRef CAS.
- C. Xu and W. Gao, Pilling-bedworth ratio for oxidation of alloys, Mater. Res. Innovations, 2000, 3(4), 231–235 CrossRef CAS.
- J. Robertson, The mechanism of high temperature aqueous corrosion of steel, Corros. Sci., 1989, 29(11–12), 1275–1291 CrossRef CAS.
- P. Marcus and I. Olefjord, Round robin on combined electrochemical and aes/esca characterization of the passive films on fe-cr and fe-cr-mo alloys, Surf. Interface Anal., 1988, 11(11), 569–576 CrossRef CAS.
- M. H. Moayed and R. C. Newman, Deterioration in critical pitting temperature of 904l stainless steel by addition of sulfate ions, Corros. Sci., 2006, 48(11), 3513–3530 CrossRef CAS.
- L.-B. Niu and K. Nakada, Effect of chloride and sulfate ions in simulated boiler water on pitting corrosion behavior of 13cr steel, Corros. Sci., 2015, 96, 171–177 CrossRef CAS.
- S.-I. Pyun and S.-M. Moon, The inhibition mechanism of pitting corrosion of pure aluminum by nitrate and sulfate ions in neutral chloride solution, J. Solid State Electrochem., 1999, 3(6), 331–336 CrossRef CAS.
- A. Bautista, Filiform corrosion in polymer-coated metals, Prog. Org. Coat., 1996, 28(1), 49–58 CrossRef CAS.
- W. H. Slabaugh and M. Grotheer, Mechanism of filiform corrosion, Ind. Eng. Chem., 1954, 46(5), 1014–1016 CrossRef CAS.
- P. P. LeBlanc and G. S. Frankel, Investigation of filiform corrosion of epoxy-coated 1045 carbon steel by scanning kelvin probe force microscopy, J. Electrochem. Soc., 2004, 151(3), B105 CrossRef CAS.
- F. Brau, S. Thouvenel-Romans, O. Steinbock, S. S. Cardoso and J. H. E. Cartwright, Filiform corrosion as a pressure-driven delamination process, Soft Matter, 2019, 15(4), 803–812 RSC.
- R. T. Ruggeri and T. R. Beck, An analysis of mass transfer in filiform corrosion, Corrosion, 1983, 39(11), 452–465 CrossRef CAS.
- G. Williams and R. Grace, Chloride-induced filiform corrosion of organic-coated magnesium, Electrochim. Acta, 2011, 56(4), 1894–1903 CrossRef CAS.
- C. Quirós, J. Mougenot, G. Lombardi, M. Redolfi, O. Brinza, Y. Charles, A. Michau and K. Hassouni, Blister formation and hydrogen retention in aluminium and beryllium: a modeling and experimental approach, Nucl. Mater. Energy, 2017, 12, 1178–1183 CrossRef.
- E. A. Henderson, G. Finch and B. Hubbs, Solutions to address osmosis and the blistering of liquid applied waterproofing membrane, Building Science and the Physics of Building Enclosure Performance, 2017, pp. 177–194 Search PubMed.
- H. Liu, G. Yuan, Q. Zhang, P. Hao, S. Dong and H. Zhang, Study on influence factors of asphalt mixtures pavement blistering on portland cement concrete bridge deck, Int. J. Pavement Eng., 2021, 22(2), 249–256 CrossRef CAS.
- B. W. Hailesilassie and M. N. Partl, Adhesive blister propagation under an orthotropic bituminous waterproofing membrane, Constr. Build. Mater., 2013, 48, 1171–1178 CrossRef.
- H. M. Künzel, Preventing damage by updating moisture control standards, XV International Conference on Durability of Building Materials and Components, 2020 Search PubMed.
- S. Ignoul, F. van Rickstal and D. van Gemert, Blistering of epoxy industrial floor on concrete substrate: phenomena and case study, International Conference on Polymers in Concrete, 2004 Search PubMed.
- F. A. Pfaff and F. S. Gelfant, Osmotic blistering of epoxy coatings on concrete, J. Prot. Coat. Linings, 1997, 14, 52–65 Search PubMed.
- S. Groth and B. Staberg, Suction blisters of the skin: a compartment with physiological, interstitium-like properties, Scand. J. Clin. Lab. Invest., 1984, 44(4), 311–316 CrossRef CAS PubMed.
- D. Herschtal and M. J. Robinson, Blisters of the skin in coma induced by amitriptyline and clorazepate dipotassium: report of a case with underlying sweat gland necrosis, Arch. Dermatol., 1979, 115(4), 499 CrossRef.
- J. J. Knapik, L. K. Reynolds, L. K. Duplantis and B. H. Jones, Friction blisters, Sports Med., 1995, 20(3), 136–147 CrossRef CAS PubMed.
- Junctional epidermolysis bullosa. https://medlineplus.gov/genetics/condition/junctional-epidermolysis-bullosa/, 2020. Accessed: 28th August 2021.
- J. A. McGrath, O. M. V. Schofield and R. A. J. Eady, Epidermolysis bullosa pruriginosa: dystrophic epidermolysis bullosa with distinctive clinicopathological features, Br. J. Dermatol., 1994, 130(5), 617–625 CrossRef CAS PubMed.
- R. Varki, S. Sadowski, J. Uitto and E. Pfender, Epidermolysis bullosa. ii. type vii collagen mutations and phenotype-genotype correlations in the dystrophic subtypes, J. Med. Genet., 2007, 44(3), 181–192 CrossRef CAS PubMed.
- J. Yan, C. D. Nadell, H. A. Stone, N. S. Wingreen and B. L. Bassler, Extracellular-matrix-mediated osmotic pressure drives vibrio cholerae biofilm expansion and cheater exclusion, Nat. Commun., 2017, 8(1), 1–11 CrossRef CAS PubMed.
- F. R. Tay and D. H. Pashley, Have dentin adhesives become too hydrophilic?, J. Can. Dent. Assoc., 2003, 69(11), 726–732 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00986a |
| This journal is © The Royal Society of Chemistry 2021 |