Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning real space microstructure characteristics from scattering data†
Matthew
Jones
 * and
Nigel
Clarke
* and
Nigel
Clarke
Department of Physics & Astronomy, University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK. E-mail: mpjones1@sheffield.ac.uk
First published on 6th October 2021
Abstract
Using tools from morphological image analysis, we characterise spinodal decomposition microstructures by their Minkowski functionals, and search for a correlation between them and data from scattering experiments. To do this, we employ machine learning in the form of Gaussian process regression on data derived from numerical simulations of spinodal decomposition in polymer blends. For a range of microstructures, we analyse the predictions of the Minkowski functionals achieved by four Gaussian process regression models using the scattering data. Our findings suggest that there is a strong correlation between the scattering data and the Minkowski functionals.
1 Introduction
De-mixing is one of the most ubiquitous examples of material self-assembly, occurring frequently in complex fluids and living systems, as well as being of great importance to the development of metallic alloys. It has enabled the development of multi-phase polymer blends and composites for use in sophisticated applications, including structural aerospace components, flexible solar cells, and filtration membranes. Even though superior functionality is derived from the microstructure, our understanding of the correlations between microstructure characteristics and material properties remains largely empirical.One of the major obstacles to developing such correlations is the challenge of characterising microstructures. Morphological image analysis (MIA) has been proposed as a method of characterising real space images of phase separated structures.1 Collectively, the key characteristics of such an image are referred to as Minkowski functionals. There are four of these in three dimensions: the total volume occupied by one of the phases, the combined surface area of the interfaces between the phases, the average curvature of the interfaces and the connectivity between the two phases. Such measures have the potential to be invaluable in enhancing our understanding of material performance since we can expect that all of them correlate with functionality. Experimentally, the determination of the Minkowski functionals of a two-phase blend requires real space three dimensional images, using techniques such as Confocal microscopy.2 Three-dimensional mapping of two-phase materials becomes challenging to obtain when the microstructures of interest are sub-micron. In contrast, scattering experiments (light, X-ray or neutron) are powerful techniques which offer the opportunity to undertake real time measurements at a wide range of length-scales, from nanometres to microns, during microstructure evolution3. The challenge in dealing with scattering data is that although model-free length scales can often be inferred directly from the peaks, for example, the extraction of other features is dependent on an appropriate choice of model to fit the data. This often leads to ambiguous, model dependent, results, partly as a consequence of limitations in the measured data introduced by the phase problem4.
In this paper, we explore the use of machine learning as a promising route to the model-free extraction of microstructure characteristics from scattering data. We will focus on the process of spinodal decomposition in binary polymer blends as an exemplar, using numerically generated data to test our approach. Spinodal topologies have generated significant interest over recent years,5–9 as has the application of machine learning to problems in the field of soft matter10. We use Gaussian process regression11 to make predictions of the Minkowski functionals of spinodal decomposition microstructures from the corresponding scattering data. Based on the quality of the predictions, we assess whether there is a correlation between the two. We are partly motivated by the well-established Porod invariant12, which provides an analytical tool to extract the volume Minkowski measure from scattering.
2 Theory
2.1 Polymeric spinodal decomposition
Spinodal decomposition occurs when a blend becomes unstable. In this stability regime, there is no energy barrier to phase separation. Therefore, infinitesimal fluctuations in composition induce a continuous phase transition to an immiscible state. The time evolution of composition fluctuations during spinodal decomposition is described by the Cahn–Hilliard equation,13–16 which, in dimensionless form, can be written as | (1) |
An experimental quantity of interest in the study of polymer blends undergoing spinodal decomposition, or any mixtures for that matter, is the structure factor.17–19 It is directly proportional to the intensity measured in scattering experiments and provides information about the amplification of composition fluctuations. The structure factor can be calculated from simulated composition data using a Fourier transform relation19. For a cubic simulation lattice with L3 lattice sites and coordinates denoted by (x, y, z), the structure factor is
 | (2) |
In scattering experiments, the scattering intensity can be used to calculate the volume Minkowski measure Vmvia the following relationship with the Porod invariant12
 | (3) |
2.2 Morphological image analysis
In most applications of MIA, some form of image processing is required as a prerequisite – this is discussed in Section 3.1. Once an image has been made amenable to MIA, the procedure for calculating the Minkowski functionals can be formulated into a straightforward counting problem1. Firstly, each pixel needs to be decomposed into its constituent parts: eight vertices, twelve edges, six faces and a cubic interior. Then the following counting relations can be employed| Vm = nc, | (4a) |
| Sm = −6nc + 2nf, | (4b) |
| 2Bm = 3nc − 2nf + ne, | (4c) |
| χm = −nc + nf − ne + nv | (4d) |
2.3 Gaussian process regression
Gaussian process regression is a non-parametric, Bayesian method for solving regression problems11. It is straight forward to implement20 and gives rise to interpretable models.To use Gaussian process regression to predict the Minkowski functionals of a given microstructure from the corresponding scattering data, we assume that the input x (a vector of the structure factor at time τ) and output y (one of the Minkowski functionals at time τ) are related through a general function f, such that y = f(x) +ε where ε is a random noise term, which is independent of x. It is assumed that the noise is additive and Gaussian distributed with zero mean and variance σn2.
To make predictions for new, previously unseen, inputs x*, assumptions need to be made about the characteristics of the function. In Gaussian process regression, this is done by defining a prior probability distribution over all possible functions. No assumptions are made about the functional form hence Gaussian process regression is a non-parametric technique. Conditioning the prior on the observations yields a posterior distribution, which contains functions from the prior that agree with the observations. By plotting the mean of the functions drawn from the posterior, predictions can be made. This is Bayesian inference: the probability distribution over functions changes as more information becomes available.
The prior distribution is constructed using a Gaussian process. Formally, a Gaussian process is defined as a collection of random variables, any number of which have a joint Gaussian distribution. Mathematically, a Gaussian process can be written as
f(x) ∼ ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (m(x), k(x, x′)) (m(x), k(x, x′)) | (5) |
m(x) = ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [f(x)] [f(x)] | (6a) |
k(x, x′) = ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [(f(x) − m(x))(f(x′) − m(x'))] [(f(x) − m(x))(f(x′) − m(x'))] | (6b) |
![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) denotes the expectation.
denotes the expectation.
The covariance function defines how ‘close’ two inputs are. Under the assumption that inputs that are close together correspond to similar values of the output, training inputs that are close to a previously unseen input should be instructive in making a prediction at that point. There are many different covariance functions to choose from. The characteristics of the functions imposed by the prior are encoded in the covariance function. Choosing a suitable covariance function can be achieved using prior knowledge, an automatic search or manual trial and error21. The precise shape of the covariance function is determined by the values of its free parameters, called hyperparameters. The values of the hyperparameters need to be learnt11.
Once a model corresponding to a particular covariance function has been trained, i.e. the values of the hyperparameters have been learnt, its performance can be assessed using previously unseen test inputs and outputs. The predictive equations for Gaussian process regression are
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) * = m* + K*[K + σn2I]−1(y − m) * = m* + K*[K + σn2I]−1(y − m) | (7a) |
 | (7b) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) * is posterior mean function, cov(f*) is the variance, m = m(X) (m* = m(X*)) is the mean vector formed by aggregating the values of eqn (6a) at each training (test) point, y is the output vector formed by aggregating the values of the training outputs, and K*, K, K** are the covariance matrices formed by evaluating eqn (6b) element-wise at all pairs of training and test points, all pairs of training points, or all pairs of test points, respectively.
* is posterior mean function, cov(f*) is the variance, m = m(X) (m* = m(X*)) is the mean vector formed by aggregating the values of eqn (6a) at each training (test) point, y is the output vector formed by aggregating the values of the training outputs, and K*, K, K** are the covariance matrices formed by evaluating eqn (6b) element-wise at all pairs of training and test points, all pairs of training points, or all pairs of test points, respectively.
3 Methodology
3.1 Building the data sets
Spinodal decomposition was simulated in ten three-dimensional polymer blends with average compositions spanning the range 0.05 ≤![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ≤ 0.5 in increments of Δ
≤ 0.5 in increments of Δ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.05. Details on the simulations of spinodal decomposition in three dimensions are provided in Section 1.1 of the ESI.† In each simulation, the microstructure of the blend was saved at integer values of τ in the range 0 < τ ≤ 39. For each microstructure, the radially averaged structure factor was calculated by taking the radial average of eqn (2). The Minkowski functionals were calculated by applying the procedure outlined in eqn (4a)–(4d). This was implemented using the algorithm provided and outlined in ref. 1 for binary images. To make the microstructures amenable to the algorithm they were first thresholded such that
= 0.05. Details on the simulations of spinodal decomposition in three dimensions are provided in Section 1.1 of the ESI.† In each simulation, the microstructure of the blend was saved at integer values of τ in the range 0 < τ ≤ 39. For each microstructure, the radially averaged structure factor was calculated by taking the radial average of eqn (2). The Minkowski functionals were calculated by applying the procedure outlined in eqn (4a)–(4d). This was implemented using the algorithm provided and outlined in ref. 1 for binary images. To make the microstructures amenable to the algorithm they were first thresholded such that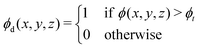 | (8) |
A lower-resolution version of the data set described above was constructed using an approximation of the scattering data. The scattering data was fit using the universal scaling function proposed by Furukawa for the late stage of spinodal decomposition22. The universal scaling function is given by
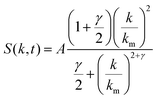 | (9) |
Spinodal decomposition was also simulated in a two-dimensional polymer blend with average composition ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5. Details on the simulation of spinodal decomposition in two dimensions are provided in Section 1.2 of the ESI.† The microstructure of the blend was saved at integer values of τ in the range 0 < τ ≤ 75. The structure factor and Minkowski functionals were calculated in the same way as described above, except for the fact that the two-dimensional equivalent1 of eqn (4b)–(4d) were used to calculate the Minkowski functionals.
= 0.5. Details on the simulation of spinodal decomposition in two dimensions are provided in Section 1.2 of the ESI.† The microstructure of the blend was saved at integer values of τ in the range 0 < τ ≤ 75. The structure factor and Minkowski functionals were calculated in the same way as described above, except for the fact that the two-dimensional equivalent1 of eqn (4b)–(4d) were used to calculate the Minkowski functionals.
To help visualise the construction of the three-dimensional data set, Fig. 1 shows the time evolution of the scattering data for the ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.25 blend. Each curve is made up of 128 points corresponding to dimensionless Fourier wave numbers in the range 1 ≤ k ≤ 128. Fig. 2 shows the time evolution of the normalised Minkowski functionals for the same blend (normalisation of the Minkowski functionals is discussed in Section 4). Each curve in Fig. 1 corresponds to one point in each of the panels in Fig. 2. This illustrates the dimensionality of the data set: each one-dimensional output (Minkowski functional) is associated with a 128-dimensional input (scattering data), and there are 39 of these pairs for each simulated polymer blend.
= 0.25 blend. Each curve is made up of 128 points corresponding to dimensionless Fourier wave numbers in the range 1 ≤ k ≤ 128. Fig. 2 shows the time evolution of the normalised Minkowski functionals for the same blend (normalisation of the Minkowski functionals is discussed in Section 4). Each curve in Fig. 1 corresponds to one point in each of the panels in Fig. 2. This illustrates the dimensionality of the data set: each one-dimensional output (Minkowski functional) is associated with a 128-dimensional input (scattering data), and there are 39 of these pairs for each simulated polymer blend.
The time evolution of the Minkowski functionals in Fig. 2 reveals a couple of interesting findings. Firstly, the volume plateaus before reaching a value of 0.25, which suggests that the phases are not pure. Secondly, the plateauing behaviour observed for each of the Minkowski functionals reveals that the simulations of spinodal decomposition reached the late-stage scaling regime, where power-law growth of the phase domains is observed.
3.2 Implementation of Gaussian process regression
Several investigations were carried out using four different Gaussian process regression models. Each model consisted of a zero mean function and one of the squared exponential, rational quadratic, Matern 5/2 and exponential covariance functions. Isotropic versions of the covariance functions were used. Since there are many covariance functions to choose from, the choice was informed by the fact that these covariance functions are well documented in the literature11,21 and that they enforce a range of smoothness assumptions on the functions f. In other words, the trial and error approach to choosing the covariance function was adopted. Further details regarding the covariance functions are provided in Section 2 of the ESI.†The models were trained and tested using the data corresponding to each value of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) separately. The training was implemented using a MATLAB code package called GPML20. In all but one of the investigations, the data used for training and testing were randomly determined (where this was not the case is made clear in Section 4). A caveat to the randomly determined training data is that the training set always included data corresponding to the first and last time steps in the spinodal decomposition simulations. This condition ensured that all testing was interpolation. To quantify how well the models were able to predict the values of the Minkowski functionals for previously unseen scattering data in the test set, the test root-mean-square fractional error (RMSE) was calculated. The RMSE is given by
separately. The training was implemented using a MATLAB code package called GPML20. In all but one of the investigations, the data used for training and testing were randomly determined (where this was not the case is made clear in Section 4). A caveat to the randomly determined training data is that the training set always included data corresponding to the first and last time steps in the spinodal decomposition simulations. This condition ensured that all testing was interpolation. To quantify how well the models were able to predict the values of the Minkowski functionals for previously unseen scattering data in the test set, the test root-mean-square fractional error (RMSE) was calculated. The RMSE is given by
 | (10) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (xi) is the predicted value for that case. Smaller values of the RMSE indicate better predictions and, therefore, better model performance. To check for overfitting, the coefficient of determination (CoD) was calculated for both the training and testing data. The CoD for the training data, subsequently referred to as the training CoD, is given by
(xi) is the predicted value for that case. Smaller values of the RMSE indicate better predictions and, therefore, better model performance. To check for overfitting, the coefficient of determination (CoD) was calculated for both the training and testing data. The CoD for the training data, subsequently referred to as the training CoD, is given by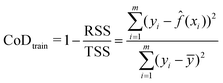 | (11) |
Training and testing were repeated one hundred times to deal with statistical fluctuations arising from the randomly determined training sets. Therefore, the median of the RMSE and CoD were calculated, as well as their interquartile ranges. The median, rather than the mean, was chosen as the most suitable measure of the average because the distributions of the values of the RMSE and CoD were skewed.
4 Results
It was found that Gaussian process regression worked best when the data corresponding to the early times in spinodal decomposition, i.e. τ < 3, were discarded; the log (base 10) of the scattering data was used and the Minkowski functionals were normalised such that1 | (12) |
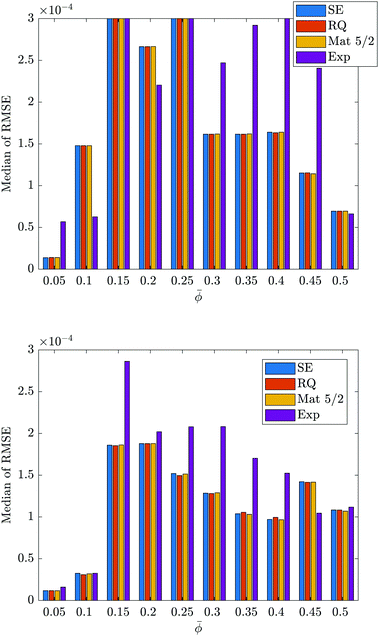
To search for a correlation between the scattering data and the Minkowski functionals, the Gaussian process regression models were trained and tested on the data set consisting of the three-dimensional Minkowski functionals and the original (not approximated) scattering data. Two different sizes of training sets were used: twenty training points and thirty training points. The average performance of the models at predicting the volume are shown in Fig. 3, where the top panel corresponds to the training set size of twenty training points, and the bottom panel corresponds to the training set size of thirty training points. The corresponding figures for the other Minkowski functionals are provided in Section 3.1 of the ESI.† Together, the figures reveal that if the average performance for each training set size is not comparable, it is better for the training set size of thirty training points. The one exception to this observation is shown in Fig. 3 for ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5, where the average performance of the models for the training set size of twenty training points is better than that for the training set size of thirty training points. The remainder of the results in this section were obtained using a training set size of thirty data points.
= 0.5, where the average performance of the models for the training set size of twenty training points is better than that for the training set size of thirty training points. The remainder of the results in this section were obtained using a training set size of thirty data points.
The bottom panels of Fig. 3 and the corresponding figures in the ESI† reveal that the highest levels of model performance were achieved for predicting the volume, followed by the surface area, curvature and connectivity. In the case of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5, a higher level of model performance was achieved for predicting the curvature rather than the connectivity. To help visualise the absolute quality of the predictions that were made by the models for each Minkowski functional, Fig. 4 shows the best predictions that were made by the Matern 5/2 model, while Fig. 5 shows some of the worst predictions that were made by any of the models. Specifically, Fig. 5 shows the worst predictions made by the exponential model for the connectivity using the original scattering data (top panel) and the approximated scattering data (bottom panel), which is discussed later. It should be noted that the plots of the best predictions achieved by the squared exponential, rational quadratic and exponential models are indistinguishable from that of the Matern 5/2 model. A summary of the best models for predicting each Minkowski functional from the original scattering data is provided in Section 3.2 of the ESI.† For each Minkowski functional, the box plots reveal that the values of the RMSE achieved in each of the one hundred instances of training and testing were often grouped closely around the median. There are some exceptions to this observation, however, and when they are considered with the small numbers of outliers that were measured, they reveal that there was significant variability in the performance of the models between some instances of training and testing.
= 0.5, a higher level of model performance was achieved for predicting the curvature rather than the connectivity. To help visualise the absolute quality of the predictions that were made by the models for each Minkowski functional, Fig. 4 shows the best predictions that were made by the Matern 5/2 model, while Fig. 5 shows some of the worst predictions that were made by any of the models. Specifically, Fig. 5 shows the worst predictions made by the exponential model for the connectivity using the original scattering data (top panel) and the approximated scattering data (bottom panel), which is discussed later. It should be noted that the plots of the best predictions achieved by the squared exponential, rational quadratic and exponential models are indistinguishable from that of the Matern 5/2 model. A summary of the best models for predicting each Minkowski functional from the original scattering data is provided in Section 3.2 of the ESI.† For each Minkowski functional, the box plots reveal that the values of the RMSE achieved in each of the one hundred instances of training and testing were often grouped closely around the median. There are some exceptions to this observation, however, and when they are considered with the small numbers of outliers that were measured, they reveal that there was significant variability in the performance of the models between some instances of training and testing.
 | ||
| Fig. 4 A comparison between the best predictions made by the Matern 5/2 model for each Minkowski functional and the true values. The predictions were made from the original scattering data. | ||
To check for overfitting, the values of the median of the training and testing CoD were calculated for each Minkowski functional using the predictions made by the models with the best average performance for each value of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) . Table 1 contains these values for the volume. The table shows that values of the median of the training and testing CoD are very close to one for all values of
. Table 1 contains these values for the volume. The table shows that values of the median of the training and testing CoD are very close to one for all values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) , apart from
, apart from ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5 where the value of the median of the training CoD is negative. For the other Minkowski functionals, the values of the median of the training and testing CoD are very close to one for all values of
= 0.5 where the value of the median of the training CoD is negative. For the other Minkowski functionals, the values of the median of the training and testing CoD are very close to one for all values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) . These results suggest that overfitting was only an issue when the models were trained to predict the volume for
. These results suggest that overfitting was only an issue when the models were trained to predict the volume for ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5.
= 0.5.
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) from the original scattering data
from the original scattering data
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif)
|
Model | Median training CoD | Median testing CoD |
|---|---|---|---|
| 0.05 | Mat 5/2 | 1.00000 | 1.00000 |
| 0.10 | RQ | 1.00000 | 0.99472 |
| 0.15 | RQ | 1.00000 | 0.99992 |
| 0.20 | SE | 1.00000 | 0.99997 |
| 0.25 | RQ | 1.00000 | 0.99996 |
| 0.30 | RQ | 1.00000 | 0.99997 |
| 0.35 | Mat 5/2 | 1.00000 | 0.99998 |
| 0.40 | Mat 5/2 | 1.00000 | 0.99995 |
| 0.45 | Exp | 1.00000 | 0.99939 |
| 0.50 | Mat 5/2 | 1.00000 | −1.81642 |
To compare the performance of the models achieved using the original scattering data with a hybrid machine learning/physics motivated model approach, the Gaussian process regression models were trained and tested on the data set consisting of the three-dimensional Minkowski functionals and the approximated scattering data. In general, the average performances of the best models trained using the approximated scattering data were worse than those trained using the original scattering data. This is exemplified in Fig. 6, which compares the average performances of the best models at predicting the surface area when trained using the original and approximated scattering data.
 | ||
| Fig. 6 A comparison of the average performance of the best models at predicting the surface area from the original scattering data and the approximated scattering data. | ||
To test whether the models were capable of making extrapolative predictions, the Gaussian process regression models were trained and tested on the data set consisting of the two-dimensional Minkowski functionals. Specifically, the models were trained once on the data corresponding to τ = 3 through to τ = 32. Then they were tested on their ability to predict the Minkowski functionals at τ = 33 and τ = 75. It should be noted that the Minkowski functionals were normalised using the two-dimensional equivalent1 of eqn (12). For each Minkowski functional, the percentage error of the prediction at τ = 75 was much greater than that at τ = 33. This is exemplified in Table 2 for the surface area. It should be noted that the percentage error of the predictions at τ = 75 for the curvature and connectivity were much larger than for the surface area. It was roughly 36% for the curvature and between 95% and 130% for the connectivity.
| Model | Percentage error of prediction for t = 33 | Percentage error of prediction for t = 75 |
|---|---|---|
| SE | 0.20 | 1.56 |
| RQ | 0.14 | 1.35 |
| Mat 5/2 | 0.03 | 1.39 |
| Exp | 0.09 | 1.46 |
To help place the performance of the Gaussian process regression models in a wider context, a comparison with a simple neural network was made. The neural network was trained and tested on the ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.25 data in the data set consisting of the three-dimensional Minkowski functionals and the original scattering data. Full details on the neural network are provided in Section 4 of the ESI.† The average performance of the Gaussian process regression models were significantly better than the neural network. This is shown in Fig. 7.
= 0.25 data in the data set consisting of the three-dimensional Minkowski functionals and the original scattering data. Full details on the neural network are provided in Section 4 of the ESI.† The average performance of the Gaussian process regression models were significantly better than the neural network. This is shown in Fig. 7.
5 Discussion
The procedure for normalising the Minkowski functionals in eqn (12) is essential to take a model trained on simulated, dimensionless data and apply it to real experimental data. To apply the normalisation procedure to simulated data, the value of L can be calculated from the number of lattice sites used in the simulation, and the value of N can be calculated by counting the number of lattice sites with ϕd = 1. It should be noted that the value of N is time-dependent. Dimensionless variables, which provide a link between the simulation and experimental length and time scales, must be defined before the normalisation procedure can be applied to experimental data. Once this has been done, the value of L can be calculated from the sample and the physical spatial discretisation, and the value of N can be calculated from eqn (3). It follows that the normalisation procedure can only be justifiably applied to experimental data in the case where the assumptions underpinning the relationship in eqn (3) hold.
Fig. 3 and the corresponding figures in the ESI† reveal several interesting findings. These include: for each Minkowski functional, the average performance of each model was different for different values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ; the highest levels of model performance were achieved for the volume, followed by the surface area, curvature and connectivity; and, a clear-cut best performing model to make predictions of the Minkowski functionals from the scattering data was not identified. We suggest that each of these findings can be understood using the concept of regression space – the space in which the Gaussian process regression models are fit to the Minkowski functionals, which are functions of the scattering data.
; the highest levels of model performance were achieved for the volume, followed by the surface area, curvature and connectivity; and, a clear-cut best performing model to make predictions of the Minkowski functionals from the scattering data was not identified. We suggest that each of these findings can be understood using the concept of regression space – the space in which the Gaussian process regression models are fit to the Minkowski functionals, which are functions of the scattering data.
First, we try to explain the finding that, for each Minkowski functional, the average performance of each model was different for different values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) . Physically, each value of
. Physically, each value of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) corresponds to a different type of microstructure: small values of
corresponds to a different type of microstructure: small values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) correspond to dispersed droplet structures, large values of
correspond to dispersed droplet structures, large values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) correspond to co-continuous structures, and intermediate values of
correspond to co-continuous structures, and intermediate values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) correspond to an in-between structure. The different types of microstructure yield different scattering data and Minkowski functionals. This affects the distribution of the Minkowski functionals in regression space. We suggest that some distributions of the Minkowski functionals are easier to fit than others, giving rise to variability in the accuracy of the predictions and, therefore, the performance of the models. This idea explains the high levels of model performance achieved for
correspond to an in-between structure. The different types of microstructure yield different scattering data and Minkowski functionals. This affects the distribution of the Minkowski functionals in regression space. We suggest that some distributions of the Minkowski functionals are easier to fit than others, giving rise to variability in the accuracy of the predictions and, therefore, the performance of the models. This idea explains the high levels of model performance achieved for ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.05 and
= 0.05 and ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.10 for each Minkowski functional. Analysis of the scattering data and Minkowski functionals reveal that the Minkowski functionals are closely bunched together in the regression space, which should make them easier to fit.
= 0.10 for each Minkowski functional. Analysis of the scattering data and Minkowski functionals reveal that the Minkowski functionals are closely bunched together in the regression space, which should make them easier to fit.
Next, we try to explain the finding that the highest levels of model performance were achieved for the volume, followed by the surface area, curvature and connectivity. Analysis of the values of each Minkowski functional reveals that, for all values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) , the volume spans the smallest relative range, followed by the surface area, curvature and connectivity. The relative range of a set of values is the range of the values divided by their mean. In terms of regression space, this means that, for each value of
, the volume spans the smallest relative range, followed by the surface area, curvature and connectivity. The relative range of a set of values is the range of the values divided by their mean. In terms of regression space, this means that, for each value of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) , the values of the volume are more closely bunched than the values of the other Minkowski functionals and, therefore, possibly easier to fit.
, the values of the volume are more closely bunched than the values of the other Minkowski functionals and, therefore, possibly easier to fit.
Now, we try to explain why a clear-cut best performing model to make predictions of the Minkowski functionals from the scattering data was not identified. Each of the Minkowski functionals has a different distribution in space according to the value of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) . Therefore, we suggest that functions with different properties (e.g. smoothness, length scale, periodicity etc.) are required to fit the Minkowski functionals for different values of
. Therefore, we suggest that functions with different properties (e.g. smoothness, length scale, periodicity etc.) are required to fit the Minkowski functionals for different values of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) . In other words, it is unlikely that there will be a one-size-fits-all model for any of the Minkowski functionals. It follows that models with low levels of average performance probably enforce the wrong assumptions on the functions f. For example, quite often, the exponential model was identified as the worst-performing. This could be because of the roughness it enforces on the functions f, which may not be suitable for fitting the Minkowski functionals.
. In other words, it is unlikely that there will be a one-size-fits-all model for any of the Minkowski functionals. It follows that models with low levels of average performance probably enforce the wrong assumptions on the functions f. For example, quite often, the exponential model was identified as the worst-performing. This could be because of the roughness it enforces on the functions f, which may not be suitable for fitting the Minkowski functionals.
Overfitting the models in training did not seem to be a problem. The only significant discrepancy between the values of the median of the training and testing CoD was obtained for the volume for ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5, as is shown in Table 1. The negative value of the median of the testing CoD reveals that the values of the volume for
= 0.5, as is shown in Table 1. The negative value of the median of the testing CoD reveals that the values of the volume for ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5 are better fit by their mean than any of the models. Indeed, analysis of the values of the volume for
= 0.5 are better fit by their mean than any of the models. Indeed, analysis of the values of the volume for ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = 0.5 showed that they fluctuate around their mean.
= 0.5 showed that they fluctuate around their mean.
Fig. 4 suggests that all of the Minkowski functionals can be excellently predicted from the scattering data. This is reflected by the small residuals between the predictions and the ‘predictions = true’ lines. Even for the relatively bad predictions shown in Fig. 5, the quality of the predictions is quite good. From the quality of the predictions made by the Gaussian process regression models, we infer that there is a strong correlation between the Minkowski functionals and the scattering data. This inference is supported by the fact that the model performance was worse when the models were trained and tested using the approximated scattering data, as is shown in Fig. 6.
As is often the case with machine learning, the performance of the models when making interpolative predictions is far better than when making extrapolative predictions. This is shown in Table 2 for the surface area. The errors in the table suggest that the models may be effective at making predictions that extrapolate beyond the training data up to a certain distance. Comparing the errors at τ = 75 for the surface area with the curvature and connectivity suggests that the extent beyond the training data for which decent extrapolative predictions can be made depends on the Minkowski functional that is being predicted.
From the above discussion, it is clear that Gaussian process regression is well suited to make predictions of the Minkowski functionals of a spinodal decomposition microstructure from the corresponding scattering data. The method is easy to implement, and it gives rise to interpretable models. It is interesting to note that the Gaussian process regression models outperformed a simple neural network, as is shown in Fig. 7. Of course, a comparison with a more sophisticated neural network may well yield a different result. However, other, potentially better, Gaussian process regression models could be developed based on different covariance functions.
To end this section, we summarise the main limitations of the method. Firstly, the normalisation procedure can only be applied to experimental data obtained from blends in which the phases are pure, and the interface between them is sharp. Secondly, the ability of the models to make extrapolative predictions is questionable, although more so for some of the Minkowski functionals than others. Thirdly, a high degree of variability is observed between the performance of some of the models. Care should be taken in the training and testing stage of their development. Fourthly, no clear-cut, best-performing model was identified, although this presents an opportunity to experiment with different models. Finally, the method has not been tested on experimental data. Thin-film polymer blends could be a good testbed.
6 Conclusion
From the quality of the predictions made by the Gaussian process regression models, we infer that there is a strong correlation between the Minkowski functionals, which are excellent measures to succinctly summarise complex microstructures, and the much more experimentally accessible scattering data. We employed four Gaussian process regression models on different data sets of scattering data and Minkowski functionals to see how well the latter could be predicted from the former. The data sets were derived from numerical simulations of spinodal decomposition in a range of blends with different average compositions![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) . The Gaussian process regression models were trained and tested on the data corresponding to each value of
. The Gaussian process regression models were trained and tested on the data corresponding to each value of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) separately.
separately.
Several investigations were carried out to assess the method and find its limitations. We suggest that the concept of regression space is useful to understand some of the findings.
Our results suggest there is an opportunity for a more complete characterisation of phase-separated microstructures using scattering data. We hope that they motivate further work into the nature of the correlation between the scattering data and the Minkowski functionals and the development of an experimental technique for analysing scattering data.
Conflicts of interest
There are no conflicts to declare.References
- K. Michielsen and H. De Raedt, Phys. Rep., 2001, 347, 461–538 CrossRef CAS.
- H. Jinnai, Y. Nishikawa, T. Koga and T. Hashimoto, Macromolecules, 1995, 28, 4782–4784 CrossRef CAS.
- J. S. Higgins and J. T. Cabral, Macromolecules, 2020, 53, 4137–4140 CrossRef CAS.
- G. Taylor, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59, 1881–1890 CrossRef PubMed.
- S. Kumar, S. Tan, L. Zheng and D. M. Kochmann, npj Computat. Mater., 2020, 6, 1–10 CrossRef CAS.
- C. M. Portela, A. Vidyasagar, S. Krödel, T. Weissenbach, D. W. Yee, J. R. Greer and D. M. Kochmann, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 5686–5693 CrossRef CAS PubMed.
- A.-L. Esquirol, P. Sarazin and N. Virgilio, Macromolecules, 2014, 47, 3068–3075 CrossRef CAS.
- S. Huang, L. Bai, M. Trifkovic, X. Cheng and C. W. Macosko, Macromolecules, 2016, 49, 3911–3918 CrossRef CAS.
- K. Hiraide, K. Hirayama, K. Endo and M. Muramatsu, Comput. Mater. Sci., 2021, 190, 110278 CrossRef CAS.
- P. S. Clegg, Soft Matter, 2021, 17, 3991 RSC.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, 2006 Search PubMed.
- J. S. Higgins and H. C. Benoit, Polymers and Neutron Scattering, Oxford University Press, 1994 Search PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- J. W. Cahn, Acta Metall., 1961, 9, 795–801 CrossRef CAS.
- P. G. de Gennes, J. Chem. Phys., 1980, 72, 4756–4763 CrossRef CAS.
- S. C. Glotzer, Annual Reviews of Computational Physics II, World Scientific, 1995, vol. 2, pp. 1–46 Search PubMed.
- J. D. Gunton, M. Sam Miguel and P. S. Sahni, Phase Transitions and Critical Phenomena, Academic Press, London, 1983 Search PubMed.
- B. F. Barton, P. D. Graham and A. J. McHugh, Macromolecules, 1998, 31, 1672–1679 CrossRef CAS.
- H. Tanaka, T. Hayashi and T. Nishi, J. Appl. Phys., 1986, 59, 3627–3643 CrossRef CAS.
- C. E. Rasmussen and H. Nickisch, The Gaussian Processes Website, http://www.gaussianprocess.org/.
- D. Duvenaud, PhD thesis, University of Cambridge, 2014.
- H. Furukawa, Phys. A, 1984, 123, 497–515 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00818h |
| This journal is © The Royal Society of Chemistry 2021 |