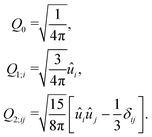DOI:
10.1039/D1SM00426C
(Paper)
Soft Matter, 2021,
17, 5613-5632
Motility-induced inter-particle correlations and dynamics: a microscopic approach for active Brownian particles
Received
18th March 2021
, Accepted 18th April 2021
First published on 19th April 2021
Abstract
Amongst the theoretical approaches towards the dynamics and phase behaviour of suspensions of active Brownian particles (ABPs), no attempt has been made to specify the motility-induced inter-particle correlations as quantified by the pair-correlation function. Here, we derive expressions for the pair-correlation function for ABPs with very short-ranged direct interactions for small and large swimming velocities and low concentrations. The pair-correlation function is the solution of a differential equation that is obtained from the Fokker–Planck equation for the probability density function of the positions and orientations of the ABPs. For large swimming Peclet numbers, λ, the pair-correlation function is highly asymmetric. The pair-correlation function attains a large value, ∼λ, within a small region of spatial extent, ∼1/λ, near contact of the ABPs when the ABPs approach each other. The pair-correlation function is small within a large region of spatial extent, ∼λ1/3, when the ABPs move apart, with a contact value that is essentially zero. From the explicit expressions for the pair-correlation function, Fick's diffusion equation is generalized to include motility. It is shown that mass transport, in case of large swimming velocities, is dominated by a preferred swimming direction that is induced by concentration gradients. The expression for the pair-correlation function derived in this paper could serve as a starting point to obtain approximate results for high concentrations, which could then be employed in a first-principles analysis of the dynamics and phase behaviour of ABPs at higher concentrations.
1 Introduction
Active matter consisting of suspensions of self-propelling particles ranges from synthetic colloidal particles to cells and bacteria. Several different types of synthetic colloidal particles have been developed over the past few years with a variety of propulsion mechanisms. Self-propulsion affects the dynamics and stability of phases, induces new phases with no counterparts in systems of passive particles, and affects phase separation kinetics. For overviews on the various types of propulsion mechanisms and motility-induced phase separation (MIPS), see, for example, ref. 1 (an introduction in German) and ref. 2–8.
The inter-particle correlations that underly the behaviour of active systems originate from direct and hydrodynamic interactions between the particles. The central quantity that specifies the degree of correlations between particles is the so-called pair-correlation function (see, for example, ref. 9 and 10). Since propulsion is achieved by forces exerted by the particles onto the surrounding fluid, there are additional contributions to their hydrodynamic interactions as compared to passive particles. These additional hydrodynamic interactions depend on the propulsion details and lead to highly anisotropic attractive/repulsive interactions depending on the relative distance between the particles (see, for example, ref. 8 and 11–16). Simulations in 3D on spherical active particles show that the differences in hydrodynamic interactions between pullers and pushers have a pronounced effect on the pair-correlation function at close contact (with a center-to-center distance of 2.01a, where a is the radius of the spheres), but a much smaller effect for somewhat larger distances (equal to 2.50a).17 The effect of hydrodynamic interactions on inter-particle correlations has been studied for model flagellum swimmers by means of simulations in ref. 18, where increased correlations between the rear parts of swimmers and decreased correlations between the rear and the front parts are found. Strong inter-particle correlations due to long-ranged hydrodynamic interactions in 3D have been observed in large-scale simulations in ref. 19, where direct interactions (for example, due to excluded-volume interactions) have been neglected. In general, self-propelled particles with a solid core, interacting hydrodynamically in addition to hard-core interactions, are referred to as squirmers. For comparison, active Brownian particles (ABPs) are introduced that do not exhibit hydrodynamic interactions. In the present paper, we study inter-particle correlations between ABPs, thus neglecting hydrodynamic interactions. It remains a largely open question to which extent inter-particle correlations of spherical ABPs and squirmers with excluded-volume interactions differ in 3D bulk.
A microscopic statistical mechanics approach towards the behaviour of active systems can be based on the so-called Smoluchowski equation, which is a Fokker–Planck-type equation of motion for the probability density function of the positions and orientations of the active particles. This approach can be used, for example, to generalize the van’t Hoff law for the osmotic pressure20 and expressions for Casimir forces between two plates21 to active systems, and explain the alignment of active colloids in a gravitational field.22 These generalizations aim at dilute active systems, and therefore depart from the Smoluchowski equation neglecting inter-particle correlations. For concentrated systems, however, such inter-particle correlations are essential.
An approach that addresses concentrated systems on a microscopic level is dynamic density functional theory (DDFT)23 (for an overview on DDFT approaches, see ref. 24). This approach is based on the equation of motion for the one-particle distribution function as obtained from the Smoluchowksi equation. Approximations are made in ref. 23 to eliminate three-particle correlation functions which arise from the coupling between the hydrodynamic and direct interactions, in favour of two-particle correlation functions. The two-particle correlation functions are then largely ignored, which is stated to be a good approximation for weak and long-ranged direct interactions. In the present paper, we are interested in the pair-correlation function for very steep and short-ranged interactions between ABPs, for which the DDFT approach in ref. 23 is inappropriate.
The Smoluchowski equation has been employed, within certain approximations, to analyse the stability of MIPS in 2D.25–29 Here, a linear decrease of the average velocity, v ∼ v0(1 − ζ ρ) (where v0 is the free-swimming velocity), of swimmers with the increasing concentration, ρ, is found, which is in accordance with semi-empirical approaches30,32–34 and simulations in 2D.35 Without the specification of the pair-correlation function, however, the coefficient ζ remains an unknown parameter. In ref. 36 and 37, the analysis of MIPS for non-chiral and chiral ABPs in 2D is similarly based on the Smoluchowki equation, where inter-particle correlations are accounted for by numerical input obtained from simulations.38 An independent calculation of the pair-correlation function is not pursued in these studies. It is the purpose of the present study to derive explicit expressions for the 3D pair-correlation function, for small concentrations where binary interactions are dominant. For an overview of several theoretical approaches, see ref. 27 and 39.
In ref. 40, an expression for the pair-correlation function has been derived on the two-particle level from a model where orientational motion is mimicked by introducing a Gaussian type of noise imposed on the propulsion velocity with a finite relaxation time. This allows for a description on the basis of position coordinates alone, thus eliminating orientational variables. Within this approach, it is possible to extract an effective potential, the Boltzmann exponent of which gives the low-density pair-correlation function. As will turn out, within the microscopic approach in the present work, where orientational motion is explicitly accounted for, it is not possible to represent activity by means of an effective pair-interaction potential.
The pair-correlation function (averaged with respect to the orientation of one of the particles) for a dilute 2D system of Brownian Janus particles with induced-charge electrophoresis activity is experimentally obtained in ref. 41, and similarly for externally driven binary mixtures in ref. 42. Good agreement is found in ref. 41 with numerical solutions of a differential equation for the pair-correlation function for weak inter-particle interactions, which is similar but not identical to the Smoluchowski equation in 2D (the difference is discussed in Section 3). It is stated in ref. 41 that “the depletion wake consists of two depletion wings”, which we will comment on at the end of Section 5.
An extensive overview of the current status and challenges concerning active systems can be found in ref. 43, and in ref. 44 with an emphasis on simulation methods.
Surely, the above-cited references represent only a biased fraction of the vast literature on active systems. There is, however, essentially no literature that addresses the analytical determination of the pair-correlation function. The aim of the present paper is to derive closed analytic expressions for the pair-correlation function for dilute 3D systems of spherical ABPs, where binary interactions dominate. It remains a future challenge to extend the theory given in the present paper to higher concentrations and to include hydrodynamic interactions.
This paper is organized as follows. In Section 2, we recapitulate the Smoluchowski equation for ABPs, the derivation of the equation of motion for the orientation-dependent local density from it, and the definition and relevance of the pair-correlation function for collective dynamics and MIPS. In Section 3, the fundamental differential equation for the pair-correlation function for small concentrations is derived, which is solved for small swimming Peclet numbers in Section 4, and for large Peclet numbers in Section 5. Section 6 discusses the collective diffusion to leading order in concentration for large Peclet numbers. The summary, conclusion, and outlook are given in Section 7.
2 Fokker–Planck approach and relevance of the pair-correlation function
A microscopic particle-based starting point to predict motility-induced collective motion and phase separation (MIPS) of active Brownian particles (ABP) with a spherically shaped core is the N-particle Smoluchowski equation. This is a Fokker–Planck equation in the over-damped limit for the (non-equilibrium) probability density function (pdf), PN, of the position coordinates, {rj}, and the orientations, {ûj}, of a total number of N ABPs within a given volume. The standard Smoluchowski equation is a generalized diffusion equation for the time-rate of change of PN, which expresses probability conservation in terms of the divergence of a probability flux. There are several contributions to the probability flux. There is a contribution arising from translational Brownian motion, which gives rise to changes of position coordinates. The position coordinates also change due to direct inter-particle interactions, while rotational Brownian motion results in changes of the orientations. Including the flux due to active swimming, the Smoluchowski equation reads as follows:| |  | (1) |
where the various contributions are displayed in the same order as discussed above. Here, D0 and Dr are the translational and rotational diffusion coefficients for a single sphere in an unbounded fluid, respectively, β = 1/kBT is the inverse thermal energy (where kB is the Boltzmann constant and T is the temperature), ∇j is the gradient operator with respect to the position coordinate, rj, of the jth particle, and| |  | (2) |
is the rotation operator, with ∇uj the gradient operator with respect to the Cartesian coordinates of the unit vector, ûj, that specifies the orientation of the jth particle. The orientation defines the direction in which an ABP would actively move when submerged in an unbounded fluid without the presence of other ABPs. Furthermore, Ψ is the total potential interaction energy of the assembly of ABPs, which depends only on the position coordinates, not on orientations, and v0 is the bare swimming velocity. The average swimming velocity in a concentrated dispersion of ABPs is different from v0 as a result of interactions between the ABPs, the calculation of which requires the solution of the Smoluchowski equation (see Section 6).
The Smoluchowski equation assumes overdamped dynamics, where inertial effects are neglected, which is a valid approximation on time scales of the order of a few tens of nanoseconds for sizes of the ABPs not larger than a few microns. An analysis of inertial effects for larger ABPs can be found in ref. 45. What has been neglected in eqn (1) are hydrodynamic interactions between the swimmers. Including hydrodynamic interactions remains a future challenge, and would enable to make a distinction between, for example, pullers and pushers.
The formulation of the Smoluchowski equation given above relates to 3D. A 2D formulation leads to a different form of the rotational operators, but is most probably amenable to the same type of analysis given in the present 3D case. Most of the experiments (like in ref. 41 and 42) have been conducted in 2D, where hydrodynamic interactions with the confining geometry will probably play a major role. Including such hydrodynamic interactions requires a major extension of the present approach. In addition, one should make a distinction whether the swimming direction is confined within the 2D plane of motion, or whether rotation in all directions is still possible. In the latter case, the rotational operators in the Smoluchowski equation remain unchanged, but the swimming contribution involves projections of the orientations onto the 2D plane.
The dynamics, phase separation kinetics, phase behaviour, spatial inhomogeneities, and local orientational order parameters can be computed from the orientation-dependent local density ρ(r,û,t) ≡ NP1(r,û,t), where P1 is the one-particle pdf for the position and orientation of an ABP, which is defined as the integral of the N-particle pdf, PN, with respect to all coordinates except for those of a single particle:
| |  | (3) |
where the integrals

range over the surface of a unit sphere, that is, over all orientations of
ûj. The orientation-dependent local density is the number concentration of ABPs at a position
r with an orientation
û. The equation of motion for
P1 is obtained by the integration of the
N-particle Smoluchowski equation with respect to all position coordinates and orientations, with the exception of a single position and orientation. This leads to the following equation:
| |  | (4) |
where the interaction energy of the assembly of ABPs is assumed to be pair-wise additive, that is,
| |  | (5) |
where
V is the pair-interaction potential. Furthermore, the pair-correlation function that appears in the integral in
eqn (4) is defined as follows:
| | | P2(r,r′,û,û′,t) = P1(r,û,t)P1(r′,û′,t)g(r,r′,û,û′,t), | (6) |
where the two-particle pdf,
P2, is equal to the integral of
PN with respect to all particle coordinates except for two of them (similar to the definition of
P1). For non-interacting ABPs,
P2 factorizes into a product of two
P1s, so that
g = 1. The pair-correlation function thus describes the degree of correlation between two particles embedded in a (concentrated) system of remaining ABPs.
For an isolated ABP, for which the last term in eqn (4) involving the pair-correlation function is absent, the following well-known expression for the mean-squared displacement W can be derived46:
| |  | (7) |
This expression has been verified experimentally in 2D in
ref. 47, in 2D for small times in
ref. 48, and by simulations in
ref. 35 and
49. For times much larger than 1/
Dr, it is found that
W(
t) = 6
Dst, where the long-time self-diffusion coefficient is equal to
Ds =
D0 +
v02/6
Dr. As will be seen in Section 6, the collective diffusion coefficient at infinite dilution is equal to the self-diffusion coefficient, just like for passive systems.
An analysis of MIPS based on the Smoluchowski equation (eqn (4)) requires an explicit expression for the pair-correlation function. The aim of the present analysis is to derive an explicit expression for the pair-correlation function, depending on the bare swimming velocity, v0. This will be done on the two-particle level, where binary interactions dominate, thus neglecting the indirect interactions between two particles via the surrounding particles. The extension of the results obtained in this work to higher concentrations requires a separate study, where, for example, a similar Ornstein–Zernike approach may be followed as for systems in equilibrium.9
3 A differential equation for the pair-correlation function
Before addressing the equation of motion for the pair-correlation function, note that the pair-correlation function in eqn (4) for the orientation-dependent local density is only needed for short distances between two ABPs, since the pair-correlation function in the integral in eqn (4) occurs as a product with the pair-interaction potential. We therefore need a closure for g(r,r′,û,û′,t) for distances |r − r′| < RV, where RV is the range of the pair-interaction potential, which is of the order of the size of the ABPs. This has two important consequences. First, the interest here is in spatial variations of the orientation-dependent local density on length scales much larger than the size of single particles. Unstable modes involve the growth of density variations with a relatively large spatial extent, much larger than the range of the pair-interaction potential. We can therefore evaluate the pair-correlation function as needed in eqn (4) for a homogeneous system, at the local density at r to within a neigbourhood of extent RV from r′. Second, since structural relaxation over small distances (of the order RV) is much faster than the relaxation or growth of inhomogeneities varying over large distances (of the order of the spatial extent of unstable density variations), the pair-correlation function may be assumed to instantaneously adapt to the local density. That is, on the time scale on which density variations relax or grow, the pair-correlation function attains its stationary form. These considerations are similar to those in ref. 50, where the Cahn–Hilliard theory for spinodal gas–liquid phase separation is derived from the Smoluchowski equation. Also, in that case, the pair-correlation function instantaneously relaxes to its equilibrium value corresponding to the local density, which may be regarded as the statistical analogon of local thermodynamic equilibrium approximations.
Note that phase separation kinetics from a meta-stable state (like nucleation and growth) cannot be described on the basis of the above-discussed local homogeneity and fast relaxation of the pair-correlation function. Such a phase separation mechanism involves the formation of a nucleus, which may have a spatial extent that is not much larger than the range RV of the pair-interaction potential.
The equation of motion for the two-particle pdf, P2, can be obtained by integrating the N-particle Smoluchowski equation (eqn (1)) with respect to all particle coordinates except for two, similar to the derivation of eqn (4) for the one-particle pdf. This leads to an equation of motion for the pair-correlation function from its definition in eqn (6). On the two-particle level, neglecting higher-order correlations related to the three-particle pdf leads to the following stationary equation of motion:
| |  | (8) |
where ∇,

, and

are understood to act on the distance
R =
r1 −
r2 between two ABPs, and the orientations
û1 and
û2 of the two ABPs, respectively. Note that the pair-correlation function is a function of the relative distance
r1 −
r2 due to the approximate homogeneity on length scales larger than
RV, and is independent of time due to the fast relaxation of correlations over short distances, as discussed above.
We note that with the so-called linearized Dean equation applied to a dilute system in ref. 41 to analyze the experimental data for the pair-correlation function in 2D, the contribution 2D0β∇·[g∇V] = (2/γ)∇·[g∇V] in eqn (8) (where γ is the Stokes–Einstein friction coefficient) is replaced by (2/γ)∇2V, thus neglecting pair-correlations to this contribution. Such a neglect is not allowed within the Smoluchowski-equation approach, neither for short-ranged nor for long-ranged pair-interaction potentials. In particular, including hard-core-excluded volume interactions, the product g∇V is proportional to the delta distribution at the contact of the two ABPs (see eqn (27) in Section 6), while ∇V by itself is undefined.
Without activity, it follows from eqn (8) that the pair-correlation function is given by the Boltzmann exponential g(R) = exp{−βV(R)}. This is the well-known leading order term in an expansion of the pair-correlation function with respect to the overall concentration for passive systems. For such low concentrations, binary inter-particle interactions are dominant. Terms that account for higher-order collisions involving more than two particles have been omitted in eqn (8). For excluded-volume interactions, it is expected that this limits the validity of our analysis to volume fractions less than about 0.10. It should be noted that activity cannot be included in eqn (8) in terms of the gradient of an interaction potential. If this would have been possible, the pair-correlation function would simply be given by the afore-mentioned Boltzmann exponential of that potential.
Specializing to hard-core interactions (in which case, V(R) = 0 for R > 2a, where a is the radius of a particle, and V(R) = ∞ for R < 2a), with a possibly super-imposed very short-ranged attractive “sticky-sphere” interaction, eqn (8) reduces for R > 2a to
| |  | (9) |
In solving this equation, the hard-core interactions are accounted for by the no-flux boundary condition:
| |  | (10) |
where
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
=
R/
R is the unit vector normal to the spherical surface with radius 2
a. This boundary condition physically means that the cores of two particles cannot interpenetrate.
The differential equation (eqn 9) and the boundary condition (eqn 10) are most conveniently rewritten in terms of dimensionless variables, introducing the dimensionless distance and gradient operator:
| |  | (11) |
Hereafter, we use the same symbols for the dimensionless distance and gradient operator as before for the distance and gradient operator with dimensions. Note that
R = 1 at the contact of the two particles. The free diffusion coefficients are equal to
D0 =
kBT/6π
η0a and
Dr =
kBT/8π
η0a3, where
η0 is the shear viscosity of the solvent, so that the dimensionless Peclet number,
| | 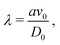 | (12) |
can be introduced (some times also denoted by Pe) to arrive at
| |  | (13) |
where
The dimensionless Peclet number,
λ, characterizes the relative importance of the swimming velocity of an isolated ABP as compared to translational and rotational diffusion. Note that it is not necessary to make a distinction between a translational and rotational Peclet number: for the spherical particles under consideration, the ratio
D0/
Dr for the translational and rotational diffusion coefficients is equal to 4
a2/3, which results in identical Peclet numbers (apart from a factor 3/2) in the dimensionless form of the stationary equation of motion
(eqn 13) for the translational and rotational contributions. The last boundary condition in
eqn (13) at infinity results from the fact that particles become uncorrelated at large separations.
We have not been able to solve this set of equations analytically for arbitrary values of the Peclet number. In the sections below, we shall therefore determine the asymptotic solutions for small and large swimming velocities.
As will turn out, these asymptotic expressions are approximately cylindrically symmetric around the direction of U, so that the pair-correlation function for these limiting Peclet numbers can be expressed in terms of the cylindrical coordinates Z = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R
Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, where Θ is the angle between R and U (as depicted in Fig. 1), that is,
Θ, where Θ is the angle between R and U (as depicted in Fig. 1), that is,
| | cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ = Θ = ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·Û, ·Û, | (15) |
where
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
and
Û are the unit vectors in the directions of
R and
U, respectively. In addition, the asymptotic expressions for the pair-correlation function depend on the magnitude of
U, which is equal to
| |  | (16) |
where
is the cosine of the angle between
û1 and
û2 (also indicated within sphere 2 in
Fig. 1). For intermediate Peclet numbers, there is an additional dependence on
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
·(
û1 +
û2). Due to the approximate independence of the asymptotic solutions for small and large Peclet numbers on this variable, the pair-correlation function might be a weak function of this variable for intermediate Peclet numbers as well.
 |
| | Fig. 1 Definition of the variables R, Z, ρ and U in relation to the previously defined orientations, û1,2, and the center-to-center distance, R. For simplicity, all vectors are drawn within the same 2D plane. The asymptotic expressions derived below are the functions of these four scalar variables. | |
4 The pair-correlation function for small Peclet numbers
For small Peclet numbers, the pair-correlation can be expanded as follows:| | | g = 1 + λg1 + λ2g2+ ⋯. | (18) |
After substitution into eqn (13), it is found that the leading order contribution satisfies the following set of equations:| | 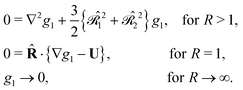 | (19) |
The solution of this set of equations is determined in Appendix A by means of a spherical harmonics series representation, leading to| | 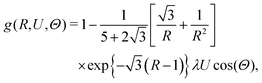 | (20) |
where the various coordinates are defined at the end of the previous section (see also Fig. 1). The contact value gc of the pair-correlation function (for which R = 1) is thus equal to| | 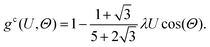 | (21) |
A little consideration (see also Fig. 1) shows that the particles move toward each other when cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ < 0, and move away from each other when cos
Θ < 0, and move away from each other when cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 0. Eqn (20) thus shows that the pair-correlation function is larger than unity when the particles move toward each other, and is equally less than unity in case they move away from each other.
Θ > 0. Eqn (20) thus shows that the pair-correlation function is larger than unity when the particles move toward each other, and is equally less than unity in case they move away from each other.
Note that the dimensionless relative velocity of two particles is equal to λU. In case U = 0, for which û1 = û2, the two particles move side-to-side along with each other with the same velocity. The motility-induced distortion of the pair-correlation is zero in that case, as the particles do not interact with each other. Hence, no matter how large the Peclet number may be, for U = 0, there is no effect of motility on the pair-correlation function. This explains why the leading order correction for small velocities in eqn (20) is proportional to λU instead of just λ.
Numerical results for g − 1 are given in Fig. 2 for λU = 1. The spherical white area with radius unity is the excluded volume by particle 1 for particle 2, within the coordinate frame that moves along with particle 1, the center of which is chosen at the origin. As discussed above, the two particles approach each other when Z < 0, leading to an increase of the pair-correlation function, and move apart when Z > 0, leading to a decrease.
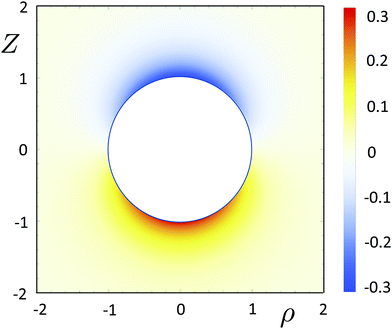 |
| | Fig. 2 Deviation of the pair-correlation function from unity for λU = 1 according to eqn (20) for small Peclet numbers. The coordinates Z = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ are the cylindrical coordinates around the direction of U, which are defined in Fig. 1. Θ are the cylindrical coordinates around the direction of U, which are defined in Fig. 1. | |
The angular average of the contact value of the pair-correlation function is zero. Beyond the linear approximation discussed here, however, this angular average will be non-zero. In particular, for the large Peclet numbers considered in the subsequent section, the angular averaged contact value varies like λ, and thus attains very large values.
5 The pair-correlation function for large Peclet numbers
For large velocities, the behavior of the pair-correlation is quite different in case the particles approach each other or move apart. We therefore define the so-called front-sector as the space where the two particles approach each other (for which cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ < 0), and the wake-sector as the space where the particles move apart (for which cos
Θ < 0), and the wake-sector as the space where the particles move apart (for which cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 0). Contrary to the behavior of the pair-correlation function for small velocities, where the increase in the front-sector is equal to the decrease in the wake sector, for large velocities, there is a much more pronounced asymmetry. When the two particles approach each other, there is a probability accumulation within a narrow region where the pair-correlation function attains large values, whereas when the two particles move apart, there is a probability shadow within an extended region where the pair-correlation function is essentially zero. The analysis in both sectors will be discussed separately in the following subsections.
Θ > 0). Contrary to the behavior of the pair-correlation function for small velocities, where the increase in the front-sector is equal to the decrease in the wake sector, for large velocities, there is a much more pronounced asymmetry. When the two particles approach each other, there is a probability accumulation within a narrow region where the pair-correlation function attains large values, whereas when the two particles move apart, there is a probability shadow within an extended region where the pair-correlation function is essentially zero. The analysis in both sectors will be discussed separately in the following subsections.
5.1 The front-sector: cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Θ < 0
Θ < 0
Multiplying eqn (13) by the small parameter 1/λ, it is obvious that this small parameter multiplies the highest order spatial Laplacian derivative. A perturbation expansion approach where the second-order Laplacian derivative would be simply neglected (as it is multiplied by the small parameter 1/λ) leads to a first-order differential equation. There are, however, two boundary conditions, which cannot be satisfied simultaneously by adjusting the single integration constant of the solution of that first-order differential equation. This implies that the second-order derivative must be very large near the contact, so that the Lapacian derivative cannot be neglected, even though it is multiplied by the small parameter 1/λ. This is the standard situation for singularly perturbed differential equations51,52 and leads, in the present case, to a narrow boundary layer near contact of the two particles where the pair-correlation function exhibits large spatial gradients, as schematically depicted in Fig. 3 in red. In this figure, the dark-grey sphere is overtaken by the light-grey sphere. Outside the boundary layer, the pair-correlation function is unity (which is the value that the pair-correlation function attains without interactions).
 |
| | Fig. 3 Schematic representation of the boundary-layer behaviour of the pair-correlation function in the front-sector, where two particles approach each other: the light-grey sphere overtakes the dark-grey sphere. As soon as the two spheres are side-to-side (where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ = 0), the light-grey sphere enters the wake-sector. Within the boundary layer (indicated in red), with a spatial extent ∼1/λ, the pair-correlation function attains large values, ∼λ. The pair-correlation function is unity outside the boundary layer (but within the front-sector). Θ = 0), the light-grey sphere enters the wake-sector. Within the boundary layer (indicated in red), with a spatial extent ∼1/λ, the pair-correlation function attains large values, ∼λ. The pair-correlation function is unity outside the boundary layer (but within the front-sector). | |
In a singular perturbation approach, the boundary layer is spatially stretched by introducing the so-called boundary-layer variable, S = λν(R − 1), where the exponent ν is determined in such a way that the second-order derivative with respect to S is of the same order as the remaining dominant terms in the differential equation, commonly referred to as “dominant balance”, which in the present case is the contribution from the motility-induced flux. The boundary-layer analysis of eqn (13) is given in Appendix B, leading to the following expression for the pair-correlation function, valid up to the leading order of the expansion:
| |  | (22) |
where the index “front” indicates that this expression is only valid in the front-sector, where cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ
Θ < 0. As before,
Θ is the angle between
R and
U =
û1 −
û2. Note that the contact value of the pair-correlation function, where
R = 1, is equal to
| |  | (23) |
For cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ
Θ = 0,
eqn (22) predicts that
g = 1, as it should be, since the particles do not interact in that configuration (the two particles are side-by-side, like the left upper light-grey sphere and the dark-grey sphere in
Fig. 3). Furthermore, the distance
R − 1 from the contact over which the pair-correlation function relaxes to unity is ∼1/
λU. This quantifies the behavior discussed above, which is schematically depicted in
Fig. 3.
As shown in Appendix B, the rotational contributions to eqn (13) can be neglected. The physical interpretation of this result is that, due to the small extent of the boundary layer, the time during which the particles interact (where the light-grey sphere rolls over the dark-grey sphere, as depicted in Fig. 3) is sufficiently short that the rotational diffusion is not effective. Note that g = 1 in case U = 0, as it should be, since in that case the two spheres move along with each other with the same velocity.
Numerical results are given in Fig. 4 for λU = 10 in the Z-versus-ρ plane as before, which shows the boundary-layer behavior of the pair-correlation function within the front-sector. The boundary-layer type of behaviour of the pair-correlation function in 3D at low concentrations is confirmed by simulations in ref. 53, where orientational averages show a very steep increase near contact. The probability accumulation in the front-sector in 2D has also been observed in simulations in ref. 28. Such a steep increase of the pair-correlation function and large contact value correspond to a sticky-sphere type of interaction for passive systems. This has been used in ref. 54 to compare the equation of state for active particles to the equation of state of a system of passive adhesive particles.
 |
| | Fig. 4 The pair-correlation function in the front-sector for λU = 10 according to eqn (22). As before, Z = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function takes large values, ∼λ, within a boundary layer of extent ∼1/λ. Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function takes large values, ∼λ, within a boundary layer of extent ∼1/λ. | |
5.2 The wake-sector: cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Θ > 0
Θ > 0
The result in eqn (22) diverges for large distances when λU![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 2, so that the above result does not describe the behavior of the pair-correlation function in the wake-sector where cos
Θ > 2, so that the above result does not describe the behavior of the pair-correlation function in the wake-sector where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 0. In the wake-sector, the behavior is very different from that in the front-sector. Once the particles enter the wake-sector (the light-grey spheres depicted in Fig. 5), there is a probability-depleted region indicated in blue in Fig. 5, which we will refer to as the probability shadow.
Θ > 0. In the wake-sector, the behavior is very different from that in the front-sector. Once the particles enter the wake-sector (the light-grey spheres depicted in Fig. 5), there is a probability-depleted region indicated in blue in Fig. 5, which we will refer to as the probability shadow.
 |
| | Fig. 5 Schematic representation of the probability shadow in the wake-sector, where the particles move away from each other. Within the blue region where ρ < 1, the pair-correlation function is essentially zero for inter-particle distances less than λ1/3, while for ρ > 1, it is unity. For large distances in the direction of U, and ρ < 1, the pair-correlation function relaxes to unity due to (rotational) diffusion into the probability shadow, as indicated by the wiggly lines for the light-grey particle on the right which overtakes the dark-grey sphere in the middle. | |
For infinite Peclet numbers, there is a cylindrical region of infinite extent in the direction of U where the pair-correlation function is zero.55 For finite Peclet numbers, there is an approximate cylindrically symmetric region around the direction of U, where the pair-correlation function is essentially zero for short distances, as time has been too short for the overtaking particle to move into the probability shadow. Therefore, the pair-correlation function attains an almost step-function-like behavior for short distances as a function of the cylindrical coordinate ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ at ρ = 1, as indicated by the solid line in Fig. 5 (see Fig. 1 for the definition of coordinates). For ρ < 1, the pair-correlation function is essentially zero, while for ρ > 1, its value is approximately unity. The pair-correlation function relaxes to unity at large distances in the direction of U due to translational and rotational diffusion into the probability shadow (as indicated by the thin solid lines for the light-grey sphere on the right in Fig. 5). In contrast to the large spatial derivatives in the direction perpendicular to U at ρ = 1, spatial derivatives in the direction of U are very small. Furthermore, the spatial derivatives along the direction of U (and for ρ < 1) decrease with the increasing swimming velocity, while the extent of the probability shadow increases with the increasing velocity. This behavior is to be contrasted to the front-sector, where the opposite occurs: here, the spatial derivatives in the direction of U are very large, and increase with the increasing swimming velocity, while the extent of the boundary layer decreases with the increasing velocity.
Θ at ρ = 1, as indicated by the solid line in Fig. 5 (see Fig. 1 for the definition of coordinates). For ρ < 1, the pair-correlation function is essentially zero, while for ρ > 1, its value is approximately unity. The pair-correlation function relaxes to unity at large distances in the direction of U due to translational and rotational diffusion into the probability shadow (as indicated by the thin solid lines for the light-grey sphere on the right in Fig. 5). In contrast to the large spatial derivatives in the direction perpendicular to U at ρ = 1, spatial derivatives in the direction of U are very small. Furthermore, the spatial derivatives along the direction of U (and for ρ < 1) decrease with the increasing swimming velocity, while the extent of the probability shadow increases with the increasing velocity. This behavior is to be contrasted to the front-sector, where the opposite occurs: here, the spatial derivatives in the direction of U are very large, and increase with the increasing swimming velocity, while the extent of the boundary layer decreases with the increasing velocity.
An approximate asymptotic solution of eqn (13) for large Peclet numbers within the wake-sector is constructed in Appendix B, the result of which is
| |  | (24) |
where
J0,1 are the Bessel functions of the first kind (of order 0 and 1). The index “wake” refers to its validity within the wake-sector. As shown in Appendix B by numerical integration, the contact value of the above expression for the pair-correlation function decays to zero faster than 1/
λ. Therefore, the contact value is zero,
to within leading order in 1/
λ, in contrast to the front-sector side where the contact value is very large. A constant contact value for the pair-correlation function, uniformly spread over the surface of the sphere, is found in
ref. 40 on the basis of a theoretical approach that does not explicitly account for orientational diffusion, as discussed in the introduction. According to the above Smoluchowski-type of approach, orientational diffusion is, however, essential for small Peclet numbers as well as for high Peclet numbers in the wake-sector.
The extent of the probability shadow can be calculated from eqn (24) as follows. In the Z-direction, we have cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ = 1, so that the Bessel function J0 in eqn (24) is equal to unity. The remaining integral can be calculated analytically as follows:56
Θ = 1, so that the Bessel function J0 in eqn (24) is equal to unity. The remaining integral can be calculated analytically as follows:56
| |  | (26) |
Note that the contact value for
Θ = 0 is exponentially small with the increasing
λ. Furthermore, this result shows that the extent
l of the probability shadow scales like
l ∼
λ1/3 for non-zero relative velocities,
U. As shown in Appendix B, this scaling is entirely due to rotational diffusion. Translational diffusion can be neglected in the wake-sector, contrary to the front-sector, where it is dominant. The scaling relation for the extent of the probability shadow can be understood as follows.
57 Let δ
θ denote a small angle over which the spheres depicted in
Fig. 5 rotate relative to each other in a direction where the overtaking light-grey sphere moves into the blue, probability-depleted region. The time δ
t it takes for such a small rotation is δ
t ∼ (δ
θ)
2/
Dr. Let
l be the extent of the probability shadow in the
Z-direction. Since the width of the probability shadow is ∼
a, we have δ
θ ∼
a/
l. Furthermore,
l ∼
v0δ
t, so that eliminating δ
θ and δ
t in favour of
l leads to (
l/
a)
3 ∼
v0/(
aDr) ∼
av0/
D0 =
λ. This confirms the scaling found in
eqn (24) and (26), and shows that the scaling is solely due to rotational diffusion.
Numerical results are given in Fig. 6 for λ = 5 and U = 2. This density plot quantifies the expected step-like function behavior for ρ = 1 in case the spheres are not too far apart, and the very slow convergence to unity in the direction along U within the probability shadow.
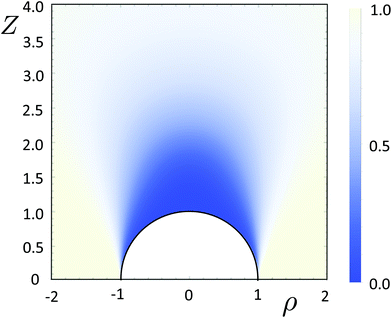 |
| | Fig. 6 The pair-correlation function in the wake-sector for λ = 5 and U = 2 according to eqn (24). As before, Z = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function is essentially a step-function as a function of ρ at ρ = 1 when the spheres are not too far apart, while it converges to unity in the direction along U within the probability shadow over large distances of order ∼λ1/3. Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function is essentially a step-function as a function of ρ at ρ = 1 when the spheres are not too far apart, while it converges to unity in the direction along U within the probability shadow over large distances of order ∼λ1/3. | |
In ref. 41, it is found that the depletion wake in 2D consists of two wings, where the two wings are surrounded by regions where the pair-correlation function is enhanced due to motility (see, for example, Fig. 1 in ref. 41). There, the pair-correlation function is plotted in a coordination frame that is fixed to the orientation, û1, of a single colloid and averaged with respect to the orientation, û2, of the second colloid. We have plotted the pair-correlation function in a coordination frame that is fixed to the relative velocity, ∼(û1 − û2). The latter allows us to make a distinction between the approaching swimmers and the swimmers moving away from each other, and thus distinguishes between what we referred to as the wake-sector and the front-sector. Averaging over the orientation, û2, mixes parts of the wake-sector and the front-sector, which probably explains the two-wing structure reported in ref. 41.
The 2D simulations in ref. 28 do not show a clear long-ranged probability shadow. These simulations have been performed at very high packing fractions, and thus indicate that higher-order inter-particle correlations affect the spatial extent of the probability shadow in the wake-sector.
6 Collective diffusion
With the expressions for the pair-correlation function derived in the previous sections, the equation of motion (eqn 4) can be evaluated in closed form. Since the pair-correlation function is evaluated to the leading order in concentration, that equation of motion is also valid up to leading order in concentration. In this section, we derive expressions for the Fickian collective diffusion coefficient and the motility-induced polarization due to concentration gradients for hard-sphere interactions.
Since the pair-correlation function is zero when the spheres overlap, we have:
| |  | (27) |
where, as before,
gc is the contact value of the pair-correlation function,
a is the radius of the particles, and
δ(·) is the delta distribution. Substitution into
eqn (4) gives
| |  | (28) |
Here,
R =
r −
r′ is the non-scaled distance between the two ABPs, and

is the integral with respect to
R ranging over a spherical surface with radius 2
a. For small spatial gradients in the orientation-dependent local density, such that the density varies linearly over distances of the order of the size of the particles, the leading order gradient expansion,
| | | ρ(r − R,û′,t) = ρ(r,û′,t) − R·∇ρ(r,û′,t), | (29) |
can be used in
eqn (28) to obtain
| |  | (30) |
where
| |  | (31) |
Since for large swimming velocities the contact value of the pair-correlation function is zero on the wake-sector side, the integrals in
eqn (31) range over the hemispherical surface corresponding to the front-sector side, as depicted in
Fig. 7. The large contact value on the front-sector side is given in
eqn (23), so that the integrations in
eqn (31) lead to
| |  | (32) |
where, as before,
U =
û −
û′ and
U = |
û −
û′|.
 |
| | Fig. 7 For large Peclet numbers, the integrations in eqn (31) range over the semi-spherical surface with radius 2a indicated in blue, corresponding to the front-sector side where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ < 0. Θ < 0. | |
The local fraction of the volume that is occupied by the cores of the particles with an orientation û, is by definition equal to
| |  | (33) |
Fick's diffusion equation is the equation of motion for the volume fraction irrespective of their orientation:
| |  | (34) |
where the so-called polarization,
| |  | (35) |
plays an important role. The polarization is proportional to the particle volume flux in the direction of the average polar alignment. This is the most important contribution to the motility-induced mass transport. We will therefore use an expansion of
φ(
r,
û,
t) (similar to what is discussed in, for example,
ref. 21,
28,
39,
58 and
59) with respect to the orthonormal polyadic products of
û up to first order (see Appendix C for the discussion of such expansions):
| |  | (36) |
The next higher-order term in the expansion is proportional to
which measures the degree of motility-induced nematic order. Since the mass transport for large Peclet numbers is severely affected by the motility-induced polar alignment and much less by nematic ordering, this higher-order contribution to
eqn (36) will not be considered.
For large swimming velocities, it is found from eqn (30) and (32), with some effort, that (see Appendix C for mathematical details)
| | 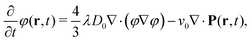 | (37) |
where only the dominant contributions for large Peclet numbers and leading order terms in spatial gradients are kept. As will be seen below,
P is of the order ∇
φ, so that
eqn (37) is valid up to second order in spatial gradients, just like the original Fick's equation for passive systems. Keeping only the leading terms in the swimming velocities for the large Peclet numbers under consideration, the equation of motion for the polarization,
P, is similarly found, noting that
λD0/
a =
v0 (again, mathematical details are given in Appendix C):
| |  | (38) |
where, as before, higher-order spatial gradients have been neglected. The solution of this equation is
| |  | (39) |
In case spatial gradients are sufficiently small, so that these evolve on time scales much larger than 1/
Dr, this expression reduces for
t ≫ 1/
Dr to
| |  | (40) |
This principle is commonly referred to as enslavement, where the non-conserved polarization,
P(
r,
t), is enslaved by the conserved concentration,
φ(
r,
t).
28,58,59 Physically, this amounts to a coarse graining to time scales where orientation is fully relaxed, while spatial gradients are sufficiently small to evolve on much larger time scales. It thus follows that,
| | 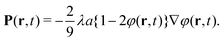 | (41) |
Terms like ∼∇
2P2 and ∼∇∇:
PP that contribute to the right-hand side of
eqn (37) (see Appendix C) are thus of fourth order in spatial gradients. Similarly, terms like ∼∇
2P,
P∇·
P, ∇·
PP, [∇
φ]·[∇
P],
etc. are neglected in
eqn (38), since these terms also contribute to higher-order gradients.
The condition for the steepness of the concentration gradients for which enslavement holds will be addressed below. Eqn (41) implies that there is a preferred orientation in the opposite direction to the concentration gradient. Thus, there is an enhanced motility-induced particle flux from high to low concentrations.
Substituting eqn (41) into the diffusion equation (eqn 37) finally leads to Fick's diffusion equation:
| | 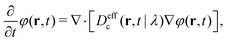 | (42) |
where the effective collective diffusion coefficient is equal to
| |  | (43) |
where terms proportional to orders of
λ less than two have been neglected. Mass transport at high Peclet numbers is thus dominated by motility due to the polar alignment along the concentration gradients.
The enslavement argument used above holds when the relaxation time of the density is much larger than the rotational relaxation time, 1/Dr. From the above result for the effective diffusion coefficient, it thus follows that enslavement requires that
| | | Λ−2D0λ2 ≪ Dr → Λ ≫ λa, | (44) |
where
Λ specifies the extent over which the concentration varies (which is the typical wavelength corresponding to the Fourier-mode decomposition of the volume fraction). This inequality is a condition for the validity of the above Fick's diffusion
eqn (42) and (43) for large
λ. Without motility, the wavelength
Λ should be much larger than the radius
a of the spheres. For Fick's equation to hold for active systems, the wavelength should be much larger than
λa. The condition
(eqn 44) physically means that the concentration should not change during the time needed for orientational relaxation, where an ABP migrates over a distance
λa.
Including all terms of second order in the spatial gradients originating from the asymptotic solution of the pair-correlation function in the equations of motion for density and polarization leads to (see Appendix C for the list of all these terms)
| |  | (45) |
Note that the collective diffusion coefficient at infinite dilution is equal to the self-diffusion coefficient for long times,
t ≫ 1/
Dr (see the discussion below,
eqn (7), in Section 2), just like for passive systems. An expression for the thermally averaged velocity,
v(
r,
t), of ABPs (including averaging with respect to the ABP orientations) can be found from the number conservation law ∂
φ/∂
t = −∇·[
vφ], in combination with
eqn (42) and (45):
| |  | (46) |
For large
λ, where the last term dominates, the velocity
v ∼ (1 − 2
φ)∇
φ thus decreases (in the opposite direction of the spatial gradients) with increasing concentration due to binary ABP interactions. For high concentrations, a similar form,
v ∼ (1 −
ζφ)∇
φ, is found in 2D simulations of disks, with
ζ = 0.9, essentially independent of
v0 and concentration.
35 Such a concentration-dependent velocity is introduced phenomenologically in, for example,
ref. 30–34, and can be semi-empirically obtained from the Smoluchowski equation (in 2D), where
ζ is related to an integral that involves the pair-correlation function, which remains unknown without specification of the pair-correlation function.
25–29 At high concentrations, the decrease of the average translational velocity with the increasing concentration is at least in part due to multi-body interactions: when several ABPs approach each other head-on, the sliding motion along one of the neighbouring ABPs is blocked by the presence of the other ABPs. When such head-on interactions occur in large clusters, the dynamics of single ABPs is kinetically arrested. Such a diminishing translational motion due to multi-particle interactions is not accounted for in the above expression for the velocity, since only binary collisions are considered. The expressions for the pair-correlation function derived in the present work may be used as a starting point to obtain the pair-correlation function for higher concentrations (for example, by means of an Ornstein–Zernike approach). This would establish a first-principles approach toward the dynamics and MIPS for ABPs with very short-ranged direct interactions.
For small Peclet numbers, it is found from the contact value in eqn (21) that the leading order contribution arising from motility varies like λ2. It may well be that the second-order contribution, g2, in the expansion of the pair-correlation function in eqn (18) contributes to the same order. We will therefore refrain here from the derivation of Fick's diffusion coefficient for small Peclet numbers. The diffusion equation as obtained from just the leading order term, g1, in eqn (18) is given at the end of Appendix C.
7 Summary and conclusions
Starting from the N-particle Smoluchowski equation, we derived analytic expressions for the low-density pair-correlation function for active Brownian particles (ABPs) in 3D for small and large swimming Peclet numbers, λ. The pair-interaction potential is assumed to be very short-ranged, consisting of an excluded-volume interaction and a possible sticky-like attractive interaction. In the analysis for large Peclet numbers, a distinction must be made between the front-sector, where two ABPs approach each other, and the wake-sector, where two ABPs move away from each other. The front-sector requires a singular perturbation analysis, leading to a boundary layer at ABP-contact with a spatial extent ∼1/λ, and contact values of the order λ. Due to the small times during which the two ABPs interact while sliding over each other, rotational diffusion does not affect the pair-correlation function in the front-sector. The behaviour of the pair-correlation function in the wake-sector is quite opposite as compared to the front-sector: there is now a large region of extent ∼λ1/3 where the pair-correlation function is essentially zero, and where rotational diffusion is solely responsible for the recovery of the pair-correlation function to unity at large distances. For passive colloids, such a pair-correlation function corresponds to a Janus particle with a very strong and short-ranged attraction at the front-sector side, and a strong but very long-ranged repulsion at the wake-side.
The same kind of behaviour of the pair-correlation function for large Peclet numbers is to be expected in 2D systems in case the orientations of the particles are also confined to the same 2D plane in which the particles move: a compact front-sector with large values of the pair-correlation function and an extended wake-sector with a near-zero pair-correlation function. In those 2D cases where rotation in all 3D directions is still possible, however, the physics may very well change, and the pair-correlation function may take a very different form.
The analytic expression for the pair-correlation function for large Peclet numbers is used to derive Fick's diffusion equation for the volume fraction of ABPs with excluded-volume interactions. We find that there is a preferred swimming direction from high to low concentrations, which dominates the relaxation of concentration inhomogeneities over translational diffusion. Motility is thus expected to suppress thermodynamically driven spinodal decomposition, where diffusion occurs from regions of low to high concentrations due to strong attractive inter-particle interactions.
The present low-density calculation of the pair-correlation function obviously accounts only for binary collisions. It remains a future challenge to construct the pair-correlation function for concentrated systems of ABPs based on the low-density expressions as derived in the present paper. One possibility to achieve this extension is through an Ornstein–Zernike type of approach, where the low-density pair-correlation function identifies the direct-correlation function. This approach towards the dynamics and MIPS of ABPs would supplement the existing theories with a firm microscopic basis without the need for semi-empirical considerations and assumptions necessary to account for inter-particle correlations. The calculation of the pair-correlation function presented here also neglects hydrodynamic interactions. Even without hydrodynamic interactions, the analysis of pair-correlations for active systems poses a highly non-trivial problem. A further future challenge is to include hydrodynamic interactions, to be able to make a distinction between, for example, pullers and pushers.
The analysis of demixing kinetics and dynamics based on Fickian-like diffusion equations requires an additional extension, where higher-order spatial gradient contributions are included. These contributions stabilize the system against the demixing of short-wavelength concentration variations, that is, they prevent the unphysical growth of concentration variations with steep spatial gradients. Not including such higher-order gradient contributions still allows us to identify the phase-stability region, but excludes the analysis of demixing kinetics.
Conflicts of interest
There are no conflicts to declare.
Appendix A: The pair-correlation function for small Peclet numbers
The set of equations (eqn 19) is most conveniently solved by expanding the pair-correlation in terms of spherical harmonics:| |  | (47) |
The Laplace operator is rewritten as follows:| |  | (48) |
where  is the rotation operator with respect to R (where ∇
is the rotation operator with respect to R (where ∇![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) is the gradient operator with respect to the Cartesian coordinates of the unit vector
is the gradient operator with respect to the Cartesian coordinates of the unit vector ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ). Using that,
). Using that,| |  | (49) |
and similarly for  and
and  , and using orthonormality of the spherical harmonics, it is found that,
, and using orthonormality of the spherical harmonics, it is found that,| |  | (50) |
where| |  | (51) |
The solution of eqn (50) that tends to zero at infinity is as follows:| |  | (52) |
where| |  | (53) |
is a modified Bessel function. The integration constants  must be determined such that the no-flux boundary condition is fulfilled. Using the addition theorem for spherical harmonics for the first-order Legendre polynomial (where Θ1 is the angle between
must be determined such that the no-flux boundary condition is fulfilled. Using the addition theorem for spherical harmonics for the first-order Legendre polynomial (where Θ1 is the angle between ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) and û1),
and û1),| |  | (54) |
and similarly for ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·û2, and using that
·û2, and using that  , it is readily found from the orthonormality of the spherical harmonics that the no-flux boundary condition is fulfilled when
, it is readily found from the orthonormality of the spherical harmonics that the no-flux boundary condition is fulfilled when| |  | (55) |
for m = −1,0,1, while all the remaining constants vanish, and  . Hence,
. Hence,| |  | (56) |
Thus, from eqn (53), it is finally found that| |  | (57) |
where| |  | (58) |
This then leads to eqn (20) in the main text.
Appendix B: The pair-correlation function for large Peclet numbers
Due to rotational and translational invariance, the pair-correlation function depends on four variables: the distance, R, between the particles; (the cosine of) the angles between R and û1,2, that is, x1 = ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·û1 and x2 =
·û1 and x2 = ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·û2; and (the cosine of) the angle between û1 and û2, that is, α = û1·û2. The differential equation (eqn (13)) in terms of these variables reads as follows:
·û2; and (the cosine of) the angle between û1 and û2, that is, α = û1·û2. The differential equation (eqn (13)) in terms of these variables reads as follows:| | | 0 = Trans + Flux + Rot, | (59) |
where the contribution “Trans” from translational diffusion is equal to| |  | (60) |
the contribution “Flux” resulting from motility is equal to| |  | (61) |
while the rotational contribution “Rot” is equal to| | 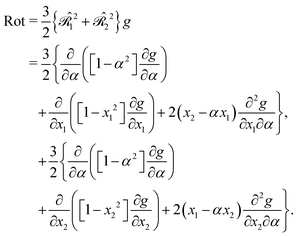 | (62) |
As will be shown below, the important related variables are as follows:| | x = x1 − x2 = ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·U = U ·U = U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, X = x1 + x2, Θ, X = x1 + x2, | (63) |
whereand Θ is the angle between R and U.
A little consideration shows that when x < 0, the two particles approach each other while for x > 0, they move apart. The region where x < 0 will be referred to as the front-sector, and where x > 0 as the wake-sector. The pair-correlation function behaves very differently in both regions, as addressed in the main text on the basis of physical arguments. The mathematical analysis in the front-sector and wake-sector will be discussed separately in the following subsections.
7.1 The front-sector: x < 0
As will be shown below, the rotational contribution in eqn (62) is of lower order in the small parameter 1/λ as compared to the translational and flux contributions. Transforming (x1,x2) to (x,X), and assuming that the pair-correlation function in this sector does not depend on X, the equation 0 = Trans + Flux, with “ Trans” and “ Flux” given in eqn (60) and (61), becomes| |  | (65) |
As will turn out, integration constants can be chosen such that the solution of this equation obeys both boundary conditions, which justifies the neglect of the X-dependence.
Multiplying the above differential equation by the small parameter 1/λ obviously shows that the highest-order derivative with respect to R is multiplied by this small parameter. This is the standard form of a singularly perturbed differential equation, the solution of which requires a boundary-layer analysis. Since the second-order derivative is needed to match two boundary conditions, this implies that the derivatives with respect to R are large near contact where R ≈ 1. Thus, there is a small region close to contact where spatial derivatives are very large, which is referred to as the boundary layer. The fact that the variables x and α do not exhibit boundary-layer behavior will be verified below. Introducing the boundary-layer variable
and insisting that the second-order derivative with respect to
S in
eqn (65) is of the same order in 1/
λ as the flux contribution implies that
By introducing the variable
S, the width 1/
λ ≪ 1 of the boundary layer in terms of the original variable
R is re-scaled to unity. This spatial stretching of the region close to contact renders the pair-correlation function a regular function of 1/
λ when expressed in terms of
S, and can therefore be expanded in a power series with respect to 1/
λ. Within the boundary layer, where
S =
λ(
R − 1) < 1,
eqn (65) thus reduces to
| |  | (68) |
As will turn out, the no-flux boundary condition can only be satisfied when the zeroth and the first-order contributions in 1/
λ arising from derivatives with respect to
S are kept. This is the reason why the first-order contribution ∼1/
λ in the above differential equation is kept. The first-order contribution arising from ∂
g/∂
x is not needed to satisfy the boundary conditions, which is therefore neglected. The solution of
eqn (68) is
| |  | (69) |
where
A and
B are the integration constants. The no-flux boundary condition in
eqn (13) in terms of the boundary variable
S is
| |  | (70) |
which leads to
| |  | (71) |
where the subscript “inner” is used to indicate that this is the solution within the boundary layer.
The outer solution, gouter, where S > 1, is simply a constant, which is unity since for infinite distances between the two particles, the pair-correlation function tends to unity:
Matching the inner and outer solutions implies that
A = 1 in
eqn (71) for the inner solution. It is thus finally found that, in terms of the original coordinates
x and
R,
| |  | (73) |
where the index “front” is used to indicate that this solution is only valid within the front-sector. Recall that
x < 0 within the front-sector.
Re-substituting this expression into eqn (59)–(62) shows that the above expression satisfies the differential equation to the leading order in 1/λ, and by construction satisfies both boundary conditions. In doing so, it is important to notice that inside the boundary layer, (R − 1) ∼ 1/λ, while outside the boundary layer, g = 1, where the exponential in eqn (73) is essentially zero. In particular, this justifies the neglect of the derivatives with respect to X and α in eqn (65), and thus shows that the rotational contribution can be neglected within the front-sector. The interpretation of the latter is that, for the large relative velocities under consideration, the time that the particles spent within the narrow boundary layer is sufficiently small that rotation does not occur. Furthermore, for x = 0 (and in particular, for U = 0), the pair-correlation function is identically equal to unity, as it should be.
7.2 The wake-sector: x > 0
The asymptotic solution in eqn (73) diverges for large distances when x > 0. This shows that the behavior in the wake-sector is quite different compared to that in the front-sector. On the basis of the discussion in the main text, spatial derivatives in the direction along the relative velocity ∼U of the two particles are expected to be very small for large λU. We therefore introduce the scaled variable (not to be confused with the S-coordinate introduced in the previous subsection),| |  | (74) |
where the function f(α) will be specified below. As a second variable, the distance ρ between the two particles perpendicular to U,| |  | (75) |
is introduced. The reason for the introduction of this cylindrical variable is, as discussed in the main text, that a step-function-like behavior at ρ = 1 is expected for small separations between the particles, since diffusion has not yet been effective for the large relative velocities under consideration. As will be shown below, an approximate solution for the boundary-value problem within the wake-sector can be found, assuming that the pair-correlation function depends on R, x1, x2, and α only through the combinations of S and ρ.
It is found by direct differentiation with respect to the Cartesian coordinates of R, or from eqn (60), that
| |  | (76) |
where terms of the order 1/
λ corresponding to the differentiations with respect to
S have been neglected. The differentiation with respect to
S in the contribution to the flux in
eqn (61) is multiplied with
λ, and should therefore be kept. It is readily found that
| |  | (77) |
Contrary to the front-sector, the rotational contribution cannot be neglected in the wake-sector. With some effort, the rotational contribution is found to be given by (the most efficient way to compute the differentiations is to first introduce the variable
ρ2, instead of just
ρ, and, after performing all differentiations, express the differentiations with respect to
ρ2 in terms of
ρ)
| |  | (78) |
where, as before,
X =
x1 +
x2. Here, the terms of the order
R/
λ resulting from differentiations with respect to
S have been neglected. As will turn out, the pair-correlation function relaxes to unity for
R ∼
λ1/3, so that the restriction of the analysis given below to distances where
R/
λ ≪ 1 is not severe. In addition, it will turn out that the solution that we find converges to unity for large distances, as it should be, which thus correctly interpolates between
R ≪
λ and
R → ∞. The variables
R and
x can be expressed in terms of
S,
ρ, and
U, using that
| |  | (79) |
leading to (here we leave
X as it occurred before)
| | 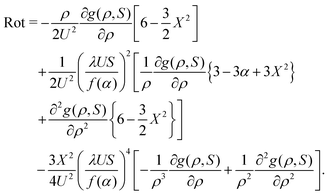 | (80) |
Adding all contributions leads to a differential equation that we were unable to solve analytically. Instead, a solution will first be obtained in the region where (
λUS/
f) =
Rx/
U =
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ
Θ ≫ 1 (note that this further limits the region where the analysis is valid, on top of the earlier condition
R ≪
λ). This is the region where the most significant relaxation of the pair-correlation function occurs. At first sight, only the last term in
eqn (80) for the rotational contribution survives in this region. However, a little thought shows that
| |  | (81) |
where
φ is the angle between
Ũ =
û1 +
û2 (the magnitude of which is

) and the projection of
R onto the plane perpendicular to
U. For
λUS/
f ≫ 1, it follows that the last term in the rotational contribution in
eqn (80) is of the order (
λUS/
f)
2 instead of the order (
λUS/
λ)
4. Expanding
eqn (80) with respect to (
f/
λUS) ≪ 1 thus leads to
| |  | (82) |
Since
V varies between 0 and 2 + 2
α (depending on the angle
φ), the combinations
U2 +
V2 and 4 −
V2 both vary between 2 − 2
α and 4. For
α = 1, we have
U = 0, for which the pair-correlation function must be trivially equal to 1 (since the relative velocity is 0 in that case). The largest relative velocity is attained for
α = −1, in which case
U2 +
V2 = 4 −
V2 = 4. We thus restrict the validity of our analysis further to values of
α which are sufficiently negative, such that
U2 +
V2 and 4 −
V2 are not very different. For such values of
α, one can average
V2 with respect to the angle
φ, for which both
U2 +
V2 and 4 −
V2 take the same value equal to 3 −
α, which also equals the average of the extreme values that both combinations take. To quantify this further, note that
| |  | (83) |
“Sufficiently negative
α” thus refers to the values of
α where 3 −
α is at least an order of magnitude larger than 1 +
α. For
α < −7/11, for example, 3 −
α is more than ten times larger than (1 +
α)(1 − 2cos
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ), for which the neglect of the last term on the right-hand side in
eqn (83) against the first term is justified. The further analysis is thus restricted to angles between
û1 and
û2 larger than about 130°. Note that 3 −
α is never smaller than (1 +
α)(1 − 2cos
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ), for any
α, so that the second term on the right-hand side in
eqn (83) is never dominant over the first term.
Since the contribution “Trans” in eqn (76) is of the zeroth order in λUS/f(α), we have Flux + Rot = 0 for the large distances under consideration. It thus follows from eqn (77), (82) and (83), with the neglect of the last term in eqn (83), that
| |  | (84) |
Choosing the function f(α) as
| |  | (85) |
reduces
eqn (84) to
| |  | (86) |
As will be seen below, this choice of
f(
α) leads to a solution of the differential equation that satisfies the required boundary conditions. Separation of variables, writing
g(
ρ,
S) =
F(
S)
H(
ρ), gives
| |  | (87) |
where
C2 is a constant. The solutions of these equations are as follows:
| |  | (88) |
where
J0 is the zeroth order Bessel function of the first kind. Hence,
| |  | (89) |
where unity is added in order to satisfy the boundary condition at infinity (the integral tends to zero for large
S and
ρ).
The final expression for the pair-correlation function has been subjected to the conditions that R/λ ≪ 1, Z = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ ≫ 1, and α < −7/11. The above expression for the pair-correlation function satisfies the boundary condition g → 1 for R → ∞, and therefore correctly interpolates between distances where R/λ is small and where R → ∞. Furthermore, as will be seen below, the function A(C) can be chosen such that g = 1 for Z = 0, as it should be. Hence, the above expression for the pair-correlation function also correctly interpolates between large values of Z and Z = 0. Finally, for U = 0 (for which α = +1 and S → ∞), g = 1, as it should be, so that there is a correct interpolation with respect to the values of α not smaller than −7/11 as well. The interpolation arguments are very similar to the matching procedure of the inner and outer solutions in the boundary-layer analysis of the front-sector as discussed in the previous subsection. The outer region in the wake-sector corresponds to the region where the conditions R/λ ≪ 1, R
Θ ≫ 1, and α < −7/11. The above expression for the pair-correlation function satisfies the boundary condition g → 1 for R → ∞, and therefore correctly interpolates between distances where R/λ is small and where R → ∞. Furthermore, as will be seen below, the function A(C) can be chosen such that g = 1 for Z = 0, as it should be. Hence, the above expression for the pair-correlation function also correctly interpolates between large values of Z and Z = 0. Finally, for U = 0 (for which α = +1 and S → ∞), g = 1, as it should be, so that there is a correct interpolation with respect to the values of α not smaller than −7/11 as well. The interpolation arguments are very similar to the matching procedure of the inner and outer solutions in the boundary-layer analysis of the front-sector as discussed in the previous subsection. The outer region in the wake-sector corresponds to the region where the conditions R/λ ≪ 1, R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ ≫ 1, and α < −7/11 are not satisfied.
Θ ≫ 1, and α < −7/11 are not satisfied.
The function A(C) is first chosen such that the expected step-function-like behavior at ρ = 1 for S ≪ 1 is reproduced. This can be achieved using the following integral identity56:
| | 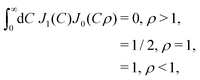 | (90) |
where
J1 is the first-order Bessel function of the first kind. This identity implies that the step-function-like behavior is obtained for
A(
C) =
J1(
C), so that
| |  | (91) |
As a last step, the no-flux boundary condition
(eqn 13) should be verified, which, in terms of the variables
R and
x, reads as follows:
| |  | (92) |
First consider the contact value,
gc =
g(
x,
R = 1,
U), of the pair-correlation function, which is equal to
| |  | (93) |
where, as before,
Θ is the angle between
R and
U, and where
| |  | (94) |
As will turn out, both terms in
eqn (92) approach zero with decreasing values of
w,
i.e., increasing values of
λ.
The combination (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ/w)gc(cos
Θ/w)gc(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ,w) = [8U3/(4 + U2)]λxgc is plotted in Fig. 8a as a function of w ∼ 1/λ for various values of cos
Θ,w) = [8U3/(4 + U2)]λxgc is plotted in Fig. 8a as a function of w ∼ 1/λ for various values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, as indicated in the plots. As can be seen, λxgc tends to zero for small w (corresponding to large λ). The particular value of w for which λxgc tends to zero, however, decreases with decreasing values of cos
Θ, as indicated in the plots. As can be seen, λxgc tends to zero for small w (corresponding to large λ). The particular value of w for which λxgc tends to zero, however, decreases with decreasing values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, and goes through a maximum. The point of contact where cos
Θ, and goes through a maximum. The point of contact where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ is zero, and therefore
Θ is zero, and therefore  , corresponds to a relative position for which R⊥U, that is, where the two particles just move from the front-sector to the wake-sector. For these positions at contact, diffusion becomes almost immediately effective, leading to a deviation from the step-function at ρ = 1. This is the physical origin of the relative large velocities required for which the contact value becomes zero for small values of cos
, corresponds to a relative position for which R⊥U, that is, where the two particles just move from the front-sector to the wake-sector. For these positions at contact, diffusion becomes almost immediately effective, leading to a deviation from the step-function at ρ = 1. This is the physical origin of the relative large velocities required for which the contact value becomes zero for small values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ. Note that these numerical results imply that the contact value of the pair-correlation function tends to zero as λ−γ, with γ > 1. Within the leading order expansion with respect to 1/λ considered here, the contact value is therefore zero.
Θ. Note that these numerical results imply that the contact value of the pair-correlation function tends to zero as λ−γ, with γ > 1. Within the leading order expansion with respect to 1/λ considered here, the contact value is therefore zero.
 |
| | Fig. 8 (a) The combination (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ/w)gc ∼ λxgc (where Θ is the angle between R and U, w ∼ 1/λ given in eqn (94), and gc is the contact value of the pair-correlation function) as a function of w, for various values of cos Θ/w)gc ∼ λxgc (where Θ is the angle between R and U, w ∼ 1/λ given in eqn (94), and gc is the contact value of the pair-correlation function) as a function of w, for various values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, as indicated in the figure. (b and c) The radial derivative of the pair-correlation function at contact as a function of w for two different ranges of the derivative. Θ, as indicated in the figure. (b and c) The radial derivative of the pair-correlation function at contact as a function of w for two different ranges of the derivative. | |
The spatial derivative in eqn (92) is plotted in Fig. 8b and c (with different scales of the vertical axes), again as a function of w for various values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ. The spatial derivatives are seen to tend to zero for large values of λ. For the same reason as for the contact value of the pair-correlation function, the spatial derivative for small values of cos
Θ. The spatial derivatives are seen to tend to zero for large values of λ. For the same reason as for the contact value of the pair-correlation function, the spatial derivative for small values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ requires larger values of λ to converge to zero. Again, this is due to the step-function-like behavior at the point where
Θ requires larger values of λ to converge to zero. Again, this is due to the step-function-like behavior at the point where  and R⊥U.
and R⊥U.
Both terms in the no-flux boundary condition (eqn 92) thus tend to zero for large λ.
In terms of the original (dimensionless) coordinates, eqn (91) finally leads to the expression (eqn 24) as given in the main text.
Appendix C: Mathematical details concerning collective diffusion
First consider the derivation of Fick's diffusion equation for large Peclet numbers. Substituting eqn (32) into the equation of motion (eqn 30) gives| |  | (95) |
where the orientation-dependent volume fraction, φ(r,û,t), has been introduced in Section 6.
Next, φ(r,û,t) is expanded in terms of orthonormal polyadic products of û (which is equivalent to an expansion with respect to spherical harmonics):
| | | φ(r,û,t) = F0(r,t)Q0 + F1(r,t)·Q1(û) + F2(r,t):Q2(û) + ⋯. | (96) |
The first few orthonormal polyadic products read as follows:
For
n ≥ 2, the orthonormal products are zero when contracted with respect to any two of its indices, so that
Fn≥2 is to zero when contracted with respect to any two of its indices without loss of generality. The poyadic products are symmetric upon interchanging any two of its indices, and therefore
Fn≥2 is similarly symmetric. These polyadic products are orthonormal in the sense that (⊙ stands for the contraction with respect to all adjacent indices)
| |  | (97) |
where
0 is the matrix with zero entries. The term
Q1(
û) ∼
û in
eqn (96) will contribute significantly to Fick's diffusion equation in case there is a preferred polar orientation induced by a concentration gradient, especially for large velocities. The last term in
eqn (96) merely characterizes the degree of nematic ordering, which contributes much less: for perfect nematic order, for example, the two particles move along with each other, so that there is no effect of activity on the pair-correlation function. From the above orthonormality relations, it is readily found that
eqn (96) reduces to
| |  | (98) |
where
| |  | (99) |
which reproduces
eqn (36) in the main text.
In order to evaluate the integrals in eqn (95), the following integral identities must be used:
| |  | (100) |
Together with the expansion
(eqn 98), these identities lead to the following results relating to each of the contributions in
eqn (95):
| |  | (101) |
Substituting these results into
eqn (95) and integrating with respect to
û leads, for each of the separate terms contributing to the equation of motion for
φ(
r,
t), to (here it is understood, for brevity, that in the right-hand sides,
φ ≡
φ(
r,
t) and
P ≡
P(
r,
t))
| |  | (102) |
Hence, from
| |  | (103) |
keeping only the leading order terms for large swimming velocities leads to
eqn (37).
The equation of motion for P is obtained by multiplying both sides of eqn (95) with û and then integrate with respect to û. The separate terms that contribute to the equation of motion for P are similarly found to be equal to
| |  | (104) |
Furthermore, using
| |  | (105) |
for
n = 1 for the evaluation of the second term in
eqn (95), including the third contribution, and adding all these integrals (similar to
eqn (103)), keeping only the leading contributions for large
λ, leads to the equation of motion
(eqn 38) for
P.
The derivation of the diffusion equation for small Peclet numbers requires relatively little effort, due to the much simpler expressions:
| |  | (106) |
as obtained from the contact value of the pair-correlation function in
eqn (21). From these expressions, the equation of motion,
| |  | (107) |
is obtained (without having to resort to the expansion in
eqn (98)). It is similarly found that (with

)
| |  | (108) |
Keeping only the leading order terms in spatial gradients, noting that
P is at least first order in such gradients, similar to what has been done for the large Peclet numbers above, this equation of motion reduces to
| |  | (109) |
As before,
P is enslaved by
φ, and hence,
| |  | (110) |
Substituting this result into
eqn (107) leads to Fick's diffusion
eqn (42), where
| |  | (111) |
The above expression reduces for
λ = 0 to the well-known diffusion coefficient for passive systems, where hydrodynamic interactions change the prefactor +8 in
eqn (111) to +1.45. Contributions from hydrodynamic interactions are therefore important for passive systems. The contributions to Fick's diffusion coefficient due to hydrodynamic interactions originating from activity might be less important, as these interactions are short-ranged.
Acknowledgements
The authors acknowledge the various very helpful discussions with Prof. Vincent Démery. In particular, he provided them with the ideas concerning the scaling relation discussed in Section 5.2.
Notes and references
- H. Stark, Phys. J., 2007, 6, 31 Search PubMed.
- W. F. Paxton, S. Sundararajan, T. E. Mallouk and A. Sen, Angew. Chem., Int. Ed., 2006, 45, 5420 CrossRef CAS PubMed.
- E. Lauga, Soft Matter, 2011, 7, 3060 RSC.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- B. Bet, G. Boosten, M. Dijkstra and R. van Roij, J. Chem. Phys., 2017, 146, 084904 CrossRef PubMed.
-
W. C. K. Poon, From clarkia to escherichia and janus: The physics of natural and synthetic active colloids, in Proceedings of the International School of Physics Enrico Fermi Course CLXXXIV Physics of Complex Colloids, ed. C. Bechinger, F. Sciortino and P. Ziherl, IOS Press, 2013, p. 317 Search PubMed.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
-
J.-P. Hansen and I. R. McDonald, Theory of simple liquids, Academic Press, London, 1986 Search PubMed.
-
J. K. G. Dhont, in An introduction to dynamics of colloids Studies in Interface Science, ed. D. Möbius and R. Miller, Elsevier, Amsterdam, 1996 Search PubMed.
- J. Clopes, G. Gompper and R. G. Winkler, Soft Matter, 2020, 16, 10676 RSC.
- T. Ishikawa, J. R. Soc., Interface, 2009, 6, 815 CrossRef PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- J. J. Molina, Y. Nakayamab and R. Yamamoto, Soft Matter, 2013, 9, 4923 RSC.
- A. W. Zantop and H. Stark, Soft Matter, 2020, 16, 6400 RSC.
- T. J. Pedley, IMA J. Appl. Math., 2016, 81, 488 CrossRef.
-
B. Delmotte, E. Climent and F. Plouraboué, in Franck hydrodynamic interactions among large populations of swimming micro-organisms, Computer Methods in Biomechanics and Biomedical Engineering, 2013, vol. 16 (supp. 1), pp. 6–8, ISSN: 1025-5842 Search PubMed.
- A. Furukawa, D. Marenduzzo and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022303 CrossRef PubMed.
- J. Stenhammar, C. Nardini, R. W. Nash, D. Marenduzzo and A. Morozov, Phys. Rev. Lett., 2017, 119, 028005 CrossRef PubMed.
- J. Rodenburg, M. Dijkstra and R. van Roij, Soft Matter, 2017, 13, 8957 RSC.
- C. M. Kjeldbjerg and J. F. Brady, Soft Matter, 2021, 17, 523 RSC.
- M. Enculescu and H. Stark, Phys. Rev. Lett., 2011, 107, 058301 CrossRef PubMed.
- A. M. Menzel, A. Saha, C. Hoell and H. Löwen, J. Chem. Phys., 2016, 144, 024115 CrossRef PubMed.
- H. H. Wensink, H. Löwen, M. Marechal, A. Härtel, R. Wittkowski, U. Zimmermann, A. Kaiser and A. M. Menzel, Eur. Phys. J.: Spec. Top., 2013, 222, 3023 Search PubMed.
- T. Speck, J. Bialké, A. M. Menzel and H. Löwen, Phys. Rev. Lett., 2014, 112, 218304 CrossRef.
- T. Speck, A. M. Menzel, J. Bialké and H. Löwen, J. Chem. Phys., 2015, 142, 224109 CrossRef PubMed.
- T. Speck, Soft Matter, 2020, 16, 2652 RSC.
- J. Bialké, H. Löwen and T. Speck, Eur. Phys. Lett., 2013, 103, 30008 CrossRef.
- R. van Damme, J. Rodenburg, R. van Roij and M. Dijkstra, J. Chem. Phys., 2019, 150, 164501 CrossRef PubMed.
- S. Hermann, P. Krinninger, D. de Las Heras and M. Schmidt, Phys. Rev. E, 2019, 100, 052604 CrossRef CAS PubMed.
- S. Hermann, D. de Las Heras and M. Schmidt, Phys. Rev. Lett., 2019, 123, 268002 CrossRef CAS PubMed.
- M. C. Marchetti, Y. Fily, S. Henkes, A. Patch and D. Yllanes, Curr. Opin. Colloid Interface Sci., 2016, 21, 34 CrossRef CAS.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef PubMed.
- Y. Fily, S. Henkes and M. C. Marchetti, Soft Matter, 2014, 10, 2132 RSC.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- J. Bickmann and R. Wittkowski, J. Phys.: Condens. Matter, 2020, 32, 214001 CrossRef CAS PubMed.
-
J. Bickmann, S. Bröker, J. Jeggle and R. Wittkowski, 2020, arXiv:2010.05262v1.
- J. Jeggle, J. Stenhammar and R. Wittkowski, J. Chem. Phys., 2020, 152, 194903 CrossRef CAS PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- U. Marini Bettolo Marconi and C. Maggi, Soft Matter, 2015, 11, 8768 RSC.
- A. Poncet, O. Bénichou, V. Deméry and D. Nishiguchi, Phys. Rev. E, 2021, 103, 012605 CrossRef CAS PubMed.
- A. Poncet, O. Bénichou, V. Démery and G. Oshanin, Phys. Rev. Lett., 2017, 118, 118002 CrossRef PubMed.
- G. Gompper,
et al.
, J. Phys.: Condens. Matter, 2020, 32, 193001 CrossRef CAS PubMed.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181 CrossRef.
- H. Löwen, J. Chem. Phys., 2020, 152, 040901 CrossRef PubMed.
- B. ten Hagen, S. van Teeffelen and H. Löwen, J. Phys.: Condens. Matter, 2011, 23, 194119 CrossRef CAS PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- M. T. Downton and H. Stark, J. Phys.: Condens. Matter, 2009, 21, 204101 CrossRef PubMed.
- J. K. G. Dhont, J. Chem. Phys., 1996, 105, 5112 CrossRef CAS.
-
A. H. Nayfeh, Intoduction to Perturbation Techniques, Wiley & Sons, New York, 1981 Search PubMed.
-
W. Eckhaus, Asymptotic Analysis of Singular Perturbations, Studies in Mathematics and its Applications, North-Holland, Amsterdam, 1979 Search PubMed.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56 CrossRef.
- F. Ginot, I. Theurkauff, D. Levis, C. Ybert, L. Bocquet, L. Berthier and C. Cottin-Bizonne, Phys. Rev. X, 2015, 5, 218103 Search PubMed.
- T. Arnoulx de Pirey, G. Lozano and F. van Wijland, Phys. Rev. Lett., 2019, 123, 260602 CrossRef CAS PubMed.
-
I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, Academic Press, London, 2007, 4th edn Search PubMed.
- Personal communication with Prof. Vincent Démery.
- M. E. Cates and J. Tailleur, Eur. Phys. Lett., 2013, 101, 20010 CrossRef CAS.
- A. Baskaran and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 011920 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
G. W.
Park
*ab,
G. W.
Park
 a and
W. J.
Briels
*ac
a and
W. J.
Briels
*ac



 range over the surface of a unit sphere, that is, over all orientations of ûj. The orientation-dependent local density is the number concentration of ABPs at a position r with an orientation û. The equation of motion for P1 is obtained by the integration of the N-particle Smoluchowski equation with respect to all position coordinates and orientations, with the exception of a single position and orientation. This leads to the following equation:
range over the surface of a unit sphere, that is, over all orientations of ûj. The orientation-dependent local density is the number concentration of ABPs at a position r with an orientation û. The equation of motion for P1 is obtained by the integration of the N-particle Smoluchowski equation with respect to all position coordinates and orientations, with the exception of a single position and orientation. This leads to the following equation:



 , and
, and  are understood to act on the distance R = r1 − r2 between two ABPs, and the orientations û1 and û2 of the two ABPs, respectively. Note that the pair-correlation function is a function of the relative distance r1 − r2 due to the approximate homogeneity on length scales larger than RV, and is independent of time due to the fast relaxation of correlations over short distances, as discussed above.
are understood to act on the distance R = r1 − r2 between two ABPs, and the orientations û1 and û2 of the two ABPs, respectively. Note that the pair-correlation function is a function of the relative distance r1 − r2 due to the approximate homogeneity on length scales larger than RV, and is independent of time due to the fast relaxation of correlations over short distances, as discussed above.


![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) = R/R is the unit vector normal to the spherical surface with radius 2a. This boundary condition physically means that the cores of two particles cannot interpenetrate.
= R/R is the unit vector normal to the spherical surface with radius 2a. This boundary condition physically means that the cores of two particles cannot interpenetrate.

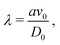

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R
Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, where Θ is the angle between R and U (as depicted in Fig. 1), that is,
Θ, where Θ is the angle between R and U (as depicted in Fig. 1), that is,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ =
Θ = ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·Û,
·Û,![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) and Û are the unit vectors in the directions of R and U, respectively. In addition, the asymptotic expressions for the pair-correlation function depend on the magnitude of U, which is equal to
and Û are the unit vectors in the directions of R and U, respectively. In addition, the asymptotic expressions for the pair-correlation function depend on the magnitude of U, which is equal to
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·(û1 + û2). Due to the approximate independence of the asymptotic solutions for small and large Peclet numbers on this variable, the pair-correlation function might be a weak function of this variable for intermediate Peclet numbers as well.
·(û1 + û2). Due to the approximate independence of the asymptotic solutions for small and large Peclet numbers on this variable, the pair-correlation function might be a weak function of this variable for intermediate Peclet numbers as well.
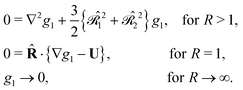
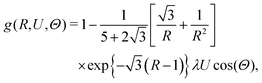
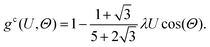
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ < 0, and move away from each other when cos
Θ < 0, and move away from each other when cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 0. Eqn (20) thus shows that the pair-correlation function is larger than unity when the particles move toward each other, and is equally less than unity in case they move away from each other.
Θ > 0. Eqn (20) thus shows that the pair-correlation function is larger than unity when the particles move toward each other, and is equally less than unity in case they move away from each other.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R
Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ are the cylindrical coordinates around the direction of U, which are defined in Fig. 1.
Θ are the cylindrical coordinates around the direction of U, which are defined in Fig. 1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ < 0), and the wake-sector as the space where the particles move apart (for which cos
Θ < 0), and the wake-sector as the space where the particles move apart (for which cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 0). Contrary to the behavior of the pair-correlation function for small velocities, where the increase in the front-sector is equal to the decrease in the wake sector, for large velocities, there is a much more pronounced asymmetry. When the two particles approach each other, there is a probability accumulation within a narrow region where the pair-correlation function attains large values, whereas when the two particles move apart, there is a probability shadow within an extended region where the pair-correlation function is essentially zero. The analysis in both sectors will be discussed separately in the following subsections.
Θ > 0). Contrary to the behavior of the pair-correlation function for small velocities, where the increase in the front-sector is equal to the decrease in the wake sector, for large velocities, there is a much more pronounced asymmetry. When the two particles approach each other, there is a probability accumulation within a narrow region where the pair-correlation function attains large values, whereas when the two particles move apart, there is a probability shadow within an extended region where the pair-correlation function is essentially zero. The analysis in both sectors will be discussed separately in the following subsections.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Θ < 0
Θ < 0
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ < 0. As before, Θ is the angle between R and U = û1 − û2. Note that the contact value of the pair-correlation function, where R = 1, is equal to
Θ < 0. As before, Θ is the angle between R and U = û1 − û2. Note that the contact value of the pair-correlation function, where R = 1, is equal to
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ = 0, eqn (22) predicts that g = 1, as it should be, since the particles do not interact in that configuration (the two particles are side-by-side, like the left upper light-grey sphere and the dark-grey sphere in Fig. 3). Furthermore, the distance R − 1 from the contact over which the pair-correlation function relaxes to unity is ∼1/λU. This quantifies the behavior discussed above, which is schematically depicted in Fig. 3.
Θ = 0, eqn (22) predicts that g = 1, as it should be, since the particles do not interact in that configuration (the two particles are side-by-side, like the left upper light-grey sphere and the dark-grey sphere in Fig. 3). Furthermore, the distance R − 1 from the contact over which the pair-correlation function relaxes to unity is ∼1/λU. This quantifies the behavior discussed above, which is schematically depicted in Fig. 3.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R
Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function takes large values, ∼λ, within a boundary layer of extent ∼1/λ.
Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function takes large values, ∼λ, within a boundary layer of extent ∼1/λ.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Θ > 0
Θ > 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 2, so that the above result does not describe the behavior of the pair-correlation function in the wake-sector where cos
Θ > 2, so that the above result does not describe the behavior of the pair-correlation function in the wake-sector where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ > 0. In the wake-sector, the behavior is very different from that in the front-sector. Once the particles enter the wake-sector (the light-grey spheres depicted in Fig. 5), there is a probability-depleted region indicated in blue in Fig. 5, which we will refer to as the probability shadow.
Θ > 0. In the wake-sector, the behavior is very different from that in the front-sector. Once the particles enter the wake-sector (the light-grey spheres depicted in Fig. 5), there is a probability-depleted region indicated in blue in Fig. 5, which we will refer to as the probability shadow.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ at ρ = 1, as indicated by the solid line in Fig. 5 (see Fig. 1 for the definition of coordinates). For ρ < 1, the pair-correlation function is essentially zero, while for ρ > 1, its value is approximately unity. The pair-correlation function relaxes to unity at large distances in the direction of U due to translational and rotational diffusion into the probability shadow (as indicated by the thin solid lines for the light-grey sphere on the right in Fig. 5). In contrast to the large spatial derivatives in the direction perpendicular to U at ρ = 1, spatial derivatives in the direction of U are very small. Furthermore, the spatial derivatives along the direction of U (and for ρ < 1) decrease with the increasing swimming velocity, while the extent of the probability shadow increases with the increasing velocity. This behavior is to be contrasted to the front-sector, where the opposite occurs: here, the spatial derivatives in the direction of U are very large, and increase with the increasing swimming velocity, while the extent of the boundary layer decreases with the increasing velocity.
Θ at ρ = 1, as indicated by the solid line in Fig. 5 (see Fig. 1 for the definition of coordinates). For ρ < 1, the pair-correlation function is essentially zero, while for ρ > 1, its value is approximately unity. The pair-correlation function relaxes to unity at large distances in the direction of U due to translational and rotational diffusion into the probability shadow (as indicated by the thin solid lines for the light-grey sphere on the right in Fig. 5). In contrast to the large spatial derivatives in the direction perpendicular to U at ρ = 1, spatial derivatives in the direction of U are very small. Furthermore, the spatial derivatives along the direction of U (and for ρ < 1) decrease with the increasing swimming velocity, while the extent of the probability shadow increases with the increasing velocity. This behavior is to be contrasted to the front-sector, where the opposite occurs: here, the spatial derivatives in the direction of U are very large, and increase with the increasing swimming velocity, while the extent of the boundary layer decreases with the increasing velocity.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ = 1, so that the Bessel function J0 in eqn (24) is equal to unity. The remaining integral can be calculated analytically as follows:56
Θ = 1, so that the Bessel function J0 in eqn (24) is equal to unity. The remaining integral can be calculated analytically as follows:56

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and ρ = R
Θ and ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function is essentially a step-function as a function of ρ at ρ = 1 when the spheres are not too far apart, while it converges to unity in the direction along U within the probability shadow over large distances of order ∼λ1/3.
Θ are the cylindrical coordinates relative to the direction of U (see Fig. 1). The pair-correlation function is essentially a step-function as a function of ρ at ρ = 1 when the spheres are not too far apart, while it converges to unity in the direction along U within the probability shadow over large distances of order ∼λ1/3.

 is the integral with respect to R ranging over a spherical surface with radius 2a. For small spatial gradients in the orientation-dependent local density, such that the density varies linearly over distances of the order of the size of the particles, the leading order gradient expansion,
is the integral with respect to R ranging over a spherical surface with radius 2a. For small spatial gradients in the orientation-dependent local density, such that the density varies linearly over distances of the order of the size of the particles, the leading order gradient expansion,



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ < 0.
Θ < 0.



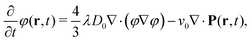



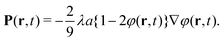
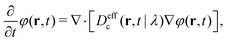





 is the rotation operator with respect to R (where ∇
is the rotation operator with respect to R (where ∇![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) is the gradient operator with respect to the Cartesian coordinates of the unit vector
is the gradient operator with respect to the Cartesian coordinates of the unit vector ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ). Using that,
). Using that,
 and
and  , and using orthonormality of the spherical harmonics, it is found that,
, and using orthonormality of the spherical harmonics, it is found that,



 must be determined such that the no-flux boundary condition is fulfilled. Using the addition theorem for spherical harmonics for the first-order Legendre polynomial (where Θ1 is the angle between
must be determined such that the no-flux boundary condition is fulfilled. Using the addition theorem for spherical harmonics for the first-order Legendre polynomial (where Θ1 is the angle between ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) and û1),
and û1),
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·û2, and using that
·û2, and using that  , it is readily found from the orthonormality of the spherical harmonics that the no-flux boundary condition is fulfilled when
, it is readily found from the orthonormality of the spherical harmonics that the no-flux boundary condition is fulfilled when
 . Hence,
. Hence,


![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·û1 and x2 =
·û1 and x2 = ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·û2; and (the cosine of) the angle between û1 and û2, that is, α = û1·û2. The differential equation (eqn (13)) in terms of these variables reads as follows:
·û2; and (the cosine of) the angle between û1 and û2, that is, α = û1·û2. The differential equation (eqn (13)) in terms of these variables reads as follows:

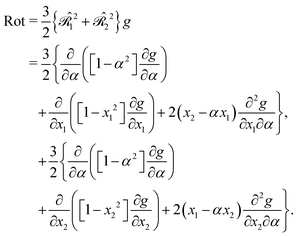
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·U = U
·U = U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, X = x1 + x2,
Θ, X = x1 + x2,











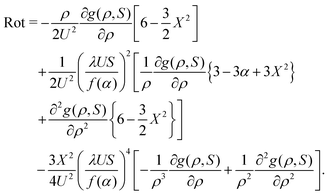
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ ≫ 1 (note that this further limits the region where the analysis is valid, on top of the earlier condition R ≪ λ). This is the region where the most significant relaxation of the pair-correlation function occurs. At first sight, only the last term in eqn (80) for the rotational contribution survives in this region. However, a little thought shows that
Θ ≫ 1 (note that this further limits the region where the analysis is valid, on top of the earlier condition R ≪ λ). This is the region where the most significant relaxation of the pair-correlation function occurs. At first sight, only the last term in eqn (80) for the rotational contribution survives in this region. However, a little thought shows that
 ) and the projection of R onto the plane perpendicular to U. For λUS/f ≫ 1, it follows that the last term in the rotational contribution in eqn (80) is of the order (λUS/f)2 instead of the order (λUS/λ)4. Expanding eqn (80) with respect to (f/λUS) ≪ 1 thus leads to
) and the projection of R onto the plane perpendicular to U. For λUS/f ≫ 1, it follows that the last term in the rotational contribution in eqn (80) is of the order (λUS/f)2 instead of the order (λUS/λ)4. Expanding eqn (80) with respect to (f/λUS) ≪ 1 thus leads to

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ), for which the neglect of the last term on the right-hand side in eqn (83) against the first term is justified. The further analysis is thus restricted to angles between û1 and û2 larger than about 130°. Note that 3 − α is never smaller than (1 + α)(1 − 2cos2
φ), for which the neglect of the last term on the right-hand side in eqn (83) against the first term is justified. The further analysis is thus restricted to angles between û1 and û2 larger than about 130°. Note that 3 − α is never smaller than (1 + α)(1 − 2cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ), for any α, so that the second term on the right-hand side in eqn (83) is never dominant over the first term.
φ), for any α, so that the second term on the right-hand side in eqn (83) is never dominant over the first term.






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ ≫ 1, and α < −7/11. The above expression for the pair-correlation function satisfies the boundary condition g → 1 for R → ∞, and therefore correctly interpolates between distances where R/λ is small and where R → ∞. Furthermore, as will be seen below, the function A(C) can be chosen such that g = 1 for Z = 0, as it should be. Hence, the above expression for the pair-correlation function also correctly interpolates between large values of Z and Z = 0. Finally, for U = 0 (for which α = +1 and S → ∞), g = 1, as it should be, so that there is a correct interpolation with respect to the values of α not smaller than −7/11 as well. The interpolation arguments are very similar to the matching procedure of the inner and outer solutions in the boundary-layer analysis of the front-sector as discussed in the previous subsection. The outer region in the wake-sector corresponds to the region where the conditions R/λ ≪ 1, R
Θ ≫ 1, and α < −7/11. The above expression for the pair-correlation function satisfies the boundary condition g → 1 for R → ∞, and therefore correctly interpolates between distances where R/λ is small and where R → ∞. Furthermore, as will be seen below, the function A(C) can be chosen such that g = 1 for Z = 0, as it should be. Hence, the above expression for the pair-correlation function also correctly interpolates between large values of Z and Z = 0. Finally, for U = 0 (for which α = +1 and S → ∞), g = 1, as it should be, so that there is a correct interpolation with respect to the values of α not smaller than −7/11 as well. The interpolation arguments are very similar to the matching procedure of the inner and outer solutions in the boundary-layer analysis of the front-sector as discussed in the previous subsection. The outer region in the wake-sector corresponds to the region where the conditions R/λ ≪ 1, R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ ≫ 1, and α < −7/11 are not satisfied.
Θ ≫ 1, and α < −7/11 are not satisfied.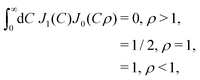




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ/w)gc(cos
Θ/w)gc(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ,w) = [8U3/(4 + U2)]λxgc is plotted in Fig. 8a as a function of w ∼ 1/λ for various values of cos
Θ,w) = [8U3/(4 + U2)]λxgc is plotted in Fig. 8a as a function of w ∼ 1/λ for various values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, as indicated in the plots. As can be seen, λxgc tends to zero for small w (corresponding to large λ). The particular value of w for which λxgc tends to zero, however, decreases with decreasing values of cos
Θ, as indicated in the plots. As can be seen, λxgc tends to zero for small w (corresponding to large λ). The particular value of w for which λxgc tends to zero, however, decreases with decreasing values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, and goes through a maximum. The point of contact where cos
Θ, and goes through a maximum. The point of contact where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ is zero, and therefore
Θ is zero, and therefore  , corresponds to a relative position for which R⊥U, that is, where the two particles just move from the front-sector to the wake-sector. For these positions at contact, diffusion becomes almost immediately effective, leading to a deviation from the step-function at ρ = 1. This is the physical origin of the relative large velocities required for which the contact value becomes zero for small values of cos
, corresponds to a relative position for which R⊥U, that is, where the two particles just move from the front-sector to the wake-sector. For these positions at contact, diffusion becomes almost immediately effective, leading to a deviation from the step-function at ρ = 1. This is the physical origin of the relative large velocities required for which the contact value becomes zero for small values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ. Note that these numerical results imply that the contact value of the pair-correlation function tends to zero as λ−γ, with γ > 1. Within the leading order expansion with respect to 1/λ considered here, the contact value is therefore zero.
Θ. Note that these numerical results imply that the contact value of the pair-correlation function tends to zero as λ−γ, with γ > 1. Within the leading order expansion with respect to 1/λ considered here, the contact value is therefore zero.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ/w)gc ∼ λxgc (where Θ is the angle between R and U, w ∼ 1/λ given in eqn (94), and gc is the contact value of the pair-correlation function) as a function of w, for various values of cos
Θ/w)gc ∼ λxgc (where Θ is the angle between R and U, w ∼ 1/λ given in eqn (94), and gc is the contact value of the pair-correlation function) as a function of w, for various values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ, as indicated in the figure. (b and c) The radial derivative of the pair-correlation function at contact as a function of w for two different ranges of the derivative.
Θ, as indicated in the figure. (b and c) The radial derivative of the pair-correlation function at contact as a function of w for two different ranges of the derivative.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ. The spatial derivatives are seen to tend to zero for large values of λ. For the same reason as for the contact value of the pair-correlation function, the spatial derivative for small values of cos
Θ. The spatial derivatives are seen to tend to zero for large values of λ. For the same reason as for the contact value of the pair-correlation function, the spatial derivative for small values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ requires larger values of λ to converge to zero. Again, this is due to the step-function-like behavior at the point where
Θ requires larger values of λ to converge to zero. Again, this is due to the step-function-like behavior at the point where  and R⊥U.
and R⊥U.





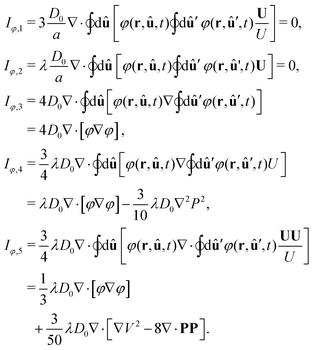

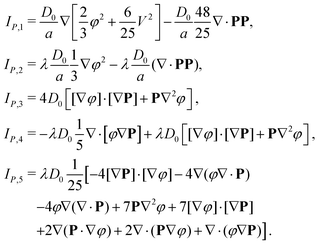



 )
)