Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A pair of particles in inertial microfluidics: effect of shape, softness, and position†
Kuntal
Patel
 * and
Holger
Stark
* and
Holger
Stark

Institut für Theoretische Physik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany. E-mail: kuntal.h.patel@tu-berlin.de
First published on 19th April 2021
Abstract
Lab-on-a-chip devices based on inertial microfluidics have emerged as a promising technique to manipulate particles in a precise way. Inertial microfluidics exploits internal hydrodynamic forces and the mechanical structure of particles to achieve separation and focusing. The article focuses on the hydrodynamic interaction of two particles. This will help to develop an understanding of the dynamics of particle trains in inertial microfluidics, which are typical structures in multi-particle systems. We perform three-dimensional lattice Boltzmann simulations combined with the immersed boundary method to unravel the dynamics of various mono- and bi-dispersed pairs in inertial microfluidics. We study the influence of different starting positions for mono- and bi-dispersed pairs. We also change their deformability from relatively soft to rigid and choose spherical and biconcave particle shapes. The observed two-particle motions in the present work can be categorized into four types: stable pair, stable pair with damped oscillations, stable pair with bounded oscillations, and unstable pair. We show that stable pairs become unstable when increasing the particle stiffness. Furthermore, a pair with both capsules in the same channel half is more prone to become unstable than a pair with capsules in opposite channel halves.
1 Introduction
Biomedical studies of biological cells play a crucial role in diagnosing several fatal diseases1 such as malaria,2 cancer,3,4 and the human immunodeficiency virus (HIV) infection,5 to name a few. In recent years, microfluidic6 lab-on-a-chip devices7 have emerged as a promising technique to precisely manipulate and control biological cells needed on a commercial level.8 Lab-on-a-chip devices for separating particles and biological cells rely on external force fields or internal hydrodynamic forces.9 Lab-on-a-chip techniques using external force fields include optical tweezers,10 dielectrophoresis,11 magnetophoresis,12 and acoustophoresis.13 On the other hand, deterministic lateral displacements at low Reynolds number using appropriately placed pillars14 and inertial microfluidics15–20 exploit internal hydrodynamic forces to achieve particle separation. In contrast to common microfluidic lab-on-a-chip devices in which fluid inertia is negligible, inertial microfluidics operates in an intermediate range between Stokes and turbulent regimes, where flow is still laminar. The possibility to attain high throughput makes inertial microfluidics an attractive option among other microfluidic particle-separation techniques. In this article, we investigate how different factors such as shape, softness, and position influence the motion of a pair of particles in a microfluidic channel.Inertial focussing was first reported by Segré and Silberberg for solid particles with the well-known tubular pinch effect21,22 and then spurred numerous theoretical,23–26 computational,19,27–30 and experimental31–34 studies to gain a deeper understanding of this phenomenon. Inertial migration of a neutrally buoyant solid particle is essentially the result of a balance between shear-gradient lift force, directed towards the channel wall,35 and a wall repulsion force, directed towards the channel center.36 Applying an external force to the solid particle along the channel axis, the resulting Saffman force37 also contributes significantly to the force balance in the cross-stream direction. For almost five decades from the observation of the Segré–Silberberg effect, inertial migration was mainly a blue-skies-research problem. In 2007 Di Carlo et al.38 demonstrated ordering and separation of particles in a microchannel using inertial focussing, which gave rise to the field of inertial microfluidics. Subsequently, Hur and co-workers39 experimentally showed inertia-driven separation and enrichment of deformable capsules. Soft capsules experience an additional lift force induced by the deformability of the cell, which drives them towards the channel center and which thereby competes with the inertial lift force.40
For biomedical applications of inertial microfluidics it is crucial to strive for a deeper understanding of the inertial migration of deformable capsules. The dynamics of soft capsules is widely studied at low Reynolds numbers in canonical flows41–45 and cellular blood flow simulations.46–49 Only recently, inertial microfluidics of deformable cells has caught attention.20,50–58 Using two-dimensional numerical simulations, Shin and Sung51 showed that the final equilibrium position for a given value of capsule elasticity varies with the Reynolds number. In their following work54 they identified different types of capsule dynamics such as tank-treading, swinging, and tumbling. According to Kilimnik et al.50 the steady-state position of a deformable capsule in the lateral direction is independent of the flow rate and it only depends on the softness. This was later verified by Schaaf and Stark20 using 3D lattice Boltzmann simulations. They also proposed that the inertial lift force in the vicinity of the channel center scales as a cube of capsule radius. More recently, Alghalibi and colleagues58 investigated cross-stream inertial migration of a soft particle in pipe flow. Interestingly, they found that irrespective of the particle's softness and the flow rate, the particle always ends up at the channel center for an initial particle diameter of 0.2 times the pipe diameter.
Practical applications require manipulation of several soft particles at a time and, hence, it is important to study how particles interact in flow. There are a few systematic studies in literature to understand the interaction of solid and soft particles in inertial microfluidics. Yan et al.59 investigated the dynamics of two solid particles in linear shear flow generated by two plates moving against each other. They observed that particles either settle down on the centerline where flow velocity is zero or exhibit oscillatory motion when released from symmetric initial positions. Schaaf et al.60 reported that for two closely placed solid particles in a channel flow, the inertial lift forces acting on the leading and lagging particles differ significantly. In their subsequent work61 they extended the understanding of a particle pair to study the behavior of particle trains62 in inertial microfluidics. At low Reynolds numbers, Lac et al.63 and Aouane et al.64 investigated the interaction of two soft capsules in shear and Poiseuille flows, respectively. The inertial counterparts of these two problems were also studied. Doddi and Bagchi65 observed a transition from irregular self-diffusion66 to different types of spiraling motions (outward, fixed orbit, and inward) with increasing Reynolds number. Lan and Khismatullin67 reported that a pair of deformable cells in a rectangular microchannel undergoes either swapping or passing trajectories, while deformable cells in a series experience damped oscillations. Like Lan and Khismatullin,67 Schaaf et al.60 also observed these swapping and passing trajectories for a pair of solid particles. Krüger et al.68 looked into the suspension of deformable capsules in Poiseuille flow at finite Reynolds numbers. They discovered that particle–particle interactions enhance the migration towards the channel center for sufficiently large Reynolds and capillary numbers.
In the present work we perform three-dimensional lattice-Boltzmann simulations combined with the immersed boundary method20,60,69 to investigate the dynamics of mono- and bi-dispersed particle pairs. They flow through a square microchannel in the inertial regime. We systematically investigate the effect of different starting positions for mono- and bi-dispersed pairs. We also vary their deformability from relatively soft to rigid and choose spherical and biconcave particle shapes. Reynolds number, particle radius, and axial particle distance are kept the same in all the cases. The observed dynamics of the different mono- and bi-dispersed particle pairs can be categorized into four types: stable pair, stable pair with damped oscillations, stable pair with bounded oscillations, and unstable pair.
The outline of the article is as follows. In Section 2 we discuss the computational setup and simulation parameters of the problem and explain the lattice Boltzmann simulations. Results from the numerical investigations are presented in Section 3 and we close with concluding remarks in Section 4.
2 Computational setup and numerical methodology
2.1 Microfluidic setup for a flowing pair of particles
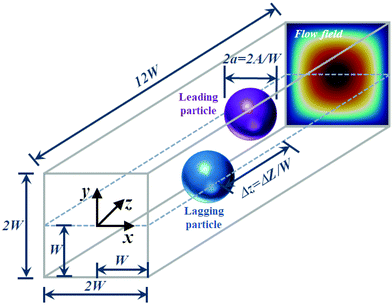
Fig. 1 shows the schematic of our microfluidic setup. We study the hydrodynamic interaction and inertial migration of a flowing pair of soft particles in a quadratic microchannel. We start from a fully-developed Poiseuille flow and place two particles in the midplane at y = 0. We apply periodic boundary conditions in the z-direction along the channel axis and the no-slip boundary condition at the channel walls in the remaining directions. The length of the microchannel is large enough so that particles do not interact with their periodic images unless the axial separation becomes as large as the channel length. The pressure gradient or force density α required to pump the fluid through the channel is calculated from the analytical expression for the velocity field of a Poiseuille flow:70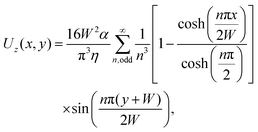 | (1) |
2.2 Coupled lattice Boltzmann finite element immersed boundary method (LBFEIBM)
 | (2) |
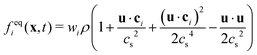 | (3) |
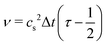 , where
, where 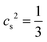 in lattice units. The last term in eqn (2) is due to the forcing scheme proposed by Guo et al.74 It takes into account the force density driving the fluid and forces exerted by particles. Based on this scheme, a body force density f is related to Fi as
in lattice units. The last term in eqn (2) is due to the forcing scheme proposed by Guo et al.74 It takes into account the force density driving the fluid and forces exerted by particles. Based on this scheme, a body force density f is related to Fi as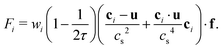 | (4) |
In order to obtain the macroscopic picture of the flow field, fluid density ρ and momentum density ρu at each lattice node can be calculated using the zeroth and first moments of the populations fi:
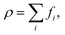 | (5) |
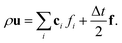 | (6) |
We enforce the no-slip condition at channel walls using the regularized method of Latt and Chopard.75,76 The numerical accuracy of our simulations is maintained by setting the relaxation time τ ≤ 1. Please refer to ref. 20 for further details. The numerical solution of the lattice Boltzmann equation is obtained using an open-source parallel lattice Boltzmann solver from the Palabos project,77 while implementation of the immersed boundary method and particle dynamics uses in-house libraries.
 elements,78i.e., linear triangular elements. Tessellation of the particle surface is achieved by dividing each triangle of an icosahedron into four triangles (for more details refer to ref. 69) and the newly created nodes are then radially shifted to the circumsphere. The process is repeated until the distance between two neighboring nodes approaches the lattice spacing. This procedure of generating mesh from a highly symmetric solid (icosahedron in the present case) enables us to achieve superior mesh quality in terms of isotropy and homogeneity.69 The same procedure is used for the solid particles as well.
elements,78i.e., linear triangular elements. Tessellation of the particle surface is achieved by dividing each triangle of an icosahedron into four triangles (for more details refer to ref. 69) and the newly created nodes are then radially shifted to the circumsphere. The process is repeated until the distance between two neighboring nodes approaches the lattice spacing. This procedure of generating mesh from a highly symmetric solid (icosahedron in the present case) enables us to achieve superior mesh quality in terms of isotropy and homogeneity.69 The same procedure is used for the solid particles as well.
The capsule dynamics is determined by a combination of strain, bending, and volume energies. For the strain energy we rely on the Skalak model79 valid for an isotropic and homogeneous capsule. It is formulated as a function of the strain invariants of the Green strain tensor and given as
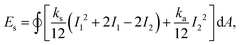 | (7) |
| I1 = λ12 + λ22 − 2, | (8) |
| I2 = λ12λ22 − 1. | (9) |
The discretized version of the bending energy proposed by Helfrich80,81 takes the form
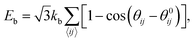 | (10) |
In this work, we consider soft particles with an impermeable membrane. To implement the constraint of constant volume, at least approximately, we choose a standard method and incorporate the volume energy82
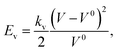 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000ρν2/W2. Note, these changes do not affect the dynamics of the particle.
000ρν2/W2. Note, these changes do not affect the dynamics of the particle.
Following Krüger et al.68 and Schaaf and Stark,20 we set ka/ks = 2 and kb/(ksa2) = 2.87 × 10−3. We can compare our parameters with the ones for red blood cells. To mimic their the mechanical behavior in blood flow simulations, the ratio kb/(ksa2) is set to 2.36 × 10−3,47 which is very close to the value in present simulations. However, the ratio ka/ks in current simulations is significantly smaller than that used for a healthy red blood cell, which allows our spherical capsules to deform significantly.
The total force acting on node i can be obtained from the principle of virtual work;83 given as Fi = ∂[Es + Eb + Ev]/∂xi. The derivatives of strain, bending, and volume energies were derived analytically and then inserted directly into the solver to save computational costs. The analytical form of the derivatives can be found in ref. 84.
| S(t + Δt) = S(t) + U(t), | (12) |
| MU(t + Δt) = MU(t) + Ffluid + FFeng, | (13) |
| Iω(t + Δt) = Iω(t) + Tfluid + TFeng, | (14) |
![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) 1 elements of the discretized particle surfaces as Lagrangian markers. The advection velocity ẋi of Lagrangian markers is obtained using an interpolation of the velocity values u from neighboring Eulerian points, which in our case are the lattice nodes of the lattice Boltzmann method:
1 elements of the discretized particle surfaces as Lagrangian markers. The advection velocity ẋi of Lagrangian markers is obtained using an interpolation of the velocity values u from neighboring Eulerian points, which in our case are the lattice nodes of the lattice Boltzmann method: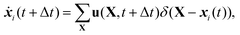 | (15) |
![[f with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0066_0303.gif) exerted by Lagrangian markers on neighboring Eulerian points is computed using the spreading operation:
exerted by Lagrangian markers on neighboring Eulerian points is computed using the spreading operation: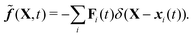 | (16) |
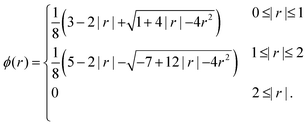 | (17) |
The interaction between soft capsules and the bulk fluid is resolved using the classical IBM. However, for solid particles we employ interpolation and spreading operations in an iterative manner85,86 to obtain the force Ffluid and torque Tfluid directly from the flow field. Then, advection velocity U is obtained using eqn (13). This particular approach is known as the multi-direct-forcing variation of the immersed boundary method.91,92
2.3 Simulation parameters
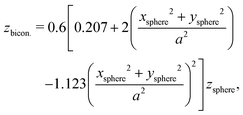
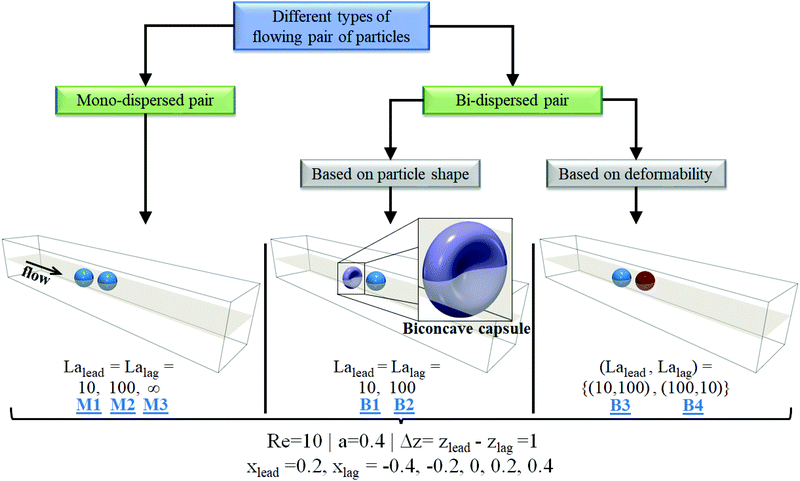
In our microfluidic setup we simulate two types of particle pairs, mono- and bi-dispersed (see Fig. 2). Mono-dispersed pairs consist of spherical particles of the same stiffness. Bi-dispersed pairs are classified into two subtypes; first, a pair with particles of different shapes but the same stiffness, and second, a pair with particles of varying stiffness but the same shape. We consider the combination of a spherical (leading) and biconcave (lagging) particle for the first type, and for the second type, two spherical particles. The initial orientation of a biconcave particle in the flow field is shown in a magnified view in Fig. 2. We apply the transformation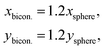 | (18) |
to the vertices of a spherical particle of radius a to model the biconcave shape.93,94
In all the cases we set the non-dimensional particle radius a and the initial axial separation Δz equal to 0.4 and 1, respectively. For the biconcave particle the radius characterizes the spherical particle from which it is generated using eqn (18). The value of the Reynolds number Re = 2WUmax/ν is fixed to 10 in all the simulations. Here, Umax is the maximum fluid velocity in the channel center and ν is the kinematic viscosity. Note, in a typical inertial microfluidics setup, the Reynolds number varies from 1 to 10017. Following Schaaf and Stark,20 we use the Laplace number to define the softness of the particle; it is given as
| La = ksa/ρν2. | (19) |
In practice, there might exist a viscosity contrast between the fluid within soft particles (cytoplasm in biological cells) and the bulk liquid (ηcyto/ηbulk > 1). For example, the cytoplasmic viscosity of the red blood cell is five times the plasma viscosity ηplasma= 1 mPa s.47 Moreover, tumour cells such as A549 can have cytoplasmic viscosity in the range of 144.8 to 1390.7 Pa s,95 which is several orders of magnitude higher than the plasma viscosity. We shortly summarize what influence this will have. An increase in the viscosity of the interior fluid or cytoplasm attenuates the deformation of soft particles and biological cells.50 Thus, while for a very soft particle a viscosity contrast close to one should not significantly alter the migration dynamics, a viscosity contrast significantly larger than one makes particles less deformable and modifies their equilibrium positions. In the case of relatively stiff particles, the viscosity contrast will have a negligible influence on the particle dynamics. Moreover, for biconcave soft particles in inertial flows with Re ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1), there exists a critical value of viscosity contrast above which the transition from tank-treading to tumbling motion takes place.52 Later, we will see that biconcave particles in the present work already exhibit tumbling motion. With this in mind, we set the density and viscosity of the soft particle identical to the values of the bulk fluid.
(1), there exists a critical value of viscosity contrast above which the transition from tank-treading to tumbling motion takes place.52 Later, we will see that biconcave particles in the present work already exhibit tumbling motion. With this in mind, we set the density and viscosity of the soft particle identical to the values of the bulk fluid.
In each simulation we fix the leading particle position in the x-direction to 0.2 and vary the position of the lagging particle from −0.4 to 0.4 in steps of 0.2. The leading particle's starting position is kept sufficiently far from the stable equilibrium point of isolated particles (see Fig. 5 and 9) so that disturbances from the lagging particle can have a significant effect on the motion of the leading particle. The implemented LBFEIBM solver has been employed in a series of works by our group19,20,60,61 (see Appendix A for benchmarking). According to our previous work we discretize the channel width with 90 lattice nodes for the case of soft particles and 75 lattice nodes for solid particles. In our simulations, the necessity of a high grid resolution arises to ensure the proper coupling between particles and the bulk fluid. Moreover, relatively more lattice nodes are required in the case of soft particles to capture the particle deformation and lift force accurately. Lastly, the surface of soft and solid particles is discretized using 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480
480  elements.
elements.
3 Results and discussion
In this section, we first explain how the overall dynamics of a particle pair is categorized in the present work for the different types of particle pairs as illustrated in Fig. 2. A detailed explanation of the hydrodynamic behavior is provided later in Sections 3.1 and 3.2 for the different mono- and bi-dispersed pairs, respectively.In Poiseuille flow the inertial lift force migrates a particle towards a specific position between channel center and wall, where softer particles are located closer to the center. Depending on the direction of migration, the particle either accelerates or slows down. For two closely placed particles the lift force acting on each particle is modified compared to the single-particle case60 and the modified cross-streamline motion causes particles to approach or move away from each other. Notably, the initial interaction and positions of particles determine their dynamics at a later stage.
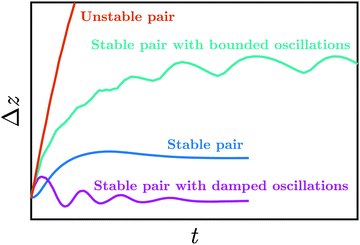
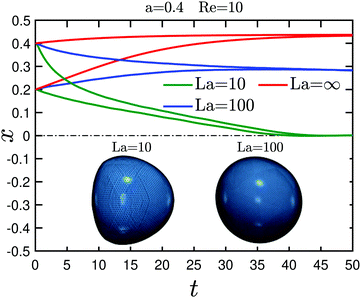
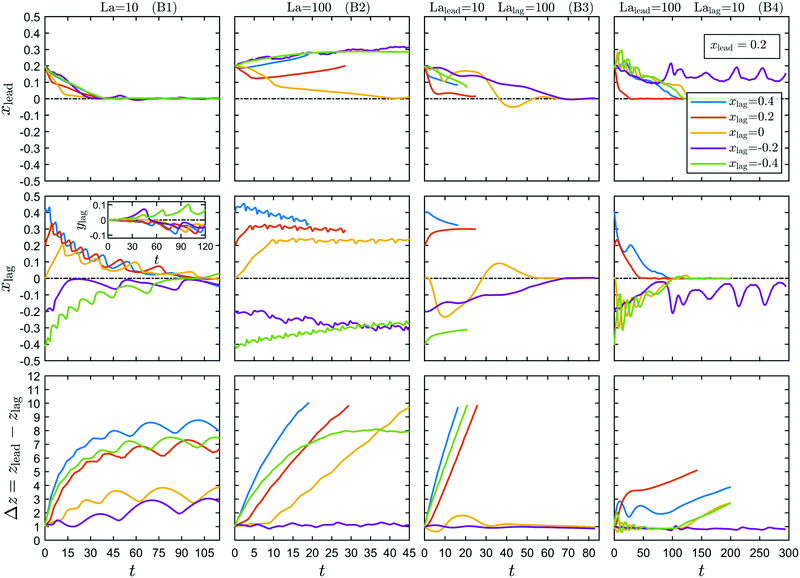
In Fig. 3 we use the time evolution of the axial particle distance Δz to identify four different types in the dynamics of a flowing particle pair: stable pair, stable pair with damped oscillations, stable pair with bounded oscillations, and unstable pair. In our notation the stable particle pair either directly approaches a constant particle separation at long times (see video M1) or the particle distance oscillates. In the second case we find both, damped oscillations ( see video M2) and ongoing bounded oscillations (see video B1). The source of damped and bounded oscillations is different as we discuss below in Sections 3.1 and 3.2. Finally, particles of an unstable pair continuously drift apart until the particle distance approaches the channel length ( see video B3).
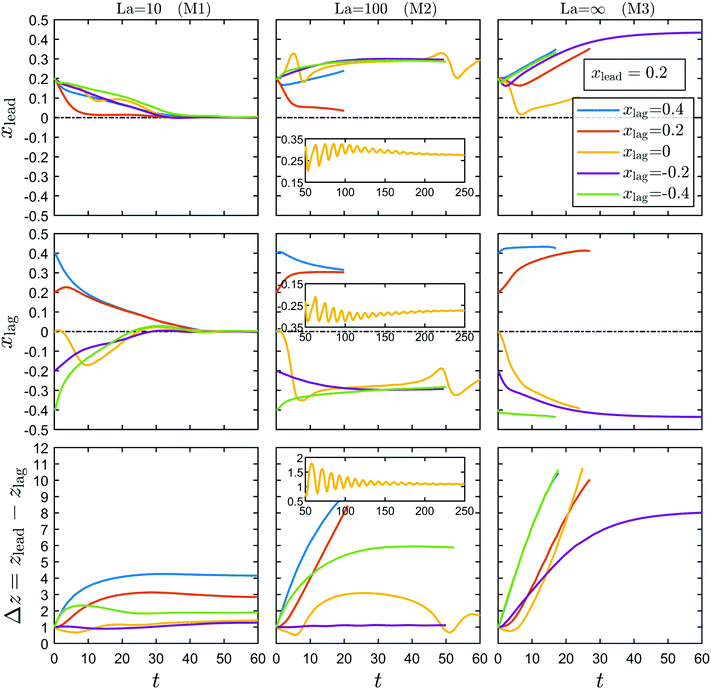
The diagram in Fig. 4 summarizes the dynamics of the particle pairs, which we observed in our simulations for different mono- and bi-dispersed pairs when the initial position of the lagging particle is varied. The mono-dispersed pair M1 with soft capsules is always stable irrespective of the starting position xlag. It is situated in the channel center as we will see below. On increasing the particle stiffness from La = 10 to La = 100 (label M2), the pair is stable when the leading and lagging particles initially occupy different channel halves and becomes unstable when the particles start in the same channel half. The transition between both cases occurs through damped oscillations. For the mono-dispersed pair M3 composed of rigid particles (La = ∞), we observe that only the symmetric pair with (xlead, xlag) = (0.2, −0.2) is stable, reminiscent of the observations in ref. 60.
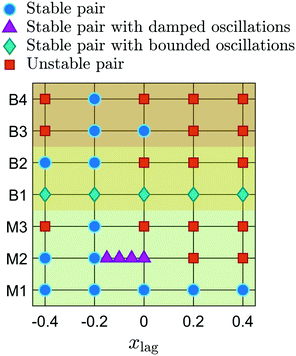 | ||
| Fig. 4 Influence of the starting position xlag on the overall dynamics of different mono- (M1–M3) and bi-dispersed (B1–B4) pairs with the leading particle starting at xlead = 0.2 (see Fig. 2 for further details on labels M1–M3 and B1–B4). | ||
The dynamics of the bi-dispersed pairs B1 and B2 is qualitatively the same as that of pairs M1 and M2, however, with the difference that now the B1 pair performs bounded oscillations. Lastly, the symmetric placement of leading and lagging particles in the B3 and B4 pairs gives a stable pair, which we also observe for the B3 pair with xlag = 0. In summary, irrespective of particle-pair type when the leading and lagging particles start from the symmetric positions (xlead, xlag) = (0.2, −0.2) the pair is stable. Also, stable pairs become unstable when increasing the particle stiffness. Finally, a pair with both particles in the same channel half is more prone to become unstable than a pair with particles starting in the opposite channel halves.
Before proceeding, we add a comment. Prohm and Stark19 demonstrated that a freely placed solid particle in Poiseuille flow might either migrate to the main axis or the diagonal depending on the particle size and cross section of a microchannel. Furthermore, these zero lift-force positions can either be stable, saddle points, or unstable. Particles located on unstable positions migrate to stable positions in response to a small perturbation. In the work of Schaaf and Stark,20 it was observed that the majority of implemented deformable capsules migrated to the channel diagonal. In our case we initialize all particles in the midplane at y = 0. We observe that in all cases they essentially stay in the midplane during migration since for symmetry reasons the lift force component normal to the midplane is zero.
3.1 Mono-dispersed pairs
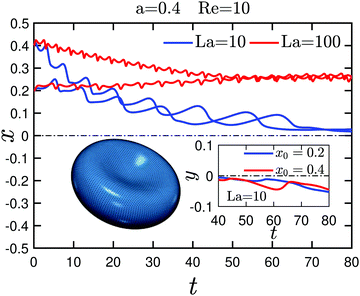
We now focus our attention on the dynamics of particles in the M2 pair. For xlag = 0.2, similar to the M1 pair, the lagging particle initially pushes the leading particle towards the channel center. Thus, leading and lagging particles drift at a different axial velocity, which continuously increases the axial distance and makes the pair unstable. Note that we stop the simulations once the axial particle distance Δz is beyond 10 and therefore close to the channel length, where a particle interacts with the image of the other particle. Continuing the simulations of the leading particle from the momentary position at x = 0.055 without the other particle present shows that it migrates towards the center instead of drifting back to the known equilibrium position at x ≈ 0.3. Thus, we identify a second type of stable position at x = 0, which we attribute to the strong wall repulsion for the large particles, we use in our simulations, and the fact that the inertial lift force is small close to the center. The M2 pair with xlag = 0.4 also turns out to be unstable since already initially, they drift with very different axial velocities. Interestingly, for xlag = −0.4 the particle pair is stable although with a larger axial distance compared to the corresponding M1 pair with La = 10, while for the symmetric initial positions with xlag = −0.2 the axial distance stays close to the starting value similar to the case La = 10.
A new feature is observed for the initial position xlag = 0. The M2 pair is stable but reaches a constant axial distance close to the initial value only after extended damped oscillations in both the lateral positions and Δz (see video M2), as the insets in Fig. 6 show. Similar oscillations in the axial distance were reported earlier in numerical simulations of a pair of solid particles60 and a train of soft particles67 in a rectangular microchannel. Experimental evidence on damped oscillations of solid particles in a microchannel can be found in Lee et al.96 Recently, based on theoretical calculations, Hood and Roper97 suggested that in such oscillations, inertia and viscosity switch their roles, i.e., viscous interactions of a particle with the channel wall and other particles initiate oscillations while inertial forces dampen them.
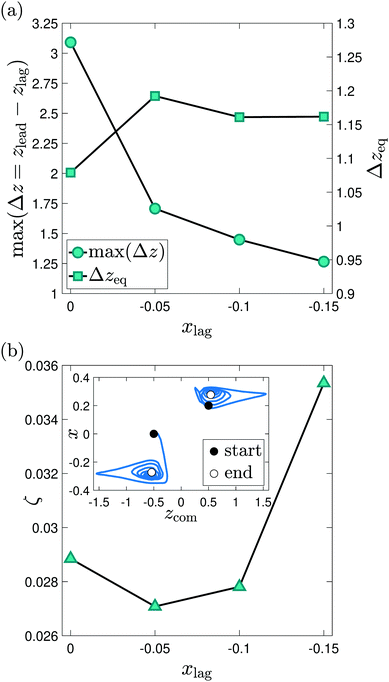
We further investigated the nature of these damped oscillations for xlag = −0.05, −0.1, and −0.15. We find that as the initial position of the lagging particle moves away from the channel center, the maximum amplitude of oscillations decreases [see Fig. 8(a)]. We assign this to the reduced viscous coupling, when the particles are further away from each other and an increased damping due to the (inertial) lift forces, which force the particle to a specific lateral position.60 In all cases, particles equilibrate with an axial separation very close to its initial value. In the inset of Fig. 8(b) we visualize the trajectories of the leading and lagging particles in the center-of-mass frame for xlag = 0. They reveal the inward spiraling motion of the leading and lagging particles. For decreasing xlag the extent of the spirals shrink because of the reduction in the value of max(Δz). As the main plot in Fig. 8(b) shows, the damping rate of the oscillations in Δz first does not vary significantly for decreasing xlag but then increases sharply.
Finally, we discuss the case of a pair of solid particles (M3) in Fig. 6. Only the symmetric placement with xlag = −0.2 and xlead = 0.2 provides a stable flowing pair, reminiscent of the findings in ref. 60. Unlike soft particles with xlag = −0.2, the initial distance between two solid particles no longer remains constant over time. It grows until the particles have reached their final lateral positions. Earlier, we saw that in mono-dispersed pairs M1 and M2 with xlag = ±0.4, the axial separation grows at the same rate only at early times. Now, the temporal increase of the axial distance Δz is the same for the whole time interval for these two cases since the lagging particles already start close to their equilibrium positions (see Fig. 5) and only the leading particle has to relax.
3.2 Bi-dispersed pairs
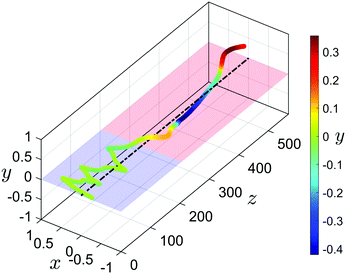
In this subsection we concentrate on the dynamics of different bi-dispersed pairs. We employ an approach similar to that in the previous discussion on mono-dispersed pairs. We first look at the migration of a biconcave particle so that later it can be compared with bi-dispersed pairs.At low Reynolds numbers a biconcave particle in shear flow undergoes either tank-treading, tumbling, or swinging motion depending on the shear rate, softness, and viscosity ratio.98 Here, for more rigid particles at La = 100 we observe a solid-body like tumbling motion in the y = 0 plane, while for the softer biconcave particle at La = 10 a deformation-driven tumbling motion is observed as illustrated in Fig. 10. Initially [Fig. 10(b and c)], the particle rotates because the lower part being closer to the center moves faster. Later, when the particle aligns itself with the flow direction [Fig. 10(d)], it transforms into a parachute-like shape [Fig. 10(f)]. Eventually, the transition to a convex disc-like shape [Fig. 10(h)] completes one tumbling cycle, during which the particle has moved closer to the channel center. This also increases the period of the tumbling motion.
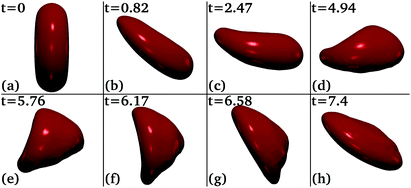 | ||
| Fig. 10 Deformation-driven tumbling motion of a biconcave particle of rigidity La = 10 starting at x0 = 0.2 in the midplane of the microchannel when looked from the top. Flow direction is from left to right and the cell tumbles counterclockwise. The snapshots are taken from the trajectory in Fig. 9. | ||
Note that the biconcave particle with La = 10 does not fully reach the channel center at x = 0 and also leaves the midplane at y = 0 [inset of Fig. 9]. Therefore, it does not have a symmetric shape and performs a tumbling motion. We call it wobbling since the tumble axis varies in time, as we explain further below in Fig. 12. This is qualitatively similar to the observation of Fedosov et al.99 for the tumbling-to-slipper transition of a red blood cell in cylindrical microchannels. A slipperlike form of the biconcave particle occurs in Poiseuille flow at low Reynolds numbers,100 which in steady state undergoes tank-treading motion. Thus, we observe a transition from deformation-driven tumbling to wobbling when the particle approaches the center. It also occurs in the bi-dispersed pair B1 as discussed below.
At stiffness La = 100 stable particle pairs only occur for xlag= −0.2 and −0.4. The pronounced bounded oscillations have vanished although modulations with small amplitudes are visible. All other B2 pairs are unstable and axially move away from each other while reaching their equilibrium positions with finite distance from the center. An exception is the case with xlag = 0. The leading particle is strongly dragged to the center by the biconcave particle and ultimately reaches the center, which we already identified as an additional stable lateral position when discussing the dynamics of the M2 pairs.
We now discuss the bi-dispersed pairs B3 and B4 where leading and lagging particles are spherical and have different stiffnesses. In Fig. 11 we plot lateral positions and axial distances versus time. When the leading particle is softer (La = 10) than the lagging particle (La = 100), the B3 pairs with xlag = 0 and −0.2 form stable pairs. The leading soft particle succeeds to drag the stiffer particle to the channel center, where it occupies the additional stable position so that the pair can stay bounded. In the remaining cases the lagging particle migrates towards the off-center stable position, which ultimately makes the B3 pairs unstable.
In the B4 pairs the rigidity values are switched between the particles. As a result both leading and lagging particles move towards the channel center. A special case occurs when both particles start from the symmetric lateral positions xlead = −xlag = 0.2. They obstruct each other from aligning at the channel center, which results in oscillations in the lateral positions. However, the axial distance between the particles only fluctuates little about its initial value and the pair is stable. In the rest of the cases the leading and lagging particles successfully align at the channel center. They drift apart at different axial velocities due to their different equilibrium shapes (see Fig. 5), which directly affect the drag acting on each particle in the axial direction. Hence, even if the leading and lagging particles have the same lateral position, their axial distance does not remain bounded. As shown in Fig. 11, for the unstable pairs the axial distance increases at the same rate once both particles are at the channel center. We did not simulate the unstable pairs for longer times because it is computationally expensive as the axial distance grows very slowly. On extrapolating the trend of the curve for xlag = 0.2, one would need ≈400 time units for Δz to reach Δz = 10. We also simulated the B4 pairs with the starting position of the leading particle xlead = 0. However, we did not find any stable configurations in these cases.
4 Concluding remarks
Inertia driven separation and focusing of soft particles in microfluidics has direct relevance for biomedical applications. Inertial microfluidics has recently emerged as a robust and precise technique for particle manipulation since it relies entirely on internal hydrodynamic forces. Moreover, inertial microfluidics functions at finite Reynolds numbers, which allows faster processing of samples. In the present article we investigated the hydrodynamics of a particle pair in inertial microfluidics using 3D numerical simulations. We combined the lattice Boltzmann method to compute the fluid flow with the finite element method to model particle dynamics. To couple fluid flow and particle motion, the immersed boundary method was used.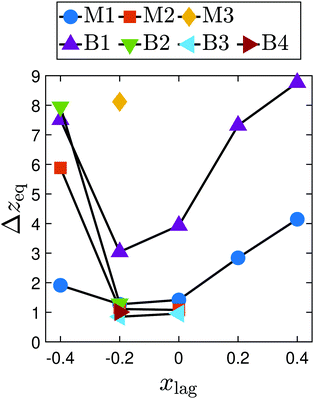 | ||
| Fig. 13 The equilibrium axial distance Δzeq between the leading and lagging particle is plotted versus xlag for stable particle pairs. | ||
In this work we considered mono- (M1–M3) and bi-dispersed (B1–B4) particle pairs of different softness and particle shape (see Fig. 2). For each pair we investigated the influence of different starting positions of the lagging particle and identified four types: stable pair, stable pair with damped oscillations, stable pair with bounded oscillations, and unstable pair.
We found that the starting position of the lagging particle does not affect the stability of the mono-dispersed pairs with stiffness La = 10 (M1). On increasing the stiffness to La = 100 (M2), the mono-dispersed pairs become unstable when the leading and lagging particles start in the same channel half. Moreover, when the lagging particle starts at xlag = 0, the pair undergoes damped oscillations. The oscillations arise due to hydrodynamic interactions between particles, while inertial forces damp them. The maximum amplitude of the damped oscillations decreases as we shift the starting position of the lagging particle away from the leading particle. Finally, from mono-dispersed pairs of perfectly solid particles (M3) only the pair with initially symmetric lateral positions about the centerline retains its stability.
When we change the shape of the lagging particle from spherical to biconcave, bi-dispersed pairs with particle stiffness La = 10 are always stable. They show bounded oscillations in the axial distance due to the tumbling motion of the biconcave particle. For La = 100 (B2) the biconcave shape does not change the qualitative behavior when compared to the mono-dispersed pairs (M2) of the same particle stiffness.
Finally, the soft leading (La = 10) and stiff lagging (La = 100) particles in the bi-dispersed pair B3 assemble at the channel center. The pair is stable when the lagging particle starts at xlag = 0 or −0.2, while the remaining starting positions result in unstable pairs. When the stiffness of the leading and lagging particles are interchanged (pair B4), both particles migrate towards the channel center irrespective of the starting position and they ultimately drift apart due to their different shapes. Only for symmetric starting positions about the channel center a stable pair with lateral oscillations occur.
Our work explores and classifies different two-particle motions, which should be observable in the flow of mono- and bi-dispersed particle suspensions in the regime of inertial microfluidic. To explicitly test the different types of pair dynamics, one could use microchannels with inlets, which place both particles at specific lateral positions.
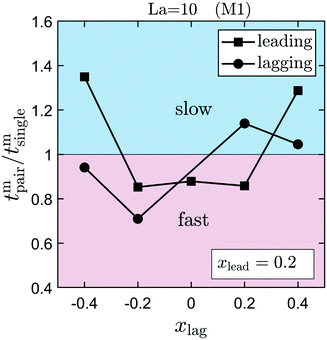
Finally, in inertial microfluidics the multi-particle states consist of linear trains either moving on the same streamline or in a staggered configuration as observed in experiments.96,101 As we demonstrated in ref. 61 for rigid particles, knowing the bounded two-particle states one can directly infer the lattice constant of the staggered trains, while the lattice constant of linear trains on the same streamline typically have a value determined by the range of the two-particle interaction. In this context, the steady-state value of the axial distance between the leading and lagging particles is summarized in Fig. 13 for mono- and bi-dispersed pairs, when they are stable. Thus, the present study will help to understand the multi-particle train configurations occurring in inertial microfluidics for soft particles and their mixtures, which will be more involved compared to the case of ref. 61, where only rigid particles of the same size were studied.
Conflicts of interest
There are no conflicts of interest to declare.Appendix A: benchmarking of the present LBFEIBM solver
We briefly present the validation of the present coupled lattice Boltzmann finite element immersed boundary method (LBFEIBM) for soft and solid particles. To benchmark the modeling of soft particles, we look at the inertial migration of a deformable capsule of radius a = 0.2 and softness La = 10 in a quadratic microchannel at Reynolds number Re = 100. In the present case, the deformable capsule is initialized on the channel diagonal. We use 120 lattice nodes to discretize the channel width, while the surface of the capsule is discretized using 5120 elements. Time-wise variation of the capsule position along the channel diagonal is shown in Fig. 14. The dashed black line in Fig. 14 indicates the equilibrium position reported by Schaaf and Stark.20
elements. Time-wise variation of the capsule position along the channel diagonal is shown in Fig. 14. The dashed black line in Fig. 14 indicates the equilibrium position reported by Schaaf and Stark.20
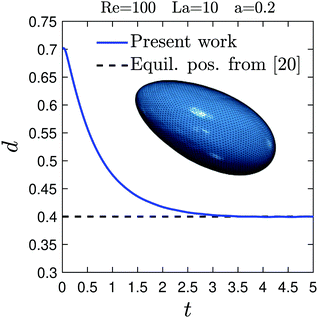 | ||
| Fig. 14 Inertial migration of a deformable capsule with La = 10 along the diagonal of a square microchannel at Reynolds number Re = 100. The dashed line shows the equilibrium position reported in ref. 20. The inset shows the equilibrium shape of the capsule. | ||
Lastly, to validate the implementation of solid particles, we demonstrate damped oscillations of the axial distance in a pair of solid particles. For this, we consider a pair of solid particles in the midplane of a rectangular microchannel with an aspect ratio 0.5. We fix the particle radius a, initial position (xlead, xlag), initial axial distance Δz, and Reynolds number Re to 0.4, (0.24, −0.2), 2, and 10, respectively. We use 75 lattice nodes to discretize the channel width. The surface of the solid particles is approximated using 20480 ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) 1 elements. The temporal evolution of the ratio Δz/a is plotted in Fig. 15, along with its steady-state value reported by Schaaf et al.60
1 elements. The temporal evolution of the ratio Δz/a is plotted in Fig. 15, along with its steady-state value reported by Schaaf et al.60
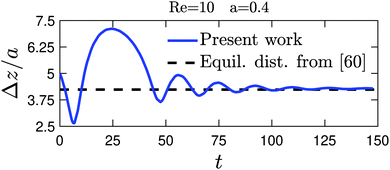 | ||
| Fig. 15 Damped oscillations of the axial distance Δz in a pair of solid particles with the initial position (xlead, xlag) = (0.24, −0.2). The dashed line shows the equilibrium distance reported in ref. 60. | ||
Acknowledgements
We thank C. Schaaf for sharing the source code. We acknowledge support from the Deutsche Forschungsgemeinschaft in the framework of the Collaborative Research Center SFB 910.References
- G. Y. Lee and C. T. Lim, Trends Biotechnol., 2007, 25, 111–118 CrossRef CAS PubMed.
- S. Suresh, J. Spatz, J. Mills, A. Micoulet, M. Dao, C. Lim, M. Beil and T. Seufferlein, Acta Biomater., 2005, 1, 15–30 CrossRef CAS PubMed.
- S. Suresh, Acta Biomater., 2007, 3, 413–438 CrossRef PubMed.
- A. van de Stolpe, K. Pantel, S. Sleijfer, L. W. Terstappen and J. M. den Toonder, Cancer Res., 2011, 71, 5955–5960 CrossRef CAS PubMed.
- X. Cheng, D. Irimia, M. Dixon, K. Sekine, U. Demirci, L. Zamir, R. G. Tompkins, W. Rodriguez and M. Toner, Lab Chip, 2007, 7, 170–178 RSC.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- E. K. Sackmann, A. L. Fulton and D. J. Beebe, Nature, 2014, 507, 181–189 CrossRef CAS PubMed.
- C. Haber, Lab Chip, 2006, 6, 1118–1121 RSC.
- A. Karimi, S. Yazdi and A. M. Ardekani, Biomicrofluidics, 2013, 7, 021501 CrossRef CAS PubMed.
- D. G. Grier, Nature, 2003, 424, 810–816 CrossRef CAS PubMed.
- B. Çetin and D. Li, Electrophoresis, 2011, 32, 2410–2427 CrossRef PubMed.
- T. P. Forbes and S. P. Forry, Lab Chip, 2012, 12, 1471 RSC.
- M. Evander, L. Johansson, T. Lilliehorn, J. Piskur, M. Lindvall, S. Johansson, M. Almqvist, T. Laurell and J. Nilsson, Anal. Chem., 2007, 79, 2984–2991 CrossRef CAS PubMed.
- A. Hochstetter, R. Vernekar, R. H. Austin, H. Becker, J. P. Beech, D. A. Fedosov, G. Gompper, S.-C. Kim, J. T. Smith, G. Stolovitzky, J. O. Tegenfeldt, B. H. Wunsch, K. K. Zeming, T. Krüger and D. W. Inglis, ACS Nano, 2020, 14, 10784–10795 CrossRef CAS PubMed.
- D. D. Carlo, Lab Chip, 2009, 9, 3038 RSC.
- J. M. Martel and M. Toner, Annu. Rev. Biomed. Eng., 2014, 16, 371–396 CrossRef CAS PubMed.
- J. Zhang, S. Yan, D. Yuan, G. Alici, N.-T. Nguyen, M. E. Warkiani and W. Li, Lab Chip, 2016, 16, 10–34 RSC.
- S. Razavi Bazaz, A. Mashhadian, A. Ehsani, S. C. Saha, T. Krüger and M. Ebrahimi Warkiani, Lab Chip, 2020, 20, 1023–1048 RSC.
- C. Prohm and H. Stark, Lab Chip, 2014, 14, 2115 RSC.
- C. Schaaf and H. Stark, Soft Matter, 2017, 13, 3544–3555 RSC.
- G. Segré and A. Silberberg, Nature, 1961, 189, 209–210 CrossRef.
- G. Segré and A. Silberberg, J. Fluid Mech., 1962, 14, 136–157 CrossRef.
- B. P. Ho and L. G. Leal, J. Fluid Mech., 1974, 65, 365–400 CrossRef.
- E. S. Asmolov, J. Fluid Mech., 1999, 381, 63–87 CrossRef CAS.
- J.-P. Matas, J. F. Morris and É. Guazzelli, J. Fluid Mech., 2009, 621, 59–67 CrossRef.
- K. Hood, S. Lee and M. Roper, J. Fluid Mech., 2015, 765, 452–479 CrossRef CAS.
- D. D. Carlo, J. F. Edd, K. J. Humphry, H. A. Stone and M. Toner, Phys. Rev. Lett., 2009, 102, 094503 CrossRef PubMed.
- X. Shao, Z. Yu and B. Sun, Phys. Fluids, 2008, 20, 103307 CrossRef.
- I. Lashgari, M. N. Ardekani, I. Banerjee, A. Russom and L. Brandt, J. Fluid Mech., 2017, 819, 540–561 CrossRef CAS.
- H. T. Kazerooni, W. Fornari, J. Hussong and L. Brandt, Phys. Rev. Fluids, 2017, 2, 084301 CrossRef.
- J.-P. Matas, J. F. Morris and É. Guazzelli, J. Fluid Mech., 2004, 515, 171–195 CrossRef.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Phys. Fluids, 2008, 20, 101702 CrossRef.
- K. Miura, T. Itano and M. Sugihara-Seki, J. Fluid Mech., 2014, 749, 320–330 CrossRef.
- C. Liu, G. Hu, X. Jiang and J. Sun, Lab Chip, 2015, 15, 1168–1177 RSC.
- J. Feng, H. H. Hu and D. D. Joseph, J. Fluid Mech., 1994, 277, 271–301 CrossRef.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS.
- P. G. Saffman, J. Fluid Mech., 1965, 22, 385–400 CrossRef.
- D. D. Carlo, D. Irimia, R. G. Tompkins and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18892–18897 CrossRef PubMed.
- S. C. Hur, N. K. Henderson-MacLennan, E. R. B. McCabe and D. D. Carlo, Lab Chip, 2011, 11, 912 RSC.
- C. K. W. Tam and W. A. Hyman, J. Fluid Mech., 1973, 59, 177–185 CrossRef.
- F. Risso, F. Collé-Paillot and M. Zagzoule, J. Fluid Mech., 2006, 547, 149 CrossRef CAS.
- S. K. Doddi and P. Bagchi, Int. J. Multiphase Flow, 2008, 34, 966–986 CrossRef CAS.
- G. Coupier, B. Kaoui, T. Podgorski and C. Misbah, Phys. Fluids, 2008, 20, 111702 CrossRef.
- L. Shi, T.-W. Pan and R. Glowinski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056308 CrossRef PubMed.
- D. S. Hariprasad and T. W. Secomb, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 033008 CrossRef PubMed.
- P. Bagchi, Biophys. J., 2007, 92, 1858–1877 CrossRef CAS PubMed.
- T. Krüger, Rheol. Acta, 2015, 55, 511–526 CrossRef.
- K. Vahidkhah, P. Balogh and P. Bagchi, Sci. Rep., 2016, 6, 28194 CrossRef CAS PubMed.
- P. Balogh and P. Bagchi, Physiol. Rep., 2019, 7, e14067 CrossRef PubMed.
- A. Kilimnik, W. Mao and A. Alexeev, Phys. Fluids, 2011, 23, 123302 CrossRef.
- S. J. Shin and H. J. Sung, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046321 CrossRef PubMed.
- Y. Kim and M.-C. Lai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 066321 CrossRef PubMed.
- D. Salac and M. J. Miksis, J. Fluid Mech., 2012, 711, 122–146 CrossRef.
- S. J. Shin and H. J. Sung, Int. J. Heat Fluid Flow, 2012, 36, 167–177 CrossRef.
- Z. Y. Luo, S. Q. Wang, L. He, F. Xu and B. F. Bai, Soft Matter, 2013, 9, 9651 RSC.
- Y.-L. Chen, RSC Adv., 2014, 4, 17908–17916 RSC.
- Z. Wang, Y. Sui, A.-V. Salsac, D. Barthès-Biesel and W. Wang, J. Fluid Mech., 2016, 806, 603–626 CrossRef CAS.
- D. Alghalibi, M. E. Rosti and L. Brandt, Phys. Rev. Fluids, 2019, 4, 104201 CrossRef.
- Y. Yan, J. F. Morris and J. Koplik, Phys. Fluids, 2007, 19, 113305 CrossRef.
- C. Schaaf, F. Rühle and H. Stark, Soft Matter, 2019, 15, 1988–1998 RSC.
- C. Schaaf and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2020, 43, 50 CrossRef CAS PubMed.
- J. F. Morris, J. Fluid Mech., 2016, 792, 1–4 CrossRef CAS.
- E. Lac, A. Morel and D. Barthès-Biesel, J. Fluid Mech., 2007, 573, 149–169 CrossRef.
- O. Aouane, A. Farutin, M. Thiébaud, A. Benyoussef, C. Wagner and C. Misbah, Phys. Rev. Fluids, 2017, 2, 063102 CrossRef.
- S. K. Doddi and P. Bagchi, Int. J. Multiphase Flow, 2008, 34, 375–392 CrossRef CAS.
- D. Leighton and A. Acrivos, J. Fluid Mech., 1987, 177, 109–131 CrossRef CAS.
- H. Lan and D. B. Khismatullin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012705 CrossRef PubMed.
- T. Krüger, B. Kaoui and J. Harting, J. Fluid Mech., 2014, 751, 725–745 CrossRef.
- T. Krüger, F. Varnik and D. Raabe, Comput. Math. Appl., 2011, 61, 3485–3505 CrossRef.
- H. Bruus, Theoretical microfluidics, Oxford University Press, Oxford New York, 2008 Search PubMed.
- S. Succi, The Lattice Boltzmann Equation for Fluid Dynamics and Beyond, Clarendon Press Oxford University Press, Oxford New York, 2001 Search PubMed.
- T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. M. Viggen, The Lattice Boltzmann Method: Principles and Practice, Springer, Berlin, Heidelberg, 2016 Search PubMed.
- T. Krüger, S. Frijters, F. Günther, B. Kaoui and J. Harting, Eur. Phys. J.-Spec. Top., 2013, 222, 177–198 CrossRef.
- Z. Guo, C. Zheng and B. Shi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 046308 CrossRef PubMed.
- J. Latt, PhD thesis, University of Geneva, 2007.
- J. Latt, B. Chopard, O. Malaspinas, M. Deville and A. Michler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 056703 CrossRef PubMed.
- J. Latt, O. Malaspinas, D. Kontaxakis, A. Parmigiani, D. Lagrava, F. Brogi, M. B. Belgacem, Y. Thorimbert, S. Leclaire, S. Li, F. Marson, J. Lemus, C. Kotsalos, R. Conradin, C. Coreixas, R. Petkantchin, F. Raynaud, J. Beny and B. Chopard, Comput. Math. Appl., 2021, 81, 334–350 CrossRef.
- H. Elman, D. Silvester and A. Wathen, Finite Elements and Fast Iterative Solvers: with Applications in Incompressible Fluid Dynamics, Oxford University Press, 2014 Search PubMed.
- R. Skalak, A. Tozeren, R. Zarda and S. Chien, Biophys. J., 1973, 13, 245–264 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CrossRef CAS PubMed.
- G. Gompper and D. M. Kroll, J. Phys. I, 1996, 6, 1305–1320 CrossRef.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- J.-M. Charrier, S. Shrivastava and R. Wu, J. Strain Anal. Eng. Des., 1989, 24, 55–74 CrossRef.
- T. Krüger, Computer simulation study of collective phenomena in dense suspensions of red blood cells under shear, Springer Spektrum, Wiesbaden, 2012 Search PubMed.
- T. Inamuro, Fluid Dyn., 2012, 44, 024001 CrossRef.
- K. Suzuki and T. Inamuro, Comput. Fluids, 2011, 49, 173–187 CrossRef.
- Z.-G. Feng and E. E. Michaelides, Comput. Fluids, 2009, 38, 370–381 CrossRef CAS.
- C. S. Peskin, Acta Numer., 2002, 11, 479–517 CrossRef.
- R. Mittal and G. Iaccarino, Annu. Rev. Fluid Mech., 2005, 37, 239–261 CrossRef.
- S. S. Jain, K. Kamrin and A. Mani, J. Comput. Phys., 2019, 399, 108922 CrossRef.
- Z. Wang, J. Fan and K. Luo, Int. J. Multiphase Flow, 2008, 34, 283–302 CrossRef CAS.
- S. K. Kang and Y. A. Hassan, Int. J. Numer. Methods Fluids, 2010, 66, 1132–1158 CrossRef.
- E. Evans and Y.-C. Fung, Microvasc. Res., 1972, 4, 335–347 CrossRef CAS PubMed.
- S. Ramanujan and C. Pozrikidis, J. Fluid Mech., 1998, 361, 117–143 CrossRef CAS.
- K. Wang, X. H. Sun, Y. Zhang, T. Zhang, Y. Zheng, Y. C. Wei, P. Zhao, D. Y. Chen, H. A. Wu, W. H. Wang, R. Long, J. B. Wang and J. Chen, R. Soc. Open Sci., 2019, 6, 181707 CrossRef CAS PubMed.
- W. Lee, H. Amini, H. A. Stone and D. D. Carlo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22413–22418 CrossRef CAS PubMed.
- K. Hood and M. Roper, Phys. Rev. Fluids, 2018, 3, 094201 CrossRef.
- A. Z. K. Yazdani and P. Bagchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 026314 CrossRef PubMed.
- D. A. Fedosov, M. Peltomäki and G. Gompper, Soft Matter, 2014, 10, 4258–4267 RSC.
- B. Kaoui, G. Biros and C. Misbah, Phys. Rev. Lett., 2009, 103, 188101 CrossRef PubMed.
- S. Kahkeshani, H. Haddadi and D. D. Carlo, J. Fluid Mech., 2016, 786, R3 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00276g |
| This journal is © The Royal Society of Chemistry 2021 |