 Open Access Article
Open Access ArticleTranslational and rotational diffusion coefficients of gold nanorods functionalized with a high molecular weight, thermoresponsive ligand: a depolarized dynamic light scattering study†
Déborah
Feller
 a,
Marius
Otten
a,
Marco
Hildebrandt
a,
Marcel
Krüsmann
a,
Gary
Bryant
a,
Marius
Otten
a,
Marco
Hildebrandt
a,
Marcel
Krüsmann
a,
Gary
Bryant
 b and
Matthias
Karg
b and
Matthias
Karg
 *a
*a
aPhysikalische Chemie I: Kolloide und Nanooptik, Heinrich-Heine-Universität Düsseldorf, 40225 Düsseldorf, Germany. E-mail: karg@hhu.de
bPhysics, School of Science, RMIT University, Melbourne, Victoria 3001, Australia
First published on 3rd March 2021
Abstract
Probing the rotational and translational diffusion and colloidal stability of nanorods is of significant fundamental interest with implications for many different applications. Recently R. Nixon-Luke and G. Bryant presented a method to analyze angle-dependent depolarized dynamic light scattering data allowing for the clear separation of the translational and rotational diffusion coefficients of gold nanorods in dilute suspension (R. Nixon-Luke and G. Bryant, Part. Part. Syst. Charact., 2018, 36, 1800388). In the present work we applied this analysis to gold nanorods decorated with high molecular weight, thermoresponsive poly-N-isopropylacrylamide ligands, which results in particles with lower effective aspect ratios. The temperature response of the ligand shell is studied. We precisely determine the translational and rotational diffusion coefficients over a broad range of temperatures and the results are compared to theoretical predictions. The results show that as temperature increases the ligands collapse, and the effective aspect ratio increases as the particle shape transitions from prolate spheroid at low temperatures to more cylindrical at high temperatures.
1 Introduction
Noble metal nanoparticles play an important role in nanotechnology due to their unique electrical and optical properties.2–4 Their interaction with light manifests in localized surface plasmon resonances (LSPRs) that result from the resonant excitation of the valence electrons by the oscillating electric field of the incident waves. Since these resonances are directly affected by parameters such as particle size, shape and composition, a lot of effort has been devoted to the synthesis of noble metal nanoparticles with defined morphologies. In particular in the field of gold nanoparticles, countless synthesis protocols have been reported with extraordinary control of particle size and shape with high yield and low dispersities.5–9 For applications such as metamaterials, sensing and photothermal actuation, gold nanorods are particularly interesting as they support intense longitudinal LSPRs with a resonance wavelength and strength that depend on the rod length.10 Simply through variation of the length, the longitudinal LSPR can be shifted from the red to the infrared spectral region.11,12 Furthermore, gold nanorods are an ideal model system for anisotropic colloids as their aspect ratio can be adjusted over a broad range. To increase the colloidal stability and be able to remove the large excess of surfactant that is commonly used in the synthesis of gold nanorods, ligand exchange with end-functionalized polymers is a well suited approach. By ligand exchange it is also possible to provide nanoparticles with additional properties, for example if stimuli-responsive polymers are used as ligands.13 These hybrid particles can yield new multifunctional materials that can exploit synergistic effects and/or feature new properties that neither of the individual components possess on their own. Along these lines gold nanoparticles have been combined with thermoresponsive polymers to allow for photothermal manipulation of the polymer via laser excitation of the plasmonic particles.14,15 Conversely, conformational changes of thermoresponsive polymers can be used to trigger LSPR shifts of plasmonic particles.16,17 In the special case of gold nanorods, thermoresponsive polymer ligands may allow for external manipulation of the effective aspect ratio via temperature, i.e. a smaller aspect ratio for good solvent conditions where the ligand shell is in an expanded state and a higher aspect ratio for bad solvent conditions where the ligand shell is collapsed onto the nanorod surface. These changes will ultimately affect the translational and rotational diffusion of the nanorods. For isotropic particles in a dilute dispersion, diffusion is commonly studied by dynamic light scattering (DLS) yielding average relaxation times that can be directly used to determine the translational diffusion coefficient. For anisotropic particles, translational as well as rotational motions contribute to the autocorrelation function recorded in DLS. Thus, the determination of particle dimensions, i.e. the length and diameter, is not possible by standard DLS. For nanorods stabilized by polymer ligands, standard DLS can also not be used to measure the shell thickness that determines the effective aspect ratio of the particles. To decouple translational and rotational motion, depolarized DLS (DDLS) has been successfully applied to various systems like tobacco mosaic virus,18 dumbbell-shaped polyelectrolyte brushes,19 and gold nanorods,1,20,21 among others.In this work, we study gold nanorods that were surface functionalized with high molecular weight, thermoresponsive polymer ligands composed of poly-N-isopropylacrylamide (PNIPAM). The structure of the particles and their response to temperature is schematically illustrated in Scheme 1. DLS and DDLS were used to study the diffusion in dilute aqueous dispersion over a wide range of scattering angles and for temperatures below and close to the lower critical solution temperature (LCST) of the polymer ligand. This allowed for the determination of the rotational and translational diffusion coefficients as a function of temperature. The ligand thickness was estimated using the isotropic scattering of polymer decorated spherical gold nanoparticles as a reference system. This in turn could be used to calculate the effective aspect ratio of the polymer decorated nanorods. Our findings were compared to the theoretical prediction for prolate spheroids.
2 Theory
2.1 DLS
In DLS, the fluctuations of the scattering intensity are measured over time and converted into the intensity–time autocorrelation function g(2)(τ).22 | (1) |
| g(2)(τ) = 1 + β|g(1)(τ)|2 | (2) |
For a dilute dispersion of monodisperse, isotropic scattering objects g(1)(τ) follows a single exponential decay function:
| g(1)(τ) = exp(−Γτ) | (3) |
| Γ = Dtq2 | (4) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) :
: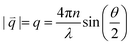 | (5) |
Using Dt the hydrodynamic radius RH can be calculated by applying the Stokes–Einstein equation:
 | (6) |
In this work all experiments were performed with incident laser light that is vertically linearly polarized. Measurements under two different polarization conditions were performed: (1) the polarizer in front of the detector is oriented vertically (VV measurement). This corresponds to a standard polarized DLS experiment. (2) The polarizer in front of the detector is oriented horizontally (H), the scattering is depolarized and is designated a VH measurement. This corresponds to a DDLS experiment.
g(1)VV(q,τ) = S0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Dtq2τ) + S2 exp(−Dtq2τ) + S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(Dtq2 + 6Dr)τ) exp(−(Dtq2 + 6Dr)τ) | (7) |
By plotting g(1)VV(q,τ) against q2τ, it is possible to identify the range of scattering angles for which Dt can be reliably determined. For these scattering angles eqn (7) can be used to determine Dt.
g(2)VH(q,τ) − 1 = β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2(q2Dt + 6Dr)τ) exp(−2(q2Dt + 6Dr)τ) | (8) |
2.2 Theoretical calculations of Dr and Dt
The theory of Tirado and Garcia de la Torre (TG)23,24 is well-established to predict the diffusion coefficients of rod like particles which have an aspect ratio p = L/D of 2 < p < 30. While this theory should hold for our gold nanorod cores (p ≈ 6), the PNIPAM ligand shell leads to a significant reduction of the effective aspect ratio (p < 2), where the TG theory is no longer applicable. For this reason, the theory established by Perrin for prolate ellipsoids is applied.20,25The translational diffusion coefficient Dt is given by:
 | (9) |
| F(p) = pS(p) | (10) |
 | (11) |
The rotational diffusion coefficient Dr is given by:
 | (12) |
 | (13) |
3 Results and discussion
3.1 Determination of size and shape of the gold nanorods
In this work, two batches of gold nanorods (AuNRs) decorated with the same PNIPAM ligand (AuNR–PNIPAM) are analysed. The nanorods vary in their diameter D and length L. Fig. 1a and b show selected bright-field TEM images of the respective AuNR–PNIPAM particles. Both samples confirm the high yield of near monodisperse nanorods with very few spherical particles. Additional images for both particle species recorded at low and high magnification as well as histograms for L and D determined from TEM are shown in the ESI,† Fig. S1–S6. Although drop-casting was used to prepare the samples, neither particle species agglomerated on the TEM grids upon drying. Both samples show a nearly constant separation between the particles. These observations can be explained by the steric hinderance of the polymer brushes during the drying process, even if the brushes collapse during this process. Further, as a result of the comparatively low contrast, the polymer brush is difficult to visualise – however, the collapsed polymer brushes on the AuNR surface can be seen in the higher magnification images shown in Fig. S3 and S6 in the ESI.† To determine the dimensions of the nanorod cores, 130 particles were measured for each sample. The core diameter and length for AuNR–PNIPAM-1 are 12.5 ± 0.8 nm and 76.0 ± 8.4 nm, respectively and for AuNR–PNIPAM-2 10.8 ± 0.9 nm and 65.7 ± 6.9 nm. The dimensions are also listed in Table 1 along with the resulting aspect ratios. Within the errors both AuNR samples possess the same aspect ratio (p = 6.1).| AuNR–PNIPAM-1 | AuNR–PNIPAM-2 | |||
|---|---|---|---|---|
| TEM | SAXS | TEM | SAXS | |
| L [nm] | 76.0 ± 8.4 | 76.0 ± 3.7 | 65.7 ± 6.9 | 65.7 ± 3.0 |
| D [nm] | 12.5 ± 0.8 | 12.4 ± 0.6 | 10.8 ± 0.9 | 10.4 ± 0.6 |
| Aspect ratio p = L/D | 6.1 ± 1.0 | 6.1 ± 0.6 | 6.1 ± 1.2 | 6.3 ± 0.7 |
To also study the size, shape and stability of the AuNR–PNIPAM samples in dispersion and as an ensemble average, we performed small-angle X-ray scattering (SAXS) measurements. The resulting SAXS profiles in Fig. 2c show a pronounced form factor (P(q)) with several minima at high q values, which supports the low polydispersity observed by TEM. Because of the low X-ray scattering length density difference between PNIPAM and the dispersion medium (water) as compared to the high contrast of the AuNR, the SAXS profiles are dominated by scattering of the AuNR cores. It is not possible to resolve the PNIPAM brushes in these measurements. In order to describe the SAXS profiles, we applied the model for a long cylindrical particle (see ESI† for a detailed discussion and equations). To account for a small fraction of aggregates in the samples, contributing only at low q, a fractal contribution was added to the cylinder form factor. In general the obtained length L and diameter D from the cylinder model (see values in Table 1) are in good agreement with the values obtained from TEM. Small differences are ascribed to the much better statistics in SAXS compared to TEM measurements due to the higher number of examined particles. Thus, in the following we will use the dimensions obtained from SAXS for further analysis.
 | ||
| Fig. 2 Results from angle-dependent DLS experiments at 25 °C. g(1)VV(q,τ) for AuNR–PNIPAM-1 (a) and AuNR–PNIPAM-2 (b) at a range of scattering angles from 20° to 140° in steps of 10°. The scattering angle increases from blue to red. Selected g(1)VV(q,τ) plotted against q2τ for AuNR–PNIPAM-1 (c) and for AuNR–PNIPAM-2 (d) only showing the range of angles where the long-time decay fully collapses onto a master curve. Example g(1)VV(q,τ) from 120° scattering angle (black lines) and fits using eqn (7) (red lines) for AuNR–PNIPAM-1 (e) and AuNR–PNIPAM-2 (f). | ||
The optical properties of the AuNR–PNIPAM samples were studied using UV/vis spectroscopy. Respective spectra are shown in Fig. S8 and S9 in the ESI.† Both samples feature a transverse LSPR at approximately 510 nm and longitudinal LSPRs at approximately 974 nm for AuNR–PNIPAM-1 and at 908 nm for AuNR–PNIPAM-2 at 15 °C. Increasing the temperature leads to a significant redshift of the longitudinal LSPR for both samples. This redshift is attributed to the increased local refractive index due to the collapse of the ligand shell confirming once more the success of the ligand exchange with the PNIPAM ligands.
3.2 DLS and DDLS measurements
We performed DLS and DDLS measurements at temperatures below and close to the LCST of the PNIPAM ligands over a wide range of scattering angles to precisely determine the translational and rotational diffusion coefficients.The decay of the correlation functions moves to shorter delay times τ with increasing scattering angle. At scattering angles from 20° to 60° (purple to blue), the curves show a clear bimodal decay behavior, while for larger angles the curves appear nearly monomodal. To precisely determine the translational diffusion coefficients from the DLS data, the correlation data are plotted as a function of q2τ as shown in Fig. S10 and S12 in the ESI.† For homogeneous and isotropic scattering objects, it is expected that all curves collapse onto a master curve if plotted against q2τ. For our AuNR–PNIPAM particles this is clearly not the case. In this case both Dt and Dr contribute to the correlation functions. One can see that the long-time decay follows the expected scaling for translational diffusion at large enough scattering angles. Fig. 2c and d shows the selected correlation functions for scattering angles from 70° to 140° where the scaling is fulfilled. It should be noted that the first decay at short delay times does not collapse for any scattering angle, which is an indication that this decay is due to a combination of rotation and translation. The second decay at longer delay times is only caused by translational motion at these scattering angles. Therefore, only curves at these angles will be fitted using eqn (7) yielding values for Dt. The high quality of the fits is demonstrated by the examples in Fig. 2e and f, for correlation functions from a scattering angle of 120 °C. The corresponding fits match almost perfectly with the experimental curves. This observation is further confirmed by the calculated deviation between the experimental and fitted curves as shown in Fig. S11 and S13 in the ESI.†
The determined values of Dt are plotted as a function of q in Fig. 3a and c. As expected for translational diffusion of a highly dilute particle dispersion, nearly constant values of Dt were obtained over the whole q-range for both samples. Thus, in the following we will use the q-average values of Dt indicated by the red lines in Fig. 3a and c for analysis of the DDLS data. The average value of Dt is significantly higher for the AuNR–PNIPAM-2 particles because of their smaller length as compared to AuNR–PNIPAM-1 (see eqn (9)).
 | ||
| Fig. 4 Results from angle-dependent DDLS measurements. g(2)VH(q,τ) − 1 for AuNR–PNIPAM-1 (a) and AuNR–PNIPAM-2 (b). Shown are data recorded for scattering angles between 20° and 140° in 10° steps. The scattering angle increases from blue to red. Representative g(2)VH(q,τ) − 1 at 120° scattering angle for AuNR–PNIPAM-1 (c) and AuNR–PNIPAM-2 (d). The red lines are the corresponding fits to the data using eqn (8). | ||
To analyse the DDLS data, g(2)VH(q,τ) − 1 was fitted using eqn (8) with the average value of Dt obtained from DLS measurements as a fixed parameter. The representative fits recorded at 120° scattering angle presented in Fig. 4c and d show only small deviations from the data, mostly at longer delay times. The deviation is calculated and shown in Fig. S14 and S15 in the ESI.† These small deviations are likely due to the (small) inherent polydispersity of the particles, which is not taken into account in this analysis.
The obtained values of Dr are plotted as a function of q in Fig. 3a and c. Despite a general trend of slightly increasing Dr with increasing q for both samples, the changes in Dr in the measured q-range are small (less than 5% from the average as indicated by the grey error corridors in Fig. 3). Thus, in the following we will use the q-average values of Dr for further analysis and discussion of temperature dependent data. Like the translational diffusion coefficient, the average value of Dr is significantly higher for the AuNR–PNIPAM-2 particles because of their smaller length compared to AuNR–PNIPAM-1 (see eqn (12)).
3.3 Comparison to theory
Although the presented light scattering measurements are well suited to determine Dt and Dr with high precision, it is not straightforward to determine the thickness of the PNIPAM brushes on the gold nanorods. This information however is needed to allow for any comparison to theory. Therefore, we chose to measure gold nanospheres that were decorated with the same PNIPAM ligand as an isotropic reference system. Since these particles are only expected to show a contribution from translational diffusion in DLS, it is possible to accurately determine their hydrodynamic radii Rh at different temperatures. The corresponding description of the synthesis and the characterization of these AuNS–PNIPAM particles by TEM, SAXS, DLS and UV/vis spectroscopy can be found in the ESI† (Fig. S17–S20). Using the radius of the gold cores from SAXS (6.89 ± 0.06 nm) and the hydrodynamic radii from DLS, we calculated the brush thickness T for a broad range of temperatures. The respective values are listed in Table S2 in the ESI.† At a temperature of 25 °C, the brush thickness is 34.5 ± 0.1 nm. This value is slightly smaller but still in good agreement to the theoretically calculated thickness of 43.2 nm using the radius of gyration and assuming good solvent conditions. More details about the theoretical calculation are provided in the ESI.† The discrepancy between the theoretical brush thickness and the experimental brush thickness can be explained by the relatively large polydispersity of our ligand. Since the theoretical calculation is based on the average molecular weight and does not take into account the high polydispersity, the theoretical brush thickness is overestimated. For the following considerations we will use the experimental values of T obtained from DLS measurements of our spherical reference particles assuming that the grafting density on the rods is comparable. To calculate the effective aspect ratio of the gold nanorods decorated with the polymer brushes, the experimental values of T are added twice to the length L and the diameter D of the gold nanorod cores obtained from the SAXS experiment. The resulting dimensions and aspect ratios for 25 °C are summarized in Table 2.| AuNR cores | AuNR–PNIPAM-1 | AuNR–PNIPAM-2 | |||
|---|---|---|---|---|---|
| AuNR-1 | AuNR-2 | ||||
| L [nm] | 76.0 ± 3.7 | 65.7 ± 3.0 | L + 2T [nm] | 145 ± 4 | 135 ± 3 |
| D [nm] | 12.4 ± 0.6 | 10.4 ± 0.6 | D + 2T [nm] | 81 ± 1 | 79 ± 1 |
| p = L/D | 6.1 ± 0.6 | 6.3 ± 0.7 | p = (L + 2T)/(D + 2T) | 1.8 ± 0.1 | 1.7 ± 0.1 |
Using the estimated total dimensions of the AuNR–PNIPAM particles we calculated the theoretical diffusion coefficients according to eqn (9) and (12). The results are listed in Tables S3 and S4 (ESI†) in direct comparison to the experimentally determined values. The experimental diffusion coefficients are larger than the theoretically calculated ones for both samples at all temperatures. The deviation is smallest for AuNR–PNIPAM-1 at 25 °C where we find Dt = 4.82 ± 0.23 μm2 s−1 and Dr = 1.48 ± 0.27 ms−1 from theory and Dt = 5.68 ± 0.10 μm2 s−1 and Dr = 1.54 ± 0.03 ms−1 from experiment. For the slightly shorter particles AuNR–NIPAM-2, we find Dt = 5.05 ± 0.29 μm2 s−1 and Dr = 1.79 ± 0.25 ms−1 from theory and Dt = 6.46 ± 0.25 μm2 s−1 and Dr = 2.75 ± 0.06 ms−1 from experiment at 25 °C. With increasing temperature the deviation between experiment and theory increases as shown by the corresponding ratios (Exp./Theo.) listed in Tables S3 and S4 (ESI†).
While the theory and experiment are in reasonable agreement, there are some differences, which can be explained as follows:
(1) The dimensions of the AuNR–PNIPAM particles used for the theoretical calculations assume the same brush thickness as experimentally determined for the spherical reference particles. While this is most likely the case for the tips of the gold nanorods where the curvature is comparable to the curvature of the spheres, we expect a different grafting density and brush thickness on the sides of the rods. Thus, the estimated total diameter (D + 2T) is only approximate. For example, a reduction in the brush thickness on the sides of 10% (everything else being equal) leads to good agreement with theory at 25 °C. Further studies of the brush thickness as a function of curvature may shed light on this effect.
(2) With increasing temperature the brush thickness decreases, leading to an increase in the effective aspect ratio. Consequently, the theoretical model becomes less appropriate as the particles become less ellipsoidal due to the ligand shell collapse.
In future works it might be interesting to study different molecular weight ligands and different grafting densities assumed that the latter quantity can be precisely determined. We expect the grafting density to have a significant influence on the temperature response of the ligand shell, i.e. for higher grafting densities, the collapse of the brush will be less pronounced and vice versa for lower grafting densities. With shorter or longer ligands, the effective aspect ratio and also its temperature-dependence will be altered allowing more tunability of the system.
4 Conclusion
We have measured intensity–time autocorrelation functions of gold nanorods decorated with thermoresponsive polymer ligands using dynamic and depolarized dynamic light scattering. Measurements were performed over a broad range of scattering angles to precisely determine the translational and rotational diffusion coefficients. Experiments at different temperatures approaching the lower critical solution temperature of the polymer ligand were used to study the increase of both diffusion coefficients with temperature. The observed changes are attributed to changes in the overall hydrodynamic particle volume and in the effective aspect ratio due to the collapse of the polymer ligand with increasing temperature. The thickness of the ligand shell and its temperature dependent changes were determined using polymer decorated gold nanoparticles of spherical shape as isotropic reference particles. Using this information, we could theoretically calculate the expected diffusion coefficients for the gold nanorods. Using a model of prolate spheroids we find very good agreement between experiment and theory. Slight deviations were attributed to the relatively large polydispersity of our ligand and potential differences in grafting density and thus brush thickness at the tips of the nanorods as compared to their sides. As the ligand shell collapses in response to an increase in temperature, the theoretical model becomes less suitable to describe the experiment. This observation is explained by the decreasing effective aspect ratio of the particles as the ligand shell collapses. Thus, the particles become less ellipsoidal and more cylindrical with increasing temperature. The ability to tune the aspect ratio offers a unique tool for understanding diffusion of anisotropic particles, and has the potential for a range of applications in colloid science, such as understanding self-assembly processes in suspensions of anisotropic particles.5 Experimental section
5.1 Materials
Cetyltrimethylammonium bromide (CTAB; VWR Chemicals, ≥99%), dimethylformamide (DMF; Aldrich, > 99.8%), 2-(dodecylthiocarbonothioylthio)-2-methylpropanoic acid (DDMAT; Aldrich, >99%), gold(III) chloride trihydrate (HAuCl4; Sigma-Aldrich, ≥99.9%), hydroquinone (Roth, ≥99.5%), N-isopropylacrylamide (NIPAM; TCI, >98%), silver nitrate (AgNO3; Fluka, ≥99.5%), sodium borohydride (NaBH4; Sigma-Aldrich, 99%) and sodium hydroxide (NaOH; Fisher Scientific, UK) were used as received. Water was purified with a Merck Milli-Q system resulting in a final water resistivity of 18 MΩ cm.5.2 Synthesis
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1. Further details can be found in the ESI.†
000 g mol−1. Further details can be found in the ESI.†
5.3 Sample preparation
The initial CTAB stabilizer on the surface of the as-prepared AuNR was exchanged by PNIPAM to render the particles with a thermoresponsive polymer shell.13 For this purpose, 0.46 g of PNIPAM were mixed with 45.9 mL Milli-Q water. 18 mL of the PNIPAM solution was added to AuNR–PNIPAM-1 and 20 mL to AuNR–PNIPAM-2. It is important that an excess of polymer is added to grant the ligand exchange of CTAB to PNIPAM. The samples were purified and centrifugated at 6810 rcf for 90 minutes at 30 °C. The residues were redispersed in water. The purification process was repeated twice. To further enhance the colloidal stability of the samples, additional ligand exchange steps were performed. For this, PNIPAM (0.77 mg for AuNR–PNIPAM-1 and 0.91 mg for AuNR–PNIPAM-2) was dissolved in 0.5 mL water and 0.1 mg of NaBH4 were added to cleave off the trithiocarbonate terminal group and render the ligand with thiol termini. After stirring for 10 minutes, the solution was added to 5 mL of the aqueous gold nanorod samples (0.625 mM). The solutions were stirred for 120 hours and then centrifuged once for 24 hours at 5985 rcf at 20 °C. The residues were dispersed in 5 mL Milli-Q water.5.4 Methods
The 2D image series for the electron tomography were recorded in bright-field mode using a high-tilt sample holder. The tilt series was acquired with automatic rectification (corrections of focus and horizontal and vertical displacement) by using the recorder software from the TEMographyTM 3-D Reconstruction software package (System in Frontier, Inc., Tachikawa, TYO, JP) on a 4096 × 4096 pixels GatanTM OneView camera (Gatan, Inc., Pleasanton, CA, USA). The tilt range was set from −67° to 75° with a basic increment of 1°, giving a total of 142 images. The tilt series data was treated for image processing and reconstruction using the Composer and Visualizer-evo software from the TEMographyTM 3-D Reconstruction software package.
Conflicts of interest
There are no conflicts to declare.Note after first publication
This article replaces the version published on the 10th March 2021, which contained errors in eqn (1).Acknowledgements
MK wants to acknowledge financial support by the German Academic Exchange service (DAAD) through its Thematic Network Melbourne-Bayreuth Polymer/Colloid Network sponsored from funds of the Federal Ministry of Education and Research (BMBF). MK thanks the German Research Foundation (DFG) for funding under grant KA3880/6-1. The authors acknowledge the DFG and the state of NRW for funding the cryo-TEM (INST 208/749-1 FUGG). The authors thank the Center for Structural Studies that is funded by the Deutsche Forschungsgemeinschaft (DFG Grant numbers 417919780 and INST 208/761-1 FUGG) for access to the SAXS instrument. Kristina Wagner (HHU Düsseldorf) and Christina Noffke (HHU Düsseldorf) are acknowledged for the synthesis of the PNIPAM ligand and the gold nanorods, respectively. The authors acknowledge Carolin Ganas for designing and preparing the table of contents graphics.Notes and references
- R. Nixon-Luke and G. Bryant, Part. Part. Syst. Charact., 2018, 36, 1800388 CrossRef.
- U. Kreibig and M. Vollmer, Optical Properties of Metal Clusters, Springer, Berlin, 1995 Search PubMed.
- S. A. Maier, M. L. Brongersma, P. G. Kik, S. Meltzer, A. A. G. Requicha and H. A. Atwater, Adv. Mater., 2001, 13, 1501–1505 CrossRef CAS.
- E. Ozbay, Science, 2006, 311, 189–193 CrossRef CAS PubMed.
- M. Grzelczak, J. Perez-Juste, P. Mulvaney and L. M. Liz-Marzan, Chem. Soc. Rev., 2008, 37, 1783–1791 RSC.
- S. J. Tan, M. J. Campolongo, D. Luo and W. L. Cheng, Nat. Nanotechnol., 2011, 6, 268–276 CrossRef CAS PubMed.
- K. Z. Liu, Z. L. He, J. F. Curtin, H. J. Byrne and F. R. Tian, Sci. Rep., 2019, 9, 7421 CrossRef.
- N. G. Bastus, J. Comenge and V. Puntes, Langmuir, 2011, 27, 11098–11105 CrossRef CAS.
- J. Perez-Juste, I. Pastoriza-Santos, L. M. Liz-Marzan and P. Mulvaney, Coord. Chem. Rev., 2005, 249, 1870–1901 CrossRef CAS.
- A. V. Alekseeva, V. A. Bogatyrev, B. N. Khlebtsov, A. G. Mel'nikov, L. A. Dykman and N. G. Khlebtsov, Colloid J., 2006, 68, 661–678 CrossRef CAS.
- L. Vigderman and E. R. Zubarev, Chem. Mater., 2013, 25, 1450–1457 CrossRef CAS.
- B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962 CrossRef CAS.
- T. Honold, D. Skrybeck, K. G. Wagner and M. Karg, Langmuir, 2016, 33, 253–261 CrossRef PubMed.
- N. Carl, J. Sindram, M. Gallei, S. U. Egelhaaf and M. Karg, Phys. Rev. E, 2019, 100, 052605 CrossRef CAS PubMed.
- S. Murphy, S. Jaber, C. Ritchie, M. Karg and P. Mulvaney, Langmuir, 2016, 32, 12497–12503 CrossRef CAS PubMed.
- M. Tagliazucchi, M. G. Blaber, G. C. Schatz, E. A. Weiss and I. Szleifert, ACS Nano, 2012, 6, 8397–8406 CrossRef CAS PubMed.
- M. Karg, S. Jaber, T. Hellweg and P. Mulvaney, Langmuir, 2011, 27, 820–827 CrossRef CAS PubMed.
- D. Lehner, H. Lindner and O. Glatter, Langmuir, 2000, 16, 1689–1695 CrossRef CAS.
- M. Hoffmann, Y. Lu, M. Schrinner, M. Ballauff and L. Harnau, J. Phys. Chem. B, 2008, 112, 14843–14850 CrossRef CAS PubMed.
- M. Glidden and M. Muschol, J. Phys. Chem. C, 2012, 116, 8128–8137 CrossRef CAS.
- J. Rodríguez-Fernández, J. Pérez-Juste, L. M. Liz-Marzán and P. R. Lang, J. Phys. Chem. C, 2007, 111, 5020–5025 CrossRef.
- B. J. Berne and R. Pecora, Dynamic Light Scattering: With Applications to Chemistry, Biology and Physics, Dover Publications, New York, 1976 Search PubMed.
- M. A. M. Tirado and J. G. A. de la Torre, J. Chem. Phys., 1980, 73, 1986–1993 CrossRef CAS.
- M. M. Tirado and J. G. A. de la Torre, J. Chem. Phys., 1979, 71, 2581–2587 CrossRef CAS.
- F. J. Perrin, J. Phys. Radium, 1936, 7, 1–11 CrossRef CAS.
- B. Ebeling and P. Vana, Macromolecules, 2013, 46, 4862–4871 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00077b |
| This journal is © The Royal Society of Chemistry 2021 |




