Open Access Article
Open Access ArticleParticle sizing for flowing colloidal suspensions using flow-differential dynamic microscopy†
James A.
Richards
 *,
Vincent A.
Martinez
*,
Vincent A.
Martinez
 * and
Jochen
Arlt
* and
Jochen
Arlt
 *
*
SUPA and School of Physics and Astronomy, University of Edinburgh, King's Buildings, Edinburgh EH9 3FD, UK. E-mail: james.a.richards@ed.ac.uk; vincent.martinez@ed.ac.uk; j.arlt@ed.ac.uk
First published on 10th March 2021
Abstract
Particle size is a key variable in understanding the behaviour of the particulate products that underpin much of our modern lives. Typically obtained from suspensions at rest, measuring the particle size under flowing conditions would enable advances for in-line testing during manufacture and high-throughput testing during development. However, samples are often turbid, multiply scattering light and preventing the direct use of common sizing techniques. Differential dynamic microscopy (DDM) is a powerful technique for analysing video microscopy of such samples, measuring diffusion and hence particle size without the need to resolve individual particles while free of substantial user input. However, when applying DDM to a flowing sample, diffusive dynamics are rapidly dominated by flow effects, preventing particle sizing. Here, we develop “flow-DDM”, a novel analysis scheme that combines optimised imaging conditions, a drift-velocity correction and modelling of the impact of flow. Flow-DDM allows a decoupling of flow from diffusive motion that facilitates successful particle size measurements at flow speeds an order of magnitude higher than for DDM. We demonstrate the generality of the technique by applying flow-DDM to two separate microscopy methods and flow geometries.
1 Introduction
Solid micron-sized particles, say from 100 nm to several μm, dispersed in a liquid are ever present in our lives. These colloidal suspensions form the basis of consumer formulations (e.g. sunscreen), construction materials, and even pharmaceuticals or food. In all these applications the particle size can be of critical importance for performance, controlling the strength of concrete1 and paint film formation,2 or the rates of drug adsorbtion.3 Particle size can even influence our sensory perception of materials, as with the taste of chocolate.4Measuring the size of particles in formulations is therefore an important task, both during development (e.g. high-throughput testing), but also in real-time during manufacture to ensure a consistent formulation. To achieve these goals it is necessary to characterise a suspension not just in a quiescent (non-flowing) state but also under flowing conditions. For quiescent samples, various approaches to particle sizing exist, for which the reference method is to determine size directly from high-resolution electron microscopy images.5 However, this requires dry particles (it is not an in situ method) and expensive equipment. More routine laboratory techniques for sizing particles in suspension include the well-established methods of static and dynamic light-scattering (SLS and DLS).6 SLS measures the particle form factor (and hence size) from the average intensity scattered; in contrast, DLS measures the free diffusion coefficient, D0, via temporal fluctuations of the scattered intensity due to Brownian motion. From D0, the particle diameter, d, can be extracted via the Stokes–Einstein relation. DLS has been extended to flowing systems for in-line testing, but the measured particle size is impacted by flow speed.7
However, for formulation science a more fundamental issue arises for both SLS and DLS, as the techniques are strongly affected by multiple scattering, where photons interact with more than one particle before reaching the detector. Although suppression of multiple scattering is possible using advanced DLS techniques,8,9 highly dilute and transparent samples are required for standard commercial DLS setups. For formulations, which may even be turbid, this is an excessively restrictive requirement.
This limitation arises from the fact that DLS operates on a large scattering volume. One can also extract size from dynamics in a smaller volume by tracking individual particles from video microscopy.10 However, this approach requires identifying individual particles, a task which becomes impracticable for smaller particles (d ≲ 500 nm) or in non-dilute, turbid systems,11 although one which machine learning is being applied to.12 Using differential dynamic microscopy (DDM),13 a digital Fourier analysis of video microscopy, we avoid both user inputs and particle location. DDM has been used to characterise the micro-rheological properties of fluids;14–16 to enable high-throughput measurements of micro-organism motility;17–19 and to measure particle diffusion in complex environments,20,21 under external fields,22 and even in dense or turbid systems.23–25
However, for flowing suspensions the fluid's velocity can impact many particle-sizing techniques, causing an apparent increase in diffusion and an underestimation of particle size.7,26 Therefore, for reliable particle sizing microscopic diffusive motion must be disentangled from the impact of bulk flow. The effect of flow on another digital Fourier microscopy technique27 related to DDM has recently been suggested, but this was limited to exploring qualitative changes in the microscopic dynamics of soft solids.28
Here, we present “flow-DDM”, a novel DDM-based analysis scheme to quantitatively measure diffusive dynamics in flowing samples using a combination of drift-velocity correction and an appropriate theoretical model. Respectively, these reduce the contribution of the flow to the dynamics and allow a careful decoupling of the diffusive dynamics from the residual effects of flow. Using dilute colloidal suspensions, we systematically validate flow-DDM as a function of flow speed for the accurate measurement of particle size. We find that flow-DDM outperforms current DDM techniques by an order of magnitude in the maximum possible flow speed. We establish a measurement protocol, bounds for reliable diffusion measurements and a guide to optimise the imaging method, which together could be widely applied for particle sizing in a multitude of flowing samples. This is demonstrated using phase-contrast microscopy of Poiseuille flow and fluorescence confocal microscopy of a rheometric shear flow.
2 Modelling the impact of flow
2.1 Differential dynamic microscopy
Before describing the impact of flow, we shall briefly cover how DDM can be used for particle sizing in a quiescent sample. DDM characterises the spatio-temporal density fluctuations within a sample by analysing microscopy movies, I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t), of a sample region. Specifically, one computes the differential intensity correlation function (DICF), also known as the image structure function:
,t), of a sample region. Specifically, one computes the differential intensity correlation function (DICF), also known as the image structure function: | (1) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ,t) the Fourier transform of I(
,t) the Fourier transform of I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) and τ the delay time. Under appropriate imaging conditions and assuming the intensity fluctuations are proportional to fluctuations in sample density (ΔI ∝ Δρ) the DICF can be written as22
,t) and τ the delay time. Under appropriate imaging conditions and assuming the intensity fluctuations are proportional to fluctuations in sample density (ΔI ∝ Δρ) the DICF can be written as22 | (2) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) characterises the signal amplitude (which will depend both on sample properties, such as the particle's form factor, and the imaging system) and B(
) characterises the signal amplitude (which will depend both on sample properties, such as the particle's form factor, and the imaging system) and B(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) accounts for uncorrelated background noise. Here f(
) accounts for uncorrelated background noise. Here f(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ,τ), often known as the intermediate scattering function (ISF), is the
,τ), often known as the intermediate scattering function (ISF), is the ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) -Fourier component of the probability of the particle displacements,
-Fourier component of the probability of the particle displacements,  ,
,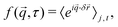 | (3) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ,τ) is a real valued function and if the underlying dynamics are isotropic it only depends on |
,τ) is a real valued function and if the underlying dynamics are isotropic it only depends on |![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) | = q, leading back to the more familiar, simplified expression: g(q) = A(q)[1 − f(q,τ)] + B(q). To extract information from the DICF, a parameterised ISF must be fitted. For non-interacting Brownian particles with diameter, d,
| = q, leading back to the more familiar, simplified expression: g(q) = A(q)[1 − f(q,τ)] + B(q). To extract information from the DICF, a parameterised ISF must be fitted. For non-interacting Brownian particles with diameter, d,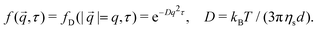 | (4) |
2.2 Impact of flow on DDM
Under flowing conditions, the total displacement of a Brownian particle, δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , is the sum of diffusive motion and ballistic motion due to flow, δ
, is the sum of diffusive motion and ballistic motion due to flow, δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) v. Using eqn (3), the ISF can be expressed as a product of separate processes:28
v. Using eqn (3), the ISF can be expressed as a product of separate processes:28 | (5) |
A uniform steady flow, with velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) , will shift the position of each particle by δ
, will shift the position of each particle by δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) v =
v = ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) τ in addition to diffusive motion, introducing a phase shift into the ISF:
τ in addition to diffusive motion, introducing a phase shift into the ISF:
 | (6) |
This is apparent in the DICF as ‘waves’ in the direction of flow, as illustrated in Fig. 1(a), which shows a typical experimental DICF, in the (qx,qy) plane at one delay time τ = 0.02 s, obtained for Brownian particles flowing with mean velocity 〈v〉 = 630 μm s−1 (see Section 3.1 for Experimental details). When diffusion is negligible, the spacing of these waves has been used to measure the flow speed of nanoparticle suspensions pumped through a capillary.29Eqn (6) also implies that flow should not contribute to the DICF in the direction perpendicular to the flow, g⊥, as ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = 0, and f⊥v = 1. However, as images are composed of finite-sized pixels, measurements of g⊥ require averaging over a finite-size sector with half-width θ and thus
= 0, and f⊥v = 1. However, as images are composed of finite-sized pixels, measurements of g⊥ require averaging over a finite-size sector with half-width θ and thus ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is only approximately perpendicular, Fig. 1(a) (cross-hatched). In practice, we found a minimum of θ ≈ 3° is required to obtain measurable g⊥ from a 256 pixel image. Therefore, this sector still contains a velocity component (∼θ|
is only approximately perpendicular, Fig. 1(a) (cross-hatched). In practice, we found a minimum of θ ≈ 3° is required to obtain measurable g⊥ from a 256 pixel image. Therefore, this sector still contains a velocity component (∼θ|![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) |), which introduces a decorrelation timescale (tv ∼ 1/qθ|
|), which introduces a decorrelation timescale (tv ∼ 1/qθ|![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) |), that for even moderate flow velocities can dominate over diffusion (tv ≪ tD = 1/Dq2). This velocity component leads to a non-monotonic (and assuredly non-diffusive) g⊥(
|), that for even moderate flow velocities can dominate over diffusion (tv ≪ tD = 1/Dq2). This velocity component leads to a non-monotonic (and assuredly non-diffusive) g⊥(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ,τ) set by fv rather than fD, Fig. 1(c) [(blue) squares]. The non-monotonic behaviour is exacerbated in the adjacent sector [(grey) circles]. We refer to a simple diffusive fit to g⊥ as “anisotropic-DDM”, a technique which has been used for particles influenced by a magnetic field.22,25
,τ) set by fv rather than fD, Fig. 1(c) [(blue) squares]. The non-monotonic behaviour is exacerbated in the adjacent sector [(grey) circles]. We refer to a simple diffusive fit to g⊥ as “anisotropic-DDM”, a technique which has been used for particles influenced by a magnetic field.22,25
 | ||
Fig. 1 Impact of flow and drift correction on DICF. (a) DICF for DDM correlator, g(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) (eqn (1)) at delay time τ = 0.02 s, for Poiseuille flow at 20 μl min−1 and 500 μm imaging depth (〈v〉 = 630 μm s−1). Colour map: light, high g values, and dark, low g values, flow direction indicated by arrow. Perpendicular (⊥, cross-hatched) and near-perpendicular (n⊥, hatched) sectors used to define g(n)⊥(q) with half-width θ = 3°. (b) DICF after drift correction, ḡ (eqn (8)), colour scale unchanged. (c) Time dependence of non-corrected DICF in (a) at q = 3 μm−1, g(τ). Symbols: dark (blue), ⊥; and, light (grey), n⊥. Line, anisotropic-DDM, diffusive fit of g⊥ (D = 6.8 μm2 s−1). (d) Drift-corrected DICF from (b): symbols, as in (c); lines, flow-DDM, eqn (9) (D = 1.55 μm2 s−1, Δv = 88 μm s−1). ) (eqn (1)) at delay time τ = 0.02 s, for Poiseuille flow at 20 μl min−1 and 500 μm imaging depth (〈v〉 = 630 μm s−1). Colour map: light, high g values, and dark, low g values, flow direction indicated by arrow. Perpendicular (⊥, cross-hatched) and near-perpendicular (n⊥, hatched) sectors used to define g(n)⊥(q) with half-width θ = 3°. (b) DICF after drift correction, ḡ (eqn (8)), colour scale unchanged. (c) Time dependence of non-corrected DICF in (a) at q = 3 μm−1, g(τ). Symbols: dark (blue), ⊥; and, light (grey), n⊥. Line, anisotropic-DDM, diffusive fit of g⊥ (D = 6.8 μm2 s−1). (d) Drift-corrected DICF from (b): symbols, as in (c); lines, flow-DDM, eqn (9) (D = 1.55 μm2 s−1, Δv = 88 μm s−1). | ||
A combination of a finite field of view and flow will also cause decorrelation due to particles leaving the image (and being replaced by on average uncorrelated particles).28 This introduces a finite-size term into the total ISF, which for flow along the x direction takes the form
| fFS = max[(1 − |vx|τ/Lx),0], | (7) |
2.3 Flow-DDM
As stated, anisotropic-DDM is quickly overwhelmed by the presence of flow and the remaining velocity component. Here, we present a new analysis scheme, flow-DDM, that allows a reduction of the flow contribution and a decoupling of the diffusive motion of Brownian particles from the background flow. Conceptually, the effect of flow on a system moving with a well defined uniform speed,![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) , can be minimized by simply observing its dynamics in a co-moving frame of reference. Recording movies directly in a co-moving frame of reference is obviously challenging, but by determining the mean drift speed 〈
, can be minimized by simply observing its dynamics in a co-moving frame of reference. Recording movies directly in a co-moving frame of reference is obviously challenging, but by determining the mean drift speed 〈![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉 in the laboratory frame of reference it is then straightforward to shift the images when computing the DICF. The resulting “drift-corrected DICF” can then be fitted with an appropriate model that takes into account diffusive motion and the fact that in most practical scenarios there will be a spread in flow speeds.
〉 in the laboratory frame of reference it is then straightforward to shift the images when computing the DICF. The resulting “drift-corrected DICF” can then be fitted with an appropriate model that takes into account diffusive motion and the fact that in most practical scenarios there will be a spread in flow speeds.
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) =
) = ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ·
·![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) τ (from eqn (6)). The drift velocity
τ (from eqn (6)). The drift velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) can then be estimated from the gradient of φ; by averaging over a sufficiently long movie segment. The method has been shown to work over a wide range of speeds, even when the displacements due to random motion start to dominate.31
can then be estimated from the gradient of φ; by averaging over a sufficiently long movie segment. The method has been shown to work over a wide range of speeds, even when the displacements due to random motion start to dominate.31
Having measured the mean flow velocity, 〈![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉, we can then compute the drift-corrected DICF:
〉, we can then compute the drift-corrected DICF:
 | (8) |
Eqn (8) allows reduction of the flow contribution, as both the ‘waves’ and non-monotonic behaviour of the DICF [Fig. 1(a) and (c)] are not apparent in the drift-corrected DICF [Fig. 1(b) and (d)]. However, we note that the drift-corrected DICF is clearly not radially symmetric, indicating that there is still some residual contribution from the flow. This is due to the fact that there is actually a distribution of flow speeds about the mean. This speed distribution must be considered to allow accurate measurements of particle size at high flow speeds.
 | (9) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) ), which we characterise by the width Δv. In the following we assume that this residual motion is purely in the direction of the original flow and we now drop vector notation for velocities (see ESI† Section S1 for comments on more general residual motion).
), which we characterise by the width Δv. In the following we assume that this residual motion is purely in the direction of the original flow and we now drop vector notation for velocities (see ESI† Section S1 for comments on more general residual motion).
Note that the width of this distribution is in principle not set by the mean speed alone, e.g. in rheometric cone-plate flow the shear rate is fixed (fixing the velocity distribution for a given optical section) but the speed varies with height. However, it is important to realise that in practice for a given imaging region the velocity distribution will increase with the mean speed in a linear fashion, Δv = k〈v〉, with the proportionally constant dependent on the flow geometry, but assumed to be less than 1 (for imaging away from the boundaries).
To size particles, we first restrict our analysis to the perpendicular sector, f⊥Δv, for which the impact of Δv is minimised (just as with 〈v〉 for f⊥v). This attempts to ensure that diffusion causes decorrelation in eqn (9). For tractability, we assume a uniform distribution of residual velocities (−Δv to +Δv) and use a small angle approximation for the phase shift, i.e.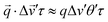 . Integration over the residual velocity distribution (Δv′) and then sector angle (θ′) thus yields:
. Integration over the residual velocity distribution (Δv′) and then sector angle (θ′) thus yields:
 | (10) |
Finite-size effects by contrast lead to tFS = 0.63Lx/vx, independent of q. Therefore decorrelation is predominantly due to diffusion for speeds up to vx ≈ 0.63q2DLx, i.e. this effect becomes less important at higher q, cf.Fig. 2(a) blue and dark grey lines. By acquiring images with a large field of view Lx and high spatial resolution (to access high q) finite size effects can be be greatly reduced. But the faster dynamics at higher q also require high frame rates, which in modern scientific cameras and confocal laser scanning systems decreases with the height Ly of the image. In practice, these requirements are most effectively achieved by taking a rectangular image, with the long axis of the field of view aligned with the flow direction: we use Lx = 4Ly throughout.
The decorrelation time caused by the distribution of speeds, from eqn (10),
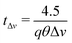 | (11) |
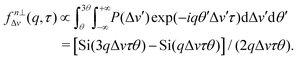 | (12) |
Decorrelation due to Δv now occurs at a more rapid rate (∼3× compared to f⊥Δv) and we can separately probe Δv by simultaneously fitting two sectors of the DICF and establish whether the measured particle size is reliable, i.e. tD ≪ {tFS, tΔv}. This combination of drift correction, imaging optimisation and fitting together we term “flow-DDM”.
3 Experimental materials and methods
We now turn to look at applying flow-DDM to measure particle size for a dilute colloidal suspension and demonstrate it using two different microscopy techniques and flow geometries.3.1 Poiseuille flow
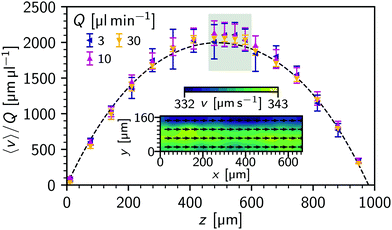
First, we use a dilute (ϕ = 0.004%) suspension of spherical polystyrene particles in water, with a nominal diameter of 300 nm flowing through a 1 mm square capillary with a controlled flow rate, giving Poiseuille flow, Fig. 3(a). Images were taken using phase contrast microscopy (20×/0.5 objective at 400 frames per second for tmax = 20 s). The rectangular images (1024 × 256 pixels image, 0.65 μm px−1 → 166 μm by 665 μm) are aligned along the centre of the capillary. At a given flow rate, Q, the capillary is then imaged at multiple focal depths, z.To establish a reference diffusion coefficient, i.e. the free-diffusion coefficient (D0), quiescent samples were recorded in the same conditions. Using standard DDM (eqn (1) and (4)), a q-dependent diffusion coefficient was extracted, Fig. 4(a). The diffusivity, D0 = 〈D(q)〉 = 1.52(1) μm2 s−1 (averaging over q = 1.0 to 3.0 μm−1) implies a particle size of d = 298(3) nm at 22 °C.
3.2 Rheo-confocal flow
To explore the general application of flow-DDM to other microscopy techniques and flow geometries, we use a confocal microscope coupled to a rotational stress-controlled rheometer33 (Anton Paar MCR 301), Fig. 3(b). Images were taken using an inverted confocal laser-scanning microscope [Leica SP8, 20×/0.75 objective)], a technique previously used with DDM to measure dense quiescent systems.23 The sample is a dilute (ϕ = 0.5%) suspension of fluorescently-dyed poly(methyl methacrylate) particles stabilised with poly(vinyl pyrrolidone); the particles are suspended in a density matched 21 wt% caesium chloride solution to prevent sedimentation and screen electrostatic interactions. Images are taken at 50 frames per second for tmax = 200 s with a 1024 × 256 resolution and 0.455 μm pixel size (466 μm × 116 μm field of view).In the quiescent state, a plateau in D(q) is seen for q = 1 to 2.5 μm−1, Fig. 4(b) (open circles). Due to the small image width (Ly) used for flow-DDM, “spectral leakage” leads to an apparent drop in diffusivity: at high q values, corresponding to length scales smaller than the particle, g(q,τ) is distorted due to particles cut off at the image boundaries.34 This effect is mitigated by smoothing the image boundaries using a Hanning window, (cf. open and filled symbols); all further diffusion measurements presented are from windowed images. Averaging D(q) from 1.0 μm−1 to 3.0 μm−1, gives D0 = 0.164(1) μm2 s−1 and a particle diameter of 2.65(1) μm at 20 °C. At low q there is an apparent rise in D due to diffusion out of the optical section.34 Additionally, we can also estimate the particle size from A(q), Fig. 4. Considering high resolution fluorescence imaging of a dilute suspension, we expect A(q) to be proportional to the particle form factor, for which a first minimum should occur at qd/2 ≈ 4.5 by considering the Fourier transform of a uniform intensity and neglecting the point spread function. The minimum at q = 3.4 μm−1, Fig. 4(d), results in an estimated diameter d ≈ 2.64 μm, in quantitative agreement with results from the measured D0.
To create flow, a 1°, 50 mm diameter cone-plate geometry generates a uniform shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , with the velocity gradient perpendicular to the imaging plane. The shear rate is set by the rotational speed of the rheometer. Imaging at an increasing depth into the sample, h = 10 and 20 μm, increases the translational speed 〈v〉 =
, with the velocity gradient perpendicular to the imaging plane. The shear rate is set by the rotational speed of the rheometer. Imaging at an increasing depth into the sample, h = 10 and 20 μm, increases the translational speed 〈v〉 = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) h; greater depths could not be used due to high sample turbidity. Images are taken at a radius of ≈20 mm from center of the cone, to ensure the direction of the rotational flow does not vary significantly along the flow direction, x.
h; greater depths could not be used due to high sample turbidity. Images are taken at a radius of ≈20 mm from center of the cone, to ensure the direction of the rotational flow does not vary significantly along the flow direction, x.
4 Results and discussion
4.1 Poiseuille flow
We now establish the effectiveness of flow-DDM and investigate the limiting factors for reliable measurement. We measured diffusivity of a dilute colloidal suspension with increasing flow rate through a capillary, which we compare to the free-diffusion coefficient D0 obtained from quiescent conditions. However, the flow velocity in a capillary varies strongly with position. We show in Fig. 5 the average flow velocity 〈v〉, measured in the (x,y)-plane center of the capillary using φDM and normalised to the flow rate Q, as a function of the height of the focal plane (z) for several Q values. We find a near parabolic flow profile, with the velocity reaching a maximum in the centre of the capillary, Fig. 5 (symbols), matching the velocity predicted by Boussinesq35 (dashed line). Temporal fluctuations in the flow speed may occur and would be included in error bars, but no systematic variation over ∼tmax was observed. Near the centre of the channel (z = 480 μm to 580 μm), 〈v〉 is near constant and we therefore average over these four positions, although we present results across the full depth in Fig. S2, ESI.† These measurements are away from the top and bottom of the channel, where the strong gradient in 〈v〉 may combine with the optical section to produce a large Δv. As with z, there is also a velocity variation across the channel width, y. Measuring 〈v〉 in sub-regions of the image we can estimate this variation at ≈3%, with a 11 μm s−1 spatial variation for 〈v〉 = 338 μm s−1, Fig. 5 (inset).From the measured 〈v〉, we computed the drift-corrected DICF for all positions (Fig. S3 for typical ḡ, ESI†). To extract a diffusion coefficient we simultaneously fit the perpendicular and near-perpendicular sectors of the drift-corrected DICF, Fig. 1(b), using eqn (4), (8)–(12) over a q range of 3.0 μm−1 to 3.5 μm−1 where A/B > 0.3. 〈v〉 is taken as an input parameter, and {D(q), Δv, A(n)⊥(q) and B(n)⊥(q)} as the fitting parameters (Fig. S3 for typical results as a function of q, ESI†).
We varied the flow rate in the range Q = 1 μl min−1 to 90 μl min−1, resulting in nearly two decades of measured 〈v〉 in the middle region of the capillary (from 34 μm s−1 to 3000 μm s−1). Plotting the extracted diffusivity 〈D〉 against 〈v〉, Fig. 6(a), we find that 〈D〉 closely matches the quiescent measurement, D0, up to 1000 μm s−1, cf. filled squares and dashed line. Correspondingly, at the minimum q used for averaging the diffusion timescale tD is far smaller than tΔv and tFS, Fig. 6(b), giving great confidence in the accuracy of the overall analysis, as discussed in Section 2.3.3. However, tD and tΔv become comparable at higher velocity 〈v〉 = 1500 μm s−1 and so the error in 〈D〉 increases, before 〈D〉 itself increases at yet higher speeds. For sizing, this would appear as a smaller particle. Based on Fig. 6, we conclude that due to the present optimal imaging conditions Δv is the limiting factor (as tΔv < tFS) and that tD ≲ tΔv/3 is necessary for reliable sizing measurements [Fig. 6(b) hatched region]. Using eqn (11), this allows us to estimate the maximum velocity, vmax = 1100 μm s−1, for reliable particle sizing by considering our measured Δv ≈ 0.1v (Fig. S4, ESI†) and θ = 3°. Using larger θ = 7.5° sectors means Δv will have a larger impact (vmax = 430 μm s−1), and correspondingly we see a larger 〈D〉 measurement at a lower 〈v〉 ≲ 1000 μm s−1 (Fig. S5, ESI†).
 | ||
| Fig. 6 Measuring diffusion with varying capillary flow rate. (a) Extracted diffusivities vs mean drift velocity, 〈v〉, averaging over 4 positions in channel centre. Symbols: filled (blue) squares, flow-DDM averaging D(q) over q = 3.0 μm−1 to 3.5 μm−1 with θ = 3° and open (black) squares, anisotropic-DDM. (b) Timescale phase diagram. Symbols, timescales at minimum q used for flow-DDM, q = 3.0 μm−1: (blue) squares, measured diffusion; solid (orange) triangles, extracted velocity distribution from flow-DDM; open (orange) triangles, velocity distribution from v(t), Fig. 5, using 0.25 s subsections and the difference between 5th and 95th percentiles; and (grey) circles, finite-size effect from 〈v〉. Lines and shading scheme as in Fig. 2, with striped shading indicating factor three timescale separation. | ||
A Δv ∼ 0.1 〈v〉 is larger than expected from variation across the width of the channel, Fig. 5 (inset). It is instead related to temporal fluctuations, with Δv measured with flow-DDM closely matched by the variation in v(t), cf.Fig. 6(b) open and filled triangles. The spatio-temporal velocity fluctuations mean that the contribution to Δv from the optical section is insignificant, which results in consistent diffusivity measurements across the capillary, even as the velocity variation across the depth of field changes, see ESI† Section 2. However, even if these measurements were not limited by flow stability, tFS would soon impact measurements [Fig. 6(b), solid dark (grey) line], even with the rectangular field of view.
Comparing flow-DDM to existing DDM-based techniques, we see a significant improvement over anisotropic-DDM, i.e. using a perpendicular sector of θ = 3° and a simple diffusive fit (eqn (4)) over the same q range, Fig. 6(a). Flow-DDM enables reliable measurement of the free diffusion coefficient, D0, and thus the particle size to 〈v〉 an order of magnitude faster than for anisotropic-DDM, for which 〈D〉 starts to significantly increase from 〈v〉 ≲ 100 μm s−1. The ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10)× improvement is consistent with Δv ∼ 0.1〈v〉 as the particle velocities are reduced 10 fold thanks to the drift-correction (eqn (8)).
(10)× improvement is consistent with Δv ∼ 0.1〈v〉 as the particle velocities are reduced 10 fold thanks to the drift-correction (eqn (8)).
Additionally, another recent technique based on DDM but using a higher-order “far-field” correlator has been suggested to eliminate the impact of translation due to flow (i.e. 〈v〉). This far-field correlator can be related to the magnitude of the ISF, which should be translation invariant.28 However, we find that even in quiescent conditions that interpretation of this correlator is challenging, as it yields a measured D(q) lower than the expected D0 (Fig. S6, ESI†), while for flowing samples the results vary proportionally with non-drift-corrected DDM (Fig. S5, ESI†). For quantitative results, we therefore use flow-DDM.
4.2 Rheo-confocal flow
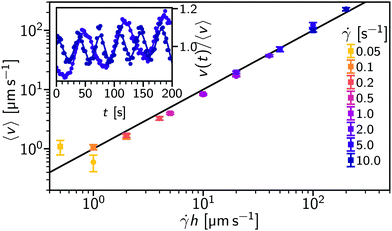
We now demonstrate the general applicability of flow-DDM by using a setup with a different microscopy method, flow geometry and particle size. Here, we performed rheo-confocal imaging of micron-sized particles, and varied the flow velocity, 〈v〉, through the imaging height, h = 10 or 20 μm, and applied shear rate,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.05 s−1 to 10 s−1. This setup allows us control of the mean speed independent of the velocity spread by imaging the flow within a well-defined optical section.
= 0.05 s−1 to 10 s−1. This setup allows us control of the mean speed independent of the velocity spread by imaging the flow within a well-defined optical section.
Fig. 7 shows 〈v〉 measured from φDM (symbols) as a function of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) h. The extracted average velocity closely matches the speed predicted for a shear flow, 〈v〉 =
h. The extracted average velocity closely matches the speed predicted for a shear flow, 〈v〉 = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) h (line). However, at high shear rates (
h (line). However, at high shear rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≥ 5 s−1) there are noticeable oscillations in the flow speed (see inset), consistent with a slight geometry misalignment.36 The drift-corrected DICF, ḡ (eqn (8)), was therefore calculated using a time-dependent drift velocity based upon a smoothed average of 〈v〉 from 2 s subsections, v(t). We then fit ḡ using the protocol developed for Poiseuille flow in Section 4.1, but now using a q range of 2.0 μm−1 to 2.5 μm−1 so that A/B remains ≳ 0.3. The lower q range consequently requires an increased θ of 7.5° to ensure an average over sufficient
≥ 5 s−1) there are noticeable oscillations in the flow speed (see inset), consistent with a slight geometry misalignment.36 The drift-corrected DICF, ḡ (eqn (8)), was therefore calculated using a time-dependent drift velocity based upon a smoothed average of 〈v〉 from 2 s subsections, v(t). We then fit ḡ using the protocol developed for Poiseuille flow in Section 4.1, but now using a q range of 2.0 μm−1 to 2.5 μm−1 so that A/B remains ≳ 0.3. The lower q range consequently requires an increased θ of 7.5° to ensure an average over sufficient ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) . Typical results for ḡ and fits thereof are shown in Fig. S3, ESI.†
. Typical results for ḡ and fits thereof are shown in Fig. S3, ESI.†
Fig. 8(a) shows the measured 〈D〉 as a function of shear rate [light (blue) symbols]. At  , 〈D〉 ≈ 0.18 μm2 s−1, giving an inferred particle diameter of d = 2.4 μm. The diffusivity is comparable to the rest measurement, D0 = 0.16 μm2 s−1, although there is an ≈10% increase that may arise from a small change in the solvent viscosity due to temperature.
, 〈D〉 ≈ 0.18 μm2 s−1, giving an inferred particle diameter of d = 2.4 μm. The diffusivity is comparable to the rest measurement, D0 = 0.16 μm2 s−1, although there is an ≈10% increase that may arise from a small change in the solvent viscosity due to temperature.
 | ||
Fig. 8 Measuring diffusion in rheometric flow. (a) Diffusion coefficient, D, as a function of applied shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , [h = 10 μm (squares) and h = 20 μm (circles)] averaging over q = 2.0 μm−1 to 2.5 μm−1. Symbols: dark (blue), D from flow-DDM; and, light (grey) anisotropic-DDM. Inset: Symbols, anisotropic-DDM vs. nominal velocity ( , [h = 10 μm (squares) and h = 20 μm (circles)] averaging over q = 2.0 μm−1 to 2.5 μm−1. Symbols: dark (blue), D from flow-DDM; and, light (grey) anisotropic-DDM. Inset: Symbols, anisotropic-DDM vs. nominal velocity (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) h). (b) Decorrelation times, ti at q = 2.0 μm−1 for given terms from flow-DDM, symbols: small, tD; large, tΔv; and filled, tFS. Shading as in Fig. 6(b). h). (b) Decorrelation times, ti at q = 2.0 μm−1 for given terms from flow-DDM, symbols: small, tD; large, tΔv; and filled, tFS. Shading as in Fig. 6(b). | ||
In order to understand the limits of flow-DDM we again need to compare the extracted decorrelation timescales shown in Fig. 8(b). First we should note that the decorrelation time associated with the spread in velocities, tΔv, decreases with shear rate rather than the velocity: tΔv is the same for the two heights, h, presented here. This experimental data implies that Δv = Δh·![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , where we find Δh = 2 μm (see ESI,† Section S4 for details). This lengthscale, Δh, is comparable to the quoted optical section of 1.8 μm for our confocal imaging configuration, which suggests that Δv arises from the velocity gradient across the depth of field in this shear flow. However, we cannot rule out a contribution from the time-dependent velocity as rapid changes may not be captured by the smooth interpolation of v(t). Our optimised imaging settings ensured that finite size effects remain negligible, with tFS the slowest of the three decorrelation processes, even at h = 20 μm. So, diffusion (or size) measurements are limited by the increasing velocity distribution, with flow-DDM again producing reliable measurements for tD ≲ tΔv/3, just as in Section 4.1.
, where we find Δh = 2 μm (see ESI,† Section S4 for details). This lengthscale, Δh, is comparable to the quoted optical section of 1.8 μm for our confocal imaging configuration, which suggests that Δv arises from the velocity gradient across the depth of field in this shear flow. However, we cannot rule out a contribution from the time-dependent velocity as rapid changes may not be captured by the smooth interpolation of v(t). Our optimised imaging settings ensured that finite size effects remain negligible, with tFS the slowest of the three decorrelation processes, even at h = 20 μm. So, diffusion (or size) measurements are limited by the increasing velocity distribution, with flow-DDM again producing reliable measurements for tD ≲ tΔv/3, just as in Section 4.1.
Using anisotropic-DDM, i.e. without drift correction, 〈D〉 shows an increase at much lower shear rates, Fig. 8(a) (black symbols), and already increases at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) ≳ 0.2 s−1 for h = 20 μm (circles). Here the rise in 〈D〉 occurs with the flow speed (see inset) rather than shear rate. The relative improvement seen for flow-DDM then depends on h, as the relevant velocity scale is changed from being set by the imaging depth (〈v〉 =
≳ 0.2 s−1 for h = 20 μm (circles). Here the rise in 〈D〉 occurs with the flow speed (see inset) rather than shear rate. The relative improvement seen for flow-DDM then depends on h, as the relevant velocity scale is changed from being set by the imaging depth (〈v〉 = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) h) to being controlled by the effective optical section (Δv =
h) to being controlled by the effective optical section (Δv = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δh): flow-DDM makes (h/Δh)× higher mean speeds accessible for size measurements. Meanwhile, the far-field correlator again significantly underestimates diffusivity in quiescent conditions (Fig. S6, ESI†). Thus, flow-DDM appears as an exciting new technique to accurately measure free-diffusion and thus size particles under general flow conditions.
Δh): flow-DDM makes (h/Δh)× higher mean speeds accessible for size measurements. Meanwhile, the far-field correlator again significantly underestimates diffusivity in quiescent conditions (Fig. S6, ESI†). Thus, flow-DDM appears as an exciting new technique to accurately measure free-diffusion and thus size particles under general flow conditions.
5 Conclusions
In summary, we have proposed flow-DDM as a novel method to accurately measure free-diffusivity, and from this determine particle size, using microscopy videos of dilute suspensions of colloidal particles under flow. We have presented its theoretical framework and practical implementation for optimal measurements.Flow-DDM is based on two main steps: (1) computing the drift-corrected DICF, ḡ, from microscopy videos, which reduces the impact of flow onto the resulting experimental signal; and (2) fitting ḡ using an appropriate model of the particle motion (including diffusion, residual flow velocities and finite-size effects) coupled with an optimised fitting protocol that allows decoupling of the residual flow velocity distribution from the diffusive motion. We have validated flow-DDM using two different particle suspensions, demonstrating its general application by studying two setups with distinct optical imaging configuration and flow geometry: phase-contrast imaging with Poiseuille flow and confocal microscopy with rheometric flow.
By performing systematic experiments as a function of flow rate and position within the sample, we have investigated the reliability and limits of flow-DDM, established its success over a large range of flow speeds and determined how to optimise imaging parameters. In particular, we have shown that under optimised conditions it is no longer the mean flow speed 〈v〉 but the width Δv of its distribution that limits the reliability of the technique. Therefore, Δv should be minimised by imaging away from regions with a large velocity gradient and by ensuring a steady flow. We have identified an empirical criterion to ensure reliable measurements based on the measured timescales of diffusion and residual velocity, tD ≲ tΔv/3, which allows estimation of the maximum accessible velocity for reliable measurements, vmax (assuming Δv = k(v)). It is important to note that vmax depends on the particle size; so, based on the measured tD and tΔv obtained from flow-DDM, the above criterion can also be used to give confidence to the user when performing flow-DDM measurements of suspensions with unknown particle-size.
Using the advantages of DDM seen in quiescent systems, flow-DDM allows particle sizing in flowing samples without user inputs or resolution of individual particles (as required for particle tracking), and without the requirement of highly dilute samples (as for DLS). This extends sample possibilities for particle sizing under flow, enabling high-throughput microfluidic testing in development or in-line testing during manufacturing of particulate suspensions, which are so ubiquitous in industry. Moreover, we expect the general framework of flow-DDM to be applicable to other imaging methods, such as bright-field,13 light-sheet,37 epifluorescence,38 and dark-field microscopy.39
Flow-DDM outperforms current digital Fourier techniques, such as a diffusive fit of anisotropic-DDM22 or far-field dynamic microscopy.28 Indeed, flow-DDM allows quantitative measurements within ≈3% of the free-diffusion coefficient at flow speeds up to one order of magnitude faster than for anisotropic-DDM. Flow-DDM has been designed to be insensitive to the details of the flow, providing some robustness against some spatio-temporal variations. Nevertheless, the method returns measurements of the mean flow velocity and an estimate for the residual velocity spread, which characterises the combination of flow geometry and imaging properties.
Finally, although we have focused entirely on probing diffusive dynamics of dilute suspensions to measure particle size, flow-DDM could also be applied to measure the collective dynamics of dense (and relatively turbid) colloidal suspensions under flow. For example, ready measurement of microscopic particle rearrangements alongside the bulk rheology could bring new insights into the understanding of non-Newtonian fluids such as shear-thickening or yield-stress suspensions40,41 and jammed emulsions.42
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no 731019 and 862559), European Soft Matter Infrastructure (EUSMI) and Novel Characterisation Platform for Formulation Industry (NoChaPFI). The authors thank Andrew Schofield for particle synthesis, and Jean-Noël Tourvieille and Sophie Galinat for enlightening discussions. All data used are available via Edinburgh DataShare at https://doi.org/10.7488/ds/2987.References
- D. P. Bentz, E. J. Garboczi, C. J. Haecker and O. M. Jensen, Cem. Concr. Res., 1999, 29, 1663–1671 CrossRef CAS.
- C. S. Kan, J. Coat. Technol. Res., 1999, 71, 89 CrossRef CAS.
- G. Sandri, M. C. Bonferoni, F. Ferrari, S. Rossi and C. M. Caramella, Particulate Products, Springer, 2014, pp. 323–341 Search PubMed.
- G. R. Ziegler, G. Mongia and R. Hollender, Int. J. Food Prop., 2001, 4, 353–370 CrossRef.
- N. C. Bell, C. Minelli, J. Tompkins, M. M. Stevens and A. G. Shard, Langmuir, 2012, 28, 10860–10872 CrossRef CAS PubMed.
- B. J. Berne and R. Pecora, Dynamic light scattering: with applications to chemistry, biology, and physics, Dover Publications, Mineola, NY, 2000 Search PubMed.
- A. B. Leung, K. I. Suh and R. R. Ansari, Appl. Opt., 2006, 45, 2186–2190 CrossRef PubMed.
- P. Pusey, Curr. Opin. Colloid Interface Sci., 1999, 4, 177–185 CrossRef CAS.
- C. Urban and P. Schurtenberger, J. Colloid Interface Sci., 1998, 207, 150–158 CrossRef CAS PubMed.
- C. Finder, M. Wohlgemuth and C. Mayer, Part. Part. Syst. Charact., 2004, 21, 372–378 CrossRef.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- J. M. Newby, A. M. Schaefer, P. T. Lee, M. G. Forest and S. K. Lai, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9026–9031 CrossRef CAS PubMed.
- R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102 CrossRef PubMed.
- P. Edera, D. Bergamini, V. Trappe, F. Giavazzi and R. Cerbino, Phys. Rev. Mater., 2017, 1, 073804 CrossRef.
- A. V. Bayles, T. M. Squires and M. E. Helgeson, Rheol. Acta, 2017, 56, 863–869 CrossRef CAS.
- M. A. Escobedo-Sánchez, J. P. Segovia-Gutiérrez, A. B. Zuccolotto-Bernez, J. Hansen, C. C. Marciniak, K. Sachowsky, F. Platten and S. U. Egelhaaf, Soft Matter, 2018, 14, 7016–7025 RSC.
- L. G. Wilson, V. A. Martinez, J. Schwarz-Linek, J. Tailleur, G. Bryant, P. N. Pusey and W. C. K. Poon, Phys. Rev. Lett., 2011, 106, 018101 CrossRef CAS PubMed.
- V. A. Martinez, R. Besseling, O. A. Croze, J. Tailleur, M. Reufer, J. Schwarz-Linek, L. G. Wilson, M. A. Bees and W. C. K. Poon, Biophys. J., 2012, 103, 1637–1647 CrossRef CAS PubMed.
- A. Jepson, J. Arlt, J. Statham, M. Spilman, K. Burton, T. Wood, W. C. K. Poon and V. A. Martinez, PLoS One, 2019, 14, 1–17 CrossRef.
- P.-L. Latreille, V. Adibnia, A. Nour, J.-M. Rabanel, A. Lalloz, J. Arlt, W. C. K. Poon, P. Hildgen, V. A. Martinez and X. Banquy, Nat. Commun., 2019, 10, 1–8 CrossRef CAS.
- K. Regan, D. Wulstein, H. Rasmussen, R. McGorty and R. M. Robertson-Anderson, Soft Matter, 2019, 15, 1200–1209 RSC.
- M. Reufer, V. A. Martinez, P. Schurtenberger and W. C. K. Poon, Langmuir, 2012, 28, 4618–4624 CrossRef CAS PubMed.
- P. J. Lu, F. Giavazzi, T. E. Angelini, E. Zaccarelli, F. Jargstorff, A. B. Schofield, J. N. Wilking, M. B. Romanowsky, D. A. Weitz and R. Cerbino, Phys. Rev. Lett., 2012, 108, 218103 CrossRef PubMed.
- E. Lázaro-Lázaro, J. A. Perera-Burgos, P. Laermann, T. Sentjabrskaja, G. Pérez-Ángel, M. Laurati, S. U. Egelhaaf, M. Medina-Noyola, T. Voigtmann, R. Castañeda Priego and L. F. Elizondo-Aguilera, Phys. Rev. E, 2019, 99, 042603 CrossRef PubMed.
- A. Pal, V. A. Martinez, T. H. Ito, J. Arlt, J. J. Crassous, W. C. K. Poon and P. Schurtenberger, Sci. Adv., 2020, 6, eaaw9733 CrossRef CAS PubMed.
- M. Tong, O. S. Brown, P. R. Stone, L. M. Cree and L. W. Chamley, Placenta, 2016, 38, 29–32 CrossRef CAS PubMed.
- A. Philippe, S. Aime, V. Roger, R. Jelinek, G. Prévot, L. Berthier and L. Cipelletti, J. Phys.: Condens. Matter, 2016, 28, 075201 CrossRef CAS PubMed.
- S. Aime and L. Cipelletti, Soft Matter, 2019, 15, 213–226 RSC.
- M. Dienerowitz, M. Lee, G. Gibson and M. Padgett, Lab Chip, 2013, 13, 2359–2363 RSC.
- R. Besseling, L. Isa, E. R. Weeks and W. C. K. Poon, Adv. Colloid Interface Sci., 2009, 146, 1–17 CrossRef CAS PubMed.
- R. Colin, R. Zhang and L. G. Wilson, J. R. Soc., Interface, 2014, 11, 20140486 CrossRef CAS PubMed.
- F. Giavazzi, D. Brogioli, V. Trappe, T. Bellini and R. Cerbino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031403 CrossRef PubMed.
- R. Besseling, E. R. Weeks, A. B. Schofield and W. C. K. Poon, Phys. Rev. Lett., 2007, 99, 028301 CrossRef CAS PubMed.
- F. Giavazzi, P. Edera, P. J. Lu and R. Cerbino, Eur. Phys. J. E, 2017, 40, 97 CrossRef PubMed.
- J. Boussinesq, J. Math Pures. Appl., 1868, 377–424 Search PubMed.
- D. J. Dudgeon and L. E. Wedgewood, J. Nonnewton. Fluid Mech., 1993, 48, 21–48 CrossRef CAS.
- D. M. Wulstein, K. E. Regan, R. M. Robertson-Anderson and R. McGorty, Opt. Express, 2016, 24, 20881–20894 CrossRef CAS PubMed.
- A. Jepson, V. A. Martinez, J. Schwarz-Linek, A. Morozov and W. C. K. Poon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 041002 CrossRef PubMed.
- A. V. Bayles, T. M. Squires and M. E. Helgeson, Soft Matter, 2016, 12, 2440–2452 RSC.
- C. Ness and J. Sun, Soft Matter, 2016, 12, 914–924 RSC.
- B. M. Guy, J. A. Richards, D. J. M. Hodgson, E. Blanco and W. C. K. Poon, Phys. Rev. Lett., 2018, 121, 128001 CrossRef CAS PubMed.
- V. V. Vasisht, S. K. Dutta, E. Del Gado and D. L. Blair, Phys. Rev. Lett., 2018, 120, 018001 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Containing details on the impact of the form of the residual velocity distribution, depth dependence, q-dependent fitting, extracted velocity distributions and far-field correlator results. See DOI: 10.1039/d0sm02255a |
| This journal is © The Royal Society of Chemistry 2021 |



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: