DOI:
10.1039/D1SC02407H
(Edge Article)
Chem. Sci., 2021,
12, 10871-10877
Control of dominant conduction orbitals by peripheral substituents in paddle-wheel diruthenium alkynyl molecular junctions†
Received
30th April 2021
, Accepted 1st July 2021
First published on 8th July 2021
Abstract
Control of charge carriers that transport through the molecular junctions is essential for thermoelectric materials. In general, the charge carrier depends on the dominant conduction orbitals and is dominantly determined by the terminal anchor groups. The present study discloses the synthesis, physical properties in solution, and single-molecule conductance of paddle-wheel diruthenium complexes 1R having diarylformamidinato supporting ligands (DArF: p-R-C6H4-NCHN-C6H4-R-p) and two axial thioanisylethynyl conducting anchor groups, revealing unique substituent effects with respect to the conduction orbitals. The complexes 1R with a few different aryl substituents (R = OMe, H, Cl, and CF3) were fully characterized by spectroscopic and crystallographic analyses. The single-molecule conductance determined by the scanning tunneling microscope break junction (STM-BJ) technique was in the 10−5 to 10−4G0 region, and the order of conductance was 1OMe > 1CF3 ≫ 1H ∼ 1Cl, which was not consistent with the Hammett substituent constants σ of R. Cyclic voltammetry revealed the narrow HOMO–LUMO gaps of 1R originating from the diruthenium motif, as further supported by the DFT study. The DFT-NEGF analysis of this unique result revealed that the dominant conductance routes changed from HOMO conductance (for 1OMe) to LUMO conductance (for 1CF3). The drastic change in the conductance properties originates from the intrinsic narrow HOMO–LUMO gaps.
Introduction
Molecular junctions, which are composed of two electrodes with a bridging molecule, are fundamental nanostructures for molecule-based devices. Control of the charge carrier transport through the molecular junction, i.e. either an electron or a hole, is an essential requirement for thermoelectric materials, where both p- (hole transport) and n-type (electron transport) materials are necessary for a high performance series circuit.1,2 Conduction orbitals close to the electrodes' Fermi energy levels determine the charge carrier and are mainly dominated by the terminal anchor groups, which connect to the electrodes.3,4 The characteristics of the bridging linkers have a subtle effect with respect to the conduction of charge carriers because common organic molecules have a large separation between the HOMO and LUMO energies, which are far away from the Fermi energies of metal electrodes and, thus, structural modifications are often ineffective. As a rare example, Venkataraman and her coworkers have reported that the conductance pathway for dithiophene molecular wires with HOMO conducting thiomethyl anchor groups can be changed from the HOMO (hole) to the LUMO (electron) by insertion of tetra(thiophene-1,1-dioxide-2,5-diyls).5 The oxidized thiophene part lowers the overall LUMO energy to change the dominant conduction orbitals, but it requires four repeating units. To date, however, control of the dominant conduction pathway via simple structural modifications, i.e. introduction of substituents, still remains elusive.
Chromium acetate (Cr2(OAc)4) synthesized in 1844 (ref. 6 and 7) and structurally characterized in 1951 was the first example of a dinuclear paddle-wheel metal complex (Fig. 1).8 Since then, various kinds of paddle-wheel dimetal complexes have been studied extensively, especially by Cotton,9,10 because they exhibit intriguing electrochemical, magnetic, and optical properties derived from the metal–metal interaction.11,12 Recent advances in single-molecule conductance measurements using break-junction (BJ) methods allow scientists to unveil the conductance properties of inorganic paddle-wheel complexes.13 For example, Chen and Peng reported that the conductance of the pentanuclear paddle-wheel complexes having the oligo-α-pyridylamine ligands and isothiocyanate anchor groups (Fig. 2a)14 was dependent on the embedded metal atoms (M = Ni, Co, and Cr) as well as the metal–metal bond order. The single-molecule conductance of the linearly arranged undecanickel complex with the tetra-naphthyridyltriamide ligand was also determined (Fig. 2b).15 On the other hand, carrier transport through the equatorial paddle-wheel ligands in the dimolybdenum complex was also reported recently (Fig. 2c).16
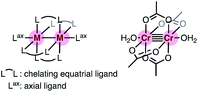 |
| | Fig. 1 Schematic representation of a paddle-wheel complex and the structure of chromium acetate with two axial water ligands. | |
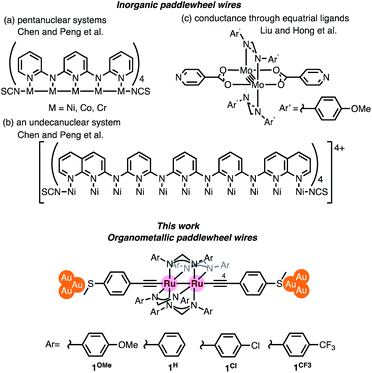 |
| | Fig. 2 Inorganic and organometallic molecular wires with paddle-wheel structural motifs. | |
Organometallic paddle-wheel diruthenium complexes with two axial alkynyl ligands constitute an interesting class of molecules for materials science due to the narrow HOMO–LUMO gaps and the rich redox properties. The first example of this class of complexes, Ru2(ap)4(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CPh), (ap = 2-anilinopyridinate), was reported by Cotton in 1986.17 Later on, Ren et al. extensively explored their application in molecular devices.18–22 To date, however, the single-molecule conductance measurement of organometallic paddle-wheel complexes remains to be studied. We describe, herein, the results of the single-molecule conductance study for a series of paddle-wheel diruthenium molecular wires 1R with diarylformamidinato supporting ligands (DArF: p-R-C6H4-NCHN-C6H4-R-p) and two axial thioanisylethynyl ligands (Fig. 2 bottom; R = OMe, H, Cl, and CF3), in which the thiomethyl anchors show high affinity toward gold electrodes. The present study revealed a unique substituent effect of the aryl moieties in the supporting DArF ligands on the conductance, suggesting the dominant conduction band as well as the charge carrier conductance changed by the substituents.
CPh), (ap = 2-anilinopyridinate), was reported by Cotton in 1986.17 Later on, Ren et al. extensively explored their application in molecular devices.18–22 To date, however, the single-molecule conductance measurement of organometallic paddle-wheel complexes remains to be studied. We describe, herein, the results of the single-molecule conductance study for a series of paddle-wheel diruthenium molecular wires 1R with diarylformamidinato supporting ligands (DArF: p-R-C6H4-NCHN-C6H4-R-p) and two axial thioanisylethynyl ligands (Fig. 2 bottom; R = OMe, H, Cl, and CF3), in which the thiomethyl anchors show high affinity toward gold electrodes. The present study revealed a unique substituent effect of the aryl moieties in the supporting DArF ligands on the conductance, suggesting the dominant conduction band as well as the charge carrier conductance changed by the substituents.
Results and discussion
Synthesis and characterization
We prepared diruthenium dialkynyl complexes 1R (R = p-OMe, H, p-Cl, and p-CF3) following the method previously reported by Ren et al.23–25 Treatment of monochloro complexes 2R with an excess amount of lithiated 4-ethynylthioanisole afforded 1R in 17–49% yields. Conventional spectroscopic methods provide characteristic structural information of 1R. The diruthenium dialkynyl complexes 1R are diamagnetic, and the single sets of 1H NMR signals for the thioanisyl and DArF ligands indicate highly symmetrical structures of 1R in solution (Fig. S1a, S2a, S4a, and S5a†). HR-ESI-TOF-MS spectra of 1R contain molecular ion peaks corresponding to the deprotonated forms (Fig. S1e, S2f, S4h, and S5e†), and the ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) vibrations appear in the range of 2092–2097 cm−1 (Fig. S1f, S2g, S4i, and S5f†). Purple crystals were grown by slow evaporation of mixed CH2Cl2/hexane solutions containing 1H, 1Cl, and 1CF3. Molecular structures of 1R (R = H, Cl, and CF3)† shown in Fig. 3 are very similar to each other regardless of the substituents. The S⋯S distance is around 21 Å, and the Ru–Ru bond distance is ca. 2.55 Å (1H; 2.5414(3) Å, 1Cl; 2.5468(3) Å, and 1CF3; 2.5521(7) Å), while short Ru–C
C) vibrations appear in the range of 2092–2097 cm−1 (Fig. S1f, S2g, S4i, and S5f†). Purple crystals were grown by slow evaporation of mixed CH2Cl2/hexane solutions containing 1H, 1Cl, and 1CF3. Molecular structures of 1R (R = H, Cl, and CF3)† shown in Fig. 3 are very similar to each other regardless of the substituents. The S⋯S distance is around 21 Å, and the Ru–Ru bond distance is ca. 2.55 Å (1H; 2.5414(3) Å, 1Cl; 2.5468(3) Å, and 1CF3; 2.5521(7) Å), while short Ru–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) bond lengths (dRu–C = 1.97–1.99 Å) are observed. These structural features are typical for dialkynyl-Ru2(DArF)4 complexes with no net formal σ bond between the two Ru centers with the π4δ2π4* electronic configuration, where the electrons in the dz2 orbitals are used for the Ru–C bonds.26 The slightly bent Ru–Ru–C
bond lengths (dRu–C = 1.97–1.99 Å) are observed. These structural features are typical for dialkynyl-Ru2(DArF)4 complexes with no net formal σ bond between the two Ru centers with the π4δ2π4* electronic configuration, where the electrons in the dz2 orbitals are used for the Ru–C bonds.26 The slightly bent Ru–Ru–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) linkages (154–166°) result from the second-order Jahn–Teller (SOJT) distortion (see below) to gain thermodynamic stability.25,27,28
linkages (154–166°) result from the second-order Jahn–Teller (SOJT) distortion (see below) to gain thermodynamic stability.25,27,28
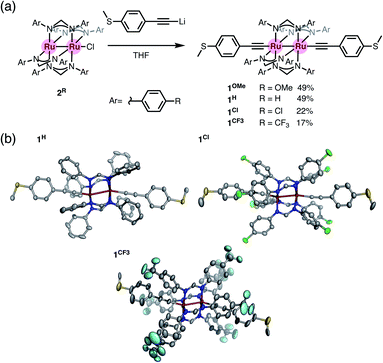 |
| | Fig. 3 (a) Synthesis of 1R (R = H, Cl, and CF3). (b) Molecular structures of 1H, 1Cl, and 1CF3 with thermal ellipsoids at the 50% probability level. Hydrogen atoms and disordered parts are omitted for clarity. | |
STM-BJ study
We carried out single-molecule conductance measurements by the scanning tunneling microscope break-junction (STM-BJ) method.29 In this method, a gold STM tip repeatedly moves in and out on a gold electrode, and the molecular junction accidentally forms during this process when molecules are present in the solution. The single process gives a long-conductance trace. A tetraglyme solution of 1R (R = OMe, H, Cl, and CF3, 0.25 mM) was soaked into the gold substrate and the break-junction measurements were performed using a gold STM-tip with 100 mV bias voltage. Individual traces show the steps in the 10−4 to 10−5G0 region (Fig. S6†). The 1D histogram constructed from 2000 successive traces reveals the peaks in the 10−4 to 10−5G0 region (Fig. 4). The 2D histogram of 1H contains features extended up to ∼1.5 nm, which correspond to the molecular junction formation. Considering the snapback distance (∼0.5 nm),30 the sum of the lengths well agrees with the S⋯S distance of 1H. On the other hand, the substituted analogues showed plateaus at shorter distances (1OMe and 1Cl: ∼1.3 nm and 1CF3: ∼0.6 nm) probably because the bulkier DArF ligands prevent the formation of molecular junctions and/or promote the breaking of molecular junctions. The single-molecule conductance was determined to be 3.4 (±1.0) × 10−4G0 (1OMe), 5.7 (±0.7) × 10−5G0 (1H), 5.6 (±1.7) × 10−5G0 (1Cl), and 1.3 (±0.2) × 10−4G0 (1CF3), with the trend of 1OMe > 1CF3 ≫ 1H ∼ 1Cl. This trend is not in accord with the expectation that replacement with electron-withdrawing substituents (cf. σ: −0.27 (OMe), 0 (H), 0.23 (Cl), and 0.54 (CF3)) deteriorates conductance because molecular wires with thioether anchor groups should prefer HOMO conductance caused by the energy alignment between the Au–sulfur lone pair bonds and the π-conjugated HOMO orbitals.3,31
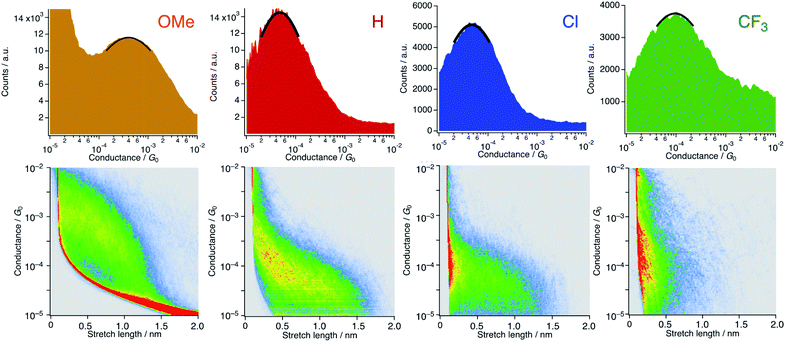 |
| | Fig. 4 1D and 2D histograms of 1R (X = OMe, H, Cl, and CF3) constructed from 2000 successive traces. [1R] = 0.25 mM in tetraglyme. No data selection was performed. | |
Cyclic voltammetry and DFT study
To estimate the frontier orbital energies, we carried out electrochemical measurements of 1R by cyclic voltammetry (Table 1, Fig. 5, [complex] = 1.0 mM in CH2Cl2, [NBu4][PF6] = 0.1 M). The paddle-wheel complexes 1R exhibit one 1e-oxidation and two successive 1e-reduction processes. The oxidation and reduction potentials cathodically shifted upon incorporation of the electron-withdrawing substituents (E1/21/E1/22; 1OMe: 0.12/−1.22, 1H: 0.19/−1.14, 1Cl: 0.38/−0.86, and 1CF3: 0.51/−0.65 V (vs. FeCp2/FeCp2+)). The potential shifts for the reduction processes caused by substitution (ΔE1/22 = E1/221CF3 – E1/221H = 0.49 V) are larger than those for the oxidation processes (ΔE1/21 = E1/211CF3 – E1/211H = 0.32 V).
Table 1 Summary of experimental and computational data for 1R (R = OMe, H, Cl, and CF3)
| Complex |
E
1/2
1 [V] |
E
1/2
2 [V] |
E
1/2
3 [V] |
HOMOCVa [eV] |
LUMOCVb [eV] |
ΔCV [eV] |
HOMODFT [eV] |
LUMODFT [eV] |
ΔDFT [eV] |
G
exp [10−5G0] |
G
calc
[10−5G0] |
HOMONEGF [eV] |
LUMONEGF [eV] |
ΔNEGF [eV] |
|
HOMOCV (in eV) = –(E1/21 (in V) + 5.1).
LUMOCV (in eV) = –(E1/22 (in V) + 5.1).
Calculated by the DFTNEGF study.
|
|
1OMe
|
0.12 |
−1.22 |
−2.20 |
−5.22 |
−3.88 |
1.34 |
−4.92 |
−3.39 |
1.53 |
34 ± 10 |
165 |
−0.13 |
0.18 |
0.31 |
|
1H
|
0.19 |
−1.14 |
−2.11 |
−5.29 |
−3.96 |
1.33 |
−5.06 |
−3.60 |
1.46 |
5.7 ± 0.7 |
1.03 |
−0.15 |
0.12 |
0.27 |
|
1Cl
|
0.38 |
−0.86 |
−1.85 |
−5.48 |
−4.24 |
1.24 |
−5.19 |
−3.84 |
1.35 |
5.6 ± 1.7 |
5.33 |
−0.16 |
0.07 |
0.23 |
|
1CF3
|
0.51 |
−0.65 |
−1.66 |
−5.61 |
−4.46 |
1.15 |
−5.27 |
−4.00 |
1.27 |
13 ± 2.4 |
49.3 |
−0.10 |
0.04 |
0.14 |
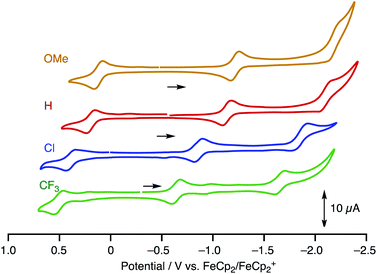 |
| | Fig. 5 CV charts of 1R (R = OMe, H, Cl and CF3) ([complex] = 1.0 mM in CH2Cl2, [NBu4][PF6] = 0.1 M, W.E. and C.E. Pt; R.E. Ag/Ag+, at the scan rate of 100 mV s−1). | |
To obtain further insights into the electronic structures of molecular wires 1R, we performed density functional theory (DFT) calculations at the B3LYP/LanL2DZ,6-31G(d) levels combined with the CPCM continuum solvent method (CH2Cl2) (Table 1, Fig. 6 and S9†). The optimized structures well reproduce the X-ray structures with the Ru2(DPhF)4 core structures distorted from D4h symmetry. The characteristics of the frontier orbitals of 1R are similar to each other. The highest occupied molecular orbitals (HOMOs), HOMO, HOMO–1 and HOMO–2, of 1R are extended over the (Ru–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C6H4SMe)2 linkages with the anti-bonding ligand π* and ruthenium dπ* character, whereas the lowest unoccupied molecular orbitals (LUMOs) are localized on the Ru2 δ* orbitals and the non-bonding N–C–N π orbitals of the DArF ligands. One notable feature of the HOMO and HOMO–1 is the overlap between the dπ* orbitals of the Ru cores due to the SOJT distortion as shown in Fig. 6.32 As a result, the Ru2 complexes gain some σ bonding nature between the two Ru atoms, which may enhance the hole transport process through the HOMO orbital.
C–C6H4SMe)2 linkages with the anti-bonding ligand π* and ruthenium dπ* character, whereas the lowest unoccupied molecular orbitals (LUMOs) are localized on the Ru2 δ* orbitals and the non-bonding N–C–N π orbitals of the DArF ligands. One notable feature of the HOMO and HOMO–1 is the overlap between the dπ* orbitals of the Ru cores due to the SOJT distortion as shown in Fig. 6.32 As a result, the Ru2 complexes gain some σ bonding nature between the two Ru atoms, which may enhance the hole transport process through the HOMO orbital.
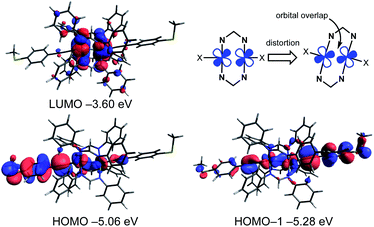 |
| | Fig. 6 Selected Kohn–Sham orbitals and their energies for 1H obtained by the DFT calculations (B3LYP/LanL2DZ,6-31G(d) and CPCM(CH2Cl2)) and the schematic representation of orbital overlap of Ru dπ* orbitals causing structural distortion. | |
The HOMO and LUMO energies (HOMODFT/LUMODFT) decrease from 1OMe (−4.92/−3.39 eV) to 1H (−5.06/−3.60 eV), 1Cl (−5.19/−3.84 eV) and then to 1CF3 (−5.27/−4.00 eV), and the values are in good agreement with those obtained from the CV analysis (HOMOCV/LUMOCV). The LUMO energies are more sensitive to the substituents on the aryl substituents (R) in accord with the CV results probably due to a subtle contribution of the aryl rings to the LUMO. As a result, the HOMO–LUMO gaps (Δ) decrease upon incorporation of the electron-withdrawing substituents (ΔDFT; 1OMe; 1.53, 1H; 1.46, 1Cl; 1.35, and 1CF3; 1.27 eV). It is noted that the plots of the HOMO and LUMO energies estimated from the CV and DFT studies against the Hammett substituent constants σ show a good linear relationship (Fig. 7), as reported for the paddle-wheel dimolybdenum complexes with the DArF ligands.33–35 Thus, the relationship between the molecule and electrode coupling should be considered to understand the unusual conductance trend by substituents.
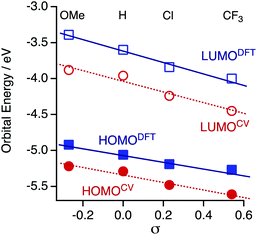 |
| | Fig. 7 Plots of the experimentally and theoretically obtained frontier orbital energies against the Hammett substituent constants σ. | |
DFT-NEGF study
To gain insights into the substituent effect of the paddle-wheel diruthenium molecular wires and the electronic structures of the molecular junctions, we carried out the DFT-non equilibrium Green's function (NEGF) calculations by using the TranSIESTA code36 and the level-broadening approach developed by Tada et al.,37 both of which gave similar results. Here, we discuss the results obtained from the TranSIESTA code for Au-1R-Au (Au: gold electrodes).38 The trend of the theoretically estimated conductance agreed well with that obtained from the break-junction study (1OMe > 1CF3 ≫ 1H ∼ 1Cl), showing the U-shaped plots (Table 1, Fig. 9a). The transmission spectra reveal many HOMO conduction orbitals within the range of 1.0 eV from the electrode's Fermi energy (EF) in contrast to the lower number of the LUMO conduction orbitals. The conduction orbitals shown in Fig. 8b are altered by the substituents. The dominant transmission eigenchannels of Au-1OMe-Au and Au-1H-Au are akin to the HOMOs of 1R without the electrodes (Fig. 6), whereas LUMO-like δ* orbitals appear for those of Au-1Cl-Au and Au-1CF3-Au. Both the HOMO and LUMO conductance peaks (HOMONEGF and LUMONEGF) shift to the negative side upon replacement of the substituents on the DArF ligands with the electron-withdrawing ones (Fig. 8a and 9b).39 For 1OMe, the HOMONEGF (−0.13 eV) is closer to EF than the LUMONEGF (0.18 eV), while the opposite trend is noted for 1CF3 (HOMONEGF: −0.10 and LUMONEGF: 0.04). These results clearly indicate that the main conduction orbital changes from the HOMO (for 1OMe) to the LUMO (for 1CF3), leading to the conductance of 1CF3 being higher than that of 1H and 1Cl. It is also noted that even the LUMO having the Ru2 δ* orbitals could be an efficient carrier transport pathway, though there is negligible contribution of the thioanisylethynyl ligands in 1R. The effect of the substituents on the single-molecule conductance and transmission spectra reported so far was moderate or, sometimes, negligible because of their large HOMO–LUMO energy gaps.40–42 The observed unique substituent effect should result from the fact that (1) the HOMO and LUMO conduction orbitals of 1R are located very close to EF and, accordingly, the HOMO–LUMO gaps become very narrow, and (2) the LUMO energies being more sensitive to the substituents causes the change of the conduction orbital from the HOMO to the LUMO.
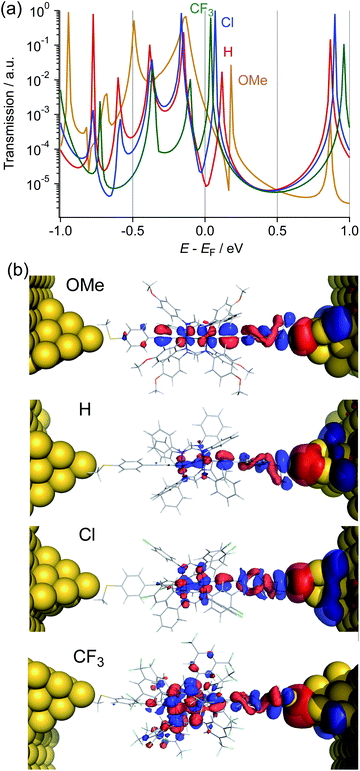 |
| | Fig. 8 (a) Transmission spectra and (b) the dominant transmission eigen channel at the Fermi level of Au-1R-Au (R = OMe, H, Cl, and CF3). | |
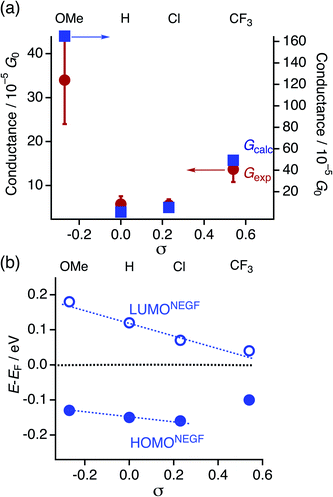 |
| | Fig. 9 Plots of (a) experimentally (Gexp) and theoretically obtained conductance (Gcalc) and (b) the HOMONEGF and LUMONEGF against Hammett substituent constants σ. | |
Conclusion
We have reported the synthesis, electrochemical properties, and single-molecule conductance of paddle-wheel diruthenium complexes 1R (R = OMe, H, Cl, and CF3) having thioanisylethynyl axial ligands. The unique trend of the single-molecule conductance caused by the replacement of the substituents on the DArF ligands with electron-withdrawing ones results from the change of the dominant conduction orbital from the HOMO (1OMe) to the LUMO (1CF3) as revealed by the DFT-NEGF study. The drastic change of the conduction orbitals is caused by the narrow HOMO–LUMO gaps of the paddle-wheel diruthenium cores. Thus, the present study reveals the importance of molecular wires embedded with metal–metal bonds with narrow HOMO–LUMO gaps, which could facilely modulate conduction orbitals. Because the control of the conduction orbitals is vital for thermoelectric materials, paddle-wheel diruthenium complexes turn out to be fascinating platforms for these purposes.
Author contributions
SO, SC, YT, and MA conceived the project. SO, SC, and YT performed experiments. YT, TO, TT, and HT performed theoretical calculations. SF and TN discussed the STM-BJ results. YT wrote the first draft and MA critically reviewed and edited the manuscript. All authors commented on drafts, and approved the final manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers 18K05139 and 21K05211. YT acknowledges research grants from the ENEOS Tonengeneral Research/Development Encouragement & Scholarship Foundation and the Asahi Glass Foundation. S. C acknowledges the Matsumae International Foundation Research Fellowship. The theoretical calculations were performed by using computers in the Research Center for Computational Science, Okazaki, Japan.
Notes and references
- S. Park, H. Kang and H. J. Yoon, J. Mater. Chem. A, 2019, 7, 14419–14446 RSC.
- K. Wang, E. Meyhofer and P. Reddy, Adv. Funct. Mater., 2020, 30, 1904534 CrossRef CAS.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 1–15 Search PubMed.
- M. Kiguchi and S. Kaneko, Phys. Chem. Chem. Phys., 2013, 15, 2253–2267 RSC.
- E. J. Dell, B. Capozzi, J. Xia, L. Venkataraman and L. M. Campos, Nat. Chem., 2015, 7, 209–214 CrossRef CAS PubMed.
- E.-M. Peligot, C. R. Acad. Sci., 1844, 19, 609–618 Search PubMed.
- E.-M. Peligot, Ann. Chim. Phys., 1844, 12, 528–579 Search PubMed.
- J. N. Van Niekerk and F. R. L. Schoening, Nature, 1953, 171, 36–37 CrossRef CAS.
- F. A. Cotton, Acc. Chem. Res., 1969, 2, 240–247 CrossRef CAS.
- F. A. Cotton, Acc. Chem. Res., 1978, 11, 225–232 CrossRef CAS.
- F. A. Cotton, C. Lin and C. A. Murillo, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4810–4813 CrossRef CAS PubMed.
- I. P.-C. Liu, W.-Z. Wang and S.-M. Peng, Chem. Commun., 2009, 4323–4331 CAS.
- Y. Tanaka, M. Kiguchi and M. Akita, Chem.–Eur. J., 2017, 23, 4741–4749 CrossRef CAS PubMed.
- I.-W. P. Chen, M.-D. Fu, W.-H. Tseng, J.-Y. Yu, S.-H. Wu, C.-J. Ku, C. Chen and S.-M. Peng, Angew. Chem., Int. Ed., 2006, 45, 5814–5818 CrossRef CAS PubMed.
- P.-J. Chen, M. Sigrist, E.-C. Horng, G.-M. Lin, G.-H. Lee, C. Chen and S.-M. Peng, Chem. Commun., 2017, 53, 4673–4676 RSC.
- M. Meng, Z. Tang, S. Mallick, M. H. Luo, Z. Tan, J. Liu, J. Shi, Y. Yang, C. Y. Liu and W. Hong, Nanoscale, 2020, 12, 10320–10327 RSC.
- P. A. Agaskar and F. A. Cotton, Inorg. Chem., 1986, 25, 15–19 CrossRef CAS.
- A. K. Mahapatro, J. Ying, T. Ren and D. B. Janes, Nano Lett., 2008, 8, 2131–2136 CrossRef CAS PubMed.
- H. Zhu, S. J. Pookpanratana, J. E. Bonevich, S. N. Natoli, C. A. Hacker, T. Ren, J. S. Suehle, C. A. Richter and Q. Li, ACS Appl. Mater. Interfaces, 2015, 7, 27306–27313 CrossRef CAS PubMed.
- A. S. Blum, T. Ren, D. A. Parish, S. A. Trammell, M. H. Moore, J. G. Kushmerick, G.-L. Xu, J. R. Deschamps, S. K. Pollack and R. Shashidhar, J. Am. Chem. Soc., 2005, 127, 10010–10011 CrossRef PubMed.
- J.-W. Ying, D. R. Sobransingh, G.-L. Xu, A. E. Kaifer and T. Ren, Chem. Commun., 2005, 357–359 RSC.
- S. Pookpanratana, I. Savchenko, S. N. Natoli, S. P. Cummings, L. J. Richter, J. W. F. Robertson, C. A. Richter, T. Ren and C. A. Hacker, Langmuir, 2014, 30, 10280–10289 CrossRef CAS PubMed.
- T. A. Stephenson and G. Wilkinson, J. Inorg. Nucl. Chem., 1966, 28, 2285–2291 CrossRef CAS.
- C. Lin, T. Ren, E. J. Valente, J. D. Zubkowski and E. T. Smith, Chem. Lett., 1997, 26, 753–754 CrossRef.
- C. Lin, T. Ren, E. J. Valente and J. D. Zubkowski, J. Chem. Soc., Dalton Trans., 1998, 571–576 RSC.
- F. A. Cotton and A. Yokochi, Inorg. Chem., 1997, 36, 567–570 CrossRef CAS.
- G. Xu, C. Campana and T. Ren, Inorg. Chem., 2002, 41, 3521–3527 CrossRef CAS PubMed.
- I. P.-C. Liu and T. Ren, Inorg. Chem., 2009, 48, 5608–5610 CrossRef CAS PubMed.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- W. Hong, D. Z. Manrique, P. Moreno-García, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304 CrossRef CAS PubMed.
- P. Moreno-García, M. Gulcur, D. Z. Manrique, T. Pope, W. Hong, V. Kaliginedi, C. Huang, A. S. Batsanov, M. R. Bryce, C. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–12240 CrossRef PubMed.
- A. Raghavan and T. Ren, Organometallics, 2019, 38, 3888–3896 CrossRef CAS.
- C. Lin, J. D. Protasiewicz, E. T. Smith and T. Ren, Inorg. Chem., 1996, 35, 6422–6428 CrossRef CAS PubMed.
- T. Ren, Coord. Chem. Rev., 1998, 175, 43–58 CrossRef CAS.
- E. Van Caemelbecke, T. Phan, W. R. Osterloh and K. M. Kadish, Coord. Chem. Rev., 2021, 434, 213706 CrossRef CAS.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B, 2002, 65, 165401 CrossRef.
- T. Tada, M. Kondo and K. Yoshizawa, J. Chem. Phys., 2004, 121, 8050–8057 CrossRef CAS PubMed.
- See the ESI.†.
- The HOMO energy of Au-1CF3-Au showed a positive shift compared to those of the other substituents. This result is in accord with that of the level-broadening approach37 (Fig. S13†).
- L. Venkataraman, Y. S. Park, A. C. Whalley, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nano Lett., 2007, 7, 502–506 CrossRef CAS PubMed.
- D. J. Mowbray, G. Jones and K. S. Thygesen, J. Chem. Phys., 2008, 128, 111103 CrossRef CAS PubMed.
- G. Yzambart, L. Rincón-García, A. A. Al-Jobory, A. K. Ismael, G. Rubio-Bollinger, C. J. Lambert, N. Agraït and M. R. Bryce, J. Phys. Chem. C, 2018, 122, 27198–27204 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis, STM-BJ study, Vis-NIR absorption spectra, and DFT and TD-DFT studies. CCDC 2057135–2057137. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc02407h |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article c,
Yuya
Tanaka
c,
Yuya
Tanaka
 *ab,
Tatsuhiko
Ohto
*ab,
Tatsuhiko
Ohto
 d,
Tomofumi
Tada
d,
Tomofumi
Tada
 e,
Hirokazu
Tada
d,
Shintaro
Fujii
e,
Hirokazu
Tada
d,
Shintaro
Fujii
 f,
Tomoaki
Nishino
f,
Tomoaki
Nishino
 f and
Munetaka
Akita
f and
Munetaka
Akita
 *ab
*ab
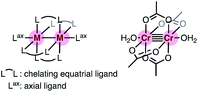
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CPh), (ap = 2-anilinopyridinate), was reported by Cotton in 1986.17 Later on, Ren et al. extensively explored their application in molecular devices.18–22 To date, however, the single-molecule conductance measurement of organometallic paddle-wheel complexes remains to be studied. We describe, herein, the results of the single-molecule conductance study for a series of paddle-wheel diruthenium molecular wires 1R with diarylformamidinato supporting ligands (DArF: p-R-C6H4-NCHN-C6H4-R-p) and two axial thioanisylethynyl ligands (Fig. 2 bottom; R = OMe, H, Cl, and CF3), in which the thiomethyl anchors show high affinity toward gold electrodes. The present study revealed a unique substituent effect of the aryl moieties in the supporting DArF ligands on the conductance, suggesting the dominant conduction band as well as the charge carrier conductance changed by the substituents.
CPh), (ap = 2-anilinopyridinate), was reported by Cotton in 1986.17 Later on, Ren et al. extensively explored their application in molecular devices.18–22 To date, however, the single-molecule conductance measurement of organometallic paddle-wheel complexes remains to be studied. We describe, herein, the results of the single-molecule conductance study for a series of paddle-wheel diruthenium molecular wires 1R with diarylformamidinato supporting ligands (DArF: p-R-C6H4-NCHN-C6H4-R-p) and two axial thioanisylethynyl ligands (Fig. 2 bottom; R = OMe, H, Cl, and CF3), in which the thiomethyl anchors show high affinity toward gold electrodes. The present study revealed a unique substituent effect of the aryl moieties in the supporting DArF ligands on the conductance, suggesting the dominant conduction band as well as the charge carrier conductance changed by the substituents.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) vibrations appear in the range of 2092–2097 cm−1 (Fig. S1f, S2g, S4i, and S5f†). Purple crystals were grown by slow evaporation of mixed CH2Cl2/hexane solutions containing 1H, 1Cl, and 1CF3. Molecular structures of 1R (R = H, Cl, and CF3)† shown in Fig. 3 are very similar to each other regardless of the substituents. The S⋯S distance is around 21 Å, and the Ru–Ru bond distance is ca. 2.55 Å (1H; 2.5414(3) Å, 1Cl; 2.5468(3) Å, and 1CF3; 2.5521(7) Å), while short Ru–C
C) vibrations appear in the range of 2092–2097 cm−1 (Fig. S1f, S2g, S4i, and S5f†). Purple crystals were grown by slow evaporation of mixed CH2Cl2/hexane solutions containing 1H, 1Cl, and 1CF3. Molecular structures of 1R (R = H, Cl, and CF3)† shown in Fig. 3 are very similar to each other regardless of the substituents. The S⋯S distance is around 21 Å, and the Ru–Ru bond distance is ca. 2.55 Å (1H; 2.5414(3) Å, 1Cl; 2.5468(3) Å, and 1CF3; 2.5521(7) Å), while short Ru–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) bond lengths (dRu–C = 1.97–1.99 Å) are observed. These structural features are typical for dialkynyl-Ru2(DArF)4 complexes with no net formal σ bond between the two Ru centers with the π4δ2π4* electronic configuration, where the electrons in the dz2 orbitals are used for the Ru–C bonds.26 The slightly bent Ru–Ru–C
bond lengths (dRu–C = 1.97–1.99 Å) are observed. These structural features are typical for dialkynyl-Ru2(DArF)4 complexes with no net formal σ bond between the two Ru centers with the π4δ2π4* electronic configuration, where the electrons in the dz2 orbitals are used for the Ru–C bonds.26 The slightly bent Ru–Ru–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) linkages (154–166°) result from the second-order Jahn–Teller (SOJT) distortion (see below) to gain thermodynamic stability.25,27,28
linkages (154–166°) result from the second-order Jahn–Teller (SOJT) distortion (see below) to gain thermodynamic stability.25,27,28


![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C6H4SMe)2 linkages with the anti-bonding ligand π* and ruthenium dπ* character, whereas the lowest unoccupied molecular orbitals (LUMOs) are localized on the Ru2 δ* orbitals and the non-bonding N–C–N π orbitals of the DArF ligands. One notable feature of the HOMO and HOMO–1 is the overlap between the dπ* orbitals of the Ru cores due to the SOJT distortion as shown in Fig. 6.32 As a result, the Ru2 complexes gain some σ bonding nature between the two Ru atoms, which may enhance the hole transport process through the HOMO orbital.
C–C6H4SMe)2 linkages with the anti-bonding ligand π* and ruthenium dπ* character, whereas the lowest unoccupied molecular orbitals (LUMOs) are localized on the Ru2 δ* orbitals and the non-bonding N–C–N π orbitals of the DArF ligands. One notable feature of the HOMO and HOMO–1 is the overlap between the dπ* orbitals of the Ru cores due to the SOJT distortion as shown in Fig. 6.32 As a result, the Ru2 complexes gain some σ bonding nature between the two Ru atoms, which may enhance the hole transport process through the HOMO orbital.





