Open Access Article
Open Access ArticleBroad-band spectroscopy of a vanadyl porphyrin: a model electronuclear spin qudit†
Ignacio
Gimeno
 a,
Ainhoa
Urtizberea
a,
Ainhoa
Urtizberea
 ab,
Juan
Román-Roche
ab,
Juan
Román-Roche
 a,
David
Zueco
a,
David
Zueco
 a,
Agustín
Camón
a,
Agustín
Camón
 a,
Pablo J.
Alonso
a,
Pablo J.
Alonso
 a,
Olivier
Roubeau
a,
Olivier
Roubeau
 *a and
Fernando
Luis
*a and
Fernando
Luis
 *a
*a
aInstituto de Nanociencia y Materiales de Aragón, CSIC and Universidad de Zaragoza, 50009 Zaragoza, Spain. E-mail: roubeau@unizar.es; fluis@unizar.es
bCentro Universitario de la Defensa, 50090 Zaragoza, Spain
First published on 17th March 2021
Abstract
We explore how to encode more than a qubit in vanadyl porphyrin molecules hosting a S = 1/2 electronic spin coupled to a I = 7/2 nuclear spin. The spin Hamiltonian and its parameters, as well as the spin dynamics, have been determined via a combination of electron paramagnetic resonance, heat capacity, magnetization and on-chip magnetic spectroscopy experiments performed on single crystals. We find low temperature spin coherence times of micro-seconds and spin relaxation times longer than a second. For sufficiently strong magnetic fields (B > 0.1 T, corresponding to resonance frequencies of 9–10 GHz) these properties make vanadyl porphyrin molecules suitable qubit realizations. The presence of multiple equispaced nuclear spin levels then merely provides 8 alternatives to define the ‘1’ and ‘0’ basis states. For lower magnetic fields (B < 0.1 T), and lower frequencies (<2 GHz), we find spectroscopic signatures of a sizeable electronuclear entanglement. This effect generates a larger set of allowed transitions between different electronuclear spin states and removes their degeneracies. Under these conditions, we show that each molecule fulfills the conditions to act as a universal 4-qubit processor or, equivalently, as a d = 16 qudit. These findings widen the catalogue of chemically designed systems able to implement non-trivial quantum functionalities, such as quantum simulations and, especially, quantum error correction at the molecular level.
Introduction
Magnetic molecules are appealing candidates to form the building blocks of future quantum technologies.1 One of their characteristic traits is the ability to tune their properties by chemical design, e.g. to enhance the spin coherence times2–4 or to gain a sufficiently fast control of their quantum states by means of external stimuli, such as microwave magnetic5 or electric6 fields and even visible light.7 Another remarkable feature is the possibility of hosting multiple qubits, or d-dimensional qudits, in a single molecule.8 This possibility allows integrating at the molecular level non-trivial functionalities, like quantum error correction9 or simple quantum codes and simulations,10 and constitutes a potential competitive advantage over other solid-state quantum platforms.A relatively straightforward strategy to embody multiple qubits is to synthesize molecules having several, weakly coupled, magnetic metal centres.8a,11 As a somewhat simpler alternative, one can also use internal degrees of freedom, arising from electronic spin projections of S > 1/2 metal ions12 or from nuclear spin states.8b,9b,13 One advantage of this second approach is that it facilitates the synthesis of magnetically diluted single crystals, which can combine sufficiently long coherence times with the ability of addressing specific quantum operations. In addition, these mononuclear complexes are often more robust, thus easier to interface with solid state devices and circuits.6a,10a,14 The choice of suitable candidates is however quite limited by the need of ensuring a proper addressability of the relevant transitions linking different levels of each qudit. Among electronic spins, the magnetic anisotropy then needs to be very weak, in order to keep resonant frequencies accessible (typically meaning within 1 to 10 GHz). In practice, this has restricted the search to Gd based qudits.12 In the case of nuclear spin qudits, the same condition imposes a sufficiently strong quadrupolar interaction. The latter criterion then seems to exclude several a priori promising systems, such as the family of vanadyl based molecules that includes among its members some of the rare examples of quantum spin coherence surviving up to room temperature15 and record spin coherence times close to milliseconds.16
In this work, we show that the sought level anharmonicity required to define multiple qubits, or a qudit, using electronuclear spin states can be achieved even when the quadrupolar interaction is negligible. A broad-band spectroscopy study of vanadyl porphyrin crystals provides direct and detailed information on the magnetic energy level structure. Extending these measurements to very low temperatures allows exploring low frequencies and magnetic fields. The entanglement of the vanadyl S = 1/2 electronic spin with its I = 7/2 nuclear spin results then in a series of unequally spaced levels. In this regime, transition rates between different nuclear spin states become also comparable to those of electronic transitions. On basis of this study, we discuss the possibility of using vanadyl molecules to perform universal quantum operations, either as 4-qubit processors or as qudits with dimension d = 16.
Results and discussion
Synthesis, structure and spin Hamiltonian of [VOTCPPEt]
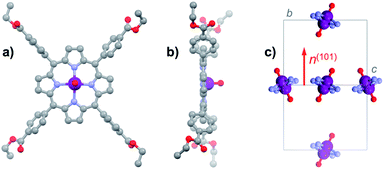
For the present study, we focus on the vanadyl porphyrin [VO(TCPPEt)] (1VO, H2TCPPEt = 5,10,15,20-tetrakis(4-carboxyphenyl)porphine tetraethyl ester), a molecule we previously used as precursor to form a 2D framework.17 Although the structure and spin dynamics of 1VO were not determined, the vanadyl porphyrin node in the 2D framework did show some reasonably long quantum coherence. Besides, 1VO is readily obtained by a simple reaction of vanadyl sulphate and the free-base H6TCPP in ethanol under solvothermal conditions, and most importantly in the form of robust large single-crystals. Interestingly, crystals of the titanyl analogue [TiO(TCPPEt)] (1TiO) can be obtained under similar synthetic conditions, albeit only with partial metallation, even using a large excess of the titanyl starting salt. The free-base ligand H2TCPPEt, obtained under the same conditions, and both vanadyl and titanyl complexes were found by single-crystal diffraction to be isostructural, which in turn allowed to isolate crystals containing the vanadyl porphyrin diluted in a diamagnetic host, 13%VO (see ESI† for details).All three materials H2TCPPEt, 1VO and 1TiO crystallize unsolvated in the monoclinic space group P21/n, the asymmetric unit coinciding with half the neutral MTCPPEt molecule (M = H2, VO, TiO). In 1VO, the V4+ ion is coordinated equatorially by the four pyrrole N (M–N bond length in the range 1.994(4)–2.172(4) Å), but lies slightly out of the N4 porphyrin plane, at 0.491 Å (Fig. 1a and b). The axial V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond (1.556(9) Å) is thus disordered over two equivalent orientations by symmetry, due to the inversion center close to the center of the porphyrin N4 square. The porphyrin ring is basically flat with no significant distortion (Fig. 1b), the largest deviation being for the external pyrrole carbons, in all cases at less than 0.102 Å from the N4 porphyrin plane. One of the two unique ethyl groups is also disordered over two positions. The molecules have two orientations in the cell as a result of the 2-fold screw axis. The average VO vector is however normal to the 101 plane, since this plane is the bisector of the N4 porphyrin plane (Fig. 1c). The molecules with identical orientation form supramolecular 1D chains through C–H⋯π interactions involving the four pyrrole rings, these chains being connected into planes through π⋯π interactions between pyrrole ring and COO ester moieties of molecules with different orientations (Fig. S1 and S2†). The shortest V⋯V separation corresponds to the translation along the a axis, at 9.394 Å, while those within the supramolecular chains and between molecules with different orientations are respectively 10.856 Å and 12.853 Å.
O bond (1.556(9) Å) is thus disordered over two equivalent orientations by symmetry, due to the inversion center close to the center of the porphyrin N4 square. The porphyrin ring is basically flat with no significant distortion (Fig. 1b), the largest deviation being for the external pyrrole carbons, in all cases at less than 0.102 Å from the N4 porphyrin plane. One of the two unique ethyl groups is also disordered over two positions. The molecules have two orientations in the cell as a result of the 2-fold screw axis. The average VO vector is however normal to the 101 plane, since this plane is the bisector of the N4 porphyrin plane (Fig. 1c). The molecules with identical orientation form supramolecular 1D chains through C–H⋯π interactions involving the four pyrrole rings, these chains being connected into planes through π⋯π interactions between pyrrole ring and COO ester moieties of molecules with different orientations (Fig. S1 and S2†). The shortest V⋯V separation corresponds to the translation along the a axis, at 9.394 Å, while those within the supramolecular chains and between molecules with different orientations are respectively 10.856 Å and 12.853 Å.
The continuous wave (CW) X-band EPR spectra of a frozen solution of 1VO in toluene:CDCl3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.46 mmol L−1), 1solVO, and of polycrystalline 1VO are shown in Fig. 2 (top traces). We have also studied the rotational CW EPR spectra of single crystals of 1VO and of 13%VO (Fig. 2 bottom and Fig. S4, S8 and S9†). All are characteristic of an axial vanadyl spin, in agreement with the local symmetry at the porphyrin site. In particular, it appears that the two orientations of the molecules in a single-crystal are magnetically equivalent when the magnetic field is applied perpendicular to the long crystal axis, labelled here as the laboratory Z axis (see Fig. S3†). From the indexing of the crystal, this corresponds to the situation where the magnetic field is applied in the 101 crystal plane, perpendicular to the average V
1, 0.46 mmol L−1), 1solVO, and of polycrystalline 1VO are shown in Fig. 2 (top traces). We have also studied the rotational CW EPR spectra of single crystals of 1VO and of 13%VO (Fig. 2 bottom and Fig. S4, S8 and S9†). All are characteristic of an axial vanadyl spin, in agreement with the local symmetry at the porphyrin site. In particular, it appears that the two orientations of the molecules in a single-crystal are magnetically equivalent when the magnetic field is applied perpendicular to the long crystal axis, labelled here as the laboratory Z axis (see Fig. S3†). From the indexing of the crystal, this corresponds to the situation where the magnetic field is applied in the 101 crystal plane, perpendicular to the average V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vector (see Fig. 1c). Moreover, there are two perpendicular orientations of the field within the laboratory XY plane, xC and yC, for which the splitting of the EPR is respectively minimal and maximal. This allows defining the magnetic axes for each molecule, taking advantage of the fact the symmetry of the rotational diagrams is solely reflecting the local molecular symmetry. Taking into account the structural information to define the angle between the two local gyromagnetic z axes, the rotational data is reproduced very satisfactorily using an axial spin-Hamiltonian for each molecule
O vector (see Fig. 1c). Moreover, there are two perpendicular orientations of the field within the laboratory XY plane, xC and yC, for which the splitting of the EPR is respectively minimal and maximal. This allows defining the magnetic axes for each molecule, taking advantage of the fact the symmetry of the rotational diagrams is solely reflecting the local molecular symmetry. Taking into account the structural information to define the angle between the two local gyromagnetic z axes, the rotational data is reproduced very satisfactorily using an axial spin-Hamiltonian for each molecule
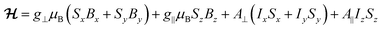 | (1) |
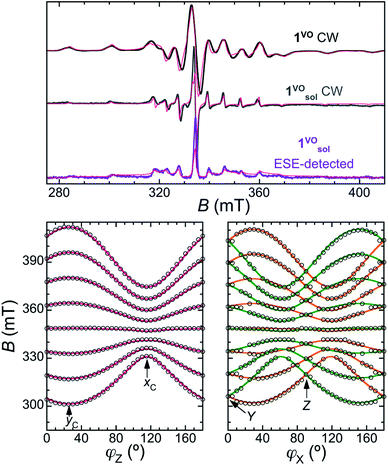 | ||
| Fig. 2 Top: X-band CW-EPR spectra of 1VO at RT (top trace) and the frozen solution 1solVO at 30 K (middle trace), and 2p-ESE-detected EPR spectrum of 1solVO (τ = 200 ns, 30 K, bottom trace). The thin red lines are simulations using an axial SH (eqn (1)) with gII = 1.963, g⊥ = 1.99, AII = 475 MHz and A⊥ = 172 MHz. Bottom: Rotational diagrams for a single crystal of 1VO at RT. The empty circles represent the positions of the center of the lines in the CW-EPR spectra upon rotating the crystal around the Z (left) and X (middle) laboratory axes (see also ESI†). Full lines are the corresponding positions calculated with the spin Hamiltonian. The contribution from the two magnetically inequivalent orientations of the molecules is represented in different colours (orange and green). | ||
The specific heat cP/R is also sensitive to the structure of magnetic energy levels. Its temperature dependence for a single-crystal of 1VO in zero-field shows a low temperature tail, which can be associated with the hyperfine splitting of the vanadyl nuclear spin levels (Fig. S24†). Under a magnetic field, a Schottky anomaly associated with the Zeeman splitting between electronic spin-up and spin down states is observed, its maximum becoming detectable in the experimental temperature range (T > 0.35 K) for fields above 2 T. At higher temperatures, the specific heat cP/R becomes dominated by excitations of vibrational modes. The Schottky broad maxima are well accounted for by numerical calculations based on the parameters of the spin Hamiltonian derived above, thus fully supporting these. An exception is observed for intermediate fields of 0.25, 0.5 and 1 T, for which the expected rise in cP/R associated with the Schottky anomaly is either not detected or reduced with respect to the simulation. As discussed below, this is due to the slow magnetization dynamics of the vanadyl spins (see also Fig. S25†).
[VO(TCPPEt)] as a spin qubit: spin coherence and spin relaxation time scales
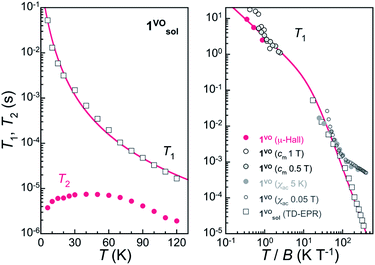
Knowledge of the temperature dependence of the spin relaxation timescales, described through the spin-lattice relaxation time T1, is important for various reasons. First, because it represents the ultimate limitation of T2 when all other sources of decoherence are suppressed, i.e. T2 ≤ T1. At higher temperatures, T2 is indeed often limited by the decreasing T1. On the other hand, 1/T1 sets the speed at which the spins decay towards the ground state at very low T, thus also the initialization process rate in quantum information applications.We have first studied the spin-lattice relaxation of the VOTCPPEt molecule in the frozen solution 1solVO through TD EPR at X-band frequencies. Inversion recovery experiments were performed between 6 K and 120 K at B = 346.6 mT, which corresponds to the most intense resonance line in the CW and ESE-detected spectra (see Fig. 2). The experimental dependence on td, the delay time after the initial inversion pulse, is reproduced by a stretched exponential, written as exp{-(td/βT1)β},18 thus allowing to derive a mean T1 value (Fig. S11 and Table S3†). From about 50 ms at 6 K, T1 decreases continuously with increasing temperature, to reach about 20 μs at 120 K (Fig. 3). The temperature dependence can be reproduced considering direct and Raman relaxation processes through the expression 1/T1 = aT + cTm, and with a = 2.2(2) s−1 K−1, c = 0.029(3) s−1 K−3 and m = 3. Although the direct process is dominant at the lowest temperature of 6 K, Raman processes are already effective and then dominate the temperature dependence of T1 at increasing temperatures.
In the solid-state, the magnetization dynamics was studied through ac magnetic susceptibility measurements on polycrystalline 1VO (Fig. S19–S21†). Upon the application of a dc field, an out-of-phase component of the susceptibility χ′′ shows up, corresponding to a decrease in the real susceptibility χ′. For spin 1/2 systems, the characteristic relaxation time is a direct measure of T1. It was determined, both at 5 K for increasing dc fields and at 500 Oe for T ranging from 2 to 20 K, by fitting the isothermal frequency dependence of χ′ and χ′′ with a generalized Debye model. The spin-lattice relaxation time was also estimated from heat capacity measurements on a single-crystal of 1VO. As mentioned above, a sharp drop is observed in the magnetic component cm measured at certain field values (see e.g. the data measured at B = 1 T in Fig. S25†). This deviation from equilibrium occurs when phonon-induced relaxation processes become too slow as compared with the time-scale of the relaxation measurement.19 By comparing measurements done with short (out of equilibrium) and long (equilibrium) experimental times, the characteristic time of the spin thermalization, which is equivalent to T1, can be derived. Finally, μ-Hall magnetization measurements performed on a single-crystal of 1VO provide yet another evidence of the slow spin dynamics. For T ≤ 1 K, T1 becomes long enough with respect to the field sweep rate of 1 T min−1, so that the system shows magnetic hysteresis (Fig. S27†) despite the absence of an activation barrier for the spin reversal. Dc relaxation measurements performed at fixed temperatures and magnetic fields indeed allow extracting T1 values in the range of seconds.
Values of T1 derived from all measurements are plotted together vs. T/B in Fig. 3 right. Overall, there is good agreement among data obtained by different methods, except for those extracted from ac susceptibility at low fields. This is understandable as the direct relaxation process becomes then less significant, while it is likely the dominant process at low temperatures and under intermediate to high fields. In fact, and quite remarkably, most data can be described considering direct and Raman processes through the expression 1/T1 = a′(T/B) + c′(T/B)3 with a′ = 0.324(9) s−1 T K−1 and c′ = 0.0145 s−1 T3 K−3, confirming that the spin relaxation is dominated by direct processes at low temperatures, at least for moderate fields in the range 0.1–1.5 T.
The relaxation times for the [VO(TCPPEt)] molecule are remarkably long, for example about two times longer than those reported recently for dicatechol vanadyl complexes as the highest for vanadyl-based compounds.20 As discussed previously, this is likely the consequence of the square pyramidal environment of the V(IV) ion and the overall rigidity of its coordination sphere. Both reduce the probability that the electronic spin couples significantly with low-lying vibrational modes. The longer T1 in 1VO with respect to other vanadyl bis-chelates (see Table S4†) can probably be ascribed to the higher rigidity of the macrocyclic tetra-chelating porphyrin. It is in this respect relevant that the phthalocyanine analogue VOPc has similarly long spin-relaxation times.15,21 Combined experimental/theoretical studies of vibrational properties are nevertheless necessary to identify the origin of differences in T1, as done so far on few occasions.22–24 Importantly, such long spin-lattice relaxation times ensure that T1 will not be limiting the coherence time-scale. On the other hand, they can represent a drawback for an efficient qubit initialization.
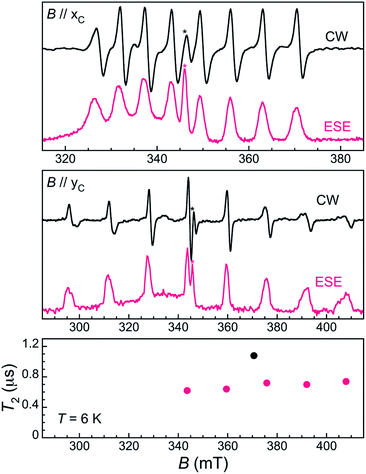
To evaluate the spin coherence times T2 of the [VOTCPPEt] molecule, we again turn to TD EPR measurements at X-band on both the frozen solution 1solVO and a diluted single crystal 13%VO. The latter were done for two orientations of the crystal, namely along the two perpendicular orientations xC and yC for which the splitting of the EPR spectrum is, respectively, minimal and maximal (see Fig. 2). Using a Hahn sequence, consisting of a π/2 pulse and a π pulse separated by a varying interval τ, an intense electron spin echo (ESE) is detected at any magnetic field in the CW-EPR spectrum, indicative of a measurable quantum coherence. The echo-induced EPR spectra are shown in Fig. 2 and 4. They are in excellent agreement with the CW-EPR spectra, being reproduced with the same Hamiltonian parameters given above (see also ESI†).
Measurements of the ESE decay as a function of τ were then applied to determine the temperature dependence of the phase memory time T2 in 1solVO. The decay (Fig. S12†) shows a significant modulation which likely arises from the interaction of the vanadyl electronic spin with deuterons from the solvent, in line with recent observations on frozen solutions of Gd complexes.12b A low frequency modulation is also present that makes the correct estimation of T2 difficult (see ESI† for details). The values of T2 given in Fig. 3, left panel, were derived by fitting a conventional stretched exponential expression, y(τ) = A0 + A1exp{−(2τ/T2)β}, to the ESE decays.
The coherence time of [VOTCPPEt] in 1solVO increases from 3.8(2) μs at 6 K to a plateau at ca. 7 μs in the range 25–60 K, and then smoothly decreases down to 1.9(2) μs at 120 K. This decrease is likely due to a parallel decrease of T1, which is only about 1 order of magnitude higher than T2 over the corresponding temperature range. The origin of the increase of T2 observed at low temperature is less clear, and could be an effect of the low frequency modulation, although a similar behavior has been reported for a vanadyl dicathechol complex.20 In any case, the observed quantum coherence compares well with those found for other VIV molecular spin qubits in frozen solution, such as [V(C8S8)3]2− (7 μs at 10 K)25 or [VO(naph-cat2]2− (6.5 μs at 25 K, see Table S4†).20 The [VOTCPPEt] molecule is therefore a valid spin-qubit candidate, especially considering that the solvent mixture used here is only partly deuterated.
In the solid-state, the ESE decay observed for a single crystal of 13%VO at 6 K is also strongly modulated, with an unassigned set of modulation frequencies (Fig. S16 and S17†). The quantum coherence of the different electronuclear transitions are very similar, with only a slight increase of T2 with the applied field, from 0.62(2) μs for the central mI = −1/2 to mI = 1/2 transition at 343.6 mT to 0.74(4) μs for the external mI = 5/2 to mI = 7/2 transition at 408.9 mT, all for the magnetic field oriented along yc (maximum splitting of the EPR spectrum). When the field is applied along xc, i.e. for the minimal splitting of the EPR spectrum, the mI = 5/2 to mI = 7/2 transition sees its coherence increase by almost 50% to 1.1(1) μs. While this is significantly lower than in 1solVO, this is likely due to the still relatively high magnetic concentration of 13%VO. Indeed, the energy scale of vanadyl–vanadyl dipolar interaction in 13%VO can be roughly estimated to be ca. 0.02 mK (or 417 MHz),26 meaning that the decoherence induced by the dipolar interaction would be of the order of 2.4 μs. Further magnetic dilution may therefore allow T2 to approach that measured in 1solVO.
Broad-band on-chip magnetic spectroscopy
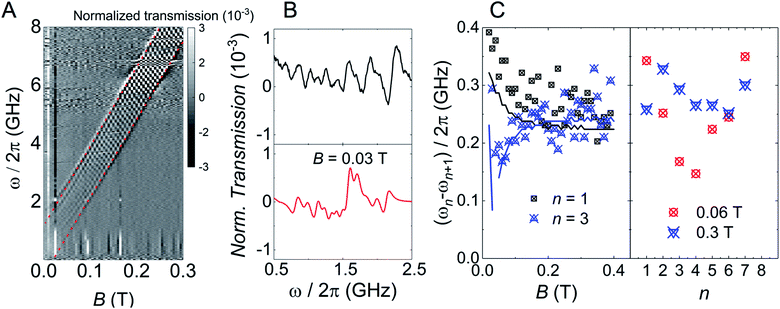
The above characterization has been completed by means of experiments performed on superconducting transmission waveguides coupled to pure crystals of 1VO. These experiments provide direct spectroscopic information at any frequency below 14 GHz and as a function of magnetic field and allow varying temperature over a wide range.12a,27 Results obtained at 4.2 K for different orientations of the magnetic field are shown in Fig. 5 and S29.† The presence of resonant spin transitions manifests in a decrease in the microwave signal transmitted through the device. The normalized transmission (see ESI†) is equivalent to the absorption derivative measured in conventional CW EPR experiments. Only, in this case one can sweep both frequency and magnetic field independently of each other, as shown in Fig. 5. The 2D transmission spectrum provides then a full picture of the Zeeman energy diagram and shows that, for B > 0.1 T, the allowed transitions correspond mainly to the reversal of the electronic spin for each nuclear spin projection. The hyperfine interaction acts here just as a kind of bias field that shifts resonances associated with different nuclear spin states. In fact, one can directly “read out” the hyperfine level splittings by looking at the frequency shifts between the 8, close to equidistant, resonance lines. This also confirms that the nuclear quadrupolar interaction is close to negligible, in agreement with previous reports for vanadium in diverse configurations.28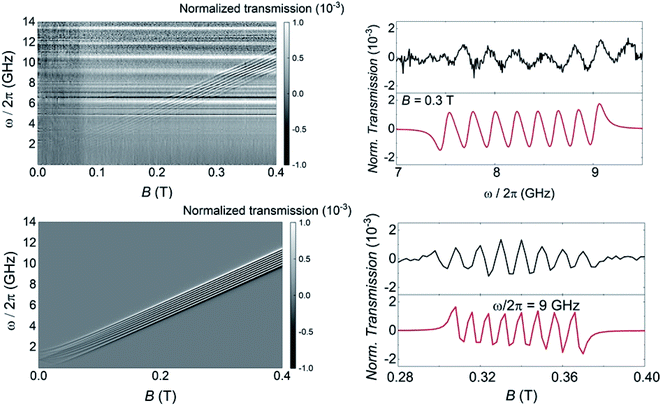 | ||
| Fig. 5 Left: Grey scale experimental (top) and simulated (bottom) plots of the normalized transmission through a superconducting wave guide coupled to a single crystal of 1VO measured at T = 4.2 K as a function of frequency and magnetic field. The magnetic field was applied along the a crystallographic axis (X axis of the laboratory frame as defined in Fig. S3†). Right: Normalized CW spectra obtained from these data at either fixed B = 0.3 T as a function of frequency (top) or at fixed ω/2π = 9 GHz as a function of magnetic field. Black and red lines show experimental and simulated data, respectively. | ||
In addition, the effective g-factor along each orientation is given by the slope of these lines. Repeating this procedure for the X, Y and Z laboratory axes (see Fig. S28 and S29†) and using the crystallographic information shown in Fig. 1, one can refine the parameters of the spin Hamiltonian, which confirm those derived from angle-dependent CW-EPR experiments. Simulations of the normalized transmission done with these parameters, shown in Fig. 5 and S29,† agree well with the experimental data.
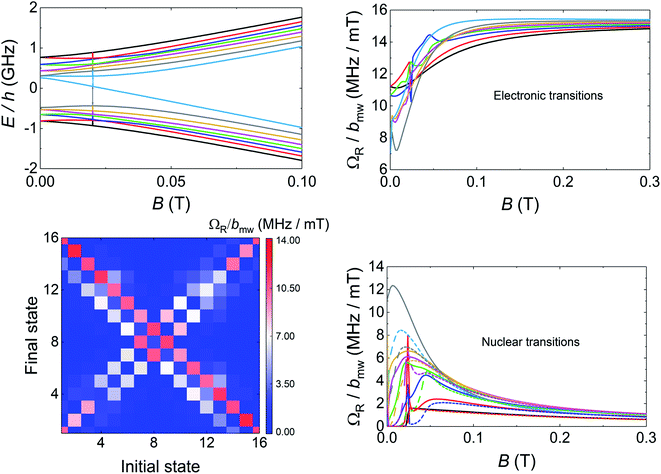
The results discussed up to now confirm that the [VOTCPPEt] molecules, like other vanadyl derivatives, are quite promising qubit candidates. Within this frame, the existence of multiple nuclear spin levels reduces to a choice between 8 different definitions for the qubit basis states ‘0’ and ‘1’. However, deviations from this simple picture are expected to occur for weaker magnetic fields, when the Zeeman and hyperfine interactions compete in intensity and the electron and nuclear spins become entangled. Eventually, for B = 0 eigenstates of the spin Hamiltonian (1) approach states of the total angular momentum F = S + I, with F = 4 and 3. The question we address in the following is whether these 16 electronuclear spin states can properly encode the basis states of a d = 16 qudit, or of a 4-qubit processor. The transmission experiments shown in Fig. 5 allow exploring this low-field low-frequency region, and hint at a deviation of the resonance lines from linearity. However, the signal becomes then also very weak, as all levels are nearly equally populated at 4.2 K. Answering the above question clearly calls for similar experiments in the temperature region below 1 K.
Very low temperature experiments: [VOTCPPEt] as a d = 16 electronuclear spin qudit
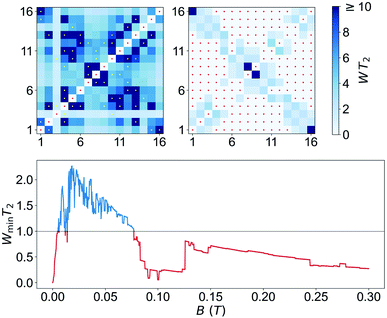
Transmission experiments have been extended to the region of very low temperatures by making use of a 3He–4He dilution refrigerator equipped with microwave lines. As it is shown in Fig. S30,† decreasing temperature gives rise to a sharp increase in the visibility of the absorption lines. A 2D plot of data measured at the lowest attainable temperature T = 0.175 K are shown in Fig. 6. Despite the still sizeable noise, the data reveal some interesting features. First, and as expected, resonance lines no longer follow a linear dependence on B. The underlying reason is the occurrence of level crossings (and also anticrossings, which become possible because F has integer values). A consequence of this, shown by the two panels on the right hand side of Fig. 6, is that the separations between nearest resonances spread in frequency. The results suggest also that some of the lines split, i.e. that additional transitions become allowed in this low-field regime. Again, this is not unexpected since transitions that are virtually forbidden when electronic and nuclear spin states factorize, cease to be so when I and S become entangled (see Fig. S31 and S32† that show the direct connection between entanglement and transition rates). Briefly, these results provide direct evidence for a change in the nature of the energy levels and spin states when the anisotropic hyperfine interactions start competing with the coupling to the external magnetic field. As we discuss below, this provides a crucial ingredient to ensure universal operations between the 16 electronuclear states. In the remaining of this section, we use this information to discuss how to exploit the multiple spin levels of 1VO as additional resources for quantum computation. The conditions that are needed to encode a qudit (or multiple qubits) in an N-level system (here N = (2S + 1) × (2I + 1) = 16) are mainly two. First, one needs to have the possibility of addressing transitions linking different states by properly selecting the frequency of a microwave resonant pulse. This implies that the energy levels must not be equally spaced. And, second, there must be a sufficient number of such transitions that are not forbidden and that have a large enough probability. As we have discussed above, and the level scheme of Fig. 7 shows, degeneracies between inter-level separations are removed, thus the first condition is fulfilled, at sufficiently low magnetic fields. Concerning the second, one must consider the Rabi frequencies ΩR of resonant transitions between any pair of spin states. A 2D plot generated for BX = 0.02 T is shown in Fig. 7. It follows from it that not only the “pure” electronic transitions are allowed, but also several others, including those that were previously associated with changes in the nuclear spin state. As B decreases, ΩR of such “NMR-like” transitions increase at the expense of a similar decrease in ΩR values associated with the former (see Fig. 7, right hand panels). The possibility of such an enhanced nuclear spin manipulation has been observed in Yb-trensal molecules by means of pulse-NMR experiments.9b For our purposes, the existence of electronuclear entanglement then contributes to generate a much larger set of available operations.The only remaining, but very important, aspect to consider is whether this set is “sufficiently large”. A rigorous criterion is to impose that the system admits universal operations, i.e. that one can generate any state within the d = 16 dimension Hilbert space via the application of (a sequence of) resonant electromagnetic pulses.29 This was recently applied to show universality of Gd-based molecular spin qudits.12 To set a quantitative criterion, we calculate the rates Wnm at which any basis state n evolves to any other m. We require that this evolution is performed by one or several addressable resonant transitions, meaning that their resonant frequencies are nondegenerate with that of any other allowed transition. Since each of them takes a finite evolution time Δt ∝ 1/ΩR, the electromagnetic pulses have an intrinsic frequency width proportional to 1/Δt. In order to take this effect into account, we consider only transitions whose frequencies differ by more than ΩR and exclude the rest. Next, we impose the condition that all Wnm brought about by such resonant transitions (for a microwave field amplitude bmw = 1 mT) be larger than a decoherence rate 1/T2 ≈ 0.2 MHz (or T2 = 5 μs, see Fig. 3). Results obtained for 1VO molecules at two different magnetic fields are given in Fig. 8. The plots show whether any two basis states can be connected by sequences of transitions being both addressable and sufficiently fast. The results confirm that 1VO affords universal operations at low magnetic fields whereas white spots, signalling the existence of disconnected pairs of states, show up as B increases (see also Fig. S33–S35†). At any B, the minimum Wnm provides a measure of the qudit universality. As can be seen from the bottom of Fig. 8, it goes to 0 as B increases, underlying the importance of electronuclear entanglement. The sudden drop observed around 0.1 T arises from accidental degeneracies between transitions that eliminate some of them (see Fig. S36†). Notice that this plot shows a most demanding condition, associated with the slowest operations, typically sequences of NMR transitions. It is likely that the characteristic T2 times of such transitions lie above the average.9b Taking this into account, or improving T2, would widen the magnetic field region that warrants universal operation and enable choosing between different situations, e.g. different ranges for the resonant frequencies or more or less factorized qudit states.
Conclusions and outlook
The results discussed in the previous sections show that [VOTCPPEt] molecules provide quite promising realizations of either a 4-qubit processor or a d = 16 qudit. Besides the relatively long spin coherence (of a few μs) and spin relaxation times (up to several s), comparable to that found for some of the best molecular qubits, a key ingredient is the possibility to introduce electronuclear spin entanglement. In [VOTCPPEt], this is done by adequately tuning the relative intensities of hyperfine and Zeeman interactions via the external magnetic field. As a result, resonant transition frequencies become non degenerate and both electronic and nuclear spin transitions can be coherently manipulated at sufficiently high, even comparable, speeds. These conditions ensure that this simple molecular system can perform universal quantum operations. This is a strong statement, meaning that it can provide a suitable implementation for any quantum algorithm.In Fig. S37 and S38,† we explore how this result depends on the details of the spin Hamiltonian. It follows that all that is needed to preserve universality is a hyperfine interaction that is not fully uniaxial nor fully isotropic, thus that A⊥ ≠ 0 and A⊥ ≠ A∥, while no quadrupolar term is required. The onset of electronuclear entanglement manifests itself (see Fig. 7) in the form of level anticrossings. It is a curious fact that the presence of such “spin-clock transitions” is here exploited as a way to enhance the connectivity between different states, rather than to reduce their sensitivity to noise.4 This finding widens the “catalogue”, and simplifies the search, of molecular systems that can implement non-trivial quantum functionalities, i.e. that can contribute to move beyond single qubits. A practical advantage is the possibility of choosing ions, such as the vanadyl center of [VOTCPPEt], with a close to 100% abundance of the relevant (high spin) nuclear isotope, thus avoiding the need, and cost, of isotopical purification.
Embedding nontrivial quantum logic in an N-level molecule opens the way to proof-of-concept implementations of some simple algorithms. Examples include Grover's search algorithm, which was recently realized in a 4-level nuclear spin qudit,10a and quantum simulations.10b But probably the most far-reaching application is the integration of quantum error correction at the molecular level. Four qubits provide a suitable basis for the simplest repetition code, based on Shor's algorithm,9a able to correct for single qubit or single phase flips. However, a better alternative seems to be the use of codes adapted to the level structure of qudits, which not even require that N be a power of 2. A particularly efficient code has been recently developed for spin qudits coupled to ancillary S = 1/2 electron spins.9b,9c Increasing the qudit dimension helps improving the state fidelity for any fixed decoherence rate. Each [VOTCPPEt] molecule, with its I = 7/2 vanadium qudit coupled to the S = 1/2 vanadyl electronic spin, provides a promising platform to implement such a code.
Using molecules as error-protected logical qubits to build increasingly complex quantum devices underlines one of the competitive advantages that chemical design can bring to the development of scalable quantum technologies. Yet, this development still faces important challenges, mainly connected with the control of individual molecular spins. Still, [VOTCPPEt] and other similar systems might allow implementing proof-of-concept realizations of these codes by much more easily affordable experiments on crystals. The experiments reported here show that nearly all of the required ingredients can be met in practice. First, it is possible to attain sufficiently long spin coherence times in diluted single crystals (see Fig. 4), without losing the spatial organization of the molecules, i.e. while keeping the possibility of selectively addressing individual transitions. This possibility has been recently used to implement single qubit operations on a related system by means of on-chip resonators.30 In order to exploit the multiple spin states, the coupling to open transmission lines allows generating broad-band control electromagnetic pulses, at the cost of reducing the electromagnetic field amplitude. In the case of [VOTCPPEt], relevant frequencies range between a few hundred MHz up to 2 GHz at low fields. For this region of frequencies, microwave pulse amplitudes of about 1 mT can be easily generated, and this value can be improved by adequate circuit design.31 This gives rise to Rabi frequencies for individual operations that are in the range of a few (tens of) MHz (see Fig. 7), thus faster than decoherence rates. Finally, the use of qudit codes simplifies also reading-out the result of the quantum operations, as it can be obtained by measuring the resonance of the electronic spin. For this, a transmission line can be combined with on-chip LC resonators with frequencies in the range of 1–2 GHz. In conclusion, these results can contribute to bring molecular spins closer to practical quantum implementations.
Author contributions
IG: formal analysis, investigation, visualization, writing – review & editing; AU: investigation, writing – review & editing; JRR: formal analysis, software, visualization, writing – review & editing; DZ: formal analysis, software, supervision, writing – original draft, review & editing; AC: investigation, writing – review & editing; PJA: formal analysis, investigation, writing – review & editing; OR: formal analysis, funding acquisition, investigation, visualization, writing – original draft, review & editing; FL: conceptualization, formal analysis, funding acquisition, investigation, supervision, writing – original draft, review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by funds from the EU (COST Action 15128 MOLSPIN, QUANTERA project SUMO, FET-OPEN grant 862893 FATMOLS), the Spanish MICINN (grants CTQ2015-68370-P, CTQ2015-64486-R, RTI2018-096075-B-C21, PCI2018-093116, PGC2018-098630-B-I00, MAT2017-86826-R) and the Gobierno de Aragón (grants E09-17R-Q-MAD, E31_17R PLATON).Notes and references
- (a) T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O'Brien, Nature, 2010, 464, 45 CrossRef CAS PubMed; (b) A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301 CrossRef PubMed; (c) M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed; (d) G. Aromí and O. Roubeau, Handbook of Physics and Chemistry of Rare-Earths, 2019, vol. 59, p. 1 Search PubMed.
- Avoiding protons and rotating methyl groups in a [Cr7Ni] ring, see C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- Avoiding nuclear spins in general, see K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2015, 5, 5304 CrossRef PubMed.
- Using clock transitions see (a) M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348 CrossRef CAS PubMed; (b) J. M. Zadrozny, A. T. Gallagher, T. D. Harris and D. E. Freedman, J. Am. Chem. Soc., 2017, 139, 7089 CrossRef CAS PubMed.
- M. Jenkins, T. Hümmer, M. J. Martínez-Pérez, J. J. García-Ripoll, D. Zueco and F. Luis, New J. Phys., 2013, 15, 095007 CrossRef.
- (a) S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS PubMed; (b) J. Liu, J. Mrozek, W. K. Myers, G. A. Timco, R. E. P. Winpenny, B. Kintzel, W. Plass and A. Ardavan, Phys. Rev. Lett., 2019, 122, 037202 CrossRef CAS PubMed.
- (a) M. S. Fataftah, S. L. Bayliss, D. W. Laorenza, X. Wang, B. T. Phelan, C. B. Wilson, P. J. Mintun, B. D. Kovos, M. R. Wasielewski, S. Han, M. S. Sherwin, D. D. Awschalom and D. E. Freedman, J. Am. Chem. Soc., 2020, 142, 20400 CrossRef CAS; (b) S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Science, 2020, 370, 1309 CrossRef CAS PubMed.
- (a) G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537 RSC; (b) E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- (a) E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, L. A. Barrios, J. I. Martínez, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337–10343 RSC; (b) R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818 CrossRef CAS PubMed; (c) A. Chiesa, E. Macaluso, F. Petiziol, S. Wimberger, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2020, 11, 8610–8615 CrossRef CAS PubMed.
- (a) C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS PubMed; (b) A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423 CrossRef CAS PubMed; (c) M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183–6192 RSC.
- (a) F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, J. Sesé, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef CAS PubMed; (b) D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215 CrossRef; (c) A. Ardavan, A. M. Bowen, A. Fernández, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Information, 2015, 1, 15012 CrossRef; (d) J. Ferrando-Soria, E. M. Pineda, A. Chiesa, A. Fernández, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed; (e) J. Salinas Uber, M. Estrader, J. Garcia, P. Lloyd-Williams, A. Sadurní, D. Dengler, J. van Slageren, N. F. Chilton, O. Roubeau, S. J. Teat, J. Ribas-Ariño and G. Aromí, Chem.–Eur. J., 2017, 23, 13648 CrossRef PubMed; (f) J. Ferrando-Soria, S. A. Magee, A. Chiesa, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. F. S. Whitehead, S. Sproules, K. M. Lancaster, A.-L. Barra, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Chem, 2016, 1, 70 CrossRef.
- (a) M. D. Jenkins, Y. Duan, B. Diosdado, J. J. García-Ripoll, A. Gaita-Ariño, C. Giménez-Saiz, P. J. Alonso, E. Coronado and F. Luis, Phys. Rev. B, 2017, 95, 064423 CrossRef; (b) F. Luis, P. J. Alonso, O. Roubeau, V. Velasco, D. Zueco, D. Aguilà, J. I. Martínez, L. A. Barrios and G. Aromí, Communications Chemistry, 2020, 3, 176 CrossRef CAS.
- E. Moreno-Pineda, M. Damjanović, O. Fuhr, W. Wernsdorfer and M. Ruben, Angew. Chem., 2017, 56, 9915–9919 CrossRef CAS PubMed.
- M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682 RSC.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS PubMed.
- A. Urtizberea, E. Natividad, P. J. Alonso, L. Pérez-Martínez, M. A. Andrés, I. Gascón, I. Gimeno, F. Luis and O. Roubeau, Mater. Horiz., 2020, 7, 885 RSC.
- D. C. Johnston, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 184430 CrossRef.
- (a) F. Luis, F. L. Mettes, J. Tejada, D. Gatteschi and L. J. de Jongh, Phys. Rev. Lett., 2000, 85, 4377 CrossRef CAS PubMed; (b) M. Evangelisti, F. Luis, L. J. de Jongh and M. Affronte, J. Mater. Chem., 2006, 16, 2534–2549 RSC.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731 CrossRef CAS PubMed.
- K. Bader, M. Winkler and J. Van Slageren, Chem. Commun., 2016, 52, 3623 RSC.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338 CrossRef CAS PubMed.
- A. Albino, S. Benci, L. Tesi, M. Atzori, R. Torre, S. Sanvito, R. Sessoli and A. Lunghi, Inorg. Chem., 2019, 58, 10260 CrossRef CAS PubMed.
- E. Garlatti, L. Tesi, A. Lunghi, M. Atzori, D. J. Voneshen, P. Santini, S. Sanvito, T. Guidi, R. Sessolli and S. Carretta, Nat. Commun., 2020, 11, 1751 CrossRef CAS PubMed.
- C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678 CrossRef CAS PubMed.
- The energy scale of the spin-spin dipolar interaction can be roughly estimated as Edip/kB ≈ (gμBS)2/V where V is the average volume per spin S, see F. Troiani, A. Ghirri, M. Affronte, S. Carretta, P. Santini, G. Amoretti, S. Piligkos, G. Timco and R. E. P. Winpeny, Phys. Rev. Lett., 2005, 94, 207208 CrossRef CAS PubMed . Considering the structure of 1VO (Vcell = 2.272 nm3; Z = 2) and 1TiO (Vcell = 2.287 nm3; Z = 2 but only 3 out of 100 sites occupied by a vanadyl), this gives ca. 0.67 mK for the pure compound and ca. 0.02 mK for the diluted 13%VO. The latter corresponds to ca. 417 MHz, meaning that the limitation of T2 by the dipolar interaction would be of the order of 2.4 μs.
- C. Clauss, D. Bothner, D. Koelle, R. Kleiner, L. Bogani, M. Scheffler and M. Dressel, Appl. Phys. Lett., 2013, 102, 162601 CrossRef.
- (a) K. Paulsen and D. Rehder, Z. Naturforsch., A: Phys. Sci., 1982, 37, 139 CrossRef; (b) T. S. Smith II, R. LoBrutto and V. L. Pecoraro, Coord. Chem. Rev., 2002, 228, 1 CrossRef; (c) C. P. Aznar, Y. Deligiannakis, E. J. Tolis, T. Kabanos, M. Brynda and R. D. Britt, J. Phys. Chem. A, 2004, 108, 4310 CrossRef CAS.
- C. V. Kraus, M. Wolf and J. I. Cirac, Phys. Rev. A, 2007, 75, 9 Search PubMed.
- C. Bonizzoni, A. Ghirri, F. Santanni, M. Atzori, L. Sorace, R. Sessoli and M. Affronte, npj Quantum Information, 2020, 6, 68 CrossRef.
- (a) A. Bienfait, J. J. Pla, Y. Kubo, M. Stern, X. Zhou, C. C. Lo, C. D. Weis, T. Schenkel, M. L. W. Thewalt, D. Vion, D. Esteve, B. Julsgaard, K. Mølmer, J. J. L. Morton and P. Bertet, Nat. Nanotechnol., 2016, 11, 253 CrossRef CAS PubMed; (b) B. Sarabi, P. Huang and N. M. Zimmerman, Phys. Rev. Appl., 2019, 11, 014001 CrossRef CAS; (c) I. Gimeno, W. Kersten, M. C. Pallarés, P. Hermosilla, M. J. Martínez-Pérez, M. D. Jenkins, A. Angerer, C. Sánchez-Azqueta, D. Zueco, J. Majer, A. Lostao and F. Luis, ACS Nano, 2020, 14, 8707 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and experimental details, crystallographic details and views of the structure, heat capacity and magnetic data, additional EPR data, micro-Hall data, additional broad-band magnetic spectroscopy data, calculated energy levels and Rabi frequencies, universality plots. CCDC 2058759–2058761. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc00564b |
| This journal is © The Royal Society of Chemistry 2021 |