Location-thinking, value-thinking, and graphical forms: combining analytical frameworks to analyze inferences made by students when interpreting the points and trends on a reaction coordinate diagram

Abstract

Reaction coordinate diagrams (RCDs) are chemical representations widely employed to visualize the thermodynamic and kinetic parameters associated with reactions. Previous research has demonstrated a host of misconceptions students adopt when interpreting the perceived information encoded in RCDs. This qualitative research study explores how general chemistry students interpret points and trends on a RCD and how these interpretations impact their inferences regarding the rate of a chemical reaction. Sixteen students participated in semi-structured interviews in which participants were asked to interpret the points and trends along provided RCDs and to compare relative reaction rates between RCDs. Findings derived from this study demonstrate the diversity of graphical reasoning adopted by students, the impact of students’ interpretations of the x-axis of a RCD on the graphical reasoning employed, and the influence of these ideas on inferences made about reaction rate. Informed by analytical frameworks grounded in the resources framework and the actor-oriented model of transfer, implications for instruction are provided with suggestions for how RCDs may be presented to assist students in recognizing the critical information encoded in these diagrams.

---

Introduction

Promoting representational competence remains a major challenge within chemistry education given the tendency for students to focus on the surface features of representations (Kozma and Russell, 2005; Graulich and Bhattacharyya, 2017; Rodriguez et al., 2020c; Xue and Stains, 2020). Reaction coordinate diagrams (RCDs), as representations, allow one to visualize the kinetic and thermodynamic parameters associated with certain chemical reactions. RCDs are relevant across a wide array of chemistry curricula and have played a representational role in the development of teaching activities and materials (Csizmar et al., 2013; Morrison et al., 2014; Kaliakin et al., 2015). Previous work has revealed difficulties that students encounter when interpreting RCDs in the context of kinetics (Lamichhane et al., 2018; Popova and Bretz, 2018b; Rodriguez et al., 2020b). This study was implemented to better understand the nature and character of these alternative conceptions and to provide recommendations to instructors on how to scaffold the development of a scientifically accurate understanding of RCDs in the chemistry classroom. We chose to explore students’ understandings of RCDs in a general chemistry setting given that these diagrams are often introduced in this classroom environment. Implications drawn from this study are intended to be most informative for practitioners when first introducing these unique chemical diagrams. However, it is important to recognize that the general chemistry classroom often introduces these diagrams in part to prepare for their application in later chemistry courses. External representation research has stressed the need for investigation of when and why external representations may be effective to implement based upon the alignment of task demands with the purpose of a representation (Goldman, 2003). Therefore, when considering how to address students’ challenges when interpreting RCDs in the general chemistry classroom, one must consider (1) where RCDs originate from and (2) the purpose of RCDs in various chemistry courses.

Origin and purpose of RCDs in the chemistry classroom

The RCD emerges from a calculated multidimensional potential energy surface (PES) which encodes simulated information about the relative energies of various molecular trajectory configurations (Sheehan, 1970; Hulse et al., 1974). The “reaction coordinate” of a RCD is the “minimum energy pathway” associated with the PES that is distinct from the “true energy pathway” of a single reaction event. While the potential energy of these trajectories may be quantified, the very nature of the “reaction coordinate” that defines the least energy pathway of this surface is dependent on the specific encounter being studied and varies in complexity from case to case (Hulse et al., 1974). Obtaining rate constants for chemical reactions from such diagrams requires statistical considerations for how an ensemble of molecules traverses this parameter space (Hulse et al., 1974).

Therefore, at the introductory level, RCDs represent an idealized depiction of the “minimum energy pathway” of a PES for the purposes of qualitative reasoning and comparison. For example, the activation energy associated with the transition state is related to the Arrhenius equation to approximate the rate constant of the reaction (Bain and Towns, 2016). In the ACS organic chemistry anchoring concept map, RCDs are used to discuss “kinetic versus thermodynamic control of a reaction” (Raker et al., 2013). Conversely, the ACS physical chemistry concept map states that RCDs present “relative energy numbers showing relationships between reactants, products and transition states as a function of an idealized reaction coordinate” (Holme et al., 2018). There is an important distinction between these two statements highlighted by the choice of the phrases “to discuss” and “function of.” Whereas RCDs are read out qualitatively in an organic chemistry context “to discuss” reaction parameters, a physical chemistry context envisions the RCD trend as a “function” defined by an idealized reaction coordinate and the potential energy of various physical states. Therefore, one could make the assertion that organic chemistry frames RCDs as qualitative diagrams, whereas physical chemistry frames RCDs as quantitative graphs (see ESI† for full discussion). Such an assertion is supported by the tendency for physical chemistry textbooks to label the x-axis of a RCD as the “reaction coordinate” to build into quantified potential energy surfaces (Levine, 2002; Atkins and de Paula, 2014), while organic chemistry textbooks use RCDs most commonly to compare kinetic and thermodynamic parameters with little, if any, reference to the x-axis (Carey and Giuliano, 2008; Loudon and Parise, 2016). Based on these points, it is evident that (1) the RCD originates from the simplification of a more complex PES and that (2) RCDs serve different purposes across chemistry curricula.

Previous research on students’ interpretations of RCDs

Previous research on students’ interpretations and understanding of RCDs has revealed a host of misconceptions. Most notably, recent studies have identified that students incorrectly associate “time” with the x-axis of a RCD (Lamichhane et al., 2018; Popova and Bretz, 2018b; Atkinson et al., 2021). In the study by Popova and Bretz (2018b), students were prompted to interpret surface features on a RCD and were shown to emergently associate meaning with the width of a RCD. The Reaction Coordinate Diagram Inventory developed by Atkinson et al. (2020) has further demonstrated undergraduate students’ tendencies to equate the width of a transition state peak or the “reaction progress” with time and how this can be effectively measured. Additional studies at the general chemistry and organic chemistry levels have identified students’ attribution of meaning to the slope and length of a RCD trend in a manner that was evocative of time and consistent with graphical reasoning (Lamichhane et al., 2018; Rodriguez et al., 2020b). The identified “x-axis as time alternative conception” has convergently emerged from the RCD literature as one of the primary challenges the chemistry education community faces when teaching with these diagrams. Students have also been shown to encounter difficulties when interpreting the information encoded in RCDs. When asking organic chemistry students about the surface features on RCDs, Popova and Bretz (2018b) found that students sometimes conflated the y-axis with “concentration” similar to other graphical representations in a chemical kinetics context. General chemistry students have also been shown to struggle with connecting correctly identified surface features on a RCD with particulate-level reaction mechanisms (Atkinson et al., 2021). Additional findings demonstrate organic chemistry students’ difficulties when labeling and describing minor reaction species, transition states, and intermediates on a RCD (Taştan et al., 2010; Popova and Bretz, 2018a). Within a kinetics context, Rodriguez et al. (2020b) examined general chemistry students’ relations of rate to RCDs through coordination class theory. This study revealed the tendency of students to use metonymy to equate the peak of a RCD and the rate constant to the rate of a reaction. The use of metonymy by students to interpret RCDs, while not addressed in this study, highlights that students may not be aware of the separate knowledge structure being referenced when the peak of a RCD is being used to make direct inferences about the rate of a reaction. While previous research has revealed a host of student misconceptions regarding RCDs, in alignment with Rodriguez et al. (2020b), we agree that more research is needed to investigate the nature and character of these alternative conceptions to draw serviceable implications that practitioners can apply (Cooper and Stowe, 2018).

Chemical kinetics and rate of change as a context

When considering the “x-axis as time alternative conception” identified in the RCD literature, the importance of chemical kinetics as a context must be considered. It is worth noting that the ACS Exam Institute defines three enduring understandings for kinetics in the general chemistry curriculum, the first of which is: “Chemical change can be measured as a function of time and occurs over a wide range of time scales” (Holme et al., 2015). A central parameter to chemical kinetics defined by the ACS Exam Institute is the “reaction rate,” which is defined as “the change in concentration of a reactant or product as a function of time.” A review of chemical kinetics research by Bain and Towns (2016) discussed students’ misconceptions regarding the definition of reaction rate and the dependence of reaction rate on various parameters, such as temperature. Within a chemical kinetics context, students have been shown to engage in conceptual blending of mathematical and chemical concepts to reason about graphical representations (Bain et al., 2018; Rodriguez et al., 2018). In particular, the role of covariational reasoning has been identified as a critical factor in distinguishing sophisticated “emergent” perceptions of chemical kinetics trends from more limited “static” interpretations (Rodriguez et al., 2019). Additionally, students have been shown to exhibit different degrees of sophistication when interpreting the rate “constant” and its relationship to activation energy and the rate of reaction (Kaya and Geban, 2012; Yalçinkaya et al., 2012; Bain et al., 2019). These degrees of sophistication are reflected by students’ inconsistent reasoning and interpretations of the rate of the reaction when provided with a RCD and the Arrhenius equation (Lamichhane et al., 2018). Furthermore, the impact of kinetics as a context on students’ interpretations of graphical trends requires additional consideration for how cross-disciplinary ideas central to kinetics, such as rate of change, contribute to students’ reasoning.

Rate of change is a pervasive crosscutting concept with widespread relevance across the fields of science and mathematics (NGSS Lead States, 2013). A mathematics education research study by Johnson (2015) investigated how students quantify rate and found that students' quantitative reasoning was highly dependent on their conceptualization of rate. In the context of derivatives, students have demonstrated a tendency to associate the independent variable with “time” even when the variable is associated with an alternative unit (Bingolbali et al., 2007; Jones, 2017). These studies have revealed a preference outside of mathematics for conceptualizing derivatives as rates of change over alternative ways of conceptualizing derivatives such as tangential lines or slopes. Additionally, it has been suggested that students may need “time” as an independent variable to understand how concavity in a graph reflects the covariation of rate of change with the independent variable (Jones, 2019). Students’ tendencies to invoke time is also reflected in chemistry education research studies in which students were asked to interpret differentials (Becker and Towns, 2012) and frequency distribution graphs (Rodriguez et al., 2020c). Associating the independent variable of a graph with time is productive in many alternative physical contexts and so students’ propensity to adopt the “x-axis as time alternative conception” across disciplines may be heavily impacted by prior experiences.

This study serves to add to a growing body of literature on students’ understanding of RCDs and to investigate the x-axis as time alternative conception by exploring how students reason about points and trends on a RCD. In particular, previously developed mathematics education research frameworks were applied to interpret the mathematical ideas, or resources, that students drew upon to reason about RCDs. Therefore, the methods and analysis employed were framed under the guiding research question: What mathematical resources do students transfer to make inferences about the points and trends on a reaction coordinate diagram?

Theoretical considerations

Theoretical frameworks

Resources framework. The crux of this study lies in understanding how students conceptualize the points and trends of a RCD and how this applied knowledge impacts the inferences students make about reaction rate. We frame knowledge as being comprised of a manifold ontology consistent with the resources framework in which fine-grained ideas or resources are activated productively or unproductively in various contexts (Hammer et al., 2005). Through this theoretical lens, the analytical frameworks chosen to perform this analysis define fine-grained mathematical resources that are commonly activated when students reason about graphical representations. However, it is important to note that when mathematical resources are activated in a specific chemical context, such as a RCD, coherent sets of resources are most often activated in order to relate chemical principles to these mathematical ideas. This study seeks to investigate how these mathematical resources inform the sets of resources that participants use to make sense of RCDs and how students draw inferences from these mathematical ideas. Therefore, the goal of this study is not to investigate the underlying resources that are activated but to distinguish how these different mathematical resources drive inferences made by participants in the unique context of RCDs. Because a student's reasoning will be comprised of both mathematical resources and the sets of resources students use to make sense of a RCD, we define a “graphical reasoning approach” to be a coherent way of coordinating mathematical and chemical resources to reason about a RCD.

Actor-oriented model of transfer. Having pre-defined mathematical resources makes the applied methods and analysis more akin to transfer of learning research. In the case of this study, the definition of transfer is clarified by viewing the foundational work used to construct the analytical frameworks employed in this study as grounded from the resources perspective. Based upon this direction, the definitions of “productive” and “unproductive” become paramount when investigating how transfer or resource activation drives the inferences made by students in the context of a RCD. Therefore, we operationalize the terms “productive” and “unproductive” according to the actor-oriented model of transfer (AOT) that reframes transfer as not a successful or unsuccessful event, but as the observed process by which the learner approaches a new task through their personal relations of similarities across contexts (Lobato, 2003). AOT has demonstrated promise as a theoretical lens in exploring students’ interpretations of transfer situations, how transfer processes are socially situated in a classroom, and the investigation of how context may play a role in productive transfer (Lobato, 2012). In particular, AOT overlaps with the resources perspective in its emphasis of context-dependence and has been previously implemented alongside the knowledge-in-pieces framework (Wagner, 2010). In the case of this study, we use AOT as an additional theoretical perspective to reflect on the impact of prior experiences and the nature of the RCD, as a context, on students’ transfer of chemical and mathematical concepts to a RCD. Findings derived from this study are used to make suggestions regarding how certain “focusing phenomena,” or the ways in which teachers direct attention, may influence students’ interpretations of RCDs within the classroom.

Analytical frameworks

Graphical forms. The identification and analysis of students’ graphical reasoning was informed by both the graphical forms and value-thinking and location-thinking frameworks derived from the chemistry and mathematics education research communities respectively (David et al., 2018; Rodriguez et al., 2020a). Graphical forms emerged from prior chemistry education research on graphs in a chemical kinetics context and describe ideas students assign to shapes in a graph (Rodriguez et al., 2018). The “registration,” or graphical feature, attended to by a participant is associated with context-specific meaning to describe the “story” that gives rise to a graph. For example, students have been shown to associate the general idea of something remaining constant when examining a straight-lined graph, straight means constant, and something with a curve as changing, curve means change (Rodriguez et al., 2018). While the granularity of a registration may vary, the graphical forms that are most relevant to the shapes associated with RCDs correspond to reasoning about regions of a graph.

Value-thinking and location-thinking. Conversely, the value-thinking and location-thinking framework showcases the context-dependence of students’ interpretations of individual points on a graph (David et al., 2018). David et al. (2018) investigated students’ interpretations of the intermediate value theorem in relation to graphs and found that some students interpret points as coordinated values, value-thinking, while others treated points as locations in space associated with inputs, location-thinking. The significance of this distinction was highlighted when students adopting location-thinking interpreted functional outputs of similar values as having different values based upon their locality. While location-thinking was generally unproductive for participants in the study by David et al. (2018), alternative representational contexts, such as a RCD, may preference location-thinking over value-thinking when physical states are associated with various regions of a graph. Location-thinking therefore serves as a bridge linking the field-specific interpretations of a RCD as a diagram or a graph according to the fluidity of the context. The value-thinking and location-thinking and graphical forms frameworks call attention to the context-dependence of students’ graphical interpretations of points and trends respectively. Therefore, these frameworks were both simultaneously considered and adopted when making analytical considerations for how students interpreted points and trends along a RCD. Additionally, the suitability of one framework versus the other may be informed by the inherent focus of the participant on a point or trend as shown in Fig. 1.

Fig. 1 A generalized distinction of how value-thinking, location-thinking, and graphical forms all frame the information encoded in a RCD where “PE” stands for potential energy (David et al., 2018; Rodriguez et al., 2020a).

Methods

This study and its research question focused primarily on exploring the scientifically inaccurate graphical understandings previously identified in the RCD literature. Therefore, we defined students’ graphical understandings as the focus of this study, in which the study's goal was to bridge these alternative conceptions with known information about students’ graphical interpretations in the chemistry and mathematics education research communities (Guba and Lincoln, 1981). A semi-structured interview methodology was employed to investigate these graphical understandings. In order to ground the findings of this study, we chose to specify the “boundary criterion” of the study, or the criterion that establishes what relevant findings may be derived from the applied methods of inquiry (Guba and Lincoln, 1981). The boundary criterion for this study was that any findings must arise from analysis of students’ interpretations of RCD representations provided by the interviewer or generated by students.

Sampling description

The study was conducted at a large public, research-intensive midwestern university. Approval was obtained from the Institutional Review Board at the university where the study was carried out prior to the recruitment of any participants. All participants were recruited from a second-semester general chemistry course for non-chemistry majors with a primary emphasis on the topics of chemical kinetics, equilibria, and thermodynamics. The textbook for the course was Chemistry: The Molecular Nature of Matter and Change, by Silberberg and Amateis (2018). The course was large (>500 students), primarily lecture-based, and accompanied by a laboratory curriculum that carried out experiments overlapping with the content discussed in lecture. In accordance with the approved IRB protocol, all interview data was made non-identifiable and a pseudonym was assigned to each student. The lead instructor of the course and lead researcher of this project met prior to the study to discuss the syllabus and to clarify the role of reaction coordinate diagrams in the course.

Reaction coordinate diagrams were first covered in the course during a 3-week period focused on chemical kinetics. RCDs were covered during both the kinetics and thermodynamics portions of the course to emphasize the role of the diagram in determining the enthalpy and rate associated with reactions respectively. For the purposes of the course, the vertical coordinate of the RCD was labeled as “potential energy,” while the horizontal coordinate was labeled as “reaction coordinate” and “progress of reaction” interchangeably. RCDs with both single transition states and multi-step mechanisms, interpreted alongside symbolic notation for a chemical reaction, were covered that modeled both exothermic and endothermic reactions. A RCD was discussed alongside a gas-phase reaction mechanism with accompanying ball-and-stick particulate representations to highlight the mechanistic information encoded in the diagram. Additionally, the relationship of the Arrhenius equation to a RCD and the effects of a catalyst on the rate of a reaction were discussed.

Interview protocol content and development

The interview protocol was divided into three phases (Fig. 2) and was structured around RCD interview prompts. Preliminary drafts of these prompts were developed based on an awareness of existing graphical reasoning frameworks (David et al., 2018; Rodriguez et al., 2020a). Additionally, the prompts were validated by the instructor of the course to ensure relevance of the features highlighted in this unique classroom context. A pilot study (n = 4) was conducted in Fall 2019 to refine the interview questions and prompts prior to the implementation of the main study. Revisions to the interview questions and prompts included the inclusion of an opening question in the prior knowledge phase and making the dashed vertical lines in Fig. 3B uniform to avoid unnecessary prompting.

Fig. 2 The progression of the interview through three separate phases: Prior Knowledge, Points and Trends, and Reaction Comparison.

Fig. 3 Phase 2 Interview Prompts. (A) A RCD highlighting various points along the curve with dashed lines to illustrate the comparability of points' energies. (B) A RCD dividing the curve into regions according to the transition state energy.

Phase 1 consisted of a highly unstructured prior knowledge phase. Participants were first asked: “What comes to mind when I use the term reaction coordinate diagram?” The purpose of this opening question was to investigate any pre-existing ideas or perceptions regarding RCDs prior to any prompting from the later phases. After providing a response, participants were encouraged to generate a drawing for the diagram that they described. Further questions were structured based upon the features of the diagrams generated during the opening portion of Phase 1. Once finished, the interviewer removed any drawings the student generated from the field of view before proceeding to Phase 2.

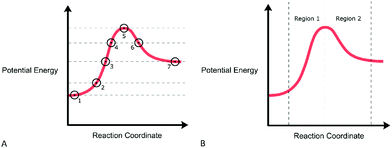
Next, students were asked a series of questions while sequentially addressing the RCDs depicted in Fig. 3. In Fig. 3A, points were included on this first diagram for the purposes of exploring students’ interpretations of specific points along the diagram. Conversely, Fig. 3B depicted the same RCD, but with the different increasing and decreasing potential energy regions highlighted. These diagrams were constructed with an awareness of existing graphical reasoning frameworks that highlight the various ways that students may interpret points and regions along a graphical trend (David et al., 2018; Rodriguez et al., 2020a). Consideration of graphical frameworks was motivated by the field-specific implications of RCDs as diagrams and graphs (see Introduction). The interviewer then proceeded to ask students to interpret the points and trends along the RCD and to describe what information was encoded in these points and trends for a hypothetical chemical reaction.

In Phase 3, students were provided an additional sequence of prompts that each contained two RCDs for comparison. Fig. 4A depicts the first RCD comparison between two RCDs, Reactions 1 and 2, with a different width for each reaction along the horizontal coordinate. The width along the horizontal coordinate is arbitrary in this context given the idealized nature of the x-axis (Sheehan, 1970; Hulse et al., 1974). The purpose of this diagram was to explore what graphical reasoning, if any, participants would employ when prompted about the relative rates of the two reactions. The interviewer first asked participants to identify any similarities and differences between the diagrams and their significance. Finally, the participants were asked “How do the rates of both reactions compare?” in order to elicit any potential graphical reasoning that may be used to make inferences about the relative rates of reaction. Afterwards, students were provided with the RCDs, for the same Reaction 1 and a new Reaction 3 (Fig. 4B) and asked an identical set of questions. The RCDs depicted in Fig. 4B display two reactions with differing activation energies and therefore the reactions exhibit different reaction constants when modeled by the Arrhenius equation. Finally, the interviewer arranged the papers such that Reactions 1, 2, and 3 were side by side and asked the participant to compare the rates of all three reactions to one another.

Fig. 4 Phase 3 Interview Prompts (A) A comparison of two RCDs wherein the second RCD maintains the energy levels of the first RCD but has different spacing along the x-axis. (B) A comparison of two RCDs wherein both RCDs have the same x-axis spacing but different peak energies.

Data collection and analysis

All participants were recruited by an email sent out by a chemistry department official who was neither an instructor for the course or researcher in this study. In the email, the lead researcher's email was provided from which students volunteered to participate. A $20 gift card incentive was provided to participants upon completion of the interview. Participants were not provided any information regarding the content of the interview besides its focus on chemistry as a topic area. Interviews were conducted within 2 weeks of the conclusion of chemical kinetics instruction by the first and second authors. A semi-structured interview protocol was used to guide the conversation and to allow for the additional flexibility of follow-up questions to investigate the unique responses of each student (Merriam and Tisdell, 2016). During the interview, students were asked to interpret provided RCDs according to the interview protocol and were allowed to draw on the diagrams. The provided RCDs were printed on Livescribe notebook paper and a Livescribe pen was provided to participants to simultaneously record audio and written work (Linenberger and Bretz, 2012). The average duration of each interview across all participants (n = 16) was 46 minutes.

All interviews were coded with NVivo software for data analysis and inter-rater reliability (IRR) calculation. Existing graphical reasoning frameworks served as a primary lens to inform the identification of emergent categories within the established boundary criterion (Guba and Lincoln, 1981). Convergence of the emergent categories was accomplished through iterative steps of data collection and refinement of categories through discussion between the research team and memoing (Guba and Lincoln, 1981; Merriam and Tisdell, 2016). A preliminary codebook was developed during the beforementioned pilot study that distinguished the different types of graphical reasoning employed. In Spring 2020, the main study (n = 16) was implemented and data collection continued until no new avenues of reasoning were identified (Guba and Lincoln, 1981). Four random main study interviews were selected for comparative analysis and IRR calculation. The codebook was revised and IRR re-calculated until the coding categories achieved sufficient agreement. A pooled kappa statistic of 0.83 was calculated across each coding category (De Vries et al., 2008) indicating sufficient reliability in the coding scheme (Hallgren, 2012).

Iterative cycles of inductive and deductive coding (Merriam and Tisdell, 2016) resulted in the emergence of seven unique graphical reasoning codes summarized in Table 1. Each graphical reasoning code, apart from the kinematic heuristic, is first designated according to the graphical reasoning frameworks that served as a lens for crafting these categories in the unique context of RCDs (David et al., 2018; Rodriguez et al., 2020a). Afterwards, each of these titles includes a descriptor, following a comma, summarizing the key attribute that distinguished the reasoning code within the coding scheme. Summarized definitions are provided alongside each code that were developed and refined throughout the data collection and analysis process (see ESI† for full definitions).

Table 1 Codes that distinguish the graphical reasoning students employed to interpret RCDs

Code	Summarized definition
Graphical Forms, Shape (GF-S)	A statement associating the shape of a RCD trend with specified parameters
Graphical Forms, Slope/Derivative (GF-SD)	A statement associating the slope or derivative of the RCD trend with the change of specified parameters
Kinematic Heuristic (KH)	A statement that frames a RCD as a kinematic system through intuitive associations
Location-Thinking, States (LT-S)	A statement associating a region of a RCD with a physical state or physical process
Location-Thinking, Trend (LT-T)	A statement associating a region or point of a RCD as an energy/value along the RCD trend
Value-Thinking, Coordinate (VT-C)	A statement associating coordinate values (x- and y-axes) to a point on a RCD
Value-Thinking, Slope/Derivative (VT-SD)	A statement associating the slope or derivative of a point with specified parameters

---

An additional coding category was developed to monitor students’ interpretations of the x-axis of a RCD during the course of the interview. The x-axis interpretation codebook was developed based on prior research that revealed the prevalent alternative conception that the x-axis of a RCD may be viewed as “time” (Lamichhane et al., 2018; Popova and Bretz, 2018b). Therefore, a student's conceptualization of the x-axis may inform how they interpret the points and trends along a RCD and what graphical reasoning they employ. In particular, the codes x-axis as time (XA as T) and x-axis as molecular distance (XA as MD) were used to distinguished between instances where students explicitly or implicitly interpreted the x-axis of the provided RCD as time or a molecular trajectory respectively (Table 2). See ESI† for the full definitions and list of x-axis interpretation codes.

Table 2 Codes designating how students interpreted the x-axis of a RCD

Codes	Summarized definition
x-axis as Molecular Distance (XA as MD)	A statement that indicates that the x-axis is associated with the relative positions of reacting molecules
x-axis as Time (XA as T)	A statement indicating explicitly or implicitly that the x-axis is associated with “time”
x-axis as Not Time (XA as NT)	A statement indicating explicitly that the x-axis is not associated with “time”
x-axis as Progress (XA as P)	A statement indicating that the x-axis is associated with the “progress” of the reaction
x-axis as Reaction Coordinate (XA as RC)	A statement indicating that the x-axis is the “reaction coordinate”
x-axis as Uncertain (XA as U)	A statement that expresses a participant's uncertainty regarding the x-axis

---

Results and discussion

Overview of emergent graphical reasoning codes

The graphical reasoning codes used to describe students’ RCD interpretations (Table 1) may be understood when considering how location-thinking, value-thinking, and graphical forms may be used to distinguish students’ reasoning. Location-thinking may be distinguished when a student ascribes meaning to specific regions of a diagram based upon their locality (David et al., 2018). In the context of a RCD, the points on the diagram encode information regarding the relative energies of states associated with an abstracted molecular trajectory. LT-S outlines reasoning in which students mapped physical states or processes onto the diagram by using their locality to distinguish them. For example, all students (n = 16) demonstrated LT-S by mapping physical states, such as reactants, products, and transition state, with regions of the diagram (Fig. 5):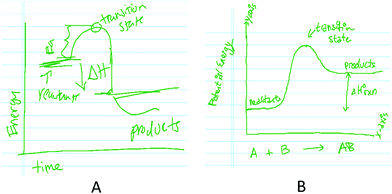

Fig. 5 Example written responses from Hayden (A) and Willa (B) during Phase 1 when asked to draw a RCD.

“So this is like the energy of your, um, reactants and then this is the energy of your products. Um, and then here, this here is your activation energy.” (Hayden, Fig. 5A)

“One like this where we have like reactants and products and then we would learn that like this is the amount of activation energy it takes for the reaction to proceed.” (Christy, Fig. 5B)

During Phase 2, students were also found to map molecular collisions, intermolecular proximity, and relative concentrations of reactants and products to various locations on the RCD in manners consistent with findings from Atkinson et al. (2021).

“There's more collisions happening towards the peak than there is towards the bottom of the curve.” (Alyson)

“…I feel like at Point 4 there's uh more, a higher concentration of reactants than products. And at Point 6 I feel as if there's a higher concentration of the products than the reactants.” (Hayden)

“Um, cause as you go to the right, um, and the energy is increasing and decreasing, the molecules are moving around and like the position of the molecules are changing.” (Susanne)

It is important to note that all students were able to recognize that the potential energy axis described the energies associated with each specified state. Therefore, all states mapped by students may be viewed as also representing a functional “output” that describes each physical state mapped onto the diagram. The close association participants made between the potential energy output and each physical state justifies the distinction of LT-S.

Students rarely ascribed meaning to a point or region based upon locality with respect to the trend and not to a specific physical state, LT-T. All recorded instances of LT-T were based upon an assessment that each point represented a separate “measurement” as indicated by Christy below:

“Um, because we're, as the reaction proceeds, the energy is like what's being measured. So we can't like change the amount of energy that is either required or is being produced.” (Christy)

While location-thinking ascribes meaning to a point or region based upon locality, value-thinking employs reasoning that requires points to be interpreted as coordinate values with a numerical input and output (David et al., 2018). Students demonstrated value-thinking reasoning when operating on points as coordinate values, VT-C, and when assessing the slope or derivative at a single point, VT-SD. Consider the following excerpt from Jessica when asked to clarify her work comparing the rates of RCDs for Reactions 1 and 3 during Phase 3:

“So I counted essentially the number of reaction coordinates that, um, throughout the graph. Yeah. So, um, I guess it was just, I mean I'm just going to draw a line [draws on Livescribe paper]. Um, so it kind of took that amount of reaction coordinates and then here it took about the same. So I'm just going to call that change in RC for change in reaction coordinates.” (Jessica)

Jessica indicates that she “counted the number of reaction coordinates” when comparing the two reactions and demonstrates this by labeling the difference in perceived reaction coordinates (Fig. 6). This statement demonstrates that Jessica was quantitatively evaluating the RCD as if the x-axis encoded numerical information that she could draw upon in this context. Because all students were able to recognize and map states onto each RCD according to their potential energies, the inclusion of numerical reasoning on the x-axis completes the coordinate system needed to identify VT-C reasoning.

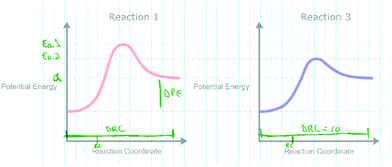Fig. 6 Jessica's annotations as she counted the “number of reaction coordinates” when comparing Reactions 1 and 3 in Phase 3.

VT-C was most commonly observed in Phase 3 when rate comparisons were made between RCDs.

Students also considered how these perceived coordinates covaried with one another at a specific point (VT-SD). Such reasoning often emerged when a student referenced the derivative and slope of a RCD interchangeably, such as in Leonard's interview:

“Uh, the release of energy is given by that negative slope. Uh, you take the derivative of any point from Point 5 to [Point] 7, and the slope is negative. So it is releasing energy.”

Conceptualizing a slope at a single point requires one to ascribe numerical meaning to the x and y-axes thereby justifying these avenues of reasoning as value-thinking.

Participants also attributed graphical ideas to perceived shapes and trends on a RCD in a manner consistent with graphical forms and prior research (Rodriguez et al., 2018, 2020b). Such reasoning differs from location-thinking and value-thinking on the basis that it does not rely on coordinate values or locality to distinguish parts of a RCD. Rather, students employ graphical forms by associating graphical ideas with a representation based upon perceived trends and features. In the context of RCDs, students adopted graphical forms to associate shapes and trends of a RCD with specified parameters (such as rate or stability). Consider the following examples in which participants assess why Point 7 would be associated with the products of the reaction:

“Uh, because the energy looks like it's kind of plateau-ing, uh, out. So, and almost going to a constant right here, uh, which would mean that no more of this forward chemical reaction would be taking place.” (Wayne)

“Because it [Point 7] starts to plateau so it doesn't need any more, any less energy to do anything else. It stays at the same level.” (Alyson)

Each student associates the flat regions as being “constant” or “staying at the same level” to justify why the end of the reaction is associated with Point 7. In these cases, the participants associate the flat region near Point 7 with an unchanging energy to justify why this is where the reaction ends. These statements are consistent with the previously identified graphical form straight means constant (Rodriguez et al., 2020a).

Students also utilized graphical forms to discuss the slopes of RCDs. Consider the following quote by Jessica:

“But, um, you could say that, uh, the, because the potential energy is slowly decreasing with the slope, um, uh, I dunno, maybe you could reason that, um, they’re colliding less often, which makes sense because if they’re colliding less often or less often with the correct orientation, then, um, the rate of reaction would also decrease if there was, um, less effective collisions.”

Jessica recognizes that “the potential energy is slowly decreasing with the slope.” No direct mention of the x-axis is made in this statement; however, the idea that a shallow slope is “slow” coincides with the graphical form steepness as rate (Rodriguez et al., 2020a). Jessica further justifies this statement by drawing upon how the frequency of collisions in a hypothetical reaction may be related to the slope of the graph based on collision theory.

Some participants appeared to “re-frame” the RCD as a kinematic system in which the transition state was a “hill” that needed to be overcome for the reaction to proceed:

“Reaction energy would be more like you would have some energy level and then more like a slope that goes up like a hill.” (Susanne)

“Also just the shape of it [the peak] kind of when you think of something in math, I don't know, it just, it's more of a, it's not a stopping point, but it's like a stalling point. Like it slows and then it either goes the other way or will stop.” (Alyson)

This interpretation of the RCD trend reflects certain analogies that are often used to describe how RCDs encode information about the progress of a reaction (i.e. a ball rolling up a hill). While this analogy is not unfounded, most students that drew upon the KH were later found to use this analogy to make scientifically inaccurate assertions when reasoning about the relative rates of reactions (see productivity of graphical reasoning codes in a kinetics context section). The KH may involve value-thinking, location-thinking, and graphical forms, but is distinguishable in that it associates intuitive physical meaning with a system that is unrelated to the chemical reaction in question. When interpreted literally, the KH relies on conceptualizing the x-axis as a physical position and not a molecular proximity. Participants’ application of the KH in this study expands upon and generalizes the findings by Popova and Bretz (2018b) that indicated organic chemistry students may relate the movement along the shape of a RCD with prior experiences, such as a rollercoaster.

The distribution of graphical reasoning codes identified across the full interview sample is included in Table 3 (see ESI† for the mapping of each interview number to its respective pseudonym). The only graphical reasoning code which emerged across all interviews was LT-S. The next most common alternative graphical reasoning codes were VT-C and GF-S which both emerged in 15 of 16 interviews. When interpreting the slope of a RCD, students more frequently adopted GF-SD than VT-SD. The emergence of graphical forms when students address RCDs is consistent with the recent study by Rodriguez et al. (2020b). Half of the participants (n = 8) were shown to have adopted the KH at some point during their interview when graphically reasoning about a RCD.

Table 3 Distribution of graphical reasoning codes across interview sample

Code	Interview number
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Note: graphical reasoning approaches have been arranged according to frequency of emergence across the interview sample.
LT-S	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
GF-S	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✗	✓	✓
VT-C	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✗
GF-SD	✓	✓	✓	✓	✗	✓	✓	✓	✓	✓	✗	✓	✓	✗	✗	✓
KH	✓	✓	✓	✗	✓	✗	✓	✓	✗	✓	✗	✗	✗	✓	✗	✗
VT-SD	✓	✗	✗	✓	✗	✓	✗	✗	✓	✗	✓	✗	✗	✗	✓	✗
LT-T	✓	✓	✓	✗	✓	✗	✗	✗	✗	✗	✗	✗	✗	✓	✗	✗
Key: Graphical Reasoning Coded (✓); Graphical Reasoning Not Coded (✗)

---

x-axis interpretation and graphical reasoning

When considering students’ interpretations of RCD trends, it is critical to consider how the various forms of graphical reasoning identified interact with the interpretation of the x-axis of the RCD. The very nature of value-thinking requires the x-axis to encode for some numerical quantity. Additionally, graphical forms and the kinematic heuristic may be associated with an x-axis from an alternative representation when assessing the graphical properties of a RCD. Conversely, LT-S uniquely associates physical states and/or processes with each point and trend on a RCD and may therefore account for the abstracted nature of the molecular trajectory encoded in a RCD.

Consistent with prior findings, all students adopted XA as T (n = 16) at some point during each interview. In general, XA as T was most commonly adopted when students applied value-thinking or graphical forms approaches. Consider the following examples from participants that adopted VT-SD and GF-SD:

“Well if you, if you took the slope as a measure of the rate of change of concentration of reactants over time, then at Point 5 and Point 7 the slope would approximately be zero for each.” (Jessica, VT-SD)

“Um, I would say the Reaction 2 is faster once the reaction actually starts because it is steeper. Even though it takes a little longer to get started, I think it would happen faster than Reaction 1.” (Alyson, GF-SD)

Jessica makes an explicit call to the x-axis, referring to it as “time” when justifying her VT-SD reasoning. Alyson's adoption of GF-SD does not explicitly use the word “time;” however, the use of the word “faster” invokes time to relate the rate of change of the RCD slope to the speed of the reaction.

Alternatively, fewer interviews (n = 4) adopted XA as MD at any point. Such an interpretation is consistent with the information encoded in a RCD and was always accompanied by LT-S reasoning. Consider the following statement from Willa during Phase 1:

“Um, when you’re modeling your reaction, the, um, like the energy of the reaction versus like, as the reaction happens and you have the coordinates of like the distances between the molecule, like the molecules and what's going on.”

All students that interpreted the x-axis as encoding information about molecular distance also indicated that the x-axis was related to time at some point during their interview. For instance, when asked about Points 3 and 7 along the RCD trend, Willa discussed each point as describing the “degree of bonding” between hypothetical atoms “A,” “B,” and “C” (Fig. 7A). Willa assigned relative bond percentages to various states in a LT-S approach as she discussed the points along the diagram (Fig. 7A):

Fig. 7 Written work from Willa (Green) during Phase 2 when asked to interpret (A) points and (B) trends along a RCD.

“I think I'd see [Point] 3 as A is 75% bonded to B and B is 25% bonded to C… Well just reasoning through this, I guess if [Point] 1 is 100% and [Point] 5 has your, like 50% on either side of B and [Point] 7 is then A with B and C bonded 100%…”

However, when asked to interpret the trends associated with a RCD she shifts to an alternative “reactant pool” explanation that relies on an implicit reference to “time” (Fig. 7B):

“Um, but then as the reaction proceeds on, some of, once, so like if these two molecules react, they're out of the, they're out of the reactant pool, right? If these two molecules react, they're out of the reactant pool, if these ones react, out of the reactant pool… Um, and so that's why as the number of available reactant molecules get smaller, it takes more time for the, um, the, uh, A, B, and the C to react.”

This initial inconsistency in Willa's interpretations demonstrates a willingness to adjust her perception of the x-axis to accommodate her reasoning. Willa would go on later in the interview to adopt VT-C reasoning when comparing reactions 1 and 2 by comparing the number of blue lines printed on the Livescribe paper and commenting that the lines:

“don't necessarily mean anything, but I'm going to make them mean something just for the purpose of making this easier… So we can say that uh reaction, so Reaction 1 takes about eight lines. I know it's not a real time measurement, but we'll just use that for now to compare.”

Other students that adopted XA as MD also weaved this interpretation with XA as T:

“I think it [the x-axis] more corresponds to like the positioning of the molecules, but like that happens, like at a certain like time. So like indirectly it's also related to time.” (Susanne)

Such an integration was clearly depicted by Mark during both Phases 1 (Fig. 8A) and 3 (Fig. 8B). When first interpreting the word “reaction coordinate diagram,” Mark discusses how molecular distances change over time:

Fig. 8 Drawings generated by Mark during (A) Phase 1 and (B) Phase 3 when discussing the relationship between time and the positioning of molecules.

“What I think of is just, maybe this would be showing time and then like if you have starting like maybe have reactants be at some point, so like maybe, and then as time progresses they could be like further spaced apart or something else could be involved.” (Fig. 8A)

The depiction of time alongside a molecular trajectory demonstrates how students might integrate an incorrect understanding of the x-axis into a reasonable framework for what information is encoded in a RCD. Later on in the interview, Mark makes the following inferences regarding reaction rate during Phase 3 (Fig. 8B):

Interviewer: “And why do you feel the narrower reaction coordinate in Reaction 2 would potentially give it a larger rate than Reaction 1?”

Mark: “Um, because like with reaction coordinates, you could have the, just to try and like have a picture representation of this. Um, the, with this distance, um, it's going to be longer before you can reach, like this part reaches this point…”

Mark integrates XA as MD and XA as T by discussing how long it takes to traverse various molecular trajectories. This interpretation ultimately led to the same VT-C approaches of a student that exclusively adopts XA as T.

Additional x-axis interpretations included the restatement of the axis label (XA as RC, n = 9) and association of the x-axis with “progress” (XA as P, n = 4). Interestingly, some students explicitly stated that the x-axis was not time (XA as NT, n = 5); however, only one of these same participants adopted the XA as MD approach (Willa). Consider the following statement by Jessica during Phase 1:

“Um, I guess it's because you're measuring the change in energy over the time of reaction but not necessarily time cause I know it's not time, but you're measuring the change in energy throughout the reaction.”

Despite this early recognition of XA as NT, Jessica goes on in Phase 3 to adopt VT-C reasoning by comparing the relative lengths of the reaction coordinates to delineate that the rates of all three reactions are identical (Fig. 6).

“Um, they're all the same. Um they're all at ten [reaction coordinates]. So in terms of that, I guess you could say that the rate of reaction is the same, but I'm not too sure in terms of time.” (Jessica)

Jessica ultimately expresses uncertainty about how to relate the reaction coordinate to time; however, her association of the length of the reaction coordinate with rate implicitly adopts XA as T. Based upon these results, the previously identified XA as T alternative conception may arise explicitly or implicitly in manners that may be congruent or incongruent with what a student has previously learned in the chemistry classroom. Participants frequently justified why they chose the XA as T interpretation by citing prior experiences:

“Um, that's just normally the standard for when you're doing graphs. The x-axis is normally your time and then the y-axis is normally whatever else you're measuring, cause time just kind of goes.” (Megan)

“Um, because a lot of what we've learned in class and also like in the lab has had to do with like how a reaction proceeds and in a sense how long the reaction takes, I would say. Um, so that's why I would put it in time, and yeah.” (Christy)

“So the x-axis represents time of the reaction from start to finish. And then the y-axis is just your energy, uh, the energy that's in the reaction. Mainly this is just like the basic way I've been taught even since middle school when we talked about, um, when we talked about like reactions and stuff.” (Haley)

These statements provide evidence that a large variety of prior experiences contribute to a convergent interpretation of XA as T. Additionally, there is reason to be concerned that these generalizing experiences may heavily sway students’ interpretations despite in-class instruction. Consider the following set of responses by Wayne:

Interviewer: “I see. Okay. Is there any, um, example of a reaction energy diagram that you can draw for me?”

Wayne: “…And then this would be tim-, uh, I don't really, this would be the energy right on this axis – well, I'm not sure about the x-axis.”

Interviewer: “I see. I think you almost said something about the x-axis. What were you going to say?”

Wayne: “Time.”

Interviewer: “Okay. And why did you hesitate in saying time?”

Wayne: “Cause it's, I don't know, it doesn't really depend on time. Maybe, yeah, I'm gonna go with time, that's usually a good x-axis label.”

Interviewer: “I see. And I noticed you mentioned that it, you said that it's usually a good x-axis label. And why would you, why would, why do you feel it, it's usually a good label?”

Wayne: “I feel like a majority of the time on the x-axis, something is always depending on time and like [the] progression of it. Especially like, I'm in physics right now too. Like almost every graph, same with, uh, like our calculus class, almost every x-axis on a two-dimensional coordinate system is time.”

Wayne was unsure about the x-axis at first, but quickly came to assume that the x-axis was associated with time based on prior experiences. The majority of participants expressed uncertainty regarding the x-axis label “reaction coordinate” during the course of the interview (XA as U, n = 10). Therefore, it is evident that students harbor general uncertainties about the x-axis; however, these uncertainties did not deter students from adopting XA as T when interpreting RCDs. Rather, the combination of students’ general uncertainty regarding the x-axis and their prior experiences with time-relevant representations seemed to support the adoption of XA as T. Participants were also shown to draw upon relations of similarity between the nature of the x-axis on a RCD and other x-axes they have seen on alternative representations. The wide array of value-thinking and graphical forms approaches that were adopted when students invoked time suggests that students may associate meaning with the x-axis to adopt these reasoning approaches. Therefore, it is important to consider the impact of a students’ x-axis interpretation on their assessment of the rate of a reaction when interpreting a RCD.

Productivity of graphical reasoning codes in a kinetics context

The graphical reasoning students employed during the course of the study demonstrated variability in their “productivity” when using a RCD to reason about the relative rates of chemical reactions. Given the relevance of graphical reasoning in other learning contexts, the actor-oriented model of transfer (Lobato, 2003, 2012) was used to develop the codes productive, unproductive, and neutral that captured whether an emergent graphical reasoning code resulted in a productive outcome when reasoning about the rate or relative rates of reaction (see ESI† for definitions). A “neutral” code was included to define instances where a student arrived at a correct answer but in a manner that was inconsistent with the information encoded in a RCD or chose not to commit to an answer based upon their own awareness of their uncertainty. This distinction was made given the potential subjectivity of “productive” based on an instructor's goals and to highlight when certain graphical reasoning approaches may give rise to intuitions that may be “unproductive” in certain contexts. The relative contributions of each graphical reasoning code to these three outcome codes is summarized in Fig. 9. A percent contribution for each graphical reasoning code was calculated by counting each instance where each graphical reasoning code contributed to each productivity code and dividing this by the total number of productivity codes. The outcome codes only include graphical reasoning codes that were used to reason about the rate or relative rates of reaction. A mapping of outcome codes onto the total graphical reasoning code distribution is included in the ESI† (Fig. S3). The character of these outcomes across each coding category is discussed in the remainder of this section.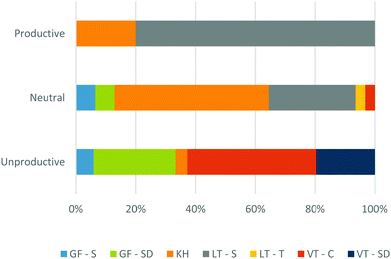

Fig. 9 The relative percent coverage of graphical reasoning codes and their association with the productivity of the transfer occurrence.

Value-thinking and graphical forms

Value-thinking and graphical forms reasoning only yielded neutral and unproductive kinetics outcome codes (Fig. 9). Many participants adopted the VT-C reasoning to unproductively associate meaning with the width of an RCD (n = 13) in alignment with previous research (Lamichhane et al., 2018; Popova and Bretz, 2018b). When comparing the relative widths between RCDs, students often used the blue lines of the Livescribe paper to attribute values to the x-axis. For example, when asked to identify the differences between the RCDs corresponding to Reactions 1 and 2 in Phase 3, Hayden marked the indicated space between the transition state peaks as shown in Fig. 10.

Fig. 10 Hayden's annotations when discussing the relative “widths” of RCDs for Reactions 1 and 2 during Phase 3.

Later on, Hayden compared the widths of all three RCDs by counting the blue lines of the notebook paper and thereby ascribing numerical values to the x-axis:

“So it [Reaction 2] takes one, two, three, four, five, six of these [referring to the blue lines on the Livescribe paper], whereas it [Reaction 3] takes, it should take seven of these if I drew it right. One, two, three, four, five, six, seven.”

Following Hayden's counting of the blue lines along the x-axis, she commented on how this information guided her assessment of the relative rates of all three RCDs:

“So at least with me, like I said, I, I kind of think rate and, and the time the reaction takes kind of go hand-in-hand. So I think, you know, the rate of Reaction 2 would be a lot faster than the rate of Reaction 1 and Reaction 3, as Reaction 1 and 3 take up basically the same amount of like, you know, these little grid spots in the paper, whereas Reaction 2 takes up less.”

Similarly, Willa came to the same conclusion based on her counting of the same blue lines (see x-axis interpretation and graphical reasoning section), despite her initial recognition that the x-axis encoded information regarding molecular distances and not time. Therefore, it is evident that this type of reasoning is attractive to students whether or not they correctly identify and adopt XA as MD. VT-C emerged in conjunction with GF-S and GF-SD in numerous cases when discussing the relative rates of reactions (discussed below).

Conversely, VT-SD arose independent of alternative graphical reasoning in all cases when participants reasoned about rate. Leonard provided a justification for his assessment that the rate of Reaction 2 is greater than Reaction 1 based on the slope and derivative of both RCDs. During this justification, Leonard drew straight lines along the RCD trend (Fig. 11). When asked why he included these lines, Leonard responded:

Fig. 11 Lines drawn by Leonard during his description of the slope and derivative of Reaction 2 during Phase 3.

“Well, I did that subconsciously because any time you're talking about a derivative, uh, of course when they're first teaching you, uh, you're, you're, you're really following that graph mentally thinking about how the, uh, linear, how the line tangent to that point, uh, what its slope is.”

Based on this statement, it is clear that the derivative at a point is influencing Leonard's assessment of the rate, resulting in an unproductive interpretation of the relative rates of reaction. It is worth noting that Leonard referenced calculus just before this example:

“Uh, well, again, going back to that calculus integration, so not integration, I mean application I guess, uh, that derivative is much higher than Reaction 1.”

This excerpt demonstrates the possible transfer of VT-SD graphical reasoning from calculus coursework into Leonard's assessment of rate when interpreting a RCD. The productivity of VT-SD in alternative social settings, such as calculus coursework, helps to support and justify Leonard's explanation for interpreting a RCD in this manner despite being unproductive in this context. Leonard's statements reflect his implicit XA as T interpretation based upon his association of numerical values with the slope of the RCD and the slope with the rate of reaction. The reference to calculus by Leonard demonstrates his relation of similarity between the nature of the x-axis of a RCD and the x-axes of familiar mathematical representations.

GF-S was used most prominently (n = 5) alongside additional graphical reasoning approaches to infer about the relative reaction rates between RCDs in Phase 3. For example, consider the excerpt from Susanne below:

Interviewer: “What differences can you identify between these two reaction coordinate diagrams?”

Susanne: “Uh, the Reaction 2, uh, the like hill is more like squished together where like for Reaction 1, it's more like spread out. Um, and that I think is the main difference between them.”

Interviewer: “I see. And is there anything you would conclude regarding these two reactions with this difference in mind?”

Susanne: “Um, yeah. So for Reaction 2 once you’ve reached the, uh, needed energy it will, because it's a steeper slope going down, it will be able to form the product quicker than Reaction 1.”

In this case, Susanne uses both GF-S and GF-SD reasoning to converge attributed meaning of the registrations “width” and “slope” to support her conclusion. The self-consistent mathematical narratives of these two observations serves to support the ultimately unproductive outcomes of Susanne's reasoning. Jesse adopted an alternative GF-S approach when asked how he had been interpreting the x-axis throughout the interview:

“I would say that, um, Reaction 1 and Reaction 2, um, definitely have, uh, different, uh, uh, rates of time, because like I was mentioning before, this horizontal compression would, would lead me to believe that this, uh, these units below this time, let's say we're in minutes while this reaction we're in seconds, or maybe Reaction 1 is in minutes and Reaction 2 is in hours. Either way, this unit of time here on Reaction 2 I would, uh, it leads me to believe that it would be, um, uh, that would be a larger time step…”

In this excerpt, Jesse transitions from GF-S to VT-C reasoning by assigning time as a unit to the x-axes to make a quantitative comparison following his initial reasoning that the units must be different due to the relative shapes of the diagrams. The unproductive mathematical narrative constructed by Jesse regarding the “width” of the RCD is supported by the assignment of values to the x-axes that may be used to compare the reactions through value-thinking approaches. Jesse does implicitly draw upon XA as T when reasoning with GF-S but adds to his inferences by explicitly adopting XA as T to further support his reasoning via a VT-C approach.

GF-SD arose both independently (n = 6) and alongside alternative graphical reasoning approaches (n = 5) when assessing the relative rates of reaction (see Susanne's quote above). In order to identify that GF-SD independently impacted a student's interpretation of rate, evidence must be acquired that the student interpreted the perceived slope of the graph and not the slope or derivative at a particular point. For example, Haley begins comparing Reactions 1 and 2 by comparing differences in slope:

“Uh, yeah, so for the slope of Reaction 1 around here compared to the slope of Reaction 2, uh the slope of Reaction 2 is a lot steeper. And what I feel is it takes, for, excuse me, for Reaction 2, it takes a less amount of time to reach that peak.”

Later on, when asked whether he needed to address the slope's relationship with the x-axis, Haley remarked that:

“Um, I just looked at the graphical representation and just, just saw the, like the grade, degrading of the, um, of the line. Like, I wouldn't need the x, I probably wouldn't need the x-axis just to show that, um, this line [draws line across Reaction 1's slope], it just feels a lot, it just appears a lot shallower compared to this line [draws line across Reaction 2's slope] because even without the x-axis it just looking at it, it Reaction 2, Reaction 2's activation energy doesn't seem to be as wide.”

Based on this response, Haley indicates that he assessed the slope without reference to the x-axis resulting in an eventual unproductive comparison of the relative rates:

“Um, I would assume that Reaction 2 would have a fast, would have a larger rate because again, the slope of the, the slope of your activation energy is much higher, is um, is more steeper than Reaction 1.”

Therefore, it is evident that Haley drew upon steepness as rate in order to interpret the relative rates of the two RCDs provided in a manner consistent with prior RCD literature findings (Rodriguez et al., 2020b). In this case, Haley implicitly draws upon XA as T to associate the slope with a familiar x-axis label (see x-axis interpretation and graphical reasoning section.)

Value-thinking and graphical forms reasoning, while productive in other contexts, are generally unproductive when applied to RCDs in the context of kinetics. Both graphical reasoning codes have been shown to be closely associated with the XA as T interpretation by participants. Therefore, it is clear that students’ adoption of XA as T supports unproductive graphical reasoning when addressing RCDs in a kinetics context.

Location-thinking

Of the emergent graphical reasoning codes, LT-S reasoning accounted for the majority of the productive assessments of reaction kinetics (Fig. 9). This is understandable given that a comparison of activation energies is the intended method for comparing the relative rates of reaction through the Arrhenius equation. A comparison of activation energies is mediated by the recognition of the major “physical states” in a RCD, thereby ascribing unique meaning to designated locations of the RCD through LT-S. Willa transitions to adopting LT-S reasoning by comparing the activation energies between RCDs in reference to a hypothetical relationship relating the reaction rate to the activation energy:

“Okay. So I can't remember now. I've got the two equations screwed up in my head and I can't remember now whether it's the bigger activation energy means the bigger k, or the, um, the bigger activation energy means the smaller k, but I can tell you that Reaction 1 and Reaction 2 are going to have, um, similar rates. And then Reaction 3 is either going to be greater or less than of those rates. I'd just be looking off the activation energies.”

In this case, Willa cannot remember the exact form of the Arrhenius equation, but upon being provided the relationship by the interviewer, Willa is eventually able to correctly reason about the relative rates of reaction:

“So Reaction 3 has a lower activation energy than Reaction 1 and 2. So since it has a lower reaction energy here, the k is going to be greater and the reaction will proceed faster.”

Similarly, Mark initially associates the relative rates of all three reactions correctly according to each RCD's activation energy:

“Um, Reaction 1 and Reaction 3, I would say have a greater change in rates for the reactions than Reaction 1 and Reaction 2, because Reaction 1 [and] Reaction 2, both had the same potential energy for the reactants.”

Mark goes on to correctly recall the Arrhenius equation, but ultimately correlates the activation energy with the rate constant incorrectly (Fig. 12):

Fig. 12 Mark's written formulation of the Arrhenius equation when comparing the relative rates of Reactions 1 and 3.

“The first thing that comes to mind is the mathematical equations involved for finding rates of reactions when the activation energy is, plays a significant role in that where, um, the greater the activation energy can affect the changes, whether or not it's greater or lesser for the rate constant, um, with a higher rate constant would have a higher rate.”

Other students made a productive comparison between the relative rates of Reactions 1 and 3 by recalling that they had been previously tasked with comparing activation energies to assess rate:

“Uh, I think it's [Reaction 3] faster just because, uh, in lecture we always talked about the lower the peak, the lower the activation energy, the faster that the reaction is. So, it needs less energy in terms of its starting point then, uh, then, uh, like Reaction 3 needs less energy to go to completion than Reaction 1 does.” (Wayne)

In only 2 of the 4 interviews in which productive LT-S reasoning emerged did students reference the Arrhenius equation. Therefore, it is possible students may recall the significance of the activation energy without a working model for why this comparison can be made. The productive outcomes associated with LT-S in this interview sample suggests that supporting students in associating physical states to regions of a RCD should be the primary target of RCD instruction. However, an awareness and understanding of the Arrhenius equation may be necessary for students to recognize why LT-S is productive in the context of kinetics.

Kinematic heuristic

Students’ adoption of the KH resulted in predominately neutral statements (Fig. 9) that in each case provided the right answer but in a manner that was inconsistent with the information encoded in RCDs (n = 5). Consider the following assessment of the relative rates of Reactions 1 and 3 by Jesse:

“…Over let's say six seconds, this reaction [Reaction 3] could reach its maximum potential energy, while Reaction 1 would reach that same value but not its maximum. So for, while Reaction 3 is then beginning to conclude its reaction, Reaction 1, um, would, would just be hitting that maximum value and by the time Reaction 3 has concluded, Reaction 1 would still be concluding. So I, it, I would say if, so, I would say that the reaction rate of [Reaction] 3 is uh greater than Reaction 1.”

Jesse associates the reaction rate with the time needed to traverse the RCD. As a result, he compared where “along” the trend the reaction will be after “say six seconds.” This reasoning is consistent with the notion that the graph encodes information about a kinematic system in which the x-axis is some distance. Haley and Mandy demonstrate a similar assessment of the relative rates of Reactions 1 and 3:

“So, um, if you observe, for instance, if you observe like five seconds of Reaction 1 versus five seconds of Reaction 3, with the less amount of time being attributed to trying to get to that transition state, there's going to be, uh, more of that five seconds in, um, product formation.” (Haley)

“If there's like a, if it's a less amount of energy they have to reach for it to be at the max point. Um, then like it wouldn't take as long, like if it's a lower, I'm thinking it wouldn't take as long, um, to reach that point [the max point] compared to Reaction 1.” (Mandy)

While students predominately used the KH to compare Reactions 1 and 3, this did not appear to conflict with inconsistent XA as T interpretations applied to Reactions 1 and 2 despite the need for the x-axis to encode distance information to support the KH. We hypothesize that this is due to a re-framing of the RCD into a kinematic system when discussing relative activation energies. As a result of this re-framing, a student may not consider the RCD a graphical representation, but a kinematic system that they can attribute intuitive meaning to via their own relations of similarity. Students attribution of meaning to the “length” of the RCD trend demonstrates that the adoption of the KH may indirectly impact how a student interprets the information encoded in a RCD and that this interpretation may even be contradicted by direct interpretations of the x-axis, such as XA as T, by the student.

Conclusions

Students adopted a diversity of graphical reasoning when confronted with interpreting points and trends along RCDs. The graphical ideas that students drew upon have been shown to arise from perceived quantitative and qualitative features of a RCD (David et al., 2018; Rodriguez et al., 2020a) and the influence of prior experiences with graphical representations. In this study, participants demonstrated flexibility in transitioning between different types of graphical reasoning to suit the task at hand. The flexibility in students’ reasoning was shown to emerge in part from the relations of similarity students made between RCDs and different representations across disciplines. It is therefore informative to consider the dependence of the transfer of these graphical ideas on the unique context of RCDs through the AOT.

Location-thinking (David et al., 2018) provides the basis for understanding how students graphically associate physical states with points or trends of a RCD via LT-S. All students demonstrated the ability to correctly label and interpret surface features of a single transition state RCD. However, students employed a host of alternative ideas and inferences regarding the processes associated with points and trends along the RCD. Rarely students associated each position of the RCD as being associated with a unique measurement giving significance to the trend rather than a physical state (LT-T). Many students employed alternative value-thinking approaches by reasoning about the coordinate (VT-C) or the slope (VT-SD) of the RCD at a point. Other students associated ideas with the shapes on the RCD trend consistent with the graphical forms framework (Rodriguez et al., 2020a). A notable distinction was made between students’ reasoning about the shape of the RCD trend (GF-S) and the perceived slope of a region (GF-SD). Additionally, some students appeared to re-frame the RCD as a kinematic diagram (KH) when reasoning about a RCD. While different forms of graphical reasoning emerged, students’ interpretations of the x-axis were monitored to explore the effects of these interpretations on the graphical reasoning employed by participants.

Findings derived from this study demonstrate that the x-axis misconception is not merely a mislabeling of the RCD by students, but rather it is an emergent phenomenon supported by a variety of generalizing experiences. While previous studies in chemistry and mathematics have highlighted students’ tendencies to invoke time across disciplines (Jones, 2017; Lamichhane et al., 2018; Popova and Bretz, 2018b), this study has explored possible origins for this reasoning through the lens of the AOT. All students in this study adopted the XA as T interpretation at some point during the interview, despite the widespread uncertainty expressed by many students regarding the x-axis label “reaction coordinate.” Even students who viewed the x-axis as encoding information about a molecular trajectory and/or not encoding information about time subsequently adopted or integrated XA as T into their explanations to suit their reasoning. Evidence derived from this study suggests that the convergence in students’ reasoning to XA as T is greatly influenced by prior experiences with graphical representations both within and outside of chemistry curricula. This finding is consistent with prior literature that has highlighted students’ preferences for invoking time when addressing graphical representations and derivatives (Jones, 2017, 2019).

The tendency for students to invoke time when addressing RCDs was shown to support students’ use of unproductive value-thinking and graphical forms reasoning when comparing relative rates of reaction between RCDs. Conversely, LT-S was demonstrated to be most productive when comparing reaction rates. Students adopting LT-S and the KH both compared the relative activation energies of RCDs to come to conclusions regarding rate. While both LT-S and the KH generally allowed students to arrive at a correct answer, LT-S reasoning was consistent with the physical information encoded on a RCD while applying the KH was generally not. The re-framing of a RCD as a kinematic path is accompanied by incorrect associations, such as attributing meaning to the “length” of a RCD path, that can misinform students of what a RCD represents as a model. In particular, the few students that adopted LT-S with a XA as MD interpretation were the most productive in physically describing the points and trends of a RCD. Students’ reasons for adopting value-thinking and graphical forms reasoning may be informed by considering the implications of kinetics as a unique context in chemistry. Within chemical kinetics as a topic area, the importance of graphical representations interpreted via covariational reasoning (Rodriguez et al., 2019) and the reaction rate as a central parameter (Holme et al., 2015) suggests that kinetics may support unproductive graphical reasoning approaches when students address RCDs.

At the general chemistry level, a RCD describes an abstracted molecular trajectory that serves as a model to describe the kinetics and thermodynamics of a reaction. However, students have been shown to draw upon prior experiences both within and outside of a chemistry context to graphically reason about RCDs in a manner inconsistent with the information encoded in RCDs. From the perspective of the AOT, it is paramount to recognize that the generally unproductive instances of value-thinking and graphical forms reasoning that emerged in this study are very productive in other learning contexts and are simply “what” many students transfer when addressing RCDs. These findings therefore shed light on how unproductive transfer may directly impact students’ abilities to learn about RCDs at the general chemistry level in a manner that properly prepares them for their reemergence in the different contexts of organic and physical chemistry curricula.

Implications

Students’ adoption of the “x-axis as time alternative conception” has been shown to support unproductive value-thinking and graphical forms reasoning when interpreting points and trends on a RCD and when making inferences about reaction rate. Value-thinking and graphical forms are highly productive within alternative contexts both within and outside the chemistry classroom as demonstrated by students’ prior experiences in this study. Therefore, it is not enough to ask instructors to “discuss” the x-axis of a RCD or to highlight that it is “not time” in a chemistry classroom. Rather, results from this study suggest it is critical that the chemistry education and chemistry education research communities revisit the purpose of these diagrams across the broader trajectory of a student's academic acculturation in chemistry.

The role of RCDs in a physical chemistry context, as graphs, and the role of RCDs in an organic chemistry context, as diagrams, suggests that the ideal methods for instruction on RCDs may depend on the intended sequence for a student's journey through chemistry. For instance, an emphasis of surface features of RCDs may be sufficient for students taking organic chemistry, but the theoretical underpinnings associated with the points and trends along a RCD may be critical for students going on to take physical chemistry. The traditional sequence of general chemistry, organic chemistry, physical chemistry suggests that the role of RCDs in the general chemistry classroom is first to build a qualitative picture for RCDs and then highlight the meaning of the points and trends on a RCD if necessary. However, the current way in which chemistry as a field portrays RCDs and the relevance of RCDs to kinetics carries with it a myriad of unproductive graphical reasoning approaches that students will inevitably draw upon because we as faculty have trained them to do so. As such, we call for a re-thinking of how RCDs are instructed through evidence-based classroom research. Innovative methods and scaffolded approaches must be developed to assist students in developing an understanding of the qualitative nature of RCDs in a general chemistry context to promote the adoption of location-thinking, states by students.

Based on the findings of this study, we suggest altering the focusing phenomena of the RCD by removing the points and trends from RCDs as these features support value-thinking and graphical forms reasoning when first introducing students to these diagrams. This suggestion is made to eliminate any perception of an x-axis given the relations of similarity students have been shown to draw between the x-axis of a RCD and alternative representations. Subsequently, points and trends may be added to the diagram and discussed in appropriate detail. This hypothetical approach would draw attention to the key features of the diagram (i.e. reactants, products, and transition state), while subsequently associating the points and trends with an instructive molecular trajectory picture. However, we challenge whether the points and trends associated with a RCD are necessary in all, or even most, chemistry curricula for students to derive the important kinetic and thermodynamic parameters from such diagrams. Whether or not points and trends are introduced, we hypothesize that a “states-based” energy diagram, such as the one included in Fig. 13, would assist in drawing students’ attention to the critical features of a RCD and encourage them to not invoke time. Chemical reaction intermediates may also be included (see ESI,† Fig. S2) with a solid line to distinguish the notable lifetime associated with intermediates when compared to transition states. We hypothesize that by removing the x-axis as a focusing phenomenon, students will be encouraged to not transfer unproductive value-thinking and graphical forms reasoning into a RCD context. Additionally, the presence of “states-based” energy diagrams in a variety of general chemistry content, such as in thermochemistry and electronic structure (Brown et al., 2015), may allow this suggested approach to support students in the productive transfer of ideas previously learned in the chemistry classroom. The curvature of a RCD can then be added in if the students of a course would benefit from discussing the dynamic and abstracted nature of the reaction coordinate based upon the demands of future coursework.

Fig. 13 A states-based RCD depiction where the curve has been replaced with discrete lines representing the potential energy associated with the reactants, transition state, and products.

Limitations

The results of this study are not generalizable beyond the context of the general chemistry course investigated in this study. Tasks and instructional materials specific to the single course investigated may have uniquely contributed to the results. We acknowledge that this unique semi-structured interview context represents a non-naturalistic setting. Additionally, the sequence of interview tasks may have prompted students to employ certain reasoning beyond addressing only one task. However, this study serves to highlight the possible role of graphical reasoning and transfer in supporting the misconceptions associated with RCDs as described in previous RCD literature (Lamichhane et al., 2018; Popova and Bretz, 2018b). We encourage future chemistry education research studies on RCDs to monitor the potential emergence of value-thinking, location-thinking, and graphical forms reasoning in addition to the surface features associated with RCDs to further build on these findings (Popova and Bretz, 2018b).

We also call attention to limitations in the application of our frameworks to the unique context of RCDs. The value-thinking and location-thinking framework distinguishes value-thinking as operative; however, the lack of explicit values in the context of RCDs means value-thinking, as it is applied in this study, is not directly operative. There is currently debate within the mathematics education research community on whether students may adopt operative reasoning with representations that do not explicitly provide values. (Moore, 2016; Thompson and Carlson, 2017; Tasova and Moore, 2020). We acknowledge any upcoming commentary on this topic and are open to various perspectives that may contribute to the limitations of this framework when bridging into a chemistry context.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors thank Dr Jon-Marc Rodriguez, Dr Libai Huang, and the attendees of the 2020 Research in Undergraduate Mathematics Education conference for critical feedback across various stages of the project. We also thank the students and the instructor of the general chemistry course.

References

1. Atkins P. and de Paula J., (2014), Physical Chemistry, 10th edn, Oxford, UK: Oxford University Press.
2. Atkinson M. B., Popova M., Croisant M., Reed D. J. and Bretz S. L., (2020), Development of the reaction coordinate diagram inventory: Measuring student thinking and confidence, J. Chem. Educ., 97(7), 1841–1851.
3. Atkinson M. B., Croisant M. and Bretz S. L., (2021), Investigating first-year undergraduate chemistry students’ reasoning with reaction coordinate diagrams when choosing among particulate-level reaction mechanisms. Chem. Educ. Res. Pract., 22(1), 199–213.
4. Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17(2), 246–262.
5. Bain K., Rodriguez J.-M. G., Moon A. and Towns M. H., (2018), The characterization of cognitive processes involved in chemical kinetics using a blended processing framework, Chem. Educ. Res. Pract., 19(2), 617–628.
6. Bain K., Rodriguez J.-M. G. and Towns M. H., (2019), Investigating student understanding of rate constants: When is a constant “constant”? J. Chem. Educ., 96(8), 1571–1577.
7. Becker N. and Towns M., (2012), Students’ understanding of mathematical expressions in physical chemistry contexts: An analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13(3), 209–220.
8. Bingolbali E., Monaghan J. and Roper T., (2007), Engineering students’ conceptions of the derivative and some implications for their mathematical education, Int. J. Math. Educ. Sci. Technol., 38(6), 763–777.
9. Brown T. L., LeMay H. E., Bursten B. E., Murphy C. J., Woodward P. M. and Stoltzfus M. W., (2015), in Jaworski A. (ed.), Chemistry the central science, 13th edn, London, UK: Pearson Education, Inc.
10. Carey F. A. and Giuliano R. M., (2008), Organic Chemistry, 8th edn, New York, NY: McGraw-Hill Publishing.
11. Cooper M. M. and Stowe R. L., (2018), Chemistry education research – From personal empiricism to evidence, theory, and informed practice, Chem. Rev., 118(12), 6053–6087.
12. Csizmar C. M., Daniels J. P., Davis L. E., Hoovis T. P., Hammond K. A., McDougal O. M. and Warner D. L., (2013), Modeling S_N2 and E2 reaction pathways and other computational exercises in the undergraduate organic chemistry laboratory. J. Chem. Educ., 90(9), 1235–1238.
13. David E. J., Roh K. H. and Sellers M. E., (2018), Value-thinking and location-thinking: Two ways students visualize points and think about graphs, J. Math. Behav., 54, 1–18.
14. De Vries H., Elliott M. N., Kanouse D. E. and Teleki S. S., (2008), Using pooled kappa to summarize interrater agreement across many items, Field Methods, 20(3), 272–282.
15. Goldman S. R., (2003), Learning in complex domains: When and why do multiple representations help? Learn. Instr., 13(2), 239–244.
16. Graulich N. and Bhattacharyya G., (2017), Investigating students’ similarity judgments in organic chemistry, Chem. Educ. Res. Pract., 18(4), 774–784.
17. Guba E. G. and Lincoln Y. S., (1981), Naturalistic solutions to methodological problems, in Effective Evaluation: Improving the Usefulness of Evaluation Results Through Responsive and Naturalistic Approaches, 1st edn, San Francisco, CA: Jossey-Bass Publishers, pp. 85–127.
18. Hallgren K. A., (2012), Computing inter-rater reliability for observational data: An overview and tutorial, Tutor. Quant. Methods Psychol., 8(1), 23–34.
19. Hammer D., Elby A., Scherr R. E. and Redish E. F., (2005), Resources, framing, and transfer, in Mestre J. P. (ed.), Transfer of Learning from a Modern Multidisciplinary Perspective, Greenwich, CT: Information Age Publishing, pp. 89–119.
20. Holme T., Luxford C. and Murphy K., (2015), Updating the general chemistry anchoring concepts content map, J. Chem. Educ., 92(6), 1115–1116.
21. Holme T. A., Reed J. J., Raker J. R. and Murphy K. L., (2018), The ACS exams institute undergraduate chemistry anchoring concepts content map IV: Physical chemistry, J. Chem. Educ., 95(2), 238–241.
22. Hulse J. E., Jackson R. A. and Wright J. S., (1974), Energy surfaces, trajectories, and the reaction coordinate, J. Chem. Educ., 51(2), 78–82.
23. Johnson H. L., (2015), Secondary students’ quantification of ratio and rate: A framework for reasoning about change in covarying quantities, Math. Think. Learn., 17(1), 64–90.
24. Jones S. R., (2017), An exploratory study on student understandings of derivatives in real-world, non-kinematics contexts, J. Math. Behav., 45, 95–110.
25. Jones S. R., (2019), Students’ application of concavity and inflection points to real-world contexts, Int. J. Sci. Math. Educ., 17(3), 523–544.
26. Kaliakin D. S., Zaari R. R. and Varganov S. A., (2015), 3D printed potential and free energy surfaces for teaching fundamental concepts in physical chemistry, J. Chem. Educ., 92(12), 2106–2112.
27. Kaya E. and Geban Ö., (2012), Facilitating conceptual change in rate of reaction concepts using conceptual change oriented instruction, Educ. Sci., 37(163), 216–225.
28. Kozma R. and Russell J., (2005), Students becoming chemists: Developing representationl competence, in Gilbert J. K. (ed.), Visualization in Science Education, Dordrecht, The Netherlands: Springer, pp. 121–146.
29. Lamichhane R., Reck C. and Maltese A. V., (2018), Undergraduate chemistry students’ misconceptions about reaction coordinate diagrams, Chem. Educ. Res. Pract., 19(3), 834–845.
30. Levine I. N., (2002), in Peterson K. A. (ed.), Physical Chemistry, 5th edn, New York, NY: McGraw-Hill Publishing.
31. Linenberger K. J. and Bretz S. L., (2012), A novel technology to investigate students’ understandings of enzyme representations, J. Coll. Sci. Teach., 42(1), 45–49.
32. Lobato J., (2003), How design experiments can inform a rethinking of transfer and vice versa, Educ. Res., 32(1), 17–20.
33. Lobato J., (2012), The actor-oriented transfer perspective and its contributions to educational research and practice, Educ. Psychol., 47(3), 232–247.
34. Loudon M. and Parise J., (2016), Organic Chemistry, 6th edn, New York, NY: W. H. Freeman and Company.
35. Merriam S. and Tisdell E., (2016), Qualitative Research: A Guide to Design and Implementation, 4th edn, San Francisco, CA: John Wiley & Sons, Inc.
36. Moore K. C., (2016), Graphing as figurative and operative thought, Paper presented at the Proceedings of the 40th Conference of the International Groups for the Psychology of Mathematics Education, Szeged, Hungary.
37. Morrison R. W., Caughran J. A. and Sauers A. L., (2014), Classroom response systems for implementing interactive inquiry in large organic chemistry classes, J. Chem. Educ., 91(11), 1838–1844.
38. NGSS Lead States, (2013), Next Generation Science Standards: For States, By States (Appendix G – Crosscutting Concepts), The National Academies Press.
39. Popova M. and Bretz S. L., (2018a), Organic chemistry students’ challenges with coherence formation between reactions and reaction coordinate diagrams, Chem. Educ. Res. Pract., 19(3), 732–745.
40. Popova M. and Bretz S. L., (2018b), Organic chemistry students’ interpretations of the surface features of reaction coordinate diagrams, Chem. Educ. Res. Pract., 19(3), 919–931.
41. Raker J., Holme T. and Murphy K., (2013), The ACS exams institute undergraduate chemistry anchoring concepts content map II: Organic chemistry, J. Chem. Educ., 90(11), 1443–1445.
42. Rodriguez J.-M. G., Santos-Diaz S., Bain K. and Towns M. H., (2018), Using symbolic and graphical forms to analyze students’ mathematical reasoning in chemical kinetics, J. Chem. Educ., 95(12), 2114–2125.
43. Rodriguez J.-M. G., Bain K., Towns M. H., Elmgren M. and Ho F. M., (2019), Covariational reasoning and mathematical narratives: Investigating students’ understanding of graphs in chemical kinetics, Chem. Educ. Res. Pract., 20(1), 107–119.
44. Rodriguez J.-M. G., Bain K. and Towns M. H., (2020a), Graphical forms: The adaptation of Sherin's symbolic forms for the analysis of graphical reasoning across disciplines, Int. J. Sci. Math. Educ., 18(8), 1547–1563.
45. Rodriguez J.-M. G., Stricker A. R. and Becker N. M., (2020b), Exploring the productive use of metonymy: Applying coordination class theory to investigate student conceptions of rate in relation to reaction coordinate diagrams, J. Chem. Educ., 97(8), 2065–2077.
46. Rodriguez J.-M. G., Stricker A. R. and Becker N. M., (2020c), Students’ interpretation and use of graphical representations: Insights afforded by modeling the varied population schema as a coordination class, Chem. Educ. Res. Pract., 21(2), 536–560.
47. Sheehan W. F., (1970), Along the reaction coordinate, J. Chem. Educ., 4(1), 254–260.
48. Silberberg M. and Amateis P., (2018), Chemistry: The Molecular Nature of Matter and Change, 8th edn, New York, NY: McGraw-Hill Publishing.
49. Tasova H. I. and Moore K. C., (2020), Constructing and representing a quantitative structure: A conceptual analysis, Paper presented at the The International Conference of the Learning Sciences, Nashville, TN.
50. Taştan Ö., Yalçinkaya E. and Boz Y., (2010), Pre-service chemistry teachers’ ideas about reaction mechanism, J. Turkish Sci. Educ., 7(1), 47–60.
51. Thompson P. W. and Carlson M., (2017), Variation, covariation and functions: Foundational ways of mathematical thinking, in Cai J. (ed.), Compendium for research in mathematics education, Reston, VA: National Council of Teachers of Mathematics, Inc., pp. 421–456.
52. Wagner J. F., (2010), A transfer-in-pieces consideration of the perception of structure in the transfer of learning, J. Learn. Sci., 19(4), 443–479.
53. Xue D. and Stains M., (2020), Exploring students’ understanding of resonance and its relationship to instruction, J. Chem. Educ., 97(4), 894–902.
54. Yalçinkaya E., Taştan-Kirik Ö., Boz Y. and Yildiran D., (2012), Is case-based learning an effective teaching strategy to challenge students’ alternative conceptions regarding chemical kinetics? Res. Sci. Technol. Educ., 30(2), 151–172.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1rp00037c

---