 Open Access Article
Open Access ArticleA low-temperature hydrothermal synthesis of submicron spherical BaF2
Xiao Liabc,
Yuxiang Zhaoab,
Bo Liab,
Shuxuan Wangab and
Xingwu Zou *ab
*ab
aKey Laboratory of Comprehensive and Highly Effificient Utilization of Salt Lake Resources, Qinghai Institute of Salt Lakes, Chinese Academy of Sciences, Xining 810008, China. E-mail: zouxingwu@isl.ac.cn
bQinghai Engineering and Technology Research Center of Comprehensive Utilization of Salt Lake Resources, Xining 810008, China
cUniversity of Chinese Academy of Sciences, Beijing 100049, China
First published on 16th December 2021
Abstract
The sub-micron spherical barium fluoride (BaF2) was successfully synthesized via a low-temperature hydrothermal method using ethylenediamine tetraacetic acid disodium salt (EDTA-2Na) as the chelating agent. The effect of pH, the molar ratio of EDTA to Ba2+, barium hydroxide octahydrate (Ba(OH)2·8H2O) concentration, hydrofluoric acid (HF) concentration, hydrothermal temperature and time, on the formation of spherical BaF2 were investigated. The formation mechanism of spherical BaF2 has been proposed based on the experimental results. The results show that the spherical BaF2, with an average size of 346.9 nm, is formed by the self-assembly of nanocubes. The optimized synthesis conditions are: pH = 14, EDTA-2Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ = 1
Ba2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Ba(OH)2 concentration is 0.1 mol L−1, HF concentration is 2.0 mol L−1, hydrothermal temperature is 80 °C and hydrothermal time is 2.0 h. The self-assembly mechanism of the spherical secondary structure was revealed from the perspective of crystal nucleation and growth, and the important role of EDTA in the spherical BaF2 formation is explained.
1, Ba(OH)2 concentration is 0.1 mol L−1, HF concentration is 2.0 mol L−1, hydrothermal temperature is 80 °C and hydrothermal time is 2.0 h. The self-assembly mechanism of the spherical secondary structure was revealed from the perspective of crystal nucleation and growth, and the important role of EDTA in the spherical BaF2 formation is explained.
1 Introduction
Barium fluoride (BaF2) has varied potential applications due to its exclusive and diverse features, such as stable chemical properties, low refractive index, strong ability to adapt to the lattice, low phonon energy, and optical transparency over a wide wavelength range. Based on these important properties, it can be used in the fields of high energy physics,1–4 optical,5,6 lasers,7–9 and semiconductor buffer layer materials.10,11 Nano-scaled barium fluoride has higher F− conductivity than single crystal or polycrystalline fluoride about 1 to 2 orders of magnitude, which has a great potential in the field of ion conductors.12–14 In addition, it also possesses novel electronic, magnetic, optical, chemical, and mechanical properties that cannot be obtained from its bulky counterparts.At present, several types of techniques have been developed to control the size, morphology and crystallinity of BaF2, such as rods,15 hollow spheres,16 whiskers,17 and cubes18–20 by microemulsion, hydrothermal and flame spray methods. Among them, the spherical structure has great potential applications on infrared glasses and catalytic materials due to its good fluidity and high specific surface area. On the one hand, in the preparation process of infrared glass, spherical particles can effectively reduce the “interlocking effect” during the mixing of glass raw materials, making the glass composition more uniform, which improves the optical properties of infrared glass. On the other hand, the high specific surface area of the spherical particles can effectively improve the catalytic efficiency and is an ideal raw material for preparing catalysts.21 However, the current research on BaF2 is more focused on preparing hollow and heterogeneous structures, but fewer BaF2 solid microsphere structures. Therefore, it is necessary to find a simple and fast method to synthesize solid microsphere BaF2.
In this study, we proposed a facile, low-cost and efficient approach for the fabrication of spherical BaF2 with high purity. Submicron solid microspheres formed by the self-assembly of BaF2 nanocubes were successfully prepared by a low-temperature hydrothermal method using Ba(OH)2·8H2O and HF as reactants, and EDTA was introduced into the reaction as the morphology-controlling agent. The effects of the EDTA to Ba2+ molar ratio, pH of the precursor solution, Ba(OH)2 and HF concentration, hydrothermal time and hydrothermal temperature on the morphology and phase of BaF2 were investigated. The formation mechanism of BaF2 solid microspheres was proposed.
2 Experimental
2.1 Reagents and materials
Barium hydroxide octahydrate (Ba(OH)2·8H2O) and ethylenediamine tetraacetic acid disodium salt (EDTA-2Na) were purchased from Sinopharm Chemical Reagents Co. Ltd. Hydrofluoric acid (HF) was purchased from Chengdu Kelong Chemicals Co. Ltd. The reagents needed for the experiment were all analytically pure, and used without further purification.2.2 Preparation of submicron spherical barium fluoride
In a typical procedure, 1.5773 g of Ba(OH)2·8H2O (5 mmol) was dissolved in 50 mL distilled water to form solution A, 1.8612 g of EDTA-2Na was added to solution A and stirred until dissolved. NaOH (4 mol L−1) was then added to adjust the pH of the solution to 14, followed by the addition of 5 mL of HF (2 mol L−1) under stirring in a Teflon beaker for 10 min. The resulting solution was transferred into a 100 mL Teflon-lined autoclave. The autoclave was sealed and maintained at 80 °C, for 2 h, and then air-cooled to room temperature. The products were washed with distilled water and absolute ethanol, and finally were vacuum-dried at 60 °C for 4 h. The effect of pH, the molar ratio of EDTA to Ba2+, Ba(OH)2 and HF concentration, hydrothermal temperature and time on the phase and morphology of BaF2 were investigated.2.3 Characterization methods
X-Ray powder diffraction (XRD) analysis was measured on a X'Pert Pro ray diffractometer with Cu Kα radiation (λ = 0.15406 nm) and 2θ ranging from 5° to 90°. Field emission scanning electron microscopy (FESEM) images were obtained on a SU8010 field emission scanning electron microscope. Transmission electron microscopy (TEM) and high-resolution transmission electron microscopy (HRTEM) images were obtained on a JEM-F200 field emission transmission electron microscope at an accelerating voltage of 200 kV.3 Results and discussion
3.1 Synthesis, morphology, and structure of submicron spherical barium fluoride prepared by the hydrothermal method
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.5
1, 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.75
1, 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1.25
1 and 1.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with hydrothermal treatment under the conditions of barium hydroxide solution with a Ba(OH)2 concentration of 0.1 mol L−1, HF concentration of 2.0 mol L−1, the pH of 14 and 80 °C for 2 h.
1 with hydrothermal treatment under the conditions of barium hydroxide solution with a Ba(OH)2 concentration of 0.1 mol L−1, HF concentration of 2.0 mol L−1, the pH of 14 and 80 °C for 2 h.XRD patterns (Fig. 1a) show that all the samples prepared under the different molar ratios are BaF2 with good crystallinity, but the half-width of the diffraction peaks of the samples after adding EDTA is more expansive, which is caused by the reduction in the particle size after adding the topography agent. According to the Scherrer formula (eqn (1)), the sample particle size decreases as the molar ratio of EDTA to Ba2+ increases (Fig. 1b).
D = Kγ/B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (1) |
The SEM image shows that the barium fluoride crystals appear as irregular cubes of different sizes in the absence of EDTA (Fig. 1d). With the increase in the molar ratio, the size of the cube particles gradually decreases, and the spherical structure formed by the self-assembly of cubes becomes obvious (Fig. 1e and f). When the molar ratio is increased to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, BaF2 cubes self-assemble into a regular and uniform spherical structure (Fig. 1g). The particle size of the spherical structure decreases when the molar ratio continues to increase (Fig. 1h). These phenomena are mainly due to the different BaF2 particle sizes caused by the EDTA–Ba complex formed by adding EDTA to the Ba(OH)2 solution (Fig. 1c).
1, BaF2 cubes self-assemble into a regular and uniform spherical structure (Fig. 1g). The particle size of the spherical structure decreases when the molar ratio continues to increase (Fig. 1h). These phenomena are mainly due to the different BaF2 particle sizes caused by the EDTA–Ba complex formed by adding EDTA to the Ba(OH)2 solution (Fig. 1c).
The reaction formula is as follows:22
| Y4− + Ba2+ → BaY2− | (2) |
| BaY2− + 2F− → BaF2 + Y4− | (3) |
According to reactions (2) and (3), when the molar ratio of EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ is lower than 1
Ba2+ is lower than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Ba2+ is not completely complexed by EDTA. The resulting barium fluoride is formed quickly after adding F−, shortening the nucleation time. Therefore, large-sized BaF2 particles can be obtained. However, when the molar ratio of EDTA
1, Ba2+ is not completely complexed by EDTA. The resulting barium fluoride is formed quickly after adding F−, shortening the nucleation time. Therefore, large-sized BaF2 particles can be obtained. However, when the molar ratio of EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ is higher than 1
Ba2+ is higher than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, excess Y4− will slow down the release rate of the Ba2+, prolonging the nucleation time, and the as-prepared BaF2 crystal grains that will be smaller will self-assemble into a spherical to reduced total surface energy.
1, excess Y4− will slow down the release rate of the Ba2+, prolonging the nucleation time, and the as-prepared BaF2 crystal grains that will be smaller will self-assemble into a spherical to reduced total surface energy.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ = 1
Ba2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 during the preparation procedure. The XRD patterns of the samples obtained at different pH values are well consistent with the BaF2 (JCPDS no. 04-0452) standard card (Fig. 2a). The strong and sharp diffraction peaks imply that the change of pH does not affect the crystal form of barium fluoride.
1 during the preparation procedure. The XRD patterns of the samples obtained at different pH values are well consistent with the BaF2 (JCPDS no. 04-0452) standard card (Fig. 2a). The strong and sharp diffraction peaks imply that the change of pH does not affect the crystal form of barium fluoride.
The morphology evolution of BaF2 under different pH values is shown in Fig. 2c–f. With the increase in the pH value, the BaF2 submicron spheres contour gradually becomes apparent. The average particle size of BaF2 cubes calculated by the Scherer formula indicates that smaller particles are easier to assemble into spheres (Fig. 2b). The particle size controlled by the crystal growth process is critical for forming a sphere of BaF2. As demonstrated in reaction (4), EDTA has a series of dissociation equilibria under acidic conditions called the acid effect that can reduce the equilibrium concentration of Y4− (complexing with Ba2+) in the system. In reaction (5), the acid effect coefficient αY(H) represents the ratio of the total concentration of the unreacted complexing agent [Y′] to the equilibrium concentration of Y that can be complexed. After obtaining the αY(H) of EDTA at each pH, the conditional stability constants of EDTA–Ba can be calculated using reaction (6). As shown in Table 1, the conditional stability constants of EDTA and Ba2+ are relatively small under acidic conditions. This means that Ba2+ in EDTA–Ba is readily dissociated and combines with F− after the addition of HF, leading to BaF2 burst nucleation, and rapid drop in the supersaturation. The system enters the crystal growth stage in the shortest time possible, resulting in relatively large particle size. With the increase in the pH value, the conditional stability constants of EDTA and Ba2+ gradually increase, Ba2+ is difficult to dissociate, making the nucleation of BaF2 crystals difficult. Therefore, the size of the crystal grains can be controlled by shortening the growth time. Hence, low pH is not suitable for the formation of spheres of BaF2.
 | (4) |
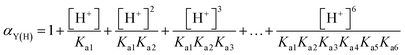 | (5) |
 | (6) |
 is the conditional stability constant of Ba2+ and EDTA, and lg
is the conditional stability constant of Ba2+ and EDTA, and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KBaY is the stability constant of Ba2+ and EDTA.
KBaY is the stability constant of Ba2+ and EDTA.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ = 1
Ba2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, pH = 14, 80 °C for 2 h at different concentrations of Ba(OH)2 (0.05 mol L−1, 0.10 mol L−1, 0.15 mol L−1 and 0.30 mol L−1).
1, pH = 14, 80 °C for 2 h at different concentrations of Ba(OH)2 (0.05 mol L−1, 0.10 mol L−1, 0.15 mol L−1 and 0.30 mol L−1).The XRD patterns show that all the samples prepared under different concentrations of Ba(OH)2 are BaF2 crystals with good crystallinity and without impurities (Fig. 3a). According to the Scherrer formula, the particle size of the samples gradually decreases as the Ba(OH)2 concentration increases (Fig. 3b). Irrespective of the Ba(OH)2 concentration being lower or higher than 0.10 mol L−1, the barium fluoride cubes could not self-assemble well into a spherical structure. At a low Ba(OH)2 concentration, the BaF2 monomers were kept in the low concentration state for a long time, leading to the size of the BaF2 cubes becoming too large to self-assemble spontaneously. On the contrary, a high Ba(OH)2 concentration increases the concentration of BaF2 monomers, resulting in the continued nucleation of BaF2 crystals. As a result, the size of the BaF2 cubes is smaller, which causes the surface energy of the cubes to be so high that cubes can only be closely packed into large-size agglomerates to reduce the surface energy, thus achieving a thermodynamically stable state. Therefore, the Ba(OH)2 solution concentration of 0.10 mol L−1 was determined as the optimal raw material concentration value for the preparation of spherical BaF2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ = 1
Ba2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, pH = 14 and the hydrothermal time was kept at 2 h to explore the influence of different hydrothermal temperatures on the formation of spherical barium fluoride.
1, pH = 14 and the hydrothermal time was kept at 2 h to explore the influence of different hydrothermal temperatures on the formation of spherical barium fluoride.The XRD patterns (Fig. 5a) of the samples obtained at different hydrothermal temperatures are in good agreement with the standard BaF2 diffraction peaks (JCPDS no. 04-0452) and without other impurity peaks.
According to SEM images, the crystal size increases with the increase in the hydrothermal temperature, which is consistent with the result calculated by the Scherrer formula (Fig. 5b). At a low temperature, the BaF2 nanocrystals can self-assemble into spherical particles but are smaller in size with poor dispersibility (Fig. 5c). On increasing the temperature to 80 °C (Fig. 5d), a spherical structure with a large size, caused by the increase in the particle size of the basic structural unit, can be obtained. With further increase in temperature, the particles can exist stably by themselves, due to the decreased surface energy caused by the increase in the nanocube size (Fig. 5e and f). At the higher temperature, EDTA shows weak chelating ability, and the crystals grow into larger particles. Therefore, 80 °C is determined as the appropriate hydrothermal temperature.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ = 1
Ba2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, pH = 14 and the hydrothermal temperature was 80 °C for different times.
1, pH = 14 and the hydrothermal temperature was 80 °C for different times.Fig. 6a displays the XRD diffraction patterns of products prepared at different times and are all barium fluoride crystals, with no intermediate products and impurities. The Scherrer formula results show that prolonged hydrothermal time promotes the crystal growth (Fig. 6b). The SEM images show the formation process of barium fluoride submicron spheres directly. BaF2 initially has an unapparent spherical morphology without hydrothermal. However, the spherical structure becomes increasingly apparent when the hydrothermal time is extended (Fig. 6c–e). Extending time to 2.0 h, resulted in all the nanocubes self-assembling into submicron spheres (Fig. 6f). The cube can exist independently, with the particle size gradually increasing with further increase in time (Fig. 6g and h). This indicates that an appropriate increase in the hydrothermal time can promote the formation of the self-assembled secondary structure of the nanoparticles. However, a long hydrothermal time will make nano-crystal grains grow reducing surface energy, and results in failure to form a spherical structure.
3.2 Characterization of BaF2 submicron solid spheres synthesized under the optimal conditions
The BaF2 submicron solid spheres were synthesized with the optimal conditions: Ba(OH)2 concentration is 0.1 mol L−1, HF concentration is 2.0 mol L−1, EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ = 1
Ba2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, pH = 14 and the hydrothermal temperature and time were 80 °C and 2 h, respectively. As indicated in Fig. 7a, the XRD pattern of BaF2 synthesized via hydrothermal synthesis agrees well with that of the standard BaF2 (JCPDS no. 04-0452). The strong and sharp diffraction peaks indicate that the as-obtained sample is highly crystallized. The SEM images (Fig. 7b) show that the obtained submicron spheres are formed by the self-assembly of nanocubic particles, with a regular morphology and average particle size of about 346.9 nm (Fig. 7c). As revealed by HRTEM images in Fig. 6d, clear and solid BaF2 was identified. The corresponding selected area electron diffraction (SAED) pattern proves that the structure is poly-crystalline and is highly consistent with each crystal plane index of BaF2 (Fig. 7e). As shown in Fig. 7f, the inter-planar distances between adjacent lattice fringes were determined to be 0.354 and 0.313 nm, indexed to the d-spacing values of the (111) and the (200) planes, respectively, in the fcc BaF2.
1, pH = 14 and the hydrothermal temperature and time were 80 °C and 2 h, respectively. As indicated in Fig. 7a, the XRD pattern of BaF2 synthesized via hydrothermal synthesis agrees well with that of the standard BaF2 (JCPDS no. 04-0452). The strong and sharp diffraction peaks indicate that the as-obtained sample is highly crystallized. The SEM images (Fig. 7b) show that the obtained submicron spheres are formed by the self-assembly of nanocubic particles, with a regular morphology and average particle size of about 346.9 nm (Fig. 7c). As revealed by HRTEM images in Fig. 6d, clear and solid BaF2 was identified. The corresponding selected area electron diffraction (SAED) pattern proves that the structure is poly-crystalline and is highly consistent with each crystal plane index of BaF2 (Fig. 7e). As shown in Fig. 7f, the inter-planar distances between adjacent lattice fringes were determined to be 0.354 and 0.313 nm, indexed to the d-spacing values of the (111) and the (200) planes, respectively, in the fcc BaF2.
3.3 The formation mechanism of sub-micron spherical BaF2
Based on the above discussions and analyses, the formation mechanism of spherical BaF2 crystal in this study is proposed and depicted in Fig. 8. The nano barium fluoride size is the decisive factor for the formation of spherical barium fluoride. The experimental results show that the cube particles as the primary unit aggregate into a spherical shape when the particle size is less than 15 nm.The small-sized particles will self-assemble into a close-packed structure to reduce the surface energy, bringing the system to a thermodynamic equilibrium state. On the contrary, large-sized grains can exist independently and stably due to a low surface energy. The growth processes control the crystal size. Illustrated by the LaMer crystal growth model, the growth of nanocrystals in a solution is mainly divided into three parts: monomer formation, nucleation and growth process (Fig. 9).23,24 In the I stage, Ba2+ and F− combine to form BaF2 monomers. When the monomer concentration exceeds the nuclear threshold, the system enters the II stage; the formation of BaF2 nuclei causes the monomer concentration to decrease. The III stage begins after the monomer concentration drops below the nuclear threshold, when nucleation is no longer taking place in the system. The consumption of monomers is only used for the crystal growth. With the addition of EDTA, Ba2+ will complex with EDTA to form metastable EDTA–Ba, which decreases the concentration of free Ba2+ in the solution. The rate of− formation BaF2 monomers relies on the release rate of Ba2+ from the composite. When the complex stability constant of EDTA–Ba is large, the release rate of Ba2+ is slower. Consequently, when the BaF2 monomer concentration is maintained in the nucleation stage for a long time, it results in the size of the crystal being so small that the as-obtained spherical BaF2 is unapparent. On the other hand, the release rate of Ba2+ is high when the stability constant is small, leading to the concentration of the monomer exceeding the nuclear threshold quickly, and drops rapidly with the outbreak-nucleation. The crystal enters the growth stage and becomes too large to self-assemble into a spherical structure.
4 Conclusion
In summary, sub-micron spherical architectures of BaF2 particles, with an average size of 346.9 nm, were synthesized through a convenient and facile hydrothermal method. During the hydrothermal synthesis of BaF2, the pH value, the ratio of EDTA to Ba2+, raw material concentration, hydrothermal temperature and time play important roles in the morphology and size of BaF2 particles. The suitable synthesis conditions for sub-micron spherical BaF2 were determined to be pH = 14, EDTA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2+ = 1
Ba2+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the concentration of Ba(OH)2 is 0.1 mol L−1, the concentration of HF is 2.0 mol L−1, T = 80 °C, and t = 2 h. The formation process of the free-standing and uniform sub-micron spherical BaF2 was proposed based on the above results.
1, the concentration of Ba(OH)2 is 0.1 mol L−1, the concentration of HF is 2.0 mol L−1, T = 80 °C, and t = 2 h. The formation process of the free-standing and uniform sub-micron spherical BaF2 was proposed based on the above results.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Qinghai National Science Foundation of China [2021-ZJ-965Q].References
- C. Hu, L. Zhang, R. Y. Zhu, A. Chen, Z. Wang, L. Ying and Z. Yu, Nucl. Instrum. Methods Phys. Res., Sect. A, 2020, 950, 162767.1–162767.7 CrossRef.
- S. Kurosawa, T. Yanagida, Y. Yokota and A. Yoshikawa, IEEE Trans. Nucl. Sci., 2012, 59(5), 2173–2176 CAS.
- P. Kagerer, C. I. Fornari, S. Buchberger, S. L. Morelho and F. Reinert, J. Appl. Phys., 2020, 128(13), 135303.1–135303.8 CrossRef.
- N. Atanov, Y. Davydov, V. Glagolev, V. Tereshchenko and V. Jmerik, IEEE Trans. Nucl. Sci., 2020, 67, 1760–1764 CAS.
- X. Chen and Y. Wu, J. Alloys Compd., 2020, 817, 153075.1–153075.6 Search PubMed.
- J. Li, X. Chen, L. Tang, Y. Li and Y. Wu, J. Am. Ceram. Soc., 2019, 102(1), 178–184 CrossRef CAS.
- O. T. Antonyak, V. V. Vistovskyy, A. V. Zhyshkovych, I. M. Kravchuk and M. S. Karkulovska, Radiat. Eff. Defects Solids, 2020, 175(7–8), 754–764 Search PubMed.
- E. E. Brown, Z. D. Fleischman, J. Mckay and M. Dubinskii, Opt. Mater. Express, 2021, 11(2), 575–584 CrossRef.
- E. I. Madirov, V. A. Konyushkin, A. N. Nakladov, P. P. Fedorov, T. Bergfeldt, D. Busko, I. A. Howard, B. S. Richards and S. V. Kuznetsov, J. Mater. Chem., 2021, 9, 3493–3503 CAS.
- J. Tang, S. Tang, G. Zhao, P. Li and W. Dou, Appl. Surf. Sci., 2020, 529, 147000.1–147000.5 CrossRef.
- I. G. Neizvestny, D. V. Ishchenko, I. O. Akhundov, S. P. Suprun and O. E. Tereshchenko, Dokl. Phys., 2020, 65(1), 15–17 CrossRef CAS.
- N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408(6815), 946–949 CrossRef CAS PubMed.
- X. X. Guo, N. Sata and J. Maier, Electrochim. Acta, 2004, 49(7), 1091–1096 CrossRef CAS.
- N. Sata, N. Y. Jin-Phillipp, K. Eberl and J. Maier, Solid State Ionics, 2002, 154–155, 497–502 CrossRef CAS.
- G. De, W. Qin, J. Zhang, J. Zhang, W. Yan, C. Cao and Y. Cui, J. Solid State Chem., 2006, 179(3), 955–958 CrossRef CAS.
- S. Hou, Y. Xing, X. Liu, Y. Zou, B. Liu and X. Sun, CrystEngComm, 2010, 12(6), 1945–1948 RSC.
- M. Cao, C. Hu and E. Wang, J. Am. Chem. Soc., 2003, 125(37), 11196–11197 CrossRef CAS PubMed.
- R. Hua, C. Zang, C. Shao, D. Xie and C. Shi, Nanotechnology, 2003, 14(6), 588–591 CrossRef CAS.
- J. H. Yan, M. Zhang, H. Z. Lian, Z. R. Ye and C. S. Shi, Chem. J. Chin. Univ., 2005, 26(6), 1006–1009 CAS.
- R. N. Grass and W. J. Stark, Chem. Commun., 2015, 13, 1767–1769 Search PubMed.
- C. Zhang, Z. Hou, R. Chai, Z. Cheng, Z. Xu, C. Li, L. Huang and J. Lin, J. Phys. Chem. C, 2010, 114(15), 6928–6936 CrossRef CAS.
- R. S. Juang, Y. J. Chen and I. P. Huang, Sep. Sci. Technol., 1999, 34(15), 3099–3112 CrossRef CAS.
- V. K. Lamer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- C. B. Whitehead, S. Ozkar and R. G. Finke, Chem. Mater., 2019, 31(18), 7116–7132 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |










