Open Access Article
Open Access ArticleExploring the symbol processing ‘time interval’ parametric constraint in a Belousov–Zhabotinsky operated chemical Turing machine†
Thomas C. Draper a,
Marta Dueñas-Díez
a,
Marta Dueñas-Díez ab and
Juan Pérez-Mercader
ab and
Juan Pérez-Mercader *ac
*ac
aDepartment of Earth and Planetary Sciences and Origins of Life Initiative, Harvard University, Cambridge, Massachusetts 02138-1204, USA
bRepsol Technology Lab, c/Agustín de Betancourt, s/n., 28935, Móstoles, Madrid, Spain
cSanta Fe Institute, Santa Fe, New Mexico 87501, USA
First published on 13th July 2021
Abstract
Chemical reactions are powerful molecular recognition machines. This power has been recently harnessed to build actual instances of each class of experimentally realizable computing automata, using exclusively small-molecule chemistry (i.e. without requiring biomolecules). The most powerful of them, a programmable Turing machine, uses the Belousov–Zhabotinsky oscillatory chemistry, and accepts/rejects input sequences through a dual oscillatory and thermodynamic output signature. The time interval between the aliquots representing each letter of the input is the parameter that determines the time it takes to run the computation. Here, we investigate this critical performance parameter, and its effect not only on the computation speed, but also on the robustness of the accept/reject oscillatory and thermodynamic criteria. Our work demonstrates that the time interval is a non-trivial design parameter, whose choice should be made with great care. The guidelines we provide can be used in the optimization of the speed, robustness, and energy efficiency of chemical automata computations.
Introduction
A simple bimolecular chemical reaction can be viewed as a computation: two molecules come together, react, and form a new species; effectively providing a system which contains an input (the molecules), a processing step (the chemical reaction), and an output (the product).1 This molecular recognition event, scaled by Avogadro's number, is the ultimate deterministic computing system. Repeatedly, reliably, and consistently yielding the same result, for the same input and conditions.This is a phenomenon which has been extensively exploited by biology, developing its own bio-architecture and computing using molecules.2 Cells regularly use deterministic molecular recognition events, from identifying targets of the immune system, to permitting access across a membrane, to processing nucleic acid strands. Indeed, some authors posit that one can even consider life itself to be both the result, and continued processing, of computation.3,4 Biology has inspired some of the man-made approaches to computation. Biochemical computing systems have been developed using many biological constructs, including enzymes,5,6 fungal colonies,7 DNA,8,9 and vesicles.10 Despite the large precedence for bio-inspired molecular computation, comparatively little work has been published on non-biological pure-chemical molecular computation. It should be noted however, that there exists a sizeable body of work (both simulations and experimental) on chemical reaction-diffusion computing.11–16
Our group recently reported the development and experimental realization of native chemical automata, i.e. computing chemical machines that use exclusively chemical means for input representation, processing, and output generation, requiring only small (non-biological) molecules in well-mixed one-pot reactors, and thus requiring neither diffusion nor geometrical aids.1,17,18 Native automata, as standard abstract automata, are language recognizers organized in a hierarchy that depends on the complexity of the languages they recognize. The chemical Turing machine is the most advanced of the realizable native chemical automata, and was designed to recognize the Chomsky type 1 Context-Sensitive Language (CSL): L3 = anbncn, where n is a natural number indicating the count of each letter.19,20 (It should be noted that, being a Turing machine,20,21 the device has also been demonstrated to be reconfigurable to encompass inclusivity to Chomsky type-2 and type-3 languages).22 In such a computer, the processing step determines whether a tested ‘word’ is part of the language (accept) or not (reject), where a ‘word’ is comprised of an inputted string of permitted characters from a given finite alphabet. In the case presented in this study, where L3 = anbncn, example in-language (IL) words include abc and aabbcc, whilst the words aaabbcc, abcc, and ac would be considered out-of-language (OoL). Due to the limitations of the universe (i.e. non-infinite space, time, energy, etc.),21 our chemical Turing machine operates as a linear-bound automaton (LBA).
In an electronic computer, the inputted word would be passed to the processor as electronic symbols. The chemical Turing machine uses solely chemistry for input, processing, and output. The chosen word is input to the system, letter-by-letter, via the addition of representative aliquots. Each letter is represented by an aliquot of a specific chemical species, at a particular volume and concentration. These letters (or symbols) are added to the device systematically and sequentially, with a specific and constant time interval (τ) between each letter. A beginning and end-of-sequence symbol (#) is used as both an anacrusis and cadence, marking the beginning and ending of the inputted word. As the aliquots/symbols are added, the state of the system changes and the device can be deemed to be processing. The chemical state of the system, post-cadence, is the output: acceptance or rejection of the word is dependent on the various properties that comprise the state of the chemical system. Note, that by following the progress of the reaction/computation in real-time, some inputs can be rejected early on.1
This chemical Turing machine has been realized through implementation of the Belousov–Zhabotinsky (BZ) oscillatory reaction.23–25 This reaction has many different flavors, though they all revolve around the oxidation of an organic species via a bromate salt and in presence of a metal catalyst with at least two accessible oxidation states. During the reaction, the oxidation state of the metal catalyst alternates (between Ru(II) and Ru(III) in the present study) in a regular and predictable manner.26 This oscillation can be observed visually as the color changes between traffic-light orange and turquoise; use of a redox meter, however, provides a relatively accurate and convenient way to quantitatively follow the reaction. The chemical state that we measure for determining acceptance or rejection of an inputted word is the ruthenium oxidation state: the period of its oscillation between +2 and +3, and (indirectly) the molar ratio of Ru(III)/Ru(II) in each oxidation/reduction cycle. These are both obtained through measurement of the frequency and amplitude of the redox oscillations.
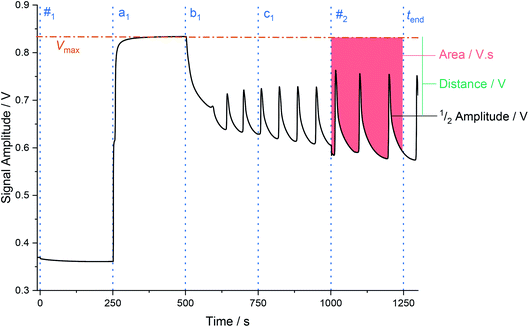
Shown in Fig. 1 is the redox trace from a BZ chemical Turing machine, processing the inputted word: abc. The blue dotted lines indicate the timepoints that the aliquots were added; using the notation mn to represent the nth addition of an aliquot of m, and tq to represent the timepoint t of event q (such as the addition of a1: ta1, or the end of the calculation: tend). The brown dot-dashed line marks Vmax, approximately the maximum value of V, calculated as the arithmetic mean of the recorded V between the timepoints (ta1 + τ − 60) and (ta1 + τ − 30). The green line marks the distance (in volts) between half of the oscillation's amplitude and Vmax. The unidimensional area metric (described below) is identified as the red shading at the end of the experimental run, above the signal trace and below Vmax, and between the timepoints (t#2 + 30) and tend. The first 30 s are excluded from the area processing, to allow for fast reaction transients to dissipate, and in particular to discard any transient shift caused by the actual phase of the oscillation at which the aliquot is added.
The area is the key accept/reject criterion used in the chemical Turing machine. It has many advantages, both practical and related to its thermodynamic significance, with respect to the other metric, the frequency–amplitude plane criterion.1 The area is equal to a constant times a functional, with the properties of the action in physics.1 That is, the final area reflects the history of the previous symbols that have been processed, and is equivalent to the value of an action. In physics this quantity is well-known to evolve in such a way that physically realizable states minimize it and describe a path in phase space. For a sequence of symbols processed by a chemical automaton, it is possible to assign such a path to the words processed and accepted by the chemical automaton.1 This can therefore be used as a criterion for acceptance/rejection of a sequence of symbols processed by a chemical automaton. Additionally, as explained in ref. 1, the area metric provides both a means of optimization of, and an interpretation for, the automaton's computation.1,22 Thus, through optimization of the chemical Turing machine, acceptance of a word can be demonstrated if the area calculated from the redox oscillations matches a certain, fixed value. This area can be further related to the Gibbs energy of oscillations via the Nernst equation.1,17,22 In this way, the chemical Turing machine accepts an inputted word if the ΔGosc = x, or rejects it if ΔGosc ≠ x; where x is the value previously obtained during system optimization, and (importantly) the same for all words in L3 = anbncn. This gives the area metric a dual thermodynamic-chemical interpretation. Furthermore, since the area can be written as a functional of the extent of reactions, the resulting native chemical computation can be understood in terms of extremal entropy production.27
It should be noted that whilst we programmed and optimized our chemical Turing machine using the ruthenium catalyzed BZ-reaction, alternative implementations of this method can be achieved with other three-reactant, non-linear, chemical oscillators – including DNA or other organic oscillators.1 Similarly, although our native chemical computations are carried out in semibatch well-mixed reactors,1,17,18,22 it is also possible to extend to continuous (CSTR) reactors with the potential advantages of automatic resetting, faster computations and longer computable sequences.27
The time interval τ is a critical design parameter in the chemical Turing machine for many reasons. Firstly, and most directly, it is pivotal in establishing the total time taken for computation, the runtime, tend. The longer the time interval, the longer the overall calculation takes, as defined by: tend = τ(3n + 2) for in-language L3 words, that are not rejected early. Secondly, τ directly relates to the area measurement (being integrated across dt), and consequently to ΔGosc. However, the complexity of the system means that this relationship is more nuanced than a direct proportional relationship, as changing the time interval has implications on both the overall reaction coordinates and the individual sub-reactions. These connections result in a non-trivial relationship between the value of τ and the area measurement. There is also an indirect effect on the distance and frequency measurements. Thirdly, each aliquot added to the chemical system transitions it to a different state, as the aliquot is processed. This processing is regulated by the rate-limiting step(s) in the reaction mechanism, e.g. in BZ one of the limiting steps is the reaction subset involved in the initially observed induction time prior to oscillations.1 Each aliquot must have sufficient time to appropriately affect the system – resulting in a minimal time interval that can be used. Note that the rate-limiting step depends on the chemistry and the reactor operating conditions (operation mode, temperature, initial reactor conditions, etc.).
Previous studies with the chemical Turing machine have always used a fixed value of τ: 450 s.1,17,22 This was chosen to ensure that the induction period of the BZ reaction would not impose unnecessary difficulties, that there would be a minimum of two oscillations between aliquot additions, and that the reaction would not reach completion before the computation had finished. The chemical parameters (concentration, volume, etc.) were then optimized around this chosen τ.
In this work, comparisons are made between the previously used value of 450 s and a reduced value of 250 s. The value of 250 s was chosen because it provides a reasonable reduction in the runtime of calculations, whilst still maintaining a minimum of three complete oscillations in the measurement zone (t#2 → t#2 + τ), and thereby ensuring that effects remain discernable. We elucidate the factors which must be contemplated when reducing τ – as is tempting, when wanting to minimize the computational runtime – and to distinguish what the overall effects are.
Experimental and methods
Tris(2,2′-bipyridyl) dichloro-ruthenium(II) hexahydrate was purchased from Sigma-Aldrich. Malonic acid and sodium bromate were purchased from Alfa-Aesar. Sulphuric acid was purchased from Fisher Scientific. Molecular-grade ultrapure water (>18 MΩ cm) and sodium hydroxide were purchased from VWR. With the exception of the ruthenium catalyst, all chemicals were reagent grade and used as received without further purification. The tris(2,2′-bipyridyl) dichloro-ruthenium(II) hexahydrate had a purity of 99.95%. Aqueous stock solutions were made according to the concentrations shown in Table 1. Solutions were made-up by inversion in a volumetric flask, whilst the sodium bromate was additionally sonicated until no further solid particulate was visible. All stock solutions were kept in amber glass bottles, and the ruthenium catalyst was additionally wrapped in aluminium foil.| Symbol | Reagent | Concentration/M | Volume/μL |
|---|---|---|---|
| # | Ru(bpy)3Cl2·6H2O | 12.5 × 10−3 | 400 |
| a | Sodium bromate | 2.00 | 1000 |
| b | Malonic acid | 3.50 | 250 |
| c | Sodium hydroxide | 5.0 | 250 |
Experiments were conducted in a semi-batch manner within a Pyrex-glass water-jacketed vessel, wrapped in aluminium foil. The vessel had an internal height of 55 mm, an internal diameter of 37 mm, and a capacity of 50 mL. The water-jacket was used to ensure thermal-continuity, and the aluminium foil prevented ambient light from affecting the reaction. A recirculating temperature-controlled water bath was used to maintain the water-jacket at a constant 20.3 °C. The reaction vessel was charged with a starting solution of aqueous sulphuric acid (19.6 mL, 0.765 M), to which the aliquots were systematically added at regular time intervals (τ). Magnetic stirring was employed, using a Teflon coated stirrer bar operating at 600 rpm.
In order to ensure timely additions of each aliquot, an automatic pipetting robot was implemented: the Opentrons OT-2. Stock solutions of each reagent were placed within the robot's reach, which was then programed to deliver an appropriate volume, of the appropriate reagent, at the appropriate timepoint. Aliquot sizes for each letter and symbol can be seen in Table 1, and a photograph of the experimental setup can be seen in Fig. 2. Automated pipetting can enable the execution of longer inputs, higher throughput of experiments, and potentially increase both the precision & accuracy of the aliquots and their timed addition.
Throughout the reaction, the redox potential of the solution was monitored and recorded using a mercury sulfate reference electrode (Koslow 5100 A) and a platinum working electrode, connected to a Vernier SensorDAQ ADC and logged using LabView (National Instruments).
Analysis of the recorded voltage was performed using MatLab 2020a (MathWorks). The timepoint of the first addition (#1) was noted, and the addition of further aliquots marked by knowing the time interval. The area of the end-state region (t#2 + 30 → t#2 + τ) was calculated through subtraction of the oscillating area from the total area, yielding the area above the oscillations, as shown in eqn (1). As previously introduced,1,17,22 this area has been shown to be proportional to the Gibbs free energy, via eqn (2), yielding eqn (3). The end period (and thereby frequency) was determined as the average time difference between oscillatory peaks in the same end-state region.
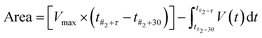 | (1) |
| ΔG = −neFV | (2) |
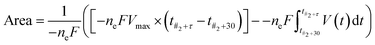 | (3) |
Simulations were performed to reproduce the experimental results using a variant of the Field–Köros–Noyes model1 of the BZ reaction in MatLab 2019a (MathWorks), using ODE solvers for stiff differential equations, and numerical integration for the area computations. Further specifics on the BZ model used can be found in the ESI.† Simulations were run on a laptop with an Intel® Core™ i7-7820HQ CPU @2.90 GH processor and Windows 64 Bit Operating System. Statistical analysis was conducted using SPSS Statistics v26 (IBM).
Results & discussion
Effects on the performance of the accept–reject criteria
The area metric is one of two accept–reject criteria that can be employed, the other being an evaluation of the distance and frequency measurements. The area metric is preferred due to its advantage of being unidimensional, as well as being easy to comprehend. Since the area metric is determined by integration across the time interval τ, changes in this parameter will impact on the metric. It is therefore important to determine that the area metric still performs when τ is reduced.Being an experimental set-up, some small variation can be expected run-to-run. This occurs regardless of the use of the automatic pipetting robot – which reduced the variance in the timing of the aliquot injection from ±2 s to less than a second.1 An example of such a slight variation can be seen in Fig. S1,† where one of the three traces is out-of-sync with the other two. This style of variation – a phase shift – can occur no matter the time interval between aliquots, and is caused by differences in the BZ induction period. These very slight natural variations between experimental runs are generally of little to no consequence chemically, however they can occasionally be detected in the final end-state of the chemical Turing machine.
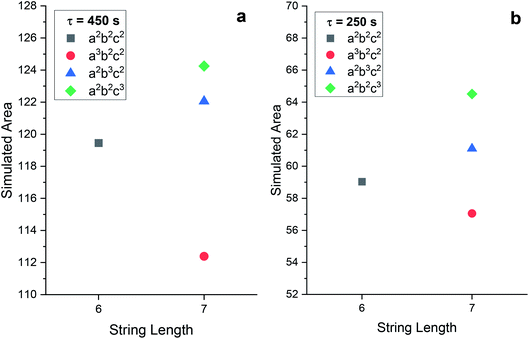
Slight variations, such as these, become visible as discrepancies when the area is measured. Fig. 3(a) shows area measurements for words conducted with a time interval (τ) of 450 s, whilst Fig. 3(b) results were recorded with τ = 250 s (the relevant experimental data is available in the ESI†). Each plot shows the area for the word a2b2c2, and each n + 1 OoL fault: a3b2c2, a2b3c2, and a2b2c3. The first point of interest is to note that the value of the area approximately halves when the time interval is reduced by 44.4%. This large decrease is logical, as the length of the abscissa being utilized is dramatically reduced. The difference is half when the word is IL, fluctuating slightly for OoL. Table 2 shows the values for each of the word and τ combinations shown in Fig. 3. When investigating the ratio of each area measurement for individual words, the same pattern as for the area measurements is noted in the ratio of the reduced time interval: IL is exactly halved, excess ‘a’ sits to one side, excess ‘b’ sits on the other, and excess ‘c’ sits in the middle. Fig. 3(c) shows the relative difference between the area measurements for each word at the different time intervals. The area is smaller than the simple 44.4% reduction marked in Fig. 3(c) as a dashed line. This is because the oscillations have a greater frequency in the measurement zone when τ = 450 s, compared to when τ = 250 s. Which, in turn, is because the extended time period permits more of the added malonic acid to be converted to the active species bromomalonic acid.
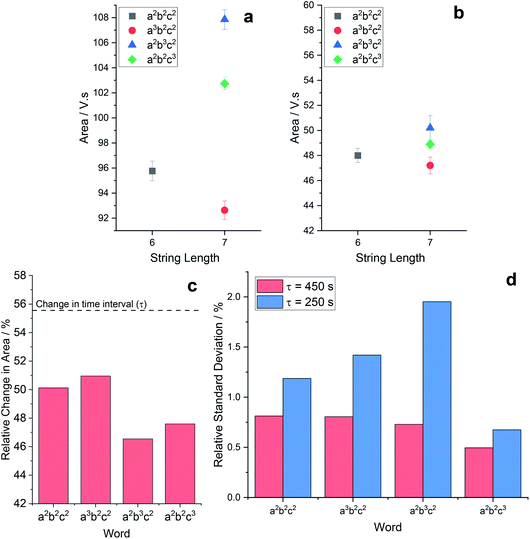 | ||
| Fig. 3 An area plot versus word length for experimental BZ chemical Turing machine reactions conducted with a time interval of (a) 450 s and (b) 250 s. The range of the y-axis is 18 in both. One can observe how the range of values is greatly reduced when the time interval is reduced. Error bars indicate the standard deviation. (c) The relative change in the area metric for each of the words indicated. The dashed line marks the 44.4% decrease in the time interval between τ = 450 s and τ = 250 s. (d) The relative standard deviation of the area for the indicated words, at both τ = 450 s and τ = 250 s. It is clear that in all circumstances, the larger the time interval (and thereby, the measurement zone), the smaller the standard deviation. All of the experimental voltage traces can be found in the ESI.† | ||
| Word | τ = 450 s area/V s | τ = 250 s area/V s | Ratio |
|---|---|---|---|
| a2b2c2 | 95.8 ± 0.78 | 48.0 ± 0.58 | 0.501 |
| a3b2c2 | 92.6 ± 0.75 | 47.2 ± 0.66 | 0.510 |
| a2b3c2 | 108 ± 0.8 | 50.1 ± 0.97 | 0.464 |
| a2b2c3 | 103 ± 0.5 | 48.9 ± 0.33 | 0.475 |
The word a3b2c2 is affected the least (i.e. has the smallest reduction in area) because the extra sodium bromate causes it to have the highest frequency (see Fig. S2(a)†) at all values of τ, and so the smallest relative change in frequency when reducing τ, resulting in the smallest reduction in the area (which is measured, as previously mentioned, above the oscillation profile).
The word a2b3c2 is most affected by this (i.e. has the greatest reduction in area) due to a greater decrease in the distance metric as the time interval is reduced from 450 s to 250 s. The distance decreases for all words as the time interval decreases, because the natural profile of the BZ reaction causes the baseline of the oscillations to gradually reduce with time as the malonic acid is consumed. Shorter time intervals result in the malonic acid being depleted less, which translates as a slower increase in the distance metric, with consequently a higher oscillation baseline. The extra malonic acid in a2b3c2 results in a greater relative decrease in distance (12%, versus 6% for a2b2c2) due to the absolute quantity of malonic acid being larger – effectively moving the oscillations up towards the Vmax value, and thereby further decreasing the area.
The reduction of word a2b2c3 is greater than the IL word a2b2c2, due to the increased pH resulting in slower and broader oscillations (see Fig. S3†), which reduces the area. It should also be noted that the pH affects many of the sub-reactions of the BZ reaction, having an overall effect on the area metric. The fact that the area of a3b2c2 is reduced the least and a2b3c2 the most, in combination with their respective positioning in Fig. 3, further promotes the reduced spacing between the different words as τ is reduced from 450 s to 250 s.
The direct effect of changing the time interval on the relative standard deviation can be seen in Fig. 3(d). Across all words tested, the larger the time interval the smaller the relative discrepancies. This trend is intuitive, and can be explained by considering that each data point (and thereby each oscillation) contains information, and the more information that is used in the calculation of the area, the more precise and reliable the result becomes.
A further point of interest, revealed in Table 2, offers insight into the primary source of the discrepancy between measurements. Whilst the area is halved when the time interval is approximately halved, the standard deviation remains roughly absolute. The area is calculated, as shown in eqn (1), through use of a time quantity and variations in the measured voltage. The range of voltages recorded for Fig. 3(a) and (b) are equivalent, it is only the time period that is different. This suggests that the primary contributor to the variance is the voltage. Of course, the factors that comprise the voltage contribution to the area measurement are non-trivial, and so the exact source of the deviations remains elusive (for example, it could be an indication of the limits of the redox meter).
The data was also analyzed as two separate metrics (as opposed to the unidimensional area metric): distance and frequency. Shown in Fig. S3,† both the τ = 450 s and the τ = 250 s data sets show the same pattern between the different words, as well as to the previously reported (different, but comparable) experiments.1 What is clearly evident is that the standard deviation of the distance measurements in the τ = 250 s data is significantly larger than for the τ = 450 s data. This further reinforces the suggestion that it is the voltage that is the primary source of variance. The inter-word range of distance measurements is also larger when τ = 450 s, as it is for the area measurements.
Statistical analysis of area measurement
In order to determine if the change in the area measurement of a2b2c2 was sufficiently affected by the addition of superfluous letters to deem the difference in their respective area measurements to be statistically significant (i.e. to confirm that the IL word can be differentiated from the OoL words), one-way analysis of variance (ANOVA) was performed on both sets of data (τ = 450 s and τ = 250 s). For each set of data the assumptions of normality were both tested and satisfied, yielding skew and kurtosis values below |2.0| and |9.0| respectively.28 Additionally, the assumptions of homogeneity were also tested and satisfied on both sets of data, based on Levene's F test: F(3,8) = 0.39 and p = 0.763 for τ = 450 s; and F(3,8) = 1.06 and p = 0.418 for τ = 250 s.The independent between-groups ANOVA for the τ = 450 s data set resulted in a statistically significant effect (F(3,8) = 184, p <0.001, η2 = 0.986), therefore the null hypothesis of all words being equal can be rejected, and 98.6% of the variance in area measurement can be attributed to the differences between words. To further investigate the difference between the words, the ANOVA was followed up with Tukey's HSD post hoc test. Importantly, the difference between each and every word was thereby found to be statistically significant, with p ≤0.01 in all cases.
The independent between-groups ANOVA for the τ = 250 s data set also resulted in a statistically significant effect (F(3,8) = 6.78, p = 0.014, η2 = 0.718), thereby also rejecting the same null hypothesis, and attributing 71.8% of the area variance to the difference between words. As before, the statistically significant ANOVA was followed up by Tukey's HSD post hoc test, which did not find all words to be statistically different. For the τ = 250 s data set, the difference in area measurement for the words a3b2c2 and a2b3c2 was statistically significant, with p = 0.011. For all other combinations of words, the difference in area measurement was found to be not statistically significant, with p >0.05.
The fact that the data set with τ = 450 s has full statistical significance, whilst the τ = 250 s data set does not, further reinforces the importance of the time interval. The data set with the greater time interval is of sufficient duration to enable the inherent natural variations to be within manageable tolerances. The full statistical results can be found in the ESI.†
Computational studies
Computational studies were also conducted using a modified version of the FKN model1,26 in MatLab, comparing the effect of reducing the time interval from 450 s to 250 s. Our (previously reported, further details in ESI†) modification to the FKN model includes both the further bromination of bromomalonic acid (inspired by the Gao-Försterling model29) and the acid-base neutralization of sodium hydroxide (letter ‘c’).1 The outcome of the simulations for τ = 450 s and τ = 250 s can be seen in Fig. 4(a) and (b), respectively. As observed in the experimental work, the simulations predict that the area is reduced as the time interval is reduced. The close grouping of the area values, caused by the reduced spacing between the IL and OoL words when τ = 250 s, is also portrayed accurately in the simulations.Improving the robustness of small τ data sets
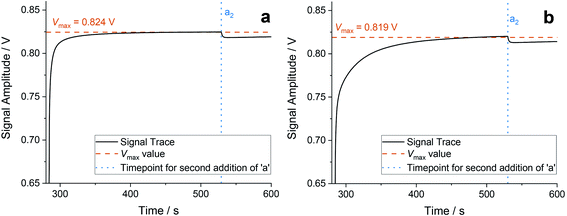
It should be noted that not all of the consequences from reducing τ are insuperable. However, there are most certainly restrictions as to how small τ can be. One such limitation is due to the dual analog-digital nature of a non-unimolecular chemical system: once an aliquot has been added, its complete effect is not instantaneous but requires a finite amount of time to be processed and fully affect the system. This phenomenon is best observed on the addition of a1, the first aliquot of sodium bromate to be added after the initial starting symbol #1. Once the sodium bromate has been added it reacts with the ruthenium catalyst, increasing its oxidation state from Ru(II) to Ru(III). This is observed through a sharp rise in the redox potential, as shown in Fig. 5. What can also be noted in Fig. 5 is that this oxidation rate varies. In some cases a value of τ = 250 s provides sufficient time for the (sub)reaction to reach completion (Fig. 5(a)), whilst in other cases oxidation is only partially within the time window (Fig. 5(b)). When the oxidation is not fully complete, the value we record for Vmax is smaller than the case of full oxidation (as defined as when the redox measurements have plateaued).This obviously has implications for the chemistry, but also for the calculation of the area measurement. As in eqn (1), the area measurement is reliant on the value of Vmax, and fluctuations in this value are a source of discrepancies between repeated experiments (as suggested above, the voltage measurements are likely the primary source of variance). One reason for the relatively smaller standard deviation when τ = 450 s (Fig. 3(d)) is that the ruthenium oxidation reaction always has sufficient time to reach completion, providing a reliable and repeatable value for Vmax.
The ideals behind the chemical Turing machine require that all information necessary for full computation, processing, and analysis is intrinsic to the chemical state of the reaction and, consequently, the redox potential that we record. Ergo, Vmax must also be an innate property of the system, and therefore cannot be replaced with a static third-party value.
We have developed a technique to obtain the true plateau value from experiments with short time intervals. By extracting the relevant section of the experimental data – from ta1 to (ta1 + τ) – and applying a curve fitting algorithm (non-linear least squares using a Trust-Region algorithm, invoked in MatLab using the fit command) to the form shown in eqn (4), where Vplat is the predicted plateau value, x0 provides an x offset equal to ta1, and b & c describe the shape of the function. This is illustrated in Fig. 6.
| f(x) = Vplat(1 − e−b(x − x0)c) | (4) |
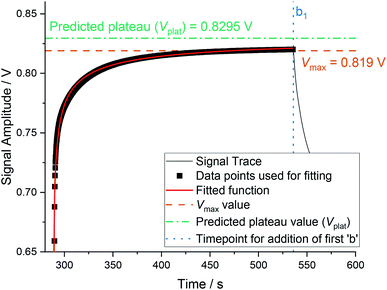 | ||
| Fig. 6 Fitting of the ruthenium oxidation curve using eqn (4), where Vplat = 0.8295, b = 1.771, c = 0.1732, x0 = 288.7. The R2 is 0.985 and the reduced χ2 is 5.97 × 10−6. The orange dot-dash line shows where the maximum value of V was reached, the green dot-dashed line shows the predicted plateau value, black squares show experimental data points (every 0.2 s), and the red solid line shows the fitting. | ||
Values for Vplat typically fall between 0.81 V and 0.84 V, for b between 1.6 and 2.3, and for c between 0.15 and 0.35. Using the example 6 and 7 letter words shown in Fig. 3 and Table 2, we have recalculated the area using the parameter Vplat, which can be seen in Table 3. There are a couple of observations to note, the first being that the standard deviations of the area have effectively either reduced or remained the same. This is expected, as the variance in the Vmax value has been reduced. The other observation is that the ranking of each word has remained the same, bar one exception: a2b2c3, which now has the largest area value. This shift is out of line with the optimized recipe and ranking previously reported.1 However, it is in line with the simulations shown in Fig. 4. It is likely that the reduced time interval (from τ = 450 s to τ = 250 s) is actually having an increased effect, which was obfuscated when Vmax is taken as the maximum value of V. The chemical difference between word a2b2c3 and the IL equivalent is an extra aliquot of sodium hydroxide. As the solvent for the BZ-reaction is aqueous sulphuric acid, addition of this extra aliquot would have a thermal component (as well as a chemical component). Whilst we perform our reactions under isothermal conditions, using a water jacket to remove and add heat, this temperature compensation takes a finite amount of time. The enthalpy of neutralization of the additional 1.25 mmol of added sodium hydroxide would release 70.6 J of heat,30 resulting in a temperature change (if adiabatic) of approximately 0.75 °C. By reducing the time interval, the system's ability to account for these changes is reduced, resulting in a larger effect from the exothermic acid–base reaction.
| Word | Using Vmax = max(V) area/V s | Using Vmax = Vplat area/V s |
|---|---|---|
| a2b2c2 | 48.0 ± 0.57 | 49.5 ± 0.57 |
| a3b2c2 | 47.2 ± 0.67 | 47.4 ± 0.45 |
| a2b3c2 | 50.2 ± 0.98 | 51.3 ± 0.51 |
| a2b2c3 | 48.9 ± 0.33 | 52.9 ± 0.37 |
Other factors
A further complication with reducing the value of τ relates to the positioning of the oscillations along the abscissa. As one may intuitively expect, the area is also partially dependent on whether the boundary of the measurement zone intersects an oscillation, or not. When the time interval is large, the effect of such an intersection is reduced by the averaging effect of a large number of oscillations. Conversely, when the time interval is small, the effect becomes amplified due to the reduced number of oscillations present in the measurement zone.It is worth noting that one cannot simply overcome the restrictions of a small τ value by arbitrarily increasing it: there are consequences for increasing τ too. The most immediately obvious is that as τ gets larger, the computation time increases proportionally, as previously mentioned. A more subtle reason is that the semi-batch BZ reaction only oscillates for a finite amount of time. If tend occurs after the oscillations have finished, the calculation will fail. We mention in passing that the finite amount of time available to perform calculations (which inherently restricts the ultimate word length) can be considered akin to the restrictions befalling the linear-bound nature of all real-life Turing machines.
The importance of τ
Throughout, it is clear that the time interval is a critically important parameter. The chemical response of the system is directly affected by it, limiting the amount of time available for sub-reactions to proceed, such as the oxidation of ruthenium after the addition of a1 or the induction period after the addition of b1. These limits also affect the total length of the chemical oscillatory regime, restricting the length of the words that can be processed. From a statistical viewpoint, it has been demonstrated that the relative variance and relative standard deviation of experimental results for the area decreases with an increase in the time period. Consequently, the area's standard error of the mean (the distance from the ‘true’ value) is also reduced as the time interval is increased. Crucially, the difference in area measurements remains statistically significant only with longer time intervals. This reduced uncertainty when τ is larger, combined with the increase in spacing between IL and OoL words, results in a more robust system that yields a better-defined criterion for the accept–reject area metric.It can be seen that the value of the time interval should be carefully considered when devising such a chemical Turing machine described herein. Whilst there is a temptation to reduce the time interval in order to decrease the computation runtime, there are several negative consequences to such an action. These consequences include risk of the induction period interfering with the addition of the initial early symbols, aliquots having insufficient time to appropriately affect the system, a poorly derived Vmax value (though this can be partly compensated for with the curve-fitting reported here), increased relative errors of the area metric, and closer grouping of IL and OoL words – all of which result in a less robust system. Conversely, the calculation runtime increases proportionally with the time interval: tend = τ(3n + 2), and so an arbitrarily increased time interval can result in an unnecessarily long runtime. This particularly becomes a problem when the calculation runtime is longer than the chemical oscillatory regime. One must consider all of these factors before selecting a value for τ.
It should be noted that, being a thermodynamics-based metric, the area quantity is also dependent on the temperature of the system, and its isothermal or adiabatic nature. This dependence stems from the chemistry of the highly complex multi-reaction BZ reaction with its many varied rate constants,26 the dependence of Gibbs free energy on temperature,31 as well as the relationship between entropy (a temperature-dependent quantity in a dynamic non-equilibrium system, such as the BZ reaction) and information.32–34 In this work, we maintained a constant isothermal system, though further investigations should consider this property.
Overall, the time interval is a key parameter of the chemical Turing machine, and must be selected with great care to balance computational, chemical, chemical engineering, statistical, and reproducibility criteria.
Conclusions
Through this work we can conclude that the time interval, τ, is a vital parameter of the chemical Turing machine. It needs to be large enough to allow for the appropriate chemical transformations from each aliquot added to sufficiently occur. However, it should not (and, indeed, cannot) be needless large that oscillations are permitted to end before the calculation. The area metric is directly dependent upon the time interval, and so it cannot be haphazardly changed: the chemical recipe and the accept–reject criterion requires optimization for each value of τ employed.Whilst there are other global factors that affect the area metric, such as temperature, the significance of the time interval should not be underestimated. We suggest that, in order to ensure maximum robustness in the system, the time interval is chosen to be as long as practically possible whilst ensuring that the chemical reaction stays within the oscillatory regime. Additionally, if the chosen time interval yields a poor value of Vmax, curve fitting should be employed (as discussed here) to obtain a truer value, Vplat. Ultimately, the value of τ cannot be arbitrarily varied, and care should be taken in choosing its value.
Conflicts of interest
Marta Dueñas-Díez and Juan Pérez-Mercader have a patent related to the work presented here.18 There are no other conflicts to declare.Acknowledgements
We thank Repsol S. A. and Harvard University Origin of Life Initiative for their support. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.References
- M. Dueñas-Díez and J. Pérez-Mercader, iScience, 2019, 19, 514–526 CrossRef.
- M. Mitchell, Ubiquity, 2011, 1–7 Search PubMed.
- G. Dodig-Crnkovic, in Language, Life, Limits, ed. A. Beckmann and E. Csuhaj-Varjú and K. Meer, LNCS, Springer, 2014, pp. 153–162 Search PubMed.
- E. Fredkin, Phys. D, 1990, 45, 254–270 CrossRef.
- I. Willner, B. Shlyahovsky, M. Zayats and B. Willner, Chem. Soc. Rev., 2008, 37, 1153 RSC.
- K.-P. Zauner and M. Conrad, Biotechnol. Prog., 2001, 17, 553–559 CrossRef CAS PubMed.
- A. Adamatzky, M. Tegelaar, H. A. B. Wosten, A. L. Powell, A. E. Beasley and R. Mayne, Biosystems, 2020, 193–194, 104138 CrossRef.
- H. Lederman, J. Macdonald, D. Stefanovic and M. N. Stojanovic, Biochemistry, 2006, 45, 1194–1199 CrossRef CAS PubMed.
- A. Okamoto, K. Tanaka and I. Saito, J. Am. Chem. Soc., 2004, 126, 9458–9463 CrossRef CAS.
- R. Mayne and A. Adamatzky, PLoS One, 2015, 10, e0139617 CrossRef.
- O. Steinbock, A. Toth and K. Showalter, Science, 1995, 267, 868–871 CrossRef CAS.
- Á. Tóth and K. Showalter, J. Chem. Phys., 1995, 103, 2058–2066 CrossRef.
- A. Hjelmfelt and J. Ross, Phys. D, 1995, 84, 180–193 CrossRef CAS.
- A. Hjelmfelt and J. Ross, J. Phys. Chem., 1993, 97, 7988–7992 CrossRef CAS.
- A. Adamatzky, B. P. J. de Lacy Costello and T. Asai, Reaction-Diffusion Computers, Elsevier, Amsterdam, 2005 Search PubMed.
- J. Gorecki, K. Yoshikawa and Y. Igarashi, J. Phys. Chem. A, 2003, 107, 1664–1669 CrossRef CAS.
- M. Dueñas-Díez and J. Pérez-Mercader, in The Energetics of Computing in Life and Machines, ed. D. H. Wolpert, C. Kempes, P. F. Stadler and J. A. Grochow, SFI Press, Santa Fe, NM, USA, 2019, pp. 105–125 Search PubMed.
- J. Pérez-Mercader, M. Dueñas-Díez and D. Case, Chemically-operated turing machine, US Pat., 9582771, 2017 Search PubMed.
- N. Chomsky, IEEE Trans. Inf. Theory, 1956, 2, 113–124 CrossRef.
- J. G. Brookshear, Theory of Computation: Formal Languages, Automata, and Complexity, Benjamin-Cummings, Redwood City, CA, 1989 Search PubMed.
- M. L. Minsky, Computation: Finite and Infinite Machine, Prentice-Hall, Englewood Cliffs, N.J., 1967 Search PubMed.
- M. Dueñas-Díez and J. Pérez-Mercader, Sci. Rep., 2020, 10, 6814 CrossRef PubMed.
- B. Belousov, Collect. Reports Radioact. Med., 1959, 147, 145 Search PubMed.
- A. T. Winfree, J. Chem. Educ., 1984, 61, 661–663 CrossRef.
- A. M. Zhabotinsky, Biofizika, 1964, 9, 306–311 Search PubMed.
- R. J. Field, E. Körös and R. M. Noyes, J. Am. Chem. Soc., 1972, 94, 8649–8664 CrossRef CAS.
- M. Dueñas-Díez and J. Pérez-Mercader, Front. Chem., 2021, 9, 611120 CrossRef PubMed.
- E. Schmider, M. Ziegler, E. Danay, L. Beyer and M. Bühner, Methodology, 2010, 6, 147–151 CrossRef.
- Y. Gao and H.-D. Foersterling, J. Phys. Chem., 1995, 99, 8638–8644 CrossRef CAS.
- H. M. Papee, W. J. Canady and K. J. Laidler, Can. J. Chem., 1956, 34, 1677–1682 CrossRef CAS.
- P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, UK, 9th edn, 2010 Search PubMed.
- R. P. Feynman, Feynman Lectures on Computation, Westview Press, Boulder, CO, USA, 1996 Search PubMed.
- C. H. Bennett, Int. J. Theor. Phys., 1982, 21, 905–940 CrossRef CAS.
- D. H. Wolpert, J. Phys. A: Math. Theor., 2019, 52, 193001 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03856g |
| This journal is © The Royal Society of Chemistry 2021 |