Chemical structure stabilities of a Si_xF_y (x ≤ 6, y ≤ 12) series

Abstract

In this paper, we construct a Si_xF_y (x ≤ 6, y ≤ 12) series optimised at the B3LYP/6-31G(d,p) level. At the same level, we perform frontline molecular orbital (FMO), Mayer bond order (MBO), molecular surface electrostatic potential (MS-EPS) and natural population analysis (NPA) calculations to study the chemical structure stabilities of these Si_xF_y molecules. The FMO and MBO results demonstrate that the chemical structure stabilities of the Si_xF_y (x ≤ 6, y ≤ 12) series are ranked (from strong to weak) as SiF₄ > Si₂F₆ > Si₃F₈ > Si₄F₁₀ > SiF₂ > Si₅F₁₂ > Si₃F₆ (ring) > Si₅F₁₀ (ring) > Si₆F₁₂ (ring) > Si₄F₈ (ring). Furthermore, the chemical structure stabilities of the chains are stronger than those of the rings, while the number of silicon atoms is the same. In addition, infrared spectroscopy analysis shows that SiF₄ is the most stable among the Si_xF_y (x ≤ 6, y ≤ 12) series, followed by Si₂F₆, and SiF₂ is unstable. The experimental results are consistent with theoretical calculations. Finally, the MS-EPS and NPA results indicate that compounds in the Si_xF_y (x ≤ 6, y ≤ 12) series tend to be attacked by nucleophiles rather than by electrophiles; also, they show poor chemical structure stability when encountering nucleophiles.

---

1. Introduction

Silicon is the main support material in the semiconductor, communications and photovoltaic industries. The main requirements for silicon are purity and configuration. In industry, the high-temperature smelting method and Siemens or modified Siemens method are used to meet these requirements. In the reported methods, the core aim is to form a flowing stream that is suitable for industrial operations. Additionally, halogen and silicon are naturally present in phosphate rock (silicon and fluorine in halogen are associated with each other in phosphate rock). In the industrial processing of phosphate rock, silicon and fluorine are naturally combined to form a gas compound, e.g. silicon tetrafluoride (SiF₄), with flow characteristics at room temperature.

To separate and purify this flowing compound directly and even effectively prepare various configurations of silicon materials (endowed with functional properties) in industrialization, it is necessary to explore the transformation between Si_xF_y (x ≤ 6, y ≤ 12) series substances. In comparison with other halogen silicon compounds, silicon fluorides (Si_xF_y) are relatively less known except for SiF₄, obviously due to the lack of understanding of the synthesis and stability of silicon fluorides. Furthermore, the chemical structure stabilities of Si_xF_y (x ≤ 6, y ≤ 12) are a highly interesting topic for the scientific and industrial community.

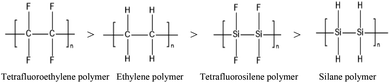
Here, we start with a common example: by calculating at the CBS-QB3 level, the corresponding C–F, C–H, Si–F and Si–H bond energies of C₂F₄, C₂H₄, Si₂F₄, and Si₂H₄ are 531, 456, 446 and 338 kJ mol⁻¹, respectively. The stabilities of the corresponding chain polymers are as follows:

Accordingly, among the compounds mentioned above, the silane polymer is the most unstable and difficult to operate in industry; meanwhile, the study of tetrafluoroethylene polymer and ethylene polymer is relatively mature, and a large number of studies have been reported. However, the structure stabilities of tetrafluorosilane polymer are in the middle, allowing the possibility of industrial operation, and it has potential application value. Therefore, increasing interest is being focused on tetrafluorosilane.

There have been some studies conducted on the macro-chemical synthesis methods of the Si_xF_y (x ≤ 6, y ≤ 12) series, distinguishing the following stable compounds: (1) SiF₄. Since Davy synthesized silicon tetrafluoride in 1812, it has become a common compound. The main synthesis methods are as follows: firstly, direct reaction preparation of high-purity silicon (or SiCl₄) and F₂; secondly, preparation with metal fluorosilicates (including Na₂SiF₆ and BaSiF₆) by pyrolysis; thirdly, co-thermal preparation with fluorosilicic acid and concentrated sulfuric acid; fourthly, reaction of fluorite and concentrated sulfuric acid or HF with solid Si at a temperature above 250 °C; finally, the reaction of CaSiF₆ and concentrated sulfuric acid under heating. (2) Disilicon hexafluoride (Si₂F₆). In 1932, Schumb et al.¹ used Si₂Cl₆ to react with anhydrous ZnF to prepare Si₂F₆; in 1994, Tosa et al.² reacted Si and Fe mixed at a ratio of 3 : 2 with Cl₂ using KCl as a catalyst to obtain Si₂Cl₆; then, the prepared Si₂Cl₆ and SbF₃ were reacted under the catalyst SbCl₅ to obtain Si₂F₆ (98%) by heating. (3) Trisilicon octafluoride (Si₃F₈). In 1967, Johannesen et al.³ studied the nuclear magnetic resonance of Si₃F₈. In 1976, Höfler et al.⁴ treated Si₃(OCH₃)₈ with BF₃ in a sealed tube to synthesize Si₃F₈ with a yield of 55%–60%, and the Raman spectrum of Si₃F₈ was obtained. Due to the poor chemical stability of Si_xF_y with long silicon chains, only a few compounds with longer chains than Si₃F₈ have been reported.

Moreover, among the unstable compounds, the preparations of SiF_n (n = 0–3) are as follows: in 1958, Pease et al.⁵ used SiF₄ to react with Si for the first time at high temperature, and a (SiF₂)_x polymer was obtained by cold polymerisation of the generated SiF₂ gas. Subsequently, Timms et al.⁶ and Bassler et al.⁷ used Ar as the carrier gas and cold-polymerised SiF₂ at 20–42 K; thus, the (SiF₂)_x polymer was also obtained. In 2008, Cruz et al.⁸ successfully synthesised Si₃N₄ using a conventional chemical vapor deposition (CVD) mixed precursor system [Na₂SiF₆(s)–N₂(g)]. Because SiF₄ and N₂ are very stable under heating and will not react directly, it is believed that the process is based on thermal dissociation to form SiF_n (n = 0–3). In 1965, Timms et al.⁹ detected SiF⁺, SiF₂⁺, SiF₃⁺, SiF₄⁺, Si₂F₄⁺, Si₂F₅⁺, Si₅F₆⁺ and Si₂F₆⁺ by performing mass spectrometry of Si₂F₆.

Moreover, Mai et al.¹⁰ used plasma-enhanced CVD and a mixed gas source (SiF₄–SiH₄–H₂) to prepare polysilicon membranes with preferred orientations at low temperature (≤400 °C); Kim et al.¹¹ used inductively coupled plasma-enhanced CVD to study F, Si, H, and Ar systems; Fisher et al.¹² successfully captured SiF_x radicals using spatially resolved laser-induced fluorescence imaging technology and generated radio frequency power and SiF₂ radicals; Takayuki et al.¹³ used SiF₄ as the raw material gas and used ultraviolet absorption spectroscopy, light-induced fluorescence and infrared laser absorption spectroscopy at 60 MHz to measure the density changes of SiF₄, SiF₂, SiF and Si.

In addition to experimental studies, there have been some theoretical calculations involving SiF_n compounds. For instance, Colvin et al.¹⁴ studied the ground state and excited state structures of SiF₂ radicals; Knizikevičius¹⁵ studied the desorption activation energy of SiF₂ radical molecules; Helluy et al.¹⁶ studied the nuclear magnetic resonance spectra of Si and F atoms in fluorosilicon compounds; Hrusak et al.¹⁷ calculated the heat of formation of SiF₂²⁺; Jiang et al.¹⁸ used density functional theory (DFT) to analyse the molecular structures and energy changes of SiX₂ (X = H, F); Zhao et al.¹⁹ used DFT to study the SiF₂ potential energy curve; Jiang²⁰ used DFT to study the structure and thermodynamic properties of the ground state of SiF₂; and Han²¹ used ab initio calculations to optimise the structure of the ground state of SiF₂. However, the studies mentioned above were mainly focused on individual compounds. As far as we know, there is no systematic study about the theoretical calculations of a Si_xF_y (x ≤ 6, y ≤ 12) series.

In this paper, systematic comparative studies on a Si_xF_y (x ≤ 6, y ≤ 12) series were performed, including stable compounds and even semi-stable intermediate substances with a short lifetime. First, we constructed the optimized models of the Si_xF_y (x ≤ 6, y ≤ 12) series at the B3LYP/6-31G(d,p) level, including stable substances such as SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂, intermediate substances such as SiF, SiF₂ and SiF₃, and cyclic substances such as i₃F₆, Si₄F₈, Si₅F₁₀, and Si₆F₁₂. Then, further frequency, frontline molecular orbital (FMO), Mayer bond order (MBO), molecular surface electrostatic potential (MS-EPS) and natural population analysis (NPA) calculations were conducted. Furthermore, the theoretical results were compared with the experimental infrared spectra of the synthesised compounds for verification.

2. Theoretical and experimental methods

2.1. Computational methods

Solid Si and SiF_n (n = 1–4) readily form Si_xF_y series or SiF₂ polymers under low-temperature conditions, as mentioned in the introduction; considering the bond length and strength of the Si–Si bond and Si–F bond, the formed Si_xF_y series are difficult to rearrange. This paper mainly studies a Si_xF_y(x ≤ 6, y ≤ 12) series, a total of 12 molecules, including chain structures, SiF, SiF₂, SiF₃, SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂, and cyclic structures, Si₃F₆, Si₄F₈, Si₅F₁₀ and Si₆F₁₂. DFT is effective in predicting the structural stability of materials.^22–25 Therefore, the calculation method in this paper mainly uses the B3LYP functional, which is located in the fourth order of Jacob's ladder.²⁶ It is the first functional that was widely used in chemical theoretical calculations. It is used in pure DFT exchange-related energy that includes part of the HF exchange energy for hybridization. According to the three-parameter hybrid method proposed by Becke²⁷ (eqn (1)),

E = A × E^Slater_x + (1 − A)E^HF_x + B × E^Becke_x + C × E^LYP_c + (1 − C)E^VWN_c (1)

where A = 0.8, B = 0.72, C = 0.81, and the three parameters are obtained by fitting the G2 test group. Using the B3LYP functional with the 6-31G(d,p) basis set to optimise their structures and calculated their vibration frequencies, we further analysed these vibrations and assessed their structural stabilities through energy values. The wave function files of the most stable structure were chosen for calculation, and related analyses were then performed. Among these, FMO and MS-EPS were calculated using Multiwfn,²⁸ and the relevant results were obtained using the visual molecular dynamics (VMD) programme correlation overlap display. Moreover, atoms in molecules (AIM), MFDD and Mayer bond order analyses were directly calculated with Multiwfn. In addition, NPA analysis was obtained by NBO analysis. All calculations except those specifically specified were performed using the Gaussian 09²⁹ software package.

2.2. Experimental methods

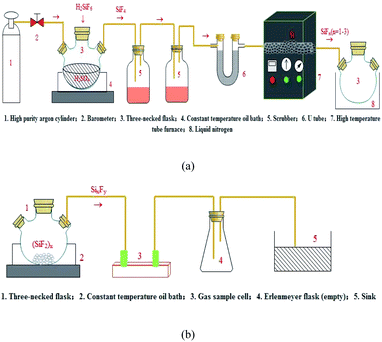
The preparation of the Si_xF_y (x ≤ 6, y ≤ 12) series was performed in two steps with silicon tetrafluoride gas and high-purity silicon as starting materials. Before the experiment, the first step was to dry the activated carbon to remove impurities such as water vapour in the activated carbon, and the experimental device was assembled according to Fig. 1(a). Then, we slowly added fluorosilicic acid to a three-necked flask containing 300 ml concentrated sulfuric acid. The resulting SiF₄ gas passed through two scrubbers containing 98% concentrated sulfuric acid and a U-shaped tube containing activated carbon. Finally, SiF₄ gas (purified by activated carbon) was introduced into the ceramic tube of the high-temperature tube furnace through the pipeline. The temperature of the high-temperature tube furnace was 1250 °C, and SiF_n (n = 1–3) gas was produced; at this time, the SiF_n (n = 1–3) gas obtained in the preparation was frozen with liquid nitrogen. The second step was obtaining SiF_n (n = 1–3) gas at 1250 °C after it was frozen in liquid nitrogen for a certain period. The polymerisation reaction generated a solid SiF₂ polymer (SiF₂)_x, which was heated to 200 °C to obtain Si_xF_y. The experimental device is shown in Fig. 1(b). In the process, the flow of silicon tetrafluoride gas and argon gas was controlled at 0.1 L min⁻¹, high-purity silicon was in excess, the outlet pressure of the pressure-reducing valve was 0.2 MP, and the reaction was controlled for 60 min. During this process, air should be strictly prevented from entering. Finally, SiF₄ gas, SiF_n (n = 1–3) gas, and Si_xF_y gas were collected using gas sampling bags, and the valve was closed to isolate the air. Under normal temperature and pressure conditions, after no storage, 1 hour storage, and 1 day storage, infrared spectrum detection was performed. The reaction device process is shown in Fig. 1.

Fig. 1 Process flows of preparing (a) silicon tetrafluoride gas and (b) Si_xF_y (x ≤ 6, y ≤ 12).

3. Results and discussion

3.1. Analysis of the equilibrium configuration

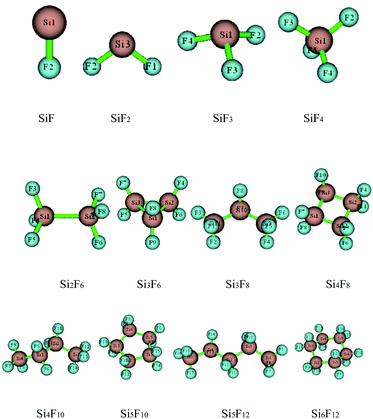
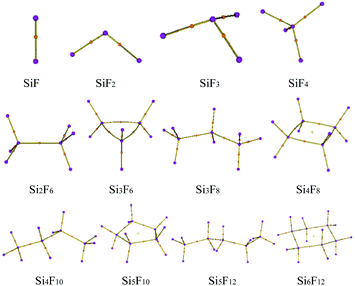
The preliminary molecular structures of the Si_xF_y (x ≤ 6, y ≤ 12) series were constructed through Gaussian view. A total of 12 molecules existed, including chain substances, SiF, SiF₂, SiF₃, SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂, and ring substances, Si₃F₆, Si₄F₈, Si₅F₁₀ and Si₆F₁₂. All of the structures were optimised at the B3LYP/6-31G(d,p) level and are shown in Fig. 2. The optimised bond lengths and bond angles are shown in Table S1 of the ESI.†

Fig. 2 The optimised configurations of Si_xF_y (x ≤ 6, y ≤ 12).

The optimized Si–F bond length and bond angle of SiF₂ are 1.616 Å and 100.9°, respectively. These results are in good agreement with the theoretical values of 1.601 Å and 100.7° from Zhao et al.³⁰ calculated at the B3P86/6-311++G(3df, 3pd) level and experimental values³¹ of 1.591 Å and 100.9°. Also, the structural comparisons of SiF₂ are shown in Table 1, indicating that the choices of the calculation method and basis set are reasonable. Therefore, the structure models of the Si_xF_y (x ≤ 6, y ≤ 12) series optimised by Gaussian 09 at the B3LYP/6-31G(d,p) level are very accurate and reliable.

Table 1 Comparisons of the molecular structures of SiF₂

Methods	E/a.u.	RSi–F (Å)	αF–Si–F (°)	Data literature
B3LYP/6-31G(d,p)	−489.25858	1.616	100.9	This text
B3P86/6-311++G(3df,3pd)	−489.93215	1.601	100.7	30
Experiment	—	1.591	100.9	31

---

From Table S1 of the ESI,† it can be seen that the Si–F bond lengths of SiF, SiF₂, SiF₃ and SiF₄ are 1.626 Å, 1.616 Å, 1.600 Å and 1.579 Å, respectively. Moreover, the F–Si–F bond angles of SiF₂, SiF₃ and SiF₄ are 100.9°, 108.0°, and 109.5°, respectively. Therefore, the Si–F bond lengths of SiF_n (n = 1–4) become shorter as the F atom numbers increase, as do the bond angles. The Si–Si bond length of Si₂F₆ is 2.317 Å, the Si–F bond lengths are 1.593 Å, the F–Si–F bond angles are both 108.4°, and the Si–Si–F bond angles are both 110.6°. The Si–Si bond lengths of the cyclic Si₃F₆ are 2.390 Å, the Si–F bond lengths are 1.609 Å, the F–Si–F bond angles are 107.6°, the Si–Si–F bond angles are 120.8°, the Si–Si bond angles are 60.0°, and other structural parameters are shown in Table S1 of the ESI.† From the bond length and bond angle parameters of the Si_xF_y (x ≤ 6, y ≤ 12) series, it can be concluded that the Si–F bonds of SiF₄ are the shortest among the Si_xF_y (x ≤ 6, y ≤ 12) series, indicating that SiF₄ is the most stable. At the B3LYP/6-31G(d, p) level, we obtained stable structures of the 8 chain substances (SiF, SiF₂, SiF₃, SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂) and the 4 cyclic substances (Si₃F₆, Si₄F₈, Si₅F₁₀ and Si₆F₁₂). On the basis of these stable structures, the frequency analyses were performed and scaled by a factor of 0.9614.³² The relevant values obtained are shown in Table S2 of the ESI.† From Table S2,† we can see that the experimental value is between the corrected and uncorrected values; therefore, it can be used to predict the peak range of the Si_xF_y (x ≤ 6, y ≤ 12) series. The difference between the theoretical and experimental values is ±20 cm⁻¹, which is caused by an experimental error.

3.2. Chemical structure stability analysis

3.2.1. Frontline molecular orbital analysis. The FMO theory^33,34 divides the electron cloud distributed around a molecule into molecular orbitals of different energy levels according to the energy. The highest energy molecular orbital (that is, the highest occupied orbital HOMO) and those that are not occupied by electrons, the lowest energy molecular orbital (that is, the lowest unoccupied orbital LUMO), are the keys to determining the chemical reaction of a system. When molecular orbitals interact, both the HOMO and LUMO play a very important role. HOMO has a weak electron binding force that readily loses electrons. LUMO has a strong electron affinity that readily receives electrons. The energy gap, ΔE, between the HOMO and LUMO is used to measure the chemical structure stabilities of molecules.^35,36 The smaller the gap value, the higher the reactivity, which means that the chemical structure stability is poorer. For the stable structures optimized at the B3LYP/6-31G(d,p) level, Multiwfn was used to perform FMO analysis, and then visual molecular dynamics (VMD) was used to map the frontline molecular orbital diagrams of the Si_xF_y (x ≤ 6, y ≤ 12) series. As shown in Fig. 3, red and dark blue represent the phases of the orbital wave function (red is positive, and dark blue is negative), which are respectively represented by the HOMO and LUMO orbitals. As shown in the figure, because SiF and SiF₃ have unbonded electrons, the unbonded electrons occupy the alpha and beta orbitals. For SiF and SiF₃, although the beta-LUMO of SiF₃ is mainly distributed near the fluorine position, the other alpha-HOMO, alpha-LUMO and beta-HOMO of SiF and SiF₃ are mainly distributed near the silicon position. The HOMO and LUMO of SiF₄ are mainly distributed in the silicon position. The HOMO and LUMO of SiF₂ are also mainly distributed in the silicon position. The intermolecular HOMO and LUMO between Si₂F₆ and Si₆F₁₂ are mainly distributed near the silicon–silicon single bond. According to the mutual attraction between the molecules derived from the interaction between the occupied orbital of one molecule and the unoccupied orbital of another molecule, the active site of the Si_xF_y (x ≤ 6, y ≤ 12) series is the silicon or silicon–silicon single bond position.

Fig. 3 FMO maps of the Si_xF_y (x ≤ 6, y ≤ 12) series.

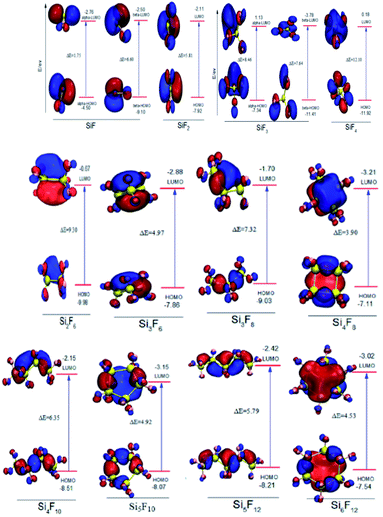
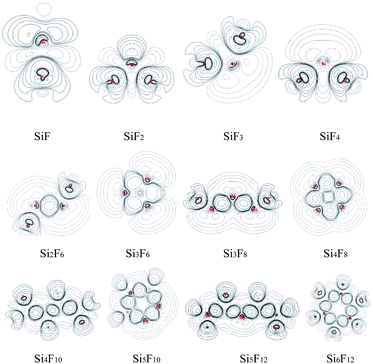
In addition, the FMO maps for the chain Si_xF_y (x ≤ 6, y ≤ 12) series are shown in Fig. 3, including SiF, SiF₂, SiF₃, SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂. As can be seen from Fig. 3, the HOMO energy values of SiF are −4.50 eV and −9.10 eV, and the LUMO energy values are −2.76 eV and −2.50 eV. Then, the ΔE values in SiF are 1.75 eV and 6.60 eV, respectively; the HOMO energy values of SiF₃ are −7.34 eV and −11.41 eV, the LUMO energy values are 1.13 eV and −3.78 eV, and the ΔE values in SiF₃ are 7.64 eV and 8.46 eV, respectively. In addition to SiF and SiF₃, the HOMO energy value of the SiF₂ molecule is −7.92 eV, and the LUMO energy value is −2.11 eV. Then, the ΔE in the SiF₂ is 5.81 eV. Accordingly, the ΔE values of SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂ are respectively 2.10 eV, 9.30 eV, 7.32 eV, 6.35 eV and 5.79 eV; therefore, the ΔE of Si_xF_y (x ≤ 6, y ≤ 12) is ranked from large to small as SiF₄(12.10 eV), Si₂F₆(9.30 eV), Si₃F₈(7.32 eV), Si₄F₁₀(6.35 eV), SiF₂(5.81 eV), Si₅F₁₂(5.79 eV). It can be concluded that the chemical structure stabilities of the chain structures in the Si_xF_y (x ≤ 6, y ≤ 12) series are ranked (from strong to weak) as SiF₄ > Si₂F₆ > Si₃F₈ > Si₄F₁₀ > SiF₂ > Si₅F₁₂.

For the cyclic structures, as can be seen from Fig. 3, the HOMO energy value of the Si₃F₆ molecule is −7.66 eV and the LUMO energy value is −2.88 eV. The ΔE in the Si₃F₆ is 4.97 eV. Accordingly, the ΔE values of Si₄F₈, Si₅F₁₀ and Si₆F₁₂ are 3.90 eV, 4.92 eV and 4.53 eV, respectively. Moreover, the order of the chemical structure stabilities (from strong to weak) is Si₃F₆ (4.97 eV) > Si₅F₁₀ (4.92 eV) > Si₆F₁₂ (4.53 eV) > Si₄F₈ (3.90 eV), and the three-membered ring structure is the most stable. The ΔE values of the three, five, and six-membered ring structures are nearly the same and are all much stronger than those of the four-membered ring structures. The ΔE in the chain Si₃F₈ molecule is 7.32 eV and that in cyclic Si₃F₆ is 4.97 eV, which indicates that chain Si₃F₈ is more stable than cyclic Si₃F₆. Recursively, when the number of silicon atoms is the same, the chemical structure stabilities of the chain substances are stronger than that of the ring substances. In addition to SiF and SiF₃, the chemical structure stabilities of molecules SiF₂ to Si₆F₁₂ are ranked as SiF₄ > Si₂F₆ > Si₃F₈ > Si₄F₁₀ > SiF₂ > Si₅F₁₂ > Si₃F₆ (ring) > Si₅F₁₀ (ring) > Si₆F₁₂ (ring) > Si₄F₈ (ring), where SiF₄ is the most stable.

3.2.2. Bond critical point analysis. AIM can effectively study and describe the interaction and properties of bonds. When two atoms form a chemical bond, there must be a BCP between the two atoms. This is the most peculiar point in the interaction region between atoms, and it is also the first-order saddle point on the scalar field of the electron density. The bond diameter is composed of two trajectories that are related to the BCP in the electron density gradient field (that is, the position of the nucleus) pointing to the bond critical point. Each point on the bond diameter is the maximum point of electron density in the direction perpendicular to the bond diameter. For the stable structures optimised at the B3LYP/6-31G(d,p) level, Multiwfn was used for electron density topological analysis. As shown in Fig. 4, purple is the nuclear critical point, which is generally at the atomic position, and orange is the bond critical dot; the brown line represents the bond diameter. It can be seen from the figure that Si, F, or Si, Si bonds interact to form the Si_xF_y (x ≤ 6, y ≤ 12) series, and Si atoms directly bond with the surrounding F and Si atoms. From the perspective of BCP and bond diameters, there are indeed chemical bonds.

Fig. 4 Bond critical points (orange balls); blue balls represent F and brown balls represent silicon.

3.2.3. Molecular electron density differences analysis. We further used Multiwfn to process dates and map figures, and the contour interval was 0.0004 to analyse the molecular electron density difference (MFDD) of the Si_xF_y (x ≤ 6, y ≤ 12) series. The area where the electron cloud ρ decreases is indicated by a dotted line, the area where the electron cloud ρ increases is represented by a solid line, and the molecular electron density differences Δρ are shown in Fig. 5. When Si and Si form a Si–Si bond, electrons move between the bonding atoms, causing a large loss of electrons near Si; the remaining electrons shrink toward the Si nucleus, and the missing electrons gather in the middle of the bond between the two atoms, finally forming covalent bonds, while Si and F atoms form polar covalent bonds.

Fig. 5 Δρ of Si_xF_y (x ≤ 6, y ≤ 12).

3.2.4. Mayer bond order analysis. The bond order can describe the chemical bond qualitatively. The most commonly used bond order is the MBO.³⁷ The MBO is often used to study the multiplicity and the strength of bonds. It can also judge whether the same atom composes the bond strength of the molecule, and the value of the same type of bond is closely related to its strength. The larger the bond sequence, the stronger the bond strength and the higher the amount of energy required, indicating that the bond is more stable. At the same time, the MBO can determine whether atoms are bonded. For the stable structures optimised at the B3LYP/6-31G(d,p) level, Multiwfn was used for MBO sequence analysis, and the results of Si–Si and Si–F of the Si_xF_y (x ≤ 6, y ≤ 12) series are shown in Table S1 and S3 of the ESI.†

For the chain Si_xF_y (x ≤ 6, y ≤ 12) series, as we can see from Table S1 of the ESI,† the main components are SiF, SiF₂, SiF₃, SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂. In addition to SiF and SiF₃, the MBO values of Si–Si are less than 1, while those of Si–F are greater than 1, indicating that the Si–F bond strength is greater than the Si–Si bond and the energy required to break the Si–F bond is greater than that of the Si–Si bond, that is, when the chain Si_xF_y (x ≤ 6, y ≤ 12) series are thermally broken, the Si–Si bond should be broken first. From the perspective of SiF_n (n ≤ 4), the MBO values of Si–F in SiF, SiF₂, SiF₃ and SiF₄ are respectively 0.9863, 1.0171, 0.9872, and 1.0538; therefore, the rank of the MBO strengths is SiF₄ > SiF₂ > SiF₃ > SiF. Therefore, SiF₄ is more stable than SiF₂, SiF and SiF₃, while Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂ are subject to the weakest chemical bonds (Si–Si bonds) when undergoing thermal breaking. The lowest MBO values of the Si–Si bonds in Si₂F₆, Si₃F₈, Si₄F₁₀, Si₅F₁₂ are 0.8471, 0.7884, 0.7312 and 0.7288, respectively. The rank of stability among them is Si₂F₆ > Si₃F₈ > Si₄F₁₀ > Si₅F₁₂.

For the cyclic Si_xF_y (x ≤ 6, y ≤ 12) series, the rank of chemical structure stabilities among the Si₄F₈, Si₃F₆, Si₅F₁₀ and Si₆F₁₂ is similarly Si₄F₈ (0.7614) > Si₆F₁₂ (0.7176) > Si₅F₁₀ (0.7031) > Si₃F₆ (0.6521), which shows that the chemical structure stability of the four-membered ring is stronger than those of the five-, the six- and three-membered rings, while the chemical structure stability of the three-membered ring is the worst.

In summary, in addition to SiF and SiF₃, the molecular chemical structure stabilities of the Si_xF_y (x ≤ 6, y ≤ 12) series ranks as SiF₄ > SiF₂ > Si₂F₆ > Si₃F₈ > Si₄F₁₀ > Si₅F₁₂ > Si₄F₈ (ring) > Si₆F₁₂ (ring) > Si₅F₁₀ (ring) > Si₃F₆ (ring). It also can be found that when the silicon atom numbers are the same, the chemical structure stabilities of the chain substances are stronger than that those the ring substances. Compared with the chemical structure stability results from the FMO, the possible reason for the difference in the stability of the cyclic substances is that the MBO only considers the role of the bond, and it is difficult to compare different chemical bonds.

3.2.5. Molecular surface electrostatic potential analysis. The stable structures optimised at the B3LYP/6-31G(d,p) level were also analysed using quantitative molecular surface electrostatic potential analysis in Multiwfn, that is, MS-EPS analysis. Based on the isovalue equal to 0.001 au for the electron density, the smooth electrostatic potential distribution, the color-filled molecular surface map and the corresponding bar graph of the surface area vs. EPS are shown in Fig. 6. The maximum and minimum values of the EPS have been marked in the figure. The red area in the figure represents a strong positive potential, and the blue area represents a strong negative potential. The more negative the electrostatic potential on the surface of the molecule, the more likely it is to be attacked by electrophiles; in contrast, the more positive the electrostatic potential on the surface of the molecule is, the more likely it is to be attacked by nucleophiles. Fig. 6 shows that the maximum point of the electrostatic potential of the Si_xF_y (x ≤ 6, y ≤ 12) series is much larger than the minimum value (positive and negative are not considered here), indicating that it is more likely to be attacked by nucleophiles than by electrophiles. According to the FMO analysis, the active site of the Si_xF_y (x ≤ 6, y ≤ 12) series is close to the silicon or silicon–silicon single bond position. Thus, the substances in the Si_xF_y (x ≤ 6, y ≤ 12) series tend to be attacked by nucleophiles rather than by electrophiles, and when encountering nucleophiles, they have poor chemical structure stabilities. The surface area diagrams of the Si_xF_y (x ≤ 6, y ≤ 12) series in each electrostatic potential range are consistent with this conclusion.

Fig. 6 Si_xF_y (x ≤ 6, y ≤ 12) surface electrostatic potential distributions and surface areas within each electrostatic potential (ESP) range.

3.2.6. Natural population analysis. Under the same method, using the natural bond orbital (NBO), the modules of the Si_xF_y (x ≤ 6, y ≤ 12) series were calculated to obtain the results of NPA. Through NPA analysis, we can know the gains and losses of the electrons of each atomic orbital as well as the change of the atomic hybrid state. The spin populations are equal to the difference between the alpha and beta populations. If the spin population is positive, alpha is greater than beta. A negative spin population means that there are more beta single electrons than alpha single electrons. The natural charge and natural population refer to the net charge and natural population of Si and F atoms, including the number of electrons in all inner orbitals of the atom (Cor). Cor usually does not participate in bonding; Val means all Si and F atoms make up the number of electrons in the molecular valence layer orbital of the Si_xF_y (x ≤ 6, y ≤ 12) series, and Val is the main part of the bonding; Ryd is the number of electrons in the excited state high-level molecular orbital of the Si_xF_y series. Val and Ryd usually participate in the bond formation; thus, the electron configuration is the number of atomic electrons contributed by each electron layer except Cor. All the results are summarised in Table S4 of the ESI,† where the populations of all silicon atoms are positive and those of all fluorine atoms are negative. The positive charge is mainly concentrated in the silicon or silicon–silicon single bond, and the electron cloud is mainly concentrated around fluorine. Generally, the more positive the atomic charge, the more readily a molecule is attacked by nucleophiles. Thus, the molecules in the Si_xF_y (x ≤ 6, y ≤ 12) series were attacked to a greater degree by nucleophiles than by electrophiles. This conclusion is consistent with the MS-EPS analysis.

3.3. Experimental results

The theoretical calculations of the stabilities of the Si_xF_y (x ≤ 6, y ≤ 12) series show that SiF₄ is the most stable among the Si_xF_y (x ≤ 6, y ≤ 12) series, followed by Si₂F₆, while SiF₂ is unstable. Because the mass spectrometer is obscure to the ion sources of SiF_n (n = 1–3), SiF₄, and Si_xF_y, infrared spectroscopy was chosen to verify the ion sources in samples stored under normal temperature and pressure. The stability after storing for 1 hour and 1 day and the stability without storage are discussed. The infrared spectra of SiF₄ were the same when it was stored for 1 hour, 1 day and without storage (immediate detection), indicating that SiF₄ is the most stable substance. Fig. 7 shows the infrared spectra of SiF_n (n = 1–3) prepared with SiF₄ and Si at a high temperature according to the process flow shown in Fig. 1 and stored for various periods. Compared with immediate detection, after 1 hour and 1 day, the peak value of SiF₂ (858 cm⁻¹) gradually decreases with increasing storage time, indicating that SiF₂ is unstable. Fig. 8 shows the infrared spectrum of the high-temperature gas Si_xF_y prepared at a high temperature and stored for different times. It can be seen that the peak value of Si₂F₆ (992 cm⁻¹) gradually decreases with storage time. Compared with SiF₄, Si₂F₆ is less stable. The theoretical calculations are consistent with the experimental results.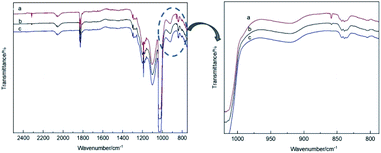

Fig. 7 Infrared spectrum of SiF_n (n = 1–3) after storage: (a) detected immediately, (b) detected after one hour, (c) detected after one day.

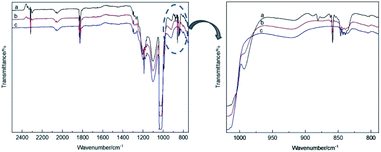Fig. 8 Infrared spectrum of Si_xF_y after storage: (a) detected immediately, (b) detected after one hour, (c) detected after one day.

4. Conclusion

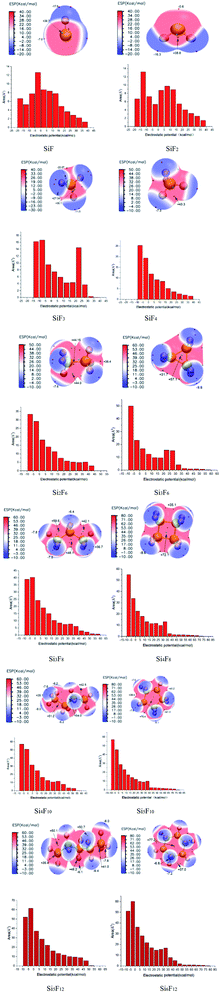
We constructed the structures of a Si_xF_y (x ≤ 6, y ≤ 12) series, including chain substances (SiF, SiF₂, SiF₃, SiF₄, Si₂F₆, Si₃F₈, Si₄F₁₀ and Si₅F₁₂) and cyclic substances (Si₃F₆, Si₄F₈, Si₅F₁₀, and Si₆F₁₂). At the B3LYP/6-31G(d,p) level, the stable structures of the Si_xF_y (x ≤ 6, y ≤ 12) series were obtained. Based on these stable structures, we explored the chemical structure stabilities using theoretical and experimental methods. The FMO analysis showed that the active site among them is at the position of the silicon or silicon–silicon single bond, and the rank of the chemical structure stabilities is SiF₄ > Si₂F₆ > Si₃F₈ > Si₄F₁₀ > SiF₂ > Si₅F₁₂ > Si₃F₆ (ring) > Si₅F₁₀ (ring) > Si₆F₁₂ (ring) > Si₄F₈ (ring), which is consistent with that obtained from MBO analysis. When the number of silicon atoms is the same, the chemical structure stabilities of the chain substances are stronger than those of the ring substances. Moreover, infrared spectroscopy shows that SiF₄ is the most stable among the Si_xF_y (x ≤ 6, y ≤ 12) series, followed by Si₂F₆, while SiF₂ is unstable. MS-EPS and NPA analyses show that the active sites close to silicon or silicon–silicon single bonds in the Si_xF_y (x ≤ 6, y ≤ 12) series are vulnerable to attack by nucleophiles. When encountering nucleophiles, these substances have poor chemical structure stabilities. These results can provide theoretical insight into the research and applications of fluorosilicon compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 21766005), the Science and Technology Planning Project of Guizhou Province (No. Qian Ke He Ping Tai Ren Cai [2019] 5609 and Qiankehezhicheng [2021]Yiban 493), Guizhou Provincial Key Laboratory of Energy Chemistry (Qianjiaohe KY Zi[2017] 009), the GIT Academic Seedling Training and Innovation Exploration Project (No. GZLGXM-11).

References

1. W. C. Schumb and E. L. Gamble, J. Am. Chem. Soc., 1932, 54, 583–590.
2. V. Tosa, S. Isomura and Y. Kuga, et al., Vib. Spectrosc., 1994, 8, 45–52.
3. B. R. Johannesen, J. Chem. Phys., 1967, 47, 955–960.
4. F. Höfler and R. Jannach, Monatsh. Chem., 1976, 107, 731–735.
5. D. C. Pease, Process for the preparation of difluorosilylene and the polymers thereof, US Pat., 2840588, 1958-06-24.
6. P. L. Timms, R. A. Kent and T. C. Ehlert, et al., J. Am. Chem. Soc., 1965, 87, 2824.
7. J. M. Bassler, P. L. Timms and J. L. Margrave, Inorg. Chem., 1966, 5, 729–732.
8. A. L. L. Cruz, J. L. D. L. Pea and M. I. P. Canul, Rev. Mex. Fis., 2008, 54, 200–207.
9. P. L. Timms, R. A. Kent, T. C. Ehlert and J. L. Margrave, J. Am. Chem. Soc., 1965, 87, 2824–2828.
10. Y. Mai, S. Klein and R. Carius, et al., J. Appl. Phys., 2005, 97, 114–119.
11. B.-H. Jun, J. S. Lee and D.-W. Kim, et al., J. Mater. Res., 1999, 14, 1688–1701.
12. K. L. Williams, C. I. Butoi and E. R. Fisher, J. Vac. Sci. Technol., A, 2003, 21, 1688–1701.
13. O. Takayuki and H. Ken-ichiro, et al., J. Appl. Phys., 2003, 94, 1428–1435.
14. M. E. Colvin, R. S. Grev III and H. F. Schaefer, et al., Chem. Phys. Lett., 1983, 99, 399–405.
15. R. Knizikevičius, Chem. Phys. Lett., 2005, 410, 177–178.
16. X. Helluy, R. Pietschnig and A. Sebald, Solid State Nucl. Magn. Reson., 2003, 24, 286–300.
17. J. Hrusak, Z. Herman and S. Iwata, Mass Spectrom., 1999, 192, 165–171.
18. L.-j. Jiang, Y.-f. Liu, Z.-z. Liu and X.-q. Han, Acta Phys. Sin., 2009, 58, 201–208.
19. J. Zhao, X.-l. Cheng and X.-d. Yang, et al., Acta Phys. Sin., 2009, 58, 5280–5284.
20. W.-s. Jiang and J.-p. Zhu, J. Sichuan Norm. Univ., Nat. Sci., 2010, 33, 519–522.
21. X.-q. Han, Acta Phys. Sin., 2014, 63, 114–119.
22. D. Bandyopadhyay and P. Sen, J. Phys. Chem. A, 2010, 114, 1835–1842.
23. D. B. andyopadhyay, P. Kaur and P. Sen, J. Phys. Chem. A, 2010, 114, 12986–12991.
24. R. Trivedi, A. Banerjee and D. Bandyopadhyay, Phys. E, 2021, 131, 114725.
25. D. Bandyopadhyay, Struct. Chem., 2019, 30, 955–963.
26. J. P. Perdew and K. Schmidt, Phys. Rev. Lett., 2001, 577, 1–20.
27. P. J. Stephens, et al., J. Phys. Chem., 1994, 98, 11623–11627.
28. L. Tian and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
29. M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision D.01, Wallingford, CT, 2013.
30. J. Zhao, X.-l. Cheng and X.-d. Yang, et al., Acta Phys. Sin., 2009, 157–161.
31. M. W. Chase, C. A. Davies and J. R. Downey, J. Phys. Chem. Ref. Data, 1985, 14, 553.
32. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
33. G.-d. Zhou and L.-y. Duan, Fundamentals of Structural Chemistry, Peking University Press, Beijing, 2008, pp. 168–171.
34. B.-r. Li, Structural Chemistry, Higher Education Press, 2004, pp. 172–178.
35. A. L. L. Cruz, J. L. D. L. Pea and M. I. P. Canul, Rev. Mex. Fis., 2008, 54, 200–207.
36. X. Helluy, R. Pietschnig and A. Sebald, Solid State Nucl. Magn. Reson., 2003, 24, 286–300.
37. I. Mayer, Chem. Phys. Lett., 1985, 117, 396.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03526f

---