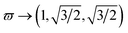Open Access Article
Open Access ArticleDynamic clock generator and memory mass device using a quantum ring driven by three-color laser fields
Dario Cricchio * and
Emilio Fiordilino
* and
Emilio Fiordilino
Dipartimento di Fisica e Chimica – Emilio Segré, Università di Palermo, Via Archirafi 36, 90123, Palermo, Italy. E-mail: dario.cricchio@unipa.it; emilio.fiordilino@unipa.it
First published on 29th July 2021
Abstract
We study the behaviour and applications of a quantum ring (QR) under a three-color laser field. In particular we study the emission of harmonics and their temporal evolution through wavelets. These results suggest the use of QR for three important applications: (1) generation of single short pulses, (2) creation of a variable clock generator, (3) a memory mass device through the angular momentum acquired by the electron.
1 Introduction
Modern technology allows us to foresee a new class of computing devices with astounding performances. Among these, we highlight computers that can learn – after being trained, they can work out problems which they have not been exposed to before, thus mimicking characteristics considered intrinsic in mammal brains1,2 and, by the same token, have high speed working features.3 Their application would be useful in the highly efficient diagnosis of diseases, translation, language recognition and efficient matrix operation.3,4 Such progress would be made possible by significant improvements in the fabrication and characterisation of new materials; among these, paramount importance is found in reduced dimensional objects such as quantum rings, nanotubes and two-dimensional (2D) lattices such as graphene.5–7 From a conceptual point of view it is possible to develop computers exploiting pure quantum effects with no classical counterparts.2Therefore, the demand for the development of new technologies that gradually allow the construction of smaller and faster logic circuits is growing. To fulfil this, technology that combines electronics and optics has been developed,1–3 however, this combination limits the speed of input/output transmission; hence it is important to create entirely new optical devices. The importance of using only optical devices is due to the much faster data transmission and to the lower energy consumption than when using traditional devices. For these reasons research is focusing on new kinds of materials and devices that show electrical and optical properties that can be suitable for the manufacturing of logic circuits. Graphene and quantum rings (QRs) (filiform structures with circular geometry) are examples, for their interesting application in nanotechnology, optics and computer science thanks to their electrical and optical properties.
Indeed, the versatility of QRs in the design of fast operating all-optical logic gates is noteworthy and has been discussed. Thus a QR driven by a two color laser field has been studied8,9 as a function of the relative intensity and phase of the two color-fields; the fine tuning of these two parameters controls the presence and absence of groups of harmonics. By assigning a logic value to the presence or absence of a particular harmonic it is possible to obtain two/three/four-state logic gates – thus extending the traditional binary logic – operating in the time range of 10−15 s, therefore in a faster range than the usual gates.
The circular symmetry of the rings makes them particularly apt to be used in the presence of a magnetic field piercing their plane. In this case, the electron spin can be exploited and fast logic gates can be investigated.10,11 A point of interest lies in large graphene annuli7 where the peculiar dispersion properties of massless Dirac electrons can be utilised to create localised filiform currents of large angular momentum apt to store many bits of information.
Atoms and molecules driven by an intense laser pulse of angular frequency ωL irradiate electromagnetic waves whose spectrum essentially contains harmonics of ωL, this processes is called high harmonic generation (HHG).12,13 The phenomenon provides an important benchmark to non-linear theories and is becoming an effective source of high frequency and coherent radiation; experimental work shows that the plateau can be as large as ωM ≈ 100ωL, i.e. using a laser wavelength λL = 800 nm ⇒ ℏωL ≅ 1.55 eV (as in this paper), to obtain a cutoff energy ℏωM ≈ 150 eV is possible. Several studies show that the use of a two-color laser field or a laser photon energy resonant between the ground state and the first excited state, can generate a spectrum with a wide plateau.14–16 Fiber lasers of constant mode are used to investigate the linear and non linear photonic properties of 2D materials.5,6,17
In this paper we study the behaviour of a QR in the presence of a three-color laser field, and evaluate the spectrum of the emitted radiation and, via a wavelet transform, its temporal evolution. All calculations are made with different combinations of the three driving frequencies, finding a relationship between these and the emitted spectrum. In particular we find configurations of the incident electric field favourable to the creation of single short pulses and other configurations that can be used for the operation of future quantum computers, namely for the creation of a variable clock generator and for a memory mass device.
2 Theory
Adopting the dipole and single active electron approximations, we consider one electron bound to a QR of radius R driven by three laser fields polarised in the x − y plane:
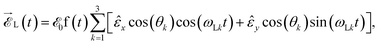 | (1) |
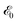 is the electric field strength,
is the electric field strength, 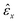 and
and 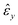 are unit vectors along the x and the y axes, θk is the angle between the k-electric field and the x axis, and f(t) the so called pulse profile. For the sake of simplicity in this paper, f(t) has been considered constant for a duration of 20 optical cycles (oc). The Hamiltonian of our system is:
are unit vectors along the x and the y axes, θk is the angle between the k-electric field and the x axis, and f(t) the so called pulse profile. For the sake of simplicity in this paper, f(t) has been considered constant for a duration of 20 optical cycles (oc). The Hamiltonian of our system is:
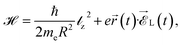 | (2) |
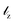 the z component of the angular momentum operator in units of ℏ and
the z component of the angular momentum operator in units of ℏ and
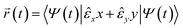 | (3) |
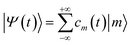 , with |m〉 the eigenvectors of the angular momentum:
, with |m〉 the eigenvectors of the angular momentum: 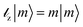
We also calculated the absorbed energy K(t) and the absorbed angular momentum Lz(t) as a function of time:
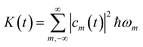 | (4) |
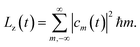 | (5) |
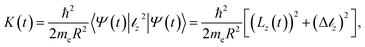 | (6) |
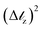 is the variance. The first term is related to the motion along the ring, and the second term to the dispersion of the wave function.
is the variance. The first term is related to the motion along the ring, and the second term to the dispersion of the wave function.
3 Results
In our calculations we use a QR with radius R = 20a0 (a0 is the Bohr radius) and with different configurations of the total field . The three colors have the same intensity I = 3 × 1014 W cm−2, but different polarisation as given by θk = 2(k − 1)π/3. The configuration of the three colors is expressed by a triplet of numbers: ϖ → (ϖ1, ϖ2, ϖ3). For example with ϖ → (1, 2, 3) we denote ωL1 = ωL, ωL2 = 2ωL, ωL3 = 3ωL. When not expressly specified, we use a laser photon energy of ℏωL = 1.55 eV. In circular coordinates, the total electric field follows the path determined by ϖ. When the three laser frequencies are equal, the total electric field is zero, when they are all different, we have an intricate path and in all other cases, we have a linear path. In Fig. (1) we show these paths calculated for an arbitrary high number of oc, and later we will see how the response of the harmonics and the generation of short pulses changes, depending on whether the fields are of integer or irrational ratio, or if they are all different or only one of them is different. All calculations are performed using 20 oc laser duration.
. The three colors have the same intensity I = 3 × 1014 W cm−2, but different polarisation as given by θk = 2(k − 1)π/3. The configuration of the three colors is expressed by a triplet of numbers: ϖ → (ϖ1, ϖ2, ϖ3). For example with ϖ → (1, 2, 3) we denote ωL1 = ωL, ωL2 = 2ωL, ωL3 = 3ωL. When not expressly specified, we use a laser photon energy of ℏωL = 1.55 eV. In circular coordinates, the total electric field follows the path determined by ϖ. When the three laser frequencies are equal, the total electric field is zero, when they are all different, we have an intricate path and in all other cases, we have a linear path. In Fig. (1) we show these paths calculated for an arbitrary high number of oc, and later we will see how the response of the harmonics and the generation of short pulses changes, depending on whether the fields are of integer or irrational ratio, or if they are all different or only one of them is different. All calculations are performed using 20 oc laser duration.
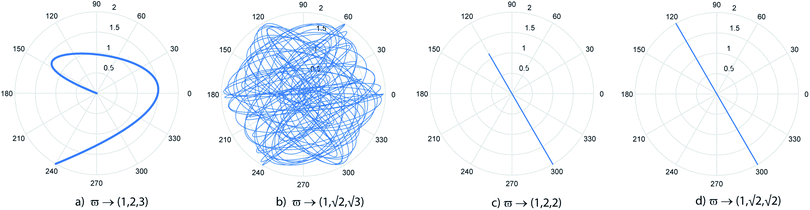 | ||
| Fig. 1 Laser field path: (a) and (b) when all the fields are different and (c) and (d) when two fields are equal. | ||
In Fig. (2) we show the energy and the angular momentum absorbed by the electron evaluated by means of eqn (4) and (5). We can therefore say that the whole process transfers energy to the electron by giving it angular momentum; by controlling the electric field duration, it is possible to transmit angular momentum which can be as large as 4 or 5 ℏ. If we call a bit one unit of angular momentum we may say that one QR can store several bits of information.
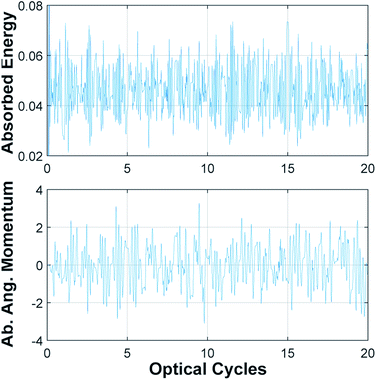 | ||
| Fig. 2 Energy (top) in au and angular momentum (bottom) in units of ℏ absorbed by the electron; ϖ → (1, 2, 3). | ||
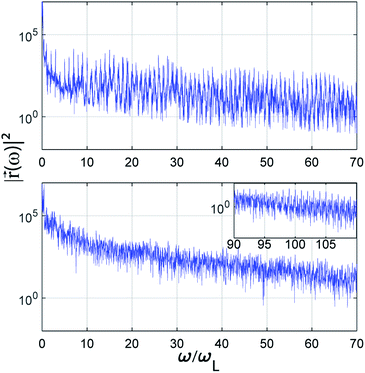
Fig. (3) shows the Fourier power spectra of 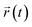 whose frequency components provide the energy spectrum emitted by the QR. We can see that there are differences depending on whether the electric fields are all different or two are equal. When the three frequencies are different we have very dense spectra with, possibly, few harmonics concentrated in the initial part and in the final part of the spectrum, while when two frequencies are equal, almost the whole spectrum is composed of both even and odd harmonics. The use of frequency ratios with integer or irrational values affects both the resolution in separated lines of the spectrum and the path of the electric field. Irrational ratios of the frequencies (spectra not shown in the present paper) produce a generally more intricate path of the electric field and a quasi-continuum spectrum. From a purely mathematical point of view this is obvious, as irrational values in ϖ destroy any form of periodicity of the field and even make the determination of a frequency and its harmonics meaningless. This may appear to be a disadvantage for the generation of harmonics but is an advantage for the generation of short pulses.18
whose frequency components provide the energy spectrum emitted by the QR. We can see that there are differences depending on whether the electric fields are all different or two are equal. When the three frequencies are different we have very dense spectra with, possibly, few harmonics concentrated in the initial part and in the final part of the spectrum, while when two frequencies are equal, almost the whole spectrum is composed of both even and odd harmonics. The use of frequency ratios with integer or irrational values affects both the resolution in separated lines of the spectrum and the path of the electric field. Irrational ratios of the frequencies (spectra not shown in the present paper) produce a generally more intricate path of the electric field and a quasi-continuum spectrum. From a purely mathematical point of view this is obvious, as irrational values in ϖ destroy any form of periodicity of the field and even make the determination of a frequency and its harmonics meaningless. This may appear to be a disadvantage for the generation of harmonics but is an advantage for the generation of short pulses.18
The Fourier power spectrum gives a perfect determination of the frequencies content of a signal s(t) but says nothing on their emission time. This information, fundamental for our purpose, can be retrieved by means of a wavelet transform which is a particular windowed Fourier transform. The wavelet transform of the signal s(t) is defined as
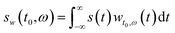 | (7) |
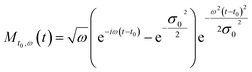 | (8) |
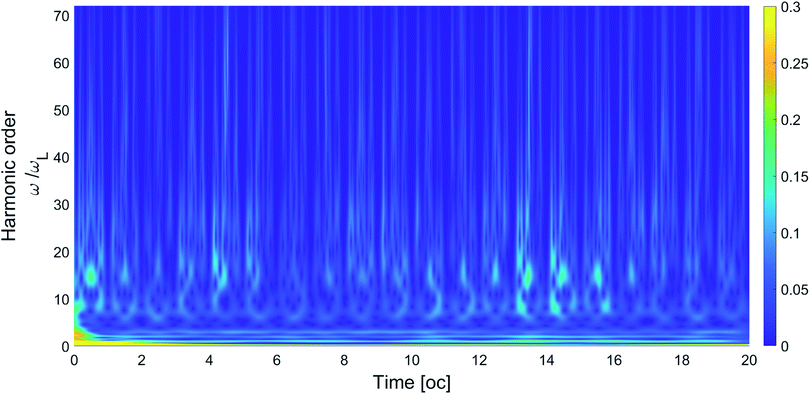
In our calculation, we choose σ0 = 1, that corresponds to one oscillation of the signal within the Morlet wavelet window. In Fig (4) we show the wavelet analysis calculated for ϖ = (1, 2, 2).
In Fig (5) we show the temporal evolution of the single 15th harmonic where we notice that the emission presents a one oc periodicity which is different from the half oc periodicity in atoms; this discrepancy flags a physical difference between the atomic and the ring case. In fact in the atomic case the emission is essentially due to impulsive collisions of the active electron with the nucleus while in the case of the ring, the reason for the emission is due to the centripetal and tangential accelerations induced by the laser on the active electron. Indeed, Fig. (4) shows that higher harmonics are emitted a few times within any optical cycle.
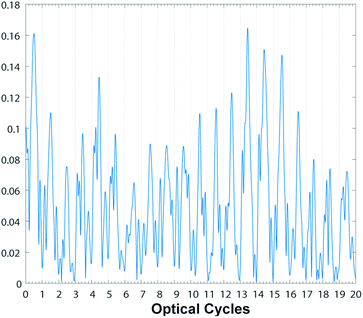 | ||
| Fig. 5 Time evolution of the 15th harmonic extracted from Fig. (4) [ϖ → (1, 2, 2)]. The emission has a periodicity of one optical cycle. | ||
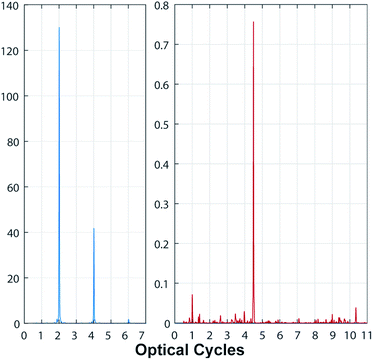
Our findings naturally lead us to look for the creation of short pulses. In fact their Fourier transform contains a broad continuum of frequency components, and such a rich spectrum is seen in the spectra of Fig (3). Thus, we calculate the inverse Fourier transform (IFT) of the signal in an appropriate range of frequencies, and we notice that it is easier to get short isolated pulses in the case of two equal frequencies, and if we choose the central region of the spectra to perform the IFT. In Fig. (6) we show the short pulses calculated for ϖ → (1, 3/2, 3/2) (left) and 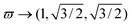 (right), with ℏωL = 3.1 eV. Their full width half maximum (FWHM) is of the order of 10−17 s. By appropriately choosing the system parameters, such as ϖ → (1, 2, 3), it is also possible to generate a train of short pulses as shown in Fig. (7).
(right), with ℏωL = 3.1 eV. Their full width half maximum (FWHM) is of the order of 10−17 s. By appropriately choosing the system parameters, such as ϖ → (1, 2, 3), it is also possible to generate a train of short pulses as shown in Fig. (7).
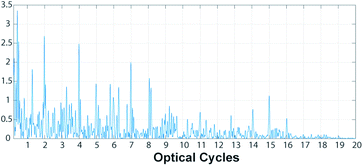 | ||
| Fig. 7 Train of short pulses with ϖ → (1, 2, 3) with ℏωL = 1.5 eV obtained by integrating the Fourier transform in the range 13–32 ω/ωL. | ||
4 Applications: quantum computing
The results can be used in quantum computing; in particular in the creation of a dynamic clock and memory mass devices. These two devices are of great importance in quantum computing. In fact, with the advancement of technology and therefore with the introduction of optical and ever faster components, there is a need for a clock to manage operations and a memory storage device to store information; and these two devices must have very high operating speeds.4.1 Dynamic clock
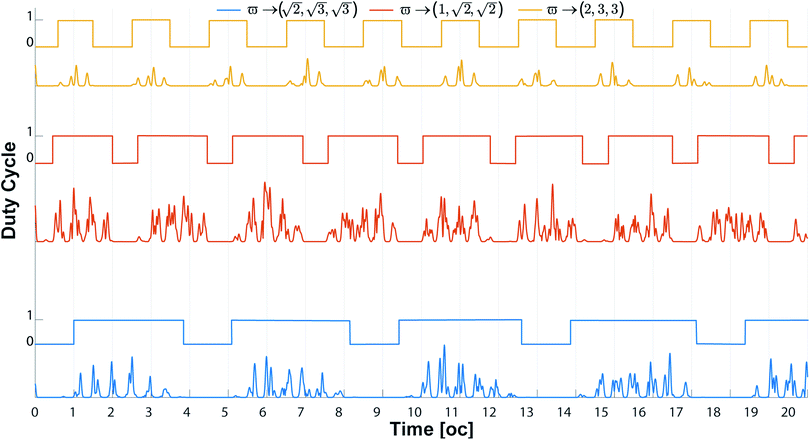
In electronics, the term clock indicates a periodic signal, generally a square wave, used to synchronize the operation of digital electronic devices. The signal consists of a voltage level that periodically makes a transition from zero to a fixed value. These two levels have binary values, 0 and 1. The clock can be generated by any oscillator, the quartz type is generally used for its high oscillation stability.We can create a clock by exploiting the emitted spectrum. In Fig (8) we show three signals by calculating the time evolution of the 51st harmonic for the cases:  ,
, 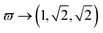 , ϖ → (2, 3, 3). If T is the total duration of the signal and P is the total time spent by the system at the high level (with value 1), we define the duty cycle D as:
, ϖ → (2, 3, 3). If T is the total duration of the signal and P is the total time spent by the system at the high level (with value 1), we define the duty cycle D as:
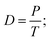 | (9) |
We can see how it is possible to vary the duty cycle, hence the clock frequency, by changing the frequency of the field components.
4.2 Memory storage
A driving circularly polarised laser field is the most efficient way for transmitting an angular momentum to the electron; also we have seen that the configuration of three laser fields can induce an average circular motion on the electron. This motion generates a current I. Let
to the electron; also we have seen that the configuration of three laser fields can induce an average circular motion on the electron. This motion generates a current I. Let  be the vector surface of the QR, and the magnetic moment generated by the motion of the electron is defined as:
be the vector surface of the QR, and the magnetic moment generated by the motion of the electron is defined as:
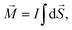 | (10) |
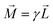 . The presence of a residual angular momentum depending on the laser configuration allows us to use the ring to store information. In fact, using three lasers with different frequencies it is possible to have a residual angular momentum, while in all other cases we will not have any. By associating the Boolean value 1 to the presence of a residual angular momentum, and the value 0 to the null case, we can use the angular momentum as an information bit. If we have a planar array of QRs and if
. The presence of a residual angular momentum depending on the laser configuration allows us to use the ring to store information. In fact, using three lasers with different frequencies it is possible to have a residual angular momentum, while in all other cases we will not have any. By associating the Boolean value 1 to the presence of a residual angular momentum, and the value 0 to the null case, we can use the angular momentum as an information bit. If we have a planar array of QRs and if 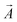 is the surface of the laser spot containing several QRs, the magnetic momentum generated will be proportional to the summation of the contributions of each QR within the laser spot surface. Then we can use the QR to store information with the magnetic momentum. These simple behaviours make the QR an interesting object to store information.
is the surface of the laser spot containing several QRs, the magnetic momentum generated will be proportional to the summation of the contributions of each QR within the laser spot surface. Then we can use the QR to store information with the magnetic momentum. These simple behaviours make the QR an interesting object to store information.
5 Conclusions
In this paper we study the response of a QR driven by three laser fields polarized along three equally spaced axes at different frequency. We have seen how it is possible to exploit various combinations of the frequencies of the incident laser to obtain different types of harmonic spectra. We have also calculated the path of the electric field and the energy and angular momentum absorbed by the electron. From these results we noticed that using two equal frequency lasers we obtain a total linear electric field that results in a spectrum rich in both even and odd harmonics, and in an average angular momentum different from zero. In all other cases the mean angular momentum was zero.This behaviour allowed us to assign Boolean values to the presence and absence of an average angular momentum, and therefore to create a bit of information. From the wavelet analysis of the spectra we have seen that the emission of harmonics occurs periodically. The importance of this phenomenon lies in the fact that obtaining periodic and regular pulses allows us to build a variable frequency clock without using resonator crystals. Finally, we have seen how this system can be considered an excellent candidate for the generation of isolated short pulses.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Prof. Tiziana Di Salvo for the generous financial support through the Fondo Finalizzato alla Ricerca (FFR) of the Dipartimento di Fisica e Chimica – Emilio Segré of the University of Palermo.Notes and references
- M. Miscuglio and V. J. Sorger, Photonic tensor cores for machine learning, Appl. Phys. Rev., 2020, 7(3), 031404 CAS.
- J. M. Arrazola, V. Bergholm, K. Brádler, T. R. Bromley, M. J. Collins, I. Dhand and A. Fumagalli, et al., Quantum circuits with many photons on a programmable nanophotonic chip, Nature, 2021, 591(7848), 54–60 CrossRef CAS PubMed.
- Y. Shen, N. C. Harris, S. Skirlo and M. et all Prabhu, Deep learning with coherent nanophotonic circuits, Nat. Photonics, 2017, 11(7), 441–446 CrossRef CAS.
- G. R. Steinbrecher, J. P. Olson, D. Englund and J. Carolan, Quantum optical neural networks, Npj Quantum Inf., 2019, 5(1), 60 CrossRef.
- J. He, L. Tao, H. Zhang, B. Zhou and J. Li, Emerging 2d materials beyond graphene for ultrashort pulse generation in fiber lasers, Nanoscale, 2019, 11, 2577–2593 RSC.
- T. Jiang, K. Yin, C. Wang, J. You, H. Ouyang, R. Miao, C. Zhang, K. Wei, H. Li, H. Chen, R. Zhang, X. Zheng, Z. Xu, X. Cheng and H. Zhang, Ultrafast fiber lasers mode-locked by two-dimensional materials: review and prospect, Photon. Res., 2020, 8(1), 78–90 CrossRef CAS.
- E. Fiordilino, Laser assisted dirac electron in a magnetized annulus, Symmetry, 2021, 13(4), 642 CrossRef.
- D. Cricchio and E. Fiordilino, Laser driven quantum rings: one byte logic gate implementation, RSC Adv., 2018, 8, 3493–3498 RSC.
- D. Cricchio and E. Fiordilino, Wavelet analysis and hhg in nanorings: their applications in logic gates and memory mass devices, Nanoscale, 2016, 8, 1968–1974 RSC.
- S. K. Maiti, NAND gate response in a mesoscopic ring: an exact result, Phys. Scr., 2009, 80(5), 055704 CrossRef.
- D. Cricchio and E. Fiordilino, Quantum ring in a magnetic field: High harmonic generation and not logic gate, Adv. Theory Simul., 2020, 3(7), 2000070 CrossRef CAS.
- M. Ferray, A. L’Huillier, X. F. Li, L. A. Lompre, G. Mainfray and C. Manus, Multiple-harmonic conversion of 1064 nm radiation in rare gases, J. Phys. B: At., Mol. Opt. Phys., 1988, 21(3), L31 CrossRef CAS.
- C. J. Joachain, N. J. Kylstra, and R. M. Potvliege. Atoms in intense laser fields. Cambridge University Press, 2012 Search PubMed.
- I. J. Kim, C. M. Kim, H. T. Kim, G. H. Lee, Y. S. Lee, J. Y. Park, D. J. Cho and C. H. Nam, Highly efficient high-harmonic generation in an orthogonally polarized two-color laser field, Phys. Rev. Lett., 2005, 94, 243901 CrossRef.
- N. F. Hinsche, A. S. Moskalenko and J. Berakdar, High-order harmonic generation by a driven mesoscopic ring with a localized impurity, Phys. Rev. A, 2009, 79, 023822 CrossRef.
- R. A. Ganeev, M. Suzuki and H. Kuroda, Quasi-phase-matching-induced enhancement of high-order harmonics during two-colour pump of multi-jet plasmas, J. Phys. B: At., Mol. Opt. Phys., 2014, 47(10), 105401 CrossRef.
- Y. Song, X. Shi, C. Wu, D. Tang and H. Zhang, Recent progress of study on optical solitons in fiber lasers, Appl. Phys. Rev., 2019, 6(2), 021313 Search PubMed.
- A. Fleischer and N. Moiseyev, Attosecond laser pulse synthesis using bichromatic high-order harmonic generation, Phys. Rev. A, Nov 2006, 74, 053806 Search PubMed.
- C. K. Chui. An Introduction to Wavelets. Academic Press, 1992 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |