Bandgap tuning strategy by cations and halide ions of lead halide perovskites learned from machine learning

Abstract

Bandgap engineering of lead halide perovskite materials is critical to achieve highly efficient and stable perovskite solar cells and color tunable stable perovskite light-emitting diodes. Herein, we propose the use of machine learning as a tool to predict the bandgap of the perovskite materials from their compositions. By learning from the experimental results, machine learning algorithms present reliable performance in predicting the bandgap of the lead halide perovskites. The linear regression model can be used to manually predict the bandgap of the perovskite with the formula of Cs_aFA_bMA_(1−a−b)Pb(Cl_xBr_yI_(1−x−y))₃ (FA = formamidinium, MA = methylammonium). The neural network (NN) algorithm, which takes the interplay of cations and halide ions into account in predicting the bandgap, presents higher accuracy (with a RMSE of 0.05 eV and a Pearson coefficient larger than 0.99). Furthermore, the compositions of the mixed halide perovskites with desirable bandgaps and high iodide ratio for suppressing halide segregation are predicted by NN algorithm. These results highlight the power of machine learning in predicting the bandgap of the perovskites from their compositions and provide bandgap tuning directions for experiments.

---

Introduction

Lead halide perovskites (APbX₃, A is the cation, X is the halide ion) are a class of incredible materials, which show unique optical, electrical, and optoelectronic performance in many applications.^1–3 Bandgap tuning is essential for the application of perovskite materials in both solar cells and light emitting diodes (LEDs). The bandgap of the perovskites can be tuned from 1.5 to 3.2 eV by adjusting I/Br and Br/Cl mixing ratio and the A-site cations (Cs, formamidinium (FA), methylammonium (MA) etc.).^4–6 Especially, mixed halide perovskites (MHPs) with wide bandgap (>1.65 eV) are gaining increasing importance for tandem solar cells (TSCs).^7,8 The TSCs with multiple junctions, which optically connect wide bandgap and narrow bandgap absorbers in series, can overcome the Shockley–Queisser limit of single junction cells and enable notably high power conversion efficiency.^9–11 The optimum bandgap for the top cell of perovskite/Si TSCs by detailed-balance calculations under standard test conditions (AM1.5G, 1 kW m⁻², 25 °C) is 1.73 eV for the series tandem and 1.81 eV for the module and the four-terminal tandem.¹² At elevated temperatures, the optimal perovskite bandgap falls below 1.68 eV (measured at 25 °C) at the radiative limit.¹³ However, the wide bandgap MHPs in the optimum bandgap range for TSCs suffer from halide segregation,^14–16 especially when Br fraction was larger than 20%, which lead to poor optoelectronic performance and device stability. To reduce halide segregation of wide bandgap MHPs, lowering the Br fraction without at the cost of lowering the bandgap is essential. Hence, to suppress the halide segregation and enhance the device performance of MHP based solar cells,^17–21 it is critical to identify the relation between the composition of the perovskites and their bandgaps, and to explore new MHPs with desired bandgaps and low Br fraction.

The physical relations between the composition of the perovskites and their bandgaps are well explored by previous work,^22–24 which provide general directions for bandgap tuning through the compositions. However, these relations are not able to be used for accurately predicting the bandgaps before experiments. To screen perovskites with desired bandgap, a traditional way is by doing trial and error experiments, which requires lots of time, materials, equipment, and manpower. Meanwhile, the fabrication of some perovskite materials may also face challenge with present techniques. For example, though triple halide strategy with partial Br replaced by Cl is proved to be effective in achieving wide bandgap MHPs with reduced Br fraction, it faces challenge in doping Cl in the crystal lattice.^25,26 It is because that Cl typically volatilizes as MACl (MA = methylammonium) or FACl (FA = formamidinium) during annealing of the perovskite film and only acts to control film crystallization.^25,27 Hence, this limits the investigation of the intrinsic material information of these materials.

Nowadays, machine-learning (ML) approach is the scientific modeling that can effectively learn from past massive datasets and mechanisms with relatively small error.^28–32 Hence, ML is beneficial for overcoming the experimental limitations to investigate the underlying mechanism of the perovskite materials. In the recent past, researchers have made progress in exploring the physical properties of the materials with their structural and chemical features,⁷ screening perovskites,^3,8 developing high-performing perovskite solar cells,²⁸ and understanding the underlying complex correlations in fullerene derivatives-based ternary OSCs.³³ In previous studies, to train the ML algorithms, the dataset is obtained mainly from either density functional theory (DFT) calculations or experimental results.^34,35 The dataset obtained from experimental results is able to reduce the deviation, and hence, the predicted results by ML algorithms are more referable to experiments. For example, Jinxin Li et al.²⁸ use the experimental bandgap results based on pure I, I–Br mixed, and I–Cl mixed perovskites as the training dataset, and learn the relations between the compositions of the perovskite materials with their bandgaps. The predicted results show high accuracy in predicting the bandgaps of the test dataset (with root mean square error of less than 0.1 eV). However, limited to the scale of the training dataset, the influences of Cl and Br, especially Cl, on the bandgap are unclear. Hence, the prediction in the bandgaps of MHPs (especially triple halide perovskites) from their compositions still face challenge.

Hence, in this work, ML approach is employed to get the bandgap tuning strategy by cations and halide ions of MHPs based on the past reported experimental dataset. The dataset covers a large range of compositions of the perovskites, including pure Cl, pure Br, pure I, Cl–Br mixed, and Br–I mixed, aiming to get a deep and accurate relation between the composition of the lead halide perovskite and its bandgap. Moreover, the dataset points are reasonably screened, which enables the ML algorithms exhibiting excellent performance in predicting the bandgaps of both the training and the test datasets. Especially, a series of MHPs with triple halide ions and low Br fraction in the optimum bandgap range for use in TSCs are predicted, which provides essential guidance for experimental composition optimization.

Results and discussion

Building dataset

To build the ML dataset, we search for the literatures reporting the bandgap of the perovskites. As for top cell of the TSCs, the bandgap of the perovskites shall be sufficiently large, so we only consider Pb-based perovskites and exclude out Sn-based perovskites. Furthermore, as Cl may be not be incorporated into the lattice of the as-reported Cl–I perovskites without Br,^25,36,37 so we also exclude the related reports. Herein, we got more than 300 data points from more than 120 recently published papers. Then we clean the data points by removing the duplicate data points with same material composition and bandgap values. For the data points with same material composition but different bandgap value, we reserve the data point with the most frequently reported and recently reported bandgap value. For example, for MAPbI₃, a typically reported value is 1.60 eV,^38,39 so we reserve the data point with a bandgap of 1.60 eV. As the reports on the bandgap information of CsPb(Cl_xBr_1−x)₃ films are quite few, we also did the experiments to obtain these information of CsPb(Cl_xBr_1−x)₃ (x = 0.1–0.5, the experimental results are shown in Fig. S1†). Finally, we got 109 data points for ML, which are listed in Table S1.† These data points cover Cl, Cl–Br mixed, Br, Br–I mixed, and I based perovskites with different A site cations including methylammonium (MA), formamidinium (FA) and cesium (Cs). The maximum bandgap of the perovskites is 3.16 eV from MAPbCl₃, while the smallest value is 1.48 eV from FAPbI₃.

Correlation between the components of perovskite with their bandgaps

We use the correlation matrix to learn the correlation between the ions and the bandgap of the perovskites. Correlation matrix presents the Pearson correlation between the components in the matrix, in which the value is the Pearson's coefficient (r value, the definition is shown in the Methods section). A larger r value means a stronger correlation between these two components. As shown in Fig. 1, the bandgap (abbreviated as E_g in Fig. 1) of the perovskites shows strong correlation with both the halide anions and the cations. As expected, the bandgap shows strong and positive correlation with Cl, so it is possible to enlarge the bandgap by a small amount of Cl. Among the three types of A-site cations (MA, FA and Cs), the bandgap has a negative correlation with FA, while it is positively changed with MA or Cs. It is proved that the observed band gap changes upon halide substitution are influenced by the electronic states of the halide anion, i.e., from Cl to Br to I, the valence band composition changes from 3p to 4p to 5p with a monotonic decrease in electron binding energy (lower ionization potential).⁴⁰ For iodide perovskites, the correlations between the bandgap and the cations are supposed to be determined by the size and the properties of the cations, which modify the bandgap through modifying the crystal lattice structure, tilting the MX₆ octahedra or by contracting the lattice isotropically in the condition of using smaller cations.^41,42 Hence, to get wide bandgap, it is important to adjust the cations and the halide ions simultaneously.

Fig. 1 Correlation matrix of the ions and the bandgap of the perovskites. Here, the ratios of FA, Cs, Cl and Br in Cs_aFA_bMA_(1−a−b)Pb(Cl_xBr_yI_(1−x−y))₃ perovskites are used as the input features for ML algorithms.

Performance of different ML algorithms

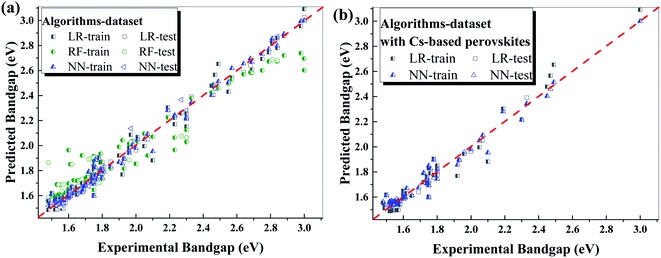
To learn the correlations between the compositions and the bandgap of the MHPs, we use R⁴³ tool employing 3 algorithms including linear regression (LR), neural network (NN) and random forest (RF). The 4 input features for the ML algorithms are the ratios of Cs, FA, Cl and Br in the perovskites with the formula of Cs_aFA_bMA_(1−a−b)Pb(Cl_xBr_yI_(1−x−y))₃, and the output is the bandgap value of the perovskite. We use 5-fold cross-validation method to optimize the performances of the ML algorithms. The dataset was randomly divided into 5 parts: 4 parts (80%, including 88 data points) for training (the training dataset) and 1 part (20%, including 21 data points) for testing (the test dataset). It means that 5 datasets used for the training, and 5 models will be obtained and are used to predict on both the training set and the test set. The model yields best performance on the test set is used for comparison and further prediction. In addition, the randomness of the dataset is also checked manually. The performances of the algorithms are evaluated using root mean square error (RMSE) and Pearson's coefficient (r value). RMSE directly evaluates the error between the predicted values and the experimental values of the dataset, which evaluates the accuracy of the algorithm in prediction. Pearson's coefficient (r value) shows the correlation between the predicted values and the experimental values of the dataset, and a larger r value means that they have a stronger correlation.

Table 1 summarizes the performances of different algorithms with RMSE and r value on the training dataset and the test dataset. Fig. 2 presents the comparison of the experimental bandgap values of the dataset and the predicted values from different algorithms including LR, NN and RF. The low RMSE value is realized by all the algorithms, indicating the high accuracy of these algorithms in predicting the bandgap values of the perovskites. Moreover, r value is higher than 0.94 for all algorithms, which means that the predicted values and the experimental values have strong correlation. In addition, the efficiencies of the algorithms are comparable, as shown in Table 1, which cost similar and short CPU time. To check the dependence of the accuracy of the ML algorithm on the size of the dataset, we carried out the NN algorithm on the datasets with different training set size. As shown by the Fig. S2,† the NN algorithm shows high accuracy on training set even at smaller dataset size, and it also shows high accuracy on test set. This reveals that the dataset size used in this work is large enough to get acceptable accuracy (RMSE < 0.05 eV).

Table 1 Performances of different ML algorithms in bandgap prediction of the perovskites

ML algorithms	Training set		Test set		Efficiency
	RMSE [eV]	r value	RMSE [eV]	r value	CPU time (s)
Linear regression	0.063	0.990	0.032	0.997	0.80
Random forest	0.134	0.973	0.145	0.947	0.77
Neural network	0.047	0.995	0.050	0.993	0.74

---

Fig. 2 Comparison of the predicted values from different algorithms and the experimental bandgaps of all perovskites (a) and Cs-based perovskites (b). The red dash line presents the condition in which the predicted value equals to the experimental value.

The high accuracy of the algorithms depends highly on data screening. To show the importance of the data screening, we evaluate the performance of LR algorithm on different datasets including the standard dataset with the data listed in Table S1† (dataset A) and the dataset with I–Cl MHPs (dataset B). Dataset B includes all 109 data points in dataset A and 3 additional datapoints with I–Cl MHPs (MAPb(Cl_0.05I_0.95)₃ (1.55 eV),⁴⁴ MAPb(Cl_0.33I_0.67)₃ (1.55 eV),⁴⁵ FA_0.3MA_0.7Pb(Cl_0.1I_0.9)₃ (1.5 eV)).⁴⁶ For dataset B, the LR model gives the RMSE of 0.085 eV (r = 0.982) and 0.056 eV (r = 0.993) on the training dataset and the test dataset, respectively. The comparison of the experimental bandgaps and the predicted values by these two models learned from dataset A and B is shown in Fig. S3.† It is clear that the model learned from dataset B is less accurate in predicting the bandgap values, especially for wide bandgap perovskites with a high content of Cl. Cl plays critical role in determining the bandgap of the perovskites, as can be seen from the importance results of the input features presented by RF algorithm (FA 22.1%, Cs 12.8%, Br 19.6%, Cl 36.6% increase in mean squared error) listed in Table S2.† As Cl may be not incorporated into the lattice of the as-reported I–Cl perovskites, the reports on their bandgap may not reflect the exact role of Cl in determining the bandgap. Hence, the real content of Cl is overestimated in these perovskites, leading to its underestimated effect on the bandgap. These results indicate the importance of the smart screening of the reported experimental dataset.

Among the three algorithms, LR and NN both perform excellent on both training and test dataset, which have quite low RMSE (<0.07 eV) and high r value (>0.99). Compared with NN algorithm, the model obtained from LR algorithm is facile to be understood and used to manually predict the bandgaps of the perovskite with unknown compositions. The relation between the bandgap (E_g) and the composition of the perovskite with the formula of Cs_aFA_bMA_(1−a−b)Pb (Cl_xBr_yI_(1−x−y))₃ can be expressed by the following equation:

E_g = 1.587 − 0.039a − 0.102b + 1.543x + 0.669y (1)

Though this correlation performs a RMSE of less than 0.07 eV in predicting the bandgaps of the perovskites, the predicted bandgaps show larger variation from the experimental results of Cs-based perovskites compared with NN algorithm. As shown in Fig. 2b, LR algorithm roughly underestimates the bandgap of Cs-based perovskites with narrow bandgaps (I and I–Br mixed perovskites), while overestimates the bandgap of Cs-based perovskites with wide bandgaps (Cl and Cl–Br mixed perovskites). In comparison, NN shows high consistency in predicting the bandgap of all the perovskites.

Optimization of LR model

The physical origin for the deviation of the predicted result by LR algorithm from the experimental results possibly correlate with the interplay of Cs and halide ions on the bandgap. In I-based perovskites, it is revealed that the introducing of small Cs cations can tilt the PbX₆ octahedra, leading to the increased bandgap.²² In Cl-based perovskites, Cs has no obvious effect in increasing the bandgap. For example, FAPbCl₃ and CsPbCl₃ have similar bandgap of 3.0 eV. Therefore, it may be retrodicted that Cs has no notable effect on tilting the PbX₆ octahedra in Cl-based perovskites. As the lattice distortion depends on the sizes of the cations and the halide ions, so we introduce a new feature R to incorporate this effect in LR algorithm. R is determined by the ratio and the size of the cations and the halide ions, which is expressed bywhere, a, b, x, y are the ratios of Cs, FA, Cl and I in Cs_aFA_bMA_(1−a−b)Pb(Cl_xBr_yI_(1−x−y))₃, respectively; r represents for the corresponding Shannon radii of the ions (r_Cs = 1.81 Å, r_FA = 2.79 Å, r_MA = 2.70 Å, r_Cl = 1.81 Å, r_Br = 1.96 Å, r_I = 2.03 Å). With the feature R, the performance of LR algorithm on Cs-based perovskites is notably improved, as shown in Fig. 3. In the improved model, the bandgap (E_g) is determined by

E_g = −4.960 + 2.214a − 0.315b + 0.814x + 0.436y + 4.913R (3)

Fig. 3 Comparison of the predicted values from LR algorithm based on different features (standard or with R feature) and the experimental bandgaps of Cs-based perovskites. The red dash line presents the condition in which the predicted value equals to the experimental value.

Compared with eqn (1), eqn (3) presents the different proportion of Cs concentration in determining the bandgap of the perovskites depending on the concentration of halide ions. This correlation shows a RMSE of 0.059 eV on training set (r = 0.992) and 0.039 eV on test set (r = 0.996). For instance, we compared the predicted results with the reported experimental values of the perovskites outside the data points shown in Table S1.† The experimental bandgaps of Cs_0.25FA_0.75Pb(Cl_0.05Br_0.15I_0.8)₃, Cs_0.25FA_0.75Pb(Br_0.2I_0.8)₃, and Cs_0.25FA_0.75Pb(Br_0.15I_0.85)₃ are >1.67 eV, 1.67 eV, and 1.63 eV,³⁶ respectively, while the predicted values are 1.689 eV, 1.647 eV, and 1.614 eV. It can be seen that the deviations between the experimental and the predicted results are less than 0.3 eV, revealing the high prediction accuracy of eqn (2) and (3). Hence, they can be used to manually predict the bandgap of the perovskites with a high accuracy.

Bandgap prediction by NN algorithm

As NN algorithm takes the interplay of cations and anions on the bandgap of the perovskites into account, so it predicts the whole range of data much accurately. Hence, we employ NN algorithm to screen perovskites with desired compositions and bandgaps. Here, the MHPs with high iodide ratio and wide bandgap are of great interest. Hence, a series of perovskite compositions, i.e., MA_(1−a−b)FA_aCs_bPb(Cl_(1−x−y)Br_xI_y)₃, (0 ≤ a, b ≤ 1, 0 < x < 0.3, 0.7 < y < 1), are predicted by NN algorithm trained by the experimental results shown Table S1.† The predicted bandgap of the perovskites varies in the scale of 1.536–2.026 eV.

To clearly shown the effects of the ion ratio on the bandgap of the perovskites, the 4D plots of the predicted bandgaps and the ion ratios are shown in Fig. 4. Fig. 4a shows the variation of the bandgap of FA_0.75Cs_0.25Pb(Cl_(1−x−y)Br_xI_y)₃ with the ratio of halide ions. It is obvious that Cl doping increases the bandgap of the perovskites, i.e., increasing the ratio of Cl from 0 to 0.15 (fixing Br ratio to be 0.1) increases the bandgap from 1.592 eV to 1.830 eV. In comparison, increasing the doping ratio of Br from 0.05 to 0.20 (fixing Cl ratio to be 0.05) increases the bandgap from 1.634 eV to 1.718 eV. Fig. 4b shows the variation of the bandgap of Cs_aFA_bMA_(1−a−b)Pb(Cl_0.05Br_0.15I_0.8)₃ with the ratio of cations. It can be seen that a high concentration of Cs benefits for obtaining wide bandgap in I-dominated perovskites. Therefore, to obtain wide bandgap and I-dominated perovskites, it is critical to increase the doping ratios of Cl and Cs.

Fig. 4 4D plots of the predicted bandgaps (unit: eV) of the perovskites with different ion ratios by neutral net algorithm trained by the experimental data listed in Table S1.† (a) Change the ratio of halide ions, while the cations ratios of FA, MA, and Cs are fixed to be 0.75, 0, and 0.25; (b) change the ratio of cations, while the halide ratios of Cl, Br, and I are fixed to be 0.05, 0.15, and 0.8.

To further explore the possible interplay of A site cations and halide ions on the bandgap of the perovskites, the bandgaps of pure halide perovskites, Cs_aFA_bMA_(1−a−b)PbX₃, (0 ≤ a, b ≤ 1, X = Cl, Br or I), are also predicted by NN algorithm trained by the experimental data listed in Table S1.† For pure iodide perovskites, increasing the ratio of Cs increases the bandgap, while increasing the ratio of FA decreases the bandgap. This is consistent with the general knowledge obtained from experimental results. For pure chloride perovskites, Cs and FA show comparable influence on the bandgap.

From these results, it can be speculated that simultaneously modifying the ratios of Cl and Cs in I-based MHPs may induce a complex change of bandgaps, which is not same to that of pure I- or Cl-based perovskites. Hence, it is critical to predict the bandgaps of the MHPs through machine learning algorithms to meet the requirements for different applications. To clearly shown the potential perovskites for TSCs, we screen a series of the perovskites with the predicted bandgaps of 1.650–1.710 eV and 1.780–1.840 eV for use in 2T and 4T TSCs, respectively, and with the following rules: (1) iodide ratio is as high as 0.8 to suppress halide segregation, (2) Br ratio is not lower than Cl ratio for ease fabrication, (3) MA ratio is 0 to enable high device stability. The screened perovskite compositions are listed in Table S2.† Table 2 shows some representative compositions, which have one kind of cations as the major cation to avoid possible phase segregation during fabrication with present techniques.^21,47 To verify the accuracy of the predicted values, we compare them with the experimental results reported in the literature and our experimental result. The experimental bandgaps of FA_0.75Cs_0.25Pb(Cl_0.05Br_0.15I_0.8)₃ and FA_0.8Cs_0.2Pb(Cl_0.05Br_0.15I_0.8)₃ are >1.67 eV (ref. 36) and 1.65 eV (our experimental result), respectively, while the predicted values are 1.688 eV and 1.680 eV. The deviations between the experimental and the predicted results are extraordinarily little, revealing the high accuracy of the prediction model. In addition, we also compared the photostability of triple-halide MHPs (FA_0.8Cs_0.2Pb(Cl_0.05Br_0.15I_0.8)₃) with that of Br–I MHPs (FA_0.8Cs_0.2Pb(Br_0.3I_0.7)₃) with similar bandgap values. FA_0.8Cs_0.2Pb(Cl_0.05Br_0.15I_0.8)₃ shows less redshift than that of FA_0.8Cs_0.2Pb(Br_0.3I_0.7)₃ after continuous irradiation for 5 h, which reveals the higher photostability of triple-halide perovskites.

Table 2 Some representative compositions of the FACsPb(Cl_xBr_(0.2−x)I_0.8)₃ perovskites with the predicted bandgaps of 1.650–1.710 eV and 1.780–1.840 eV by NN algorithm trained by the experimental data listed in Table S1

TSCs	Predicted bandgap	Experimental bandgap	FA/(FA + MA + Cs)	Cs/(FA + MA + Cs)	Br/(Cl + Br + I)	Cl/(Cl + Br + I)
2T	1.651	—	0.70	0.30	0.2	0
	1.697	—	0.70	0.30	0.15	0.05
	1.688	>1.67	0.75	0.25
	1.680	1.65	0.80	0.20
	1.672	—	0.85	0.15
	1.664		0.90	0.10
	1.657		0.95	0.05
4T	1.783	—	0	1	0.2	0
	1.827	—	0	1	0.15	0.05
	1.818		0.05	0.95
	1.808		0.1	0.9
	1.798		0.15	0.85
	1.788		0.20	0.80

---

Methods

R (version 3.6.2) tool was employed as the platform for machine learning. Correlation matrix analysis was carried out based on Pearson correlation and using corr function. The linear regression (LR), neural network (NN) and random forest (RF) algorithms were used for learning based on glm, neuralnet, and randomForest functions, respectively. The NN algorithm has 3 layers, which have 4, 4 and 4 neurons, respectively. The tree number in RF algorithm was 100. The number of neurons, the layer number, the tree number and other important parameters used in NN and RF algorithms were optimized in advance. The performances of the algorithms are evaluated by root mean square error (RMSE) and Pearson's coefficient (r value) on the test set. Here,

X_i, Y_i, X̄, Ȳ, and n represent for the i^th value of experimental bandgap dataset, the i^th value of predicted bandgap dataset, the mean value of the experimental bandgap dataset, the mean value of the predicted bandgap data set, and the number of the dataset points, respectively. The ratio of the test dataset is 0.2. To train the ML algorithms, we use 5-fold cross-validation, which employed the createFolds function and randomly divided the dataset into 5 parts (80% data points for training and 20% for test) and did the learning for 5 times. The model of the algorithm performing the lowest RMSE on test set was screened for further learning.

Conclusion

In summary, the bandgap tuning strategy by cations and halide ions is revealed by machine learning, and the neural network algorithm presents high accuracy in predicting the bandgap of the perovskites from their components. In addition, we show that A site cations and halide ions have synergetic effect on the bandgap, which makes the bandgap prediction in triple halide MHPs more complicated than commonly used Br–I MHPs. Considering this effect, we modify the linear regression model and presents a function of the bandgap with the change of the ion ratios for manual prediction. Moreover, a series of mixed halide perovskites with required bandgaps and high iodide ratio for suppressing halide segregation are predicted by neural network, which have great potential for application in highly efficient stable perovskite solar cells and are referable for experiments. These results reveal that machine learning is an efficient tool to explore and design new mixed halide perovskites, which will greatly reduce the time and material cost in experiments.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Beijing Natural Science Foundation (No. 2192045), the National Natural Science Foundation of China under Grant No. 61775013, and 62075006, the Educational Research Project of Young and Middle-Aged Teachers in Fujian Province (No. JAT190072), National Natural Science Foundation (No. 52002070).

References

1. Y. R. Park, S. Eom, H. H. Kim, W. K. Choi and Y. Kang, Sci. Rep., 2020, 10, 1–10.
2. G. Kim, H. Min, K. S. Lee, S. M. Yoon and S. I. Seok, Science, 2020, 370, 108–112.
3. C. Xie, X. Zhao, E. W. Y. Ong and Z.-K. Tan, Nat. Commun., 2020, 11, 1–5.
4. J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764–1769.
5. J. Albero, A. M. Asiri and H. García, J. Mater. Chem. A, 2016, 4, 4353–4364.
6. G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988.
7. D. P. McMeekin, G. Sadoughi, W. Rehman, G. E. Eperon, M. Saliba, M. T. Hörantner, A. Haghighirad, N. Sakai, L. Korte and B. Rech, Science, 2016, 351, 151–155.
8. Z. Yu, Z. Yang, Z. Ni, Y. Shao, B. Chen, Y. Lin, H. Wei, Z. J. Yu, Z. Holman and J. Huang, Nat. Energy, 2020, 5, 657–665.
9. K. Jayawardena, S. Silva and R. Misra, J. Mater. Chem. C, 2020, 8, 10641–10675.
10. F. Fu, T. Feurer, T. Jäger, E. Avancini, B. Bissig, S. Yoon, S. Buecheler and A. N. Tiwari, Nat. Commun., 2015, 6, 1–9.
11. Z. Wang, X. Zhu, S. Zuo, M. Chen, C. Zhang, C. Wang, X. Ren, Z. Yang, Z. Liu and X. Xu, Adv. Funct. Mater., 2020, 30, 1908298.
12. M. H. Futscher and B. Ehrler, ACS Energy Lett., 2016, 1, 863–868.
13. E. Aydin, T. G. Allen, M. De Bastiani, L. Xu, J. Ávila, M. Salvador, E. Van Kerschaver and S. De Wolf, Nat. Energy, 2020, 5, 851–859.
14. E. T. Hoke, D. J. Slotcavage, E. R. Dohner, A. R. Bowring, H. I. Karunadasa and M. D. McGehee, Chem. Sci., 2015, 6, 613–617.
15. I. L. Braly, R. J. Stoddard, A. Rajagopal, A. R. Uhl, J. K. Katahara, A. K.-Y. Jen and H. W. Hillhouse, ACS Energy Lett., 2017, 2, 1841–1847.
16. D. W. DeQuilettes, W. Zhang, V. M. Burlakov, D. J. Graham, T. Leijtens, A. Osherov, V. Bulović, H. J. Snaith, D. S. Ginger and S. D. Stranks, Nat. Commun., 2016, 7, 1–9.
17. A. J. Knight and L. M. Herz, Energy Environ. Sci., 2020, 13, 2024–2046.
18. Y. Li, D. Song, J. Meng, J. Dong, Y. Lu, X. Huo, A. Maqsood, Y. Song, S. Zhao and B. Qiao, J. Mater. Sci., 2020, 55, 9787–9794.
19. H. Tan, F. Che, M. Wei, Y. Zhao, M. I. Saidaminov, P. Todorović, D. Broberg, G. Walters, F. Tan and T. Zhuang, Nat. Commun., 2018, 9, 1–10.
20. W. Fan, Y. Shi, T. Shi, S. Chu, W. Chen, K. O. Ighodalo, J. Zhao, X. Li and Z. Xiao, ACS Energy Lett., 2019, 4, 2052–2058.
21. K. A. Bush, K. Frohna, R. Prasanna, R. E. Beal, T. Leijtens, S. A. Swifter and M. D. McGehee, ACS Energy Lett., 2018, 3, 428–435.
22. R. Prasanna, A. Gold-Parker, T. Leijtens, B. Conings, A. Babayigit, H.-G. Boyen, M. F. Toney and M. D. McGehee, J. Am. Chem. Soc., 2017, 139, 11117–11124.
23. N. K. Kumawat, A. Dey, A. Kumar, S. P. Gopinathan, K. L. Narasimhan and D. Kabra, ACS Appl. Mater. Interfaces, 2015, 7, 13119–13124.
24. S. Gharibzadeh, B. Abdollahi Nejand, M. Jakoby, T. Abzieher, D. Hauschild, S. Moghadamzadeh, J. A. Schwenzer, P. Brenner, R. Schmager, A. A. Haghighirad, L. Weinhardt, U. Lemmer, B. S. Richards, I. A. Howard and U. W. Paetzold, Adv. Energy Mater., 2019, 9, 1803699.
25. M. Kim, G.-H. Kim, T. K. Lee, I. W. Choi, H. W. Choi, Y. Jo, Y. J. Yoon, J. W. Kim, J. Lee and D. Huh, Joule, 2019, 3, 2179–2192.
26. J. Jeong, H.-B. Kim, H. Kim, B. Walker, S. Song, J. Heo, Y. J. Yoon, Y. Jo, H. Choi and G.-H. Kim, ACS Energy Lett., 2016, 1, 712–718.
27. C. Zuo and L. Ding, Nanoscale, 2014, 6, 9935–9938.
28. J. Li, B. Pradhan, S. Gaur and J. Thomas, Adv. Energy Mater., 2019, 9, 1901891.
29. A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331.
30. P. Raccuglia, K. C. Elbert, P. D. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76.
31. C. Chen, Y. Zuo, W. Ye, X. Li, Z. Deng and S. P. Ong, Adv. Energy Mater., 2020, 10, 1903242.
32. G. H. Gu, J. Noh, I. Kim and Y. Jung, J. Mater. Chem. A, 2019, 7, 17096–17117.
33. J. Li, B. Pradhan, S. Gaur and J. Thomas, Adv. Energy Mater., 2019, 9, 1901891.
34. H. Park, R. Mall, F. H. Alharbi, S. Sanvito, N. Tabet, H. Bensmail and F. El-Mellouhi, Phys. Chem. Chem. Phys., 2019, 21, 1078–1088.
35. J. Im, S. Lee, T.-W. Ko, H. W. Kim, Y. Hyon and H. Chang, npj Comput. Mater., 2019, 5, 1–8.
36. J. Xu, C. C. Boyd, J. Y. Zhengshan, A. F. Palmstrom, D. J. Witter, B. W. Larson, R. M. France, J. Werner, S. P. Harvey and E. J. Wolf, Science, 2020, 367, 1097–1104.
37. V. L. Pool, A. Gold-Parker, M. D. McGehee and M. F. Toney, Chem. Mater., 2015, 27, 7240–7243.
38. S. Draguta, O. Sharia, S. J. Yoon, M. C. Brennan, Y. V. Morozov, J. S. Manser, P. V. Kamat, W. F. Schneider and M. Kuno, Nat. Commun., 2017, 8, 1–8.
39. D. Luo, R. Su, W. Zhang, Q. Gong and R. Zhu, Nat. Rev. Mater., 2020, 5, 44–60.
40. A. Walsh, J. Phys. Chem. C, 2015, 119, 5755–5760.
41. C. Yi, J. Luo, S. Meloni, A. Boziki, N. Ashari-Astani, C. Grätzel, S. M. Zakeeruddin, U. Röthlisberger and M. Grätzel, Energy Environ. Sci., 2016, 9, 656–662.
42. M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate and A. Hagfeldt, Energy Environ. Sci., 2016, 9, 1989–1997.
43. https://github.com/wxAMPS/wxAMPS3.
44. W. Nie, H. Tsai, R. Asadpour, J.-C. Blancon, A. J. Neukirch, G. Gupta, J. J. Crochet, M. Chhowalla, S. Tretiak and M. A. Alam, Science, 2015, 347, 522–525.
45. S. Sajid, A. M. Elseman, D. Wei, J. Ji, S. Dou, H. Huang, P. Cui and M. Li, Nano Energy, 2019, 55, 470–476.
46. L. Chen, G. Wang, L. Niu, Y. Yao, Y. Guan, Y. Cui and Q. Song, RSC Adv., 2018, 8, 15961–15966.
47. Y. Zhou, Y. H. Jia, H. H. Fang, M. A. Loi, F. Y. Xie, L. Gong, M. C. Qin, X. H. Lu, C. P. Wong and N. Zhao, Adv. Funct. Mater., 2018, 28, 1803130.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03117a

‡ These authors contributed equally: Yaoyao Li, Yao Lu.

---