Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revisiting the valence stability and preparation of perovskite structure type oxides ABO3 with the use of Madelung electrostatic potential energy and lattice site potential
Masahiro Yoshimura†
 *a and
Kripasindhu Sardarb
*a and
Kripasindhu Sardarb
aTokyo Institute of Technology, Tokyo, Japan. E-mail: yoshimur@ncku.edu.tw
bDepartment of Material Science and Engineering, National Cheng Kung University, Tainan, 701, Taiwan
First published on 10th June 2021
Abstract
Valence stability of aliovalent ions is mostly correlated with lattice site potential in ionic crystals. Madelung electrostatic potential is obtained by adding all the lattice site potentials for all the ions present in a crystal structure. Therefore, valence stability and the stability of a crystal structure can be better understood with consideration of both the lattice site potential and Madelung electrostatic potential. This was first demonstrated more than four decades ago by one of the present authors. We revisit this situation by using re-calculated lattice site potential and Madelung electrostatic potential for perovskite structure type ABO3 compounds using a new computer program VESTA. We show that the formation of a perovskite structure type compound with the general formula ABO3 (where A and B are cations and O is an oxide ion) becomes energetically favorable when it has a higher Madelung electrostatic potential than the combined Madelung electrostatic potential of parent binary compounds AO and B2O3 or BO2. It is further shown that strong lattice site potential results in stability of high valence or high valence ions can be stabilized in a lattice site with strong lattice-site potential. It further follows that certain ions experience maximum lattice site potential at the B ion lattice site of the perovskite structure when compared to other structures such as fluorite BO2, rutile BO2 and corundum B2O3. Therefore, (i) the stability of an ion with a high (and uncommon) valence state at the B site being higher than that at the A site, (ii) occurrence of point defects at A or O sites with weak lattice site potentials, respectively and (iii) instability of perovskite A4+B2+O3, and A5+B1+O3 compounds, respectively can be rationalized by lattice site potential and Madelung electrostatic potential analysis.
Introduction
An enormous number of solids show crystallographic structural similarity to the mineral perovskite (CaTiO3) and have the general formula ABX3. Metal oxides with chemical formula ABO3 are a subclass of this large family of compounds. For many years, perovskite oxides have been studied extensively in the literature of chemistry, physics and geology for a large variety of solid state phenomena associated with electric, optical, thermal and magnetic properties. A large number of oxides with perovskite type structures are possible to synthesise in a laboratory for applications in vast areas spanning from electronics to catalysis. It is of immense importance to understand the factors that may correlate with the formation and stability of perovskite structure type ABO3 compounds for the design of new compounds with novel structures containing desired valence states of B cations.The reason for why many compounds would take perovskite structure type ABX3 had been explained from ion-packing & tolerance factor, by Goldschmidt in 1926.1 Even now, most of the research articles and text books on the assessment of stability of perovskite structure type ABO3 oxides focus on the geometric parameters such as tolerance factor, and structure-field map.2–5 However, lattice and valence stabilities should be more related to thermodynamic energy and originate from thermodynamic principles rather than numerical geometrical parameters. Crystal chemistry and thermodynamic energy of ionic solids are reflected into Madelung electrostatic potential as shown by Van Gool and Piken in 1969.6,7 “The valence stability using lattice site-potential” of perovskite structure type ABO3 was demonstrated by one of the authors of this article (M. Yoshimura) and was considered for the first time in 1974.8 This was referred by Rustam Roy in 1975 in a plenary lecture presented as the Robert B. Sosman Memorial Lecture at the 77th annual meeting of the American ceramics society and was published in 1977.9 This is a novel and very less explored concept. We also note that not many researchers have been able to consider this concept perhaps due to the inaccessibility of the original article.8 Here, the present article is written by re-visiting Madelung lattice energy and site potentials based upon recent data calculated using VESTA10 program and recent crystallographic (structural) and thermodynamic data. We emphasize on the fact that ionic solids are stabilized due to the gain in lattice energy that is reflected in Madelung electrostatic potential (EM). Nevertheless, recently, Hoppe demonstrated that the enthalpy of formation of solids is reflected in Madelung electrostatic potential in 199511 and Glasser has shown that for ionic solids the lattice energy and Madelung electrostatic potential energy (EM) has a linear relationship in 2012.12
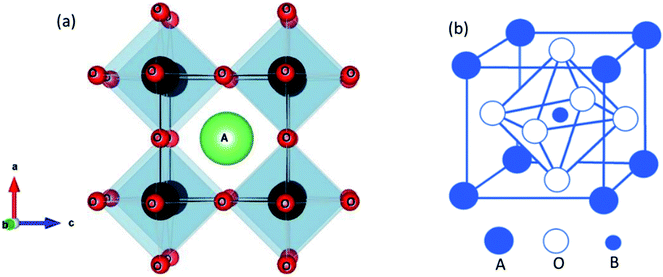
The ideal perovskite structure type of ABO3 compound has a cubic unit cell. This structure can be constructed from corner shared BO6 octahedra with A cation being present at the 12 coordinated interstitial position within the octahedral network (Fig. 1a). A and B cations are coordinated by 12 and six O2− ions, respectively and O2− ion is coordinated by four A and two B cations. Several structural modification of cubic perovskite structure has been identified such as tetragonal, orthorhombic, rhombohedral, hexagonal, and monoclinic, respectively either as polymorph of ABO3 or upon chemical modification. The most important chemical fact of ABO3 perovskite compound is that, apart from noble gasses and nonmetals, A or B in ABO3 can be chosen from almost all elements and several aliovalent A or B ions such as 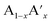 or
or 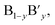 respectively can be combined in a single compound. Furthermore, non-ideal stoichiometry of oxygen or A such as ABO3−z or A1−xBO3, respectively are regularly observed. It is further interesting that many BO3 compounds can adopt perovskite type structure where A cation is completely absent for example ReO3. Therefore, the structural skeleton formation by BO3 sub lattice is generally regarded as prerequisite for the formation of perovskite structure type compounds.2 Furthermore, the BO3 sub lattice skeleton is primarily stabilized by the electrostatic potential energy gain by ionic arrangements in solid phase and additional stability of perovskite type ABO3 compounds can arise from (i) the presence of large A cation within the interstitial position, (ii) crystal field splitting and (iii) hybridization of orbitals.2
respectively can be combined in a single compound. Furthermore, non-ideal stoichiometry of oxygen or A such as ABO3−z or A1−xBO3, respectively are regularly observed. It is further interesting that many BO3 compounds can adopt perovskite type structure where A cation is completely absent for example ReO3. Therefore, the structural skeleton formation by BO3 sub lattice is generally regarded as prerequisite for the formation of perovskite structure type compounds.2 Furthermore, the BO3 sub lattice skeleton is primarily stabilized by the electrostatic potential energy gain by ionic arrangements in solid phase and additional stability of perovskite type ABO3 compounds can arise from (i) the presence of large A cation within the interstitial position, (ii) crystal field splitting and (iii) hybridization of orbitals.2
The total internal energy of ionic solids may be expressed as
| E = EM + EN | (1) |
The analysis of Madelung electrostatic potential and lattice site potential of a large number ABO3 compounds (with varying combination of A and B) led to a set of fundamental criteria for the formation of perovskite structure type ABO3 with varying combination and valence states of A and B and summarized by Yoshimura et al.8,14 as follows: oxides of A can be reacted with oxides of B to form perovskite structure type ABO3 compounds if: (i) B ion is smaller than A ion, (ii) valence of B ion is larger or equal to A ion and (iii) sum of valence of A and B ion is six (including mixed valence situation 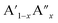 or
or 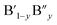 ). An in depth analysis showed that the valence stability originates from gain of lattice site potential. Recently, there have been some excellent research work reported in the literature based on the use of Madelung electrostatic potentials energy for understanding the stability of perovskite structure type compounds. Shan et al. investigated Li ion insertion in perovskite structure type SrVO3−δ, La2/3TiO3−δ and (La, Li)TiO3−δ, from the lattice site potential analysis and found that the insertion of lithium ion is limited by the effect of lattice site potential on the valence stability of V and Ti.15 In these perovskite structure type oxides, the valence state of tetravalent V and Ti can be reduced to 3 upon insertion of monovalent Li ion at an interstitial site. It is interesting to note that for spinel structure type LiMn2O4 compounds, Ragavendran et al. have shown that the Madelung electrostatic potential of LixMn2O4 almost linearly correlates with x and therefore voltage of Li-ion battery made using LiMn2O4 can be easily estimated from the Madelung electrostatic potential.16 Furthermore, the perovskite structure-type is not limited to ABO3 and a large number of organic–inorganic halide crystallise into perovskite type structure with general formula ABX3. A bottle neck for the realization of full potential of so called ‘perovskite solar cells’ and related electronic devices has been the degradation of electronic devices fabricated using hybrid organic–inorganic ABX3 compounds.17 The degradation of these devices arise from instability of the perovskite structure type hybrid compounds and can also be understood from Madelung electrostatic potential analysis.18 Furthermore, it has also been shown that the stability of oxides such as Li4SiO4 towards the reaction Li4SiO4 + CO2 → Li2SiO3 + Li2CO3 has direct consequence on the CO2 capture and storage abilities and recent study by Oh-ishi et al. had successfully employed lattice site potentials analysis of all Li+ ions in the unit cells of Li4SiO4, Li2SiO3, and Li2CO3 to evaluate the extraordinary stability.19
). An in depth analysis showed that the valence stability originates from gain of lattice site potential. Recently, there have been some excellent research work reported in the literature based on the use of Madelung electrostatic potentials energy for understanding the stability of perovskite structure type compounds. Shan et al. investigated Li ion insertion in perovskite structure type SrVO3−δ, La2/3TiO3−δ and (La, Li)TiO3−δ, from the lattice site potential analysis and found that the insertion of lithium ion is limited by the effect of lattice site potential on the valence stability of V and Ti.15 In these perovskite structure type oxides, the valence state of tetravalent V and Ti can be reduced to 3 upon insertion of monovalent Li ion at an interstitial site. It is interesting to note that for spinel structure type LiMn2O4 compounds, Ragavendran et al. have shown that the Madelung electrostatic potential of LixMn2O4 almost linearly correlates with x and therefore voltage of Li-ion battery made using LiMn2O4 can be easily estimated from the Madelung electrostatic potential.16 Furthermore, the perovskite structure-type is not limited to ABO3 and a large number of organic–inorganic halide crystallise into perovskite type structure with general formula ABX3. A bottle neck for the realization of full potential of so called ‘perovskite solar cells’ and related electronic devices has been the degradation of electronic devices fabricated using hybrid organic–inorganic ABX3 compounds.17 The degradation of these devices arise from instability of the perovskite structure type hybrid compounds and can also be understood from Madelung electrostatic potential analysis.18 Furthermore, it has also been shown that the stability of oxides such as Li4SiO4 towards the reaction Li4SiO4 + CO2 → Li2SiO3 + Li2CO3 has direct consequence on the CO2 capture and storage abilities and recent study by Oh-ishi et al. had successfully employed lattice site potentials analysis of all Li+ ions in the unit cells of Li4SiO4, Li2SiO3, and Li2CO3 to evaluate the extraordinary stability.19
On the other hand, lattice site potential can be used for the estimation of the oxygen to metal charge transfer and bandgap of perovskite type ABO3 oxides using an ionic model developed by Zaanen et al.20 and demonstrated in a large number of oxides by Torrance et al.21 and Arima et al.22 Kato et al. employed lattice site potential analysis to show that the valence band structure can be tailored by designing the stacking sequence of layers of a number of layered compounds BiOX (X = Cl, Br, I), Bi4NbO8X (X = Cl, Br), Bi2GdO4X (X = Cl, Br), and SrBiO2X (X = Cl, Br, I) and therefore, lattice site potential analysis may be useful for designing new photocatalysts.23 Here we look back at the development of Madelung electrostatic potential and lattice site potential only for perovskite type ABO3 oxides. We show that the lattice and valence stabilities of perovskite structure type ABO3 compounds can be understood from simple Madelung electrostatic potential view point and valence stability is directly related to the lattice site potential. Based on the existing literatures, our hypothesis is that the stability and properties of perovskite type ABO3 oxides can be rationalized better in terms of change in Madelung electrostatic potential energies rather than structural perturbation such as distortions and tolerance factors.24,25
The Madelung electrostatic potential and lattice site potentials can be calculated using commercial first principle calculation software packages. We have used freely available software VESTA10 to recalculate the lattice site potentials and Madelung electrostatic potential directly from the known crystal structures. The Madelung electrostatic potential EM obtained from VESTA has the unit of MJ mol−1 asymmetric unit. In order to compare EM per mole of each compound with different crystal symmetry (space groups), the EM output of each compound from VESTA was multiplied by the multiplicity of general Wyckoff position and divided by the number of formula units in the unit cell.
Results and discussion
According to Van Gool and Piken,6,7 the Madelung electrostatic potential energy EM can be expressed as
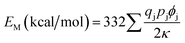 | (2) |
The Madelung constant can be expressed as
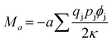 | (3) |
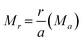 | (4) |
From eqn (2)–(4) the Madelung electrostatic potential can be expressed by
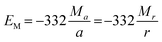 | (5) |
In VESTA,10 lattice site potential ϕi and Madelung electrostatic potential EM of a given structure is calculated using following equations
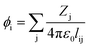 | (6) |
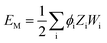 | (7) |
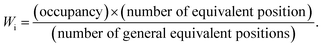
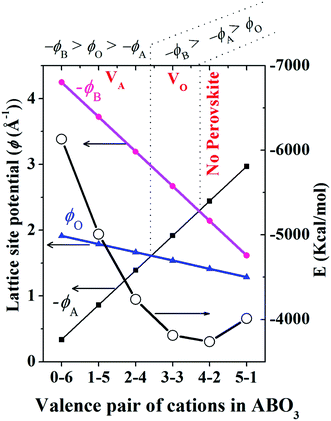
For similar structures with fixed atomic position (e.g. NaCl, CsCl), the lattice site potential ϕj for each site in the crystal structure is inversely proportional to the characteristic length. However, if the characteristic length is fixed, for the first time Yoshimura et al.8 had analyzed that, lattice site potential ϕj, the Madelung constant Ma and Madelung electrostatic potential energy EM varies with the valence states. Fig. 2 shows the relationship between valence state and lattice site potentials ϕj as well as Madelung electrostatic potential EM in ideal cubic perovskite type structure of ABO3 with fixed lattice constant of 3.881 Å. Based on eqn (5) the Madelung constant Ma also shows similar trend with valence. Fig. 2 shows that the lattice site potential at A site (ϕA) and O site (ϕO) increase with the valence (0–6), (1–5), (2–4), (3–3) (the first number indicates valence of A and second number indicates valence of B) while the lattice site potential of B ion (ϕB) decreases. This re-calculated trend of lattice potential with valence pairs is in excellent agreement with that obtained from method developed by Van Gool and Piken,6,7 and adapted by Yoshimura et al. in 1974.8 All calculations were performed using VESTA10 employing the radius of ionic sphere and reciprocal space range of 1.6 Å and 10 Å−1, respectively. For the calculation of ϕ and EM of A0B6+O3, a dummy A such as Na atom was placed at (½ ½ ½) and B cation Re6+ at (0 0 0) atomic coordinates, respectively of space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (221) with both valence and occupancy, respectively of A were set to zero. The calculation for valence pairs (4–2) and (5–1) assumed hypothetical A4+B2+O3 and A5+B1+O3 perovskite structure type compounds because they rarely exist.
m (221) with both valence and occupancy, respectively of A were set to zero. The calculation for valence pairs (4–2) and (5–1) assumed hypothetical A4+B2+O3 and A5+B1+O3 perovskite structure type compounds because they rarely exist.
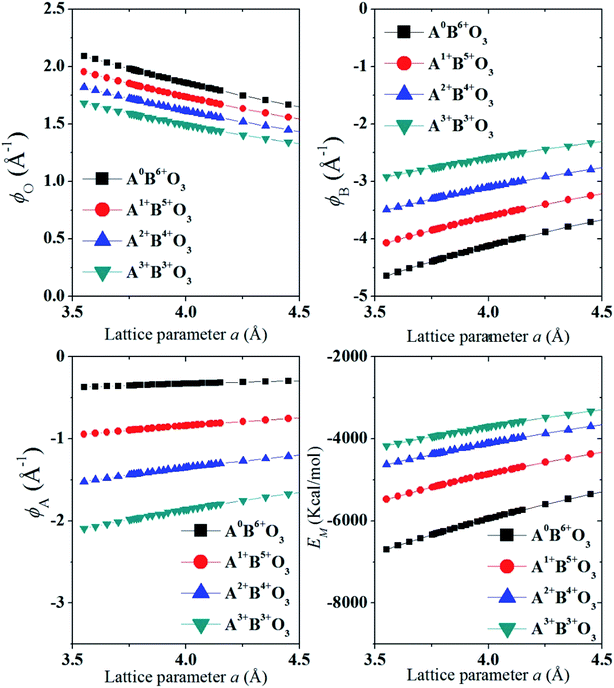
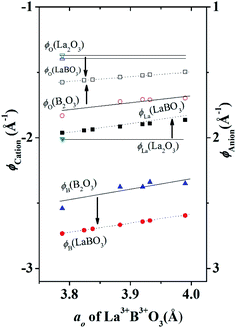
In Fig. 3 we show that, how the lattice site potential (ϕ) of each ionic site and Madelung electrostatic potential (EM) energy changes with lattice parameter when valence is fixed, for each valence pair in each perovskite structure type ABO3. The variation observed in Fig. 3 is consistent with the observation of Sabry et al. in 2000 (ref. 24). From Fig. 2 and 3 it is observed that lattice site potential for all sites change significantly with valence pairs. Lattice site potential for oxygen in A3+B3+O3 is lowest. Therefore, it can be expected that oxygen can be easily removed from the perovskite type compounds with A3+B3+O3 than A0+B6+O3. Indeed, the occurrence of oxygen vacancy is very common in A3+B3+O3 and this may be of importance during designing catalysts for the availability of active lattice oxygen or designing materials for p- or n- type conductivity.24,26
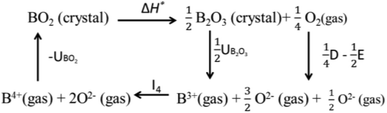
Valence stability is related to lattice energy which mainly arises from Madelung electrostatic potential and more directly related to lattice site potential. We first consider the valence stability of B ions in oxides where both 4+ and 3+ valence state of B ion is known. Example of such B ions are Ce3+/4+, Pr3+/4+ and Tb3+/4+. In order to understand the relative stability of B4+O2 and B23+O3 we consider the enthalpy change (8) of the decomposition reaction BO2 → ½B2O3 + ¼O2 and corresponding Born–Haber cycle (Scheme 1)
| ΔH* = (UBO2 − ½UB2O3) − I4 − ¼D + ½E | (8) |
Eqn (8) suggests that high valence of B in oxide BO2 can be stable if its lattice energy is compensated by other energy terms. Since, the lattice energy is enthalpy at T = 0 K (ΔHo = ΔUo = ΔGo; the energy terms such as ΔS and RT do not contribute at T = 0 K), one can postulate that the stability of high valence ions is enhanced in crystal structure with large lattice energies. A similar analogy can be drawn for the valence stability in complex oxides where multiple ions are present such as in perovskite type ABO3 compounds. Furthermore, cations provide large electrostatic potential contribution to the total Madelung electrostatic potential in crystal structure as shown in the plots of ϕA and ϕB in Fig. 3. This is in excellent with the trend of cation site potentials observed by Sabry et al.24 Therefore, the valence stability of cation is rather directly related to the lattice-site potential of the cation site in a crystal structure and the stability enhances when they are present in lattice site with strong lattice site potential such as B site in perovskite structure type ABO3 oxides.
A number of experimental study has indicated that high valence of some B cation is stable in perovskite type A2+B4+O3 oxides but not in fluorite type B4+O2. For example, investigation on the synthesis of perovskite type ABO3 compounds had revealed that several stable perovskite type A2+B4+O3 compounds (with A = Ba, Sr and B = Ce, Tb, Pr) can be synthesized and are stable at room temperatures in spite of the poor ambient condition stability of Pr4+O2 and Tb4+O2 and existence of both Ce23+O3 and Ce4+O2.27 In order to explain this experimental fact, an in depth analysis of lattice site potential and Madelung site potential was presented in.8 Here, we have recalculated the lattice site potential and Madelung electrostatic potential using VESTA10 and presented in Table 1. Our recently calculated values show excellent matches with that using the procedure of Van Gool and Piken.8 In Table 1 the lattice site potential of A ion in all perovskite structure type compounds appear to be close to those of AO but for B ion, the perovskite structure provides significant lattice site potential gain than that in fluorite structure. Except for BaTbO3 which we believe due to not so accurate estimation of lattice parameter for TbO2.
| Compound | Crystal structure | Lattice constanta (Å) | Madelung electrostatic potential EM (kcal mol−1) | Difference ΔEMb (kcal mol−1) | Lattice site potential (Å−1) | ||
|---|---|---|---|---|---|---|---|
| ϕA | ϕB | ϕO | |||||
| a Pseudocubic lattice parameters from a: ref. 31 and b: ref. 27.b ΔEM = EM(ABO3) − [EM(AO) + EM(BO2)]. | |||||||
| CeO2 | Fluorite | 5.411a | −2855.431 | −2.801 | 1.504 | ||
| PrO2 | 5.393a | −2864.947 | −2.811 | 1.509 | |||
| TbO2 | 5.22a | −2959.725 | −2.904 | 1.559 | |||
| BaO | NaCl | 5.523a | −840.791 | −1.269 | 1.269 | ||
| SrO | 5.160a | −899.696 | −1.358 | 1.358 | |||
| BaCeO3 | Perovskite | 4.396b | −3738.779 | −42.6 | −1.228 | −2.822 | 1.469 |
| BaPrO3 | 4.372b | −3759.255 | −53.5 | −1.234 | −2.837 | 1.477 | |
| BaTbO3 | 4.280b | −3839.885 | −39.4 | −1.261 | −2.898 | 1.509 | |
| SrCeO3 | 4.291b | −3830.060 | −74.9 | −1.258 | −2.890 | 1.505 | |
| SrPrO3 | 4.280b | −3839.885 | −75.2 | −1.261 | −2.898 | 1.509 | |
| SrTbO3 | 4.186b | −3925.916 | −66.5 | −1.289 | −2.963 | 1.543 | |
Therefore, the experimental observation that B4+ was not stable in fluorite structure type B4+O2 but stable in perovskite structure type A2+B4+O3 is in accordance with the data presented in Table 1. The strong lattice site potential at B site results in large total Madelung electrostatic potential of perovskite structure. In general, Fig. 4 shows that lattice site potential of B site is stronger than A or O site in perovskite type ABO3 in each valence state situation. Therefore, we find that the formation of these perovskite type oxides are associated with significant gain in Madelung electrostatic potential (ΔEM) calculated by subtracting the combined EM of rock salt structure type AO and fluorite structure type BO2 from the EM of perovskite crystal structure type of final ABO3 (Table 1). For example, one can reasonably expect that Ba2+O + Ce4+O2 → Ba2+Ce4+O3 reaction may proceed as there is gain in Madelung electrostatic potential ΔEM of ∼ −43 kcal mol−1. It should be noted that this discussion of lattice site potential and Madelung electrostatic potential is first approximation but still can be useful to explain experimental observations. For the calculation of the EM and ϕ, an ideal cubic structure for ABO3 has been assumed and all the ions have been considered as point charges. In real crystals however, ions will have certain degree of polarization in their site, and various structural distortion generally leads to the deviation from cubic symmetry of the crystal structure of the perovskites. High structural distortion can lead to the decomposition of ABO3 to component oxides. Therefore, the practical stability of these perovskite structure type ABO3 oxides may not be very high.
Takayama-Muromachi et al. experimentally obtained change in heat of formation (ΔHf) for the reaction A2+O + B4+O2 → A2+B4+O3 of several oxides (A = Ca, Sr, Ba, Pb and Cd; B =Ti and Zr).13 They also calculated change in Madelung electrostatic potential (ΔEM) from the EM of A2+B4+O3, AO and BO2 and showed that heat of formation of perovskite structure type compounds can be written as
| ΔHf ≈ ΔE = ΔEM + ΔEN | (9) |
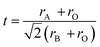 | (10) |
The valence stabilization due to strong lattice potential at B site as described above for A2+B4+O3 can be further extended to A3+B3+O3. For example, hexagonal structured A2O3 (such as La2O3) can be reacted with rhombohedral (corundum) structured B2O3 (such as Cr2O3) or rutile structured BO2 (such as CrO2) to form perovskite structure type A3+B3+O3 compounds. However, high valence Ni3+ and Co3+ in corundum structure Ni2O3 and Co2O3 respectively are not stable but LaNi3+O3, LaCo3+O3 are stable. Lattice parameters and atomic coordinates for corundum structure Ni2O3 and Co2O3 is unavailable. In this situation the Madelung electrostatic potential and lattice site potential, can be calculated using a different characteristic length r = rB + rO for each known A2O3, B2O3, BO, BO2, and ABO3 using eqn (3)–(5) and graphically estimated for unknown compounds.8 Further detailed discussion on the characteristic length and Madelung electrostatic potential can be found in.8,12 However, for comparison purposes, here all lattice site potentials were obtained using VESTA10 that uses eqn (6) and (7) for lattice site potential and Madelung electrostatic potential and presented in Tables 1 and 2. The lattice site potential obtained from compounds with general formula LaB3+O3 (B = Al, Co, Cr, Fe Ni, Ti and V) and B23+O3 (B = Al, Co, Cr, Fe, Ti and V), are given in Table 2. Fig. 4 shows the gain in lattice site potentials of all the sites in La3+B3+O3. It can be clearly seen that there is significant enhancement of lattice site potential for B site for all La3+B3+O3 from that of corundum structure B23+O3. Thus, high valence state of Ni and Co is stable in La3+B3+O3 is due to this large lattice site potential at B site and consistent with similar high valence stability situation of A2+B4+O3 as discussed in the previous section. Furthermore, from Fig. 4 it can be stated that the lattice site potential for oxygen is much lower in perovskite structure than corundum structure and therefore, corundum structure of B2O3 is more difficult to form oxygen related point defects than perovskite structure type La3+B3+O3. Indeed, a similar analysis has been performed for rutile BO2 structure as-well8 and therefore it may be understandable that why oxygen vacancy is rarely seen in rutile or corundum structure although plenty of vacancy present in perovskite structure type A3+B3+O3 compounds. Therefore, lattice site potential analysis provides reasonable understanding of the defect formation in perovskite structure ABO3 compounds and preparation of many perovskite structure type ABO3 phases from constituent binary oxides could be understood due to the strong B site potential and gain of Madelung electrostatic potential ΔEM.
| Compound | Structure | Lattice parameter (Å) | Refb | Madelung electrostatic potential EM (kcal mol−1) | Difference ΔEM (kcal mol−1) | Lattice site potential (Å−1) | ||
|---|---|---|---|---|---|---|---|---|
| ϕA | ϕB | ϕO | ||||||
| a ϕA, ϕB, and ϕO are lattice site potentials for A, B and oxygen sites, respectively.b References for lattice parameters (i) mp-1968; (ii) COD1000032; (iii) mp-19399; (iv) mp-19770; (v) mp-458; (vi) mp-18937; (vii) F. S. Galasso ‘‘Structure, properties and preparation of perovskite type compounds'’, Pergamon Press, New York (1969); mp stands for materials project, and COD stands for crystallography open database. | ||||||||
| La2O3 | Hexagonal | a = b = 3.938, c = 6.180, α = β = 90°, γ = 120° | i | −3381 | −2.0095 | 1.3945, 1.3687 | ||
| Al2O3 | Rhombohedral | a = b = 4.761, c = 12.996, α = β = 90°, γ = 120° | ii | −4352 | −2.5402 | 1.8320 | ||
| Cr2O3 | a = b = 5.07, c = 13.872, α = β = 90°, γ = 120° | iii | −4081 | −2.3757 | 1.7241 | |||
| Fe2O3 | a = b = 5.105, c = 13.913, α = β = 90°, γ = 120° | iv | −4064 | −2.3754 | 1.7070 | |||
| Ti2O3 | a = b = 5.113, c = 13.984, α = β = 90°, γ = 120° | v | −4031 | −2.3392 | 1.7097 | |||
| V2O3 | a = b = 5.126, c = 14.134, α = β = 90°, γ = 120° | vi | −4030 | −2.3510 | 1.6972 | |||
| LaAlO3 | Pseudocubic | 3.788 | vii | −3904 | −37 | −1.9630 | −2.7337 | 1.5765 |
| LaCoO3 | 3.824 | −3867 | — | −1.9446 | −2.7081 | 1.5616 | ||
| LaNiO3 | 3.838 | −3853 | — | −1.9375 | −2.6982 | 1.5559 | ||
| LaCrO3 | 3.883 | −3808 | −77 | −1.9152 | −2.6670 | 1.5379 | ||
| LaTiO3 | 3.92 | −3772 | −67 | −1.8971 | −2.6419 | 1.5234 | ||
| LaFeO3 | 3.932 | −3761 | −39 | −1.8914 | −2.6339 | 1.5188 | ||
| LaVO3 | 3.99 | −3706 | −1 | −1.8640 | −2.5957 | 1.4967 | ||
The perovskite structure type compound A4+B2+O3 with valence pair (4–2) cannot be prepared and rarely exist. This can be rationalized from Madelung electrostatic potential view point as well. For example, the calculation of ΔEM of a hypothetical chemical reaction ThO2 + MgO → Th4+Mg2+O3 revealed that a net Madelung electrostatic potential loss of 184 kcal mol−1 (calculated assuming lattice the parameter of ThMgO3 as a = 4.008 Å, equivalent to CaZrO3 due to similarity of ionic radius of Ca2+ and Th4+ as well as Mg2+ and Zr4+ since the lattice parameter of ThMgO3 is not available) would occur for the formation of perovskite structure type Th4+Mg2+O3.14 Thus this reaction will not proceed because there is no Madelung electrostatic potential or lattice energy gain in this perovskite type A4+B2+O3 compound and the same hypothesis is applicable to A5+B1+O3. We also note that very recently A4+B2+O3 compounds Bi4+Ni2+O3 and Pb4+Ni2+O3 have been reported to be made only under very high pressure conditions and these can be considered as very special valence combinations where stability is perhaps favored due to other energy factors such as covalency due to hybridization.29,30
In Scheme 2 we show similar (see Table 2) calculation of the difference in Madelung electrostatic potential ΔEM in the preparation of perovskite structure type EuTiO3 from EuO or Eu2O3 and TiO2 or Ti2O3. The calculated ΔEM in Scheme 2 suggests that Eu2+Ti4+O3 will be more stable than Eu3+Ti3+O3 and usually any preparation will lead to the formation of Eu2+Ti4+O3. This analysis may be expanded to other compounds which are of importance for stabilizing Eu2+ at specific ionic sites for the development of visible light emitting phosphor materials.
 | ||
| Scheme 2 Change in Madelung electrostatic potential ΔEM for the formation of EuTiO3. The EM were calculated using similar conditions as described for other systems using VESTA,10 assuming perovskite type Eu3+Ti3+O3 and Eu2+Ti4+O3 may have same lattice parameter of 3.904 Å (as the lattice parameter of Eu3+Ti3+O3 is not available). | ||
In conclusion, we have revisited some fundamental aspects of synthesis, stability and properties of perovskite structure type ABO3. With the use of lattice site potential and Madelung electrostatic potential we have been able to demonstrate that (1) perovskite structure type ABO3 compounds can be synthesized from their parent binary oxides because of gain in Madelung electrostatic potential which directly correlates with lattice energy, (2) Madelung electrostatic potential and lattice site potentials dictates the stability of perovskite structure and valence stability of cation in perovskite structure is direct consequence of strong cation lattice site potential and (3) the formation of defects such as oxygen vacancy or excess is driven by intrinsic lower lattice site potential of oxygen site. These results (1)–(3) can be seen various experimental data13,32–34 however, have not been explained in terms of lattice site potential by the authors. Thus, the present article will contribute to understanding of synthesis, structures and properties of functional perovskite type oxides for various areas of applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful for calculation of some Madelung electrostatic potentials by Dr Alex Lee, and help from profs. Jow-Lay Huang and Jyh-Ming Ting of Department of Materials Science and Engineering of National Cheng Kung University, Tainan, Taiwan. This work was financially supported by the Hierarchical Green-Energy Materials (Hi-GEM) Research Center, from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) and the Ministry of Science and Technology (MOST 110-2634-F-006 -017) in Taiwan.References
- V. M. Goldschmidt, Die Naturwissenschaften, 1926, 21, 477–485 CrossRef.
- K. Zhang, J. Sunarso, Z. Shao, W. Zhou, C. Sun, S. Wang and S. Liu, RSC Adv., 2011, 1, 1661–1676 RSC.
- Q. Sun and W.-J. Yin, J. Am. Chem. Soc., 2017, 139, 14905–14908 CrossRef CAS PubMed.
- S. Svarcova, K. Wiik, J. Tolchard, H. J. M. Bouwmeester and T. Grande, Solid State Ionics, 2008, 178, 1787–1791 CrossRef CAS.
- C. Li, K. C. K. Soh and P. Wu, J. Alloys Compd., 2004, 372, 40–48 CrossRef CAS.
- W. Van Gool and A. G. Piken, J. Mater. Sci., 1969, 4, 95–104 CrossRef CAS.
- W. Van Gool and A. G. Piken, J. Mater. Sci., 1969, 4, 105–111 CrossRef CAS.
- M. Yoshimura, T. Nakamura and T. Sata, Bull. Tokyo Inst. Technol., 1974, 120, 13–27 CAS.
- R. Roy, J. Am. Ceram. Soc., 1977, 60, 350–363 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. Hoppe, Z. Naturforsch., 1995, 50, 555–567 CAS.
- L. Glasser, Inorg. Chem., 2012, 51, 2420–2424 CrossRef CAS PubMed.
- E. Takayama-Muromachi and A. Novartsky, J. Solid State Chem., 1988, 72, 244–256 CrossRef CAS.
- T. Ishigaki, Z. S. Nikolic, T. Watanabe, N. Matsushita and M. Yoshimura, Solid State Ionics, 2009, 180, 475–479 CrossRef CAS.
- J. Shan, Y. Inaguma and M. Itoh, Solid State Ionics, 1995, 79, 245–251 CrossRef.
- K. Ragavendran, D. Vasudevan, A. Veluchamy and B. Emmanuel, J. Phys. Chem. B, 2004, 108, 16899–16903 CrossRef CAS.
- N. Ashurov, B. L. Oksengendler, S. Maksimov, S. Rashiodva, A. R. Ishteev, D. S. Saranin, I. N. Burmistrov, D. V. Kuznetsov and A. A. Zakhisov, Mod. Electron. Mater., 2017, 3(1), 1–25 CrossRef.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. V. Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- K. Oh-ishi, R. Kobayash and K. Oka, J. Ceram. Soc. Jpn., 2017, 125(5), 383–386 CrossRef CAS.
- J. Zaanen, G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1985, 35(4), 418–421 CrossRef PubMed.
- J. B. Torrance and P. Lacorre, Physica C, 1991, 182, 351–364 CrossRef CAS.
- T. Arima, Y. Tokura and J. B. Torrance, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17006–17009 CrossRef CAS PubMed.
- D. Kato, K. Hongo, R. Maezono, M. Higashi, H. Kunioku, M. Yabuuchi, H. Suzuki, H. Okajima, C. Zhong, K. Nakano, R. Abe and H. Kageyama, J. Am. Chem. Soc., 2017, 139(51), 18725–18731 CrossRef CAS PubMed.
- A. Sabry, M. Ayadi and A. Chouikh, Comput. Mater. Sci., 2000, 18, 345–354 CrossRef CAS.
- A. Sabry and M. Ayadi, Int. J. Mod. Phys. C, 2001, 12(3), 325–332 CrossRef CAS.
- E. W. Arnold III and S. Sundaresan, Chem. Eng. Commun., 1987, 58(1–6), 213–230 CrossRef.
- M. Yoshimura, T. Nakamura and T. Sata, Chem. Lett., 1973, 2, 923–928 CrossRef.
- K. Kamata, T. Nakamura and T. Sata, Mater. Res. Bull., 1975, 10, 373–378 CrossRef CAS.
- S. Ishiwata, M. Azuma, M. Takano, E. Nishibori, M. Takata, M. Sakata and K. Kato, J. Mater. Chem., 2002, 12, 3733–3737 RSC.
- Y. Inaguma, K. Tanaka, T. Tsuchiya, D. Mori, T. Katsumata, T. Ohba, K. Hiraki, T. Takahashi and H. Saitoh, J. Am. Chem. Soc., 2011, 133(42), 16920–16929 CrossRef CAS PubMed.
- R. W. G. Wycoff, Crystal structure (II), Interscience, New York, 1964 Search PubMed.
- H. Yamamoto, K. Toda, Y. Sakai, T. Nishikubo, I. Yamada, K. Shigematsu, M. Azuma, H. Sagayama, M. Mizumaki, K. Nitta and H. Kimura, Chem. Mater., 2020, 32, 6892–6897 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martinez, J. M. Garcia-Lastra, M. Mogensen and J. Rossmeisl, Angew. Chem., Int. Ed., 2010, 49, 7699–7701 CrossRef CAS PubMed.
- Z. H. Zeng, F. Calle-Vallejo, M. B. Mogensenc and J. Rossmeisl, Phys. Chem. Chem. Phys., 2013, 15, 7526–7533 RSC.
Footnote |
| † Present address: Hierarchical Green-Energy Materials (Hi-GEM) Research Center and NCKU 90 and beyond project, Distinguished Visiting Chair Professor, Department of Materials Science and Engineering, National Cheng Kung University, Tainan, Taiwan, 701 |
| This journal is © The Royal Society of Chemistry 2021 |