Open Access Article
Open Access ArticleUltra-high Seebeck coefficient of a thermal sensor through entropic optimisation of ligand length of Fe(II) spin-crossover (SCO) materials†
Hazirah Che Hassana,
Suhana Mohd Said*a,
Nik Muhd Jazli Nik Ibrahima,
Megat Muhammad Ikhsan Megat Hasnanb,
Ikhwan Syafiq Mohd Noorc,
Rozalina Zakariad,
Mohd Faiz Mohd Salleha,
Nur Linahafizza Md. Noore and
Norbani Abdullahe
aDepartment of Electrical Engineering, Faculty of Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia. E-mail: smsaid@um.edu.my
bMicroelectronic and Nanotechnology – Shamsuddin Research Centre (MiNT-SRC), Faculty of Electrical and Electronic Engineering, University Tun Hussein Onn, Parit Raja, 86400 Batu Pahat, Johor, Malaysia
cPhysics Division, Centre of Foundation Studies for Agricultural Science, University Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia
dDepartment of Physics, Faculty of Science, University of Malaya, 50603 Kuala Lumpur, Malaysia
eDepartment of Chemistry, Faculty of Science, University of Malaya, 50603 Kuala Lumpur, Malaysia
First published on 14th June 2021
Abstract
In this work, we present a spin-crossover (SCO) complex molecular formulation [Fe(Ln)2](BF4)2 in an electrochemical single couple solution. A Seebeck voltage arises when an electrochemical single couple solution is subjected to a temperature difference, resulting in a single couple reaction at either terminal of the electrochemical cell. The ultrahigh Seebeck coefficients were obtained due to a number of molecular optimisation strategies. The [Fe(L16)2](BF4)2 complex demonstrated a maximum Seebeck coefficient of 8.67 mV K−1, achieved through a six-pronged approach to maximise entropy during the transition from low spin (LS) to high spin (HS) through: (i) a change in spin state, (ii) a change in physical liquid crystalline state, (iii) the spin Seebeck effect, (iv) the kosmotropic and chaotropic effect, (v) the fastener effect and (vi) thermal heat absorbance. A reduction of the Seebeck coefficient to 1.68 mV K−1 during the HS–LS transition at higher temperatures is related to the single spin state transition entropy change. In summary, this paper presents a systematic study to identify the contributing factors in the production of a sensor with an ultrahigh Seebeck coefficient for energy harvesting through the optimisation of its molecular entropy elements.
1. Introduction
The thermoelectrochemical effect offers an effective way of converting heat directly into electrical potential, and thus can become a generator of electricity.1 However, there is still a challenge in the thermoelectrochemical generator (TEG) system that should be overcome from the low current, as well as the electrical potential due to the material properties, which ultimately affect their performances.1 Therefore, this work explores an alternative application of the thermoelectrochemical effect as thermal sensors by using spin-crossover (SCO) complexes. The thermal sensor studied in this work has the same operating principle as the TEG, but the ultrahigh Seebeck (Se) coefficient is achieved using the SCO complex by primarily exploiting its intrinsic phase and magnetic transitions, namely the liquid crystal (LC) effect and spin Seebeck effect (SSE).2–5 The sensitivity of the SCO complex to a thermal stimulus has driven entropy changes, which subsequently drives a Seebeck voltage. The entropy change (ΔS) and the transport properties of the charge carrier affect the magnitude and sign of Se. The performance of the thermal sensor based on the Seebeck effect can be defined according to the figure of merit (ZT) below:
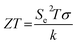 | (1) |
Here, T is the absolute temperature, Se is the Seebeck coefficient, σ is the ionic conductivity and κ is the thermal conductivity.6
This work introduces three new novel spin-crossovers (SCO) based Fe(II) complexes which are [Fe(L12)2](BF4)2 (complex 1), [Fe(L14)2](BF4)2 (complex 2) and [Fe(L16)2](BF4)2 (complex 3) where L12,14,16 were N3 Schiff bases appended with linear C12,14,16 carbon chains at the N atoms. These Fe(II) SCO complexes are characterized for their Seebeck voltage as a function of temperature in order to identify the effect of ligand length on the Seebeck voltage. Previously, Ibrahim et al.7,8 have reported the use of similar Fe(II) metal centre with different structural complexes, and provided the structural correlations between molecular and ionic structures with spin state behaviour and on thermoelectric performance. The results exhibited the Seebeck coefficient with −0.51 mV K−1 for [Fe(L)3](BF4)2·2H2O (Fe2+-mono), −0.57 mV K−1 for [Fe2(CH3COO)4(L)2]·2H2O (Fe-dinuc) and −0.52 mV K−1 for [Fe2(CH3COO)4(L)2.7,8 SCO complexes have indicated great potential in thermal sensor applications, owing to their high Se values between −0.088 mV K−1 and 1.8 mV K−1, reported by other researchers, listed in Table 1.
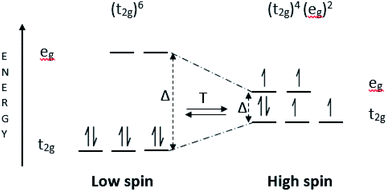
The switchable behaviour of the SCO material between high-spin (HS) to low-spin (LS) or vice versa as shown in Fig. 1 distinguishes this material for its capacity to convert electrochemical energy to electrical potential, in response to temperature gradients.12 Fe(II) complexes are the most extensively studied SCO materials,13,14 as the change of spin state transition during electron transferring is capable of producing high entropy. Theoretically, Fe(II) complexes have good thermoelectric behaviour due to its large ΔS value. The ΔSspin for Fe(II) = R[ln(2S + 1)HS − ln(2S + 1)LS] is 13.4 J K−1 mol−1, is higher than Fe(III) of 9.1 J K−1 mol−1 and Co(II) of 5.8 J K−1 mol−1.15 This is due to the electronic transition of Fe(II) complexes occurring between LS with no unpaired electrons (S = 0), and HS with four unpaired electrons (S = 2), as referred to the diagram in Fig. 1.16,17 In terms of metal–ligand (M–L) bonding (between Fe and ligand), the LS state has a shorter bond which induces the N-donor on the ligand to easily donate electrons to the Fe centre. The positive charge at the Fe centre becomes unbalanced as the number of electrons are donated to the metal centre. The coulombic attraction between cation and anion becomes weak and easy for bonds to break, thus increasing entropy.7 In contrast to the HS state which has a longer bond between Fe–L, the N-donor ligand has difficulty in contributing electrons to the Fe centre. The number of charges positive (at the metal centre) and negative (at N-donor ligand) cause the interaction between cation and anion to become stronger, thus requiring high energy to break the coulombic attraction, and hence lower the entropy. This is the reason why the LS state of Fe(II) complexes can produce higher entropies compared to the HS state, and in turn result in a higher Seebeck coefficient. Entropy is one of the important parameters in determining the Seebeck coefficients of thermal sensors.18–21 Seebeck coefficients, Se can be described by the following equation:22
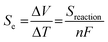 | (2) |
In eqn (2), parameter n refers to the number of electrons involved in the redox reaction, F is the Faraday constant and ΔV is the potential generated by the temperature difference, ΔT. If the Se is in a positive value, the entropies of the cations are increased.11
The advances in SCO material development can be seen through the combination of this material with its liquid crystal properties, otherwise known as metallomesogens (thermotropic liquid crystals). The liquid crystal phase transition results from the transition process between the crystal phase and liquid phase which can be observed through polarizing optical microscopy (POM). Metallomesogens complexes provide advantages for processing SCO materials in the form of thin films, enhanced spin transition signals, switching and sensing in different temperature regimes and achievement of photo- and thermochromism.13,23 This complex structure change associated with the crystalline (Cr) ↔ liquid crystal induces the spin state transition, thus contributing to an increase in entropy and Seebeck values, as reported by Gaspar et al.24
The spin Seebeck effect (SSE) refers to the generation of spin voltage as a result of a temperature gradient in magnetic materials. SSE have been introduced as one of the novelties that can be induced for high entropy and Seebeck coefficient through charge transport properties in SCO materials. Megat Hasnan et al. has reported that SSE of polymer-based electrolyte in a thermoelectrochemical cell study has induced the spin Se and can act as a thermal booster to enhance ionic mobility and diffusivity.5 Besides that, the spin state transition can cause two other effects such as the kosmotropic and chaotropic effect. The kosmotropic effect (inducing structure) is the ordered structure of complexes by stabilizing intramolecular interactions between Fe–ligand, whilst the chaotropic effect (inducing disorder) produces the opposite effect by disrupting and destabilizing the complex structure.25 Hence, the kosmotropic and chaotropic effects involve the structure of complexes from an ordered structure to a disordered structure, brought to increase the entropy and consequently enhance the Seebeck effect.26
The alkyl ligand lengths that are attached to the metal centre can provide variation in entropy and Seebeck measurements. A long alkyl ligand has a fastener effect where it forms a flexible and soft space field around the central metal complex moiety through the thermal motions.27 The flexible alkyl chains cause the emergence of a strong cooperative effect called interchain interaction, formed between the adjacent chains of the surrounding ligands. This flexibility can contribute to enhance the entropy and Seebeck values by facilitating the formation of spin state transition of the centre metal ions.28,29 The thermal heat absorbance can contribute to maximise the entropy. This thermal heat can be measured using differential scanning calorimetry (DSC) where it records the phase change of SCO complexes during the heating and cooling process by observing the endothermic and exothermic peaks. The SCO complexes will absorb the heat to break the bond since ligands will begin to dissociate at certain temperatures, hence promoting the heat capacity and increasing the entropy.
Throughout this work, we have focused on a six-pronged strategy which contributes to maximizing entropy during the transition from low spin (LS) to high spin (HS): (i) change in spin state, (ii) change in physical liquid crystalline state, (iii) spin Seebeck effect (iv) kosmotropic and chaotropic effect, (v) fastener effect, (vi) thermal heat absorbance and its impact on the Seebeck coefficient, which is especially apparent in the heating range between 298 K and 373 K.
2. Methodology
This section describes the synthesis of each complexes by the facile one pot reaction method, the preparation of Fe(II) complex electrolytes, and the characterization of each of the complexes on physical, electrochemical and thermal sensor properties.2.1. Materials
Tetrabutylammonium tetrafluoroborate (TBATFB) with a molecular weight of 327.29 g mol−1, purchased from Merck, was used as a charge supplier in the Fe(II) complexes electrolyte. Dimethyl sulfoxide (DMSO), anhydrous 99.9% with a molecular weight of 78.13 g mol−1, purchased from Sigma Aldrich, was used as a solvent to dissolve the solute. All the chemicals were of analytical grade and used without further purification.2.2. Syntheses of complexes
2.3. Fe(II) SCO electrolyte preparation
Three electrolytes based Fe(II) SCO complexes with different ligand length, i.e., [Fe(L12)2](BF4)2 (1), [Fe(L14)2](BF4)2 (2) and [Fe(L16)2](BF4)2 (3) were prepared. The compositions of electrolyte based Fe(II) complexes is listed in Table 2. 0.002 M of Fe(II) complexes and 0.1 M of TBATFB as the charge supplier were dissolved in 5 ml of DMSO. The mixture was stirred for 1 h at 353 K until the mixture became homogeneous.| Complex | TBATFB | DMSO |
|---|---|---|
| 1 [0.002 M] | 0.1 M | 5 ml |
| 2 [0.002 M] | 0.1 M | 5 ml |
| 3 [0.002 M] | 0.1 M | 5 ml |
2.4. Physical characterization of Fe(II) SCO complexes
The characterizations of Fe(II) SCO complexes with different ligand lengths are as listed below:(a) Fe(II) SCO complexes
(i) Magnetic susceptibility was used to indicate the condition of the complex either in low spin or high spin at room temperature.
(ii) Mesomorphism was observed during the transition of liquid crystal properties of complexes by using polarizing optical microscopy.
(iii) A thermal study was used to evaluate the mass loss by thermogravimetric analysis.
(iv) Determination of enthalpy and predicted peak for endothermic and exothermic reactions were used to observe the spin state transition peak by differential scanning calorimetry.
(b) Fe(II) SCO electrolytes
(v) Cyclic voltammetry was used to observe the single couple potential reaction and estimate the diffusion, mobility and electrochemical bandgap.
(vi) Electrochemical impedance spectroscopy was used to measure the ionic conductivity.
(vii) Thermal sensor properties were studied to measure the Seebeck value and power output.
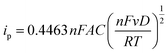 | (3) |
Here, n is the number of electrons exchanged per molecule, A is the electrode area, C is the compound concentration, v is the potential scan rate, F is the Faraday constant and R is the gas constant. The electrochemical bandgap, Ee was then calculated using the relationship as shown below:
| Ee = |HOMO − LUMO| | (4) |
In eqn (4), HOMO = (onset oxidation peak voltage + 4.4) eV and LUMO = (onset reduction peak voltage + 4.4) eV. The mobility (μ) of the charge carrier was estimated using the Nernst–Einstein relationship.
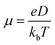 | (5) |
The diffusion (D) value in eqn (5) was obtained from Randles–Sevcik's equation. Parameter kb refers to the Boltzmann's constant (1.38 × 10−23 m2 kg s−2 K−1), where e is the electron charge (1.602 × 10−19 coulomb) and T is the absolute temperature.
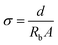 | (6) |
Here, A is the electrode–electrolyte contact area, and d is the distance between two electrodes in the Teflon holder. Parameter Rb is the bulk resistance of the Fe(II) SCO electrolyte which was obtained from the intersection of the complex impedance plot with the real impedance axis.
3. Results and discussion
3.1. Syntheses and structural deduction
The ionic complexes, [Fe(L12)2](BF4)2 (1), [Fe(L14)2](BF4)2·H2O (2) and [Fe(L16)2](BF4)2 (3) where L12,14,16 were N3 Schiff bases appended with linear C12,14,16 carbon chains at the N atoms. These were obtained as dark powders in good yields by facile one-pot reactions involving a methanolic solution of 2,6-pyridinedicarboxaldehyde, Fe(BF4)2·6H2O and CnH2n+1NH2 (n = 12, 14, 16). These complexes are readily soluble in common organic solvents such as methanol (CH3OH), ethanol (C2H5OH), chloroform (CHCl3), dichloromethane (CH2Cl2) and methanenitronate (CH2(NO2)2). These complexes have octahedral Fe(II) atoms as the structural formula (Fig. 3) is deduced from a combination of instrumental techniques.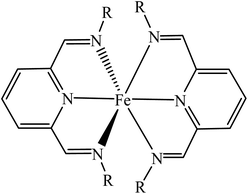 | ||
| Fig. 3 General structural formula for 1–3 (R = CnH2n+1; n = 12, 14, 16). BF4− ion and lattice H2O are not shown. | ||
Fe(II) SCO compounds often exhibit thermochromism (dark purple ↔ white colour change) due to the rearrangement in the molecules of the complexes. The LS state absorbs visible light more strongly than the HS state and usually at distinctly different wavelengths, making UV-vis spectroscopy a useful tool for observing SCO. The HS state has more electrons in the antibonding eg orbitals compared to the LS state, thus has longer metal–ligand bond lengths. The electronic absorption spectral data in CHCl3 tabulated in Table 3 shows d–d bands at approximately 700 nm assigned to the overlapping of 1A1g(F) → 1T1g and 1A1g → 1T2g electronic transitions respectively. Three other bands that were observed were metal-to-ligand charge transfer (MLCT) and intraligand charge transfers. It is interesting to note that the MLCT band occurred at low energies for all complexes.
| SCO complex | λ/nm (εmax/M−1 cm−1) |
|---|---|
| a λ is wavelength and εmax is molar extinction coefficient. | |
| 1 | 721(510), 599(9444), 573(7610), 472(7083) |
| 2 | 715(682), 676(888), 597(15255), 571(12145), 473(11289) |
| 3 | 721(470), 596(8710), 576(7100), 473(6475) |
3.2. Magnetic susceptibilities
The magnetic data (χMT) obtained by the Gouy method at 298 K is used to deduce the spin state of Fe(II) atom either at LS or HS. In the case of Fe(II), the HS state (S = 2) is paramagnetic, while the LS state (S = 0) is diamagnetic. Thus, the Fe(II) SCO switches the paramagnetism to “on” and “off”. The room temperature magnetic susceptibilities (χ) for complex 1 to 3 were initially measured at 298 K and are tabulated in Table 4.| Complex | Magnetic (χMT/cm3 K mol−1) | Assignment |
|---|---|---|
| 1 | 0.31 | 89.7% LS, 10.3% HS |
| 2 | 0 | 100.0% LS |
| 3 | 0.27 | 91.0% LS, 9.0% HS |
From Table 4, complexes 1 and 3 gave almost identical χMT values. Complex 1 gave a χMT value of 0.31 cm3 K mol−1 made up of 10.3% of HS and 89.7% LS. Complex 3 has a χMT value of 0.27 cm3 K mol−1 which consists of 9.0% HS and 91.0% LS. The χMT value for complex 2 obtained 0 cm3 K mol−1 with 100% LS. It is reported that a full HS Fe(II) SCO complex (S = 2) typically exhibits at χMT ≈ 3.00 cm3 K mol−1 and a LS Fe(II) SCO complex (S = 0) is visible at χMT ≈ 0 cm3 K mol−1.29–33 Based on this study, it may be inferred that the prepared complexes are mostly LS Fe(II) at this temperature. Hence, this is in line with the data obtained from electronic absorption spectra. The SQUID magnetometry elucidated a low spin state for Fe(II) complexes at room temperature, revealing a diamagnetic electronic structure.34
3.3. Thermal properties
The decomposition temperatures and thermal properties of Fe(II) SCO complexes with different ligand length [Fe(L12)2](BF4)2 (1) and [Fe(L16)2](BF4)2·H2O (3) were studied by thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) respectively. Table 5 tabulated the major mass losses and strongest peaks obtained for both samples. From the TGA, the major mass losses for each complex agreed with the values calculated from the loss of two BF3 and two ligands.2 Besides that, complex 1 suffered initial mass losses of 0.8% (temperature ranged from 357 K to 513 K) due to the evaporation of lattice H2O. Thus, the thermal stability of complex 1 (Tdec = 515 K) is higher than complex 3 (Tdec = 463 K) due to a higher HS of complex 1. This produced a strong coulombic attraction in the ionic complex, and as a result, longer metal-to-ligand bonds.7 Based on Table 5, it can be seen that the measured mass loss (percentage) is in good agreement with the theoretical results (percentage) obtained from their structural formula, as it indicates the purity of the complexes and supports the proposed structural formula.| Complex | TGA | DSC | ||
|---|---|---|---|---|
| T range (K) | Mass loss (%) found (calc.) | Heating T/K (ΔH/kJ mol−1) | Cooling T/K (ΔH/kJ mol−1) | |
| 1 | 515–1023 | 91.4 (90.6) | 344.0 (+65.1) | No peak |
| 3 | 463–911 | 92.4 (93.3) | 317.8 (+79.2) | 316.5 (−32.2) |
From the DSC, the strongest peak for all complexes in the temperature range of 315 K to 350 K was assigned to Cr-to-Col transitions. It is in agreement with the polarizing optical microscopy (POM). During the heating process, the endothermic peak corresponds to the first order phase transition that accompanies the spin-crossover. The enthalpy of transition from LS to HS state for complex 3 (ΔH = +79.2 kJ mol−1) is higher than the enthalpy during the endothermic peak of complex 1. This can be attributed to the ligand length effect which was aided to promote the reaction enthalpy formed for this complex.35 Therefore, the reaction entropy produced for complex 3 (0.25 kJ mol−1 K−1) is higher compared to complex 1 (0.19 kJ mol−1 K−1). During the cooling process, complex 3 exhibited the highest exothermic peak of ΔH = −32.2 kJ mol−1 and showed a phase transition from isotropic to solid. Complex 3 was expected to produce a better Seebeck performance as the thermal sensor material of this complex can generate a higher entropy reaction than complex 1. As a result, a spin-crossover behaviour occurred in the former complex. Moreover, complex 3 can undergo a reversible spin-state transition during the heating and cooling process. This is of great importance its application as the complex can absorb more heat easily due to the convection process that takes place in the thermal sensor cell on the cold electrode. This is to promote high reaction entropy which contributes to the Seebeck effect. It is noted that there were no corresponding peaks on cooling for complex 1, indicating the slow rate of phase formation.
3.4. Mesomorphic properties
The mesomorphic properties of complex 1 to 3 were studied by polarizing optical microscopy (POM). Under POM, complex 1 was observed to melt at about 343 K, in agreement with the DSC data, and cleared to an isotropic liquid (Iiso) at 402 K during the heating process. Upon cooling from the isotropic liquid phase, the dendritic-like optical textures36–38 was developed at 398 K, which corresponds to a columnar mesophase (Col) as shown in Fig. 4(a). This texture gradually transformed to the mosaic character of a crystalline phase when further cooled to room temperature. Similarly, complex 2 melted at about 348 K and cleared to an isotropic liquid at 437 K. After further cooling, an optical texture like complex 1 (Col) was developed at 404 K. This texture then transformed to a broken-fan texture at 390 K.Subsequently, complex 3 melted at approximately 362 K, and cleared to an isotropic liquid at 472 K. Upon cooling, a focal conic fan-like (Col) optical texture39–41 was formed at 397 K (Fig. 4(b)). The results showed that the melting point and the phase transition from clear crystalline to isotropic liquid point became higher with an increase in the ligand length of the complexes. These behaviours were ascribed to the fastening effect of the long alkyl chains. The weaker van der Waals interactions of the long alkyloxy chains of ligand bonded to the LS Fe(II) is due to the less flexible geometry at this site. It possesses a stronger Fe–L bond compared to those bonded to the HS Fe(II). As a result, L at the HS site melted at a lower temperature, which enabled the Fe–L bonds to become shorter (stronger), leading to a change in its electronic configuration to LS.3 Hence, complex 3 revealed a high Seebeck generation owing to the fastening effect of the long alkyl chain that affects the melting point and phase transition point.
3.5. Electrochemical reversibility of the Fe(II) SCO complexes
The ligands that surround the Fe2+ ion will create a ligand field (spin state). This causes a redistribution of the electrons over the orbitals. This condition results in different spin states depending on the strength of the ligand field, thus influencing the single couple potential. In order to investigate the electrochemical properties of complex 1 to 3, a cyclic voltammetry (CV) was carried out. The measurements were conducted at various temperature ranges and repeated by three cycles for each temperature. The complexes showed good electrochemical reversibility. The charge supplier (TBATFB) was added into the solution as it easier to undergo oxidation and reduction processes due to the lower single couple potential. As electron transfer occurs at the electrodes, the charge supplier will migrate to balance the charge and complete the electrical circuit.42 The CV scan for the complexes shows the anodic and cathodic peaks, as indicated respectively in ESI 1.†All complexes showed the anodic and cathodic potential peaks in the range outside −1 V and +1 V. These peaks can be assigned to the oxidation of L to L+ and the reduction of L+ to L.43 The Fe ion peak is absent during the oxidation and reduction for all complexes. This is attributed to the spin state transition either in LS or HS, where the HS state have longer bonds between Fe–L. Hence, the Fe metal centre was shielded by the long alkyl ligands which acted as an insulating layer, hindering from further participation of the Fe in the single couple reaction at the electrode.11,44 In contrast, complexes in LS have shorter bonds between Fe–L, allowing donation of electron to take part easily. Many negative charges surrounded the Fe metal centre and made it more difficult for the Fe ion to oxidize due to repulsion towards the BF− anion. The aromatic structure of complexes have shielded the solvent to oxidize at the metal centre, thus limiting the solvent reorganisation of the entropy.45 Referring to Table 6 and ESI 1,† the increase of temperature gave the anodic peak shift towards positive voltage and the cathodic peak shift towards negative voltage. This behaviour is characteristic of a diffusion-controlled reaction.
| Complex | Temperature (K) | Anodic peak potential, Epa1 (V) | Anodic peak potential, Epa2 (V) | Cathodic peak potential, −Epa1 (V) | Cathodic peak potential, −Epa2 (V) |
|---|---|---|---|---|---|
| 1 | 303 | +1.12 | No peak | −1.17 | No peak |
| 333 | +1.15 | No peak | −1.05 | No peak | |
| 363 | +1.21 | +1.63 | −1.19 | No peak | |
| 2 | 303 | No peak | No peak | No peak | No peak |
| 333 | No peak | No peak | No peak | No peak | |
| 363 | +1.01 | +1.40 | −0.92 | −1.39 | |
| 3 | 303 | +1.61 | No peak | −1.67 | No peak |
| 333 | +1.67 | No peak | −1.67 | No peak | |
| 363 | +1.72 | No peak | −1.78 | No peak |
Subsequently, ESI 2† showed the comparison of the CV graph changes between three complexes at temperatures of 303 K, 333 K and 363 K. At temperatures of 303 K and 333 K, complex 1 and complex 3 indicated ligand peaks for oxidation and reduction, but no peak was observed for complex 2. At 363 K, all complexes are observed to have cleared oxidation and reduction peaks. This indicates that the complexes are easier to undergo oxidation and reduction at high temperatures.46 The diffusion, electrochemical band gap and mobility are calculated by using eqn (3)–(5), as summarised in Table 7.
| Complex | Temperature, T (K) | Diffusion, D (×10−7 cm2 s−1) | Mobility, μ (×10−6 cm2 V s−1) | Electrochemical bandgap, Ec (eV) |
|---|---|---|---|---|
| 1 | 303 | 0.10 | 0.39 | 1.72 |
| 333 | 0.49 | 1.69 | 1.83 | |
| 363 | 3.07 | 9.82 | 1.91 | |
| 2 | 303 | — | — | — |
| 333 | — | — | — | |
| 363 | 3.48 | 11.10 | 1.20 | |
| 3 | 303 | 2.98 | 11.40 | 2.60 |
| 333 | 7.66 | 26.70 | 2.74 | |
| 363 | 20.50 | 65.40 | 2.74 |
Referring to Table 7, the values of diffusion, mobility and electrochemical bandgap for all complexes increased with temperature. The diffusion coefficient is related to the movement of ions in the electrolyte caused by an external forced field such as the temperature. This occurred when the ion is removed from the electrolyte by the discharge at an electrode. Besides that, the diffusion coefficient is related to the ionic mobility where the higher diffusion affects the ionic mobility of the charge carrier. This is based on the Einstein relation in eqn (5) that showed the ionic mobility is proportional to diffusion. The diffusion coefficient for complex 3 is higher than complex 1 and complex 2 at 333 K due to weaker Fe–L bonds of the HS. A weaker coulombic interaction enabled the ion to move easily, this resulted in high diffusion as well as high mobility.27,47 Moreover, complex 1–3 experienced a spin Seebeck effect due to the increasing value of diffusion and ion mobility of the charge carrier that have arisen after the spin state transition. In Table 7, it can be seen that the electrochemical bandgap for complex 3 is lower (2.60 eV), as compared to after the spin state transition LS–HS which is of higher value (2.74 eV). This indicated that the ion transfer can occur easily before the spin state transition and cause a higher Seebeck value compared to after the spin state transition. This leads to inducing the electrochemical bandgap to become bigger, thus reducing the Seebeck value.
3.6. Effect of ligand length Fe(II) SCO complexes on the ionic conductivity
Results in Fig. 5 and Table 8 presented the ionic conductivity at various temperatures for each Fe(II) SCO electrolyte. The ionic conductivity of complex electrolytes were calculated using the eqn (6). From Fig. 5, it is observed that the ionic conductivity increased linearly with temperature for complex 1, complex 2 and complex 3. The values of conductivity are tabulated in Table 8. At room temperature (298 K), complex 2 gave the highest conductivity value compared to complex 1. As discussed before, complex 2 is 100% LS. Complexes in the LS state are more conductive compared to the HS state. This is due to shorter bonds between Fe–L which has compressed the structure, hence easing the donation of the electrons.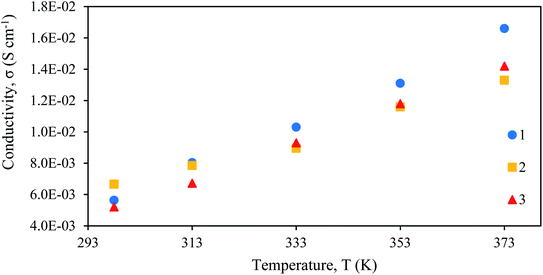 | ||
| Fig. 5 Plot of conductivity–temperature dependence for [Fe(L12)2](BF4)2 (1), [Fe(L14)2](BF4)2 (2), and [Fe(L16)2](BF4)2 (3) electrolytes. | ||
| Temperature (K) | Ionic conductivity, σ (×10−3 S cm−1) | ||
|---|---|---|---|
| [Fe(L12)2](BF4)2 (1) | [Fe(L14)2](BF4)2 (2) | [Fe(L16)2](BF4)2 (3) | |
| 298 | 5.63 | 6.66 | 5.21 |
| 313 | 8.04 | 7.85 | 6.72 |
| 333 | 10.30 | 8.95 | 9.30 |
| 353 | 13.10 | 11.60 | 11.80 |
| 373 | 16.60 | 13.30 | 14.20 |
At temperatures of 313 K and above, it can be seen that complex 1 revealed the highest conductivity value compared to other complexes. This observation can be attributed to the shorter 12-carbon linear alkyl chains that assisted in improving the ionic conductivity, as compared to complex 2 and complex 3 that have relatively lower ionic conductivity due to long alkyl chains. The graph presented a linear ionic conductivity trend for all complexes due to the spin Seebeck effect that has developed the charge transport properties after the spin state transition. The ionic conductivity is highly sensitive to the changes induced by the spin-crossover transition. This is through changes in ionic conductivity via chemical compression, driven by the structural changes.48
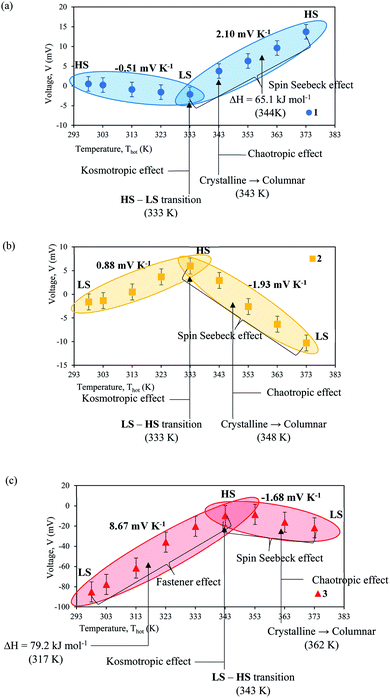
3.7. Effect of ligand length Fe(II) SCO complexes on the Seebeck coefficient
Analysis of the Seebeck coefficient of [Fe(L12)2](BF4)2 (complex 1), [Fe(L14)2](BF4)2·H2O (complex 2) and [Fe(L16)2](BF4)2·H2O (complex 3) were performed. The maximised entropy molecular reaction of Fe(II) SCO electrolytes can be observed through six factors: (i) spin state transition, (ii) liquid crystal physical changes, (iii) spin Seebeck effect, (iv) kosmotropic and chaotropic effect, (v) fastener effect and (vi) thermal heat absorbance. In particular, it is the phase change of the liquid crystal order in solution that was thought to have somewhat retained and contributed to one of the causes for the increase in entropy.49 Any perturbations will result in higher entropy change. This event will then be elucidated from the view of ligand length of the SCO complex. Fig. 6(a)–(c) depicted the results of potential difference as a function of the temperature of hot electrode (Thot). The result indicates two sign gradients for the Seebeck coefficient of each complex, as tabulated in Table 9. A higher boiling point of DMSO (462 K) solvent allows the complex solution to be heated up to 373 K at the hot electrode. Most significantly, the maximum Seebeck coefficient achieved by complex 3 (8.67 mV K−1) is to the best of our knowledge, one of the highest achieved Seebeck coefficient for electrochemical single couple solution compared to ferri/ferrocyanide (−1.4 mV K−1)50 and cobalt-based redox couples [Co2+/3+(2,2′-bipyridyl)3 (NTf2)2/3] (2.19 mV K−1).9 This is due to the dependency of the Seebeck coefficient on entropy, and in such SCO systems, the significant enhancement in entropy of SCO complexes comes from a six-pronged approach, as shown in Fig. 6(c).| Complex | First gradient Seebeck coefficient (mV K−1) | Second gradient Seebeck coefficient (mV K−1) | Spin state transition (K) |
|---|---|---|---|
| 1 | −0.51 | +2.10 | 333 |
| 2 | +0.88 | −1.93 | 333 |
| 3 | +8.67 | −1.67 | 343 |
Complex 3 shows the spin state transition from LS–HS occurred at 343 K which caused the structural changes and the enhancement of the entropy. During the LS state, complex 3 has short metal–ligand bonds that easily allowed the N-donor to donate electrons to the metal centre. The increase of charge density at the metal centre causes the metal–ligand bonds to break down due to a weak coulombic attraction. The kosmotropic effect occurred during the spin state transition of LS–HS. This effect increased the order structure of complex 3 by providing the pathway for electron transfer.51 The fastener effect is another factor which contributed to the enhancement of entropy through the interchain interaction formed by long alkyl chains of complex 3. The flexibility of long alkyl chains of complex 3 formed a strong cooperative effect between the adjacent chains of surrounding ligands that enhanced the entropy and Seebeck value. The spin state transition of centre metal ions was affected by the flexibility of long alkyl chains of complex 3.28,29 The endothermic peak at 317 K with 79.2 kJ mol−1 belongs to the first order phase transition that promoted the enthalpy reaction, thus significantly increasing its entropy. All four factors contribute to maximising the entropy activity, resulting in the highest Seebeck value of 8.67 mV K−1 for complex 3.
The second gradient showed the spin state transition which occurred from HS–LS at 343 K to 373 K. The metal–ligand bond during the HS state is longer and is difficult for the N-donor to donate the electron to the metal centre. The charge density was maintained at the metal centre and anion ligand due to the stronger coulombic attraction, making the breaking of the bond more difficult. Between the temperature ranges, the phase transition from Crystalline to Columnar also occurred at 362 K, as observed by the POM. Moreover, the enhancement of the chaotropic effect contributed to the entropy due to the disordered structure of complex 3.11 The spin Seebeck effect has developed after the spin transition and contributing to give the Seebeck coefficient of 1.68 mV K−1 which is lower than a second gradient of complex 2.
Referring to Fig. 6(a), the Seebeck coefficient of complex 1 was the lowest (0.51 mV K−1) compared to other complexes as the spin state transition from the HS–LS and the kosmotropic effect at 293 K to 333 K contributed to the entropy. Referring to the second gradient, complex 1 produced the highest Seebeck coefficient of 2.10 mV K−1. This can be attributed to the spin Seebeck effect of complex 1 from the LS–HS, in which the chaotropic effect and the endothermic peak occurred at 344 K with ΔH = 65.1 kJ mol−1, accompanied by the contribution from the phase transition (Crystalline → Columnar) which commenced at 343 K. These four factors resulted in the Seebeck coefficient for the second gradient of complex 1 to be the highest by transition from LS–HS. From Fig. 6(b), it is observed that the Seebeck coefficient of complex 2 is 0.88 mV K−1 which is higher than complex 1. This event is due to the spin state transition from LS–HS, as well as the kosmotropic effects which occurred from 298 K to 333 K. The second gradient for complex 2 produced the Seebeck coefficient of 1.93 mV K−1 which is higher than the second gradient of complex 3. This circumstance is related to the spin Seebeck effect from HS–LS, the chaotropic effect and the phase transition (Crystalline → Columnar) at 348 K. All six effects mentioned above have contributed to maximising the entropy, hence increasing the Seebeck value.
3.8. Effect of different ligand length of SCO Fe(II) complexes on the thermal sensor performance
The performance of [Fe(L12)2](BF4)2 (complex 1), [Fe(L14)2](BF4)2·H2O (complex 2), and [Fe(L16)2](BF4)2·H2O (complex 3) were tested in a thermal sensor that were connected with two platinum electrodes and a resistor in parallel to the circuit. The hot sided electrode was heated from 298 K to 403 K. The highest power output was produced when the applied external resistance is equal to the internal resistance of the cell.52Referring to Fig. 7, it can be seen that complex 2 revealed the highest power density with the value (Pmax = 0.166 mW m−2) at the temperature of 373 K compared to other SCO electrolytes. This is attributed to a combination of a higher Seebeck coefficient at the second gradient and spin state transition from HS–LS which occurred at 373 K. Complex 2 in a LS state is higher in charge density, indicating a higher capability to transport charge to the respective electrodes and accumulate on the electrode surface. However, higher ion concentrations have the effect of reducing the ion diffusivity (3.48 × 10−7 cm2 s−1) and mobility (11.10 × 10−6 cm2 V s−1). In addition, additional factors also come from the changes in physical liquid crystalline (Crystalline → Columnar state) and chaotropic effect. The spin Seebeck effect that has occurred after the spin state transition contributed to the high charge transport properties.5 During these occurrences, the potential in the thermal sensor increased dramatically. As a result, high cell power density is obtained. Although the highest power density obtained in this present study is 0.166 mW m−2 for thermal sensor with complex 2, this value is still considered low if compared to the reported value by Abraham et al.9 of 499 mW m−2 with a cell consisting of 0.1 M CoII/III(bpy)3(NTf2)2/3 in MPN electrolyte. This can be due to the fact that power density is directly proportional to concentration. The low concentration of complex 2 (0.002 M) has restricted the performance of the thermal sensor device due to the diffusion limitations.53 Another important factor that limits the device performance is through the observation of the relationship between the current and potential of electrochemical device.
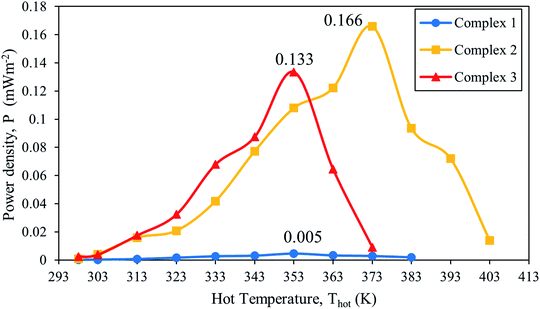 | ||
| Fig. 7 Plot of power density as a function of temperature of thermal sensor for [Fe(L12)2](BF4)2 (1), [Fe(L14)2](BF4)2 (2), and [Fe(L16)2](BF4)2 (3). | ||
In Fig. 8(a) and (b), the current and power density obtained are low for all complexes systems which led to the limitation of diffusion, thus revealing a smaller power output. This clearly showed that the power output and current–voltage relation have influenced the overall performance of the device. The following are strategies to improve the performance of thermal sensor device; (i) optimization of the electrolyte concentration must be conducted,9,53 (ii) the use of the redox couple instead of the single couple can increase the redox reaction,11 (iii) the electrode surface area should be increased by replacing them with carbon nanotubes which increases the number of reaction sites, hence producing a higher power output. Baughman et al.54 proved that high surface area carbon nanotube electrodes perform better than platinum in aqueous thermoelectrochemical systems. This strategy has been proved by Abraham et al.9 where the thermocell power density increased from 499 to 522 mW m−2 for the MPN-based device and from 183 to 240 mW m−2 for [C2mim][B(CN)4]. Furthermore, another strategy is to focus on the device level by introducing a thermal separator between hot and cold electrodes can increase the thermal gradient within the electrolyte. The optimization of the thermal separator thickness can contribute to maximizing the performance of the device.55
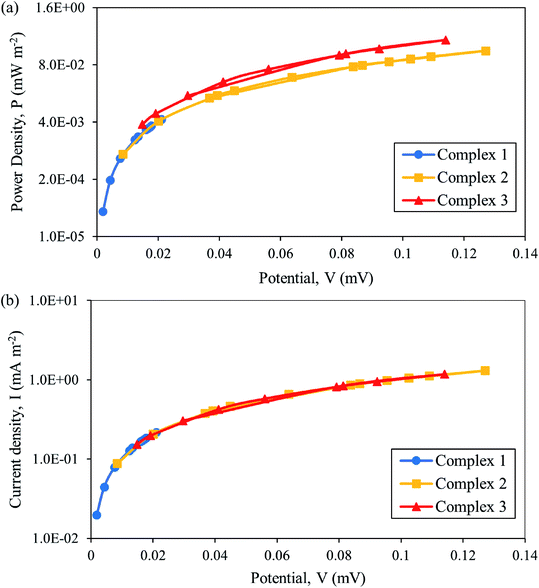 | ||
| Fig. 8 Plot of (a) power density and (b) current density as a function of potential for thermal sensor for [Fe(L12)2](BF4)2 (1), [Fe(L14)2](BF4)2 (2) and [Fe(L16)2](BF4)2 (3). | ||
4. Conclusions
This work has successfully investigated the factors to maximise the entropy of three spin-crossover (SCO) Fe(II) complexes, [Fe(L12)2](BF4)2 (complex 1), [Fe(L14)2](BF4)2·H2O (complex 2) and [Fe(L16)2](BF4)2·H2O (complex 3) as new thermal sensor materials. The synthesis and structural deduction, thermal properties, mesomorphic properties, single couple behaviour, transport properties on the Seebeck coefficient and the thermal sensor performance were carried out. Results showed that [Fe(L16)2](BF4)2·H2O (complex 3) with the longest carbon chain length of ligand yielded an ultrahigh Seebeck value of 8.67 mV K−1 due to a six-pronged strategy that increased the entropy of the molecular SCO system. This contributed to changes during spin state, physical phase (liquid crystal mesophase), spin Seebeck effect, kosmotropic and chaotropic effect, fastener effect and thermal heat absorbance. Additionally, in a real thermal sensor (where one terminal is hot whilst the other is cold), an enhancement of the thermal property of the SCO solution due to a strong endothermic peak (as illustrated by the DSC analysis) further enhances the entropy of the reaction. Ultimately, all these properties point towards a structured strategy for the optimization of stable SCO based electrolytes for ultrahigh Seebeck thermal sensor. These materials are electrochemically reversible and hence, demonstrate a long lifetime use of these solutions in thermal sensor.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank University of Malaya for the University Malaya Student Financial Aid (UMSFA); the Frontier Research Grant [FG009-17AFR]; the Faculty Grant [GPF022A-2018]; the UM Research Grant [IIRG002A-1911SS]; the Nippon Glass Sheet Grant [IF009-2020]; and the Partnership 2020 (UM Research Grant) for their generous financial support for the PhD fellowship.References
- B. Yang and G. Portale, Ionic thermoelectric materials for waste heat harvesting, Colloid Polym. Sci., 2021, 299(3), 465–479 CrossRef CAS.
- N. Abdullah, et al., Spin-crossover, mesomorphic and thermoelectrical properties of cobalt(II) complexes with alkylated N-3-Schiff bases, J. Mater. Chem. C, 2015, 3(11), 2491–2499 RSC.
- N. Abdullah, et al., Magnetic, thermal, mesomorphic and thermoelectric properties of mononuclear, dimeric and polymeric iron (II) complexes with conjugated ligands, RSC Adv., 2015, 5(63), 50999–51007 RSC.
- A. Z. S. Bin Zulkifli, et al., Conductivity studies on the effect of a nematic liquid crystal on polyvinyl alcohol-based electrolytes, in Advanced Materials Research, Trans Tech Publ, 2014 Search PubMed.
- M. M. I. Megat Hasnan, et al., Enhancement of spin Seebeck effect of reverse spin crossover Fe (II) micellar charge transport using PMMA polymer electrolyte, Appl. Organomet. Chem., 2021, e6268 Search PubMed.
- S. Wang, et al., High performance n-type (Bi, Sb)2 (Te, Se)3 for low temperature thermoelectric generator, J. Phys. D: Appl. Phys., 2010, 43(33), 335404 CrossRef.
- N. Ibrahim, et al., Optimisation of octahedral iron (II) and cobalt (II) spin-crossover metal complex for thermoelectric application, Mater. Chem. Phys., 2019, 232, 169–179 CrossRef CAS.
- N. N. Ibrahim, et al., Molecular design strategies for spin-crossover (SCO) metal complexes (Fe (II) and Co (II)) for thermoelectricity, Mater. Res. Bull., 2020, 126, 110828 CrossRef.
- T. J. Abraham, D. R. MacFarlane and J. M. Pringle, High Seebeck coefficient redox ionic liquid electrolytes for thermal energy harvesting, Energy Environ. Sci., 2013, 6(9), 2639–2645 RSC.
- J. H. Kim and T. J. Kang, Diffusion and Current Generation in Porous Electrodes for Thermo-electrochemical Cells, ACS Appl. Mater. Interfaces, 2019, 11(32), 28894–28899 CrossRef CAS PubMed.
- M. M. Hasnan, et al., Thermo-electrochemical generation capabilities of octahedral spin crossover complexes of Mn (II), Fe (II) and Co (II) with N-donor ligands and benzoate counter ion, Electrochim. Acta, 2018, 261, 330–339 CrossRef CAS.
- A. Gaspar, M. Seredyuk and P. Gütlich, Spin crossover in iron (II) complexes: Recent advances, J. Mol. Struct., 2009, 924, 9–19 CrossRef.
- Y. Bodenthin, et al., Spin-crossover phenomena in extended multi-component metallo-supramolecular assemblies, Coord. Chem. Rev., 2009, 253(19–20), 2414–2422 CrossRef CAS.
- R. J. Wei, et al., Anion-Dependent Spin Crossover and Coordination Assembly Based on [Fe (tpa)]2+ [tpa= tris (2-pyridylmethyl) amine] and [N(CN)2]−: Square, Zigzag, Dimeric, and [4+1]-Cocrystallized Complexes, Eur. J. Inorg. Chem., 2013, 2013(5–6), 916–926 CrossRef CAS.
- S. Hayami, et al., Spin-crossover in cobalt (II) compounds containing terpyridine and its derivatives, Coord. Chem. Rev., 2011, 255(17–18), 1981–1990 CrossRef CAS.
- S. Roy Chowdhury and S. Mishra, Ab initio investigation of magnetic anisotropy in intermediate spin iron (iii) complexes, J. Chem. Phys., 2018, 149(23), 234302 CrossRef PubMed.
- R. W. Hogue, S. Singh and S. Brooker, Spin crossover in discrete polynuclear iron (II) complexes, Chem. Soc. Rev., 2018, 47(19), 7303–7338 RSC.
- S. Sahami and M. J. Weaver, Solvent effects on the kinetics of simple electrochemical reactions: part I. Comparison of the behavior of Co (III)/(II) trisethylenediamine and ammine couples with the predictions of dielectric continuum theory, J. Electroanal. Chem. Interfacial Electrochem., 1981, 124(1–2), 35–51 CrossRef CAS.
- J. T. Hupp and M. J. Weaver, Solvent, ligand, and ionic charge effects on reaction entropies for simple transition-metal redox couples, Inorg. Chem., 1984, 23(22), 3639–3644 CrossRef CAS.
- E. L. Yee, et al., A survey of ligand effects upon the reaction entropies of some transition metal redox couples, J. Am. Chem. Soc., 1979, 101(5), 1131–1137 CrossRef CAS.
- S. Sahami and M. J. Weaver, Entropic and enthalpic contributions to the solvent dependence of the thermodynamics of transition-metal redox couples: part ii. Couples containing ammine and ethylenediamine ligands, J. Electroanal. Chem. Interfacial Electrochem., 1981, 122, 171–181 CrossRef CAS.
- T. J. Abraham, D. R. MacFarlane and J. M. Pringle, Seebeck coefficients in ionic liquids–prospects for thermo-electrochemical cells, Chem. Commun., 2011, 47(22), 6260–6262 RSC.
- P. G. Bomben, et al., Cyclometalated ruthenium chromophores for the dye-sensitized solar cell, Coord. Chem. Rev., 2012, 256(15–16), 1438–1450 CrossRef CAS.
- A. Gaspar, M. Seredyuk and P. Gütlich, Spin crossover in metallomesogens, Coord. Chem. Rev., 2009, 253(19–20), 2399–2413 CrossRef CAS.
- Y. Marcus, Effect of ions on the structure of water: structure making and breaking, Chem. Rev., 2009, 109(3), 1346–1370 CrossRef CAS PubMed.
- J. Duan, et al., Aqueous thermogalvanic cells with a high Seebeck coefficient for low-grade heat harvest, Nat. Commun., 2018, 9(1), 1–8 CrossRef PubMed.
- Y. Komatsu, et al., Spin-Crossover Behaviors Based on Intermolecular Interactions for Cobalt (II) Complexes with Long Alkyl Chains, Eur. J. Inorg. Chem., 2012, 2012(16), 2769–2775 CrossRef CAS.
- S. Hayami, et al., A Photoinduced Spin Transition Iron (II) Complex with Liquid-Crystal Properties, Adv. Mater., 2004, 16(11), 869–872 CrossRef CAS.
- S. Hayami, et al., Spin-crossover cobalt (II) compound with banana-shaped structure, Inorg. Chem., 2005, 44(21), 7295–7297 CrossRef CAS PubMed.
- T. Quickenden and C. Vernon, Thermogalvanic conversion of heat to electricity, Sol. Energy, 1986, 36(1), 63–72 CrossRef CAS.
- J. Agar and W. Breck, Thermal diffusion in non-isothermal cells. Part 1.—Theoretical relations and experiments on solutions of thallous salts, Trans. Faraday Soc., 1957, 53, 167–178 RSC.
- A. Hauser, Ligand field theoretical considerations, in Spin Crossover in Transition Metal Compounds I, Springer, 2004, pp. 49–58 Search PubMed.
- C. J. O'Connor, Magnetochemistry—Advances in Theory and Experimentation, in Progress in Inorganic Chemistry, John Wiley & Sons, Inc., 2007, pp. 203–283 Search PubMed.
- Y. Zhang, et al., Reversible Redox, Spin Crossover, and Superexchange Coupling in 3d Transition-Metal Complexes of Bis-azinyl Analogues of 2, 2′: 6′, 2′′-Terpyridine, Eur. J. Inorg. Chem., 2018, 2018(10), 1212–1223 CrossRef CAS.
- G. Nancollas, The Thermodynamics of Formation of Metal Complexes and Ion-Pairs in Solution, Croat. Chem. Acta, 1970, 42(2), 299–310 CAS.
- V. Percec, et al., Self-Assembly of Semifluorinated Janus-Dendritic Benzamides into Bilayered Pyramidal Columns, Angew. Chem., 2005, 117(30), 4817–4823 CrossRef.
- G. Zanchetta, Spontaneous self-assembly of nucleic acids: liquid crystal condensation of complementary sequences in mixtures of DNA and RNA oligomers, Liq. Cryst. Today, 2009, 18(2), 40–49 CrossRef CAS.
- I. Dierking, Textures of liquid crystals, John Wiley & Sons, 2003 Search PubMed.
- J. Grolik, Ł. Dudek and J. Eilmes, Tuning the mesomorphic properties of liquid-crystalline dibenzotetraaza [14] annulenes—discotic nematic phases of tetraalkoxy-substituted derivatives, Tetrahedron Lett., 2012, 53(38), 5127–5130 CrossRef CAS.
- C. F. Fitié, et al., Nanostructured materials through orthogonal self-assembly in a columnar liquid crystal, Chem. Mater., 2008, 20(6), 2394–2404 CrossRef.
- M. Iliş and V. Circu, Discotic liquid crystals based on Cu (I) complexes with benzoylthiourea derivatives containing a perfluoroalkyl chain, J. Chem., 2018, 2018, 1–10 CrossRef.
- N. Elgrishi, et al., A practical beginner's guide to cyclic voltammetry, J. Chem. Educ., 2018, 95(2), 197–206 CrossRef CAS.
- M. M. Dîrtu, et al., Room temperature hysteretic spin transition in 1D iron (II) coordination polymers, in Journal of Physics: Conference Series, IOP Publishing, 2010 Search PubMed.
- N. Abdullah, et al., Room-temperature magnetic liquid complexes of 2-hexyldecanoato ligand with Cu (II), Ni (II) and Co (II) ions, Asian J. Chem., 2014, 26(4), 987 CrossRef CAS.
- E. L. Yee and M. J. Weaver, Functional dependence upon ligand composition of the reaction entropies for some transition-metal redox couples containing mixed ligands, Inorg. Chem., 1980, 19(4), 1077–1079 CrossRef CAS.
- C. Schulzke, Temperature dependent electrochemistry—a versatile tool for investigations of biology related topics, Dalton Trans., 2009,(34), 6683–6691 RSC.
- H. L. Chum, Review of thermally regenerative electrochemical systems, Solar Energy Research Institute, 1981, vol. 1 Search PubMed.
- K. Murata, et al., High-pressure research in organic conductors, J. Phys. Soc. Jpn., 2006, 75(5), 051015 CrossRef.
- I. Dierking and S. Al-Zangana, Lyotropic liquid crystal phases from anisotropic nanomaterials, Nanomaterials, 2017, 7(10), 305 CrossRef PubMed.
- M. Dupont, D. MacFarlane and J. Pringle, Thermo-electrochemical cells for waste heat harvesting–progress and perspectives, Chem. Commun., 2017, 53(47), 6288–6302 RSC.
- C. D. Simpson, et al., From graphite molecules to columnar superstructures–an exercise in nanoscience, J. Mater. Chem., 2004, 14(4), 494–504 RSC.
- A. Taheri, et al., Flexible and non-volatile redox active quasi-solid state ionic liquid based electrolytes for thermal energy harvesting, Sustain. Energy Fuels, 2018, 2(8), 1806–1812 RSC.
- T. J. Kang, et al., Electrical power from nanotube and graphene electrochemical thermal energy harvesters, Adv. Funct. Mater., 2012, 22(3), 477–489 CrossRef CAS.
- R. Hu, et al., Harvesting waste thermal energy using a carbon-nanotube-based thermo-electrochemical cell, Nano Lett., 2010, 10(3), 838–846 CrossRef CAS PubMed.
- L. Zhang, et al., High Power Density Electrochemical Thermocells for Inexpensively Harvesting Low-Grade Thermal Energy, Adv. Mater., 2017, 29(12), 1605652 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra01387d |
| This journal is © The Royal Society of Chemistry 2021 |