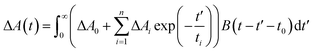Open Access Article
Open Access ArticleSinglet fission from upper excited singlet states and polaron formation in rubrene film†
Tong Wua,
Wenjun Nia,
Gagik G. Gurzadyan *a and
Licheng Sun
*a and
Licheng Sun *abc
*abc
aState Key Laboratory of Fine Chemicals, Institute of Artificial Photosynthesis, Dalian University of Technology, 116024 Dalian, China. E-mail: gurzadyan@dlut.edu.cn; lichengs@kth.se
bDepartment of Chemistry, School of Engineering Sciences in Chemistry, Biotechnology and Health, KTH Royal Institute of Technology, 10044 Stockholm, Sweden
cCenter of Artificial Photosynthesis for Solar Fuels, School of Science, Westlake University, 310024, Hangzhou, China
First published on 22nd January 2021
Abstract
Femtosecond fluorescence up-conversion and transient absorption pump-probe setups are applied to study the relaxation dynamics of the lower and upper excited singlet electronic states in easy-to-make rubrene films. Upon 250 nm (4.96 eV) excitation, singlet fission was observed directly from S2 state bypassing S1 state within 30 fs i.e. breaking the classical Kasha rule. From the transient absorption measurements, polaron formation was also detected on the same time scale. Both singlet fission and polaron formation are accelerated from upper excited states compared with S1 state. Our work shows that rubrene films with low degree of crystallinity could display efficient singlet fission, notably in the case of excitation to upper lying electronic states. This can strongly expand the applications of rubrene in organic electronics. Moreover, our results will provide a new direction for synthesizing novel materials with optimized excited state properties for organic photovoltaic applications.
1. Introduction
Singlet fission is a spin-allowed process in which a singlet excited state molecule shares its energy with an adjacent ground state molecule to generate two triplet excited state molecules.1 Singlet fission has attracted a great deal of interest for its potential to increase photovoltaic efficiency above the Shockley–Queisser limit,2,3 and has been observed in crystals,4–6 films,7,8 dimers,9,10 nanoparticles11,12 and concentrated solutions.13 Singlet fission is very fast in solid tetracene and pentacene; triplet yield is reached 200%.14–16 Rubrene as a derivative of tetracene, due to its high carrier mobility17–19 and long exciton diffusion length,20–22 has received extensive attention in recent years. Singlet fission has already been confirmed in rubrene crystal.23–25 In our previous publications,26,27 we studied rubrene crystal by femtosecond pump-probe spectroscopy; triplet states are formed within 2–20 ps via singlet fission from lowest excited singlet state under 500 nm excitation and within 200 fs from upper excited singlet states under 250 nm excitation. In ref. 28, by combining spectroscopic measurements and theoretical modeling, formation of correlated triplet pairs was confirmed in rubrene crystal within 20 fs. Miyata et al. reported that SF takes place through both the coherent and the incoherent pathways. Coherent phonons of singlet and triplet exciton states were observed in a rubrene single crystal at 35 K.29,30 Apart from single crystal, triplet states are also studied in amorphous rubrene film, which originate from not only singlet fission but also polarons.31 In ref. 32, it is reported that both singlet fission and triplet fusion (TF) can happen in amorphous rubrene; singlet fission undertakes a charge transfer state mediated channel and competes well with TF. In rubrene film, suppression of singlet fission at low temperatures was reported.33–35 Earlier, it was also demonstrated in rubrene crystal.27 Zhang's group reported the competition between singlet fission, fluorescence and dissociation in rubrene doped amorphous films.36 They have also demonstrated that transition rate of singlet fission exponentially decreased with increasing distance between rubrene molecules.37 Finton et al. presented the time-resolved fluorescence results of various film samples.38 They have not observed quenching of fluorescence in fully amorphous samples, which indicates absence of singlet fission in this rubrene film. In the samples which contain some degree of crystallinity, fluorescence is strongly quenched, which is a sign for singlet fission.It should be mentioned that the time-resolved spectroscopic data on dynamics of polaron and triplet formation are rather scarce and restricted to time-resolved fluorescence. Moreover, all pump-probe measurements involving upper excited singlet electronic states in rubrene film is still missing. In the present work, we draw the detailed picture of the relaxation pathways from the upper excited states in easy-to-make rubrene film. This may lead to advantageous applications in photovoltaics. Our approach is, by using molecular systems and crystals which have strong absorption in blue/UV, to produce triplet states via singlet fission directly from higher lying electronic states bypassing relaxed S1 state. Thus it will necessarily lead to increase of efficiency of photon-to-electron conversion. Harnessing the entire UV/blue/Vis spectrum of the Sun for producing free charge careers via singlet fission may have far-reaching advantages and enormous industrial benefits.
There are few possible detection methods: magnetic field effect to recognize SF qualitatively;39,40 time-resolved fluorescence to identify the quenching of singlet state,41,42 time-resolved resonance Raman and time-resolved two-photon photoemission spectroscopy to distinguish various intermediate states,43–46 2D, 3D spectroscopy47,48 and ultrafast pump-probe method to track the decay of singlet state and the formation of triplet state and, possibly, also identifying intermediate states.
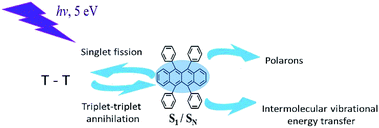
In this work, we used time-resolved fluorescence and pump-probe transient absorption techniques with time resolution of 30 fs, in order to study various photoreactions after excitation of upper excited electronic states of rubrene film, i.e. singlet exciton fission, triplet–triplet annihilation, polaron formation (Scheme 1).
2. Materials and methods
2.1 Sample preparation
Rubrene was thermally evaporated in Vacuum Evaporation Pump device with a pressure below 10−4 Pa [QHV-Z350C, Pana Instruments]. Before installing in the chamber, the quartz substrates were cleaned by ethanol in ultrasonic bath for 10 minutes and stood in ethanol for 12 hours. After that, the quartz substrates were treated with plasma in an O3-filled environment for 8 minutes in order to remove organic impurities and contaminants. X-ray diffraction (XRD) measurements were performed to characterize crystal structure of our films, using data acquisition mode 1D. Besides, the surface of our films was investigated by use of scanning electron microscopy (SEM) and atomic force microscopy (AFM). SEM images were measured under 5 kV accelerating voltage and 10 A current. AFM was conducted on Tecnai F30 operated at 300 kV, in non-contact mode with the scan rate of 1.0 Hz.2.2 Experimental
The steady state absorption spectra were obtained by using UV-Visible spectrophotometer (Cary 100, Agilent) and fluorescence spectra are recorded by spectrofluorometer (Flurorolog-3, HORIBA Jobin Yvon). In both cases the wavelength resolution was 1 nm.Time-resolved up-conversion measurements were carried out by a fluorescence spectrometer (TRFLS, Newport) with 100 fs resolution in combination with a mode-locked Ti-sapphire laser (Mai Tai DeepSee, Spectra-Physics). Briefly, the femtosecond laser system generated light pulses at 800 nm of duration 150 fs at a repetition rate 80 MHz, average power of 2.9 W. The frequency of the laser pulse was doubled with a BBO crystal and served for excitation (pump), gate pulse was split from the pump beam with beam splitter. The emitted fluorescence was focused into a BBO crystal together with the gate beam (800 nm) to create the up-converted signal at the sum-frequency generation (SFG). The fluorescence decay curve is obtained by varying the optical path of the delay stage for the gate beam. Fluorescence lifetimes in the range 10 ps to 100 ns were measured by time-correlated single photon counting (TCSPC) technique (PicoHarp 300, PicoQuant). By use of deconvolution/fit program (FluFit, PicoQuant) the time resolution was reached down to 10 ps. The second harmonic of a Titanium–sapphire laser (Mai Thai DeepSee, Spectra-Physics) at 400 nm (150 fs, 80 MHz) was used as the excitation source.
The transient absorption (TA) spectra were measured by optical femtosecond pump-probe spectroscopy. The output of a mode-locked Ti-sapphire amplified laser system (Spitfire Ace, Spectra-Physics) with wavelength 800 nm, pulse-width 35 fs, repetition rate 1 kHz, average power 4 W was split into two beams (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Pump beam in the range of 240–2400 nm is acquired by use of Optical Parametric Amplifier (TOPAS, Light Conversion). 10% of 800 nm laser pulse was focused in a 3 mm thickness rotated CaF2 plate to produce a white light continuum (WLC), which was used as a probe beam ranging between 350 and 850 nm. Home-built pump-probe setup was used for obtaining transient absorption spectra and kinetics. The relative polarizations between pump and probe beam were arranged to the magic angle (54.7°) to avoid rotational depolarization effects (except for λpump = 250 nm). The experimental data were fitted to a multiexponential decay function convoluted with the instrument response function B(t − t0) centered at t0:
1). Pump beam in the range of 240–2400 nm is acquired by use of Optical Parametric Amplifier (TOPAS, Light Conversion). 10% of 800 nm laser pulse was focused in a 3 mm thickness rotated CaF2 plate to produce a white light continuum (WLC), which was used as a probe beam ranging between 350 and 850 nm. Home-built pump-probe setup was used for obtaining transient absorption spectra and kinetics. The relative polarizations between pump and probe beam were arranged to the magic angle (54.7°) to avoid rotational depolarization effects (except for λpump = 250 nm). The experimental data were fitted to a multiexponential decay function convoluted with the instrument response function B(t − t0) centered at t0:
Global fit of time-resolved experimental results was done by Glotaran software.52 The decay associated spectra (DAS) allow separating several overlapping emission spectra in parallel model, whereas the evolution associated spectra (EAS) shows the global fit results in a sequential model.
3. Results and discussion
3.1 Characterization of rubrene film
Our film was fully characterized by use of XRD, SEM and AFM techniques (Fig. S1†). In the XRD spectrum (Fig. S1a†), there exists a peak at 27° repeating the reference rubrene crystal, similar to previous observations.53 It is indicative of certain amount of crystallinity of orthorhombic form in our films. Besides, the SEM image exhibits clear polycrystalline morphology of 10–20 micrometer size. The AFM picture (inset of Fig. S1b†) gives a proof of smooth and uniform film surface. Note that the beam size during pump-probe and time-resolved fluorescence is about 100 μm, i.e. fully covering both amorphous and crystalline regions.3.2 Steady state and time-resolved PL characterizations
Steady-state absorption, fluorescence and excitation spectra of rubrene in hexane and film are presented in Fig. 1a and b, respectively. We use absorptance (1 − T, where T is transmittance) as a linear scale of absorption instead of absorbance. Absorption spectrum of rubrene solution shows four maxima at 522, 487, 457 and 431 nm, ascribed to the S0 → S1 band54 with a vibronic progression of Δω = 1300 cm−1, which corresponds well to literature data.26 The fluorescence spectrum exhibits two maxima, at 551 and 589 nm, with vibronic progression Δω = 1170 cm−1. Absorption and excitation spectra match well, in agreement with Kasha rule.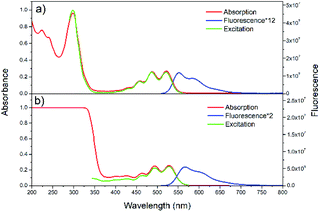 | ||
| Fig. 1 Steady-state absorption, fluorescence, and excitation spectra of rubrene in hexane (a) (λex = 500 nm, λem = 570 nm) and film (b) (λex = 480 nm, λem = 600 nm). | ||
Absorption spectrum of rubrene film also shows four maxima, at 528, 494, 464 and 434 nm with vibronic progression Δω = 1300 cm−1, which are red shifted by 7 nm compared with solution. The fluorescence spectrum shows two maxima, at 566 and 604 nm, indicative of a vibronic progression with Δω = 1110 cm−1; it is also red shifted relative to solution (15 nm), which is due to excitonic states originated from intermolecular interactions54,55 and reabsorption.54 The other reason for red shift is higher polarizability and the broadening of spectra as a result of static disorder.33
TCSPC map of rubrene solution at λex = 400 nm (Fig. S2a†) corresponds well with the steady state fluorescence spectrum. The kinetics at different emission wavelengths (Fig. S2b†) shows mono-exponential decay with τ = 10 ns.
Fig. 2 presents the TCSPC measurements of rubrene film under 400 nm excitation. We have observed a strong fluorescence quenching which indicates presence of a new nonradiative relaxation channel. Lifetimes are emission wavelength dependent and kinetics at all probe wavelengths are well fitted by 3 components (Table S1†): τ1 = 68–380 ps (A1 = 0.78–0.21), τ2 = 580–1400 ps (A2 = 0.17–0.49) and τ3 = 3700–5000 ps (A3 = 0.04–0.30). The initial decay τ1, which we assign to prompt fluorescence, is followed by a long component τ3. This decay feature is typical for singlet fission followed by triplet–triplet annihilation (TTA), which has previously been observed in rubrene27 and tetracene crystals.14 We therefore suggest that in our case as well the observed delayed fluorescence is a result of singlet fission and further TTA. τ2 most probably originates from oxidized rubrene.26,56,57 Other reason can be existence of rubrene molecules with poor packing geometry where SF does not occur efficiently.
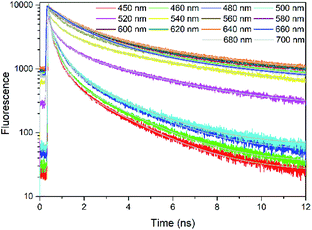 | ||
| Fig. 2 TCSPC kinetics of rubrene film at different probe wavelengths, λex = 400 nm. Pump fluence: 3.49 × 10−8 J cm−2. | ||
In order to obtain precise fluorescence lifetimes, the up-conversion measurements with 100 fs resolution were performed. Up-conversion fluorescence with higher time resolution (Fig. S3†) leads to an additional shorter time component of τ1 = 1.4–9.6 ps (Table S1†), which is due to direct fission from higher vibrational states and τ2 = 30–300 ps corresponds to the thermally activated singlet fission.27
From transient fluorescence results, we identify that singlet fission takes place in rubrene film. Further proof was obtained by combining the fluorescence data with the transient absorption measurements described below.
3.3 Femtosecond transient absorption spectra
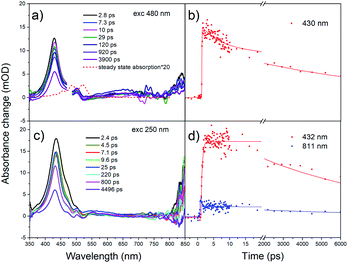
In order to make proper assignments of the TA spectral bands, the pump-probe measurements were first performed in solution. Femtosecond transient absorption spectra under different excitation wavelengths are shown in Fig. 3. At λex = 480 nm, a strong ESA at 430 nm appears promptly after photoexcitation and decays within 8.0 ns (Fig. 3b), is due to singlet–singlet absorption (S1 → SN).26 The negative part at 520–550 nm, which corresponds to maximum of steady state absorption, is due to ground state bleaching (GSB). The amplitude of GSB is small, similar to rubrene crystal26,28 and film.31 There are several reasons for the absence of GSB. One reason is an unfavorable orientation of the S0 → S1 transition dipole in crystal.28 Other reason is that the photoinduced absorption band between 2.4 and 2.6 eV overlaps substantially with the GSB in film.31 The third reason is that the excited state absorption is much stronger than the GSB,26 i.e. the molar extinction coefficient of the singlet–singlet absorption S1 → SN is significantly larger than that of S0 → S1, ε = 9550–12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1.58,59 Because of small quantum yield of intersystem crossing (Φ < 0.01),60 we did not observe formation of triplet states (no triplet–triplet absorption TA band at about 500 nm).
000 M−1 cm−1.58,59 Because of small quantum yield of intersystem crossing (Φ < 0.01),60 we did not observe formation of triplet states (no triplet–triplet absorption TA band at about 500 nm).
Further, we have excited rubrene in hexane with λex = 250 nm, thus populating higher vibrational levels of S2 state; transient absorption spectra are shown in Fig. 3c. The peak at 432 nm, i.e. ESA due to S1 → SN transition, decays within 7.5 ns (S1 lifetime). The kinetics (Fig. 3d) shows a rise time of 0.39 ps, which is due to S2 → S1 internal conversion. Relatively long S2 lifetime is due to large S1–S2 energy gap (∼2 eV), which is supported by DFT and TD-DFT calculations (ESI, Pages S8–S13†). Strong ESA band at 800–850 nm appears promptly after excitation; it is assigned to radical cation and anion.61,62 These radicals form only at 250 nm (4.96 eV) excitation, and not at 480 nm (2.58 eV) or 340 nm (3.65 eV) which is indicative of an energy threshold for their formation. The ionization energy threshold is 6.4 eV in gas,63 4.95 eV for rubrene crystal and 5.3 eV for amorphous film.64 The lifetime of the cation/anion is 0.50 ps (Fig. 3d). Similar results were obtained after excitation of the lower vibrational levels of S2 (λex = 340 nm, Fig. S4†).
Global fit of spectra under λex = 250 nm (Fig. S5†) results in two time components: τ1 = 0.90 ps with maximum at 445 nm and τ2 = 7.9 ns with maximum at 433 nm. Time component of 7.9 ns corresponds to S1 → SN absorption, in agreement with fluorescence lifetime. The short component, 0.9 ps, is assigned to S2 → SM transition; decay of S2 state is accompanied with the rise of S1 population with the same time component.
The pump-probe measurements were carried out in rubrene film under different excitation wavelengths. For transient absorption spectra under λex = 480 nm (Fig. S6†), we only observed one positive band at 439 nm. Similar to rubrene solution, we assign 439 nm band to singlet–singlet absorption. We do not observe triplet transient, indicating the absence of singlet fission. However, in rubrene crystal, singlet fission proceeds at even longer excitation wavelengths, e.g. λex = 500 nm.26 The explanation is that in film, although molecules packed tightly, short-range molecular order matching the molecular arrangement in orthorhombic rubrene crystals is not favoured. Overall films are of low degree of crystallinity. Therefore, in rubrene film singlet fission undergoes under higher excitation photon energies 3–5 eV (400–250 nm, see below).
Under 400 nm excitation, the transient absorption spectra (Fig. 4a) present one small peak at 439 nm and another strong one at 489 nm. The 439 nm peak is assigned to singlet–singlet absorption, i.e. at the same position as with λex = 480 nm. The band at 489 nm has a long decay time (over 100 ns, A = 0.41). We assign it to triplet absorption according to previous publications on the rubrene solution, film and crystal: 472 and 505 nm in solution,65 504 nm in film,31 510 nm in crystal.24,26,27 Existence of decay times 29 ps (A = 0.34) and 2.4 ns (A = 0.25) in triplet ESA kinetics is due to overlap with singlet–singlet absorption band (439 nm). We suggest that triplet formation is due to singlet fission.
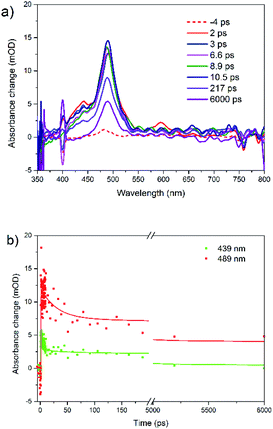 | ||
| Fig. 4 (a) Femtosecond transient absorption spectra for rubrene film at λex = 400 nm and (b) transient kinetics at 439 and 489 nm, pump fluence: 1.27 × 10−3 J cm−2. | ||
Similar results were obtained under 340 nm excitation (Fig. S7†). However, there is only triplet–triplet absorption peak locating at 490 nm, which is the result of singlet fission. The singlet–singlet TA band is much weaker and therefore is fully covered by strong triplet TA band. Moreover, both bands are strongly overlapping with polaron band (see below), overall causing some distortion.
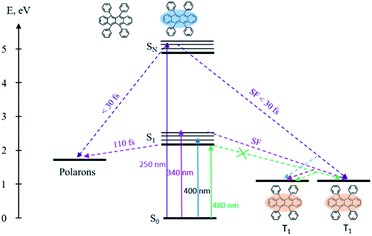
The transient absorption spectra of rubrene film under 250 nm excitation are presented in Fig. 5a. At 441 nm (singlet–singlet absorption), we observed an ultrashort decay time of 0.26 ps (Table S2†). The shortening is due to direct singlet fission from S2 state, i.e. S2 → 2T1, which agrees well with 0.2 ps fission from SN states in rubrene crystal.26 No risetime was observed for the triplet transient, i.e. singlet fission proceeds within 30 fs (time resolution of our setup). Singlet fission competes well with ultrafast internal conversion S2 → S1. As was indicated above, this is due to relatively long S2 lifetime as a result of large S1–S2 energy gap: (∼2 eV). We can also rule out participation of upper triplet states in population of T1 via intersystem crossing SN → TN and further internal conversion TN → T1 because TN (n = 2) lifetimes of organic molecules are in pico- or nanosecond time scale [ref. 66 and references therein]. Polarons are observed at 706 nm which appears immediately after excitation, i.e. they are generated within instrument resolution 30 fs. Compared with 0.11 ps upon 340 nm excitation, polaron formation is faster under higher excitation photon energy. The ultrafast formation of polarons has also been observed in other molecules, e.g. the relaxation time of free exciton to form an exciton polaron is determined as 50 ± 23 fs in MEH-PPV67 and 60–100 fs in the polymer PHTDMABQ.68
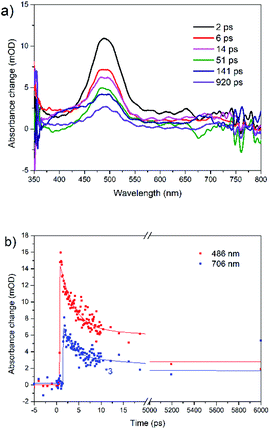 | ||
| Fig. 5 (a) Femtosecond transient absorption spectra for rubrene film at λex = 250 nm, pump fluence: 1.27 × 10−3 J cm−2. (b) Transient kinetics at different wavelengths. | ||
In film, we did not observe isosbestic point in the 400–550 nm region as in rubrene crystal,26 which is indicative of more than one process contributing to the transient absorption. Here, under 250 nm excitation, the ESA band is broader, which indicates polarons absorb at 400–550 nm, i.e. strongly overlapping with triplet states. The decay times 220 ps (λex = 340 nm) and 140 ps (λex = 250 nm) at 490 nm are assigned to polarons lifetime, which recombine due to a secondary recombination processes via diffussion.69 At “minus delays” (i.e. delay times of 1 ms) we observed TA signal in the range of 400–550 nm (Fig. S8†), indicating the polarons lifetime is longer than 1 ms. In our case, polarons absorb in the whole range of 400–800 nm. Singlet fission competes with polaron generation in our films with certain degree of crystallinity. Note that polarons are also formed in fully amorphous films.70–72
Our sample contains both amorphous and polycrystalline morphology. The beam size during pump-probe and time-resolved fluorescence is about 100 μm, which can fully cover both amorphous and crystalline regions. Considering all above, we conclude that rubrene films with low degree of crystallinity could display efficient singlet fission, which can strongly expand the applications of rubrene in organic electronics.
The overall relaxation processes after excitation with various photon energies are presented in Scheme 2. Population of the lowest singlet state results in the generation of polarons, moreover singlet fission is fully suppressed. Excitation of upper electronic states leads to 3 times faster polaron formation and to ultrafast singlet fission.
4. Conclusions
We have studied the excited state dynamics of easy-to-make rubrene film by femtosecond pump-probe and fluorescence spectroscopy under various excitation conditions. Upon excitation at 250 nm, an ultrafast (30 fs) singlet fission directly from higher excited singlet states was observed. Moreover, an ultrafast polaron formation was also detected at this excitation conditions. Both SF and polaron formation are accelerated after excitation of upper states compared with S1 excitation. TD-DFT calculations support our observations.Our film which contains both amorphous and polycrystalline morphology could display efficient singlet fission. The present results highlight potential of simple-fabricated and commercially attractive rubrene film in organic photovoltaic applications. Moreover, our work gives new insight into the dynamics of excited states in rubrene film, which will contribute in understanding of singlet fission in various organic crystals and films.
Author contributions
T. W. prepared and characterised the film, T. W., W. N. and G. G. G. performed all spectroscopic measurements and analysis, G. G. G. and L. S. supervised the research. All authors contributed in discussion and writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are indebted to Prof. Maxim Gelin (Hangzhou Dianzi University) for valuable comments and suggestions. This work was supported by DUT startup grant and by DUT basic research funding (DUT18GJ205).Notes and references
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS.
- M. B. Smith and J. Michl, Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS.
- K. Aryanpour, A. Shukla and S. Mazumdar, J. Phys. Chem. C, 2015, 119, 6966–6979 CrossRef.
- R. J. Dillon, G. B. Piland and C. J. Bardeen, J. Am. Chem. Soc., 2013, 135, 17278–17281 CrossRef CAS.
- N. Renaud and F. C. Grozema, J. Phys. Chem. Lett., 2015, 6, 360–365 CrossRef CAS.
- S. T. Roberts, R. E. McAnally, J. N. Mastron, D. H. Webber, M. T. Whited, R. L. Brutchey, M. E. Thompson and S. E. Bradforth, J. Am. Chem. Soc., 2012, 134, 6388–6400 CrossRef CAS.
- J. N. Schrauben, J. L. Ryerson, J. Michl and J. C. Johnson, J. Am. Chem. Soc., 2014, 136, 7363–7373 CrossRef CAS.
- E. G. Fuemmeler, S. N. Sanders, A. B. Pun, E. Kumarasamy, T. Zeng, K. Miyata, M. L. Steigerwald, X. Y. Zhu, M. Y. Sfeir, L. M. Campos and N. Ananth, ACS Cent. Sci., 2016, 2, 316–324 CrossRef CAS.
- W. Ni, G. G. Gurzadyan, J. Zhao, Y. Che, X. Li and L. Sun, J. Phys. Chem. Lett., 2019, 10, 2428–2433 CrossRef CAS.
- R. D. Pensack, A. J. Tilley, S. R. Parkin, T. S. Lee, M. M. Payne, D. Gao, A. A. Jahnke, D. G. Oblinsky, P. Li, J. E. Anthony, D. S. Seferos and G. D. Scholes, J. Am. Chem. Soc., 2015, 137, 6790–6803 CrossRef CAS.
- M. J. Y. Tayebjee, K. N. Schwarz, R. W. MacQueen, M. Dvořák, A. W. C. Lam, K. P. Ghiggino, D. R. McCamey, T. W. Schmidt and G. J. Conibeer, J. Phys. Chem. C, 2016, 120, 157–165 CrossRef CAS.
- B. J. Walker, A. J. Musser, D. Beljonne and R. H. Friend, Nat. Chem., 2013, 5, 1019–1024 CrossRef CAS.
- J. J. Burdett, A. M. Müller, D. Gosztola and C. J. Bardeen, J. Chem. Phys., 2010, 133, 144506 CrossRef.
- C. Jundt, G. Klein, B. Sipp, J. Le Moigne, M. Joucla and A. A. Villaeys, Chem. Phys. Lett., 1995, 241, 84–88 CrossRef CAS.
- A. Rao, M. W. B. Wilson, J. M. Hodgkiss, S. Albert-Seifried, H. Bässler and R. H. Friend, J. Am. Chem. Soc., 2010, 132, 12698–12703 CrossRef CAS.
- V. Podzorov, E. Menard, A. Borissov, V. Kiryukhin, J. A. Rogers and M. E. Gershenson, Phys. Rev. Lett., 2004, 93, 86602 CrossRef CAS.
- V. C. Sundar, Science, 2004, 303, 1644–1646 CrossRef CAS.
- T. Hasegawa and J. Takeya, Adv. Mater., 2009, 10, 024314 Search PubMed.
- P. Irkhin and I. Biaggio, Phys. Rev. Lett., 2011, 107, 17402 CrossRef.
- J. C. Johnson, A. J. Nozik and J. Michl, J. Am. Chem. Soc., 2010, 132, 16302–16303 CrossRef CAS.
- H. Najafov, B. Lee, Q. Zhou, L. C. Feldman and V. Podzorov, Nat. Mater., 2010, 9, 938–943 CrossRef CAS.
- K. Bera, C. J. Douglas and R. R. Frontiera, J. Phys. Chem. Lett., 2017, 8, 5929–5934 CrossRef CAS.
- L. Ma, G. Galstyan, K. Zhang, C. Kloc, H. Sun, C. Soci, M. E. Michel-Beyerle and G. G. Gurzadyan, J. Chem. Phys., 2013, 138, 184508 CrossRef.
- A. Ryasnyanskiy and I. Biaggio, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 193203 CrossRef.
- L. Ma, K. Zhang, C. Kloc, H. Sun, M. E. Michel-Beyerle and G. G. Gurzadyan, Phys. Chem. Chem. Phys., 2012, 14, 8307–8312 RSC.
- L. Ma, K. Zhang, C. Kloc, H. Sun, C. Soci, M. E. Michel-Beyerle and G. G. Gurzadyan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 201203 CrossRef.
- I. Breen, R. Tempelaar, L. A. Bizimana, B. Kloss, D. R. Reichman and D. B. Turner, J. Am. Chem. Soc., 2017, 139, 11745–11751 CrossRef CAS.
- K. Miyata, Y. Kurashige, K. Watanabe, T. Sugimoto, S. Takahashi, S. Tanaka, J. Takeya, T. Yanai and Y. Matsumoto, Nat. Chem., 2017, 9, 983–989 CrossRef CAS.
- K. Miyata, S. Tanaka, T. Sugimoto, K. Watanabe, T. Uemura, J. Takeya and Y. Matsumoto, et al., Ultrafast Phenomena XIX, ed. K. Yamanouchi, Spring-Verlag, Berlin, 2015, pp. 218–221 Search PubMed.
- V. Jankus, E. W. Snedden, D. W. Bright, E. Arac, D. Dai and A. P. Monkman, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224202 CrossRef.
- P. Sher, C. Chen, T. Chiu, C. Lin, J. Wang and J. Lee, J. Phys. Chem. C, 2019, 123, 3279–3284 CrossRef CAS.
- G. B. Piland, J. J. Burdett, D. Kurunthu and C. J. Bardeen, J. Phys. Chem. C, 2013, 117, 1224–1236 CrossRef CAS.
- J. Li, Z. Chen, Q. Zhang, Z. Xiong and Y. Zhang, Org. Electron., 2015, 26, 213–217 CrossRef CAS.
- Y. Zhang, Y. Lei, Q. Zhang and Z. Xiong, Org. Electron., 2014, 15, 577–581 CrossRef CAS.
- J. Li, Z. Chen, Y. Lei, Z. Xiong and Y. Zhang, Synth. Met., 2015, 207, 13–17 CrossRef CAS.
- X. Tian, L. Zhou, X. Chen, Y. Meng, Z. Xiong, X. Zhou and Y. Zhang, Org. Electron., 2017, 50, 429–434 CrossRef CAS.
- D. M. Finton, E. A. Wolf, V. S. Zoutenbier, K. A. Ward and I. Biaggio, AIP Adv., 2019, 9, 95027 CrossRef.
- S. Kawata, Y. Pu, A. Saito, Y. Kurashige, T. Beppu, H. Katagiri, M. Hada and J. Kido, Adv. Mater., 2016, 28, 1585–1590 CrossRef CAS.
- T. Yago, K. Ishikawa, R. Katoh and M. Wakasa, J. Phys. Chem. C, 2016, 120, 27858–27870 CrossRef CAS.
- B. Manna, A. Nandi and R. Ghosh, J. Phys. Chem. C, 2018, 122, 21047–21055 CrossRef CAS.
- G. B. Piland and C. J. Bardeen, J. Phys. Chem. Lett., 2015, 6, 1841–1846 CrossRef CAS.
- A. J. Musser, M. Maiuri, D. Brida, G. Cerullo, R. H. Friend and J. Clark, J. Am. Chem. Soc., 2015, 137, 5130–5139 CrossRef CAS.
- C. Wang and M. J. Tauber, J. Am. Chem. Soc., 2010, 132, 13988–13991 CrossRef CAS.
- W. L. Chan, M. Ligges, A. Jailaubekov, L. Kaake, L. Miaja-Avila and X. Y. Zhu, Science, 2011, 334, 1541–1545 CrossRef CAS.
- W. Chan, M. Ligges and X. Zhu, Nat. Chem., 2012, 4, 840–845 CrossRef CAS.
- A. C. Jones, N. M. Kearns, J. Ho, J. T. Flach and M. T. Zanni, Nat. Chem., 2020, 12, 40–47 CrossRef CAS.
- A. Mandal, M. Chen, E. D. Foszcz, J. D. Schultz, N. M. Kearns, R. M. Young, M. T. Zanni and M. R. Wasielewski, J. Am. Chem. Soc., 2018, 140, 17907–17914 CrossRef CAS.
- J. Shang, S. Yan, C. Cong, H. Tan, T. Yu and G. G. Gurzadyan, Opt. Mater. Express, 2012, 2, 1713 CrossRef CAS.
- J. Shang, T. Yu, J. Lin and G. G. Gurzadyan, ACS Nano, 2011, 5, 3278–3283 CrossRef CAS.
- S. Ullrich, T. Schultz, M. Z. Zgierski and A. Stolow, Phys. Chem. Chem. Phys., 2004, 6, 2796 RSC.
- J. J. Snellenburg, S. P. Laptenok, R. Seger, K. M. Mullen and I. H. M. Stokkum, J. Stat. Softw., 2012, 49, 1–22 Search PubMed.
- K. Lin, Y. Wang, K. Chen, C. Ho, C. Yang, J. Shen and K. Chiu, Sci. Rep., 2017, 7, 40824 CrossRef CAS.
- P. Irkhin, A. Ryasnyanskiy, M. Koehler and I. Biaggio, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085143 CrossRef.
- X. Zeng, D. Zhang, L. Duan, L. Wang, G. Dong and Y. Qiu, Appl. Surf. Sci., 2007, 253, 6047–6051 CrossRef CAS.
- C. Kloc, K. J. Tan, M. L. Toh, K. K. Zhang and Y. P. Xu, Appl. Phys. A, 2009, 95, 219–224 CrossRef CAS.
- O. Mitrofanov, D. V. Lang, C. Kloc, J. M. Wikberg, T. Siegrist, W. Y. So, M. A. Sergent and A. P. Ramirez, Phys. Rev. Lett., 2006, 97, 166601 CrossRef.
- C. Burgdorff, S. Ehrhardt and H. G. Loehmannsroeben, J. Phys. Chem., 1991, 95, 4246–4249 CrossRef CAS.
- T. Petrenko, O. Krylova, F. Neese and M. Sokolowski, New J. Phys., 2009, 11, 15001 CrossRef.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- A. Saeki, S. Seki, T. Takenobu, Y. Iwasa and S. Tagawa, Adv. Mater., 2008, 20, 920–923 CrossRef CAS.
- S. Tao, H. Matsuzaki, H. Uemura, H. Yada, T. Uemura, J. Takeya, T. Hasegawa and H. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075204 CrossRef.
- N. Sato, K. Seki and H. Inokuchi, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 1621 RSC.
- Y. Nakayama, S. Machida, T. Minari, K. Tsukagishi, Y. Noguchi and H. Ishii, Appl. Phys. Lett., 2008, 93, 173305 CrossRef.
- D. K. K. Liu and L. R. Faulkner, J. Am. Chem. Soc., 1977, 99, 4594–4599 CrossRef CAS.
- W. Yang, J. Zhao, G. Tang, X. Li and G. G. Gurzadyan, J. Phys. Chem. Lett., 2019, 10, 7767–7773 CrossRef CAS.
- T. Kobayashi, M. Yamashita, J. Du, J. Zhang and I. Iwakura, Chem. Phys. Lett., 2013, 579, 51–57 CrossRef CAS.
- J. Du, Z. Wang, W. Feng, K. Yoshino and T. Kobayashi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 19 Search PubMed.
- P. Muller, Pure Appl. Chem., 1994, 66, 1077–1184 Search PubMed.
- K. H. Wu, T. Y. Hsu, H. C. Shih, Y. J. Chen, C. W. Luo, T. M. Uen, J. Y. Lin, J. Y. Juang and T. Kobayashi, J. Appl. Phys., 2009, 105, 43901 CrossRef.
- Z. Wu, H. Li, L. Yan, B. Liu and Q. Tian, Superlattices Microstruct., 2013, 55, 16–25 CrossRef CAS.
- M. Menšík, J. Pfleger and P. Toman, Chem. Phys. Lett., 2017, 677, 87–91 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10780h |
| This journal is © The Royal Society of Chemistry 2021 |