Open Access Article
Open Access ArticleSimultaneous and continuous particle separation and counting via localized DC-dielectrophoresis in a microfluidic chip
Yongxin Songa,
Xiaoshi Hana,
Deyu Lia,
Qinxin Liub and
Dongqing Li *c
*c
aDepartment of Marine Engineering, Dalian Maritime University, Dalian, 116026, China
bThe 601st Institute the 6th Academy, China Aerospace Science and Industry Corporation Limited, Hohhot, 010076, China
cDepartment of Mechanical and Mechatronics Engineering, University of Waterloo, Waterloo, ON N2L 3G1, Canada. E-mail: dongqing@uwaterloo.ca
First published on 19th January 2021
Abstract
A novel microfluidic method of counting the number of particles while they are separated by a localized DC-dielectrophoresis force was presented. Liquid flow from a wide microchannel forces the to-be-detected particles to pass over a small orifice on a side wall of the sample input channel. A direct current (DC) voltage applied across the small orifice and a strong electric field gradient is generated at the corners of the orifice for dielectrophoretic particle separation. Particle counting is achieved by detecting the electric current change caused by the being-separated particle near the sensing orifice. In this way, particles can be separate and in situ counted at the same time. Numerical simulations show that particle separation is achieved at the edge of the sensing orifice where the strength of the electric field gradient is the largest. Separation and counting of polystyrene particles of two and three different sizes with 1 μm resolution were demonstrated experimentally.
1. Introduction
Dielectrophoresis (DEP) is a well-known electrical method for particle manipulation at micro and nano scales.1–5 Recently, there have been some investigations on integrating DEP with some detection means to improve detection sensitivity or achieve selective detection. One popular approach is to integrate DEP with an impedance detection system.6–16 The DEP force is utilized to enrich the target particles at the detection region or deplete the unwanted ones from the suspension. Due to the greatly concentrated sample, the detection sensitivity was improved. Such a concept was successfully applied for the detection of bacteria,6,7 DNA,8,9,17 amyloid beta10,16 and cancer cells.15,16There are some other types of detection means which were combined with DEP also. Do et al.18 designed a device which utilizes DEP to enrich and immobilize the target cells on an electrode covered with specific anti-EGFR biomarker. Afterwards, the target cells on the electrode were detected on the changed capacitance. Cherukulappurath et al.19 achieved a rapid and ultrasensitive surface-enhanced Raman spectroscopy (SERS) detection by forming nanometer-sized gaps with Au nanoparticles which are subjected to DEP force. Under the DEP force, the nanoparticles with the to-be-detected-analyte covered were chained with sub-10 nm gaps near the DEP electrodes. As a result, an order of 108 enhanced detection was achieved.
To selectively detect target individual molecular species, Tian et al.20 used a polycationic nanocarrier to bind the target biomelecules. As a result, the size of the target biomolecule is greatly increased, making DEP capture easy and possible. The captured target DNA will be pulled to pass through a nanopore where it is detected. The non-target nucleric acides are repelled from entering into the nanopore.
Another strategy for selective detection in DEP device is to measure the fluorescence signals generated by the target biomolecules or particles immobilized on microparticles21 or DEP electrodes.22 Similarly, DEP force was utilized to manipulate the targets to the detection region and thus increase the immuno-capture efficiencies22 or to different locations for more than one targets detection.21 To detect target bioparticles at single cell level, Chen et al.23 counted the number of DEP trapped bacterial which are stained with fluorescence with a customer-made image program.
In summary, DEP force is generally utilized as a pre-treatment means, such as trapping the targets at the detection region, concentrating the wanted and filtering the unwanted. Detection and counting were performed as the next step. In this paper, we present a microfluidic method for simultaneously and continually counting the number of particles at a single particle level while they are being separated by a localized DC-dielectrophoresis force. The two functions of DEP separation and resistive pulse sensing are achieved at the same time by generating an electric field at a much smaller orifice that connects two much wider microchannels. Experimental demonstration of separating and counting particles from a mixed suspension were performed.
2. Experimental system and working principle
2.1 Detection system and chip structure
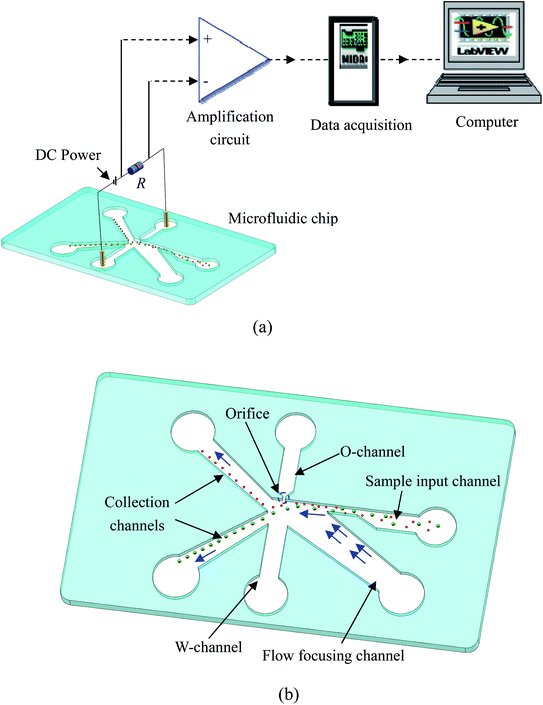
Fig. 1(a) schematically shows the working principle of the dielectrophoretic particle separation and counting system. Briefly, the system consists of a microfluidic chip, an electrical resistor (R), a DC power supply, a signal amplification circuit (AD620) and a data acquisition device (NI USB6259, NI, USA). For the microfluidic chip (Fig. 1(b)), it can be functionally divided into three sections: particle transportation section, separation and counting section and particle collection section. In the particle transportation section, there are one sample input channel and one flow-focusing channel. A microchannel with a small orifice (named as ‘O-channel’) and a wide microchannel (W-channel) form the separation and counting section where particles are separated and counted near the small orifice. The particle collection section is composed of two microchannels where particles of different sizes are collected. DC electric filed is applied by connecting the Pt electrodes in the O-channel and W-channel to the positive and negative ends of the DC power supply respectively. The two ends of the electrical resistor are connected to the DC power supply and the Pt electrode of W-channel respectively. Moreover, the two ends of the electrical resistor (R) are also connected with the two input ends of the amplifier whose output is connected to the data acquisition device.2.2 Principle of particle separation, detection and counting
To begin particle separation and detection, firstly, PBS buffer was added to all of the channels of the microfluidic chip. Then after sample solution was added into the well of the sample input channel and a DC voltage (100 V) was applied. Fig. 2 shows the electric field distributions around the sensing orifice (orifice: 1 μm × 5 μm (width × length)). It can be seen that both the electric strength (E) (Fig. 2(a)) and the gradient of the square of electric strength (∇|E|2) (Fig. 2(b)) are maximum at the two corners (indicated by the red circles) of the sensing orifice. In this study, the sample particles were focused by a sheath flow to pass by the orifice as closely as possible. When a particle is at the corner of the orifice where the strength of the electric field is the largest (Fig. 2(a)), it has the following two effects. In one aspect, the moving particle is subject to a DEP force at the corner due to the strong gradient of the square of electric strength generated by the orifice-microchannel structure.17 The DEP force (FDEP) exerted on a particle is given by:| FDEP = 2πεsr3Re(fCM)(∇|E|2) | (1) |
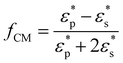 | (2) |
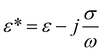 | (3) |
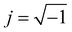 .
.
 | ||
| Fig. 2 (a) Distributions of electric field and (b) gradient of the square of electric strength (the arrow shows the direction of FDEP and Fd). | ||
For a polystyrene particle, its dielectric constant is much smaller than that of an electrolyte solution. Therefore, the fCM in eqn (2) is a negative value. Consequently, a polystyrene particle at the corner of the orifice is subject to a negative DEP force directing from the orifice to the W-channel. Since DEP force is proportional to the volume (i.e., r3 in eqn (1)) of the particle, different particles (different diameters) will be pushed away from the orifice to different distances, and finally, follow different stream lines to be transported to different collection channels. In this way, particle separation are achieved.
It should be noted that the fluid velocity will also affect the separation process. The flowing of the fluid will exert a drag force (Fd in Fig. 2(b)) exerted on the particle. The DEP force and the drag force determine the moving velocity and the trajectory (the position) in the microchannel. The fluid velocity will affect the drag force, of course, the trajectory (also the separation efficiency) of the particles. For example, increasing the fluid velocity will tend to drag particles to the upper collection channel.
On the other aspect, a particle at the orifice will increase the electric resistivity of the channels (by displacing the electrolyte solution). Accordingly, the voltage shared by the resistor is decreased. Such a voltage change will be detected by the system as a voltage pulse whose magnitude depends on the size of the particle.24 Furthermore, detection sensitivity can be increased by generating a larger resistance change (ΔR) by the particle which can be achieved by increasing the volume ratio of the particle to the orifice.25 In this study, the electric field is applied via the two electrodes, one in O-channel well, another in W-channel well. The electric field lines or the current will go from the O-channel to the W-channel and pass through the orifice. When a particle passes over the orifice, it will replace the liquid and hence change the local electric conductivity, and consequently generate detectable electric signals for particle counting. That is, the numbers of particles can be counted by counting the numbers of the pulse. It should be emphasized that the O-channel is connected to W-channel by a small orifice. This innovative structure is responsible to generate a unique electric field that produces not only DEP force for particle separation by size but also electric signals for counting particles by size.
Since the orifice is of micro size, there will be electroosmotic flow (EOF) from the O-channel to the W-channel. Such a liquid flow will influence the position of a particle at the orifice and thus the magnitudes of the detected resistive signal and DEP force. To minimize this side effect, on one side, all of the channels and the bottom glass slide of the microfluidic chip were coated with 0.6% PB to reduce the zeta potential to about 3.7 mV.26 Furthermore, the Pt electrode in O-channel was connected with the positive end of the DC power supply. Therefore, the EOF is towards the orifice which will move particles towards the orifice and thus is favor of signal particle detection and separation.
3. Experiments
3.1 Chip fabrication
In the microfluidic chips used in this study, the dimension of the W-channel is 200 μm × 5 mm (width × length). For the O-channel, it is 105 μm × 5 mm (width × length). The dimension of the flow focusing channel is 120 μm wide and 11 mm long. To achieve a good sample focusing, the sample channel has a narrow region (15 μm wide and 300 μm long) at the joint of the focusing channel and the sample channel. The rest region of the sample channel is 120 μm wide and 7 mm long. The collection channel is 60 μm wide and 10 mm long. In this study, two different sizes of orifice were used and the height of all channels is 10 μm.The masters with the microstructure shown in Fig. 1(b) was fabricated by the soft lithography method,27 using the negative photo-resist of SU-8 3010 (MicroChem Co., Newton, MA). The PDMS microstructures were fabricated by pouring onto the master the liquid PDMS (Sylgard 184, Dow Corning, USA) mixed with curing agent with a mass ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Afterheating the master with the liquid PDMS at 80 °C in an oven (Isotemp model 280A, Fisher Scientific, Pittsburgh, PA, USA) for 1–2 hours. Then the PDMS layer was peeled off from the master. Then the PDMS layer and a glass slide (25.66 × 75.47 × 1.07 mm, CITOGLAS, China) were treated with 0.6% polybrene (PB) solution following the procedures described in the reference paper.26 Finally, the PB-treated PDMS layer and glass slide were bonded with a plasma cleaner (HARRICK PLASMA, Ithaca, NY, USA).
1. Afterheating the master with the liquid PDMS at 80 °C in an oven (Isotemp model 280A, Fisher Scientific, Pittsburgh, PA, USA) for 1–2 hours. Then the PDMS layer was peeled off from the master. Then the PDMS layer and a glass slide (25.66 × 75.47 × 1.07 mm, CITOGLAS, China) were treated with 0.6% polybrene (PB) solution following the procedures described in the reference paper.26 Finally, the PB-treated PDMS layer and glass slide were bonded with a plasma cleaner (HARRICK PLASMA, Ithaca, NY, USA).
3.2 Sample preparation and experimental procedure
Polystyrene particles (Fluka, Shanghai, China) were used to demonstrate the performance of this system in this study. The particle samples were prepared by adding 1 μL particle solution (at a particle concentration of 2%) into 1× PBS buffer (pH = 7.5) to decrease the concentration to be about 0.013‰.The following procedures were followed for each of the experiments. Firstly, the microchannels were primed with 10 μL PBS buffer (pH = 7.5), followed by loading 5 μL of sample solution into the sample input channel well. Afterwards, 30 μL PBS buffer solution (pH = 7.5, focusing solution) was added into the well of the flow focusing channel. While particle focusing effect can be achieved by increasing the liquid level of the well of the focusing channel, the particle may move too fast which is hard for observation. Therefore, in this study, additional buffer solution was added to the well of the W-channel. This will also make the particles move as close to the orifice as possible without significantly increasing particles' moving velocity. Based on lots of experiments, the best volume of buffer solution added to the well of W-channel was found to be 7 μL. The flow rates at the sample channel and focusing channel was estimated by numerical simulations and found to be 42.5 μm s−1 and 400 μm s−1 respectively. During the experiments, the movement of the particles around the orifice were observed under a microscope (Ti-e, Nikon, Japan), aiming to make sure if the detected signals indeed were generated by the particles.
4. Results and discussions
4.1 Detection and separation of particles of two sizes
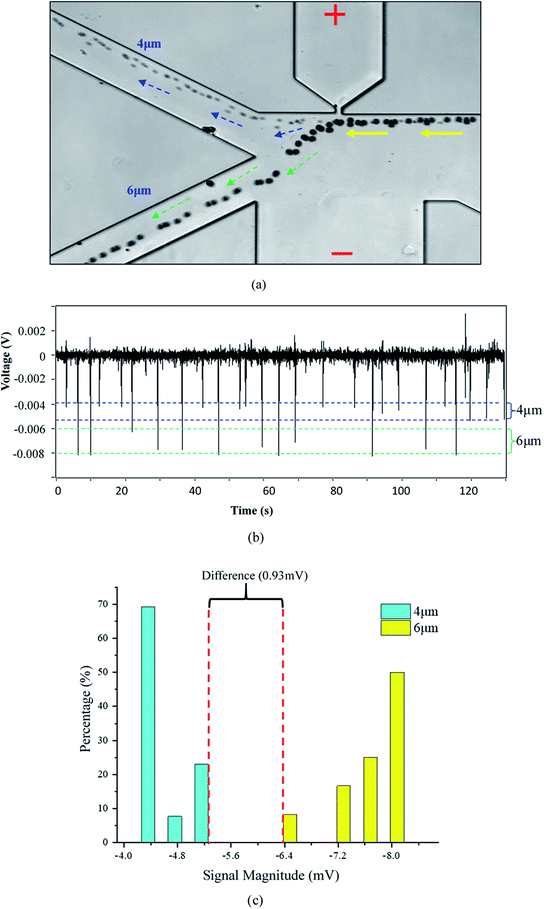
To verify the working principle of this system, 6 μm and 4 μm polystyrene particles were mixed and employed as the sample. The typical trajectories of the particles near the orifice were shown in Fig. 3(a). It can be found from Fig. 3(a) that the smaller particles (4 μm) are less deviated away from the orifice and go to the right collecting channel. The 6 μm particles are pushed much far away from the orifice and go to the left collecting channel. Because the gradient of the square of electric field is the largest at the orifice, the DEP force at the orifice region will force the particles deviate from their original stream lines. Furthermore, since the DEP force acting on the particle is proportional to the particle's volume, the DEP force acting on 6 μm particles is thus larger than that on the 4 μm particles. Therefore, 6 μm particles will be pushed a little further away from the orifice. By careful designing the structure of the collecting channels and adjusting the flow speed of the solution in the channels (by changing the liquid level difference in the wells), the larger particles will be pushed into stream lines which go into the left collecting channel. In this way, size-based particle separation can be achieved.Recall that the particles passing over the orifice will also cause changes in electric resistivity which will be detected by the two electrodes inserted in O-channel and W-channel, respectively (Fig. 1). Fig. 3(b) shows the detected voltage signals generated by the passing particles. The signals generated by the particles passing over the orifice were confirmed under the microscope. It was found that the signals with a magnitude range of 0.004–0.005 V were generated by the 4 μm particles. For the 6 μm particles, the magnitude of the generated signals is within the range of 0.006–0.008 V. For the signal noise, its magnitude is only about 0.0004 V. Therefore, the averaged signal to noise ratios (S/N) of the 4 μm and 6 μm particles are about 10 and 17 respectively. From Fig. 3(c), it's clear that there is an obvious difference (0.93 mV) in the magnitude of signals generated by 4 μm particles and by 6 μm particles. This method, therefore, can be utilized for size-based particle counting. It should be noted that, in Fig. 3(b), the downward peaks with magnitudes less than 0.002 V and the upward peaks were generated by the smoothing Labview program which was used to obtain a straight baseline during the measurement.
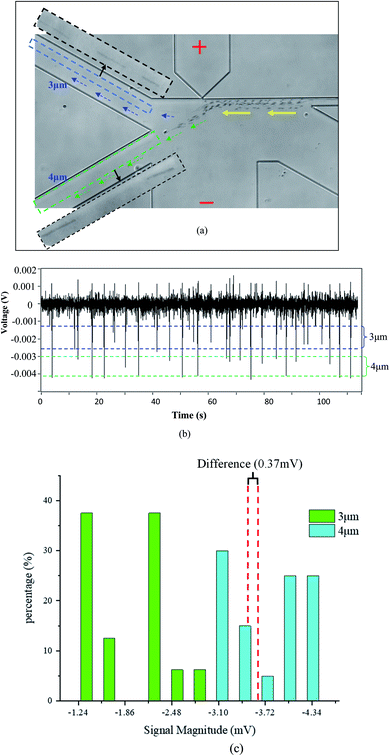
To evaluate the resolution of this method, polystyrene particles with 1 μm diameter difference, i.e., 3 μm and 4 μm particles, were mixed together and tested with an orifice of 1 μm × 2.5 μm. Fig. 4 shows the trajectories and the detected signals of the particles. As can be seen from Fig. 4(a), the particles were successfully separated into the two different collection channels. It should be noted that the trajectories for the 3 μm particles are not so obvious due to their small size and much fast-moving velocities. As regards to the generated signals, the magnitude of the downward signals is within the range of 0.0012 V to 0.0026 V for the 3 μm particles. For the 4 μm particles, the magnitude is larger than 0.003 V. From Fig. 4(c), it can be found that there is a 0.37 mV difference in magnitude which is sufficient enough for differentiating these particles. In Fig. 3(c) and 4(c), it should be further noted that the peaks are not uniform for one specific particle size. The thing is that the particles are not ideally focused into one line to pass the orifice. Such deviations from the orifice will cause different peak height.
4.2 Detection and separation of particles of three sizes
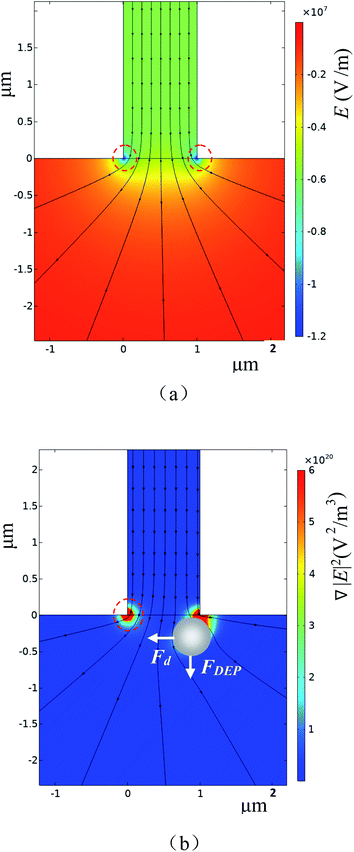
In practice, it's possible that a sample may have particles with more than two different sizes. To test the capability of this system presented in this paper in more complex sample analysis, 4 μm, 6 μm and 7 μm polystyrene particles were mixed and tested. A typical result is shown in Fig. 5. It can be found that the 4 μm particles are separated into one collection channel and the 6 μm and 7 μm particles are collected into another channel (Fig. 5(a)). For the averaged magnitudes of the detected signals, they are about 0.005 V, 0.0075 V and 0.0125 V for the 4 μm, 6 μm and 7 μm particles, respectively. It should be noted that there is one signal (pointed with a red arrow) in Fig. 5(b) with much bigger magnitude. This signal is most possibly generated by some impurities in the solution or more than one particle passing by the orifice at the same time. These results clearly demonstrate the ability of this system for analyzing complex particle samples.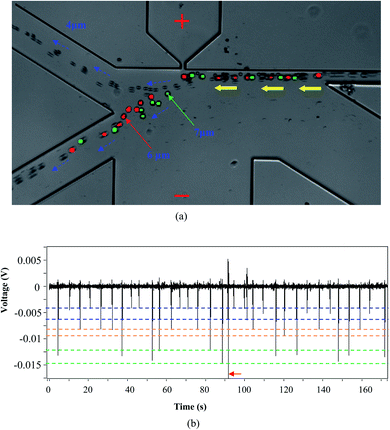 | ||
| Fig. 5 Separating and counting 4 μm, 6 μm and 7 μm particles, (a) trajectories of moving particles; (b) the detected signals (orifice: 5 μm × 10 μm; applied voltage V = 80 V). | ||
4.3 Other discussions
In this study, the demonstrated separation results (particle trajectories) are those that one kind of particle was 100% separated into one collection channel. Such results are based on lots of experiments to find the optimized operation parameters, such as the applied electric field and the flow rates in the sample channel and the focusing channel. Since this is a size-based separation method, the pre-determined best operation parameters can be reliably applied for separating particles with known sizes in practice.The voltages applied between the O-channel and W-channel determines the gradient of the electric field. Specifically, the larger of the applied voltage, the larger of the gradient of the electric field. For the DEP force, its magnitude increases with the increase in the electric field gradient. Which will in turn influence particle separation. Larger DEP force is in favor of achieving a higher separation resolution. For this method, however, to achieve a high detection resolution, it is preferred that the particle is as close as possible to the orifice. On the other aspect, large DEP force is preferred for high separation accuracy. However, large DEP force will force particles to be far away from the orifice, which is adverse to particle detection. Therefore, the detection resolution and separation accuracy have to be well balanced.
The throughput depends both on the concentrations of and the flow velocity of the sample solution. The purpose of this study is to show the capability of this system on simultaneously counting and separating particles of different sizes. Therefore, the concentration and flow velocity were not deliberately control. From Fig. 3(b), 4(b) and 5(b), it is estimated that the throughput is between 10–20 particles per min. It should be noted that the throughput can be easily increased by increasing the concentration and flow velocity of the sample solution. Furthermore, there are several different approaches that can be used to improve the throughput. More details can be found in the reference paper.28
At last, this is a DC voltage-based method and there is a relative strong electric field at the orifice. If the sample can be easily damaged under electric field, this method cannot be used.
5. Conclusion
An electric method of simultaneously counting and separating particles with a side-orifice was developed in this paper. The resistive particle counting and DEP separation can be realized by the strong electric field gradient at the corners of the small sensing orifice. Separating and counting polystyrene particles of two and three sizes with 1 μm resolution were achieved successfully. The idea of using only one side-orifice for particle counting and separation at the same time is advantageous in detecting mixed particle samples without the risk of orifice clogging.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank the financial support of the National Natural Science Foundation of China (51979019), Liaoning BaiQianWan Talents Program and Liaoning Nature Science Foundation (2019MS027) to Y. Song, the Fundamental Research Funds for the Central Universities (3132019336) and the Natural Sciences and Engineering Research Council of Canada through a research grant (RGPIN-03622) to D. Li. The financial support from the State Key Laboratory of Clean Energy Utilization (Project No. ZJUCEU2019015) is greatly appreciated.References
- H. A. Pohl, Dielectrophoresis: The behavior of neutral matter in nonuniform electric fields (Cambridge Monographs on physics), Cambridge University Press, Cambridge/New York, 1978 Search PubMed.
- K. Zhao, L. Larasati, B. P. Duncker and D. Li, Anal. Chem., 2019, 91, 6304–6314 CrossRef CAS.
- K. Zhao, R. Peng and D. Li, Nanoscale, 2016, 8, 18945–18955 RSC.
- Y. Kang, B. Cetin, Z. Wu and D. Li, Electrochim. Acta, 2009, 54, 1715–1720 CrossRef CAS.
- I. Barbulovic-Nad, X. Xuan, J. S. H. Lee and D. Li, Lab Chip, 2006, 6, 274–279 RSC.
- R. Hamada, H. Takayama, Y. Shonishi, L. Mao, M. Nakano and J. Suehiro, Sens. Actuators, B, 2013, 181, 439–445 CrossRef CAS.
- R. Wang, Y. Xu, H. Liu, J. Peng, J. Irudayaraj and F. Cui, Biomed. Microdevices, 2017, 19, 34 CrossRef.
- G. Bhatt, K. Mishra, G. Ramanathan and S. Bhattacharya, Sens. Actuators, B, 2019, 288, 442–453 CrossRef CAS.
- M. Nakano, Z. Ding, H. Kasahara and J. Suehiro, Europhys. Lett., 2014, 108, 28003 CrossRef.
- H. J. Kim, D. Park, S. Y. Baek, S. H. Yang, Y. Kim, S. M. Lim, J. Kim and K. S. Hwang, Biosens. Bioelectron., 2019, 128, 166–175 CrossRef CAS.
- M. Nakano, S. Kalsi and H. Morgan, Biosens. Bioelectron., 2018, 117, 583–589 CrossRef CAS.
- J. Chung, Y. Chen and S. J. Kim, Sens. Actuators, B, 2018, 266, 106–114 CrossRef CAS.
- N. V. Nguyen and C. P. Jen, Biosens. Bioelectron., 2018, 121, 10–18 CrossRef CAS.
- N. C. Chen, C. H. Chen, M. K. Chen, L. S. Jang and M. H. Wang, Sens. Actuators, B, 2014, 190, 570–577 CrossRef CAS.
- Y. Demircan, A. Koyuncuoğlu, M. Erdem, E. Özgür, U. Gündüz and H. Külah, Electrophoresis, 2015, 36, 1149–1157 CrossRef CAS.
- H. J. Kim, J. Kim, Y. K. Yoo, J. H. Lee, J. H. Park and K. S. Hwang, Biosens. Bioelectron., 2016, 85, 977–985 CrossRef CAS.
- M. Nakano, S. Kalsi and H. Morgan, Biosens. Bioelectron., 2018, 117, 583–589 CrossRef CAS.
- L. Q. Do, H. T. T. Thuy, T. T. Bui, V. T. Dau, N.-V. Nguyen, T. C. Duc and C.-P. Jen, BioChip J., 2018, 12, 114–122 CrossRef CAS.
- S. Cherukulappurath, S. H. Lee, A. Campos, C. L. Haynes and S.-H. Oh, Chem. Mat., 2014, 26, 2445–2452 CrossRef CAS.
- K. Tian, K. Decker, A. Aksimentiev and L.-Q. Gu, ACS Nano, 2017, 11, 1204–1213 CrossRef CAS.
- J. Ramón-Azcón, T. Yasukawa and F. Mizutani, Biosens. Bioelectron., 2011, 28, 443–449 CrossRef.
- L. Yang, Talanta, 2009, 80, 551–558 CrossRef CAS.
- X. Chen, Z. Liang, D. Li, Y. Xiong, P. Xiong, Y. Guan, S. Hou, Y. Hu, S. Chen, G. Liu and Y. Tian, Biosens. Bioelectron., 2018, 99, 416–423 CrossRef CAS.
- W. H. Coulter, US Pat., 2656508, 1953 Search PubMed.
- T. Zhou, Y. Song, Y. Yuan and D. Li, Anal. Chim. Acta, 2019, 1052, 113–123 CrossRef CAS.
- Y. Song, J. Li and D. Li, Electrophoresis, 2016, 37, 567–572 CrossRef CAS.
- Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 CrossRef CAS.
- Y. Song, J. Zhang and D. Li, Micromachines, 2017, 8(7), 204 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |