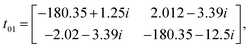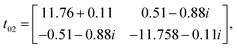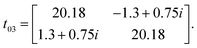Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Complex magnetism of the two-dimensional antiferromagnetic Ge2F: from a Néel spin-texture to a potential antiferromagnetic skyrmion
Fatima Zahra
Ramadan
 *a,
Flaviano
José dos Santos
b,
Lalla Btissam
Drissi
abc and
Samir
Lounis
bd
*a,
Flaviano
José dos Santos
b,
Lalla Btissam
Drissi
abc and
Samir
Lounis
bd
aLPHE, Modeling & Simulations, Faculty of Science, Mohammed V University in Rabat, Rabat, Morocco. E-mail: f.ramadan88@gmail.com
bPeter Grünberg Institut, Institute of Advanced Simulation, Forschungszentrum Jülich, JARA, D-52428, Jülich, Germany
cCPM, Centre of Physics and Mathematics, Faculty of Science, Mohammed V University in Rabat, Rabat, Morocco
dFaculty of Physics, University of Duisburg-Essen, 47053 Duisburg, Germany
First published on 24th February 2021
Abstract
Based on density functional theory combined with low-energy models, we explore the magnetic properties of a hybrid atomic-thick two-dimensional (2D) material made of germanene doped with fluorine atoms in a half-fluorinated configuration (Ge2F). The Fluorine atoms are highly electronegative, which induces magnetism and breaks inversion symmetry, triggering thereby a finite and strong Dzyaloshinskii–Moriya interaction (DMI). The magnetic exchange interactions are of antiferromagnetic nature among the first, second and third neighbors, which leads to magnetic frustration. The Néel state is found to be the most stable state, with magnetic moments lying in the surface plane. This results from the out-of-plane component of the DMI vector, which seems to induce an effective in-plane magnetic anisotropy. Upon application of a magnetic field, spin-spirals and antiferromagnetic skyrmions can be stabilized. We conjecture that this can be realized via magnetic exchange fields induced by a magnetic substrate. To complete our characterization, we computed the spin-wave excitations and the resulting spectra, which could be probed via electron energy loss spectroscopy, magneto-Raman spectroscopy or scanning tunneling spectroscopy.
I. Introduction
The realization of complex spin-textures hinges on the presence of competing magnetic interactions, which are heavily explored in various materials. While hosting fundamentally exciting phenomena, such magnetic states have great potential in spintronics with possible impact on information technology. For example, going beyond the conventional ferromagnetic (FM) materials for practical applications, such as the antiferromagnetic (AFM) ones1–4 can have various interesting advantages. AFMs are expected to be robust against perturbation due to magnetic fields, they produce no stray fields, display ultrafast dynamics, and are capable of generating large magnetotransport effects.1The emergence of complex magnetic states is favored by the presence of competing magnetic interactions, which can lead to frustration. Spin–orbit driven interactions, such as the Dzyaloshinskii–Moriya interaction (DMI), also favor non-collinearity with the additional injection of a potential chiral magnetic behavior. Indeed, broken inversion symmetry and spin–orbit coupling triggers a finite DMI, which stabilizes a unique sense of rotation of the magnetic moments. Various chiral spin-swirling states can then be produced, such as chiral spin spirals, chiral domain walls or magnetic skyrmions. The latter are topological protected vortex lines in which the spins point in all the directions wrapping a sphere,5–7 which are promising for potential high-density and low-power spintronics technology.8–10 In this field, there is currently a great interest in going beyond FM skyrmions by discovering AFM skyrmions,11–18 which would combine the advantages of skyrmions19–25 and AFM properties.
The goal of this manuscript is to prospect the presence of chiral complex spin textures in two dimensional (2D) magnetic materials. They not only offer unique physical and chemical properties, but also an unprecedented flexibility in system design. When grown in a multilayer fashion, their flexibility stems from van-der-Waals bonding between neighboring atomic-thick layers of potentially very different properties, which permits virtually unlimited combinations and stackings of individual layers. The resulting properties, usually conveyed via proximity effects, can be very distinct from the original building block materials. Most of 2D materials do not exhibit DMIs because of their centrosymmetric crystal structure.
To break such a symmetry, some approaches consist on creating 2D structures within which different atoms are mixed in an alternating manner to generate one-atom thick hybrids.26,27 Other strategies such as applying a bias voltage or strain are also used.28–30 Chemical functionalization, impurities, boundaries and defects are other efficient ways employed in 2D sheets to tune their physical properties and induce magnetic order.29,31–35 In particular, chemisorption using radicals such as oxygen, hydrogen or fluorine atoms on the surface of 2D honeycomb structures leads to long-range magnetism.36–40 Another example consists of Sn monolayer on SiC(0001) surface, where a strong spin–orbit coupling was found on the basis of a generalized Hubbard model. This mainly contributes in the formation of a nanoskyrmion state at realistic magnetic fields and temperatures.41
Half-functionalization is also a powerful and widely-used tool to tailor spin and magnetic behavior in 2D materials.42,43 A particularly interesting adatom is fluorine since it is the most electronegative element of the periodic table. Half fluorination is an exothermic adsorption that generates stable 2D hexagonal structures.44 In half-fluorinated graphene, C2F, where F-atoms form strong covalent bonds with carbon, a threshold of the antiferromagnetic–ferromagnetic instability with strong Dzyaloshinskii–Moriya interaction was predicted46 with the potential presence of ferromagnetic skyrmions. The latter work challenged the ab initio results obtained by Rudenko et al.,45 which revealed finite AFM interactions on the triangular lattice of magnetic moments, leading to the instability of the collinear magnetic ordering due to frustration and the stabilization of a 120° Néel state. Mazurenko et al.46 proposed that the direct exchange interaction between spin orbitals, not accounted in ref. 45, leads to a ferromagnetic interaction, which is capable of compensating the antiferromagnetc indirect exchange interactions in C2F.
Remarkably, half-fluorination can trigger opposite magnetic behavior in hybrid 2D monolayers. While half-fluorinated BN sheet is an antiferromagnetic direct semiconductor, half-fluoro-GaN monolayer shows ferromagnetic character.47 In silicene–graphene (SiC), interesting magnetic properties can emerge depending on which host atom (C or Si) fluorine is attached.48
In this paper, we study the presence of chiral spin-textures in half fluorinated germanene using density functional theory (DFT) combined with low-energy models with spin–orbit coupling in the spirit of the methodology followed by Mazurenko et al.46 We found that the Ge2F is antiferromagnetic with strong DMI between the first nearest magnetic germanium neighbors. The spin dynamics simulations demonstrate the stability of the antiferromagnetic Néel state, resulting from magnetic frustration. In the latter configuration, the magnetic moments lie in the surface plane, which is induced by the out-of-plane component of the DMI vector. Extremely large magnetic fields can stabilize an antiferromagnetic skyrmion. We conjecture that this can be enabled by a proximity-effect induced by an underlying magnetic substrate. Noting that magnons in 2D structures have been probed with magneto-Raman spectroscopy49 and scanning tunneling microscopy,50 we finally explore the spin-wave excitations characterizing the obtained complex spin-textures.
II. Computational details
The electronic and magnetic properties have been obtained using the Quantum espresso code,51 which is based on density functional theory (DFT). Exchange and correlation effects were taken into account using the local spin density approximation (LDA). Spin–orbit (SO) coupling was included on the basis of fully relativistic pseudopotentials. In these calculations, we set the energy cutoff to 60 Ry for the plane-wave basis. For the Brillouin-zone integration a 30 × 30 × 1 Monkhorst Pack mesh was used. To avoid the artificial interactions between layers, the thickness of the vacuum space was fixed at 20 Å.To extract the magnetic exchange interactions required for the exploration of the magnetic properties, we built a low-energy model using an effective Hamiltonian following the work of Mazurenko et al.:46
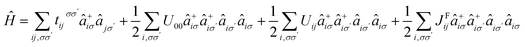 | (1) |
Moreover, we used the Spirit atomistic spin dynamics simulation code55 to solve the Landau–Lifshitz–Gilbert (LLG) equation:
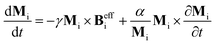 | (2) |
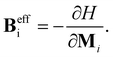 We assume a supercell of a size of 100 × 100 × 1 atoms.
We assume a supercell of a size of 100 × 100 × 1 atoms.
Once the ground state or a metastable state is found, we compute the adiabatic spin-wave modes and the corresponding inelastic scattering spectrum, based on time-dependent perturbation theory. The associated theoretical framework was presented in ref. 56 and 57 and used for various problems.58,59 The spin-wave eigenvalues ω(k) and eigenvectors k are then obtained after diagonalization of the system's dynamical matrix in the reciprocal space. We arrive to the total dynamical structure factor (summing up all the scattering channels), which is given by
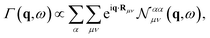 | (3) |
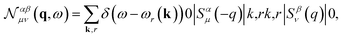 | (4) |
Within this framework we have access to several distinct scattering channels. In this work we present results for the total inelastic scattering spectrum due to spin waves (the sum over all scattering channels), as one would measure in an experiment with an unpolarized scattering experiment such as electron energy loss spectroscopy (EELS). The various scattering channels will also be analyzed, which could be detected via the recent theoretical proposal, spin-resolved EELS (SREELS), shown in ref. 57. Within the latter, a spin-polarized beam of electrons is used to probe the magnetic material. The scattered electrons are then spin-filtered with the spin analyzer collinear with the incident beam polarization. This gives rise to four scattering channels, one for each possible combinations of [incoming spin]–[outgoing spin]. Two of these channels correspond to non-spin-flip processes, namely the up–up and the down–down channels. The other two, up-down and down-up, account for spin-flip events, where angular momentum is exchanged with the sample.
III. Results and discussion
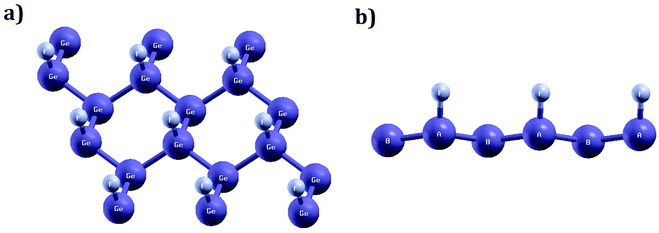
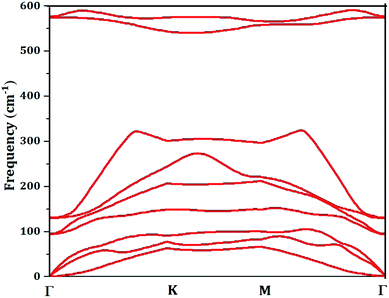
In this paper, we study the magnetic properties of 2D half-fluorinated germanene where F-atoms bind Ge-atoms occupying the A-sites of each hexagonal lattice while B-sites remain undecorated as shown in Fig. 1. The bond lengths are dGe–Ge = 2.52 Å and dGe–F = 1.80 Å. The structure is slightly puckered, with a buckling parameter of 0.74 Å. The interatomic angles ranging between 111.70° and 111.80° indicate an sp3 hybridization between Ge atoms. According to ref. 60, the Ge2F is an antiferromagnetic semiconductor, with a small gap energy.To check and examine the stability of free-standing monolayer materials, various computational methods can be used such as molecular dynamics,61,62 the computation of formation energy and binding energy,60 as well as translational symmetry based on the relaxation of a finite nanocluster.63,64 In this work, the stability of half fluorinated germanene, confirmed in ref. 60 calculating the formation energy, is rechecked through the analysis of the phonon dispersion, the Fig. 2 displays the phonons dispersion. Analysis of the phonon spectrum shows the absence of imaginary frequency along the high-symmetry directions of the Brillouin zone for all phonon branches. It is a signature of stability of our material.
Fig. 3a illustrates the LDA band-structure, including SO coupling. The metallic character of Ge2F is in good agreement with recent work.66 As expected, a small gap energy of 0.19 eV is reported for Ge2F using the generalized gradient approximation (GGA).60 It is worth noting that the standard DFT approximations, namely the LDA and the GGA, are known to successfully describe the ground-state properties and to underestimate the results of excited states. Thus to include quasiparticle corrections, which reproduce a band gap in accordance with the experimental measurements, one should use the GW approximation that goes beyond the scope of this work.67,68Fig. 3(a) also shows the bands around the Fermi level slightly overlap with other bands at the Γ-point similarly to what was found for the half fluorinated graphene (C2F)46 but with a larger spin–orbit splitting induced by the heavier Ge atoms. The splitting characterizing the band crossing the Fermi energy reaches a maximum of 48 meV, as shown in Fig. 3(b), which is larger than 38 meV, the maximum value reported for the half-fluorinated graphene C2F.46
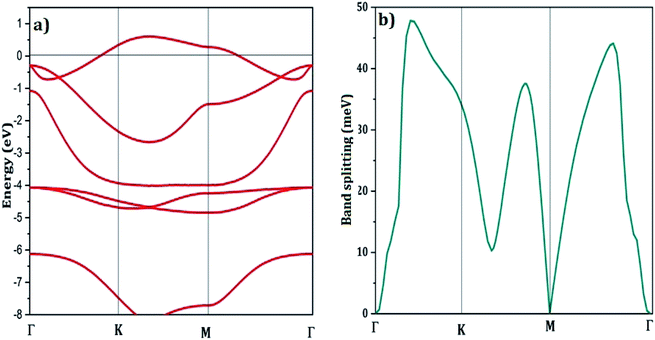 | ||
| Fig. 3 (a) The LDA band-structure with respect to the Fermi energy of half fluorinated germanene including spin–orbit coupling. Similarly to ref. 46, the impact of spin–orbit coupling on the band crossing the Fermi energy is monitored in terms of the band splitting (b). | ||
For the bands located at the Fermi level, Fig. 4 reveals that the Wannier functions, obtained from the projection of the pz orbitals on the non-fluorinated Ge-atoms, are positioned at the centre of these atoms. The spread value of 2.04 indicates the delocalization of the Wannier function in real space. Besides, as shown in Fig. 4, the Wannier functions overlap on three nearest neighboring (NN) germanium decorated sites, giving rise to the Coulomb contribution to the total exchange interaction.
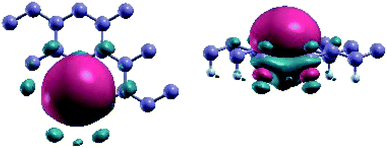 | ||
| Fig. 4 Representation of Maximally-Localized Wannier functions obtained from the projection of the pz band at the Fermi level on the non-decorated Ge. | ||
The spin up/down channel of the partial density of states, displayed in Fig. 5, shows that the magnetism, which is relevant for Ge2F near the Fermi level, is principally originated from pz orbitals of the non-functionalized Ge atoms. This is due to the broken π–bonding network of pure non magnetic germanene. More precisely, in Ge2F, the F-atoms form strong bonds with saturated Ge-atoms leaving pz electrons of the non-decorated Ge-atoms free and localized.
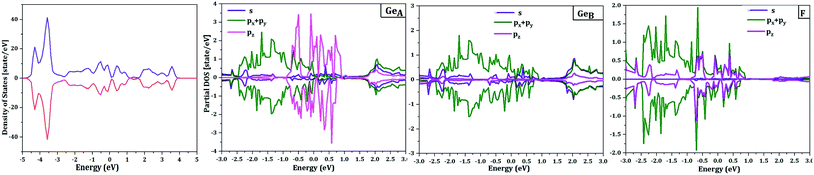 | ||
| Fig. 5 Total density of states (DOS) and partial density of states of half-fluorinated germanene as obtained with the antiferromagnetic (AFM) state described in the main text and shown in Fig. 6. The upper pannel corresponds to the majority-spin (up) channel, while the lower one hosts the minority-spin (down) channel. | ||
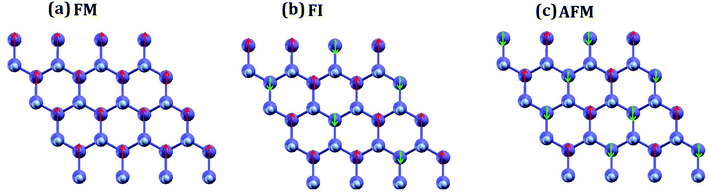 | ||
| Fig. 6 Three possible magnetic configurations of half-fluorinated germanene: (a) ferromagnetic, (b) ferrimagnetic and (c) antiferromagnetic, as explored from ab initio. | ||
Within the ab initio formalism, we explored various magnetic configurations of Ge2F, namely, antiferromagnetic (AFM), ferromagnetic (FM), and ferrimagnetic (FI), utilizing the 4 × 4 supercell shown in the Fig. 6. The AFM state is found to be the lowest in energy. The energy differences with respect to the non-magnetic (NM) state are: ENM − EAFM = 16.93 meV, ENM − EFI = 15.78 meV and ENM − EFM = 10.85 meV.
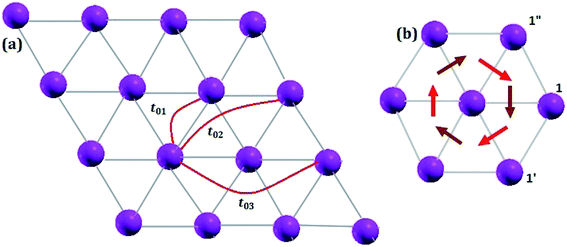
Owing to the presence of spin–orbit coupling, the hopping integrals are 2 × 2 matrices in spin-space. They are listed below in meV for the case of first NN (01), second NN (02) and third NN (03) germanium atoms (see the schematic representation in Fig. 7(a)):
We note that (i) the hopping matrix between the first nearest neighbors contain large imaginary and non-diagonal elements, which are responsible for the antisymmetric anisotropic exchange interactions (DMI), and (ii) tij ≪ U. In this case, Heisenberg Hamiltonian can be constructed within the superexchange theory69 as follows:70
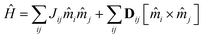 | (5) |
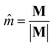 is the classical Heisenberg vector of unit length, Jij and Dij are the isotropic exchange coupling and the DMI vector, respectively. The summation runs twice over all pairs.
is the classical Heisenberg vector of unit length, Jij and Dij are the isotropic exchange coupling and the DMI vector, respectively. The summation runs twice over all pairs.
A Isotropic exchange interaction
A mapping of the previous Heisenberg Hamiltonian to eqn (1) leads to the following form of the isotropic exchange interaction: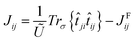 | (6) |
![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ij is the hopping energy taking into account spin–orbit coupling and Ũ = U00 − U01 (ref. 46) corresponds to the effective local partially-screened Coulomb interaction calculated via constrained random phase approximation (cRPA).52Uij and JFij, with i ≠ j, are often much smaller than U00, which usually motivates their neglect. However, Mazurenko et al.46 has shown that JFij needs to be taken into account when extracting the magnetic exchange interactions in C2F and C2H. Our analysis of the case of Ge2F shows that in contrast to C2F, the non-local JFij are negligible. This can be explained by the extremely weak spin-polarization of the non-fluorinated Ge atoms, which play an important role in mediating the interactions between the fluorinated Ge atoms.65 The local Coulomb interaction U00 and non local Coulomb interaction U01 are respectively equal to 2.80 eV and 0.92 eV, which leads to Ũ = 1.88 eV.
ij is the hopping energy taking into account spin–orbit coupling and Ũ = U00 − U01 (ref. 46) corresponds to the effective local partially-screened Coulomb interaction calculated via constrained random phase approximation (cRPA).52Uij and JFij, with i ≠ j, are often much smaller than U00, which usually motivates their neglect. However, Mazurenko et al.46 has shown that JFij needs to be taken into account when extracting the magnetic exchange interactions in C2F and C2H. Our analysis of the case of Ge2F shows that in contrast to C2F, the non-local JFij are negligible. This can be explained by the extremely weak spin-polarization of the non-fluorinated Ge atoms, which play an important role in mediating the interactions between the fluorinated Ge atoms.65 The local Coulomb interaction U00 and non local Coulomb interaction U01 are respectively equal to 2.80 eV and 0.92 eV, which leads to Ũ = 1.88 eV.
The first term in eqn (6) represents the Anderson superexchange, while the non-local JFij is the ferromagnetic term that could originate from the direct overlap of the neighboring Wannier functions. In contrast to C2F,46 however, JFij is rather negligible in Ge2F because of the weak magnetic moment carried by germanium. Therefore, we use in practice the usual form:
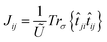 | (7) |
Using LDA+SO calculations by integrating the corresponding combination of the Wannier functions, one deduces that the isotropic exchange interaction between the first nearest neighbors J01 = 1.4 meV is very important when compared to the second nearest neighbors J02 = 0.11 meV and the third nearest neighbors J03 = 0.15 meV. The positive sign J01 confirms that the half fluorinated-germanene is antiferromagnetic.
B Dzyaloshinskii–Moriya interaction
The anisotropic exchange interaction resulting from the spin–orbit interaction, is expressed as follows: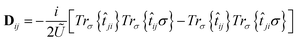 | (8) |
C Spin-dynamics simulations
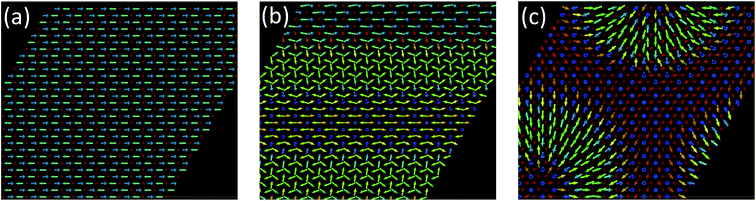
After solving the LLG equation, eqn (2), utilizing the extracted magnetic exchange interactions, we obtained as the ground state a Néel state with a zero net magnetization as shown in Fig. 8(a). The nearest neighboring AFM interactions favor the realization of such a magnetic state. Interestingly, we find that the z-component of the DMI imposes to have the moments in the surface plane. If one removes the z-component of the DMI, the resulting Néel state is characterized by out-of-plane components of the magnetic moments (Fig. 9(a)). In this particular case, a metastable spin-spiral state can be stabilized (Fig. 9(b)) which has an energy of 0.031 meV per atom above that of the ground state.When applying a large magnetic field (up to 4000 T) along the x-axis, applied to the right in Fig. 8b, a modified Néel state is obtained if keeping the z-component of the DMI finite. However, one can also obtain at higher energies the spin spirals shown in Fig. 8(c and d). Without the z-component of the DMI, an antiferromagnetic skyrmion can even be stabilized with a field of 2000 T along the z-axis (Fig. 8(c)). We conjecture that such large magnetic fields can be induced via a proximity effect if the 2D material is deposited on a magnetic substrate. The equivalent magnetic exchange energy for the 2000 T field is 32.41 meV, which could potentially be accessed.
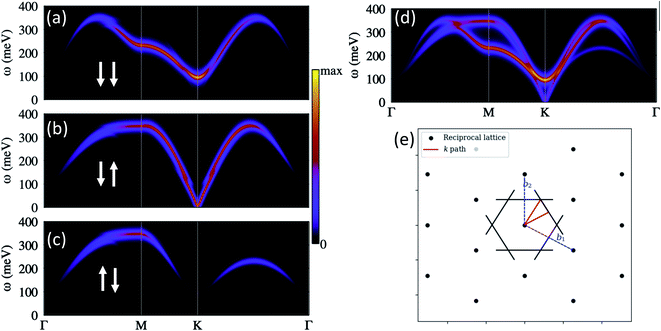
The spin-excitations spectra corresponding to the Néel ground state [Fig. 8(a)] as they would be measurable with SREELS or EELS are depicted in Fig. 10(a–d). We computed the spectra along the Brillouin-zone path indicated in Fig. 10(e). Fig. 10(d) shows the total inelastic spectrum as they would be probed by an unpolarized electronic beam.
Notice the strong scattering intensities around the K point and the vanishing intensities at the Γ, which are common spectroscopy features of antiferromagnets.58,59 We can count up to three spin-wave branches which can be individually detected through the spin-resolved spectroscopy. Fig. 10(a–c) represent the spin-resolved spectra that arise from the possible spin orientations of the incoming and outgoing electrons. We chose the polarization of the probing electrons perpendicular to the magnetic film. Fig. 10(a) corresponds to the non-spin-flip scattering channels, such that when we send electrons with spin down we measure only scattered electrons with the same spin. The spectrum displays a single spin-wave branch with an energy minimum (100 meV) at the K point. In Fig. 10(b) and (c), we have the spectra for the excitations which require spin flips of the probing electrons. In these processes, angular momenta is exchange between the probing electrons and the spin waves. The spin-wave mode in Fig. 10(b) has a linear dispersion at low energies, which are the characteristical spin-wave feature of antiferromagnets (see for example ref. 59).
IV. Conclusion
To summarize our study, we performed an ab initio investigation of the complex magnetic properties of a half-fluorinated germanene (Ge2F) and use a low-energy model to map the first-principles calculations and extract the magnetic exchange interactions as well as the Dzyaloshinskii–Moriya interaction vector. The latter is induced by the strong spin–orbit coupling of Germanium atoms and by the fact that the fluorine atoms break inversion symmetry.The magnetic exchange interactions are antiferromagnetic among the first, second and third nearest neighbors, which stabilize a Néel state where the magnetic moments are lying in the surface plane. This particular configuration is favored by the out-of-plane component of the DMI vector. Antiferromagnetic spin spirals are found as metastable states once a magnetic field is applied. Interestingly, if the out-of-plane component of the DMI vector is set to zero, antiferromagnetic skyrmions can be found. For the realization of such chiral magnetic textures, we propose to use a potential magnetic substrate to induce the requested large magnetic fields. Finally, we explored for completeness the spin-waves excitations and presented the spectra that could be measurable with electron energy loss spectroscopy or its spin-resolved version.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. Z. Ramadan and L. B. Drissi would like to acknowledge “Académie Hassan II des Sciences et Techniques-Morocco” for financial support. L. B. Drissi acknowledges the Alexander von Humboldt Foundation for financial support via the George Forster Research Fellowship for experienced scientists (Ref 3.4-MAR-1202992). The work of F. J. dos Santos and S. Lounis was supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (ERC-consolidator grant no. 681405-DYNASORE). We gratefully acknowledge the computing time granted by JARA-HPC on the supercomputer JURECA at Forschungszentrum Jülich and by RWTH Aachen University.References
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono and Y. Tserkovnyak, Antiferromagnetic spintronics, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Antiferromagnetic spintronics, Nat. Nanotechnol., 2016, 11, 231–241 CrossRef CAS.
- P. Wadley, B. Howells, J. Železný, C. Andrews, V. Hills and R. P. Campion, et al., Electrical switching of an antiferromagnet, Science, 2016, 351, 587–590 CrossRef CAS.
- K. Olejník, T. Seifert, Z. Kašpar, V. Novák, P. Wadley and R. P. Campion, et al., Terahertz electrical writing speed in an antiferromagnetic memory, Sci. Adv., 2018, 4, eaar3566 CrossRef.
- A. N. Bogdanov and D. Yablonskii, Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets, J. Exp. Theor. Phys., 1989, 95, 178 Search PubMed.
- U. K. Rössler, A. N. Bogdanov and C. Pfleiderer, Spontaneous skyrmion ground states in magnetic metals, Nature, 2006, 442, 797–801 CrossRef.
- S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch and A. Neubauer, et al., Skyrmion lattice in a chiral magnet, Science, 2017, 323, 915–919 CrossRef.
- W. Jiang, P. Upadhyaya, W. Zhang, G. Yu, M. B. Jungfleisch and F. Y. Fradin, et al., Blowing magnetic skyrmion bubbles, Science, 2015, 8, 283–286 CrossRef.
- Y. Zhou and M. Ezawa, A reversible conversion between a skyrmion and a domain-wall pair in a junction geometry, Nat. Commun., 2014, 1, 1–8 Search PubMed.
- H. Du, R. Che, L. Kong, X. Zhao, Ch. Jin and C. Wang, et al., Edge-mediated skyrmion chain and its collective dynamics in a confined geometry, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- J. Barker and O. A. Tretiakov, Static and dynamical properties of antiferromagnetic skyrmions in the presence of applied current and temperature, Phys. Rev. Lett., 2016, 116, 147203 CrossRef.
- H. Velkov, O. Gomonay, M. Beens, G. Schwiete, A. Brataas, J. Sinova and R. A. Duine, Phenomenology of current-induced skyrmion motion in antiferromagnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 18, 075016 Search PubMed.
- R. Keesman, M. Raaijmakers, A. E. Baerends, G. T. Barkema and R. A. Duine, Skyrmions in square-lattice antiferromagnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 054402 CrossRef.
- X. Zhang, Y. Zhou and M. Ezawa, Antiferromagnetic skyrmion: stability, creation and manipulation, Sci. Rep., 2016, 6, 24795 CrossRef CAS.
- B. Göbel, A. Mook, J. Henk and I. Mertig, Spin eigenexcitations of an antiferromagnetic skyrmion, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 184429 CrossRef.
- V. P. Kravchuk, O. Gomonay, D. D. Sheka, D. R. Rodrigues and K. Everschor-Sitte, et al., Spin eigenexcitations of an antiferromagnetic skyrmion, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 122, 184429 CrossRef.
- Z. Liu, M. dos Santos Dias and S. Lounis, Topological Magnons and Edge States in Antiferromagnetic Skyrmion Crystals, Phys. Rev. Lett., 2019, 122, 187203 CrossRef.
- Z. Liu, M. dos Santos Dias and S. Lounis, Theoretical investigation of antiferromagnetic skyrmions in a triangular monolayer, J. Phys.: Condens. Matter, 2020, 32, 425801 CrossRef CAS.
- N. Nagaosa and Y. Tokura, Topological properties and dynamics of magnetic skyrmions, Nat. Nanotechnol., 2013, 8, 899–911 CrossRef CAS.
- R. Wiesendanger, Nanoscale magnetic skyrmions in metallic films and multilayers: a new twist for spintronics, Nat. Rev. Mater., 2016, 1, 16044 CrossRef CAS.
- A. Fert, N. Reyren and V. Cros, Magnetic skyrmions: advances in physics and potential applications, Nat. Rev. Mater., 2016, 2, 1–15 Search PubMed.
- X. Zhang, Y. Zhou, M. Ezawa, G. P. Zhao and W. Zhao, Magnetic skyrmion transistor: skyrmion motion in a voltage-gated nanotrack, Sci. Rep., 2015, 5, 11369 CrossRef.
- D. M. Crum, M. Bouhassoune, J. Bouaziz, B. Schweflinghaus, S. Blügel and S. Lounis, Perpendicular reading of single confined magnetic skyrmions, Nat. Commun., 2015, 6, 1–8 Search PubMed.
- I. L. Fernandes, M. Bouhassoune and S. Lounis, Defect-implantation for the all-electrical detection of non-collinear spin-textures, Nat. Commun., 2020, 11, 1–9 Search PubMed.
- W. Kang, Y. Huang, C. Zheng, W. Lv, N. Lei and Y. Zhang, et al., Voltage controlled magnetic skyrmion motion for racetrack memory, Sci. Rep., 2016, 6, 23164 CrossRef CAS.
- E. J. Kan, H. J. Xiang, F. Wu, C. Tian, C. Lee and J. L. Yang, et al., Monolayer honeycomb structures of group-IV elements and III-V binary compounds: first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 15, 155453 Search PubMed.
- L. B. Drissi, N. B. Kanga, S. Lounis, F. Djeffal and S. Haddad, Electron-phonon dynamics in 2D carbon based-hybrids XC (X= Si, Ge, Sn), J. Phys.: Condens. Matter, 2019, 31, 135702 CrossRef CAS.
- W. Yao, D. Xiao and Q. Niu, Valley-dependent optoelectronics from inversion symmetry breaking, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 77, 235406 CrossRef.
- J. Liu, M. Shi, J. Lu and M. P. Anantram, Analysis of electrical-field-dependent Dzyaloshinskii–Moriya interaction and magnetocrystalline anisotropy in a two-dimensional ferromagnetic monolayer, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 97, 054416 CrossRef.
- K. K. Bai, Y. C. Wei, J. B. Qiao, S. Y. Li, L. J. Yin and W. Yan, et al., Detecting giant electron–hole asymmetry in a graphene monolayer generated by strain and charged-defect scattering via Landau level spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 121405 CrossRef.
- L. B. Drissi, K. Sadki, M. H. Kourra and M. Bousmina, Strain-engineering of Janus SiC monolayer functionalized with H and F atoms, Phys. Chem. Chem. Phys., 2018, 123, 185106 Search PubMed.
- S. C. Zhu, C. T. Yip, S. J. Peng, K. M. Wu, K. L. Yao and C. L. Mak, et al., Half-metallic and magnetic semiconducting behaviors of metal-doped blue phosphorus nanoribbons from first-principles calculations, Phys. Chem. Chem. Phys., 2018, 20, 7635–7642 RSC.
- Y. Mao, H. Xu, J. Yuan and J. Zhong, Functionalization of the electronic and magnetic properties of silicene by halogen atoms unilateral adsorption: a first-principles study, J. Phys.: Condens. Matter, 2018, 30, 365001 CrossRef.
- M. Sun, Q. Ren, Y. Zhao, J. P. Chou, J. Yu and W. Tang, Electronic and magnetic properties of 4d series transition metal substituted graphene: a first-principles study, Carbon, 2017, 120, 265–273 CrossRef CAS.
- L. B. Drissi, F. Z. Ramadan and S. Lounis, Halogenation of SiC for band-gap engineering and excitonic Functionalization, J. Phys.: Condens. Matter, 2017, 29, 455001 CrossRef CAS.
- E. J. Kan, H. J. Xiang, F. Wu, C. Tian, C. Lee and J. L. Yang, et al., Prediction for room-temperature half-metallic ferromagnetism in the half-fluorinated single layers of BN and ZnO, Appl. Phys. Lett., 2010, 97, 122503 CrossRef.
- Y. Ma, Y. Dai, M. Guo, C. Niu, L. Yu and B. Huang, Magnetic properties of the semifluorinated and semihydrogenated 2D sheets of group-IV and III-V binary compounds, Appl. Surf. Sci., 2018, 257, 7845–7850 CrossRef.
- H. M. Le, T. T. Pham, T. S. Dinh, Y. Kawazoe and D. Nguyen-Manh, First-principles modeling of 3d-transition-metal-atom adsorption on silicene: a linear-response DFT+ U approach, J. Phys.: Condens. Matter, 2016, 28, 135301 CrossRef.
- F. Marsusi, N. D. Drummond and M. J. Verstraete, The physics of single-side fluorination of graphene: DFT and DFT+ U studies, Appl. Surf. Sci., 2019, 144, 615–627 CAS.
- J. Zhou, Q. Wang, Q. Sun and P. Jena, Electronic and magnetic properties of a BN sheet decorated with hydrogen and fluorine, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 8, 085442 CrossRef.
- D. I. Badrtdinov, S. A. Nikolaev, A. N. Rudenko, M. I. Katsnelson and V. V. Mazurenko, Nanoskyrmion engineering with s p-electron materials: Sn monolayer on a SiC (0001) surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 184425 CrossRef CAS.
- F. B. Zheng and C. W. Zhang, The electronic and magnetic properties of functionalized silicene: a first-principles study, Nanoscale Res. Lett., 2012, 144, 1–5 Search PubMed.
- W. X. Zhang, Y. B. Wang, P. Zhao and C. He, Tuning the electronic and magnetic properties of graphene-like SiGe hybrid nanosheets by surface functionalization, Phys. Chem. Chem. Phys., 2016, 18, 26205–26212 RSC.
- L. B. Drissi, F. Z. Ramadan and N. B.-J. Kanga, Fluorination-control of electronic and magnetic properties in GeC-hybrid, Chem. Phys. Lett., 2016, 659, 148–153 CrossRef CAS.
- A. N. Rudenko, F. J. Keil, M. I. Katsnelson and A. I. Lichtenstein, Exchange interactions and frustrated magnetism in single-side hydrogenated and fluorinated graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 081405 CrossRef.
- A. N. Mazurenko, S. A. Rudenko, D. S. Nikolaev, A. Medvedeva, I. Lichtenstein and M. I. Katsnelson, Role of direct exchange and Dzyaloshinskii–Moriya interactions in magnetic properties of graphene derivatives: C2F and C2H, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 214411 CrossRef.
- Y. Ma, M. Dai, M. Guo, C. Niu, L. Yu and B. Huang, Strain-induced magnetic transitions in half-fluorinated single layers of BN, GaN and graphene, Nanoscale, 2011, 3, 2301–2306 RSC.
- L. B. Drissi, F. Z. Ramadan, E. H. Saidi, M. Bousmina and O. F-Fehri, Fluorination effects on electronic and magnetic properties of silicene/graphene hybrids, J. Phys. Soc. Jpn., 2013, 82, 104711 CrossRef.
- J. Cenker, B. Huang, N. Suri, P. Thijssen, A. Miller and T. Song, et al., Direct observation of two-dimensional magnons in atomically thin CrI3, Nat. Phys., 2020, 1–6 Search PubMed.
- D. R. Klein, D. MacNeill, J. L. Lado, D. Soriano, E. N-Moratalla and K. Watanabe, et al., Probing magnetism in 2D van der Waals crystalline insulators via electron tunneling, Nat. Phys., 2018, 360, 1218–1222 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car and C. Cavazzoni, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- B. Amadon, T. Applencourt and F. Bruneval, Screened Coulomb interaction calculations: cRPA implementation and applications to dynamical screening and self-consistency in uranium dioxide and cerium, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 125110 CrossRef.
- X. Gonze, F. Jollet, F. A. Araujo, D. Adams, B. Amadon and T. Applencourt, et al., Recent developments in the ABINIT software package, Comput. Phys. Commun., 2016, 205, 106–131 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Wannier90: A tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- G. P. Müller, M. Hoffmann, C. Dißelkamp, D. Sch ürhoff, S. Mavros, M. Sallermann, N. S. Kiselev, H. Jónsson and S. Blügel, Spirit: Multifunctional framework for atomistic spin simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 224414 CrossRef.
- F. J. Dos Santos, M. dos Santos Dias and S. Lounis, First-principles investigation of spin-wave dispersions in surface-reconstructed Co thin films on W(110), Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 134408 CrossRef.
- F. J. Dos Santos, M. dos Santos Dias, F. S. M. Guimarães, J. Bouaziz and S. Lounis, Spin-resolved inelastic electron scattering by spin waves in noncollinear magnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 024431 CrossRef CAS.
- F. J. D. Santos, M. D. S. Dias, and S. Lounis, Nonreciprocity of spin waves in noncollinear magnets due to the Dzyaloshinskii–Moriya interaction, Scientific reports, 2020, ArXiv:2003.11649 Search PubMed.
- F. J. D. Santos, M. D. S. Dias, and S. Lounis, Voltage controlled magnetic skyrmion motion for racetrack memory, Scientific reports, 2020, arXiv:2005. 07250 Search PubMed.
- P. Liang, Y. Liu, S. Xing, H. Shu and B. Tai, Electronic and magnetic properties of germanene: surface functionalization and strain effects, Solid State Commun., 2016, 226, 19–24 CrossRef CAS.
- S. Sun, F. Meng, H. Wang, H. Wang and Y. Ni, Novel two-dimensional semiconductor SnP 3: high stability, tunable bandgaps and high carrier mobility explored using first-principles calculations, J. Mater. Chem. A, 2018, 6, 11890–11897 RSC.
- M. Ashton, J. Paul, S. B. Sinnott and R. G. Hennig, Topology-scaling identification of layered solids and stable exfoliated 2D materials, Phys. Rev. Lett., 2017, 118, 106101 CrossRef.
- P. Avramov, V. Demin, M. Luo, C. H. Choi, P. R. Sorokin, B. Yakobson and L. Chernozatonskii, Translation symmetry breakdown in low-dimensional lattices of pentagonal rings, J. Phys. Chem. Lett., 2015, 6, 4525–4531 CrossRef CAS.
- A. V. Kuklin, H. Agren and P. V. Avramov, Structural stability of single-layer PdSe2 with pentagonal puckered morphology and its nanotubes, Phys. Chem. Chem. Phys., 2020, 22, 8289–8295 RSC.
- V. V. Mazurenko, S. L. Skornyakov, V. I. Anisimov and F. Mila, First-principles investigation of symmetric and antisymmetric exchange interactions of SrCu2(BO3)2, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 7, 195110 CrossRef.
- M. Goli, S. M. Mozvashi, P. Aghdasi, S. Yousefi, and R. Ansari. A DFT study on the mechanical properties of hydrogenated and fluorinated germanene sheets, 2020, arXiv preprint arXiv:2005.07583 Search PubMed.
- L. B. Drissi and F. Z. Ramadan, Many body effects study of electronic and optical properties of silicene-graphene hybrid, Phys. E, 2015, 68, 38–41 CrossRef CAS.
- L. B. Drissi and F. Z. Ramadan, Excitonic effects in GeC hybrid: Many-body Green's function calculations, Phys. E, 2015, 74, 377–381 CrossRef CAS.
- P. W. Anderson, Anisotropic spin Hamiltonians due to spin-orbit and Coulomb exchange interactions, Phys. Rev., 1959, 115, 2–13 CrossRef CAS.
- T. Yildirim, A. B. Harris, A. Aharony and O. Entin-Wohlman, Anisotropic spin Hamiltonians due to spin-orbit and Coulomb exchange interactions, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 10239–10267 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |