Open Access Article
Open Access ArticleAtmospheric oxidation of Folpet initiated by OH radicals, NO3 radicals, and O3†
Chenxi Zhang ab,
Xiaomin Sun
ab,
Xiaomin Sun b,
Wei Tanc and
Hengjun Peng*d
b,
Wei Tanc and
Hengjun Peng*d
aCollege of Biological and Environmental Engineering, Binzhou University, Binzhou 256600, P. R.China
bEnvironment Research Institute, Shandong University, Qingdao 266200, P. R. China
cShandong Provincial Eco-environment Monitoring Center, Jinan 250100, P. R. China
dLogistics Support Department, Shandong University, Jinan 250100, P. R. China. E-mail: phj@sdu.edu.cn
First published on 11th January 2021
Abstract
Folpet, a nonspecific sulfenimide fungicide, is widely used to protect crops against mildew. It can be dispersed and transported over long distances. The residence time of Folpet in the atmosphere depends on the oxidation processes initiated by atmospheric oxidants such as O3, OH and NO3 radicals. In this study, the reactions of Folpet with gas-phase O3, OH and NO3 radicals were investigated via quantum chemical calculation methods, which can effectively provide information about the reaction intermediates and pathways. The obtained results show that the room-temperature rate constants of the reactions between Folpet and OH radicals, NO3 radicals and O3 are about 3.69 × 10−14, 5.40 × 10−15, and 1.73 × 10−22 cm3 per molecule per s at 298 K, respectively. Considering the oxidant concentration in the atmosphere, Folpet seems to be mainly scavenged by NO3 radicals, especially at night. This study can contribute to a better understanding of the atmospheric fate of Folpet, elucidating a significant impact of NO3 radicals on its degradation process in comparison with other oxidants such as O3 and OH radicals.
Introduction
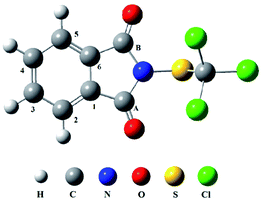
Pesticides are widely used to kill pests and increase crop yields around the world. This inevitably leads to a release of environmental and foodborne contaminants, which has been shown to cause many diseases including cancer.1 Thus the environmental fate of pesticides has become a hot topic. Up to 90% of pesticides applied in the agricultural field do not reach the target site, but end up being found in the soil, water and atmosphere.2 It is worth noting that 30–50% of pesticides are transferred to the atmosphere via spray drift, evaporation, volatilization and windblown soil.2–5Folpet (N-trichloromethyl-thio-phthalimide) is a nonspecific sulfenimide fungicide, which consists of a phthalimide moiety (PI) and a trichloromethylthio group (SCCl3) (Fig. 1). Since 1952, Folpet has been widely employed on grapevines and other fruit trees to prevent diseases caused by mildew, grey mould, spoilage fungi and wood-decay fungi.6,7 In addition, Folpet is also used as a raw material in the production of oil-based paints, coatings and plastics.8
Due to a low vapor pressure (2.1 × 10−5 Pa at 25 °C), Folpet is expected to found in both gas phases and particulate phases of the atmosphere. In general, the reported values are the sum of the pesticides present in both the gas and particulate phases, although some studies have separately reported the distribution in gases and particles. The air Folpet concentrations assessed in different places of the world range from pg to ng per m3. A study by Raina et al. in the Lower Fraser Valley agricultural region of Canada reveals a maximum air Folpet total concentration of 1.7 ng m−3.9 The maximum Folpet total concentration detected by Coscollà et al. in the Central Region of France during a period of 2006–2008 was as high as 82.2 ng m−3.10 In turn, Folpet concentrations in the Centre of Reims (France), were reported to be not higher than 4.70 ng m−3.11 Furthermore, these assessed during sampling campaign by Schummer et al. varied from 0.39 to 11.3 ng m−3, and Folpet was mostly present in the gas phase (about 68%).12 Finally, high levels of PM10 Folpet concentrations from 11.4 to 162.0 pg m−3 were found within 24 hours of sampling in Spain.13
Once in the atmosphere, the fate of pesticides is dictated by dry and wet deposition,14 as well as by the chemical processes including photolysis and oxidation initiated by atmospheric oxidants such as O3, OH, and NO3 radicals.15–20 Wet and dry deposition are physical removal processes and will not be removed from the environment. In turn, the efficiency of photolysis depends on three factors: absorption cross section, quantum yield for photo-induced reactions, and actinic flux of solar radiation. While the photon flux can be accurately calculated as a function of time of day, season and latitude, the measurement of absorption cross-sections and quantum yield can not presently be estimated.21 Thus, photolysis rates can not be estimated reliably. Oxidation induced by atmospheric oxidants is expected to play a major role in the atmospheric chemistry of pesticides. In this respect, studying the mechanism and kinetics of atmospheric chemical reactions to understand the behavior of pesticides in the environment is an important task.
Earlier studies reveal that pesticides undergo oxidation reactions with atmospheric oxidants. Dang et al. investigated the atmospheric oxidation of p,p′-dicofol by OH and NO3 radicals, and the rate constants for the reactions of p,p′-dicofol with OH and NO3 radicals are 1.51 × 10−12 and 8.88 × 10−14 cm3 per molecule per s, respectively.22 El Masri et al. studied the kinetics and mechanism of heterogeneous oxidation of chlorpyrifos (CLP) and chlorpyrifos oxon (CLPO) by O3 and OH radicals at room temperature using a photochemical reactor coupled to a GC/MS analytical system.23 The result shown that the rate constants for the reactions of CLP and CLPO with O3 are (1.2 ± 0.1)×10−19 cm3 per molecule per s and (2.9 ± 0.7)×10−21 cm3 per molecule per s, respectively. And the rate constants of CLP and CLPO with OH radical range between 6 × 10−12 and 2 × 10−14 cm3 per molecule per s. There are also some pesticides with atmospheric oxidants has already been studied. But unfortunately, there are still a few studies concerning the degradation of Folpet by atmospheric oxidants.24,25 To date, there are still a few studies concerning the degradation of Folpet by atmospheric oxidants. Among them, two works were dedicated to the determination of the kinetic rate constants for the reactions between Folpet, O3 and OH radicals in the heterogeneous phase.26,27 Their values were (2.6 ± 0.2) × 10−20 cm3 per molecule per s for the reaction induced by O3 and (1.6 ± 0.9) × 10−13 cm3 per molecule per s in the case of the process involving the OH radical. Furthermore, it was shown that pesticide reactivity in the heterogeneous phase may be affected by the chemical properties of the supporting surface.26 In this study, the degradation processes of the gas-phase Folpet with O3, OH and NO3 radicals were investigated via the quantum chemical calculation approaches, which can effectively provide information on the reaction intermediates and pathways. The rate constants of all initial pathways were then used to assess the fate and resistance of Folpet in the atmosphere.
Computational methods
Mechanism computations
All thermodynamics calculations were performed using Gaussian 09 software.28 The geometrical parameters of reactants, intermediates, transition states (TS) and products in each elementary reaction were optimized by applying M06-2X functional with a standard 6-31+G(d,p) basis set. Zheng et al. has employed 348 model chemistries to calculate the 24 barrier heights in the DBH24/08 database, which including heavy-atom transfer (HATBH6), nucleophilic substitution (NSBH6), unimolecular and association (UABH6), and hydrogen-transfer (HTBH6) reactions.29 The selected M06-2X/6-31+G(d,p) was proven to meet the need of both high accuracy and low computational cost. In this paper, TSs were examined by vibrational frequency analysis. A larger basis set, 6-311++g(3df,3pd), was used in the same method to obtain more accurate single energies.Kinetics computations
Using the above calculated potential energy surface, the kinetics were obtained using KisThelP software based on the Transition State Theory (TST) with a Eckart tunneling correction factor.30,31 The following thermodynamic equivalent is employed in KiSThelP:32
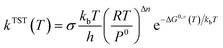 | (1) |
Results and discussion
Reactions with OH radicals
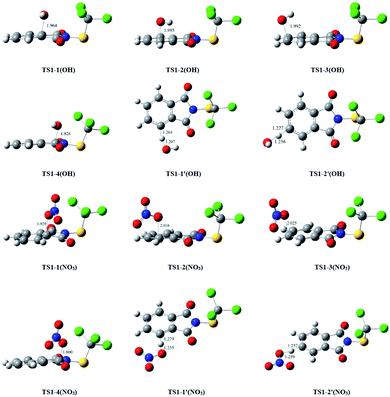
Atmospheric OH radical mainly originates from the photolysis of ozone in the presence of water (O(1D) + H2O → 2OH).34 It is often called the “detergent” of the troposphere: reacting with many organic compounds and pollutants, it decomposes them through “cracking”, often acting as the first step to their removal. Furthermore, OH radical plays an important role in eliminating some greenhouse gases like methane and ozone, as well as inactivating pathogenic viruses and bacteria and neutralising allergenic pollens and mould spores. The reaction of the OH radical with an organic compound can be described by the two general processes: OH radical addition and H-atom abstraction.35 For convenience, the atom number of Folpet is labeled in Fig. 1. As seen, a Folpet structure has four different carbon sites relative to the –SCCl3 group, which can be attacked by OH radicals: the carbon atom of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (CA, CB), α-position carbon (Cα-C1, C6), β-position carbon (Cβ-C2, C5), and λ-position carbon (Cλ-C3, C4). To avoid repetition, C1, C2 and C3 positions were described in following article. H-atom abstraction will occur at the H atom linked with Cβ and Cλ atoms. C2 and C3 positions were described as examples. The reaction pathways of OH radical addition and H atom abstraction are depicted in Fig. 2. In this figure, the potential barriers (Eb) and the reaction heat (Er) are marked as well. The optimized transition state structures of Folpet with OH radicals are shown in Fig. 3.
O (CA, CB), α-position carbon (Cα-C1, C6), β-position carbon (Cβ-C2, C5), and λ-position carbon (Cλ-C3, C4). To avoid repetition, C1, C2 and C3 positions were described in following article. H-atom abstraction will occur at the H atom linked with Cβ and Cλ atoms. C2 and C3 positions were described as examples. The reaction pathways of OH radical addition and H atom abstraction are depicted in Fig. 2. In this figure, the potential barriers (Eb) and the reaction heat (Er) are marked as well. The optimized transition state structures of Folpet with OH radicals are shown in Fig. 3.
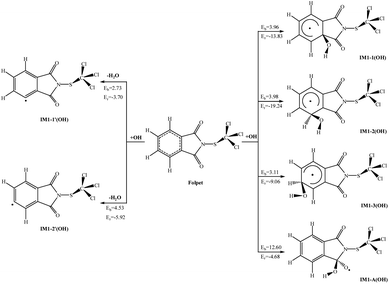 | ||
| Fig. 2 The potential barriers Eb (kcal mol−1) and reaction heats Er (kcal mol−1) at 298 K for the possible reactions of Folpet with OH radicals. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond generates IM1-A(OH) with a higher potential barrier (12.60 kcal mol−1). The length of a newly formed CA–O bond in TS1-A(OH) is 1.826 Å. This process is also exothermic, but the amount of energy released (4.68 kcal mol−1) is less than that during the addition to the aromatic ring. Thus, OH radical addition to the aromatic ring is an energetically more favorable reaction pathway.
O bond generates IM1-A(OH) with a higher potential barrier (12.60 kcal mol−1). The length of a newly formed CA–O bond in TS1-A(OH) is 1.826 Å. This process is also exothermic, but the amount of energy released (4.68 kcal mol−1) is less than that during the addition to the aromatic ring. Thus, OH radical addition to the aromatic ring is an energetically more favorable reaction pathway.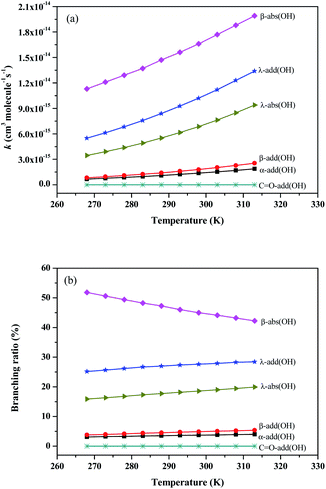 | ||
| Fig. 4 The rate constants and branching ratios of the reaction of Folpet with OH radical at 268-313 K using the TST theory. | ||
As seen in Fig. 4(a), the rate constants of α-add, β-add, λ-add, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-add, β-abs and λ-abs reactions are 1.38 × 10−15, 1.80 × 10−15, 1.02 × 10−14, 1.48 × 10−21, 1.66 × 10−14, and 6.86 × 10−15 cm3 per molecule per s at 298 K and 1 atm pressure, respectively. Since the rate constant of C
O-add, β-abs and λ-abs reactions are 1.38 × 10−15, 1.80 × 10−15, 1.02 × 10−14, 1.48 × 10−21, 1.66 × 10−14, and 6.86 × 10−15 cm3 per molecule per s at 298 K and 1 atm pressure, respectively. Since the rate constant of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-add reaction is much lower than others, this pathway is not dominant and can be negligible. The kadd(OH) and kabs(OH) values are found to be 1.34 × 10−14 and 2.35 × 10−14 cm3 per molecule per s, respectively, thus both OH radical addition reactions and H atom abstraction are important for Folpet. The ktotal(OH) parameter is 3.69 × 10−14 cm3 per molecule per s, which is slightly lower than that of (1.6 ± 0.9) × 10−13 cm3 per molecule per s in the heterogeneous phase.27
O-add reaction is much lower than others, this pathway is not dominant and can be negligible. The kadd(OH) and kabs(OH) values are found to be 1.34 × 10−14 and 2.35 × 10−14 cm3 per molecule per s, respectively, thus both OH radical addition reactions and H atom abstraction are important for Folpet. The ktotal(OH) parameter is 3.69 × 10−14 cm3 per molecule per s, which is slightly lower than that of (1.6 ± 0.9) × 10−13 cm3 per molecule per s in the heterogeneous phase.27
The branching ratio (R) can more intuitively express the contribution of each pathway. Fig. 4(b) shows the R values of all reaction pathways. Here, the dominant pathways are β-abs and λ-add, whose R values are around 47% and 27% within a studied temperature range. While the R value of β-abs pathway decreases from 51.8 to 42.3% with increasing temperature, that of λ-add rises from 25.2 to 28.5% within the above range of temperatures, implying that the increase of temperature is beneficial to λ-add pathway. As for other pathways, their degrees of contribution to the OH-initiated transformation of Folpet can be described by the following sequence: λ-abs > β-add > α-add > C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-add.
O-add.
Based on these results, it can be concluded that both OH radical addition and H-abstraction are important in the reactions between Folpet and OH radicals. Among them, β-abs is a dominant abstraction process, whereas the OH radical addition mainly acts on the Cλ sites.
Reactions with NO3 radicals
The atmospheric NO3 radical is derived from the reactions NO + O3 → NO2 + O2 and NO2 + O3 → NO3 + O2.36 Since this is a short-lived component with a lifetime of just about 5 s, its concentration remains low during the day, but it can be accumulated at night. Similar to the reactions with OH radicals, the NO3 radical can be attached to the aromatic ring or the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, or can abstract an H atom from the C–H bond. The possible reactions of Folpet with NO3 radicals are illustrated in Fig. 5, and the total rate constants (k) along with branching ratios (R) of each reaction site at 298 K are listed in Table 1.
O bond, or can abstract an H atom from the C–H bond. The possible reactions of Folpet with NO3 radicals are illustrated in Fig. 5, and the total rate constants (k) along with branching ratios (R) of each reaction site at 298 K are listed in Table 1.
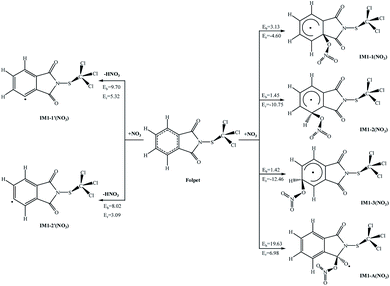 | ||
| Fig. 5 The potential barriers Eb (kcal mol−1) and reaction heats Er (kcal mol−1) at 298 K for the possible reactions of Folpet with NO3 radicals. | ||
| Reaction | k298 K (cm3 per molecule per s) | R (%) |
|---|---|---|
| Folpet + NO3 → IM1-α(NO3) | 1.03 × 10−16 | 1.9 |
| Folpet + NO3 → IM1-β(NO3) | 2.88 × 10−15 | 53.3 |
| Folpet + NO3 → IM1-λ(NO3) | 2.42 × 10−15 | 44.8 |
Folpet + NO3 → IM1-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(NO3) O(NO3) |
4.19 × 10−28 | 0 |
| Folpet + NO3 → IM1-β′(NO3) | 2.07 × 10−21 | 0 |
| Folpet + NO3 → IM1-λ′(NO3) | 4.28 × 10−20 | 0 |
According to data in Fig. 5, the addition reactions at the aromatic rings seem to be energetically favorable reaction pathways. These processes are exothermic, releasing energies of 4.60–12.46 kcal mol−1, and possess low potential barriers (1.42–3.13 kcal mol−1), being in contradiction to the reactions of OH radical addition and H atom abstraction that proceed with high activation barriers (Eb = 8.02–19.63 kcal mol−1, Er = 3.09–6.98 kcal mol−1).
A comparative analysis of the k and R parameters at 298 K (Table 1) allows one to conclude that the rate constants for the addition reactions are much greater than those associated with the abstraction reactions, thus indicating a 100% contribution of the addition reactions to the total process. The total rate constant is found to be 5.40 × 10−15 cm3 per molecule per s, which is close to the values of reference compounds, such as 4.0 × 10−15 cm3 per molecule per s of benzyl alcohol,37 6.8 × 10−14 cm3 per molecule per s of dibenzo-p-dioxins,38 and 9.3 × 10−15 cm3 per molecule per s of dibenzofurans.39
Reactions with O3 radicals
O3 is a powerful oxidizing agent, which comes from eddy diffusion in the stratosphere or the photolysis of NO2.35,40 Unlike OH and NO3 radicals, the reaction of O3 with Folpet is only possible via the addition to the aromatic ring or the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, but never through the H-atom abstraction from a C–H bond. For O3 added to Folpet, there are five eventual pathways (see Fig. 6).
O bond, but never through the H-atom abstraction from a C–H bond. For O3 added to Folpet, there are five eventual pathways (see Fig. 6).
 | ||
| Fig. 6 The potential barriers Eb (kcal mol−1) and reaction heats Er (kcal mol−1) at 298 K for the possible reactions of Folpet with O3 radicals. | ||
According to the thermodynamic perspective, the addition to the aromatic ring is easier to occur than that to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. In all the pathways, the addition of O3 to C2
O bond. In all the pathways, the addition of O3 to C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3 and C3
C3 and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bonds results in the lowest barriers and the highest energies released. Table 2 show the total rate constants (k) and branching ratios (R) of each reaction site. The total rate constant of Folpet with O3 is 1.73 × 10−22 cm3 per molecule per s at 298 K, which is two orders of magnitude lower than that obtained in the heterogeneous phase.26 As seen in Table 2, the addition reactions involving Cβ
C4 bonds results in the lowest barriers and the highest energies released. Table 2 show the total rate constants (k) and branching ratios (R) of each reaction site. The total rate constant of Folpet with O3 is 1.73 × 10−22 cm3 per molecule per s at 298 K, which is two orders of magnitude lower than that obtained in the heterogeneous phase.26 As seen in Table 2, the addition reactions involving Cβ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cλ and C3
Cλ and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bonds dominate over those with Cα
C4 bonds dominate over those with Cα![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cβ and C1
Cβ and C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C6 bonds within a studied temperature range. Consequently, the addition to a C
C6 bonds within a studied temperature range. Consequently, the addition to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond can basically be ignored. It is worth noting that, while the branching ratios for the reactions with Cβ
O bond can basically be ignored. It is worth noting that, while the branching ratios for the reactions with Cβ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cλ and C3
Cλ and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bonds exhibit a slightly downward trend over the investigated temperature range, others are gradually rising.
C4 bonds exhibit a slightly downward trend over the investigated temperature range, others are gradually rising.
| Reaction site | k298 K (cm3 per molecule per s) | R (%) |
|---|---|---|
Cα![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cβ (O3) Cβ (O3) |
8.43 × 10−24 | 5.0 |
Cβ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cλ (O3) Cλ (O3) |
5.25 × 10−23 | 31.2 |
C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 (O3) C4 (O3) |
1.02 × 10−22 | 59.9 |
C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C6 (O3) C6 (O3) |
6.59 × 10−24 | 3.9 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (O3) O (O3) |
4.22 × 10−34 | 0 |
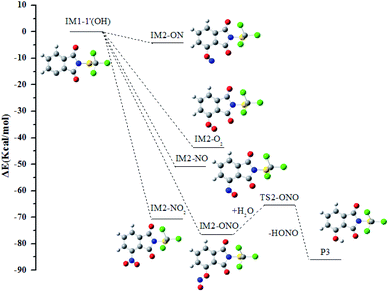
The subsequent reactions of IM1-3(OH) and IM1-1′(OH)
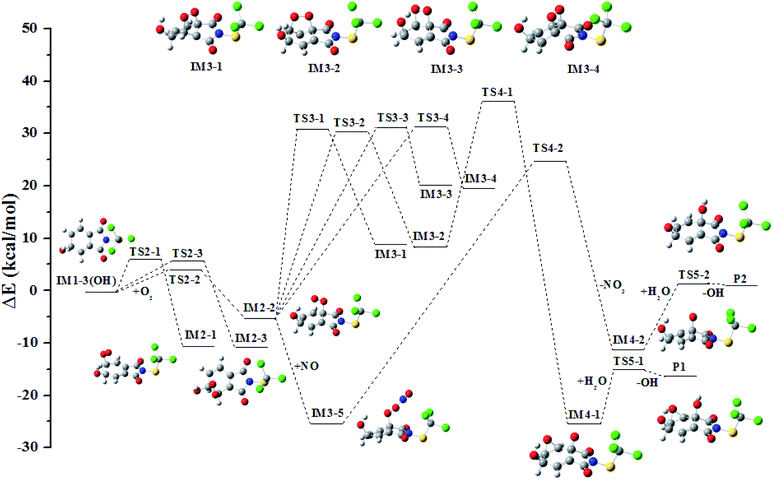
In all the reactions, the OH radical addition to λ-site and H atom abstraction from β-site are most kinetically favored, thus IM1-3(OH) and IM1-1′(OH) are chosen as examples to illustrate the subsequent reaction in the atmosphere. The reaction paths are shown in Fig. 7 and 8, respectively.Under low-NOx conditions, the O atom of O2 can attack the C atom of benzene ring to form five-member ring adduct (IM3-1 and IM3-2) or the four-member ring adduct (IM3-3 and IM3-4). All the isomerization reactions will pass through a high potential barrier and require heat absorption. Among them, the reaction forming IM3-2 has the lowest barrier. It will open up the O–O bond to form the intermediate IM4-1 subsequently. A three-member ring is formed simultaneously with the rupture of the O–O bond. The carbonyl free radical IM4-1 can abstract the H atom from H2O to reach a stable state P1 and the OH radical will be regenerated simultaneously. The regenerated OH radical will initiate a new round of reaction.
Under high-NOx conditions, it includes three elementary reactions: NO addition, NO2 elimination, and reaction with H2O. It should be pointed out that NO addition is a barrier-free combination and a strong exothermic process, resulting in an energy-rich intermediate that can be further reacted through unimolecular decomposition. The NO2 elimination reaction has a high potential barrier of 51.35 kcal mol−1, so it is the rate-determining mining step in the reaction path. The carbonyl free radicals IM4-2 can abstract the H atom in H2O to regenerate OH radical and P2.
The atmospheric lifetimes
The atmospheric lifetimes (τ) of Folpet corresponding to its reactions with highly reactive oxidants are defined by the formula: τ = 1/(kx[X]), where [X] is the atmospheric oxidant concentration. The concentration ranges of OH radical, NO3 radical and O3 are 3.5 × 105 to 2.00 × 106, 3 × 107 to 9 × 108 and 4.67 × 1011 to 1.17 × 1012 molecules per cm3, respectively.40–42 Using the above determined rate constants k, the lifetimes of Folpet with respect to O3 is hundreds of years (159.2–398.9 years) in comparison to 5.2–29.8 months and 2.38 days to 2.38 months against OH radical and NO3 radical. If the average concentration of OH radicals for 12 h daytime (1.6 × 106 molecule cm3)43 and the average concentration of NO3 radicals for 12 h nighttime (1.1 × 108 molecule cm3)42 are used, the lifetime of about 6.5 months and 19.5 days are obtained, which shows that Folpet is relatively persistent towards oxidation removal processes.Conclusions
The atmospheric oxidation mechanisms and kinetic phenomena arising in the reactions of Folpet with OH radicals, NO3 radicals and O3 were investigated using the DFT method. Two general reaction mechanisms were used to describe the above processes: (1) addition to the aromatic rings and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, initiated by the OH radicals, NO3 radicals and O3 and (2) H-abstraction from C–H bonds, induced by OH and NO3 radicals. While both the addition and H-abstraction were shown to be important for the OH radical-initiated reactions, the addition to the aromatic ring was found to dominate over the H-abstraction in the case of processes with NO3 radicals. The room-temperature rate constants of the reactions involving OH radicals, NO3 radicals and O3 were about 3.69 × 10−14, 5.40 × 10−15, and 1.73 × 10−22 cm3 per molecule per s, respectively. Considering the atmospheric oxidant concentrations, Folpet was shown to be mainly scavenged by NO3 radicals, especially at night time.
O bonds, initiated by the OH radicals, NO3 radicals and O3 and (2) H-abstraction from C–H bonds, induced by OH and NO3 radicals. While both the addition and H-abstraction were shown to be important for the OH radical-initiated reactions, the addition to the aromatic ring was found to dominate over the H-abstraction in the case of processes with NO3 radicals. The room-temperature rate constants of the reactions involving OH radicals, NO3 radicals and O3 were about 3.69 × 10−14, 5.40 × 10−15, and 1.73 × 10−22 cm3 per molecule per s, respectively. Considering the atmospheric oxidant concentrations, Folpet was shown to be mainly scavenged by NO3 radicals, especially at night time.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by National Natural Science Foundation of China (21607011 and 21976109), Key Research and Development Project of Shandong Province (2019GSF109021 and 2019GSF109037), Natural Science Foundation of Shandong Province (ZR2018MB043), the Fundamental Research Funds of Shandong University (2018JC027).References
- E. S. O'Leary, J. E. Vena, J. L. Freudenheim and J. Brasure, Environ. Res., 2004, 94, 134–144 CrossRef.
- Y. Gil and C. Sinfort, Atmos. Environ., 2005, 39, 5183–5193 CrossRef CAS.
- F. Van Den Berg, R. Kubiak, W. G. Benjey, M. S. Majewski, S. R. Yates, G. L. Reeves, J. H. Smelt and A. M. Van Der Linden, Water, Air, Soil Pollut., 1999, 115, 195–218 CrossRef CAS.
- O. Zivan, Y. Bohbot-Raviv and Y. Dubowski, Chemosphere, 2017, 177, 303–310 CrossRef CAS.
- O. Zivan, M. Segal-Rosenheimer and Y. Dubowski, Atmos. Environ., 2016, 127, 155–162 CrossRef CAS.
- H. Teisseire and G. Vernet, Pestic. Biochem. Physiol., 2001, 69, 112–117 CrossRef CAS.
- J. F. Huertas-Pérez, M. Ernest, J. Varela and F. Badoud, Food Chem., 2018, 260, 213–220 CrossRef.
- K. Chen, J. C. Mackie, E. M. Kennedy and B. Z. Dlugogorski, Environ. Sci. Technol., 2011, 452, 554–560 CrossRef.
- R. Raina, W. Belzer and K. Jones, Water, Air, Soil Pollut., 2009, 2, 41–49 CAS.
- C. Coscollà, P. Colin, A. Yahyaoui, O. Petrique, V. Yusà, A. Mellouki and A. Pastor, Atmos. Environ., 2010, 3915–3925 CrossRef.
- A. Villiot, E. Chrétien, E. Drab-Sommesous, E. Rivière, A. Chakir and E. Roth, Atmos. Environ., 2018, 174, 82–91 CrossRef CAS.
- C. Schummer, E. Mothiron, B. M. R. Appenzeller, A. Rizet, R. Wennig and M. Millet, Environ. Pollut., 2010, 158, 576–584 CrossRef CAS.
- E. Hart, C. Coscollà, A. Pastor and V. Yusà, Atmos. Environ., 2012, 62, 118–129 CrossRef CAS.
- M. S. Majewski, R. H. Coupe, W. T. Foreman and P. D. Capel, Environ. Toxicol. Chem., 2014, 33, 1283–1293 CrossRef CAS.
- R. Atkinson, R. Guicherit, R. A. Hites, W. U. Palm, J. N. Seiber and P. de Voogt, Water, Air, Soil Pollut., 1999, 115, 219–243 CrossRef CAS.
- E. Borras, M. Rodenas, T. Vera, T. Gomez and A. Munoz, Sci. Total Environ., 2017, 579, 1–9 CrossRef CAS.
- J. Socorro, P. S. J. Lakey, L. Han, T. Berkemeier, G. Lammel, C. Zetzsch, U. Poeschl and M. Shiraiwa, Environ. Sci. Technol., 2017, 51, 13749–13754 CrossRef CAS.
- W. H. Wang, K. Z. Aregahegn, S. T. Andersen, A. Z. Ni, A. F. Rohrbacher, O. J. Nielsen and B. J. Finlayson-Pitts, J. Agric. Food Chem., 2019, 67, 1638–1646 CrossRef CAS.
- C. Mattei, H. Wortham and E. Quivet, Atmos. Environ., 2019, 211, 170–180 CrossRef CAS.
- C. Mattei, H. Wortham and E. Quivet, Sci. Total Environ., 2018, 625, 1544–1553 CrossRef CAS.
- R. Atkinson, R. Guicherit and R. A. Hites, Water, Air, Soil Pollut., 1999, 115, 219–243 CrossRef CAS.
- J. Dang, S. Tian and Q. Z. Zhang, Chemosphere, 2018, 219, 645–654 CrossRef.
- A. El Masri, M. Al Rashidi, H. Laversin, A. Chakir and E. Roth, RSC Adv., 2014, 4, 24786–24795 RSC.
- O. Rokbani, S. Fattouch, A. Chakir and E. Roth, Sci. Total Environ., 2018, 694, 133745 CrossRef.
- T. Vera, E. Borras, J. M. Chen, C. Coscolla, V. Daele, A. Mellouki, M. Rodenas, H. Sidebottom, X. M. Sun and V. Yusa, Chemosphere, 2015, 138, 112–119 CrossRef CAS.
- M. Al Rashidi, A. Chakir and E. Roth, J. Phys. Chem. A, 2013, 117, 2908–2915 CrossRef CAS.
- M. Al Rashidi, A. Chakir and E. Roth, Atmos. Environ., 2014, 82, 164–171 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel and G. E. Scuseria, et al., Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- J. J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 808–821 CrossRef CAS.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- H. Eyring, Chem. Rev., 1935, 17, 65–77 CrossRef CAS.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS.
- R. Guicherit and M. Roemer, Chemosphere: Global Change Sci., 2000, 2, 167–183 CrossRef CAS.
- R. Atkinson and J. Arey, Atmos. Environ., 2003, 37, S197–S219 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. R. F. Hampson and J. Troe, J. Phys. Chem. Ref. Data, 1997, 26, 1329–1499 CrossRef CAS.
- J. C. Harrison and J. R. Wells, Int. J. Chem. Kinet., 2012, 44, 778–788 CrossRef CAS.
- E. S. C. Kwok, R. Atkinson and J. Arey, Int. J. Chem. Kinet., 1994, 26, 511–525 CrossRef CAS.
- R. Atkinson, Environ. Sci. Technol., 1996, 6, 53–72 CAS.
- J. A. Logan, J. Geophys. Res., 1985, 90, 10463–10482 CrossRef.
- M. G. Lawrence, P. Jockel and R. von Kuhlmann, Atmos. Chem. Phys., 2001, 1, 37–49 CrossRef CAS.
- M. Vrekoussis, M. Kanakidou, N. Mihalopoulos, P. J. Crutzen, J. Lelieveld, D. Perner, H. Berresheim and E. Baboukas, Atmos. Chem. Phys., 2004, 4, 169–182 CrossRef CAS.
- R. Prinn, D. Cunnold, P. Simmonds, F. Alyea, R. Boldi, A. Crawford, P. Fraser, D. Gutzler and D. R. Rosen, J. Geophys. Res., 1992, 97, 2445–2461 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09429c |
| This journal is © The Royal Society of Chemistry 2021 |