Novel structural phases and the properties of LaX (X = P, As) under high pressure: first-principles study

Abstract

The particle swarm optimization algorithm and density functional theory (DFT) are extensively performed to determine the structures, phase transition, mechanical stability, electronic structures, and thermodynamic properties of lanthanide phosphates (LaP and LaAs) in the pressure range of 0 to 100 GPa. Two novel high-pressure structures of LaP and LaAs are first reported here. It is found that LaX (X = P, As) undergo a phase transition from NaCl-type structure (Fm3m) to CsCl-type structure (P4/mmm) at 19.04 GPa and 17.22 GPa, respectively. With the elevation of the pressure, C2/m-LaP and Imma-LaAs are the most stable structures up to 70.08 GPa and 85.53 GPa, respectively. Finally, the analysis of the elastic constants and hardness confirms that the C2/m-LaP possesses hardness values up to 23.24 GPa due to the strong covalent P–P bonding and ionic La–P bonding, indicating that it is a potential hard material.

---

1. Introduction

Rare-earth (RE) monopnictides have attracted extensive attention due to their excellent properties of high melting point, extreme magnetoresistance, and high superconductivity. These properties make them widely applied in many fields, such as sensors, spintronics, infrared (IR) detectors, and magnetic storage devices.^1–11 As the first member of the rare earth monopnictides family, it is very important to understand lanthanum monopnictides in order to look for more interesting properties of this family. In the past decades, a series of studies have been carried out on the fundamental properties of lanthanum pnictides (including electronic, elastic, optical and mechanical properties). For example, Charifi et al.¹² and Shoaib et al.⁹ used full-potential linearized augmented plane wave (FP-LAPW) calculations on the electronic structures of lanthanum pnictides. Vaitheeswaran et al.¹³ studied the structural and electronic properties of lanthanum pnictides by means of the self-consistent tight binding linear muffin tin orbital (TB-LMTO) method. In addition, Kwon et al.¹⁴ measured the optical properties of these compounds. Tütüncü et al.¹⁵ determined the elastic properties of these compounds using ultrasonic measurement techniques and through experimental phonon spectroscopy.

High pressure is an effective tool to discover new phenomena and explore new materials. Presently, there are some reports on the structural phase transition and electronic properties of LaX (X = P, As) under high pressure.^12,16–19 At ambient conditions, LaX (X = P, As) are cubic structures of NaCl type (B1 phase) with space group of Fm3m. Under lower pressure, they undergo a structure phase transition into a tetragonal distorted structure of CsCl type (PT phase) with a space group of P4/mmm. In theory, Charifi et al.¹² showed that LaX (X = P, As) transformed from cubic structure to tetragonal structure in the range of 14.6 to 22.6 GPa for LaP and 11.2 to 19.6 GPa for LaAs, respectively. Vaitheeswaran et al.²⁰ investigated the electronic structure and the relative stability of LaP and LaAs at high pressure. They found that the phase transition from rocksalt to tetragonal occurred around 18 GPa and 11.2 GPa in the case of LaP and LaAs, respectively. In experiments, high-pressure synchrotron X-ray diffraction experiment revealed that the phase transition was found at around 24 GPa for LaP¹⁶ and the pressure-volume relationship extracted from the synchrotron X-ray diffraction pattern showed that the phase transition of LaAs occurred at around 20 GPa.¹⁹ Similar transformations have also been observed in other rare earth family members, such as PrAs,²¹ NdAs,²¹ SmAs,²¹ and PrSb.²² Recently, Khalid et al.⁴ found that the hydrostatic pressure can induce the p–d crossing of LaAs, showing a topological phase transition at about 7 GPa. However, there are few studies on lanthanide phosphates LaX (X = P, As) under higher pressures.

The purpose of this work is to study the structural, dynamical, mechanical, thermodynamic properties and electronic structures of lanthanide phosphates LaX (X = P, As) under high pressures. Using CALYPSO method,^23,24 the structures of LaX (X = P, As) are investigated under pressures up to 100 GPa. It is found that the Fm3m-LaX (X = P, As) phases undergo structural phase transitions to P4/mmm-LaX (X = P, As) phases at lower pressure (19.04 GPa and 17.22 GPa). Moreover, two novel structural phases C2/m-LaP and Imma-LaAs have been proved to be the most stable structures under higher pressures.

2. Computation details

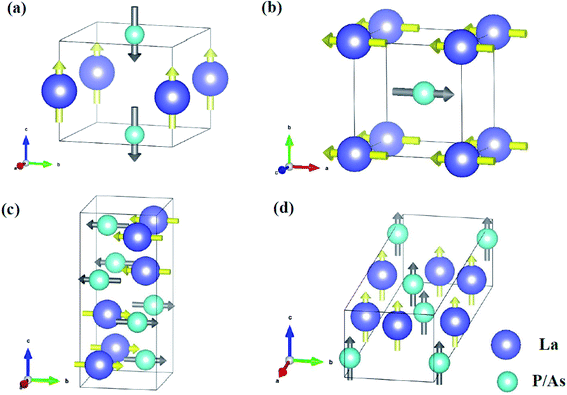
We search for the high-pressure structures of LaP and LaAs using the global structural optimization CALYPSO code with the particle-swarm optimization (PSO) algorithm,^23,24 which is not affected by any prior known structure information and has successfully predicted the high-pressure structures of different systems.^25–28 The calculations of structural relaxations, total-energy and electronic structure are carried out in the framework of density functional theory (DFT) with the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE)²⁹ exchange-correlation functional with the projector augmented wave (PAW)³⁰ method as implemented in Vienna ab initio simulation package (VASP).³¹ The plane-wave kinetic energy cutoff is set up to 800 eV, and the Brillouin zone sampling is performed by using k-grids with a spacing of 2π × 0.02 Å⁻¹. The convergence of the total energy and forces is 1 × 10⁻⁶ eV per atom and 0.01 eV Å⁻¹, respectively. The phonon calculations are carried out by applying the real-space supercell approach (finite-displacement) and density function perturbation theory (DFPT)³² implemented in the PHONOPY³³ program. The figures of crystal structures, atomic displacement patterns and electron localization function (ELF)^34,35 are produced using the VESTA software.

3. Results and discussion

3.1 Phase transition and structural properties

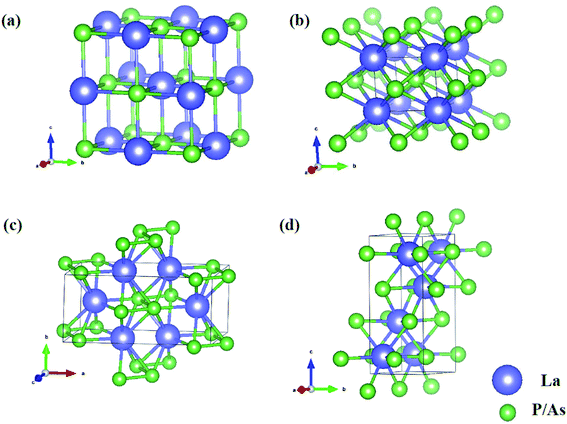
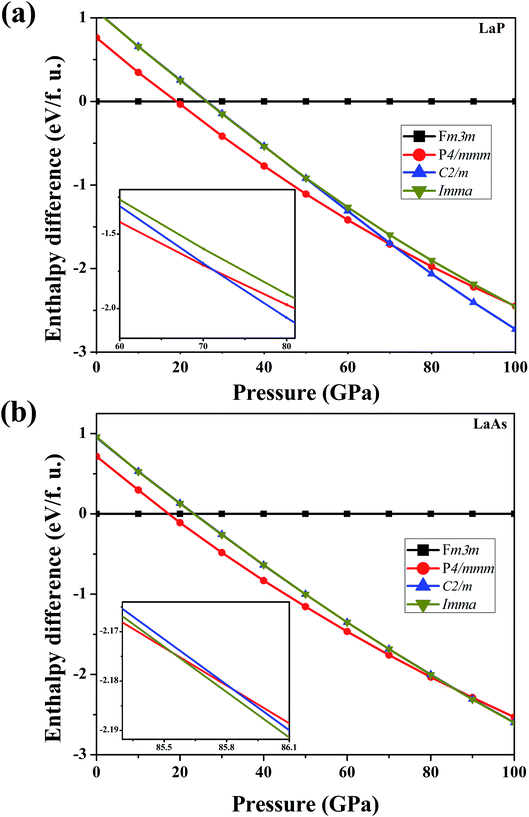
In order to determine the high-pressure crystal structures of LaX (X = P, As), we performed the crystal structures prediction in the pressure range of 0–100 GPa with simulation sizes from one to eight formula units (f.u.) per cell. The results showed that Fm3m-LaX (X = P, As) (Fig. 1a) are the most stable structures at 0 GPa and P4/mmm-LaX (X = P, As) (Fig. 1b) become the most stable structures at 50 GPa, consistent with the previous results,^{9,12,19,20,36,37} showing the reliability of our research. At the higher pressure of 100 GPa, two novel structures (C2/m-LaP and Imma-LaAs) are predicted, as shown in (Fig. 1c and d). The structural stability and other properties of them will be studied in the following.

Fig. 1 Crystal structures of (a) Fm3m-LaX (X = P, As) at 0 GPa; (b) P4/mmm-LaX (X = P, As) at 50 GPa; (c) C2/m-LaP at 100 GPa; (d) Imma-LaAs at 100 GPa. The purple and green spheres represent the La and P/As atoms, respectively.

To verify the stable phase at high pressure, the variations of enthalpy differences of LaP and LaAs with pressures are presented in Fig. 2. The relationships between volume and pressure are shown in Fig. 3. Our results show that, when the pressure increases, the cubic structures (Fm3m-LaP/LaAs) will be transformed into tetragonal structures (P4/mmm-LaP/LaAs). The corresponding phase transition pressures of LaP and LaAs are 19.04 GPa and 17.22 GPa, respectively, with the volume collapse are about 10.2% and 9.8%, which are consistent with other available researches.^19,20,37 In the inset of Fig. 2a and b, the enthalpy differences are additionally presented to show clearly the phase transition at higher pressures. It is found that the lowest enthalpies for LaP and LaAs are different. For LaP, C2/m has the lowest enthalpy, while for LaAs, the enthalpy of Imma is lower than that of C2/m, so C2/m is the most stable phase of LaP and Imma is the stable phase of LaAs at 100 GPa. The corresponding transformation pressures are 70.08 GPa and 85.53 GPa, and the changes in volume collapse are about 3.1% and 1.3%, respectively. Therefore, the sequence of phase transition is Fm3m → P4/mmm → C2/m for LaP and Fm3m → P4/mmm → Imma for LaAs, respectively.

Fig. 2 Calculated enthalpy differences of LaP (a) and LaAs (b) with respect to Fm3m-LaX (X = P, As) as functions of pressure range from 0 to 100 GPa. Insets show (a) enthalpy differences of LaP in the range of 60–80 GPa and (b) that of LaAs in the range of 85–86 GPa.

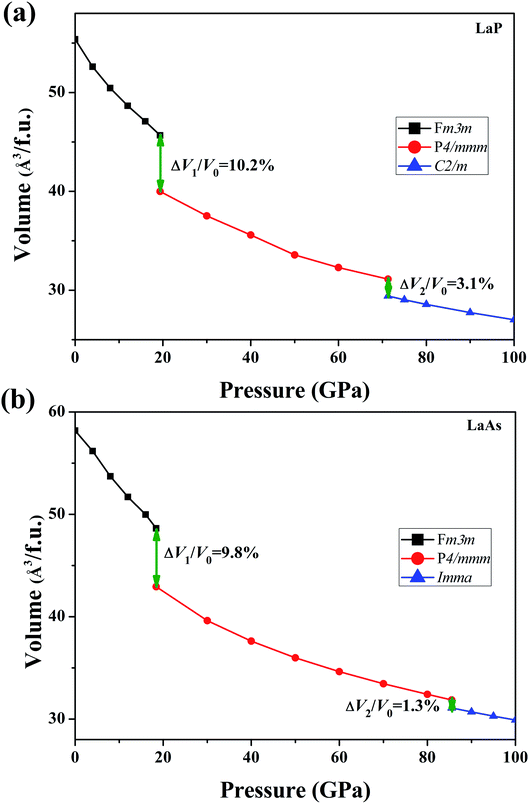Fig. 3 Calculated volumes as a function of pressure for (a) LaP and (b) LaAs, where V₀ represents the equilibrium volume of Fm3m-LaX (X = P, As).

The lattice parameters, atomic coordinates and relative formation enthalpies of the three phases at several pressures are listed in Table 1. The formation enthalpies are defined by ΔH = H(LaX) − H(La) − H(X), where X represents P and As atom, respectively. H is the enthalpy per formula unit of the most stable structure under a given pressure. The discussions of Fm3m structures of LaP and LaAs have been mentioned in our previous studies.^38,39 In the P4/mmm phase, which contains two atoms per primitive unit-cell, each La atom is surrounded by four P/As atoms. The bond lengths of La–P and La–As are 2.80 and 2.87 Å, respectively. The calculated lattice constants of LaP are a = 3.507 Å and c = 3.004 Å at 20 GPa, well consistent with the experimental value (a = 3.460 Å, c = 3.007 Å)¹⁶ and theoretical lattice constants (a = 3.530 Å, c = 3.059 Å calculated by Vaitheeswaran et al.,²⁰ a = 3.711 Å, c = 3.82 Å calculated by Charifi et al.¹²). The lattice constants of LaAs are a = 3.684 Å and c = 3.108 Å at 20 GPa, consistent well with the available experimental data (a = 3.625 Å, c = 3.06 Å)¹⁹ and other theoretical value (a = 3.645 Å, c = 3.171 Å).²⁰ Upon compression, the P4/mmm-LaP/LaAs are predicted to be the monoclinic structure C2/m for LaP and the orthorhombic structure Imma for LaAs. For the C2/m-LaP and Imma-LaAs structures, the obtained equilibrium lattice parameters are: a = 4.063 Å, b = 3.589 Å, c = 8.202 Å and a = 4.063 Å, b = 3.589 Å, c = 8.201 Å, respectively. We noticed that there is no experimental and theoretical information on the structural behavior of LaP and LaAs under high pressures. These results are of great significance for further understanding of the high-pressure characteristics of lanthanide phosphates.

Table 1 Calculated lattice parameters, atomic coordinates and formation enthalpy ΔH(eV per f.u.) of LaX (X = P, As)

LaP	Structures	Pressures	Lattice parameters (Å, deg.)	Atomic coordinates		ΔH
	Fm3m	0	a = b = c = 6.050	La	(0.000, 0.000, 0.000)	−2.026
			α = β = γ = 90	La	(0.000, 0.500, 0.500)
				La	(0.500, 0.000, 0.500)
				La	(0.500, 0.500, 0.000)
				P	(0.500, 0.500, 0.500)
				P	(0.500, 0.000, 0.000)
				P	(0.000, 0.500, 0.000)
				P	(0.000, 0.000, 0.500)
	P4/mmm	50	a = b = 3.407, c = 2.892	La	(0.000, 0.000, 0.500)	−0.863
			α = β = γ = 90	P	(0.500, 0.500, 0.000)
	C2/m	100	a = 4.063, b = 3.589, c = 8.202	La	(0.859, 0.500, 0.609)	−0.137
			α = β = 90, γ = 137	La	(0.141, 0.500, 0.391)
				La	(0.358, 0.000, 0.609)
				La	(0.641, 0.000, 0.391)
				P	(0.907, 0.000, 0.157)
				P	(0.093, 0.000, 0.843)
				P	(0.407, 0.500, 0.157)
				P	(0.593, 0.500, 0.843)

---

LaAs	Structures	Pressures	Lattice parameters (Å, deg.)	Atomic coordinates		ΔH
	Fm3m	0	a = b = c = 6.151	La	(0.500, 0.500, 0.500)	−1.846
			α = β = γ = 90	La	(0.500, 0.000, 0.000)
				La	(0.000, 0.500, 0.000)
				La	(0.000, 0.000, 0.500)
				As	(0.000, 0.000, 0.000)
				As	(0.000, 0.500, 0.500)
				As	(0.500, 0.000, 0.500)
				As	(0.500, 0.500, 0.000)
	P4/mmm	50	a = b = 3.506, c = 2.928	La	(0.000, 0.000, 0.000)	−0.686
			α = β = γ = 90	As	(0.500, 0.500, 0.500)
	Imma	100	a = 4.063, b = 3.589, c = 8.201	La	(0.000, 0.750, 0.872)	−0.255
			α = β = γ = 90	La	(0.500, 0.750, 0.628)
				La	(0.500, 0.250, 0.372)
				La	(0.000, 0.250, 0.128)
				As	(0.500, 0.250, 0.883)
				As	(0.000, 0.250, 0.617)
				As	(0.000, 0.750, 0.383)
				As	(0.500, 0.750, 0.117)

---

3.2 Elastic properties

Through the strain-stress method, we obtained the elastic constants C_ij of LaX (X = P, As) at different pressures, which are listed in Table 2. The positive values of the elastic constant matrix of LaAs at different pressures indicate that they are elastically stable. According to the criteria of crystal mechanical stability, if the elastic constants of each phase satisfy the generalized elastic stability criteria, they can be considered mechanically stable.⁴⁰ The mechanical stability criteria are as follows:⁴¹

Table 2 Calculated elastic constants (GPa) of LaX (X = P, As) at different pressures

	LaP			LaAs
	Fm3m (0 GPa)	P4/mmm (50 GPa)	C2/m (100 GPa)	Fm3m (0 GPa)	P4/mmm (50 GPa)	Imma (100 GPa)
C11	162.02	355.55	640.99	164.64	340.87	602.52
C22			646.96			452.63
C33		381.12	444.72		392.67	595.21
C44	33.65	105.32	373.69	29.46	100.68	232.98
C55			162.44			165.22
C66		199.68	251.30		207.64	308.71
C12	27.39	225.75	112.16	22.84	230.87	359.86
C13		158.09	199.50		159.31	124.87
C23			286.86			162.29
C14
C15			48.81
C25			−77.01
C35			35.48
C46			−53.87

---

For Fm3̄m structures:

C₁₁ > 0, C₄₄ > 0, C₁₁ > |C₁₂|, C₁₁ + 2C₁₂ > 0

For P4/mmm structures:

C₁₁ > |C₁₂|, 2C₁₃² < C₃₃ (C₁₁ + C₁₂), C₄₄ > 0, C₆₆ > 0

For Imma structures:

C₁₁ > 0, C₄₄ > 0, C₅₅ > 0, C₆₆ > 0, C₁₁C₂₂ > C₁₂², C₁₁C₂₂C₃₃ + 2C₁₂C₁₃C₂₃ − C₁₁C₂₃² − C₂₂C₁₃² − C₃₃C₁₂² > 0

For C2/m structures:

C₁₁ > 0, C₂₂ > 0, C₃₃ > 0, C₄₄ > 0, C₅₅ > 0, C₆₆ > 0, (C₂₂ + C₃₃) − 2C₂₃ > 0, (C₃₃C₅₅ − C₃₅²) > 0, (C₄₄C₆₆ − C₄₆²) > 0, C₁₁ + C₂₂ + C₃₃ + 2(C₁₂ + C₁₃ + C₂₃) > 0, C₂₂(C₃₃C₅₅ − C₃₅²) + 2C₂₃C₂₅C₃₅ − C₂₃²C₅₅ − C₂₅²C₃₃ > 0, 2[C₁₅C₂₅(C₃₃C₁₂ − C₁₃C₂₃) + C₁₅C₃₅(C₂₂C₁₃ − C₁₂C₂₃) + C₂₅C₃₅(C₁₁C₂₃ − C₁₂C₁₃)] − [C₁₅²(C₂₂C₃₃ − C₂₃²) + C₂₅²(C₁₁C₃₃ − C₁₃²) + C₃₅²(C₁₁C₂₂ − C₁₂²)] + C₅₅C₁₁C₂₂C₃₃ − C₁₁C₂₃² − C₂₂C₁₃² − C₃₃C₁₂² + 2C₁₂C₁₃C₂₃ > 0

It is found that the calculated elastic constants for LaX (X = P, As) (including C2/m-LaP) all satisfy the above conditions at pressure, confirming their mechanical stabilities. The calculated elastic constants for Fm3m-LaX (X = P, As) are basically consistent with the previous theoretical values.^9,42,43 For P4/mmm-LaX (X = P, As), the values of C₁₁ and C₃₃ are similar, indicating that they have an almost isotropic linear incompressibility. For the higher-pressure phases C2/m-LaP and Imma-LaAs, their elastic constants (C₁₁, C₂₂ and C₃₃) are larger than those of other phases, suggesting that they are more difficult to compress.

In addition to checking the mechanical stability, the elastic properties can also be used to explain various phenomena, such as inter-atomic potentials, phonon spectra, specific and thermal expansion.⁴⁴ Table 3 gives the results of bulk modulus B (GPa), shear modulus G (GPa), G/B ratio, Young's modulus E (GPa), Poisson's ratio and Vickers hardness H_v (GPa) of LaX (X = P, As). It can be seen that C2/m-LaP and Imma-LaAs possess the larger values of bulk, shear and Young's modulus, implying the potential hard properties. Our results show that P4/mmm-LaP and P4/mmm-LaAs exhibit ductility, and others are brittle. The type of the bonding can be measured by Poisson ratio (the threshold value of Poisson's ratio is 0.25,⁴⁵ the covalent bonding (ν < 0.25) corresponds to ionic materials and the ionic bonding (ν ≥ 0.25) corresponds to ionic materials. The Poisson's ratios of P4/mmm-LaX (X = P, As) and Imma-LaAs are larger than 0.25, suggesting that they are ionic crystals and the ionic bond component is dominant. While for the Poisson's ratio of C2/m-LaP, its small value implies that there are a lot of strong covalent bonds.

Table 3 Bulk modulus B (GPa), shear modulus G (GPa), G/B ratios, Young's modulus E (GPa), Poisson's ratios ν and Vickers hardness H_v (GPa) of LaX (X = P, As) at different pressures

LaP	B (GPa)	G (GPa)	G/B	E (GPa)	ν	Hv (GPa)
Fm3m	72.26	44.59	0.62	110.95	0.244	7.48
P4/mmm	241.51	111.61	0.46	290.00	0.289	9.79
C2/m	323.69	204.38	0.63	506.53	0.239	23.24

---

LaAs	B (GPa)	G (GPa)	G/B	E (GPa)	ν	Hv (GPa)
Fm3m	70.11	42.24	0.60	105.53	0.249	6.88
P4/mmm	241.43	107.23	0.44	279.95	0.292	8.92
Imma	324.10	186.17	0.57	468.76	0.259	19.24

---

The hardness can be estimated by Vickers hardness H_v proposed by Chen et al.⁴⁶ This empirical model is expressed as H_v = 2(k²G)^0.585 − 3 (where H_v is the Vickers hardness, G is the shear modulus, and k is the value of G/B), which has been successfully applied to a wide range of material systems.^47–51 For C2/m-LaP and Imma-LaAs, the hardness values are 23.24 GPa and 19.24 GPa, respectively. The hardness are much higher than those of other phases. Especially for C2/m-LaP phase whose hardness is similar to those of ReB₂ (ref. ⁵²) and WB₂,²⁷ indicating that it is a potential hard material.

For engineering materials, elastic anisotropy is an important factor affecting their applications. Fig. 4 shows the direction dependence of the Young's modulus for LaX (X = P, As) and the corresponding slice in the xy, yz, xz planes. The cubic phases of LaP and LaAs exhibit the isotropic Young's modulus. It can be seen that the anisotropy of Young's modulus of LaP-P4/mmm and LaAs-P4/mmm is basically the same. Structural anisotropy can cause the orientation difference of these compounds. The maximum values of Young's modulus are 625 GPa along xy plane for C2/m-LaP and 536 GPa along yz plane for Imma-LaAs. Accordingly, their minimum values are 388 GPa and 312 GPa, respectively. The ratios of E_max/E_min are 1.61 and 1.72, respectively, indicating the comparable anisotropy of Young's modulus.

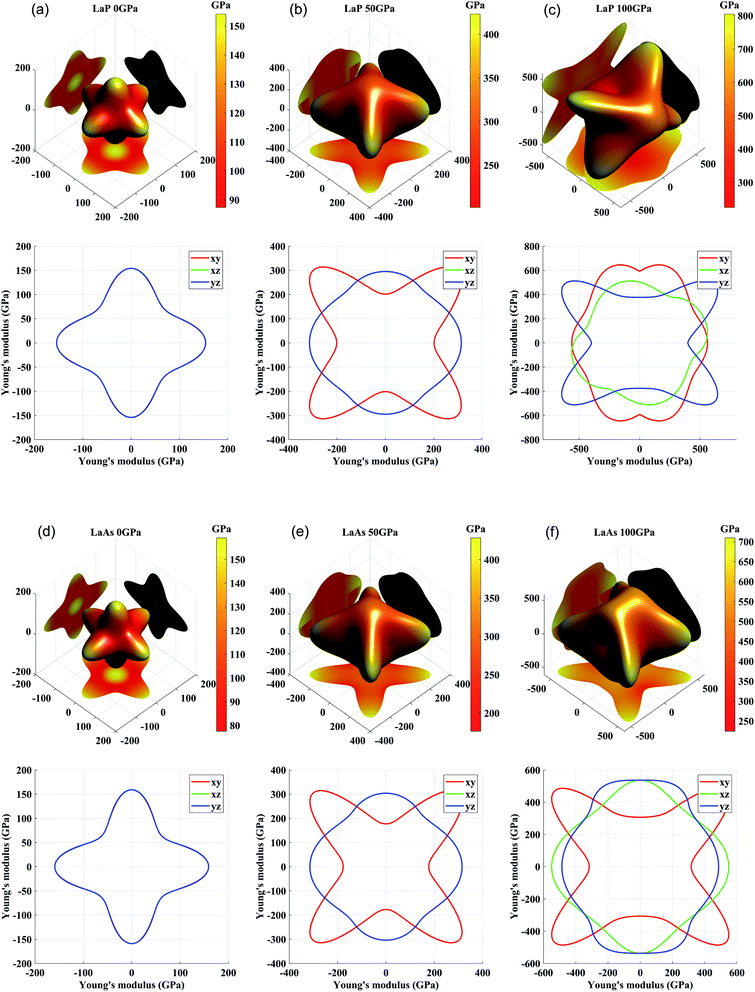Fig. 4 Three-dimensional and two-dimensional surface representations of Young's modulus for (a) LaP-Fm3m, (b) LaP-P4/mmm, (c) LaP-C2/m, (d) LaAs-Fm3m, (e) LaAs-P4/mmm, and (f) LaAs-Imma.

3.3 Lattice dynamic properties

To confirm their dynamical stabilities, we calculated a series of phonon dispersion curves of stable structures at different pressures. Through our previous researches,^38,39 it has been proved that Fm3m-LaP and Fm3m-LaAs are stable at 0 GPa, and the phonon spectra have no imaginary frequency. The phonon spectra of the P4/mmm-LaP and P4/mmm-LaAs at 50 GPa and C2/m-LaP and Imma-LaAs at 100 GPa are shown in Fig. 5. There are no imaginary phonon frequencies in the all considered structures, indicating these phases are all dynamically stable. Because of the structural similarity of LaP and LaAs at 50 GPa, their phonon spectra are generally similar. However, due to the different atomic weights of La and P atoms, there are phonon gaps in the phonon spectra of LaP. It can be seen from the phonon DOS that the vibrations of La and P are completely decoupled in P4/mmm-LaP and C2/m-LaP, and the main contribution of acoustic branches comes from La atoms, while the high-frequency branches mainly correspond to the P/As atoms.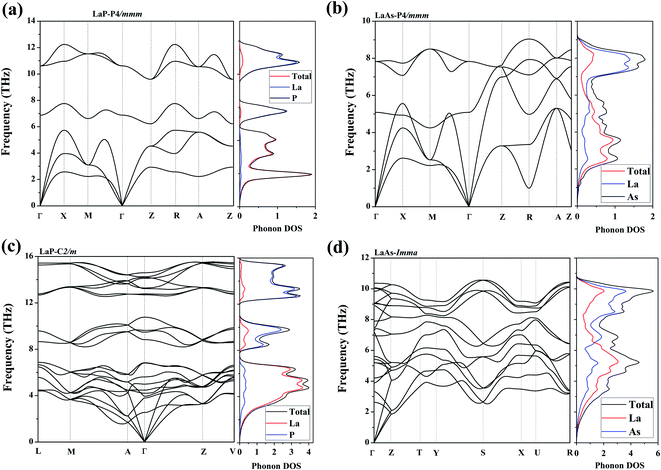

Fig. 5 Phonon dispersions and the total and partial phonon density of states (DOSs) for (a) LaP-P4/mmm, (b) LaAs-P4/mmm, (c) LaP-C2/m and (d) LaAs-Imma.

Phonon velocities are closely related to the phonon transportation, the phonon velocities of LaX (X = P, As) at different pressures are obtained from the phonon dispersions. The two phonon velocities (v_p is the phase velocity and v_g is the group velocity) are defined as:^53,54 ν_p = ω(k)/k,ν_g = ∇_kω(k), where k is the distance between two points in the Brillouin zone, ω(k) is the dispersion relation. Considering the anisotropy of P4/mmm-LaP and P4/mmm-LaAs, Fig. 6a–d shows the phonon phase velocities and group velocities along [100] and [001] directions. As we can see, the phase velocities of optical branches are much larger than those of acoustic modes, but in contrast, the group velocities of acoustic branches are about three times as large as those of optical branches. This phenomenon can also be found in the phonon velocities of C2/m-LaP and Imma-LaAs, as shown in the Fig. 6e and f. These results can be understood from the equations of phase velocity and group velocity. The phase velocity is directly proportional to the phonon frequency, and the phase velocities of the optical branches are larger than those of the acoustic branches because of their larger phonon frequencies. While the group velocities are obtained from the slope of the phonon dispersion, and the acoustic branches are steeper near the Γ point, so their group velocities are larger than those of the optical branches.

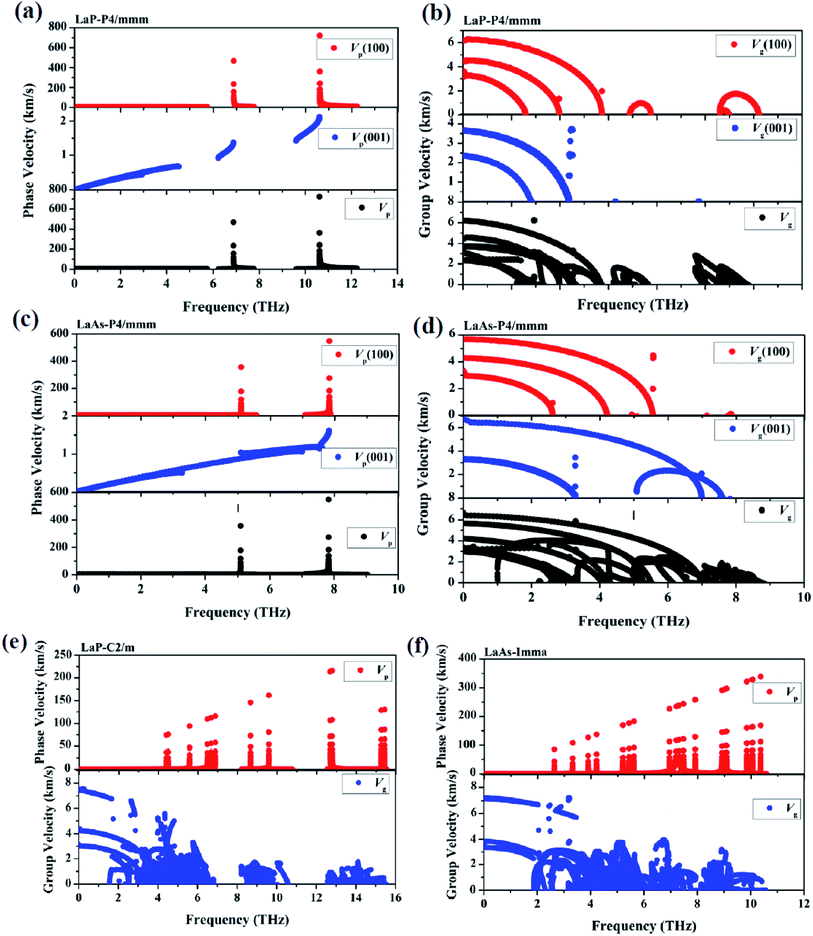Fig. 6 The calculated phonon phase velocities and group velocities of LaP-P4/mmm (a) and (b), LaAs-P4/mmm (c) and (d), LaP-C2/m (e) and LaAs-Imma (f).

Fig. 7 shows the atomic displacements of LaP and LaAs at different pressures. The displacements of La and P/As atoms are indicated by yellow and grey arrows, respectively. For P4/mmm-LaP/LaAs, the vibration direction of La atom is opposite to that of P/As atoms. For Imma-LaAs, the structure is a layered along the c direction. The two adjacent layers are composed of the same atoms, forming a folded layered structure. The vibration directions of different atoms in each layer are opposite. The most intricate one is LaP-C2/m, similar to the combination of two interactive vibrations. We assume that the primitive cell is divided into left and right parts along the b axis, and the vibration direction of different atoms in each part is different.

Fig. 7 Main atomic displacements of (a) P4/mmm-LaP, (b) P4/mmm-LaAs, (c) LaP-C2/m and (d) LaAs-Imma. The displacements of La and P/As atoms are indicated by yellow and grey arrows, respectively.

3.4 Electronic structure

Electronic properties play a key role in the study of other properties of solid materials.^55–57 Fig. 8 presents the density of state (DOS) over their stable pressure ranges. From the calculated DOS curves, we can see that P4/mmm-LaX (X = P, As), C2/m-LaP and Imma-LaAs all exhibit metallic characteristics, confirmed by the non-zero electronic DOS at the Fermi level. It is obvious that the DOS near Fermi level is mainly composed of La-d states mixed with La-f and P/As-p, while the contributions of La-p and P/As-s states are mainly located far away from the Fermi level. For P4/mmm-LaX (X = P, As) structures, it is notable that P/As-p orbital is the main supplier in the energy range of −7–0 eV, while from 0–3 eV, the DOS is mainly dominated by the La-d orbital. The allopatric distribution of P/As-p and La-d may be responsible for the lower hardness of the two tetragonal phases. For C2/m-LaP, the peaks of La-d/f and P-p orbitals overlap from −3–3 eV, indicating that there is strong hybridization between La and P atoms, which is regarded as covalent bonds nature. While for Imma-LaAs, the peaks overlap becomes fewer, which means that the covalent bond becomes weaker.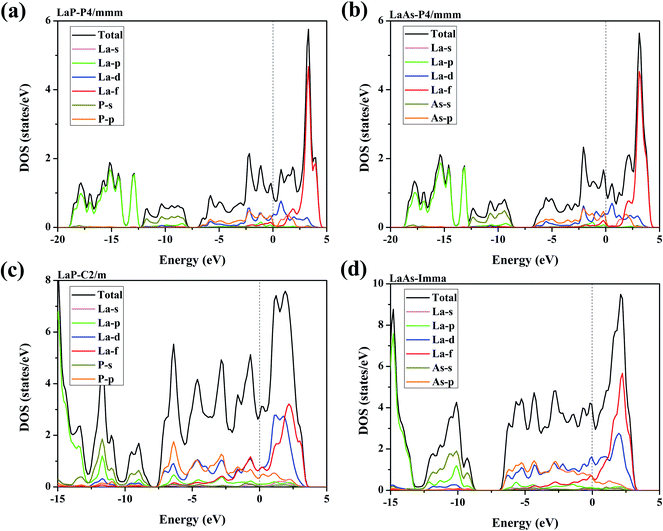

Fig. 8 Calculated total and projected DOS for (a) LaP-P4/mmm, (b) LaAs-P4/mmm, (c) LaP-C2/m and (d) LaAs-Imma. The vertical dash lines represent the Fermi level.

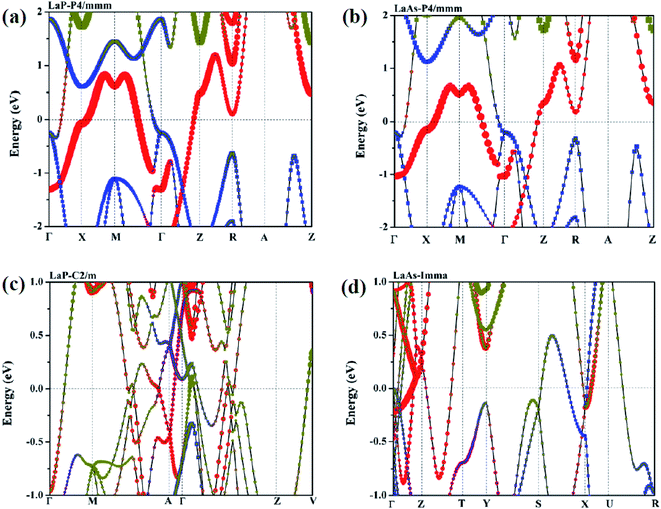
In order to further explore the contribution of each orbit near Fermi level, Fig. 9 presents the projected band structures of LaX with the spectral weight of La-f, La-d orbitals and P/As-p orbitals. The results also demonstrate the metallic characteristics of these high-pressure structures due to the absence of the band gap at the Fermi level. The observation of the projected band structures shows that P4/mmm-LaP and P4/mmm-LaAs have similar electronic distributions near Fermi level, which is in good agreement with the results of density of state (DOS). The valence band is mainly composed of mixed states of P/As-p and La-d states, while the conduction band is mainly composed of La-d states with a significant contribution from La-f and P/As-p states. For the C2/m-LaP and Imma-LaAs, their band structures remain metallic; however, the contributions of La-f orbitals near the Fermi surface are larger than those of P4/mmm-LaP and P4/mmm-LaAs.

Fig. 9 Calculated projected band structures for (a) LaP-P4/mmm, (b) LaAs-P4/mmm, (c) LaP-C2/m and (d) LaAs-Imma. The red and yellow bubbles represent the contributions of La-d and La-f orbitals. The blue squares represent the contributions of P/As-p orbitals.

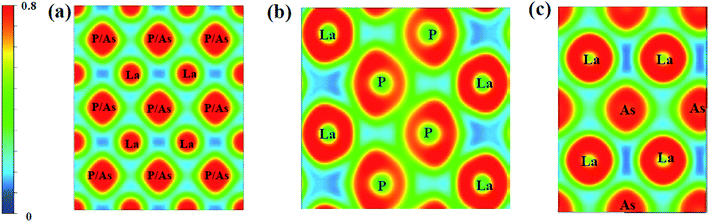
To further study the chemical bonds properties of the La–P/As combinations, the electronic localization function (ELF) of LaX (X = P, As) are calculated as depicted in Fig. 10, which can imply the localizing degree of electrons in the certain regions.⁵⁸ ELF values can provide useful information about the chemical bonding properties by qualitatively defining the bonding nature to iconicity, covalency or metallicity.⁴⁴ The localizing degree of electrons in the related regions gradually increases from 0 to 1. It can be seen that the electronic localization function of P4/mmm-LaX (X = P, As) gradually changes between La and As/P atoms, which means there exist P–P covalent bonds and La–P ionic bonds. In the Fig. 10b and c, the electronic localization function for C2/m-LaP and Imma-LaAs are similar, while the overlap of electronic localization function for La–P and P–P atoms in C2/m-LaP is much larger in Imma-LaAs. This indicates the La–P ionic bonds and P–P covalent bonds in LaP-C2/m are stronger, that is to say, C2/m-LaP has larger bonding strength, so the hardness is higher than other phases. The results of electronic localization function of each phase of LaX are consistent with the analysis of density of states. The bonding strength and the proportion of the covalent play a key role in the incompressibility and hardness of the compounds.

Fig. 10 Electron localization function of LaX (X = P, As) in (100) plane at different pressures: (a) LaP-P4/mmm and LaAs-P4/mmm at 50 GPa, (b) LaP-C2/m at 100 GPa, (c) LaAs-Imma at 100 GPa, respectively.

4. Conclusions

In summary, the CALYPSO is used to search the possible structures of LaX (X = P, As) under pressures up to 100 GPa. We have predicted two novel high-pressure phases of lanthanide phosphates LaP and LaAs in the pressure range of 0–100 GPa. The phase transition, mechanical, thermodynamic properties, and electronic structures of these compounds are further studied by first principles. The predicted phase transition sequence of LaP is Fm3m → P4/mmm → C2/m with transition pressures of 19.04 GPa and 70.08 GPa, and the phase transition sequence of LaAs is Fm3m → P4/mmm → Imma with transition pressures of 17.22 GPa and 85.53 GPa. The calculations of phonon dispersions, elastic constants and formation enthalpies showed that these phases are stable. According to the elastic properties, we have evaluated the hardness values of C2/m-LaP and Imma-LaAs are 23.24 and 19.24 GPa, respectively, indicating that they are potential hard materials. In addition, the electronic properties of these compounds at dominating pressures are also investigated to explore the intrinsic chemical bonding characteristics and to find out the reason for their higher hardness. These results are of great significance for further understanding of the high-pressure characteristics of the rare earth phosphates and for providing guidance of the applications in modern industry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 12074274), the NSAF (Grant No. U1830101), and the Science Challenge Project (Grant No. TZ2016001). We also acknowledge the support for the computational resources by the State Key Laboratory of Polymer Materials Engineering of China in Sichuan University.

References

1. G. A. Prinz, Science, 1999, 283, 330.
2. S. S. Sun, Q. Wang, P. J. Guo, K. Liu and H. C. Lei, New J. Phys., 2016, 18, 082002.
3. M. Zhang, X. Q. Wang, A. Rahman, R. C. Dai, Z. P. Wang and Z. M. Zhang, Phys. Rev. B, 2020, 101, 064106.
4. S. Khalid, A. Sharan and A. Janotti, Phys. Rev. B, 2020, 101, 125105.
5. Y. Wu, T. Kong, L. L. Wang, D. D. Johnson, D. X. Mou, L. N. Huang, B. Schrunk, S. L. Bud'ko, P. C. Canfield and A. Kaminski, Phys. Rev. B, 2016, 94, 081108.
6. L. Petit, Z. Szotek, M. Luders and A. Svane, J. Phys.: Condens. Matter, 2016, 28, 223001.
7. H. Y. Yang, T. Nummy, H. Li, S. Jaszewski, M. Abramchuk, D. S. Dessau and F. Tafti, Phys. Rev. B, 2017, 96, 235128.
8. F. F. Tafti, Q. D. Gibson, S. K. Kushwaha, N. Haldolaarachchige and R. J. Cava, Nat. Phys., 2016, 12, 272–277.
9. M. Shoaib, G. Murtaza, R. Khenata, M. Farooq and R. Ali, Comput. Mater. Sci., 2013, 79, 239–246.
10. A. Svane, V. Kanchana, G. Vaitheeswaran, G. Santi, W. M. Temmerman, Z. Szotek, P. Strange and L. Petit, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71.
11. F. Hulliger and H. R. Ott, J. Less-Common Met., 1977, 55, 103–113.
12. Z. Charifi, A. H. Reshak and H. Baaziz, Solid State Commun., 2008, 148, 139–144.
13. G. Vaitheeswaran, V. Kanchana and M. Rajagopalan, Phys. B, 2002, 315, 64–73.
14. Y. S. Kwon, M. Takeshige, T. Suzuki and T. Kasuya, Phys. B, 1990, 163, 328–330.
15. H. M. Tütüncü, S. Bagci and G. P. Srivastava, J. Phys. Condens. Matter, 2007, 19, 156207.
16. T. Adachi, I. Shirotani, J. Hayashi and O. Shimomura, Phys. Lett. A, 1998, 250, 389–393.
17. A. Hasegawa, J. Phys. Soc. Jpn., 1985, 54, 677–684.
18. Y. Kaneta, O. Sakai and T. Kasuya, Phys. B, 1993, 186–88, 156–158.
19. I. Shirotani, K. Yamanashi, J. Hayashi, N. Ishimatsu, O. Shimomura and T. Kikegawa, Solid State Commun., 2003, 127, 573–576.
20. G. Vaitheeswaran, V. Kanchana and M. Rajagopalan, J. Alloys Compd., 2002, 336, 46–55.
21. I. Shirotani, K. Yamanashi, J. Hayashi, Y. Tanaka, N. Ishimatsu, O. Shimomura and T. Kikegawa, J. Phys.: Condens. Matter, 2001, 13, 1939–1946.
22. G. Vaitheeswaran, L. Petit, A. Svane, V. Kanchana and M. Rajagopalan, J. Phys.: Condens. Matter, 2004, 16, 4429–4440.
23. Y. C. Wang, J. A. Lv, L. Zhu and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
24. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
25. Y. M. Chen, H. Y. Geng, X. Z. Yan, Y. Sun, Q. Wu and X. R. Chen, Inorg. Chem., 2017, 56, 3867–3874.
26. J. J. Wang, G. L. Sun, P. L. Kong, W. G. Sun, C. Lu, F. Peng and X. Y. Kuang, Phys. Chem. Chem. Phys., 2017, 19, 16206–16212.
27. H. Y. Zhang, F. Xi, Z. Y. Zeng, X. R. Chen and L. C. Cai, J. Phys. Chem. C, 2017, 121, 7397–7403.
28. C. Z. Zhang, G. L. Sun, J. J. Wang, C. Lu, Y. Y. Jin, X. Y. Kuang and A. Hermann, ACS Appl. Mater. Interfaces, 2017, 9, 26169–26176.
29. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
30. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
31. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
32. X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368.
33. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
34. A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. Vonschnering, Angew. Chem., Int. Ed., 1992, 31, 187–188.
35. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
36. X. Z. Yan, Y. M. Chen, X. Y. Kuang and S. K. Xiang, J. Appl. Phys., 2014, 116, 083707.
37. A. H. Reshak, Z. Charifi and H. Baaziz, J. Phys.: Condens. Matter, 2008, 20, 325207.
38. Y. Zhou, Y. Cheng, X. R. Chen, C. E. Hu and Q. F. Chen, Philos. Mag., 2018, 98, 1900–1918.
39. Y. Zhou, W. L. Tao, Z. Y. Zeng, X. R. Chen and Q. F. Chen, J. Appl. Phys., 2019, 125, 045107.
40. F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
41. Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
42. E. Deligoz, K. Colakoglu, Y. O. Ciftci and H. Ozisik, J. Phys.: Condens. Matter, 2007, 19, 436204.
43. G. Pagare, S. P. Sanyal and P. K. Jha, J. Alloys Compd., 2005, 398, 16–20.
44. L. Chen, J. L. Xu, M. G. Zhang, Z. R. Wen and Z. Y. Jiang, J. Alloys Compd., 2020, 813, 152246.
45. J. Haines, J. M. Leger and G. Bocquillon, Annu. Rev. Mater. Res., 2001, 31, 1–23.
46. X. Q. Chen, H. Y. Niu, D. Z. Li and Y. Y. Li, Intermetallics, 2011, 19, 1275–1281.
47. A. Misra and W. Y. Ching, Sci. Rep., 2013, 3, 1488.
48. X. Q. Chen, H. Y. Niu, C. Franchini, D. A. Z. Li and Y. Y. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 121405.
49. H. Y. Gou, Z. P. Li, L. M. Wang, J. Lian and Y. C. Wang, AIP Adv., 2012, 2, 012171.
50. Y. C. Liang, Y. P. Gou, X. Yuan, Z. Zhong and W. Q. Zhang, Chem. Phys. Lett., 2013, 580, 48–52.
51. M. G. Zhang, H. Y. Yan and Q. Wei, J. Alloys Compd., 2019, 774, 918–925.
52. X. F. Hao, Y. H. Xu, Z. J. Wu, D. F. Zhou, X. J. Liu, X. Q. Cao and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224112.
53. Y. C. Ding and B. Xiao, RSC Adv., 2015, 5, 18391–18400.
54. X. Feng, J. W. Xiao, R. Melnik, Y. Kawazoe and B. Wen, J. Chem. Phys., 2015, 143, 104503.
55. M. H. Zhang, X. L. Chen, W. X. Ji, P. J. Wang, Y. Min and C. W. Zhang, Appl. Phys. Lett., 2020, 116, 172105.
56. A. N. Ma, S. S. Li, S. F. Zhang, C. W. Zhang, W. X. Ji, P. Li and P. J. Wang, Phys. Chem. Chem. Phys., 2019, 21, 5165–5169.
57. S. Q. Feng, Y. Yang, F. Guo, L. Su, X. R. Cheng, C. S. Yuan and K. Yang, J. Alloys Compd., 2020, 844, 156098.
58. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.

---