Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Designing bioinspired green nanosilicas using statistical and machine learning approaches†
Luc
Dewulf
,
Mauro
Chiacchia‡
,
Aaron S.
Yeardley
,
Robert A.
Milton
,
Solomon F.
Brown
 and
Siddharth V.
Patwardhan
and
Siddharth V.
Patwardhan
 *
*
Department of Chemical and Biological Engineering, University of Sheffield, Mappin Street, Sheffield S1 3JD, UK. E-mail: s.patwardhan@sheffield.ac.uk
First published on 4th March 2021
Abstract
The in vitro bioinspired synthesis of silica, inspired from in vivo biosilicification, is a sustainable alternative to the conventional production of high value porous silicas. The short reaction time, mild reaction conditions of room temperature and its use of benign precursors make this an eco-friendly, economical and scalable route with great industrial potential. However, a systematic optimisation of critical process parameters and material attributes of bioinspired silica is lacking. Specifically, statistical approaches such as design of experiments (DoE) and global sensitivity analysis (GSA) using machine learning could be highly effective but have not been applied to this “green” nanomaterial yet. Herein, for the first time, a sequential DoE strategy was developed with pre-screening experiments to outline the feasible design space. A successive screening using 23 full factorial design determined that from the initially investigated three factors (the ratio of the reactant concentrations, pH, and precursor concentration), only the first two were statistically significant for silica yield and surface area. The subsequent concatenated optimisation using central composite design located a maximum yield of 90 mol% and a maximum surface area of 300–400 m2 g−1. Since for successful commercialisation, high yields and large specific surface areas are desirable, their simultaneous optimisation was also achieved with high predictability regression models. For complementation, a variance-based GSA was successfully applied to bioinspired silica for the first time. This method rapidly identified key parameters and interactions that control the physicochemical properties and provided insights in the wide parameter space, which was validated by the extensive DoE campaign. This work is the starting point in holistically modelling the multidimensional factor–response relationship over a large experimental space in order to complement efforts for resource-efficient product and process development and optimisation of bioinspired silica and beyond.
Design, System, ApplicationDespite many studies on bioinspired silica and its vast potential in many applications, efforts for a systematic optimisation of its properties, such as the silica yield and surface area, have been missing. Given the lack of clarity over the factor–response relationship, the tailored synthesis of silica towards ideal process parameters and desired material attributes has been held back, which in turn has been a barrier to its production, despite its potential to provide sustainable manufacturing of high-value porous nanomaterials. This work integrated design of experiments and machine learning tools, harnessing the capabilities of both techniques that have been identified as a research frontier for inorganic materials synthesis. The application of a novel sequential strategy, presented in this manuscript, in combination with a machine learning approach to bioinspired silica is of significant novelty. Employing this unique DoE strategy in combination with multivariate analysis enabled constructing reliable models with good predictability. Machine learning using the Sobol' index was successfully applied to bioinspired silica for the first time. This work is the starting point in holistically modelling the complex multidimensional synthesis of bioinspired silica to complement sustainable and resource-efficient product and process optimisation and development of this nanomaterial. |
1. Introduction
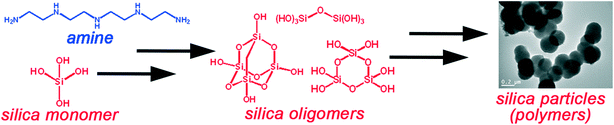
Silica is amongst the top traded commodity chemicals worldwide,1,2 and it is the most mass-produced nanomaterial both in Europe and worldwide3,4 for applications in pharmaceuticals, cosmetics, foodstuffs and coatings to name a few sectors. The bottom-up synthesis of silica nanomaterials, from smaller molecules to structures of 1 to 100 nm, has prominent examples such as the MCM-41, SBA-15 and Stöber silicas, which however require harsh synthesis conditions such as high temperatures, toxic solvents and reagents of high purity and cost.5,6 The drive for greener yet economical silica nanomaterials calls for a paradigm shift away from conventional manufacturing routes.One particular technique of sustainable silica production was inspired by the 550 million-year-old biosilicification process producing diatoms (microalgae) of well-defined structures in nature. This is achieved by using highly-specialised organic biomolecules, especially amines, that act as catalysts, templates, and scaffolds.7,8 Learning from biology, bioinspired silica synthesis has been developed by us and others as a hybrid sol–gel/precipitation route that mimics the natural silicification process and employs the same or structurally similar reactants.9 Specifically, in bioinspired silica synthesis, an amine additive is dissolved in water together with a silicon source, which in solution is present as silica monomers (Fig. 1). Addition of acid then causes the monosilicic acid to condense and polymerise to form oligomers, which subsequently undergo growth and maturation to a solid silica “polymer” that precipitates. This method has been extensively reported and reviewed elsewhere;2,6,8,10,11 below a brief summary of investigations relevant to the optimisation and modelling of this synthesis is provided.
Recent investigations sought to gain a better understanding of this chemistry and the relationship between reaction conditions (factors) and materials physicochemical properties (responses) in order to optimise the bioinspired silica synthesis in a twofold way. On the one hand, for developing commercial products with profitability, critical process parameters need to be maximised. Although rarely appraised in this area of research, the yield has been identified as a crucial measure, and for this type of silica it is conventionally expressed as the molar percentage of elemental silicon in the final polymeric silica product (mol%).12 On the other hand, optimisation must enable control of critical materials attributes, such as its porosity, so as to manufacture silica with predictable properties and consistent quality. Porosity is a key parameter for most porous nanomaterials where a material's specific surface area is used commonly.13,14
Previous literature found that properties of bioinspired silica depended on multiple synthesis parameters such as the pH, the type of amine additive, the type of silicon precursor, the ratio of the concentrations of the silicon precursor and amine additive (Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N), the reagent concentration ([Si]), and the reaction time, amongst others.11 Generally, the silica yield increased from initially 0 to 100 mol% with decreasing Si
N), the reagent concentration ([Si]), and the reaction time, amongst others.11 Generally, the silica yield increased from initially 0 to 100 mol% with decreasing Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio and increasing reaction time.15–17 Small straight chain amines such as tetraethylenepentamine (TEPA), as well as polymeric ones such as poly(ethylene imine) (PEI) were found to produce yields of around 50 mol%.11,18 Annenkov et al. investigated how two different sizes of poly(vinyl amine) (PVA) affected the concentration of silicic acid monomers over a certain time range15 and their results showed that the initial silicic acid concentration decreased with increasing reaction time. Although, a direct correlation to the yield could not be established, the data suggests that the yield generally increased with increasing reaction time.
N ratio and increasing reaction time.15–17 Small straight chain amines such as tetraethylenepentamine (TEPA), as well as polymeric ones such as poly(ethylene imine) (PEI) were found to produce yields of around 50 mol%.11,18 Annenkov et al. investigated how two different sizes of poly(vinyl amine) (PVA) affected the concentration of silicic acid monomers over a certain time range15 and their results showed that the initial silicic acid concentration decreased with increasing reaction time. Although, a direct correlation to the yield could not be established, the data suggests that the yield generally increased with increasing reaction time.
The silica yield response, studied by Patwardhan and Perry,16 observed that the silica yield increased with reaction time. As the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio and [Si] were changed simultaneously, no conclusions could be drawn for those two factors individually, apart from a 100 mol% silica yield at 5 min reaction time, regardless of the factor levels. Manning et al. investigated how the silica yield changed when the type of additive and the reaction pH were both varied.11 They found that the amount of coagulated silica decreased from 66 to 47 mol% when decreasing the pH from 7 to 6.65.
N ratio and [Si] were changed simultaneously, no conclusions could be drawn for those two factors individually, apart from a 100 mol% silica yield at 5 min reaction time, regardless of the factor levels. Manning et al. investigated how the silica yield changed when the type of additive and the reaction pH were both varied.11 They found that the amount of coagulated silica decreased from 66 to 47 mol% when decreasing the pH from 7 to 6.65.
Unlike yield, the Brunauer–Emmett–Teller (BET) surface area13 has been widely reported. Short chain and polymeric amines produced a range of surface areas from 10 to 700 m2 g−1.19,20 However, the BET surface area generally decreased with increasing mixing time, whereas the yield increased with reaction time, highlighting a typical optimisation problem whereby the best compromise between different responses must be found.21,22 Belton et al. reported the BET surface area of bioinspired silica which was prepared by varying a range of factors.21–23 They found that the surface area reduced (e.g. from ∼700 to 400 m2 g−1 or even to 0 m2 g−1) with either increasing additive length (with or without changing the amines per molecule) or decreasing Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio. As the three factors (amine type, reaction time, and silicon to nitrogen ratio) were investigated one-factor-at-a-time (OFAT), it was not possible to estimate how the surface area varied with a simultaneous change in all three factors. Many other studies on bioinspired silica did not investigate the BET surface area as their focal point and therefore only reported individual values, which is insufficient to develop predictive models.
N ratio. As the three factors (amine type, reaction time, and silicon to nitrogen ratio) were investigated one-factor-at-a-time (OFAT), it was not possible to estimate how the surface area varied with a simultaneous change in all three factors. Many other studies on bioinspired silica did not investigate the BET surface area as their focal point and therefore only reported individual values, which is insufficient to develop predictive models.
Other parameters such as the pH and [Si], which have known influences on the kinetics, reaction mechanism and silica formation pathways24 were generally kept constant within and between different studies and thus the effect of those factors and the impact of the interplay between them on the yield and BET surface area remains unknown. Table 1 summarises recent literature on the optimisation of bioinspired silica. It reveals that studies were unsuccessful in holistically optimising silica by accounting for multiple factors, as the experiments were unsystematic and also did not attempt to optimise several responses simultaneously. Moreover, previous studies aimed to gain a qualitative understanding and experiments were carried out in an OFAT or univariate way. This is likely due to a complex nature of the parameter space and interdependencies, which in turn is a barrier to unlock the potential of bioinspired silica. As such an empirical quantitative understanding can be gained by more systematic experimentation.
| Additivea | Si precursorb | Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N (mol mol−1) N (mol mol−1) |
pH | [Si] (mM) | Time (min) | Observation | Ref. |
|---|---|---|---|---|---|---|---|
| a PVA-238 = poly(vinyl amine) 238 units, PVA-1100 = poly(vinyl amine) 1100 units, PEHA = pentaethylenehexamine, PEI = poly(ethylene imine), PDPA23–PDMA68 = poly(2-(diisopropyl-amino)ethyl methacrylate)-block-2-(dimethylamino)ethyl methacrylate, TETA = triethylenetetramine, DETA = diethylenetriamine, MEDA = monoethylenediamine, SPDN = spermidine, SPN = spermine, TEPA = tetraethylenepentamine, DA4 = 1,4-diaminobutane, DA6 = 1,6-diaminohexane, DA8 = 1,8-diaminooctane, DA10 = 1,10-diaminodecane, propylamines = N,N′-(bis-3-diaminopropyl)-1,3-diaminopropanes. b Na2SiO3·9H2O = sodium metasilicate nonahydrate, TMOS = tetramethyl orthosilicate, Na2SiO3·5H2O = sodium metasilicate pentahydrate, SiCat = dipotassium tris(1,2-benzenediolato-O,O′)silicate. c Not available or could not be calculated from the data provided. | |||||||
| Silica yield | |||||||
| PVA-238, PVA-1100 | Na2SiO3·9H2O | 1.5 | 10 | 10 | 0–1440 | n/ac | 15 |
| PEHA | Na2SiO3·9H2O | 0.5, 1, 2 | 6.5, 7 | 20–40 | 0–5 | Max 100 mol% | 16 |
| PEI | TMOS | n/ac | n/ac | 2.3 | 40 | 12–15 mol% | 26 |
| PDPA23–PDMA68 | TMOS | 1057 | 7.2 | 185 | 20 | 58 mol% | 18 |
| PEHA, TETA, DETA, PEI | Na2SiO3·5H2O | 1 | 7 | 30 | 5 | 47–66 mol% | 27 |
| Silica BET surface area | |||||||
| MEDA, DETA, SPDN, TETA, SPN, TEPA, PEHA | SiCat, TMOS | 1.7–0.08 | 7 | 30 | 1440–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 080 |
0–700 m2 g−1 | 21 |
| MEDA, DA4, DA6, DA8, DA10 | SiCat | 1 | 6.8 | 30 | 1440–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 080 |
400–700 m2 g−1 | 22 |
| Poly(ethylene amine), propylamine | SiCat | 1 | 6.8 | 30 | 1440 | 0–650 m2 g−1 | 23 |
| TETA, TEPA, PEHA | Na2SiO3·5H2O | 1 | 7 | 30 | 5 | 12.8–15.6 m2 g−1 | 19 |
| DETA, TETA, TEPA, PEHA | Na2SiO3·5H2O | 1 | 7 | 30 | 2 | 19–37 m2 g−1 | 28 |
| PEHA | Na2SiO3·5H2O | 2 | 7 | 30 | 5 | 45 m2 g−1 | 12 |
| PEHA | Na2SiO3·5H2O | 1 | 2–7 | 30 | 5 | 30–300 m2 g−1 | 29 |
| PEI | TMOS | n/ac | n/ac | 2.3 | 40 | 71 m2 g−1 | 26 |
Beyond bioinspired silica, conventional types of silica nanomaterials were previously successfully developed using organised statistical approaches, in particular design of experiments (DoE), which allows product and process optimisation by sound mathematical evidence. As part of the DoE framework, efficient designs determine the combination of synthesis factors and factor levels for each treatment in order to provide a robust groundwork of experimental results (observations) with the least amount of experiments necessary. After the experiments, the statistical analysis employs multivariate statistical methods to determine the significance of synthesis factors and their interactions. A powerful advantage is the possibility to construct linear regression models to establish empirical relationships for prediction of product responses as a function of synthesis factors.25
Full and fractional factorial designs have been successfully used previously to screen the synthesis of Stöber silica,30–32 SBA-15,33 and silica via dissolution precipitation.34 Whereas factorial designs are regarded as resource-efficient for identification of significant synthesis factors, they often do not contain a sufficiently large number of treatments for response modelling with more precise second-order regression polynomials. As such, more elaborate central composite designs were used to model the complex relationship between multiple synthesis factors and product property responses for sol–gel silica.35,36 However, the risk with using designs that necessitate many treatments at an early stage of the optimisation process is that not all factors might be statistically significant, and thus the resulting models may be unnecessarily complex. Experimentation was performed more efficiently with the stepwise approach used for zeolite-X and mesoporous TUD-1 silica, in which compact screening designs were employed upfront for factor selection, followed by more detailed designs for modelling the remaining few significant factors.37,38 A holistic DoE strategy could have reduced the numbers of required trials further by re-using some of the treatments from the screening study for the optimisation by concatenating both designs. Additionally, it must be noted that all DoE studies constructed the regression models with the design factor levels, which might have differed slightly from the factor levels attained during the experiments. More realistic models could have made use of actual factor levels instead.
Another important strategy to identify and optimise key factors is through a sensitivity analysis, which characterises the relationship between the model's inputs and outputs.39 Sensitivity analysis can be split into three key approaches: screening,40,41 local sensitivity analysis42,43 and global sensitivity analysis (GSA).44,45 Specifically, GSA is powerful because it quantifies the variation of the model output, fully exploring the input space within the entire parameter domain. The most popular GSA method is a variance-based decomposition analysis that calculates Sobol' sensitivity indices.44–47 However, the calculations require a significant number of data points evaluations to ensure convergence of integrals to a satisfactory precision level. Therefore, in a wide range of disciplines, surrogate models are used to reduce the number of evaluations by directly interrogating the model. For example, polynomial chaos expansion was used for CO2 pipeline safety,48 artificial neural networks studied combustion kinetics,49 and Gaussian processes (GPs) analysed lithium ion battery safety.50 However, their application in materials chemistry is rarely reported.
As can be seen, efforts for a systematic optimisation of bioinspired silica properties, such as the silica yield and BET surface area, have been unfruitful so far. Given the lack of clarity over the factor–response relationship, the tailored synthesis of silica towards ideal process parameters and desired material attributes has been held back, which in turn has been a barrier to its commercialisation, despite its potential to provide sustainable manufacturing of high-value porous nanomaterials. As shown in the literature above, DoE has been employed for similar silica syntheses, but most studies conducted a single standalone type of design and rarely combined multiple ones in an integrated strategic approach.
As a result of these limitations, this work aims to, for the first time, quantitatively model the multivariate input–output relationship between the factors (pH, Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, [Si]) and the responses (silica yield, silica BET surface area) for the bioinspired silica synthesis. A novel methodical sequential strategy was devised consisting of pre-screening, screening, and optimisation experiments shown in Fig. 2, with the aim of not only synthesising a sustainable silica material, but also of rendering the material's product development pathway more resource-efficient. Further, we also apply the GSA methodology for the first time to bioinspired silica in order to explore its suitability and compare the results with the DoE outcomes for complementation and cross-validation. While there may be other techniques for multi-dimensional modelling, they can generally be described as statistical methods (e.g. multivariate or Bayesian approaches) and/or machine learning approaches (e.g. artificial neural networks, GPs).51 The combined use of DoE with GSA was reported for the identification of significant parameters in in silico simulation of cell growth in batch reactors,52in silico modelling of metabolic networks,53 and for biopharmaceuticals freeze-drying,54 leaving a research gap in its application to materials synthesis. Indeed, the integrated employment of specifically DoE and machine learning tools, harnessing the capabilities of both techniques, has been identified as a research frontier for inorganic materials synthesis.55 This review also mentions that, owing to more input variables such as synthesis and process history, and more output variables including structure and texture, materials synthesis generally faces more complexity than small molecules preparation. As such, the application of a novel sequential strategy in combination with a machine learning approach to bioinspired silica is of significant novelty.
N, [Si]) and the responses (silica yield, silica BET surface area) for the bioinspired silica synthesis. A novel methodical sequential strategy was devised consisting of pre-screening, screening, and optimisation experiments shown in Fig. 2, with the aim of not only synthesising a sustainable silica material, but also of rendering the material's product development pathway more resource-efficient. Further, we also apply the GSA methodology for the first time to bioinspired silica in order to explore its suitability and compare the results with the DoE outcomes for complementation and cross-validation. While there may be other techniques for multi-dimensional modelling, they can generally be described as statistical methods (e.g. multivariate or Bayesian approaches) and/or machine learning approaches (e.g. artificial neural networks, GPs).51 The combined use of DoE with GSA was reported for the identification of significant parameters in in silico simulation of cell growth in batch reactors,52in silico modelling of metabolic networks,53 and for biopharmaceuticals freeze-drying,54 leaving a research gap in its application to materials synthesis. Indeed, the integrated employment of specifically DoE and machine learning tools, harnessing the capabilities of both techniques, has been identified as a research frontier for inorganic materials synthesis.55 This review also mentions that, owing to more input variables such as synthesis and process history, and more output variables including structure and texture, materials synthesis generally faces more complexity than small molecules preparation. As such, the application of a novel sequential strategy in combination with a machine learning approach to bioinspired silica is of significant novelty.
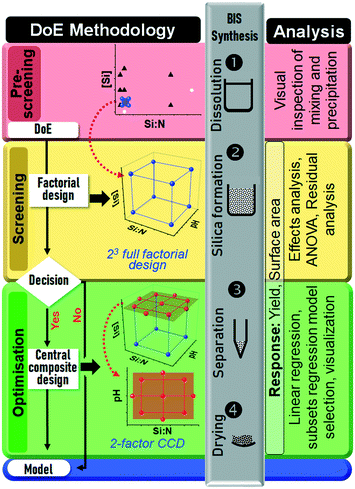 | ||
| Fig. 2 Holistic design of experiments strategy for the bioinspired silica synthesis. Each of the three consecutive experiments (pre-screening, screening and optimisation) were conducted in four consecutive steps: design selection according to the algorithm partly adapted from ref. 56, experimental design, bioinspired silica synthesis, and statistical analysis. The designs are detailed further in Fig. 3 and the text. The “Decision” involved identifying if there is a curvature to the responses and if there were any unimportant factors, see text for details. | ||
2. Materials and methods
2.1 Design of experiments methodology
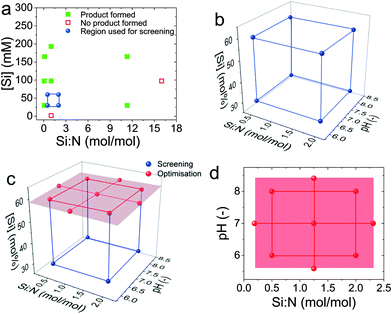
Fig. 2 shows a unique methodical DoE strategy developed, which was divided into three experiments:1. A pre-screening experiment to locate a feasible design space (Fig. 3a),
2. a screening experiment using a full factorial design (FFD) to identify the significant synthesis factors (Fig. 3b), and
3. an optimisation experiment for regression modelling using a central composite design (CCD), Fig. 3c and d.
Each of the three experiments was conducted in four consecutive steps: first the type of design was chosen based on the DoE algorithm partly adapted from ref. 56. Secondly, the experimental design was constructed, then bioinspired silica (BIS) was synthesised and characterised according to the treatments prescribed by the design and according to the method described in section 2.2, and finally the measured observations were statistically analysed using methods appropriate for the purpose of each experiment. These four steps were completed for one experiment (e.g. pre-screening) before the next experiment was commenced (e.g. screening).
At the initial stage, the pre-screening experiment (shown in a red box in Fig. 2) used a semi-systematic approach using two additives to visually identify under which conditions of the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and [Si] factors the synthesis produced bioinspired silica (also shown in Fig. 3a and Table S1 in the ESI†). For the subsequent screening experiment, a 23 full factorial design (3 factors each at 2 levels) was selected with the additional factor pH at levels pH 6 and 8, resulting in the blue cube in Fig. 2 (also shown in Fig. 3b). The combination of factors and levels is also tabulated in Table 2 and runs were carried out randomly to avoid bias. After synthesis, for segregation of the significant from the insignificant factors for both responses, evidence was drawn from an effects analysis, an analysis of variance (ANOVA), and a residual analysis as described below.
N and [Si] factors the synthesis produced bioinspired silica (also shown in Fig. 3a and Table S1 in the ESI†). For the subsequent screening experiment, a 23 full factorial design (3 factors each at 2 levels) was selected with the additional factor pH at levels pH 6 and 8, resulting in the blue cube in Fig. 2 (also shown in Fig. 3b). The combination of factors and levels is also tabulated in Table 2 and runs were carried out randomly to avoid bias. After synthesis, for segregation of the significant from the insignificant factors for both responses, evidence was drawn from an effects analysis, an analysis of variance (ANOVA), and a residual analysis as described below.
| Treatment | Factors | Responses | |||||||
|---|---|---|---|---|---|---|---|---|---|
| pH (−) | Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N (mol mol−1) N (mol mol−1) |
[Si] (mM) | Silica yield (mol%) | Silica BET surface area (m2 g−1) | |||||
| Design level | Actual levela | Design level | Actual levela | ||||||
| a Actual factor levels replaced with a dash (—) were irrelevant since the full factorial design assumed factor levels to be fixed. | |||||||||
| Full factorial design (Treatments 1–9) | 1 | 6 | — | 0.5 | — | 30 | 54 | 46 | |
| 6 | — | 0.5 | — | 30 | 54 | 52 | |||
| 2 | 8 | — | 0.5 | — | 30 | 72 | 15 | ||
| 8 | — | 0.5 | — | 30 | 58 | 13 | |||
| 3 | 6 | — | 2 | — | 30 | 12 | 118 | ||
| 6 | — | 2 | — | 30 | 24 | 184 | |||
| 4 | 8 | — | 2 | — | 30 | 70 | 18 | ||
| 8 | — | 2 | — | 30 | 70 | 14 | |||
| 5 | 6 | 5.82 | 0.5 | 0.50 | 60 | 40 | 105 | Central composite design (Treatments 5–13) | |
| 6 | 5.72 | 0.5 | 0.50 | 60 | 35 | 98 | |||
| 6 | 8 | 8.01 | 0.5 | 0.50 | 60 | 90 | 31 | ||
| 8 | 8.02 | 0.5 | 0.50 | 60 | 89 | 30 | |||
| 7 | 6 | 5.95 | 2 | 2.00 | 60 | 19 | 264 | ||
| 6 | 5.98 | 2 | 2.00 | 60 | 24 | 397 | |||
| 8 | 8 | 8.04 | 2 | 2.00 | 60 | 86 | 16 | ||
| 8 | 8.00 | 2 | 2.00 | 60 | 87 | 17 | |||
| 9 | 5.59 | 5.58 | 1.25 | 1.25 | 60 | 31 | 182 | ||
| 5.59 | 5.58 | 1.25 | 1.25 | 60 | 23 | 217 | |||
| 10 | 8.41 | 8.45 | 1.25 | 1.25 | 60 | 88 | 22 | ||
| 8.41 | 8.45 | 1.25 | 1.25 | 60 | 87 | 20 | |||
| 11 | 7 | 6.87 | 0.19 | 0.19 | 60 | 90 | 33 | ||
| 7 | 6.84 | 0.19 | 0.19 | 60 | 90 | 33 | |||
| 12 | 7 | 7.05 | 2.31 | 2.31 | 60 | 80 | 46 | ||
| 7 | 7.00 | 2.31 | 2.31 | 60 | 74 | 47 | |||
| 13 | 7 | 7.01 | 1.25 | 1.25 | 60 | 80 | 46 | ||
| 7 | 7.00 | 1.25 | 1.25 | 60 | 81 | 56 | |||
After this point, the algorithm contained a decision gate, and because the screening experiment revealed interacting factors causing curvature in the silica yield and BET surface area responses, a subsequent optimization experiment was justified. The benefit of sequential experimentation became apparent here. As described in the discussion below (section 3.2), the [Si] factor was identified to be an unimportant factor and was hence removed, allowing the central composite design to be run with one less factor. For the optimisation design, the distance between the centre and the outer point was α = 1.414, hence superimposing the CCD onto the FFD at the high level of [Si] was possible. This enabled the reuse of four treatments from the previous experiments, as can also be seen from Fig. 3c and Table 2. If a CCD had been chosen to run immediately without a preceding FFD, 15 treatments would have been required, whereas sequential experimentation and design concatenation required only 13 treatments to screen and optimise the silica synthesis. Experimental efficiency of this methodical strategy could be expected to increase with an increasing number of factors investigated.
In order to mathematically relate the significant factors to the responses, second-order linear regression models were constructed of the form
| y = β0 + ∑βixi + ∑βijxixj + ∑βiix2i | (1) |
2.2 Experimental methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Mw/Mn = ∼2.5; Mw: weight-average molecular weight, Mn: number-average molecular weight) were purchased from Sigma Aldrich; tetraethylenepentamine (TEPA, ≥95%), and anhydrous oxalic acid (98%) from Acros; and hydrochloric acid solution (1 M), 4-methylaminophenol sulfate (metol, 99%), and anhydrous sodium sulfite (98%) from Fisher. All chemicals were used as received without further purification. Water was purified to 15 MΩ in-house.
000, Mw/Mn = ∼2.5; Mw: weight-average molecular weight, Mn: number-average molecular weight) were purchased from Sigma Aldrich; tetraethylenepentamine (TEPA, ≥95%), and anhydrous oxalic acid (98%) from Acros; and hydrochloric acid solution (1 M), 4-methylaminophenol sulfate (metol, 99%), and anhydrous sodium sulfite (98%) from Fisher. All chemicals were used as received without further purification. Water was purified to 15 MΩ in-house.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, pH and [Si] were re-calculated for more realistic data analysis. The white particle suspension at the end of the reaction (after 5 min) was centrifuged for 15 min at 5000 rpm (Sorvall ST16, Thermo Fisher Scientific). After the first centrifugation, supernatant was collected for determination of the silica yield and precipitated silica was washed with fresh water and centrifuged a total of three times before being dried at 60 °C for 1 week.
N, pH and [Si] were re-calculated for more realistic data analysis. The white particle suspension at the end of the reaction (after 5 min) was centrifuged for 15 min at 5000 rpm (Sorvall ST16, Thermo Fisher Scientific). After the first centrifugation, supernatant was collected for determination of the silica yield and precipitated silica was washed with fresh water and centrifuged a total of three times before being dried at 60 °C for 1 week.
The silica yield was evaluated using an adaptation of the silicomolybdic acid spectrophotometric method.24 The molybdate reagent was prepared by dissolving 1 g of ammonium molybdate tetrahydrate with 6 mL 37% hydrochloric acid and making up to 100 mL with water. The reducing agent was prepared by dissolving 10 g oxalic acid, 3.35 g metol, 2 g anhydrous sodium sulfite and 50 mL sulfuric acid with the balance water to make 500 mL of solution. For determination of unreacted monomeric silicic acid at the end of the reaction, 10 μL of supernatant was added to 3 mL water and 0.3 mL molybdate reagent. After exactly 15 minutes, 1.6 mL reducing agent was added and the assay left to develop overnight, before absorbance measurement at 810 nm against a linear calibration curve. For the determination of oligomeric and precipitated “polymeric” silica, supernatant or the precipitate were first depolymerised to monomeric silicic acid by heating for 1 hour at 80 °C with an equal volume of 2 M NaOH before being subjected to the same silicomolybdic acid spectrophotometric method. The BET surface area of the dry silica samples was determined by nitrogen adsorption analysis at 77 K (TriStar II 3020, Micromeritics), after overnight degassing at 105 °C. In alignment with the relevant standards, the BET isotherm was applied to the relative pressure range 0.05 ≤ p/p0 ≤ 0.3 where completion of the monolayer was expected.59,60
2.3 Global sensitivity analysis methodology
This work utilises a GP surrogate model to calculate the Sobol' indices as a variance-based GSA technique. Sobol' indices describe how much of the variance of an output can be decomposed into terms that are dependent on the input factors.61 Each input factor has different levels of Sobol' indices corresponding to the amount of inputs that the variance is expressed by. The first-order Sobol' index (Si) corresponds to the amount of variance solely attributable to a factor xi. Whereas total Sobol' index (STi) expresses the whole effect of xi including its interactions with all other input factors. Thus, the effect due to interactions with the remaining input factors is calculated by the difference between STi and Si.The calculation of Sobol' indices is performed through a decomposition method presented by Sobol'62 which evaluates each term through multidimensional integrals that require a large sampling cost.63 Therefore, this work encapsulated the experimental data from Tables 2 and S1† using a machine learning technique to produce a model that captures the behaviour in a cheaper, simpler framework. GP regression predicts the model response (silica yield or silica BET surface area) by taking a (1 × 3) row vector of input factors x (pH, Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, [Si]) and returns a Gaussian random variable y, through calculations using the predictive equations presented by Yeardley et al.64 Within the predictive equation, the automatic relevance determination (ARD) kernel function expresses the correlation between responses to input samples65 as follows:
N, [Si]) and returns a Gaussian random variable y, through calculations using the predictive equations presented by Yeardley et al.64 Within the predictive equation, the automatic relevance determination (ARD) kernel function expresses the correlation between responses to input samples65 as follows:
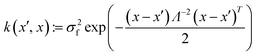 | (2) |
3. Results and discussion
3.1 Pre-screening experiment
The aim of the stepwise strategy was to first find a suitable range of factors that were commonly employed and to identify the best performing additive, before employing other factors in the study. Therefore, initially a pre-screening campaign with 56 experiments was performed using two additives – poly(ethylene imine) (PEI) and tetraethylenepentamine (TEPA), see Table S1† and Fig. 3a. The syntheses were performed by varying the silica precursor concentrations between 2 and 193 mM and the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio from 16 to 1/16, while keeping the pH at 7 according to previous methods.11,17 As polymers and small molecules exhibit different mechanisms in the formation of bioinspired silica due to the effects from polymeric chain conformation, dynamic cooperative assembly between additive and silicates, and increased density of cationic charge,67,68 here we discuss qualitatively the results obtained from PEI and TEPA separately. These results feed into the DoE by identifying areas in the reaction space (not) to focus on. With the use of PEI (Fig. 4a), yields of up to 100% were observed with highest surface area reaching ∼440 m2 g−1. Two scenarios were clearly identified where no precipitation occurred. They include low Si
N ratio from 16 to 1/16, while keeping the pH at 7 according to previous methods.11,17 As polymers and small molecules exhibit different mechanisms in the formation of bioinspired silica due to the effects from polymeric chain conformation, dynamic cooperative assembly between additive and silicates, and increased density of cationic charge,67,68 here we discuss qualitatively the results obtained from PEI and TEPA separately. These results feed into the DoE by identifying areas in the reaction space (not) to focus on. With the use of PEI (Fig. 4a), yields of up to 100% were observed with highest surface area reaching ∼440 m2 g−1. Two scenarios were clearly identified where no precipitation occurred. They include low Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratios (<0.09 or <1/11), i.e. high additive concentrations and low precursor concentration ([Si] ≈ 2 mM). This finding is supported by the literature where high concentration of additive has resulted in stabilisation of silica oligomers, leading to reduced or no precipitation even after centrifugation.21 While it is known that precursor concentrations much lower than 20 mM does not lead to significant precipitation within the 15 min synthesis timescales used herein,69 2 mM is close to equilibrium solubility of silica and hence lack of precipitation at this concentration is expected.70 In order to assess the experimental errors associated with the synthesis and characterisation, samples 17–28 were prepared with identical conditions. The results show that while the average yield of 93 mol% was highly reproducible (with a low standard deviation of 4 mol%), the average surface area of 158 m2 g−1 was spread wider (standard deviation = 58 m2 g−1). Although a similar systematic study has not been reported before, previous experience suggests that variation in surface areas of bioinspired silica obtained from polymeric additives is not surprising due to the effects from polymeric solubility, conformation and assembly, which are not yet fully understood.
N ratios (<0.09 or <1/11), i.e. high additive concentrations and low precursor concentration ([Si] ≈ 2 mM). This finding is supported by the literature where high concentration of additive has resulted in stabilisation of silica oligomers, leading to reduced or no precipitation even after centrifugation.21 While it is known that precursor concentrations much lower than 20 mM does not lead to significant precipitation within the 15 min synthesis timescales used herein,69 2 mM is close to equilibrium solubility of silica and hence lack of precipitation at this concentration is expected.70 In order to assess the experimental errors associated with the synthesis and characterisation, samples 17–28 were prepared with identical conditions. The results show that while the average yield of 93 mol% was highly reproducible (with a low standard deviation of 4 mol%), the average surface area of 158 m2 g−1 was spread wider (standard deviation = 58 m2 g−1). Although a similar systematic study has not been reported before, previous experience suggests that variation in surface areas of bioinspired silica obtained from polymeric additives is not surprising due to the effects from polymeric solubility, conformation and assembly, which are not yet fully understood.
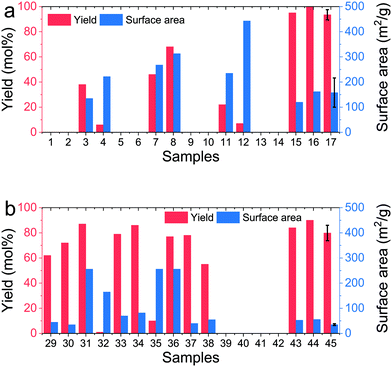 | ||
| Fig. 4 Yield and surface areas obtained from samples listed in Table S1† using (a) PEI or (b) TEPA as the additive. Samples 17 and 45 show results from identical repeats (samples 17–28 and 45–56 respectively for PEI and TEPA as show in Table S1†). | ||
In the case where TEPA was used as the additive, most samples produced silica precipitate except for very low [Si] (sample no. 41 and 42 in Table S1†) or very high Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N (sample no. 39 and 40). Although high yields were obtained with TEPA, they did not reach 100% as observed for PEI (Fig. 4b). This supports the literature findings that generally, cationic polymers are more effective in flocculating and precipitating silica when compared to smaller amines.67,71 Further, samples obtained using TEPA were generally low in surface area, again consistent with the literature.21 Sample no. 45–56 were identical and used for measuring the experimental errors. Unlike the case of PEI, when TEPA was used, the reproducibility was much higher (average yield = 80 ± 6 mol% and average surface area 35 ± 4 m2 g−1). Based on these findings of the pre-screening study, prior knowledge of the system described in the literature above, and a profitability analysis described elsewhere,12 a narrow feasible screening region was constructed, which is depicted with a blue box in Fig. 3a, which is bound by the levels of 0.5 and 2 mol mol−1 for the Si
N (sample no. 39 and 40). Although high yields were obtained with TEPA, they did not reach 100% as observed for PEI (Fig. 4b). This supports the literature findings that generally, cationic polymers are more effective in flocculating and precipitating silica when compared to smaller amines.67,71 Further, samples obtained using TEPA were generally low in surface area, again consistent with the literature.21 Sample no. 45–56 were identical and used for measuring the experimental errors. Unlike the case of PEI, when TEPA was used, the reproducibility was much higher (average yield = 80 ± 6 mol% and average surface area 35 ± 4 m2 g−1). Based on these findings of the pre-screening study, prior knowledge of the system described in the literature above, and a profitability analysis described elsewhere,12 a narrow feasible screening region was constructed, which is depicted with a blue box in Fig. 3a, which is bound by the levels of 0.5 and 2 mol mol−1 for the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N factor, and 30 and 60 mM for the [Si] factor.
N factor, and 30 and 60 mM for the [Si] factor.
3.2 Screening experiment
Moving from the pre-screening campaign, as described in the methods section above, a novel DoE approach was developed using a full factorial design (FFD) followed by a central composite design (CCD), leading to 13 “treatments” in total (see Table 2), each run in duplicate. This was followed with optimisation (described in section 3.3). These stages are also shown in Fig. 3b–d, indicating the reaction space mapped herein. Briefly, in addition to [Si] and Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, pH as a third factor was also included. pH is known to affect silica synthesis,24 however, it has not been systematically varied before in the context of bioinspired silica. Each factor was investigated at two levels. Due to the variability observed when using PEI, the screening study was focussed on TEPA. The responses observed for each treatment are tabulated in Table 2, which were first visualised in Fig. 5 and then used in a detailed statistical analysis described below.
N, pH as a third factor was also included. pH is known to affect silica synthesis,24 however, it has not been systematically varied before in the context of bioinspired silica. Each factor was investigated at two levels. Due to the variability observed when using PEI, the screening study was focussed on TEPA. The responses observed for each treatment are tabulated in Table 2, which were first visualised in Fig. 5 and then used in a detailed statistical analysis described below.
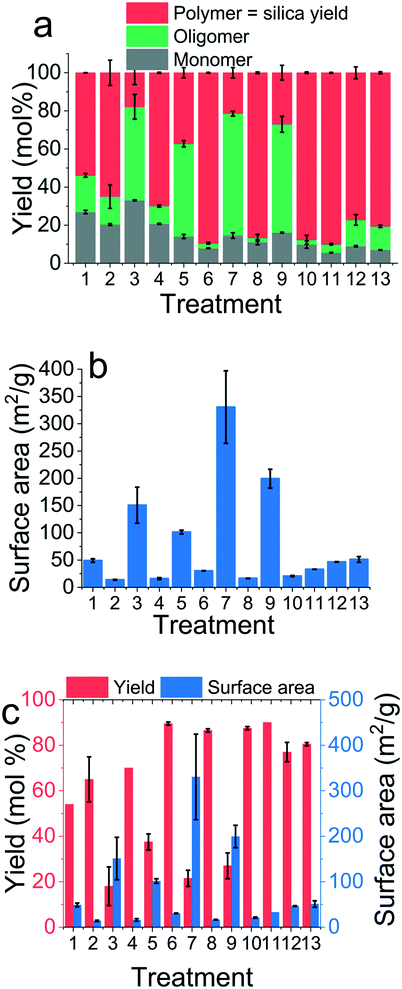
Fig. 5 depicts the experimental results for the treatments of the screening and optimisation experiment for the yield and surface area responses. Fig. 5a shows the distribution of silica species – the monomer, oligomers and the polymer (or the precipitate). Of these, only the polymeric silica precipitate was used as the silica yield response. These results indicate that generally a low pH leads to low yield, either due to poor conversion of monomers (e.g. treatments 1 and 3) or stabilisation of oligomers (e.g. treatments 5, 7 and 9). The precipitates collected were dried and then analysed using N2 adsorption followed by BET analysis to obtain specific surface areas. A typical nitrogen adsorption–desorption isotherm obtained for bioinspired silica is shown in Fig. S1.† The general shape of the isotherm and the hysteresis over the entire relative pressure range suggests a product with heterogeneous texture and a mixture of micro-, meso- and macropores. The BET surface areas calculated for each treatment are shown in Fig. 5b. When the yields and surface areas are superimposed in a single graph (Fig. 5c), it becomes clear that there is a tension between these two responses (e.g. see treatment 6 vs. 7). We will return to this point in the optimisation section below.
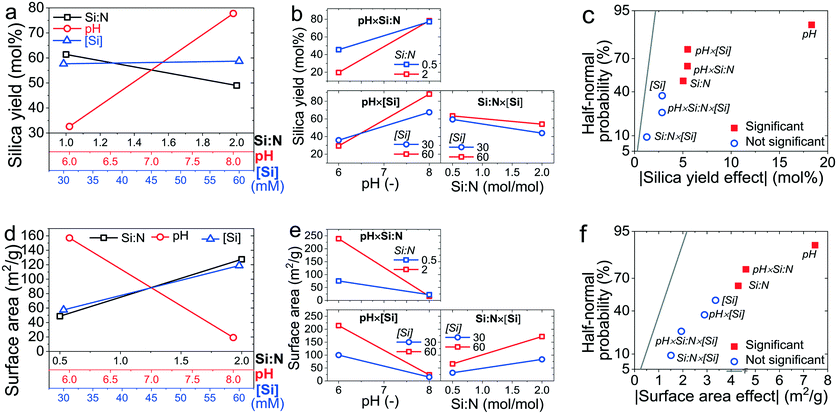
In order to identify which of the synthesis factors and their interactions caused a statistically significant change in the yield and surface area, an effects analysis, an analysis of variance, and a residual analysis were performed. In Fig. 6a and d, the “main effects” of factors relative to each other were compared in an effects plot, which is customarily constructed as a set of straight lines where the slope of the line is a direct indication of the importance of the factor.57 A “main effect” is the difference between the average observations at the high and low level of a factor. For example, the value of the main effect of pH on silica yield was 32.8 mol% at low pH and 77.8 mol% at high pH. Fig. 6a evidences that the pH had the largest effect on the silica yield, which increased positively with increasing pH. The Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio impacted the yield in the opposite direction, but to a lesser extent, while the almost negligible variation of the yield with a change in [Si] suggests that this factor could be insignificant within the range of the reaction space considered herein. Similarly, the BET surface area (Fig. 6d) was most heavily impacted by the pH, but the trend was in opposite direction to the yield. This highlighted again the tension between the two desired outcomes and hence the need to find an optimum between yield and surface area. Both Si
N ratio impacted the yield in the opposite direction, but to a lesser extent, while the almost negligible variation of the yield with a change in [Si] suggests that this factor could be insignificant within the range of the reaction space considered herein. Similarly, the BET surface area (Fig. 6d) was most heavily impacted by the pH, but the trend was in opposite direction to the yield. This highlighted again the tension between the two desired outcomes and hence the need to find an optimum between yield and surface area. Both Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and [Si] positively influenced the surface area, i.e. increasing these factors increased the surface area. However, the effects were indiscernible from each other by visual inspection, which is a drawback of main effects plots and hence further analysis was performed with interaction plots and half-normal probability plots (Fig. 6b, c, e and f).
N and [Si] positively influenced the surface area, i.e. increasing these factors increased the surface area. However, the effects were indiscernible from each other by visual inspection, which is a drawback of main effects plots and hence further analysis was performed with interaction plots and half-normal probability plots (Fig. 6b, c, e and f).
 | ||
| Fig. 6 Effects plots for the silica yield (a–c) and BET surface area (d–f). (a and d) Main effects plot, (b and e) interaction effects plot, and (c and f) half-normal probability plot. | ||
In the interaction effects plots (Fig. 6b and e), lines representing two factors that are severely not parallel or even intersecting (although the latter is not a requirement) indicate opposing or synergistic effects between two factors. The greater the difference between their slopes, the higher the intensity of their interactions. When two lines are parallel or almost parallel, then the interaction of two factors is insignificant. The less the difference between their slopes, the less the intensity of their interactions. For the silica yield (Fig. 6b), the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH and the pH × [Si] interactions were found to be important, given the differences in the slopes of the lines shown, while the Si
N × pH and the pH × [Si] interactions were found to be important, given the differences in the slopes of the lines shown, while the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × [Si] interaction was insignificant. A similar pattern emerged for the surface area (Fig. 6e), but it was unclear whether the pH × [Si] interaction was significant. In order to confirm the important factors and their interactions, the effects analysis was concluded by half-normal probability plots (Fig. 6c and f). In such analysis, factors and their interactions with negligible effects (shown in blue) are normally distributed and lie on a straight line, whereas significant factors (shown in red) are non-normally distributed and lie far apart from the normal distribution line. Again, for both the silica yield and surface area, pH stood out as an important factor. However, a more quantitative method in addition to this qualitative graphical analysis is required to objectively assign statistical significance to the other factors and their coupled effects.
N × [Si] interaction was insignificant. A similar pattern emerged for the surface area (Fig. 6e), but it was unclear whether the pH × [Si] interaction was significant. In order to confirm the important factors and their interactions, the effects analysis was concluded by half-normal probability plots (Fig. 6c and f). In such analysis, factors and their interactions with negligible effects (shown in blue) are normally distributed and lie on a straight line, whereas significant factors (shown in red) are non-normally distributed and lie far apart from the normal distribution line. Again, for both the silica yield and surface area, pH stood out as an important factor. However, a more quantitative method in addition to this qualitative graphical analysis is required to objectively assign statistical significance to the other factors and their coupled effects.
To complement the visual effects analysis shown in Fig. 6, an ANOVA (Table 3) was conducted for both responses. The basis of the ANOVA was an F-test, which compared the amount of variability present between and within treatments, analogously to a signal-to-noise ratio, and which is summarised in the p-value. In order to be 99% confident that a given factor or interaction is statistically significant, the level of confidence was set to α = 0.01. Thus, a factor or interaction was deemed significant if p < 0.01. As the F-distribution was based on a normal distribution, normality of the experimental observations was checked with normal probability plots of residual (Fig. S2 and S3†). Since no gross departure from normality was detected, the ANOVA was considered a valid and applicable technique.
| Factor | Yield (mol%) | Surface area (m2 g−1) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSa | DFb | MSc | F-Value | p-Value | Significant? | SSa | DFb | MSc | F-Value | p-Value | Significant? | |
| a Sum of squares. b Degrees of freedom. c Mean square. | ||||||||||||
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N N |
616 | 1 | 616 | 25.37 | 0.001 | Yes | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
1 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
18.44 | 0.003 | Yes |
| pH | 8158 | 1 | 8158 | 336.06 | 0.000 | Yes | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 038 |
1 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 038 |
55.90 | 0.000 | Yes |
| [Si] | 199 | 1 | 199 | 8.18 | 0.021 | No | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 509 |
1 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 509 |
11.25 | 0.010 | No |
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH N × pH |
729 | 1 | 729 | 30.01 | 0.001 | Yes | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 331 331 |
1 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 331 331 |
21.28 | 0.002 | Yes |
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × [Si] N × [Si] |
39 | 1 | 39 | 1.60 | 0.242 | No | 3131 | 1 | 3131 | 2.27 | 0.170 | No |
| pH × [Si] | 735 | 1 | 735 | 30.27 | 0.001 | Yes | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575 575 |
1 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575 575 |
8.40 | 0.020 | No |
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH × [Si] N × pH × [Si] |
196 | 1 | 196 | 8.09 | 0.022 | No | 5171 | 1 | 5171 | 3.75 | 0.089 | No |
| Error | 194 | 8 | 24 | 8 | 1378 | |||||||
| Total |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 866 866
|
15 | 15 | |||||||||
From the ANOVA of the yield and surface area, the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, pH, and Si
N, pH, and Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH factors were found to be significant. This also confirmed that the change in silica yield resulting from the intentional variation of Si
N × pH factors were found to be significant. This also confirmed that the change in silica yield resulting from the intentional variation of Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and pH was more significant than any random experimental error. The only difference is that for silica yield, the pH × [Si] interaction emerged as an additional significant effect, although the [Si] factor was not important on its own (p = 0.021 > 0.01). According to non-hierarchy, it is indeed possible that a factor exhibits no significant main effect but is involved in a large factor interaction.72,73 On the other hand, for surface area, the [Si] factor was marginally significant on its own (p = 0.01
N and pH was more significant than any random experimental error. The only difference is that for silica yield, the pH × [Si] interaction emerged as an additional significant effect, although the [Si] factor was not important on its own (p = 0.021 > 0.01). According to non-hierarchy, it is indeed possible that a factor exhibits no significant main effect but is involved in a large factor interaction.72,73 On the other hand, for surface area, the [Si] factor was marginally significant on its own (p = 0.01  0.01), and certainly not significant when in an interaction. This statistical analysis of systematically designed experimental campaign identified statistically significant effects and further helped to reduce the number of synthesis factors for further optimisation. As such, based on the effects analysis, ANOVA, and non-hierarchy principle, the Si
0.01), and certainly not significant when in an interaction. This statistical analysis of systematically designed experimental campaign identified statistically significant effects and further helped to reduce the number of synthesis factors for further optimisation. As such, based on the effects analysis, ANOVA, and non-hierarchy principle, the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio and pH were selected for the consecutive optimisation experiment discussed below.
N ratio and pH were selected for the consecutive optimisation experiment discussed below.
3.3 Optimisation experiment
The objective of the optimisation experiment was to obtain a mathematical model of appropriate complexity for the purpose of predicting and optimising both the yield and surface area. The statistical analysis employed linear regression modelling and a best subsets regression model selection to find the most suitable relationship between a given response (yield or surface area), and the factors identified earlier to be statistically relevant (Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and pH). The [Si] factor was found unimportant during the screening experiment and was therefore held constant during optimisation. For both responses, the 31 possible regression models of different complexity were calculated in the form of eqn (1), using the observations from Table 2 as input. We used the actual factor levels as input instead of the design factor levels as they allowed the construction of more realistic regression models. This approach is rarely reported for DoE-based experimentation. However, the benefits from using our approach are clear from the fact that results from the modelling between design and actual differed by up to 50% even though the input values did not differ greatly, and sometimes the actual level was identical to the designed level.
N and pH). The [Si] factor was found unimportant during the screening experiment and was therefore held constant during optimisation. For both responses, the 31 possible regression models of different complexity were calculated in the form of eqn (1), using the observations from Table 2 as input. We used the actual factor levels as input instead of the design factor levels as they allowed the construction of more realistic regression models. This approach is rarely reported for DoE-based experimentation. However, the benefits from using our approach are clear from the fact that results from the modelling between design and actual differed by up to 50% even though the input values did not differ greatly, and sometimes the actual level was identical to the designed level.
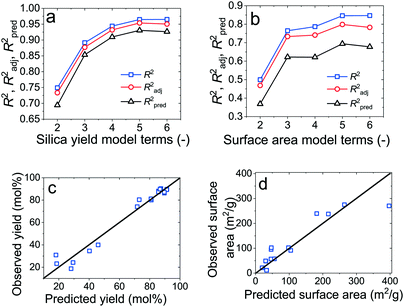
The selection of the most appropriate regression model was then performed graphically using the best subsets regression method for the yield (Fig. 7a) and the BET surface area (Fig. 7b). The plots show the maxima of three coefficients of multiple determination for models containing 2 to 6 terms. R2 always increases with additional model terms, thus models with the peak R2 values might be too complex. Instead, the adjusted R2 (R2adj) accounts for statistically significant terms and decreases in value if redundant terms are present in the model. Similarly, the prediction R2 (R2pred) evaluates how well a given model predicts a response by removing a particular observation, fitting a model to the remaining observations and testing how precisely the model predicts that missing observation. It is also highest for the model with the greatest predicting capabilities, which does not necessitate to be the most complex correlation.57
Given the fact that models left of the peak R2adj and R2pred are generally underfitting, and models right of these values tend to overfit the experimental data, the most appropriate models were chosen to be the models with 5 terms, which yielded the following correlations:
Yield (mol%) = −701.6 − 59.8 × Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N + 211.8 × pH + 7.3 × Si N + 211.8 × pH + 7.3 × Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH − 14.1 × pH2 N × pH − 14.1 × pH2 | (3) |
BET surface area (m2 g−1) = 1556.3 + 631.0 × Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N − 471.7 × pH − 84.1 × Si N − 471.7 × pH − 84.1 × Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH + 35.7 × pH2 N × pH + 35.7 × pH2 | (4) |
Three-dimensional representation of regression models allowed direct visualization of the trend in silica yield (Fig. 8a) and BET surface area (Fig. 8b) and of the close fit between experimental observations (black spheres) and the response surface. Further, literature values were also plotted, which compared very well with the models. This robust prediction of the effect of synthesis factors on product characteristics and optimisation of the bioinspired silica system was only possible with this holistic model accounting for multiple factors over a large experimental range. The only literature exception was the red points in Fig. 8a where the yields from continuous flow tubular reactors16 exceeded the predictions. As continuous processes generally show better yields, this underestimation of yield using our models developed from small scale batch experiments is not unexpected.
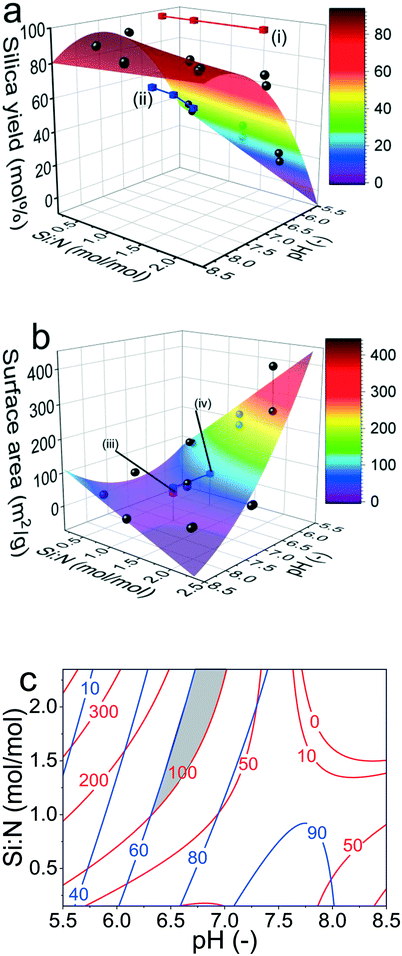 | ||
| Fig. 8 Three-dimensional response surfaces of the selected regression models for (a) the silica yield and (b) the BET surface area. Black spheres represent the data collected herein while other points show additional literature values obtained from (i) ref. 16, (ii) ref. 11, (iii) ref. 19 and (iv) ref. 29. (c) Overlaid contour plot of the model for silica yield (blue) and silica BET surface area (red) for optimisation of both responses simultaneously. The grey region enables to synthesise silica with the constraints that the yield should exceed 60 mol% and the BET surface area should exceed 100 m2 g−1. | ||
Fig. 8a and the model shown in eqn (3), in alignment with the earlier analysis, shows that the silica yield was most drastically affected by the pH and increased from 20 mol% at pH 5.5 to 80 mol% at pH 8.5. The impact caused by the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N factor was less pronounced and the yield increased only slightly with decreasing Si
N factor was less pronounced and the yield increased only slightly with decreasing Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N. The surface area plateaued at about 50 m2 g−1 and increased steeply with decreasing pH and increasing Si
N. The surface area plateaued at about 50 m2 g−1 and increased steeply with decreasing pH and increasing Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N. Although these observations are consistent with the literature,1,8,9 this study incorporated both factors simultaneously and hence was able to explain the trend in greater detail accounting for interactions between factors. For example, the strong curvature of the model towards the top right-hand corner for surface area (Fig. 8b) was indicative of a strong Si
N. Although these observations are consistent with the literature,1,8,9 this study incorporated both factors simultaneously and hence was able to explain the trend in greater detail accounting for interactions between factors. For example, the strong curvature of the model towards the top right-hand corner for surface area (Fig. 8b) was indicative of a strong Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH interaction. From a mechanistic perspective, eqn (3) and (4), and Fig. 8a and b show a strong influence of pH on both responses. There are three factors that are likely to contribute to this pH dependency. Firstly, the rate of silica formation decreases with the pH below ∼pH 8 (i.e. the reaction is slow at low pH), while it is maximum at around pH 7–8 (p177 of ref. 24). We have shown this mechanism is also valid for bioinspired silica,69 while in the present work, we have discovered the quantitative relationships. Secondly, silica particle growth follows distinct pathways at acidic and basic pH (p174 and p519 of ref. 24). At acidic pH, formation of a network of primary particles leads to higher surface areas. At higher pH, individual particles grow without forming a network, thereby forming low surface area particles. Finally, as bioinspired silica synthesis is driven by the protonation and deprotonation of the additives, eqn (3) and Fig. 8a show a significant role of pH in controlling the yield. At higher pH, the silicates are highly negatively charged, leading to stronger interactions with the additive (positively charged amines). At low pH, these interactions diminish due to the protonation of ≡Si–O− ions to ≡Si–OH. These interactions between the pH and amine (Si
N × pH interaction. From a mechanistic perspective, eqn (3) and (4), and Fig. 8a and b show a strong influence of pH on both responses. There are three factors that are likely to contribute to this pH dependency. Firstly, the rate of silica formation decreases with the pH below ∼pH 8 (i.e. the reaction is slow at low pH), while it is maximum at around pH 7–8 (p177 of ref. 24). We have shown this mechanism is also valid for bioinspired silica,69 while in the present work, we have discovered the quantitative relationships. Secondly, silica particle growth follows distinct pathways at acidic and basic pH (p174 and p519 of ref. 24). At acidic pH, formation of a network of primary particles leads to higher surface areas. At higher pH, individual particles grow without forming a network, thereby forming low surface area particles. Finally, as bioinspired silica synthesis is driven by the protonation and deprotonation of the additives, eqn (3) and Fig. 8a show a significant role of pH in controlling the yield. At higher pH, the silicates are highly negatively charged, leading to stronger interactions with the additive (positively charged amines). At low pH, these interactions diminish due to the protonation of ≡Si–O− ions to ≡Si–OH. These interactions between the pH and amine (Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) are clearly identified by the models (eqn (3) and (4)).
N) are clearly identified by the models (eqn (3) and (4)).
This multidimensional study visualised the interplay between factors, which traditional experimentation techniques failed to achieve. As a result, unlike any previous studies, the maximum economic viability of the process could be obtained with the maximum silica yield of 90 mol%, achieved at Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N = 0.5 mol mol−1 and pH = 7.6. Such direct prediction of process chemistry was not available prior to this work. The maximum surface area of 300–400 m2 g−1 was achieved for silica synthesised at Si
N = 0.5 mol mol−1 and pH = 7.6. Such direct prediction of process chemistry was not available prior to this work. The maximum surface area of 300–400 m2 g−1 was achieved for silica synthesised at Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N = 2 mol mol−1 and pH = 5.5.
N = 2 mol mol−1 and pH = 5.5.
From comparison of the two response surface plots, it was observed that the silica yield and surface area increased in opposite directions, that is, the silica yield had its maximum in the top left-hand corner, while the BET surface area was highest in the top right-hand corner. Although in some circumstances maximization of individual responses is required, for which the optimum conditions have been stated, frequently an optimum compromise between responses is required for profitable operations at the same time as meeting customer demands. An overlaid contour plot was constructed in Fig. 8c for a typical scenario, where manufacturing bioinspired silica becomes economically viable at yields >60 mol%,12 with surface area >100 m2 g−1. The intersection of these two criteria is shown as the grey shaded region. Due to the two models' high precision, this response library enables the prediction of the optimised synthesis conditions required to produce silica with desired attributes, which in the present case would be for example Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N = 2 and pH = 6.75.
N = 2 and pH = 6.75.
3.4 Global sensitivity analysis using machine learning
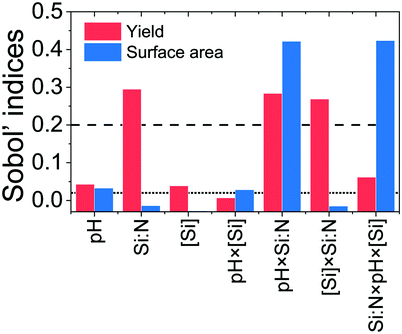
As described in section 2.3, a machine learning technique was used to efficiently conduct a GSA to support the DoE study in decision making of the relevant synthesis factors. Therefore, the GP surrogate model was validated using leave-one-out cross-validation ensuring inaccuracies were not carried through to the Sobol' indices.A criterion for the calculated Sobol' indices has been set to assign a qualitative level of importance for each factor and its interactions. A total Sobol' index value STi was calculated for each factor. A maximum value of STi = 1 shows i corresponds to 100 % of the response's variance. Whereas a minimum value of STi = 0 shows i has a negligible impact on the response. For the factor i, the importance of itself and each interaction is known by splitting the factors STi into i's first-order Sobol' index value Si, plus its interactions with j Sij and k Sik, plus the interactions between all three factors Sijk as shown below in eqn (5):
| STi = Si + Sij + Sik + Sijk | (5) |
From Fig. 9 (red bars), it can be seen that the yield is strongly dependent on the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio and the interactions Si
N ratio and the interactions Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH and Si
N × pH and Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × [Si]. GSA also predicted that pH and [Si] could be marginally important, however, their Sobol' indices were very close to the “low” cut-off (0.02). Further, GSA identified the three factor interactions as somewhat important for the silica yield. When considering the surface area, GSA analysis suggests that only Si
N × [Si]. GSA also predicted that pH and [Si] could be marginally important, however, their Sobol' indices were very close to the “low” cut-off (0.02). Further, GSA identified the three factor interactions as somewhat important for the silica yield. When considering the surface area, GSA analysis suggests that only Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH and the three factor interactions are important, while other factors were found not to be important at all or marginally important (Fig. 9, blue bars). When comparing the GSA results with the DoE outcomes (Table 4), there are good agreements. For example, both methods identified Si
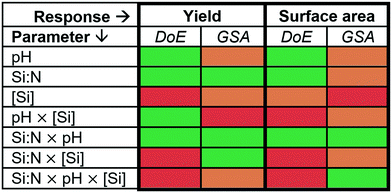
N × pH and the three factor interactions are important, while other factors were found not to be important at all or marginally important (Fig. 9, blue bars). When comparing the GSA results with the DoE outcomes (Table 4), there are good agreements. For example, both methods identified Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N × pH interaction as a key factor for controlling both the silica yield and the surface area. This is a valuable outcome as it provides a single factor that can be used in experimental optimisation of two key properties of silica. There are some factors where a weak disagreement between DoE and GSA results is seen. For example, while the DoE analysis suggested that pH × [Si] is important for the silica yield, the Sobol' index identified this interaction as not important. Similarly, for the surface area, the three-parameter interaction was not considered to be important based on DoE analysis, while it had one of the highest Sobol' index. Such differences between these two methods are expected as they employ fundamentally different mathematical analyses (classical regression and machine learning). Further, the different approaches in defining significance or non-significance using p-values or Sobol' indices and their respective thresholds could add to the discrepancies (p = 0.01 for DoE, Si = 0.02 and 0.2 for GSA).
N × pH interaction as a key factor for controlling both the silica yield and the surface area. This is a valuable outcome as it provides a single factor that can be used in experimental optimisation of two key properties of silica. There are some factors where a weak disagreement between DoE and GSA results is seen. For example, while the DoE analysis suggested that pH × [Si] is important for the silica yield, the Sobol' index identified this interaction as not important. Similarly, for the surface area, the three-parameter interaction was not considered to be important based on DoE analysis, while it had one of the highest Sobol' index. Such differences between these two methods are expected as they employ fundamentally different mathematical analyses (classical regression and machine learning). Further, the different approaches in defining significance or non-significance using p-values or Sobol' indices and their respective thresholds could add to the discrepancies (p = 0.01 for DoE, Si = 0.02 and 0.2 for GSA).
While the methodologies developed herein have been successfully applied for green nanomaterials for the first time, it is clear that further refinements will be beneficial. A wider range of input factor levels with more treatment replicates would enable to cover a wider design space while gaining a better estimate of the variance. Additionally, not all potentially relevant synthesis factors could be investigated in this study, such as reaction time, temperature, and mixing regime. For the GSA, it would be beneficial to extend this to wider ranges of key factors and use more data which has a normal distribution. Given the similarity of the DoE approach to a nested quadrature (Clenshaw–Curtis) method, in future studies, it may be possible to calculate the Sobol' indices directly without needing a GP. Optimisation of the DoE directly with a GP approach could likely be beneficial such that experiments could be focussed to where it is statistically ‘optimal’ for producing a GP representation.74
A comparison of DoE and GSA is novel for nanomaterials. As a consequence of this comparison, we have identified interesting aspects and they need future work. There is little literature comparing the application of DoE ANOVA with GSA.55 This is likely because the two techniques appeal to different communities, and the focus has been either on the practicalities of implementation (i.e. when should one method be used over the other75) or application of DoE to improve GSA (largely ignoring other ANOVAs).76 Given that the two techniques are now in quite widespread, but largely non-overlapping, use across a range of applications, a direct comparison from the application of both techniques to the same problem is highly fruitful. To the authors' knowledge the only occurrence of machine learning for silica production was by Paulson et al. (published a few months ago).76 However, they optimised a single response (particle size) for the flame spray pyrolysis (not using green synthesis) using a GP surrogate model. This, in combination with the findings from a recent review,55 highlight the novelty of our approach using machine learning for sensitivity analysis with the sequential DoE strategy. This comparison may lead to a potentially significant area of future research (not least to the disparate communities employing the two techniques), which our findings aim to point toward and initiate.
Although the potential for improvement has been identified, the present findings are transferable beyond this work. Future research in the area of bioinspired silica synthesis will benefit from identification of the significant synthesis factors and the nonlinear trends in pH and Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, as identified by both the DoE and GSA method. In addition, these results provide a foundation to explore larger scale and/or various reactor geometries in order to enable scale-up of this sustainable synthesis. Applications of bioinspired silica will value the accurate mapping of the factor-response relationship at different scales to guide research towards an optimum direction. The combined use of DoE and GSA for inorganic materials synthesis is a research frontier, aiming to tackle the complexity inherent to materials design. Having highlighted above the benefits and difficulties of a combined method, this work thus acts as one of the earliest case studies at the interface of DoE and GSA for inorganic materials synthesis that has wider applicability.
N, as identified by both the DoE and GSA method. In addition, these results provide a foundation to explore larger scale and/or various reactor geometries in order to enable scale-up of this sustainable synthesis. Applications of bioinspired silica will value the accurate mapping of the factor-response relationship at different scales to guide research towards an optimum direction. The combined use of DoE and GSA for inorganic materials synthesis is a research frontier, aiming to tackle the complexity inherent to materials design. Having highlighted above the benefits and difficulties of a combined method, this work thus acts as one of the earliest case studies at the interface of DoE and GSA for inorganic materials synthesis that has wider applicability.
4. Conclusion
This study aimed at establishing robust factor-response relationships to optimise and predict two properties of bioinspired silica (yield and surface area) as a function of three synthesis parameters (silicon-to-nitrogen concentration ratio Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, pH, and precursor concentration [Si]). This study confirmed that solid polymeric bioinspired silica only precipitates out of the reaction suspension within a certain Si
N, pH, and precursor concentration [Si]). This study confirmed that solid polymeric bioinspired silica only precipitates out of the reaction suspension within a certain Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and [Si] range, beyond which no precipitate forms. In order to minimise the number of required experiments, a sequential design of experiments strategy was developed with a pre-screening, a screening, and an optimisation experiment. In addition, global sensitivity analysis (GSA) using Sobol' index was successfully applied to this case of green nanomaterials for the first time. The main new findings from this work are as follows:
N and [Si] range, beyond which no precipitate forms. In order to minimise the number of required experiments, a sequential design of experiments strategy was developed with a pre-screening, a screening, and an optimisation experiment. In addition, global sensitivity analysis (GSA) using Sobol' index was successfully applied to this case of green nanomaterials for the first time. The main new findings from this work are as follows:
• The 23 full factorial design and subsequent statistical analysis efficiently identified that, within the design space investigated, only the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and pH factor were significant for the responses (as summarised in Table 3).
N and pH factor were significant for the responses (as summarised in Table 3).
• Expanding the factorial design to a central composite design and employing multivariate analysis enabled to construct reliable empirical regression models for each response with good predictability (R2 = 96% for yield, R2 = 85% for surface area).
• 3D response surface and overlaid contour plot visualizations identified the synthesis conditions for maximum yield or surface area individually, or for both responses simultaneously towards an optimum.
• GSA-based method was shown to rapidly provide insights in a wide parameter space and supported the extensive DoE campaign.
• Specifically, GSA identified key parameters and interactions between factors that control the physicochemical properties of nanomaterials, thus demonstrating a strong potential of GSA in green chemistry and engineering in conjunction with classical statistics.
We believe this work is the starting point in holistically modelling the complex multidimensional synthesis of bioinspired silica to complement sustainable and resource-efficient product and process optimisation and development of this nanomaterial.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
SP and LD thank EPSRC (projects EP/P006892/1 and EP/R025983/1) for the financial support to perform this research. SB would like to acknowledge the support of the Royal Academy of Engineering through the Industrial Fellowship reference: IF\192046.References
- J. I. Kroschwitz and M. Howe-Grant, in Kirk-Othmer Encyclopedia of Chemical Technology, ed. R. E. Kirk and D. F. Othmer, Wiley, New York, 2nd edn, 1997, pp. 1963–1972 Search PubMed.
- S. V. Patwardhan, Chem. Commun., 2011, 47, 7567 RSC.
- A. A. Keller, S. McFerran, A. Lazareva and S. Suh, J. Nanopart. Res., 2013, 15, 17 CrossRef.
- F. Piccinno, F. Gottschalk, S. Seeger and B. Nowack, J. Nanopart. Res., 2012, 14, 11 CrossRef.
- R. W. Kelsall, I. W. Hamley and M. Geoghegan, Nanoscale science and technology, John Wiley, Chichester, England, 2005 Search PubMed.
- S. V. Patwardhan, J. R. H. Manning and M. Chiacchia, Curr. Opin. Green Sustain., 2018, 12, 110–116 CrossRef.
- J. C. Compton, Diatoms: Ecology and Life Cycle, Nova Science Publishers, Incorporated, Hauppauge, United States, 2011 Search PubMed.
- S. V. Patwardhan, S. J. Clarson and C. C. Perry, Chem. Commun., 2005, 1113, 10.1039/b416926c.
- S. V. Patwardhan and S. S. Staniland, Green nanomaterials : from bioinspired synthesis to sustainable manufacturing of inorganic nanomaterials, IOP Publishing, Bristol, UK, 2019 Search PubMed.
- S. V. Patwardhan and J. R. H. Manning, Silica synthesis, WO2017037460, 2017 Search PubMed.
- J. R. H. Manning, E. Routoula and S. V. Patwardhan, J. Visualized Exp., 2018, 57730, DOI:10.3791/57730.
- C. Drummond, R. McCann and S. V. Patwardhan, Chem. Eng. J., 2014, 244, 483–492 CrossRef CAS.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- British Standards Institution, Nanotechnology – Nanoparticles in powder form – Characteristics and measurements, BS EN ISO 17200, 2020 Search PubMed.
- V. V. Annenkov, E. N. Danilovtseva, V. A. Pal'Shin, V. O. Aseyev, A. K. Petrov, A. S. Kozlov, S. V. Patwardhan and C. C. Perry, Biomacromolecules, 2011, 12, 1772–1780 CrossRef CAS PubMed.
- S. V. Patwardhan and C. C. Perry, Silicon, 2010, 2, 33–39 CrossRef CAS.
- J. R. H. Manning, PhD thesis, The University of Sheffield, 2019 Search PubMed.
- J.-J. Yuan, O. O. Mykhaylyk, A. J. Ryan and S. P. Armes, J. Am. Chem. Soc., 2007, 129, 1717–1723 CrossRef CAS PubMed.
- C. Forsyth and S. V. Patwardhan, J. Mater. Chem. B, 2013, 1, 1164 RSC.
- S. Takahashi, Y. Kurita, T. Ikeda, M. Miyamoto, S. Uemiya and Y. Oumi, Dalton Trans., 2016, 45, 16335–16344 RSC.
- D. J. Belton, S. V. Patwardhan and C. C. Perry, J. Mater. Chem., 2005, 15, 4629 RSC.
- D. Belton, S. V. Patwardhan and C. C. Perry, Chem. Commun., 2005, 3475 RSC.
- D. J. Belton, S. V. Patwardhan, V. V. Annenkov, E. N. Danilovtseva and C. C. Perry, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5963–5968 CrossRef CAS PubMed.
- R. K. Iler, The chemistry of silica : solubility, polymerization, colloid and surface properties, and biochemistry, Wiley, New York, 1979 Search PubMed.
- British Standards Institution, Statistics – Vocabulary and symbols Part 3: Design of experiments, BS ISO 3534-3, 2013 Search PubMed.
- J. J. Yuan, P. X. Zhu, N. Fukazawa and R. H. Jin, Adv. Funct. Mater., 2006, 16, 2205–2212 CrossRef CAS.
- J. R. H. Manning, E. Routoula and S. V. Patwardhan, J. Visualized Exp., 2018,(138), e57730 Search PubMed.
- P. J. Baker, S. V. Patwardhan and K. Numata, Macromol. Biosci., 2014, 14, 1619–1626 CrossRef CAS PubMed.
- J. R. H. Manning, T. W. S. Yip, A. Centi, M. Jorge and S. V. Patwardhan, ChemSusChem, 2017, 10, 1683–1691 CrossRef CAS PubMed.
- H.-J. Won, Y.-S. Pyo, S.-S. Oh, Y.-C. Kim, Y.-S. Kim and J.-H. Hwang, Met. Mater. Int., 2006, 12, 95–99 CrossRef CAS.
- M. S. Elazazy, A. A. Issa, M. Al-Mashreky, M. Al-Sulaiti and K. Al-Saad, Adv. Powder Technol., 2018, 29, 1204–1215 CrossRef CAS.
- H. Beygi, E. Z. Karimi, R. Farazi and F. Ebrahimi, J. Alloys Compd., 2016, 654, 308–314 CrossRef CAS.
- T. Klimova, A. Esquivel, J. Reyes, M. Rubio, X. Bokhimi and J. Aracil, Microporous Mesoporous Mater., 2006, 93, 331–343 CrossRef CAS.
- H. Khorsand, N. Kiayee and A. H. Masoomparast, Part. Sci. Technol., 2013, 31, 366–371 CrossRef CAS.
- M. Shekarriz, R. Khadivi, S. Taghipoor and M. Eslamian, Can. J. Chem. Eng., 2014, 92, 828–834 CrossRef CAS.
- I. Ong-On, B. Embley, Y. Chisti and N. Hansupalak, Microporous Mesoporous Mater., 2016, 233, 1–9 CrossRef CAS.
- P. Doumit, M. W. Clark, L. H. Yee and A. Rose, J. Mater. Sci., 2019, 54, 14677–14689 CrossRef CAS.
- G. Pomalaza, M. Capron and F. Dumeignil, Appl. Catal., A, 2020, 591, 117386 CrossRef.
- A. Saltelli, S. Tarantola, F. Campolongo and M. Ratto, Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models, John Wiley & Sons, Chichester, 2004 Search PubMed.
- B. Bettonvil and J. P. C. Kleijnen, Eur. J. Oper. Res., 1997, 96, 180–194 CrossRef.
- M. D. Morris, Technometrics, 1991, 33, 161–174 CrossRef.
- V. Czitrom, Am. Stat., 1999, 53, 126–131 Search PubMed.
- E. Castillo, A. J. Conejo, R. Mínguez and C. Castillo, Eng. Optim., 2006, 38, 93–112 CrossRef.
- B. Iooss and P. Lemaître, arXiv, 2014, 1404.2405.
- T. Homma and A. Saltelli, Reliab. Eng. Syst., 1996, 52, 1–17 CrossRef.
- I. M. Sobol', Matem. Mod., 1990, 2, 112–118 Search PubMed.
- I. M. Sobol', Math. Comput. Simulat., 2001, 55, 271–280 CrossRef.
- S. Brown, J. Beck, H. Mahgerefteh and E. S. Fraga, Reliab. Eng. Syst., 2013, 115, 43–54 CrossRef.
- S. Li, B. Yang and F. Qi, Combust. Flame., 2016, 168, 53–64 CrossRef CAS.
- A. S. Yeardley, P. J. Bugryniec, R. A. Milton and S. F. Brown, J. Power Sources, 2020, 456, 228001 CrossRef CAS.
- R. G. Brereton, Chemometrics for Pattern Recognition, Wiley, 2009 Search PubMed.
- A. Kiparissides, C. Georgakis, A. Mantalaris and E. N. Pistikopoulos, Ind. Eng. Chem. Res., 2014, 53, 7517–7525 CrossRef CAS.
- A. Kiparissides and V. Hatzimanikatis, Metab. Eng., 2017, 39, 117–127 CrossRef CAS PubMed.
- P.-J. Van Bockstal, S. T. F. C. Mortier, J. Corver, I. Nopens, K. V. Gernaey and T. De Beer, Eur. J. Pharm. Biopharm., 2018, 123, 108–116 CrossRef PubMed.
- E. J. Braham, R. D. Davidson, M. Al-Hashimi, R. Arróyave and S. Banerjee, Dalton Trans., 2020, 49, 11480–11488 RSC.
- M. J. Anderson and P. J. Whitcomb, in Kirk-Othmer Encyclopedia of Chemical Technology, ed. C. Ley, Wiley, Hoboken, NJ, 2010 Search PubMed.
- D. C. Montgomery, Design and analysis of experiments, Wiley, Hoboken, NJ, 8th edn, 2013 Search PubMed.
- D. C. Montgomery, E. A. Peck and G. G. Vining, Introduction to linear regression analysis, Wiley, Hoboken, NJ, 4th edn, 2006 Search PubMed.
- British Standards Institution, Determination of the specific surface area of solids by gas adsorption – BET method, BS ISO 9277, 2010 Search PubMed.
- British Standards Institution, Pore size distribution and porosity of solid materials by mercury porosimetry and gas adsorption – Part 2: Analysis of mesopores and macropores by gas adsorption, BS ISO 15901-2, 2006 Search PubMed.
- B. Iooss and P. Lemaître, in Uncertainty Management in Simulation-Optimization of Complex Systems, ed. G. Dellino and C. Meloni, Springer, Boston, 2015 Search PubMed.
- I. M. Sobol', Mathematical Modelling Computational Experiments, 1993, vol. 1, pp. 407–414 Search PubMed.
- A. Saltelli, M. Ratto, T. Andres, F. Campolongo, J. Cariboni, D. Gatelli, M. Saisana and S. Tarantola, Global Sensitivity Analysis. The Primer, John Wiley & Sons, 2007 Search PubMed.
- A. S. Yeardley, D. Roberts, R. A. Milton and S. F. Brown, presented in part at the 30th Eur Symp Comput Aided Process Eng, 2020 Search PubMed.
- D. P. Wipf and S. Nagarajan, in Proceedings of the 20th International Conference on Neural Information Processing Systems, NIPS'07, 2007, pp. 1625–1632 Search PubMed.
- R. A. Milton and S. F. Brown, ROMCOMMA, The University of Sheffield, 2019, https://github.com/C-O-M-M-A/rom-comma Search PubMed.
- D. Belton, G. Paine, S. V. Patwardhan and C. C. Perry, J. Mater. Chem., 2004, 14, 2231–2241 RSC.
- S. V. Patwardhan, R. Maheshwari, N. Mukherjee, K. L. Kiick and S. J. Clarson, Biomacromolecules, 2006, 7, 491–497 CrossRef CAS PubMed.
- D. J. Belton, O. Deschaume, S. V. Patwardhan and C. C. Perry, J. Phys. Chem. B, 2010, 114, 9947–9955 CrossRef CAS PubMed.
- S. V. Patwardhan, G. E. Tilburey and C. C. Perry, Langmuir, 2011, 27, 15135–15145 CrossRef CAS PubMed.
- S. V. Patwardhan and S. J. Clarson, Silicon Chem., 2002, 1, 207–214 CrossRef CAS.
- B. E. Ankenman and A. M. Dean, in Handbook of Statistics, Elsevier, 2003, vol. 22, pp. 263–317 Search PubMed.
- D. C. Montgomery, R. H. Myers, W. H. Carter and G. G. Vining, Qual. Reliab. Eng. Int., 2005, 21, 197–201 CrossRef.
- E. Burnaev and M. Panov, in Statistical Learning and Data Sciences, Lecture Notes in Computer Science, ed. A. Gammerman, V. Vovk and H. Papadopoulos, Springer, Cham, 2015, vol. 9047, pp. 116–125 Search PubMed.
- A. Saltelli and P. Annoni, Environ. Model. Softw., 2010, 25, 1508–1517 CrossRef.
- N. H. Paulson, J. A. Libera and M. Stan, Mater. Des., 2020, 196, 108972 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0me00167h |
| ‡ Present address: Nexeon Limited, 136 Eastern Avenue, Milton Park, Abingdon, Oxon, OX14 4SB UK. |
| This journal is © The Royal Society of Chemistry 2021 |