Long-term repeatability and interlaboratory reproducibility of high-precision ID-TIMS U–Pb geochronology

Abstract

Age determination of minerals using the U–Pb technique is widely used to quantify time in Earth's history. A number of geochronology laboratories produce the highest precision U–Pb dates employing the EARTHTIME ²⁰²Pb–²⁰⁵Pb–²³³U–²³⁵U tracer solution for isotope dilution, and the EARTHTIME ET100 and ET2000 solutions for system calibration and laboratory intercalibration. Here, we report ET100 and ET2000 solution data from the geochronology laboratory of University of Geneva obtained between 2008 and 2021 and compare the most recent data with results from the geochronology laboratories of Princeton University and ETH Zürich. This compilation demonstrates that (i) the choice of the thermal ionization mass spectrometer model has no influence on precision and accuracy of the data; (ii) the often observed excess scatter of apparent ET100 solution ²⁰⁶Pb/²³⁸U dates can be mitigated by more careful tracer-sample equilibration; and (iii) natural zircon reference materials are not suitable for evaluating intra-laboratory repeatability and inter-laboratory reproducibility, since they combine several phenomena of natural system complexities (especially domains of different age within the same zircon grain, and residual loss of radiogenic lead in domains of high decay damage after chemical abrasion pre-treatment). We provide our best estimates of apparent dates for the ET100 solution (²⁰⁶Pb/²³⁸U date, 100.173 ± 0.003 Ma), for ET2000 solution (²⁰⁷Pb/²⁰⁶Pb date, 1999.935 ± 0.063 Ma), as well as for natural reference zircon Temora-2 (²⁰⁶Pb/²³⁸U date, 417.353 ± 0.052 Ma). These data will allow U–Pb laboratories to evaluate their analytical performance and to independently calibrate non-EARTHTIME tracer solutions in use.

---

Introduction

Uranium–lead geochronology by isotope dilution thermal ionization mass spectrometry (ID-TIMS) applied to U-bearing minerals is considered to be the “gold standard” of geochronology. Zircon (ZrSiO₄) is a particularly useful accessory mineral phase for this purpose, as it incorporates abundant U up to 1000's of ppm, with negligible initial Pb (e.g., ref. 1). As a result, it is commonly used to reconstruct the precise durations and rates of geological processes, including the duration and tempo of magmatism (e.g., ref. 2–8), timescales of tectonic activity (e.g., ref. 9 and 10), the formation of ore deposits (e.g., ref. 11–14), dynamics of sedimentary systems (e.g., ref. 15), timescales of global climate and biotic change (e.g., ref. 16–18), and potential causal relationships between volcanic activity in large igneous provinces and global biotic and environmental deterioration (e.g., ref. 19–25). Precise U–Pb dates are crucial tools in the reconstruction of geological processes, therefore it is of paramount importance to know their accuracy, and to intercalibrate different mass spectrometry equipment and analytical protocols that are employed in different laboratories.

A series of breakthroughs in chemical and mass spectrometric techniques, refined workflows, and new calibration and tracer solutions were at the origin of an improvement of the precision and accuracy in U–Pb geochronology to approximately 0.1% of single crystal ²⁰⁶Pb/²³⁸U ages. Possibly the most important improvement was the introduction of the chemical abrasion pre-treatment of zircon prior to analysis.^26,27 Method advancements have been mainly fostered through the international EARTHTIME consortium,^28–31 which achieved the objective that data obtained over long periods of time and in different laboratories should be comparable at the same level of precision. Further development has since moved the initially defined target of a 0.1% uncertainty on a ²⁰⁶Pb/²³⁸U age towards the goal of a 0.01% threshold. Increased precision, and accuracy, requires very careful quantification of random and systematic uncertainties, and their accurate propagation throughout the age calculation. In U–Pb geochronology, accuracy and repeatability are tested through the repeated analysis of synthetic and natural reference materials, allowing the testing of the different components of the analytical workflow. Therefore, a record of reference material data and their variance is necessary to assess published U–Pb zircon datasets in terms of a potential inter-laboratory or mass spectrometer bias as well as intra-laboratory repeatability.

In order to assess potential mass spectrometer bias, long term laboratory reproducibility and the quality of available natural zircon reference materials, we present data from synthetic EARTHTIME ET100 and ET2000 standard solutions, used worldwide to assess repeatability and intra-laboratory reproducibility, via the analysis of an apparent ²⁰⁶Pb/²³⁸U or ²⁰⁷Pb/²⁰⁶Pb date, respectively.³² In addition, we analyzed natural reference zircon materials Temora-2 and GJ-1 using state-of-the-art isotope dilution thermal ionization mass spectrometry (ID-TIMS) preceded by chemical abrasion.²⁷ The data from University of Geneva (abbreviated UNIGE) were collected on two different thermal ionization mass spectrometers, a Thermo Scientific TRITON and an IsotopX PHOENIX. These data are compared to data from a PHOENIX mass spectrometer of the U–Pb laboratory at Princeton University (abbreviated PU) and a TRITON Plus at ETH Zürich (abbreviated ETH). This data set therefore presents an excellent case for the evaluation of inter-spectrometer bias and inter-laboratory reproducibility. It sheds light on the limits of precision, accuracy, repeatability and reproducibility of these techniques, applied to both synthetic and natural materials, and raises questions about the sources for short-term and long-term variance in data sets. Our results indicate that some of the commonly used natural zircon reference materials are heterogeneous, and while solution standards are likely a better option, commonly used techniques for processing these solutions introduce scatter presumably due to inter-element fractionation during preparation.

Developing U–Pb geochronology towards higher temporal resolution

In order to test increasingly precise and discrete hypotheses, Earth scientists require U–Pb age determinations at the highest possible levels of precision obtained from small sample volumes. This is necessary for resolving complex growth textures of natural zircon (e.g., ref. 5), variable decay damage related Pb-loss due to parent/daughter zonation of natural zircon (e.g., ref. 33), and complex systematic behavior as a result of post-crystallization thermal or hydrothermal overprint (e.g., ref. 14, 34, and 35). As an illustration, U–Pb geochronology in 1980 needed 2 mg of zircon, which represents thousands of zircon grains in order to obtain 1 μg of Pb for determining an isotopic composition of the sample. The analysis also featured a procedural blank of 200 pg (2 × 10⁻¹⁰ g) of Pb, eventually achieving a precision ∼1% on a ²⁰⁶Pb/²³⁸U ratio. As of 2021, we are currently dissolving either a single grain or a fragment of a zircon with a weight of a few μg, separate and commonly analyze less than 10 pg (1 × 10⁻¹¹ g) of Pb, with a procedural blank of 100–300 fg (1– × 10⁻¹³ g) of Pb. Under optimal conditions (optimal blank, 10–20 pg of measured radiogenic Pb), we are able to achieve a precision of ∼0.02% on a ²⁰⁶Pb/²³⁸U ratio from a single measurement.

Approaching the present level of precision and accuracy in U–Pb geochronology required a series of fundamental achievements by the community during the last 15 years: (i) production and distribution of calibrated EARTHTIME ²⁰⁵Pb–²³³U–²³⁵U (ET535) and ²⁰²Pb–²⁰⁵Pb–²³³U–²³⁵U (ET2535) tracer solutions (“spikes”) for isotope dilution analysis;³⁶ (ii) reduction of the procedural Pb blanks to <300 fg, allowing for increase of precision and analysis of smaller samples at high radiogenic Pb/common Pb ratios (Pb*/Pb_c); (iii) improvement of the collector sensitivity through development of more stable multiplier devices on one hand, and of high-sensitivity, high-ohmic resistor-based^37–39 or capacitive transimpedance based Faraday technologies;⁴⁰ (iv) further development and improved calibration of the chemical abrasion method, which allows for removal of alpha-decay damaged lattice portions of the host mineral zircon and reduction of damage-related data scatter;^26,27,41 (v) standardized data treatment algorithms and software.^29,30

We here define the different terms that will be used throughout this manuscript: “Precision” refers to the sum of the random analytical uncertainties from mass spectrometry (mainly from ion counting statistics of multiplier measurements and the signal to noise ratio of the collector) and correction for laboratory Pb and U blank. “Accuracy” compares a result to the (unknown) “true” value and is mainly influenced by non-random (“systematic”) uncertainty, such as spike calibration, or correction of mass spectrometric variables (the most important are mass fractionation in the spectrometer source, and collector calibration). “Repeatability” refers to the variance of a series of individual measurements of reference materials in the same laboratory (which is identical to “intra-laboratory reproducibility”). “Reproducibility” is the variance of mean dates of reference materials in between different laboratories. Ideally, the stated precision of an individual analysis or a weighted mean age will take the external sources of error into account. The uncertainty of U–Pb ages is commonly stated following a X/Y/Z notation proposed by Schoene et al.,⁴² with [X] equal to random, “internal” uncertainty, [Y] to systematic, “external”, mostly tracer calibration uncertainty, and in [Z] adding the decay constant uncertainty. It has to be noted that this latter uncertainty notation does not contain neither a repeatability nor a reproducibility component.

Due to potential heterogeneities within natural zircon reference materials, a homogeneous, synthetic solution containing U and radiogenic Pb in proportions equivalent to an age of interest has been thought to be the best approach to thoroughly assess the accuracy, repeatability and reproducibility of high precision ID-TIMS U–Pb dates, within an individual laboratory and also for inter-laboratory calibration. Such solutions can be aliquoted in abundances optimal for analytical conditions, such as for optimized ion counting statistics, using the maximum linear range of the multiplier device for measuring Pb isotope composition, and arriving at the highest possible Pb*/Pb_c. Here, we compare a long-term series of data obtained at UNIGE from the nominally 100 Ma old ET100 solution distributed through the EARTHTIME consortium³² with results from the U–Pb ID-TIMS laboratories at PU and ETH. Analyzing the synthetic ET100 solution mixed with a calibrated U–Pb isotope tracer (i.e., ET535 and ET2535) with TIMS allows for a direct assessment of mass spectrometer performance and isotope dilution procedures. While there is no formally agreed age for the solution, publications from various labs report ²⁰⁶Pb/²³⁸U dates scattering between 100.0 and 100.3 Ma, and it has been used to directly intercalibrate EARTHTIME and non-EARTHTIME U–Pb isotope tracers for studies involving data from multiple labs (e.g., ref. 21 and 43). Unfortunately, there is no standard procedure for preparing these solutions for ID-TIMS analysis; the discussion of the repeatability and reproducibility of the ET100 and ET2000 solutions is a main point of this contribution and will be further explored below.

Two different TIMS instruments have been used in this study at UNIGE: (A) a Thermo Scientific TRITON purchased in 2005, featuring a MasCom discrete-dynode secondary electron multiplier (SEM) used for Pb isotope analysis in ion counting mode and a multicollector Faraday cup array featuring initially five 10¹¹ Ω and five 10¹² Ω resistance amplifiers. The latter were upgraded with five 10¹³ Ω resistance amplifiers in 2017; (B) a PHOENIX (IsotopX Ltd.) TIMS purchased in 2016, equipped with a Daly-multiplier ion counting system and Faraday cups backed by 10¹² Ω resistance amplifiers. The ET100 data from PU were obtained from the same generation PHOENIX TIMS; the data measured at ETH come from a TRITON Plus mass spectrometer, equipped with 10¹³ Ω resistance amplifiers. Cross calibration between the TRITON and PHOENIX models of has not previously been established for high precision U–Pb geochronology. Therefore, in order to ensure that the community is producing and publishing comparable data, a thorough comparison is a necessary exercise.

In this contribution we present a unique long-term data set of synthetic and natural reference materials obtained at UNIGE, which allows us to: (i) demonstrate that TRITON (Thermo Scientific) and PHOENIX (IsotopX) TIMS deliver results from ET100 solution identical within an internal precision of 0.01% of the ²⁰⁶Pb/²³⁸U date; (ii) quantify excess scatter of ET100 apparent ²⁰⁶Pb/²³⁸U dates, and show that uncontrolled effects in solution chemistry lead to the overdispersion of data, unrelated to the mass spectrometer platform; (iii) demonstrate and explain why ²⁰⁶Pb/²³⁸U dates of natural zircon standard materials may only be reproducible at the 0.1% level.

Reference materials and applied methods

Optimizing conditions for ET100 solution measurements

A compilation of 112 zircon U–Pb isotope determinations on single zircon grains analyzed in the UNIGE lab covering the range of 0.3–229 pg Pb*, and Pb*/Pb_c ratios of 0.5–1370 has been used to evaluate the proportions of the three main sources of uncertainty in U–Pb dating (isotopic fractionation of Pb [alpha Pb], Pb_c in analysis [blank], and Pb*/Pb_c; Table S1†). The most important source of uncertainty is the Pb*/Pb_c ratio of the measured material, while alpha Pb is corrected from the measured ²⁰²Pb/²⁰⁵Pb. From these data we conclude that a minimum Pb*/Pb_c of above 15–20 is required to obtain results of optimal precision, which has been adopted for the preparation of the ET100 solution aliquots (Fig. S1†); see an analogous plot in ref. 44. It is important to note that the different batches of the ET100 solution used by different EARTHTIME laboratories appear to have different abundances of Pb_c and are measured at different ²⁰⁶Pb/²⁰⁴Pb ratios at very similar blanks. Therefore, measured Pb_c abundances are a mixture of loading/procedural blank and Pb_c in the solution. However, all Pb_c present in analysis has been corrected with the measured isotope composition of the laboratory procedural blank in all three laboratories (Table S2†).

Synthetic ET100 solution

Consequently, given a known concentration of Pb* in the ET100 solution and the typically measured abundances of Pb_c, aliquots were tailored to have a Pb*/Pb_c ratios largely in excess of 15, in most cases between 50 and 200 (Tables S3–S5†). We prepared aliquots of the ET100 solutions with 50 to 150 pg of Pb*, and spiked them with 10 to 12 mg EARTHTIME ²⁰²Pb + ²⁰⁵Pb + ²³³U +  ²³⁵U (ET2535) tracer solution (calibration version 3;^31,36), targeting a ²⁰⁶Pb/²⁰⁵Pb ratio ranging from 1 to 2, and drying down with traces of 0.02 M H₃PO₄ on a hot plate at a temperature of around 120 °C. It should be noted that this procedure diverges from the standard zircon chemical treatment (see below), since the ET100 solution did not undergo high-temperature-pressure re-equilibration in a PARR™ pressure vessel (“bomb”) for the measurements reported in Tables S3 and S4† nor ion-exchange column chromatography. As a word of caution, these Pb isotopic composition determinations from the synthetic solutions were prepared with elevated Pb concentrations and Pb*/Pb_c ratios and are therefore more precise than real unknowns analyzed for their U–Pb age. We therefore do not use the ET100 data to address aspects of real sample precision and repeatability that mainly arise through the Pb_c correction and decay-damage related Pb loss but assess the analytical performance and long-term repeatability of our labs.

To evaluate if the sample preparation described above is sufficient to equilibrate the sample (ET100) and spike (ET2535), three additional preparation techniques have been tested:

(i) At UNIGE a set of 15 analyses of ET100 solutions were prepared in 2021 using a two-step equilibration procedure at high-pressure. First, ET100 solution, ET2535 tracer and HF + HNO₃ were added to two individual microcapsules inside the PARR bomb with its bottom covered with HF, and then placed in the oven for 48 hours at 210 °C. Following this flux, they were dried down on a hotplate, re-precipitated in 3 drops of 6 M HCl, and placed back in the same PARR bomb again to flux at 210 °C overnight. After this conversion to chlorides, the solutions in the two microcapsules were dried down and then redissolved in 3 M HCl. Subsequently, 7 and 8 aliquots were pipetted into individual 7 ml Savillex vials from the two microcapsules, respectively. After adding phosphoric acid, the sample solutions were dried down for loading onto the TIMS.

(ii) At PU, larger amounts of the ET100 solution were transferred into a 7 ml screw-top Savillex vial together with the ET2535 tracer solution in 1 M HNO₃ and left for 4 to 8 days on a hotplate at 80 °C for equilibration, then pipetted into individual Savillex vials and dried with phosphoric acid.

(iii) At ETH, prior to adding the ET2535 spike to the ET100 solution, the two solutions were shaken before putting two drops of each solution in individual Savillex vials. After adding >200 μl of 3 M HCl and phosphoric acid, the sample-spike mixture was dried.

Synthetic ET2000 calibration solution

This solution has been measured intermittently over a period of 8 years from 2008 to 2016 on the TRITON TIMS at UNIGE, in 2019 on the PHOENIX TIMS at PU, and in 2018 at ETH Zürich, in order to assess mass spectrometry repeatability for ²⁰⁷Pb/²⁰⁶Pb ages. The ET2535 tracer was added to the synthetic solution aliquots and the sample-spike mixture was dried.

Zircon reference material

Selected grains or fragments of zircon reference materials Temora-2 (ref. 45) and GJ-1 (ref. 46; crystal #67) were treated with the standard chemical abrasion, dissolution, column chemistry and dry-down procedures used for zircon in the UNIGE: this involved annealing in a muffle furnace at 900 °C for 48 hours, and subsequent chemical abrasion at either 180 °C or 210 °C for 12 hours in concentrated HF in 3 ml Savillex beakers placed in a PARR digestion vessel.^27,41 The data are presented in Table S6† along with details about the temperature of the partial dissolution step of chemical abrasion. Remaining grain fragments after chemical abrasion were further cleaned in 6 N HCl on a hotplate at 80 °C overnight, followed by washing in 7 N HNO₃ in combination with ultrasonication. Individual cleaned zircon crystals or fragments were then loaded into individual 200 μl Savillex microcapsules, spiked with 5 to 10 mg of either ET2535 or ET535 tracer solution, and dissolved with about 70 μl HF and trace HNO₃ in a PARR digestion vessel at 210 °C for 48 hours. Following dissolution, the samples were dried down and converted to a chloride by placing them back in an oven at 210 °C overnight in 6 N HCl. The samples were then dried down again and re-dissolved in 3 N HCl and purified to U and Pb through anion exchange column chromatography. Once purified, the U and Pb fractions were dried down in cleaned 7 ml Savillex beakers with trace H₃PO₄.

Mass spectrometry

All samples were loaded on outgassed, zone-refined Re ribbon filaments with a Si-gel emitter that contains a concentration of silicic acid four times higher than the original recipe of ref. 47.

At UNIGE, the Pb measurements on the TRITON were done in dynamic mode on a MasCom SEM, respecting a yield window of 93–94% and a maximum dark noise of 15–20 cpm. Uranium isotope compositions were analyzed as an oxide in static mode using Faraday cups coupled to 10¹² Ω resistance amplifiers until mid-2017, and on Faraday cups coupled to 10¹³ Ω resistance amplifiers from fall 2017. The extended linear range of the latter allowed for U isotope analysis at higher signal to noise ratios, higher ion currents, providing better in-run statistics. The Pb isotope analyses on the PHOENIX TIMS were carried out in dynamic mode using a Daly photomultiplier, a subset of data using a one-jump dynamic procedure on Faraday cups coupled to 10¹² Ω resistance Faraday cups, using the ²⁰⁵Pb intensity for Daly–Faraday intercalibration and measuring ²⁰⁴Pb intensity on the Daly multiplier. U isotope composition was measured as an oxide in static mode using 10¹² Ω resistance Faraday cups. At PU, analyses were measured on a PHOENIX TIMS closely following the measurement routines outlined above for the PHOENIX TIMS UNIGE. At ETH, the first block of analyses was carried out on a TRITON Plus, measuring the Pb isotope composition on a discrete dynode SEM following closely the procedures outlined above for UNIGE. The second bock of analyses (N = 13) measured Pb isotope compositions on 10¹³ Ω resistance amplifiers following the procedures outlined in ref. 38 (Table S3†).

The ¹⁸O/¹⁶O oxygen isotope ratio in UO₂ was determined to be 0.00205 ± 0.00002 for both mass spectrometer types and in all laboratories based on repeat measurements of the U500 standard. This ratio was applied to all data assuming no inter-sample variation of oxygen isotope ratio. Mass fractionation of Pb and U was corrected for using isotopic ratios ²⁰²Pb/²⁰⁵Pb = 0.99923913 (±0.0265% 1σ), ²³³U/²³⁵U = 0.995062 (±0.0054% 1σ) in the ET2535 tracer, and a natural ²³⁸U/²³⁵U ratio of 137.818 ± 0.045 (2σ),⁴⁸ as outlined in ref. 30. For analyses of zircon reference materials using ET535 spike, fractionation factors of 0.13 ± 0.02% per a.m.u. and 0.20 ± 0.03% per a.m.u. were used for TRITON and PHOENIX in the UNIGE lab, respectively. All common Pb was considered laboratory blank and was corrected using the measured Pb isotopic composition of total procedural blanks (using ET2535 tracer) over the entire duration of the study (Table S2†).

Data treatment and presentation

All data were processed using the Tripoli and Redux U–Pb software packages.^29,30 Weighted mean values are given with the [X] internal error⁴² at the 2σ level of uncertainty, or with 95% confidence limits of [tσ√MSWD] in the case the MSWD values are outside of the acceptable range for the indicated degree of freedom.⁴⁹

Results

Long-term repeatability of ET100 solution measurements (2008–2021, UNIGE)

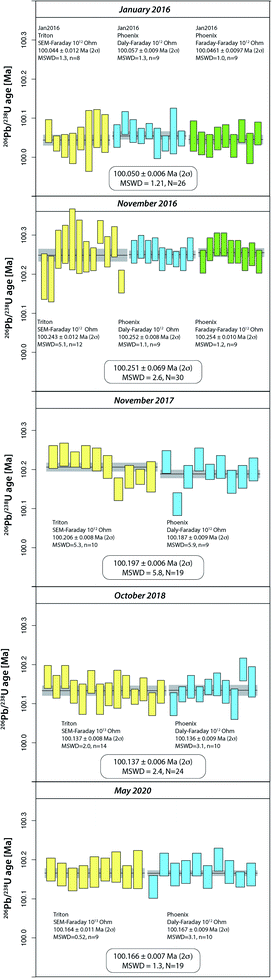
The compilation of data in Fig. 1 (Tables S2–S4†) represents 264 ET100 measurements over 13 years on the TRITON TIMS (2008–2015) and on both TRITON and PHOENIX TIMS (2016–2021) at UNIGE. During this period, four different secondary electron multipliers (SEM) were used on the TRITON (SEM#2 to #5 in Fig. 1), following a standard exchange procedure that is required due to the gradual saturation of the first dynode.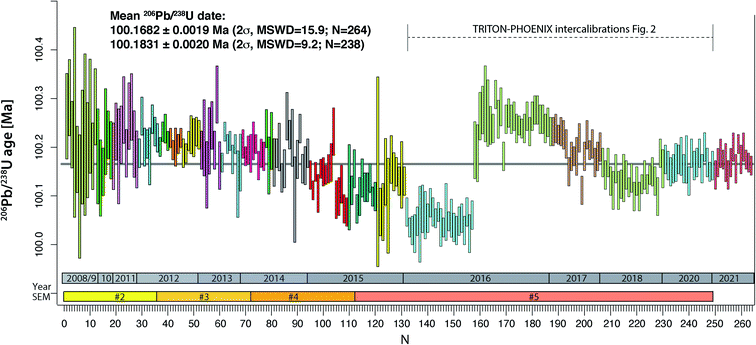

Fig. 1 Measurements of apparent ²⁰⁶Pb/²³⁸U age from ET100 synthetic solution at UNIGE 2008–2015 on TRITON TIMS, 2016–2020 on both TRITON and PHOENIX TIMS, 2021 on PHOENIX only. TRITON data were measured using four subsequent secondary electron multipliers (#2 to #5). The color-coded blocks refer to blocks defined in Tables S1 and S2,† measurements #132–249 are shown in more detail in Fig. 2. See text for further details.

The results are in chronological order, the approximate timing is indicated in Fig. 1. The first batch of 131 ET100 measurements on the TRITON TIMS scatter around a mean ²⁰⁶Pb/²³⁸U date of 100.18 Ma, starting at higher values at around 100.25 Ma and decreasing towards an average at ∼100.12 Ma. Clear outliers of data set have been excluded for a variety of reasons such as elevated Pb_c in analysis (bad loading blank), non-ideal sample load (not in the filament center or dispersed across the length of the filament), or faulty mass spectrometer operation (measurement at inappropriate filament temperature, bad source vacuum). Despite this, after data screening, the remaining data still show significant overdispersion. The second batch of 118 ET100 analyses were measured on both TRITON and PHOENIX TIMS in order to intercalibrate the two mass spectrometers at UNIGE, as discussed below. The data were screened in the same way as described above. The last batch of 15 analyses in Fig. 1 was carefully equilibrated at high pressure in a PARR bomb before aliquoting and analyses on the PHOENIX TIMS in January 2021. No outlier rejection was necessary for this batch.

An apparent weighted-mean ²⁰⁶Pb/²³⁸U date of 100.1698 ± 0.0019 Ma (2σ) can be calculated from all 264 data, the significant excess scatter leads to a MSWD of 16. By removing an outlier block (run numbers #132–157, beginning of 2016) we arrive at a mean apparent ²⁰⁶Pb/²³⁸U date of 100.1837 ± 0.0020 Ma (2σ, MSWD = 9.3, N = 238).

Intercalibration of TRITON and PHOENIX TIMS at UNIGE using ET100 solution (2016–2020)

The purchase of a PHOENIX TIMS in 2015 at the UNIGE required careful intercalibration of the two mass spectrometers. The results from five intercalibration exercises between January 2016 and May 2020 are reported as run numbers #132 to 249 in Fig. 1, and data from each intercalibration exercise are reported in Fig. 2 separately. The solution preparation, filament loading and measurements were done at the same time on both mass spectrometers to ensure identical experimental conditions. For the first two exercises, two different Pb isotope measurement procedures were applied on the PHOENIX TIMS, (i) dynamic measurement of all Pb isotopes using only the Daly photomultiplier system, and (ii) multi-dynamic Pb isotope measurement using 10¹² Ω resistance Faraday cups for masses 202, 205, 206, 207 and 208, while 204 and 205 were measured on the Daly multiplier to apply an in-run Daly–Faraday intercalibration routine. There was no outlier rejection applied, and all data are reported in Table S4.†

Fig. 2 Apparent ²⁰⁶Pb/²³⁸U ages of ET100 synthetic solution from five TRITON–PHOENIX intercalibration exercises at UNIGE between 2016 and 2020. Yellow – TRITON measurements, blue – PHOENIX measurements utilizing Daly ion counting for Pb isotope analysis; green – PHOENIX measurements using a mixed 10¹² ohm Faraday–Daly ion counting array for Pb isotope ratio measurement.

The data show (i) excellent internal repeatability for both mass spectrometers within the same exercise at an internal uncertainty of 0.01% in apparent ²⁰⁶Pb/²³⁸U age, (ii) various degrees of overdispersion within individual measurement blocks (MSWD values as high as 5.9), (iii) large variations in ²⁰⁶Pb/²³⁸U dates at the level of 0.1% between the different exercises, with the January 2016 exercise being an outlier with an average age 0.13% lower than the average apparent ²⁰⁶Pb/²³⁸U date of all other analyses (i.e., 100.1831 ± 0.0020 Ma). These measurements were done after a long period of consistently decreasing values, presumably produced through a constant, minor U/Pb fractionation during solution aliquot removal (Fig. 1 and 2). During 2016, the UNIGE lab changed from bottle #1 to bottle #2 of the ET2535 tracer, resulting in a marked jump in apparent ²⁰⁶Pb/²³⁸U date from 100.050 ± 0.006 Ma (January 2016) up to 100.251 ± 0.0056 Ma (November 2016; Fig. 1).

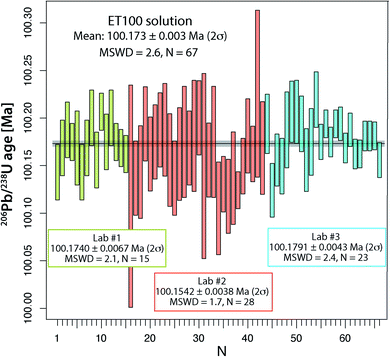
Sample-spike equilibration test and laboratory intercalibration (UNIGE, PU and ETH, 2020–2021)

From all ET100 solution data presented so far, it is evident that there is a considerable degree of excess scatter not accounted for by the propagation of analytical uncertainties. A potential explanation for this excess scatter is that with the used analytical protocol for the synthetic ET100 solution, sample-spike equilibration is not achieved. Therefore, at UNIGE, two separate batches of ET100 solution were equilibrated with ET2535 spike in two individual microcapsules inside a PARR bomb at 210 °C, identical to the treatment normally applied to zircon (see above). The two batches were measured in 2021 and yielded respectively 8 and 7 apparent ²⁰⁶Pb/²³⁸U dates that agree within their uncertainty and yield a weighted mean apparent ²⁰⁶Pb/²³⁸U date of 100.1740 ± 0.0067 Ma (2σ, MSWD = 2.1; N = 15; Fig. 3 and Table S5†), without any outlier rejection. These results are similar to the experiment in the laboratory of PU, where large aliquots of ET2535 tracer and ET100 synthetic solution were mixed in a 7 ml Savillex vial and left equilibrating on a hotplate for several days, yielding a mean apparent ²⁰⁶Pb/²³⁸U date of 100.1542 ± 0.0076 Ma (2σ, MSWD = 1.7; N = 28; Fig. 3 and Table S5†). The third experiment performed at ETH, where the synthetic ET100 solution and the ET2535 isotope spike were shaken, mixed and then evaporated in 200 μl of 3 M HCl, yield an apparent mean ²⁰⁶Pb/²³⁸U date of 100.1791 ± 0.0043 Ma (2σ, MSWD = 2.4; N = 23; Fig. 3 and Table S5†) with only a small component of overdispersion. The difference of only 0.025% between the average ²⁰⁶Pb/²³⁸U dates of the three laboratories could potentially be due to small variations in multiplier behavior, and oxygen isotope fractionation during UO₂ isotope analysis. More importantly, different proportions of total procedural blank Pb_cversus Pb_c hosted by the ET100 solution may lead to data scatter, since all Pb_c is corrected with the isotope composition of the procedural blank in the respective labs.

Fig. 3 Apparent ²⁰⁶Pb/²³⁸U ages of ET100 synthetic solution from University of Geneva, Princeton University and ETH Zürich labs. For details on measurement conditions see text. Variable precision mainly results from differences in Pb*/Pb_c of the individual aliquots due to variable amounts of ET100 solution analyzed.

By pooling all analyses together, we obtain a mean apparent ²⁰⁶Pb/²³⁸U age of 100.173 ± 0.003 Ma (2σ, MSWD = 2.62; N = 67), which we consider to be our best estimate for the apparent age of the ET100 solution. These analyses demonstrate that more careful sample-spike homogenization is able to remove most, albeit not all, of the excess scatter identified in an earlier stage, and leads to more reproducible data between different batches of ET100 solution and between different geochronology laboratories.

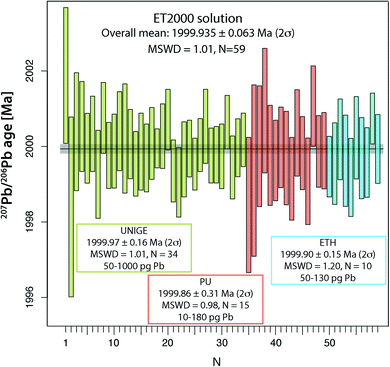
Reproducibility of ²⁰⁷Pb/²⁰⁶Pb dates of ET2000 synthetic solution at UNIGE, PU and ETH

The main aim of analyzing the synthetic ET2000 solution is to evaluate the repeatability of the ²⁰⁷Pb/²⁰⁶Pb dates, which does not include any additional uncertainty from chemical treatment or from the sample/tracer equilibration. The overall mean ²⁰⁷Pb/²⁰⁶Pb date of 1999.97 ± 0.16 Ma (2σ, MSWD = 1.01, N = 34; Fig. 4 and Table S6†) from the UNIGE lab demonstrates perfect repeatability and a correct propagation of analytical uncertainties from mass spectrometry. Identical values of 1999.86 ± 0.31 Ma (2σ, MSWD = 0.86, N = 15) and 1999.90 ± 0.15 Ma (2σ, MSWD = 1.20, N = 10; Fig. 4 and Table S6†) are reported from PU and ETH labs. Pooling the data from the three laboratories together we can establish a ²⁰⁷Pb/²⁰⁶Pb date of 1999.935 ± 0.063 Ma (2σ, MSWD = 1.01, N = 59), which we suggest here as the best estimate of the mean ²⁰⁷Pb/²⁰⁶Pb date for this solution.

Fig. 4 Data compilation of apparent ²⁰⁷Pb/²⁰⁶Pb dates from ET2000 synthetic solution at University of Geneva on TRITON TIMS, from Princeton University on PHOENIX TIMS, and from ETH Zürich TRITON Plus TIMS.

U–Pb analyses of natural reference zircons Temora-2 and GJ-1

The two widely used zircon reference materials Temora-2 and GJ-1 were dated at UNIGE and are presented in Table S7† and Fig. 5 and 6. Since there is no offset between the two TIMS platforms, the data are not specified for the mass spectrometer in Fig. 5 and 6, but these details are specified in Table S7.†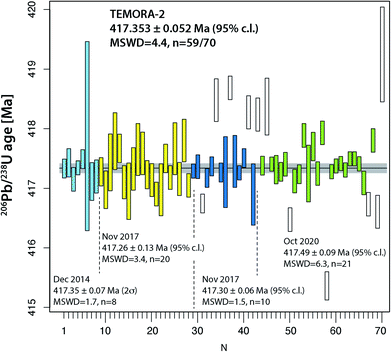

Fig. 5 Compilation of ²⁰⁶Pb/²³⁸U age determinations of reference zircon Temora-2 at University of Geneva.

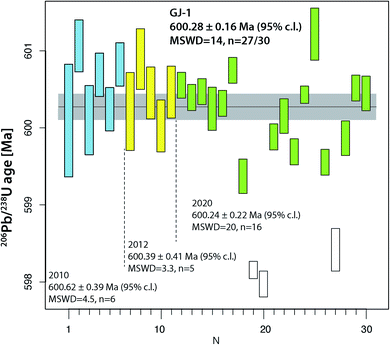Fig. 6 Compilation of ²⁰⁶Pb/²³⁸U age determinations of reference zircon GJ-1 at University of Geneva.

Temora-2. A total of 70 analyses are reported in Table S7,† color coded for 4 measurement blocks between December 2014 and October 2020. Each block contains results from both TRITON and PHOENIX TIMS and differs in terms of used isotopic tracer (normally ET2535, except for the November 2017 block, which was measured with ET535 spike), in terms of spike bottle (#1 and #2), and in terms of selected temperature for the partial dissolution step (180 °C or 210 °C) during chemical abrasion. The data set is characterized by variable total Pb abundance, variable Pb_c and therefore variable Pb*/Pb_c, partly below the critical threshold value of 15, and significant scatter beyond pure analytical error as defined by the long-term repeatability of the synthetic ET100 solution of below ±0.1% (see above) (Fig. S1†). These effects lead mainly to large differences in ²⁰⁷Pb/²³⁵U date uncertainty but may also bias the ²⁰⁶Pb/²³⁸U date. A mean ²⁰⁶Pb/²³⁸U date of 417.353 ± 0.052 Ma (95% c.l., MSWD = 4.4, n = 59) can be calculated after removal of the following outliers: analyses #34, 37, 41, 43, 45 and 70, all of which may belong to an older age component at 418.5–419.0 Ma; and analyses #31, #50, 58, 67 and 69 that were likely biased by residual Pb loss and have been removed from the mean as well. All other analyses were used to calculate the mean date, assuming that the scatter is of analytical nature only. The variance is beyond analytical scatter in all measurement blocks, which prevents us from considering single blocks, e.g., of different partial dissolution temperature separately.

GJ-1, crystal #67. The three measurement blocks of a total of 30 analyses reported in Table S7† were acquired between 2010 and 2020 and are heterogeneous in terms of the tracer used (ET535, ET2535 bottles #1 and #2), as well as the chosen temperatures for partial dissolution (180 °C and 210 °C). The original TIMS GJ-1 data published in ref. 46 were discordant, and due to this, the SIMS and LA-ICP-MS community has adopted the ²⁰⁷Pb/²⁰⁶Pb date as the standard age. Therefore, not only ²⁰⁶Pb/²³⁸U dates, but the degree of discordance needs to be evaluated for our data set as well (see Fig. S2†). The three measurement blocks demonstrate the increase of precision of the Geneva laboratory over 10 years, at the detriment of the repeatability. Block 1 (2010) provides a cluster of 6 concordant data with a mean ²⁰⁶Pb/²³⁸U date of 600.62 ± 0.39 Ma (²⁰⁷Pb/²⁰⁶Pb date = 605.39 ± 1.1 Ma); block 2 was spiked with ET535 tracer solution and yields a mean date of 5 concordant points of 600.39 ± 0.41 Ma (²⁰⁷Pb/²⁰⁶Pb date = 603.71 ± 1.5 Ma); block 3 shows excessive scatter, which is mostly produced from the PHOENIX measurements #17 to 30. Interestingly, all 30 analyses overlap within uncertainty with the Concordia band; discarding the three youngest analyses (with suspected lead loss bias) a mean ²⁰⁶Pb/²³⁸U date of 600.28 ± 0.16 Ma (MSWD = 14, N = 27) can be calculated as an estimate for the GJ-1 reference material, but this date is not statistically significative. The mean ²⁰⁷Pb/²⁰⁶Pb date for crystal #67 of GJ-1 is 605.2 ± 4.8 Ma (MSWD = 7, N = 30).

Discussion

In the following, we discuss the cross-calibration of the different mass spectrometer models and address different problems that arise from our data set that are likely responsible for the observed batch-to-batch and within-batch overdispersion of data from the synthetic ET100 solution and for the heterogeneity among natural reference zircon analyses. Finally, we suggest some best-practices in order to minimize these observed problems.

Comparison of the analytical performance of the TRITON and the PHOENIX mass spectrometers

As a main result of this study, our repeated intercalibration exercises demonstrate that these two spectrometers yield identical apparent ²⁰⁶Pb/²³⁸U dates of a synthetic ET100 solution with a precision of roughly 100 ppm (0.01%) within individual batches prepared at the same time within the same lab. The cross-calibration between TRITON and PHOENIX mass spectrometers is of paramount importance for the high-precision U–Pb geochronology community, which uses both TIMS platforms, but very rarely within the same laboratory. Therefore, any existing interlaboratory bias cannot be explained solely by the use of different TIMS platforms and likely has other reasons.

Potential reasons for excess data scatter of the synthetic ET100 solution

A conspicuous result is the fact that repeated measurement of ET100 solution under ideal analytical conditions (high Pb*/Pb_c; correct sample/spike ratio) creates significant overdispersion within a large data set (Fig. 1). Possible sources of excess data scatter may come from mass spectrometry, such as Daly or Faraday gain and yield instability, potentially variable interferences on ²⁰²Pb and ²⁰⁵Pb spike masses, or variable blank and blank isotope composition. However, the perfect data overlap observed within all 5 intercalibration exercises (Fig. 2) points to a source of scatter originating earlier in the procedure, prior to analysis by TIMS. The perfect repeatability of the apparent ²⁰⁷Pb/²⁰⁶Pb age of the ET2000 synthetic solution (Fig. 4) suggests that the Pb isotope measurement is perfectly reproducible within analytical uncertainty, and highlights how performing inter-element isotopic analysis (Pb/U) is significantly more challenging. Assuming that the Faraday-based U isotope analyses does not introduce significant scatter, we therefore suggest that U/Pb fractionation occurs during the preparation of the sample-spike mixture prior to mass spectrometry.

The strong, long-term fluctuations of the apparent ²⁰⁶Pb/²³⁸U age of the ET100 solution (Fig. 1), may be explained by non-reproducible fractionation of the U/Pb ratio (i) during the process of sampling from the ET100 solution, (ii) through adding the ET2535 tracer solution to the sample, or (iii) because of imperfect sample-tracer equilibration prior and during evaporation. Both ET100 and tracer solutions are stored in dropper bottles and from both solutions an aliquot is removed by adding one to several drops directly into a Savillex vial. We speculate that U/Pb fractionation may happen during several steps of the process, such as differential adsorption of U⁴⁺ and Pb²⁺ ions on the Teflon container walls, differential condensation of the two molecules and non-complete re-introduction of condensate into the solution before sampling. Empirically, shaking the ET100 solution bottle before aliquoting solution has proved to decrease the data scatter (as shown by the ETH data set, Fig. 3).

In addition to these issues, the 0.2% jump in apparent ²⁰⁶Pb/²³⁸U ages shown between the January and November 2016 TRITON–PHOENIX intercalibration exercises coincides with the change from ET2535 spike bottle #1 to #2 at UNIGE, after the level of liquid in spike bottle #1 dropped to a few percent of the initial volume of the tracer solution. It seems that there may be some U/Pb fractionation associated with the incremental removal of solution over time. This fractionation becomes apparent at low remnant levels of tracer solution therefore the tracer solutions must be regularly checked through, e.g., repeat measurements of the ET100 solution, and discarded before being completely depleted. We therefore consider the data collected during the January 2016 intercalibration exercise (run numbers #132–158) as outliers that are not representative of the overall ET100 scatter.

It is important to note that the pretreatment of ET100 solution is different from natural zircon: sample-spike mixtures do not undergo equilibration in chloride form under pressure as it is the case for zircon. We therefore suggest that a simple dry-down of two drops of ET100 solution with the same amount of tracer on a hotplate at ∼120 °C, as previously done in the UNIGE and presumably in other labs is not assuring complete spike-sample equilibration. The three labs involved in this study have introduced different methodologies to overcome this problem: (i) a two-step equilibration was introduced in the UNIGE lab, which resembles the common sample/spike equilibration procedure for zircon more closely. The last set of 15 analyses of ET100 solution from two individual microcapsules (Fig. 1 and data in Table S5†) indicate that when utilizing this approach, we get closer to an equivalent population of data with a MSWD of 2.1 at N = 15. (ii) Very comparable results were obtained in the PU lab, where a large batch of ET100 solution and tracer was equilibrated on the hotplate during several days, leading to a data set with an MSWD of 1.7, N = 28 as well (Fig. 3). (iii) The ETH lab achieves similar repeatability by shaking the ET100 and tracer bottles followed by a dry-down on the hotplate in 200 μml of 3 M HCl. We therefore suggest that any of the presented homogenization procedures either at elevated temperature and pressure, or in larger volumes of HCl will lead to more reproducible ET100 solution data, as the three data sets from UNIGE, PU and ETH suggest (Fig. 3). However, we will need to evaluate whether and how much these adjusted solution preparation techniques increase the repeatability of the apparent ²⁰⁶Pb/²³⁸U age of the ET100 solution on a long term (months to years).

Comparison of synthetic solution with natural zircon data sets

Natural zircon is used as a reference material to calibrate matrix-dependent fractionation effects in SIMS and LA-ICP-MS U–Pb dating. A homogeneous zircon material of well-known age is essential for the accuracy of these dating techniques. A series of international reference zircon materials have been proposed, for which high-precision ID-TIMS ages are available (see compilation in, e.g., ref. 50). For the Temora-2 and GJ-1 reference zircon materials, recent high-precision ages using an EARTHTIME tracer have been published.^38,51 Despite the availability of high-precision ages for these zircon, most spot-dating laboratories use the values of ref. 45 and 46 instead.

For Temora-2, our ²³⁰Th disequilibrium uncorrected ²⁰⁶Pb/²³⁸U date of 417.353 ± 0.052 Ma (95% c.l., MSWD = 4.4) is slightly outside the uncertainty limits of the ²⁰⁶Pb/²³⁸U date of 416.78 ± 0.33 Ma from ref. 45 which was obtained on mechanically and not chemically abraded grains. Our age is very similar to the date reported in ref. 38, 417.361 ± 0.072 Ma (N = 9, MSWD = 1.8). We suggest that 417.353 ± 0.052 Ma (95% c.l., MSWD = 5) is the best estimate for the age of this reference zircon.

The data compilation in Fig. 5 provides evidence that the Temora-2 data set is biased by non-mitigated residual lead loss, and inheritance. The too young analyses #67 and 69 were chemically abraded at only 180 °C, while #31, #50 and 58 belong to a series that underwent partial dissolution at 210 °C for 12 hours, which is the recommended temperature and time of Widmann et al.⁴¹ Incomplete removal of radiation damaged portions of the analyzed grains may therefore be dependent on factors other than temperature and duration of the partial dissolution step.^41,52

The reference zircon GJ-1 is distributed as individual, large grains purchased from a Sidney gem dealer.⁴⁶ Therefore, we could anticipate that analyses from different crystals and different labs do not necessarily coincide and we consider our results valid for grain #67 only. Jackson et al.⁴⁶ reported eight discordant analyses from fragments of four different grains obtained by F. Corfu at the U–Pb laboratory at the R.O.M., Toronto. They did not undergo any abrasion (neither mechanical nor chemical) and show considerable scatter along a Pb loss line with an upper intercept age of around 608.5 Ma and a zero-age lower intercept. Their mean ²⁰⁷Pb/²⁰⁶Pb age of 608.5 ± 0.4 Ma is frequently used as a reference value by LA-ICP-MS laboratories. The new analyses of GJ-1 reported in ref. 51 reproduce the old values but with largely increased precision: they report measurably discordant values at a Th-uncorrected ²⁰⁶Pb/²³⁸U date of 601.87 ± 0.37 Ma, and a mean ²⁰⁷Pb/²⁰⁶Pb date of 607.7 ± 0.7 Ma. First doubts about the validity of a ²⁰⁷Pb/²⁰⁶Pb age around 607 Ma for crystal #67 were raised with the ²⁰⁶Pb/²³⁸U date of 600.5 ± 0.4 Ma mentioned in ref. 53, however the data were not presented. The data referred to in ref. 53 data are those shown in the first block (run numbers #1–6) in Table S6.† Analyses from crystal #67 reported in this study were obtained over a time span of more than 10 years and document the improvement in precision in the UNIGE lab over this time period. Most importantly, none of our 30 analyses reported in Table S6† are analytically discordant, they all at least overlap the limits of uncertainty band of the concordia (Fig. S2†). It is evident that our data set shows significant dispersion, even after rejection of three young outliers possibly related to residual lead loss. The latter provide a ²⁰⁶Pb/²³⁸U age of ∼598 Ma and are in quite good agreement with the youngest analysis in ref. 46. We may propose a ²³⁰Th disequilibrium-uncorrected average ²⁰⁶Pb/²³⁸U age of 600.28 ± 0.16 Ma (95% c.l., MSWD = 14) as our best age estimate for crystal #67 of this reference material (Fig. 5). Our data have a 0.26% lower ²⁰⁶Pb/²³⁸U age that does not overlap with the precise U–Pb dates reported in ref. 51. We may speculate that the data from zircon #67 are not directly comparable to the data from other GJ-1 grains, but the excess scatter makes our data set inconclusive. GJ-1 grain #67 is frequently used for LA-ICP-MS dating in the laboratory at University of Lausanne and its accuracy using an age of 600.4 Ma is repeatedly confirmed through comparison with ID-TIMS dates (e.g., ref. 54 and 55); by applying the Jackson et al.⁴⁶²⁰⁷Pb/²⁰⁶Pb age value, these data would suffer from a ∼1% systematic inaccuracy, however that would not be identifiable with the 2% analytical uncertainty of the technique⁵¹ and the inherent inaccuracy through the analysis of non-chemically abraded zircon.

Overall, the analyses of the two natural zircon reference materials do not contribute to the resolution of the above discussed problems of excess scatter of ²⁰⁶Pb/²³⁸U dates. Analysis of natural material is always linked to higher degrees of uncertainty (e.g., variable and non-ideal sample-spike isotope ratios; variable concentrations of blank (Pb_c) and therefore of Pb*/Pb_c). In addition, incomplete mitigation of radiation-damage related lead loss is likely a main reason for age scatter, the other being natural age variation from protracted growth, the presence of antecrystic or xenocrystic domains, or discrete zones of alteration. These effects are very likely present in our zircon data from Temora and GJ-1. In conclusion, repeated analysis of synthetic solutions under optimal analytical conditions is the best way to quantify the level of precision and repeatability of our dating procedure.

As a further development, a solution prepared from a zircon population and already spiked with an isotope tracer may more closely match the procedures of natural zircon analysis. This would include the ion chromatography step, making it a more systemic test. This zircon solution is in preparation in the EARTHTIME consortium and will allow labs to test their analytical precision, repeatability and enable interlaboratory calibration at higher precision and accuracy than via the analysis of individual grains of a zircon reference material.

Can we derive best practices?

It is evident that natural age dispersion from decay damage related Pb-loss and/or xenocrystic or antecrystic inheritance remain the biggest obstacles in achieving perfect accuracy in U–Pb dating. An empirical but quantitative assessment of the duration of the partial dissolution step of chemical abrasion demonstrated that a 12 hour dissolution in HF + HNO₃ at 210 °C gets closest to a pristine zircon lattice in the residual material.⁴¹ Unfortunately, in many cases, such treatment is impossible due to excessive decay damage from old age and/or high U concentration, leaving us with a residual inaccuracy that is impossible to resolve. However, we need to be aware that we may bias our results towards a higher or a lower age through this treatment, depending on whether the highest-U growth zones are in the center or the rim of the zircon.

Apart from Pb loss, we identify the isotope dilution and equilibration procedure as a significant source of ²⁰⁶Pb/²³⁸U age scatter in ET100 analyses. It is evidently insufficient to let one drop of each ET100 solution and tracer simply dry down in a beaker. Therefore, we recommend following one of the procedures described above that lead towards an improved spike-sample equilibration.

As an additional potential sources of data scatter, evaporative loss from the spike bottle would not change the calculated age as long as U is not fractionated from Pb; however, drops of condensate have to be re-introduced into the solution either by carefully swiveling the bottle around or by gently shaking it. This applies to both tracer solution and synthetic standard solution. Smallest droplets of condensate in the capillary tubing of both solution and tracer bottle may have the same effect and may need to be removed by discarding the first drop.

Summary and outlook

(1) The EARTHTIME ET100 solution is currently the best reference material to check repeatability and accuracy at the 100 ppm level of a ²⁰⁶Pb/²³⁸U date, if the reagents are prepared and measured quasi-simultaneously, and the conditions outlined in this paper are respected. Natural materials do not reproduce at the same level, due to the combination of natural age variation and residual lead loss. Therefore, we suggest that U–Pb ID-TIMS labs present relevant ET100 data when publishing new data, in order to allow for more comparable data sets across the field.

(2) Using different mass spectrometers for isotope analysis is not the limiting factor for the accuracy of high-precision U–Pb dates obtained by ID-TIMS. U–Pb dates of the synthetic EARTHTIME ET100 solution from both TRITON (Thermo Scientific) and PHOENIX (IsotopX) TIMS coincide at the 0.01% level of uncertainty of ²⁰⁶Pb/²³⁸U age. The main factors that limit repeatability of U–Pb ages are instead: (i) the heterogeneity of natural sample material, and (ii) fractionation phenomena that occur due to inappropriate procedures not ensuring complete spike-sample equilibrium in solution.

(3) Achieving high precision is not the main challenge of U–Pb geochronology but instead ensuring repeatability and accuracy of the obtained dates. For an assessment of precision and short-term repeatability, aliquots of ET100 solution have to be prepared and measured in batches. By choosing ideal measurement conditions at Pb*/Pb_c above 15, we could achieve a short-term repeatability and a cross-calibration between the two TIMS models in at a precision of 100 ppm or better in ²⁰⁶Pb/²³⁸U date. However, testing repeatability through continuous analysis of the EARTHTIME ET100 solution is flawed by non-ideal sample-spike equilibration, which requires a careful homogenization of the sample-spike mixture at elevated temperature (and possibly pressure).

(4) For natural zircon, decay damage related partial loss of radiogenic Pb remains partly uncontrolled despite optimized conditions during the partial dissolution step of the chemical abrasion treatment (12 hours at 210 °C (ref. 41)). These effects, combined with natural age variability, are the reason that our data from natural reference zircon material (Temora, GJ-1) do not allow assessment of precision and accuracy at better than 0.1% of a ²⁰⁶Pb/²³⁸U date, and are one order of magnitude worse than it is possible with the ET100 solution.

(5) We suggest that production and distribution of a natural zircon solution would make it possible to carry out tests of precision, repeatability and interlaboratory reproducibility more closely matching natural zircon analysis at high precision.

(6) As an outlook beyond the work presented here, we anticipate that the shift from SEM and Daly-based ion counting to high-sensitivity Faraday based Pb isotope analysis using high-resistance Faraday analysis on the TRITON,³⁸ or to ATONA Faraday analysis on the PHOENIX,⁴⁰ as well as the direct determination of the U isotope composition⁵⁶ will contribute to a better precision and accuracy of U–Pb age determinations in the future.

Author contributions

MO, SPG, BS, JFW, JFHLD, FF, NG and DS carried out the isotopic analyses, US compiled all the data, all authors participated in the writing of the text.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful for technical support from the staff at UNIGE (M. Senn, F. Arlaud, M. Chiaradia). US acknowledges the continuous support of the Swiss National Science Foundation for funding of the University of Geneva isotope laboratories (ongoing projects CRSII5_180253, 200020_182007). This study was funded by US National Science Foundation grants EAR-1726099 and EAR-1735512 to BS. We thank the two journal reviewers for interesting and constructive comments. We also like to acknowledge the longstanding good relationship and open information exchange with people from both mass spectrometry companies (Thermo Scientific, Bremen, D; IsotopX Ltd., Cheshire, U.K.) that made this work possible.

References

1. P. W. Hoskin and U. Schaltegger, Rev. Mineral. Geochem., 2003, 53, 27–62.
2. D. Coleman, W. Gray and A. Glazner, Geology, 2004, 32, 433.
3. B. Schoene, U. Schaltegger, P. Brack, C. Latkoczy, A. Stracke and D. Günther, Earth Planet. Sci. Lett., 2012, 355–356, 162–173.
4. J. F. Wotzlaw, U. Schaltegger, D. A. Frick, M. A. Dungan, A. Gerdes and D. Günther, Geology, 2013, 41, 867–870.
5. K. M. Samperton, B. Schoene, J. M. Cottle, C. B. Keller, J. L. Crowley and M. D. Schmitz, Chem. Geol., 2015, 417, 322–340.
6. F. Farina, A. Dini, M. Ovtcharova, J. H. F. L. Davies, N. D. Greber, A.-S. Bouvier, L. Baumgartner, A. Ulyanov and U. Schaltegger, Earth Planet. Sci. Lett., 2018, 495, 213–223.
7. S. P. Gaynor, D. S. Coleman, J. M. Rosera and M. J. Tappa, J. Geophys. Res.: Solid Earth, 2019, 124, 2457–2468.
8. D. Szymanowski, B. S. Ellis, J. F. Wotzlaw and O. Bachmann, Earth Planet. Sci. Lett., 2019, 510, 103–115.
9. M. P. Eddy, O. Jagoutz and M. Ibanez-Mejia, Geology, 2017, 45, 527–530.
10. C. R. Martin, O. Jagoutz, R. Upadhyay, L. H. Royden, M. P. Eddy, E. Bailey, C. I. O. Nichols and B. P. Weiss, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 29487–29494.
11. C. Chelle-Michou, M. Chiaradia, M. Ovtcharova, A. Ulianov and J. F. Wotzlaw, Lithos, 2014, 198–199, 129–140.
12. Y. Buret, J. F. Wotzlaw, S. Roozen, M. Guillong, A. von Quadt and C. A. Heinrich, Geology, 2017, 45, 623–626.
13. S. J. E. Large, A. von Quadt, J. F. Wotzlaw, M. Guillong and C. Heinrich, Econ. Geol., 2018, 13, 39–61.
14. S. P. Gaynor, J. M. Rosera and D. S. Coleman, Geosphere, 2019, 15, 548–575.
15. T. M. Herriott, J. L. Crowley, M. D. Schmitz, M. A. Wartes and R. J. Gillis, Geology, 2019, 47, 1044–1048.
16. M. Ovtcharova, H. Bucher, U. Schaltegger, T. Galfetti, A. Brayard and J. Guex, Earth Planet. Sci. Lett., 2006, 243, 463–475.
17. T. Galfetti, H. Bucher, M. Ovtcharova, U. Schaltegger, A. Brayard, T. Brühwiler, N. Goudemand, H. Weissert, P. A. Hochuli, F. Cordey and K. Guodun, Earth Planet. Sci. Lett., 2007, 258, 593–604.
18. U. Linnemann, M. Ovtcharova, U. Schaltegger, A. Gaertner, M. Hautmann, G. Geyer, P. Vickers-Rich, T. Rich, B. Plessen, M. Hofmann, J. Zieger, R. Krause, L. Kriesfeld and J. Smith, Terra Nova, 2019, 31, 49–58.
19. B. Schoene, J. Guex, A. Bartolini, U. Schaltegger and T. J. Blackburn, Geology, 2010, 38, 387–390.
20. T. J. Blackburn, P. E. Olsen, S. A. Bowring, N. M. Mclean, D. V. Kent, J. Puffer, G. McHone, E. T. Rasbury and M. Et-Touhami, Science, 2013, 340, 941–945.
21. F. Corfu, H. Svensen and A. Mazzini, Earth Planet. Sci. Lett., 2016, 434, 349–352.
22. J. H. F. L. Davies, A. Marzoli, H. Bertrand, N. Youbi, M. Ernesto and U. Schaltegger, Nat. Commun., 2017, 8, 15596.
23. B. Schoene, M. P. Eddy, K. M. Samperton, C. B. Keller, G. Keller, T. Adatte and S. F. R. Khadri, Science, 2019, 363, 862–866.
24. N. D. Greber, J. H. F. L. Davies, S. P. Gaynor, F. Jourdan, H. Bertrand and U. Schaltegger, Results in Geochemistry, 2020, 1, 100005.
25. J. H. F. L. Davies, A. Marzoli, H. Bertrand, N. Youbi, M. Ernesto, N. D. Greber, M. Ackerson, G. Simpson, A.-S. Bouvier, L. Baumgartner, T. Pettke, F. Farina, H. V. Ahrenstedt and U. Schaltegger, Contrib. Mineral. Petrol., 2021, 176, 9.
26. R. Mundil, K. Ludwig, I. Metcalfe and P. Renne, Science, 2004, 305, 1760.
27. J. Mattinson, Chem. Geol., 2005, 220, 47–66.
28. S. A. Bowring, D. Erwin, R. R. Parrish and P. Renne, Geochim. Cosmochim. Acta, Suppl., 2005, A316.
29. J. F. Bowring, N. M. Mclean and S. A. Bowring, Geochem., Geophys., Geosyst., 2011, 12, Q0AA19.
30. N. M. Mclean, J. F. Bowring and S. A. Bowring, Geochem., Geophys., Geosyst., 2011, 12, Q0AA18.
31. N. M. McLean, D. J. Condon, B. Schoene and S. A. Bowring, Geochim. Cosmochim. Acta, 2015, 164, 481–501.
32. D. J. Condon, N. M. Mclean, B. Schoene, S. A. Bowring, R. R. Parrish and S. Noble, Geochim. Cosmochim. Acta, Suppl., 2008, A175.
33. J. W. Valley, D. A. Reinhard, A. J. Cavosie, T. Ushikubo, D. F. Lawrence, D. J. Larson, T. F. Kelley, D. R. Snoeyenbos and A. Strickland, Am. Mineral., 2015, 100, 1355–1377.
34. T. Geisler, U. Schaltegger and F. Tomaschek, Elements, 2007, 3, 43–50.
35. M. Ovtcharova, N. Goudemand, Ø. Hammer, K. Guodun, F. Cordey, T. Galfetti, U. Schaltegger and H. Bucher, Earth-Sci. Rev., 2015, 146, 65–76.
36. D. J. Condon, B. Schoene, N. M. Mclean, S. A. Bowring and R. R. Parrish, Geochim. Cosmochim. Acta, 2015, 164, 464–480.
37. J. M. Koornneef, C. Bouman, J. B. Schwieters and G. R. Davies, Anal. Chim. Acta, 2014, 819, 49–55.
38. A. von Quadt, J. F. Wotzlaw, Y. Buret, S. J. E. Large, I. Peytcheva and A. Trinquier, J. Anal. At. Spectrom., 2016, 31, 658–665.
39. J. F. Wotzlaw, Y. Buret, S. J. E. Large, D. Szymanowski and A. von Quadt, J. Anal. At. Spectrom., 2017, 32, 579–586.
40. D. Szymanowski and B. Schoene, J. Anal. At. Spectrom., 2020, 35, 1207–1216.
41. P. Widmann, J. H. F. L. Davies and U. Schaltegger, Chem. Geol., 2019, 511, 1–10.
42. B. Schoene, J. Crowley, D. J. Condon, M. Schmitz and S. A. Bowring, Geochim. Cosmochim. Acta, 2006, 70, 426–445.
43. J. M. Rosera, S. P. Gaynor and D. S. Coleman, Econ. Geol., 2021, 1–24.
44. B. Schoene and E. F. Baxter, Rev. Mineral. Geochem., 2017, 83, 231–260.
45. L. P. Black, S. L. Kamo, C. M. Allen, D. W. Davis, J. N. Aleinikoff, J. W. Valley, R. Mundil, I. H. Campbell, R. J. Korsch, I. S. Williams and C. Foudoulis, Chem. Geol., 2004, 205, 115–140.
46. S. Jackson, N. Pearson, W. Griffin and E. Belousova, Chem. Geol., 2004, 211, 47–69.
47. H. Gerstenberger and G. Haase, Chem. Geol., 1997, 136, 309–312.
48. J. Hiess, D. J. Condon, N. M. McLean and S. R. Noble, Science, 2012, 335, 1610.
49. I. Wendt and C. Carl, Chem. Geol., 1991, 86, 275–285.
50. U. Schaltegger, A. K. Schmitt and M. S. A. Horstwood, Chem. Geol., 2015, 402, 89–110.
51. M. S. A. Horstwood, J. Košler, G. Gehrels, S. E. Jackson, N. M. McLean, C. Paton, N. J. Pearson, K. Sircombe, P. Sylvester, P. Vermeesch, J. F. Bowring, D. J. Condon and B. Schoene, Geostand. Geoanal. Res., 2016, 40, 311–332.
52. M. H. Huyskens, T. Iizuka and Y. Amelin, J. Anal. At. Spectrom., 2012, 27, 1439.
53. F. Boekhout, R. Spikings, T. Sempere, M. Chiaradia, A. Ulianov and U. Schaltegger, Lithos, 2012, 146–147, 48–64.
54. H. Rezeau, R. Moritz, J. F. Wotzlaw, R. Tayan, R. Melkonyan, A. Ulianov, D. Selby, F. X. D'Abzac and R. A. Stern, Geology, 2016, 44, 627–630.
55. U. Schaltegger, A. Nowak, A. Ulianov, C. M. Fisher, A. Gerdes, R. Spikings, M. Whitehouse, I. N. Bindeman, P. Brack, J. Hanchar, J. Duff, J. D. Vervoort, T. Sheldrake, L. Caricchi and O. Müntener, J. Petrol., 2019, 60, 701–722.
56. F. L. H. Tissot, M. Ibanez-Mejia, P. Boehnke, N. Dauphas, D. McGee, T. L. Grove and T. M. Harrison, J. Anal. At. Spectrom., 2019, 34, 2035.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ja00116g

---