Determination of the microscopic mineralogy of inclusion in an amygdaloidal pillow basalt by fs-LIMS†
Marek
Tulej
 *a,
Rustam
Lukmanov
a,
Valentine
Grimaudo
a,
Andreas
Riedo
*a,
Rustam
Lukmanov
a,
Valentine
Grimaudo
a,
Andreas
Riedo
 a,
Coenrad
de Koning
a,
Coenrad
de Koning
 a,
Niels F. W.
Ligterink
b,
Anna
Neubeck
a,
Niels F. W.
Ligterink
b,
Anna
Neubeck
 c,
Magnus
Ivarsson
d,
Sean
McMahon
c,
Magnus
Ivarsson
d,
Sean
McMahon
 e and
Peter
Wurz
e and
Peter
Wurz
 a
a
aSpace Research and Planetary Sciences, Physics Institute, University of Bern, Switzerland. E-mail: marek.tulej@space.unibe.ch
bCentre for Space and Habitability, University Bern, Switzerland
cDepartment of Geological Sciences, Uppsala University, Sweden
dDepartment of Paleobiology, Swedish Museum of Natural History, Sweden
eSchool of Physics and Astronomy, University of Edinburgh, Room 1508, James Clerk Maxwell Building, Peter Guthrie Tait Road, Edinburgh, EH9 3FE, UK
First published on 10th November 2020
Abstract
We present chemical depth profiling studies on mineralogical inclusions embedded in amygdale calcium carbonate by our Laser Ablation Ionisation Mass Spectrometer designed for in situ space research. An IR femtosecond laser ablation is employed to generate ions that are recorded by a miniature time-of-flight mass spectrometer. The mass spectra were measured at several locations on the sample surface and yield chemical depth profiles along the depth length of about 30 μm. The presence of oxides and sulphides within inclusion material allows us to derive elemental abundance calibration factors (relative sensitivity coefficients, RSCs) for major and minor elements. These are obtained from the atomic intensity correlations performed on the depth profiling data. With the RSCs corrections the quantitative analysis of more complex mineralogical phases within the inclusion is conducted by correlating atomic abundance fractions in ternary diagrams, typically used in geology. The spatial resolution of the depth profiles was sufficient to study chemically distinct micrometre-sized objects, such as mineralogical grains and thin layers of minerals including micrometre-sized filamentous structures. The method presented here is well-suited for the quantitative chemical analyses of highly heterogeneous materials where the ablation condition can vary locally with the material composition making the application of standard reference materials less accurate. The presented method is developed to distinguish between abiotic and biological material while searching for micrometre-sized extinct or extent life forms on the surfaces of Solar System bodies.
Introduction
One of the major objectives of current space research and planetology is the search for signatures of extant and extinct life on other planetary bodies. With the assumption that life on other planets should be based on the same physical and chemical rules as life we know from Earth and evolved along similar pathways, these searches should follow known terrestrial practice. Ancient extinct life can be identified by finding remains of organic material, stromatolitic layers, and individual microfossils within planetary rocks and soils.1 Identification of metabolic products together with the deciphering of fossilization mechanisms can be essential in such searches. Among available analytical instrumentation, only those instruments, which can deliver selective and sensitive chemical measurements of microscopic structures can be employed for this task.2,3For conducting analyses on planetary bodies only small, light, low-powered and sufficiently robust instrumentation can be used. Several space-borne instruments including Laser-Induced Breakdown Spectroscopy (LIBS), X-Ray Fluorescence (XRF), and Laser Raman Spectroscopy have proved their capabilities in delivering composition measurements of the sample surface and important biosignatures in numerous performance studies. However, their measurement sensitivity might not be sufficient to investigate the chemical composition of microscopic structures of sparse life.2,4 An example of the instrument combining Raman, LIBS and IR techniques is the SuperCam instrument designed on the NASA Mars2020 with the performance figures of each of applied technique described in recent publication and references therein.5,6 Compared to these techniques, laser-based mass spectrometry adds complementary information. With current LIMS spatial resolution (lateral and vertical) and sensitivity, detailed analyses of grain-size objects can be conducted with the determination of context mineralogy and detection of micro-sized fossils.7–9
Laser ablation ionisation mass spectrometry (LIMS) based on time-of-flight mass analysers is a well-known technique with its origin in the mid-1970s. In the beginning, the technique suffered from various drawbacks, which mostly were affecting the quantification and the measurement procedure. With the continuous advances in electronics, vacuum, and laser systems, this technology has re-emerged for laboratory and field application for chemical analysis of solid-state samples.10–12 Over the years, a high degree of miniaturisation of the LIMS instrument has been achieved with the objective to become a space-borne instrument.8,13–15 Robustness of the time-of-flight mass analyser, flexible operation of the laser ablation ion source, the control over the ion optics settings and detector gain allow direct and sensitive chemical analysis of raw samples providing efficient ion production and nearly 100% ion transmission from the measurement spot to ion detector.15,16 For the analysis of micrometre-sized objects such as grains or microfossils, the integration of a microscope camera system into the system helps in an initial characterisation of micro-sized objects and improving overlap of the laser spot with the object of interest.8,17
LIMS with an fs laser ablation ion source shows an increasingly higher performance. It delivers improved quantitative chemical composition information with considerably reduced element fractionation.18–20 Several recent studies show that LIMS can be considered as a standardless technique delivering semi-quantitative results.18–22 Further improvements to the quantitative analysis can be achieved by adding to atomic abundance derived from the single-charged atomic mass peaks also multiple ionised atomic mass peaks.23 An improved efficiency of the atomic ion production and quantification of atomic ions can be achieved applying a double pulse laser ablation/ionisation ion source.24 In double pulse system, the first pulse is ablating the sample surface and the second, shortly delayed pulse interacts with freshly formed plasma plume resulting in additional plasma heating, atomisation and ionisation. These processes influence also post-plasma chemistry efficiency. The presence of isobaric multiple-charged atomic ions and clusters in ion beam can introduce uncertainty in the quantification of the atomic signal measurement; hence, by applying double pulse laser ion source, the isobaric interferences can be minimized. It has been demonstrating also that the isobaric interferences due to clusters could be reduced by implementing collisional cell which allows partial temporal separation of the cluster and atomic ion distributions.25 High-resolution time-of-flight mass spectrometric measurements of atomic ions produced in laser ablation are typically difficult due to wide kinetic energy distributions of produced ions. Only, recently a high-resolution (M/ΔM ∼104) laboratory LIMS system with a double reflectron system was developed to resolve most of mass peaks of cluster ions, hence, the isobaric interferences resulting from polyatomic species can be avoided.26 In miniature LIMS systems designed for in situ applications not all these implementations can be made. Here, we propose alternative method of the abundance calibration. The applied method uses depth-profiling data and requires presence of simple chemical compounds such as oxides and sulphides within the sample material.
In recent years, fs-LIMS proved its capabilities for chemical analysis with high spatial (lateral, vertical) resolution. High lateral resolution is achieved by focusing laser radiation onto the surface to a spot size of a few micrometres and by tuning over the pulse energy, ablation rate and thickness of the ablated layer can be well controlled so that the measurements can be conducted with the depth resolution down to a few nanometres.27–32 In our recent studies on the Ni/Cr NIST standard, we have accomplished a depth resolution of about 30 nm applying UV femtosecond laser radiation arranged in a double pulse configuration.24,32 3D chemical mapping analysis with LIMS were recently presented.33,34
There are other laboratory analytical techniques, which offer high spatial resolution depth profiling capabilities such as Glow Discharge Mass Spectrometry (GD-MS), Laser Ablation Inductively Coupled Mass Spectrometry (LA-ICP-MS) and Secondary Ion Mass Spectrometry (SIMS).35–40 These instruments in current state of development are less suitable for application to space research but can be useful in applications in terrestrial environments. Current LIMS systems fulfil the requirements of size, weight or power consumption necessary available aboard a spacecraft, either a rover or a lander.7
In the current contribution, we introduce a procedure for the in situ atomic abundance calibration using micrometre-sized inclusion embedded in a calcium carbonate host mineral. The procedure uses the depth profiling data e.g. the measurements of atomic intensities in a function of ablation layer. By correlating the intensities of atomic species measured at specific ablation layers and observation of linear correlation, we can deduce the presence of the molecular compounds and determine corrections to the measured atomic intensities. These corrections are obtained by comparison of the measured slopes of the correlations and the expected values from the actual chemical formula. From the measurements of various oxides and sulphides we obtain the correction coefficients for most of major and minor elements. Determination of these corrections on simple compounds allows for a more detailed analysis of complex mineralogical phases present in the sample at microscopic scales. Having the obtained corrected elemental abundances, atomic abundance fractions are plotted in ternary diagrams allowing the investigation of more complex mineralogical phases. A similar procedure which is known as LRS-linear regression slope method was applied in earlier MC-ICP-MS studies to improve accuracy and precision of isotope ratios.41–43 This data reduction protocol used the simultaneous responses of all isotopes measured. In the current study, the simultaneous response of elements is expected while ablating specific molecular compound.
Similar materials to that studied here are found on Mars and can be considered as a distinct astropaleontological target. The calcium carbonate phase in basalts can host veins and voids, which are recognised as habitats for endolithic microorganisms and form secondary infilling mineralisation in volcanic environments.44–47 Thus, extended characterisation of these materials and understanding their heterogeneities are important to account for their biological or abiotic origin.
Experimental
Materials
The sample of an amygdaloidal pillow basalt from Kinghorn, Fife, Scotland48 was processed to a 30 μm thick thin-section, mounted on a stainless-steel sample holder and introduced into the vacuum chamber for its mass spectrometric analysis (Fig. 1). The left panel of Fig. 1 shows the thin-section of basalt with an inclusion of calcium carbonate. The right panel shows a close-up image of the dark inclusion, which contains a number of needle-shaped microscopic structures. The enclosure into the calcium carbonate host happened some 360–320 Ma ago.48The LIMS instrument
The mass spectrometric investigations were conducted with our miniature laser ablation ionisation mass spectrometer designed for in situ space research applications. The instrument combines a femtosecond-laser ablation ion source with a miniature time-of-flight mass analyser.22 Current studies are conducted with a NIR-fs-laser radiation (pulse width, Δt ∼190 fs, λ = 775 nm, laser pulse repetition rate of 1 kHz) focused to a circular spot of about 10 μm in diameter. In all measurements, a pulse energy of about 8 μJ on the sample surface was applied. The resulting craters were inspected with an optical microscope.17 The detailed crater morphology analyses can be found in our previous publications.31 The measurements were computer-controlled using our custom-designed operating system.15 The sample was attached to the xyz-micro-translation stages. The stage allows for about 2 μm positioning accuracy of the location of interest on the sample by using prior measurements size calibration with an in situ microscope camera system.17Mass spectrometric measurements
Mass spectra were collected at ten locations on the sample, starting from the pure calcium carbonate mineral, across the interface of the calcium carbonate host all the way into the dark inclusion, and on the inclusion's surface seen as a dark area in the centre of Fig. 1b. The dark inclusion consists of needle-shaped micrometre-sized structures that are embedded in complex mineralogical phases other than calcium carbonate. For each location 300 mass spectra were acquired corresponding to 300 ablated layers. The individual layer spectrum is measured by accumulation mass spectra of 200 laser shots on board of the acquisition system. Additionally, mass spectra on the calcium carbonate host were collected by drilling through the 30 μm thin-section, which corresponds to about 366 layers. The mass calibration of the spectra, mass peak integration and principles of depth profiling analysis were discussed in detail in our previous publications.49,50Relative sensitivity coefficients
The Relative Sensitivity Coefficient (RSC) for an element in the sample is obtained by dividing measured element concentration, Xm by the expected concentration, X: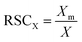 | (1) |
The LIMS instrument delivers measurement of atomic intensities. These intensities are calculated by integrating mass peaks of this element in the mass spectrum. Thus, the atomic concentrations are presented as the atomic fractions. To derive the RSC of an element, one compares the measured and expected atomic fractions:
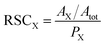 | (2) |
Knowing concentration ratio between elements Xi and reference element Y in the sample, we can derive another formula for calculating RSCs:
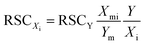 | (3) |
Using depth profiling data and the signal intensity correlation, we can identify elements, which form simple chemical compounds even they are distributed within sample volume irregularly. In addition to their intensity relationship, the linear intensity correlation of the measuring signals also yields the location where the signals are measured in the sample i.e., where these minerals are present in the sample. Hence, we can identify these compounds at specific ablation layers. The determination of RSCs from the signal intensity correlation between species in a simple chemical compound can be made this way, e.g., two or three-element compounds such as oxides or sulphides present in the sample as layers or grains can be made this way. For the correlation, we select the atomic signals of a compound, which originate from various ablation layers. Atomic signals emerging from the same compound will always create a linear correlation, since the element ratio will be constant in all different layers, independently of the amount of the compound. The slope of a linearly correlated data set is then the effective abundance ratio of the two correlating atomic species.
Results and discussion
Mass spectra of the calcium carbonate phase and the dark inclusion
Fig. 2a shows the mass spectrum measured on the pure calcium carbonate with C, O, and Ca as the major elements that are characteristic for the calcium carbonate mineral composition, CaCO3. From purely mass spectrometric perspective, it is hard to identify polymorphic modifications. The calcium carbonate could be calcite, aragonite, or vaterite, but earlier it was determined to be calcite.7 Additionally, we also observe mass peaks of the elements Na and K. The dynamic range of the spectrum is close to 104, which allowed for simultaneous detection of the major elements and trace elements with a bulk concentration of at least 100 ppm (atomic fractions). In addition to C, O and Ca also Li, B, F, Mg, S, Cl, and Sr elements are identified in the spectrum. These elements are known impurities in the calcium carbonate minerals. Other mass peaks within the low atomic mass range are double- and triple-charged ions of C, O, and Ca. Non-equilibrium chemistry in the expanding and cooling ablation plume leads to the formation of hydrocarbons, CxHy, and oxides, CaxOy (where x = 1–3 and y = 1–4), which ions are also observed in the mass spectrum. Similar mass spectra are recorded at locations 1–4 (see also Fig. 1b), indicating chemical homogeneity of the host mineral.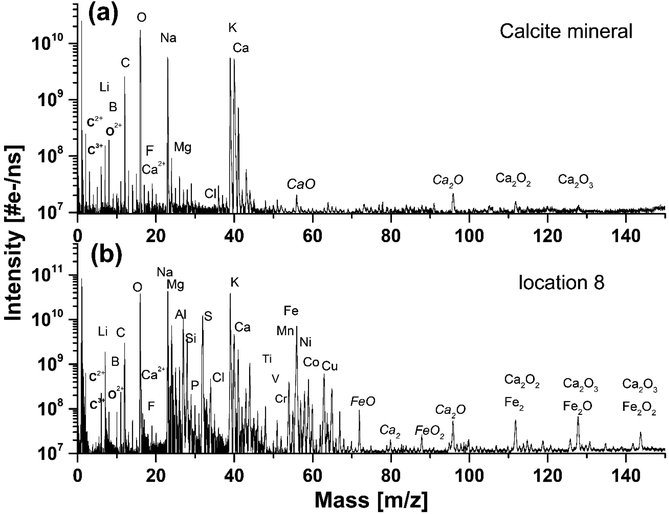 | ||
| Fig. 2 (a) The mass spectrum recorded on a pure calcium carbonate mineral on location 4, (b) and on the inclusion on location 8. | ||
The mass spectrum displayed in Fig. 2b was measured on the inclusion at location 9 (see also Fig. 1). The major and minor elements observed are O, Na, K, Fe and C, Mg, Al, Si, S, Ca, Ni, Co, respectively, including also the trace elements, Li, N, P, Ti, V, Cr, Cu, Zn and Sr. The dynamic range in the spectra is larger than 104. In addition, multiple charged ions, hydrocarbons and oxides of the main constituents C, O, Ca, and Fe can be identified in the mass spectra. The resemblance of the mass spectra at location 9 and at locations 6, 7 and 8 is large, indicating negligible chemical heterogeneity in the dark inclusion. However, the depth profiling analysis shows that the inclusion material is heterogeneous.
Chemical depth profiling on calcium carbonate mineral
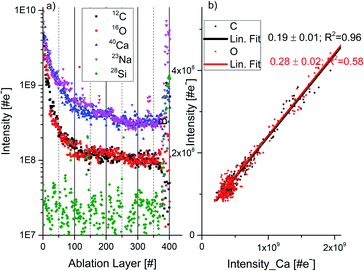
Fig. 3a shows the chemical depth profiles measured for the elements C, O, Na, and Si along the 30 micrometre-thick calcium carbonate sample as a function of the ablation layer number. The measured mass peak intensities are observed to decrease fast for about first 30 ablation layers and for the remaining ablation layers – approximately monotonically with the ablation layer number. Because of the mass peak shape distortions and peak intensity fluctuations in the spectra recorded during an initial ablation phase (here for the first 30 ablation layers) these spectra are removed from the analysis. Above the ablation layer number 366 we observe a sudden signal increase for all elements, including Na and Si. The Na and Si signals show the transition to the soda lime glass substrate, which indicates that the laser has drilled a crater through approximately 30 μm thick thin-section sample. Approximately circular craters with a diameter of about ø10 μm were produced as observed with the internal optical microscope.17 More advanced analyses of the crater characteristic were not conducted in the current study.Mass peak intensity correlation of C, O and Ca and RSC values
Inclusion material, heterogeneities
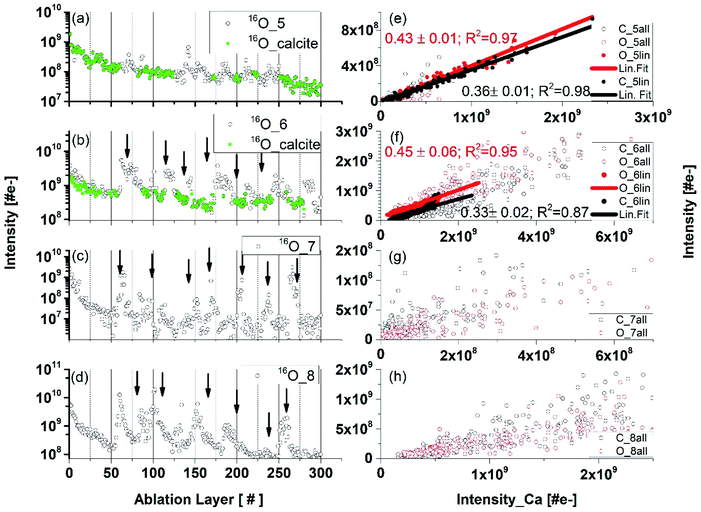
Fig. 4 compares the O depth profiles in a function of ablation layer number recorded at various locations on the inclusion including also location at the interface between pure calcium carbonate and inclusion material (Fig. 4, panel (a), see also location 5 in Fig. 1b). Similar depth profiles are observed for C and Ca although some differences at specific ablation layers in the profile shapes can be noticed. An increase of mass peak intensities at specific ablation layer form characteristic peaks on the depth-profiling curve. A systematic shift of these peaks towards lower ablation layer numbers is observed while the measurement locations become closer to the centre of the inclusion, as indicated by the arrows in Fig. 4(b–d). This shift is likely due to measurement of the same assembly of dark needles embedded in the matrix with a certain angle to the surface normal. The closer one gets to the centre of the dark inclusion, the earlier one measures the needle assembly because the darker area is closer to the surface and the needles were growing in opposite direction, along the direction of depth of the thin section. Fig. 4 (panels (e) to (h)) displays the mass peak intensity correlations of C with Ca, and O with Ca, measured at locations from 5 to 8. At location 5, the mass peak intensities correlate linearly well and only a small group of data points lay outside the correlation line. Contrary, at location 6, the linear correlation is observed only for a small part of data points (Fig. 4, panel (f)). At locations 7 and 8, no obvious linear correlation can be observed; the data points form a diffuse distribution with a large intensity spread. The data points in the depth profiles measured in locations 5 and 6 (Fig. 4, panels (a) and (b), respectively), for which the calcium carbonate mineral was identified via the linear correlations (red and black data points on the linear regression in panels (e) and (f)) are indicated as green circles in panels (a) and (b), respectively. These are found at the ablation layer numbers between regions of increased peak intensities on the depth-profiling curve. These layers with calcium carbonate, if present, are not easy to detect at locations 7–9. By fitting the fraction of the data that correlates to the calcium carbonate mineral at location 6, one obtains slope coefficient values for O, which are larger compared to that determined at the location of a pure calcium carbonate. The slope coefficient values in correlation of C and Ca are observed to be similar to each other at these locations with the slope coefficient values of 0.41 ± 0.06 and 0.31 ± 0.02 at location 6 and 0.45 and 0.33 at location 7 for C/Ca and O/Ca correlations, respectively (Fig. 4e and f). Considering data at locations 6 we can repeat the procedure applied for pure calcium carbonate phase and derive RSC coefficients of C, O and Ca at the inclusion location (see ESI Section A, Table 3†) using the composite spectrum obtained by summing up only the contributing the data points to linear correlations. These calculations yield RSCs of C, O, and Ca of 0.91 ± 0.05, 0.44 ± 0.05 and 2.71 ± 0.04, respectively. Applying again eqn (3) with RSC of Ca equal 2.71 ± 0.04 as reference and considering slope coefficients C/Ca and O/Ca we can obtain the RSC of C and O equal to 0.97 ± 0.09 and 0.38 ± 0.05, respectively. The RSC of Ca is chosen as the reference (see Section A, Tables 3 and 4 in ESI for more details†).Depth profiles at location 9
Fig. 5 shows depth profiles of several major and minor elements recorded at location 9. Significant mass peak intensity variations for all elements can be observed along the depth profiles at specific ablation layer numbers. Signal intensity variations indicate either a deficit or an increase of the element concentration at these specific ablation layers. Some increase of the ablation efficiency can occur because of the increased absorption of laser radiation at darker spots such as needles. In agreement with the signal intensity correlation studies at locations 7 and 8, we also observe that the Ca, C, and O signals do not correlate linearly. Moreover, at certain depths, a depletion of Ca is observed shown as shaded areas in Fig. 5a. At the ablation layer ranges 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58, 65
58, 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71, 128
71, 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132, 156
132, 156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161, and 165
161, and 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171, we can observe that the drop of the K intensity is accompanied by an increase of the intensities of Na, C, and Ca (Fig. 5a). Considering correlations of the minor elements, an increase of the S, Ni, Co, Mg, Mn, Cu, and B at several locations is typically accompanied by a decrease of the Fe and Ti mass peak intensities (see shaded areas in Fig. 5b and c). Only at the ablation, layer 110 all peaks intensities are observed to correlate. From the microscope images of the needle-like structures we can estimate their size to be in the range of 0.8–2 μm (Fig. 1b). The narrowest peaks in the depth profile involve 5 ablation layers (see Fig. 5). Thus, the thickness of the measured individual ablation layers is estimated to be in a range 0.2–0.4 μm.
171, we can observe that the drop of the K intensity is accompanied by an increase of the intensities of Na, C, and Ca (Fig. 5a). Considering correlations of the minor elements, an increase of the S, Ni, Co, Mg, Mn, Cu, and B at several locations is typically accompanied by a decrease of the Fe and Ti mass peak intensities (see shaded areas in Fig. 5b and c). Only at the ablation, layer 110 all peaks intensities are observed to correlate. From the microscope images of the needle-like structures we can estimate their size to be in the range of 0.8–2 μm (Fig. 1b). The narrowest peaks in the depth profile involve 5 ablation layers (see Fig. 5). Thus, the thickness of the measured individual ablation layers is estimated to be in a range 0.2–0.4 μm.
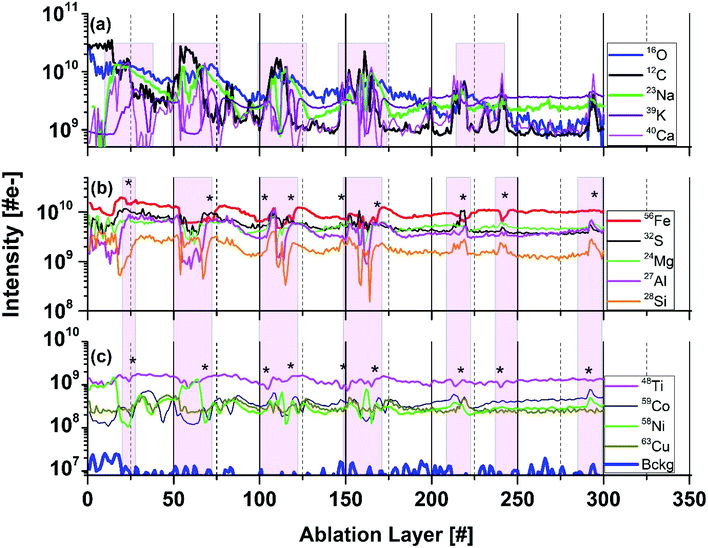 | ||
| Fig. 5 Variation of the intensities as function of ablation layer number for several elements (isotopes) measured on the dark inclusion at location 8 (Fig. 1b). Panel (a) shows the intensity variations of the C, O, Ca, Na, and K intensities. Panel (b) shows variations of the Fe, S, Mg, Al, and Si intensities. Panel (c) shows variations of Ti, Ni, Co, and Cu intensities. At ablation layers marked by (*) the intensities of Ni and Co correlate well with S, and anticorrelate with Fe. Shaded area highlights layer with specific element correlation, respectively anticorrelations. The traces are shifted to each other vertically for better visualisation of their shapes. | ||
Determination of RSCs from the data collected at locations 6 to 9
If the atomic signals were measured stoichiometric, the slope in the correlation would represent the abundance ratios of the elements of the relevant chemical formula. So far, we have determined RSCs for the elements C and O through their abundance correlation with Ca. Based on our previous studies we know that in the inclusion material other small chemical compounds are present including oxides and sulphides.By correlating the intensities of other elements with oxygen and sulphur intensities, we can gain the information about the RSCs for these elements providing that they form oxides and/or sulphides. The details of RSCs calculations are given in ESI, Section A Tables 5–7.† Here we briefly discussed the results obtained with the linear intensity correlation method.
In Fig. 6, the intensities of several elements are set in correlation with S (left panel) and O (right panel) intensities, respectively. For some parts of the data set, a linear correlation, either with oxygen or sulphur is observed indicating that these elements may have their origin in oxides and/or sulphides. This agrees with the results of our earlier studies, where identification of oxides and sulphides with other analytical methods were performed.7 Typically, the fs-LIMS measurements on Standard Research Materials show that RSCs for almost all metallic elements are, generally, close to one within about 15%. An exception are Al, Ti, Cu and Mg. RSCs of non-metallic elements such as C, S, O, Si and Ca various within broader range and depends sensitively on the ablation conditions and material properties.19,22
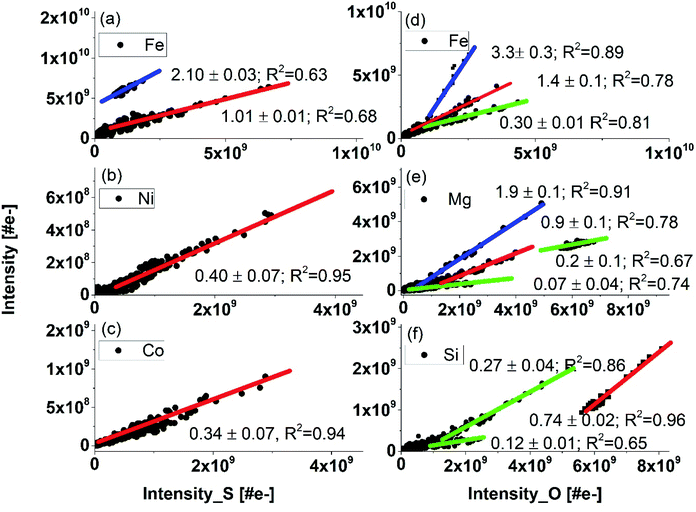 | ||
| Fig. 6 The correlation of Fe, Ni, and Co with S (panels (a–c)), and the correlation of Fe, Mg, and Si with O (panels (d–f)) based on all data measure on locations 6 to 9 (see Fig. 1b). The y-axis represents the intensity of the indicated element in the legend. The slopes (blue) are given for each correlation curve for the oxides and sulphides. RSCs are determined from the blue slopes. Lower slope values than expected for sulphides and oxides indicates that the analysed element was within another compound or a more complex. | ||
Iron is an abundant element in the inclusion. Typically, iron occurs ubiquitously in hydrothermal ore deposits in sulphides, oxides, silicates, and in carbonate minerals. In the correlation of the Fe with O intensities, we observe three different linear slopes (Fig. 6d). The coefficient values for the red and blue slope are 1.4 ± 0.1 and 3.3 ± 0.3, respectively. With RSC of O derived in the analysis of calcium carbonate on the inclusion equal to 0.38 ± 0.05, we derive RSC of Fe equal 1.25 ± 0.04 considering chemical formulas FeO for blue slope. From the slope coefficient of the red curve we can derive RSC of Fe equal to 1.05 ± 0.05 assuming that FeO2 is present in the sample (Fig. 6 panel (d)). From these data we obtain average RSC of Fe equal to 1.15 ± 0.05. RSC value for Fe is typically close to 1 (within 15% uncertainty) as it can be determined in the analyses of various materials including metallic or rock samples.19,22,51 The latter compound, FeO2, however, is unlikely to be present in our sample. The most common oxidation states of Fe are +2 and +3. With these valences Fe can be found in minerals such FeO (ferric oxide), Fe2O3 (hematite) or Fe3O4 (magnetite). Most viable candidate instead can be iron(II) hydroxide or ferrous hydroxide with the formula Fe(OH)2. Ferrous hydroxide is produced when iron(II) salts, e.g., iron(II) sulphate is treated with hydroxide ions. This process is likely to occur in aqueous environments including hydrothermal systems.52 The slope coefficient of the third correlation of Fe with O observed in Fig. 6c is smaller than the one assigned to the oxides. This result implies that those measured atomic signals may originate from more complex mixture of relevant chemical compounds or mineral phases. For a sample consisting of heterogeneities within a volume smaller than the sampled volume, the determination of RSC from the mass spectrum at this location would yield inaccurate results, because an unique element composition is assumed for the entire volume, thus entire data set. Using depth profiling, the mass peak intensity correlation method can be applied for each individual layer and can yield more accurate results. The specific chemical composition of each layer is preserved and the spatial resolution with the profiling depth is expected to be in sub-micrometre range. In this way an isolation between various compound can be achieved and the different mineralogical phases are recognised by means of their unique elemental composition (abundance ratio) within the various ablation layers. Hence, they can be identified from the correlation studies. Nevertheless, the lateral resolution of this study is at least order of magnitude lower and may affect an isolation of the signals if more than one unique mineralogical grains will be ablated simultaneously.
In similar analysis conducted for the correlation of Fe with S, we observe two linearly correlated populations (Fig. 6a). Taking the RSC value of Fe as 1.15 ± 0.05, we can determine the RSC value of S. The two correlation curves give the slope coefficients 2.10 ± 0.03 (blue) and 1.01 0.01 (red), respectively. Assigning the blue and red slopes as being due to the compounds FeS and FeS2, we can derive RSC of S equal to 0.54 ± 0.06 and 0.57 ± 0.04, respectively. The FeS and FeS2 are the most common forms of iron sulphides known in natural environments, such as mackinawite (metastable form of FeS), pyrrhotite (thermodynamically more stable form of FeS), cubic FeS, (formed in presence of foreign ions e.g. chloride ions), and pyrite (FeS2). These compounds are formed frequently also in hydrothermal environments. In our previous study, no pyrite could be identified in the inclusion though this compound is the most important sulphide gangue mineral and occurs in virtually all major hydrothermal base and precious metal mineral deposits. Nevertheless, if the deposits are subjected to high-grade metamorphism, pyrrhotite (FeS) replaces pyrite. This occurs typically by dissolution of pyrite from aqueous solutions and presence of Fe(SH)2 instead FeS2 in inclusion material.52–54
Similar analyses of RSCs of other elements including Mg, Al, Si, and Ca are conducting assuming that these elements can be present as sulphides and oxides. For the Mg and O intensity correlation, we observe four slopes and with S one slope. The slope with the coefficient 1.9 ± 0.1 corresponds likely to MgO. The correlation slope coefficient 0.91 ± 0.06 indicates that MgO2 could be present in the inclusion. Again, in this case similarly to other above cases, it is more likely that Mg(OH)2 is present instead. The slope value in correlation Mg and S is consistent with the measurement on MgS. Three linear correlations of Si with O are observed. Quartz (SiO2) is typically, the gangue mineral, most commonly encountered in ore-forming hydrothermal systems. Slope coefficient 0.74 in correlation with O is taken to derive the RSC of this element. It is likely that again Si(OH)2 instead of SiO2 is present in the sample. The correlation curves with smaller slope coefficients can reflect the presence of other mineralogical phases with a lower Si fraction in the compound. Similarly, for Al correlation with O, the measured slope coefficient is consistent with presence Al(OH)3 rather than common compound Al2O3. The analysis of Mg and Ca correlation curves with S yield RSCs similar to that obtained for correlation with O or from the analysis of calcium carbonate. The correlation of Ca with S with measured slope coefficient indicates presence of Ca(SH)2 and the analysis of correlation Al with S is consistent with Al2S3. The results of calculations of RSCs are given in Table 7.†
The slope coefficients of the Ni S, and Co and S correlation curves are 0.34 ± 0.07 and 0.4 ± 0.07, respectively, yield however much lower values of RSCs as expected for these metals (Table 7†). These coefficients are somewhat too small to yield the expected chemical formula NiS and CoS, assuming that RSCs of these elements are typically close to one.22,51 One of the reason for these RSCs being lower than 1 can be that the compounds NiS and CoS are well mixed and effectively a (Ni, Co)S compound is sampled in our experiment. The determination of RSC for S (from Fe-sulphides) also allows to conclude that the size of the other Ni and Co sulphides inclusions are smaller than the ablated layer thickness (≲150 nm). The ablation layers where NiS and CoS are measured cannot be resolved to see separate compounds. The optical imaging of the inclusion area shows large density of needles characteristic of millerite mineral.7 In addition to Co, also Cu, Mn, and Fe are known impurities, which are identified in millerite. Fig. 5 shows that at the ablation layers at which an increase of the Ni, Co and S signals is observed also signals of Mn, Cu or Mg increases. An exception are Fe and Ti signals, which decrease for these specific ablation layers.
A small part of data points of Ti are observed to linearly correlate with the slope coefficient 0.22 ± 0.03 indicating that Ti may be a part of more complex mineralogical phase(Fig. 5, panel (c)). In the analysed locations on the inclusion there is also no correlation of Ti with O observed. TiO2 (anatase mineral) was identified, however, in the previous studies in other inclusion locations. For the other trace elements including B, V, Cr, Mn, Zn and Cu measured here the correlation curves are too diffuse and the linear fit is not applied. However, their RSCs are expected to be close to one.18,20,51 The RSCs for non-metals such as Si, C, O, S or P are typically smaller than one. RSCs of Na and K are typically larger than 1, because it is relatively easy to ionise alkali elements comparing to other elements. RSCs of Na and K could not be derived from the correlation of these elements with O or S. For the minor and trace elements, the measurement intensities have larger statistical fluctuations resulting in less accurate determination of the slope coefficients. There are ablation layers in which the relevant atomic signals are weak or not detectable. For too large signals, the mass peak intensities can be under-measured due to the detector saturation effects. For large differences in material properties from one ablation layer to the other, the ablation process and efficiency of ion production may change affecting linearity of the atomic intensity correlation. The effects affecting the mass peak intensity measurements are discussed in more detail in our recent publication.55 The RSCs of investigated elements are summarised in Table 1.†
For a sample consisting of heterogeneities within a volume smaller than the sampled volume, the determination of RSC from the mass spectrum at this location would yield inaccurate results, because an unique element composition is assumed for the entire volume, thus entire data set. Using depth profiling, the mass peak intensity correlation method can be applied for each individual layer, which yields more accurate results.55 The specific chemical composition of each layer is preserved and the spatial resolution with the profiling depth is expected to be in sub-micrometre range. In this way an isolation between various compounds can be achieved and the different mineralogical phases are recognised by means of their unique elemental composition (abundance ratio) within the various ablation layers. Hence, they can be identified from the correlation studies. Nevertheless, the lateral resolution of this study is at least order of magnitude lower and may affect an isolation of the signals if more than one unique mineralogical grains will be ablated simultaneously.
Only, RSCs of major and some minor elements can be obtained using present method (see also ESI†). The corrections were applied to the atomic intensities of the major species Ca, O, S, Mg and Si. Such corrections can be important when the analysis of mineralogical phases are conducted as the rock chemistry depends on the concentrations of these elements. In ESI,† Section B, we show also the atomic intensities (background level value 107) and atomic fractions of all elements identified in this study.
Mineralogical phases
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
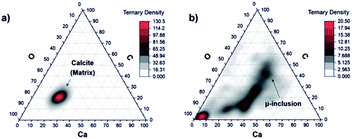
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60) that agrees with the chemical formula CaCO3. Contrary, the plot of the data representing the measurements on locations 6 to 9 shows very diffuse distribution with large spread from the area expected for the calcite mineral (Fig. 7, panel (b)). This may indicate that the other minerals instead a calcium carbonate are present at the inclusion location. This goes along with our previous investigations with spectroscopic methods, which identified the presence of mineralogical phases such as clinochlore [(Mg5Al)(AlSi3)O10(OH)8], clinochlore-transformed augite (Ca,Na)(Mg,Fe,Al,Ti)(Si,Al)2O8 and plagioclase (feldspar group) [NaAlSi3O8–CaAl2Si2O8].
60) that agrees with the chemical formula CaCO3. Contrary, the plot of the data representing the measurements on locations 6 to 9 shows very diffuse distribution with large spread from the area expected for the calcite mineral (Fig. 7, panel (b)). This may indicate that the other minerals instead a calcium carbonate are present at the inclusion location. This goes along with our previous investigations with spectroscopic methods, which identified the presence of mineralogical phases such as clinochlore [(Mg5Al)(AlSi3)O10(OH)8], clinochlore-transformed augite (Ca,Na)(Mg,Fe,Al,Ti)(Si,Al)2O8 and plagioclase (feldspar group) [NaAlSi3O8–CaAl2Si2O8].
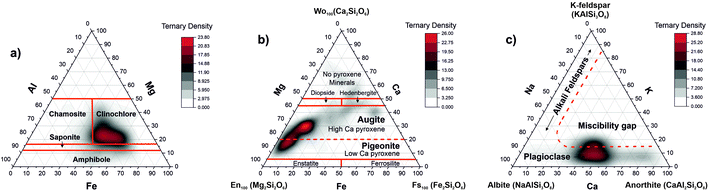
Clinochlore-transformed augite mineral is a member of pyroxene group namely calcic clinopyroxenes (diopside, hedenbergite, augite). Pure diopside of CaMgSi2O6 chemical composition can undergo as a complete solid solution to hedenbergite CaFeSi2O6 or augite (Ca,Mg,Fe2+,Fe3+,Al)2(Si,Al)2O6. In another chemical formula proposed for pyroxene group (CaxMgyFez)(Mgy1Fez11)Si2O, for augite, the relative composition of Ca can vary within the range 0.4 ≤ x ≤ 0.9 where x + y + z = 1 and y1 + z1 = 1.56 The ternary plot of Mg, Fe, and Ca proportions indicates presence of magnesian augite in the inclusion material (Fig. 8b).
Fig. 8c shows the ternary diagram of the abundances of the elements K, Na, and Ca, which is applied for the classification of feldspar minerals. One can identify the distribution of data along the base of the K coordinate, and the miscibility gap in the centre. The sequence of minerals along the base of the triangle indicate the presence of the plagioclase mineral or the solid solution series of plagioclase being a mixture between albite (sodium aluminosilicate: [Na(AlSi3O8)]) and anorthite (calcium aluminosilicate: [Ca(Al2Si2O8)]) and the notable absence of alkali feldspars.57 The red line denoting location of the feldspars is schematic. The RSC values of K and Na are chosen 1, which can be the reason that we observe the plagioclase on ternary diagram shifted more in the alkali region. The RSCs of K and Na are expected to be larger than 1 but they cannot here be derived accurately using the abundance correlation method applied to simple compounds.
In our previous studies the analyses conducted by various analytical techniques showed that the dark inclusion investigated here is highly weathered basalt with olivine, and pyroxene (augite) phenocrysts with a dominating amygdales phase.7 Typically, amygdales in basaltic lavas are formed after lava cools down, and hydrothermal fluids pass through the cavities. Their precipitation in the bubbles form secondary minerals such as calcium carbonate, zeolites, and quartz, depending on the fluid composition. The depth profiles indicate also presence of layers of various mineralogical phases around the millerite needles. Oxides and sulphides of several metals are present as separate entities and some of the metals fill the sites of complex mineralogical compounds.52
Summary
We describe the mass spectrometric measurements conducted by fs-laser ablation/ionisation time-of-flight mass spectrometry and introduce principles of data analysis, which yields to true elemental abundances. The corrections to measured atomic abundances are obtained by analysing atomic intensity correlations using depth-profiling data. In heterogeneous sample such as analysed inclusion embedded in a calcium carbonate mineral, chemical compounds are present at specific depths and can be identified in specific ablation layers. By correlating the measured atomic intensities, one can select the data points for which atomic intensities, correlate linearly. With the slope coefficients of these correlations, the relative abundances of the correlated elements are derived. The method was tested successfully on a pure calcium carbonate phase followed by locations at the interface between inclusion and calcite mineral and on the inclusion. RSCs for major and minor elements were derived by correlating atomic intensity of these elements with either oxygen or sulphur. Subsequently, with the corrected elemental abundances more complex mineralogical phases were analysed by applying the ternary atomic abundance fraction correlations on specific elements typically chosen in geological analysis of the mineralogical context.The mass spectrometric results are consistent with the results presented in our former studies of this sample conducted with several other instruments. However, LIMS studies cannot differentiate between minerals with the same chemical formula such as calcium carbonate mineral, which can occur as aragonite, calcite or vaterite. To conduct such analysis the Raman measurements will be necessary. Similarly, with the IR analysis one would approve our ambiguous assignment of presence of hydroxides or hydrosulphides in the sample. The presented method can be important in studies of highly heterogeneous materials, because matrix-matched reference materials are often not available for complex natural samples. The in situ determined RSCs can overcome the problems associated with the local heterogeneity, which can occur in the micrometre range similar to the sample probing laser spot. Thus, the in situ atomic abundance calibration introduced here can allow quantitative chemical composition investigation of heterogeneous structures. With the detection of heterogeneity in the micrometre scale, one can analyse grain-size objects such as microsized minerals or microfossils in detail. The presented method can be also of interest in searches for ancient fossilised life forms on planetary surfaces because in addition to context mineralogy, high depth profiling resolution provides means for isolation and analyses of microfossils embedded in mineralogical phases.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. Wurz acknowledges financial support by Swiss Science Foundation (SNSF). A. Neubeck acknowleges Swedish Research Council (contract no. 2017-05018).References
- K. E. Peters, J. M. Walters and J. M. e. Moldowan, The Biomarker Guide, Cambridge University Press, 2005 Search PubMed.
- A. H. Stevens, A. McDonald, C. de Koning, A. Riedo, L. J. Preston, P. Ehrenfreund, P. Wurz and C. S. Cockell, Sci. Rep., 2019, 9, 9706 CrossRef.
- A. Riedo, C. de Koning, A. H. Stevens, C. S. Cockell, A. McDonald, A. C. Lopez, V. Grimaudo, M. Tulej, P. Wurz and P. Ehrenfreund, Astrobiology, 2020, 20, 1224–1235 CrossRef CAS.
- A. Riedo, C. de Koning, A. Stevens, A. C. o. L. p. McDonald, A. Tulej, P. Wurz, C. S. Cockell and P. Ehrenfreund, Astrobiology, 2020, 20, 1224–1235 CrossRef CAS.
- J. M. Reess, M. Bonafous, L. Lapauw, O. Humeau, T. Fouchet, P. Bernardi, P. Cais, M. Deleuze, O. Forni, S. Maurice, S. Robinson, R. C. Wiens and S. Team, Proc. SPIE, 2018, 11180 Search PubMed.
- P. Sarrazin, D. Blake, M. Gailhanou, F. Marchis, C. Chalumeau, S. Webb, P. Walter, E. Schyns, K. Thompson and T. Bristow, J. Instrum., 2018, 13, C04023 CrossRef.
- A. Neubeck, M. Tulej, M. Ivarsson, C. Broman, A. Riedo, S. McMahon, P. Wurz and S. Bengtson, Int. J. Astrobiol., 2016, 15, 133–146 CrossRef CAS.
- M. Tulej, A. Riedo, M. B. Neuland, S. Meyer, P. Wurz, N. Thomas, V. Grimaudo, P. Moreno-Garcia, P. Broekmann, A. Neubeck and M. Ivarsson, Geostand. Geoanal. Res., 2014, 38, 441–466 CrossRef CAS.
- M. Tulej, A. Neubeck, M. Ivarsson, A. Riedo, M. B. Neuland, S. Meyer and P. Wurz, Astrobiology, 2015, 15, 669–682 CrossRef CAS.
- Y. M. Lin, Q. A. Yu, W. Hang and B. L. Huang, Spectrochim. Acta, Part B, 2010, 65, 871–883 CrossRef.
- A. A. Sysoev and A. A. Sysoev, Eur. J. Mass Spectrom., 2002, 8, 213–232 CrossRef CAS.
- A. A. Sysoev, A. V. Karpov, V. V. Milyaeva and A. A. Sysoev, Eur. J. Mass Spectrom., 2018, 24, 96–107 CrossRef CAS.
- U. Rohner, J. A. Whitby and P. Wurz, Meas. Sci. Technol., 2003, 14, 2159–2164 CrossRef CAS.
- M. Tulej, M. Iakovleva, I. Leya and P. Wurz, Anal. Bioanal. Chem., 2011, 399, 2185–2200 CrossRef CAS.
- A. Riedo, A. Bieler, M. Neuland, M. Tulej and P. Wurz, J. Mass Spectrom., 2013, 48, 1–15 CrossRef CAS.
- R. Wiesendanger, M. Tulej, A. Riedo, S. Frey, H. Shea and P. Wurz, J. Anal. At. Spectrom., 2017, 32, 2182–2188 RSC.
- R. Wiesendanger, D. Wacey, M. Tulej, A. Neubeck, M. Ivarsson, V. Grimaudo, P. Moreno-Garcia, A. Cedeno-Lopez, A. Riedo and P. Wurz, Astrobiology, 2018, 18, 1071–1080 CrossRef CAS.
- J. He, R. F. Huang, Q. Yu, W. Hang and B. L. Huang, Chem. J. Chin. Univ., 2009, 30, 57–59 CAS.
- B. C. Zhang, M. H. He, W. Hang and B. L. Huang, Anal. Chem., 2013, 85, 4507–4511 CrossRef CAS.
- S. D. Zhang, B. C. Zhang, W. Hang and B. L. Huang, Spectrochim. Acta, Part B, 2015, 107, 17–24 CrossRef CAS.
- Z. B. Yin, L. Hang, R. Liu, W. Hang and B. L. Huang, J. Mass Spectrom., 2018, 53, 435–443 CrossRef CAS.
- A. Riedo, M. Neuland, S. Meyer, M. Tulej and P. Wurz, J. Anal. At. Spectrom., 2013, 28, 1256–1269 RSC.
- V. V. Milyaeva, E. E. Sil'nikov, A. M. Mikhailov and A. A. Sysoev, Eur. J. Mass Spectrom., 2017, 23, 167–173 CrossRef CAS.
- M. Tulej, R. Wiesendanger, A. Riedo, G. Knopp and P. Wurz, J. Anal. At. Spectrom., 2018, 33, 1292–1303 RSC.
- R. F. Huang, Y. M. Lin, L. F. Li, W. Hang, J. He and B. L. Huang, Anal. Chem., 2010, 82, 3077–3080 CrossRef CAS.
- R. Wiesendanger, V. Grimaudo, M. Tulej, A. Riedo, R. Lukmanov, N. Ligterink, R. Fausch, H. Shea and P. Wurz, J. Anal. At. Spectrom., 2019, 34, 2061–2073 RSC.
- M. B. Neuland, S. Meyer, K. Mezger, A. Riedo, M. Tulej and P. Wurz, Planet. Space Sci., 2014, 101, 196–209 CrossRef CAS.
- S. Frey, R. Wiesendanger, M. Tulej, M. Neuland, A. Riedo, V. Grimaudo, P. Moreno-Garcia, A. C. Lopez, M. Mohos, B. Hofmann, K. Mezger, P. Broekmann and P. Wurz, Planet. Space Sci., 2020, 182, 104816 CrossRef CAS.
- A. Riedo, M. Tulej, U. Rohner and P. Wurz, Rev. Sci. Instrum., 2017, 88 CrossRef CAS.
- V. Grimaudo, P. Moreno-Garcia, A. C. Lopez, A. Riedo, R. Wiesendanger, M. Tulej, C. Gruber, E. Lortscher, P. Wurz and P. Broekmann, Anal. Chem., 2018, 90, 5179–5186 CrossRef CAS.
- V. Grimaudo, P. Moreno-Garcia, A. Riedo, M. B. Neuland, M. Tulej, P. Broekmann and P. Wurz, Anal. Chem., 2015, 87, 2037–2041 CrossRef CAS.
- V. Grimaudo, M. Tulej, A. Riedo, R. Lukmanov, N. F. W. Ligterink, C. de Koning and P. Wurz, Rapid Commun. Mass Spectrom., 2020, 34, e8803 CrossRef CAS.
- V. Grimaudo, P. Moreno-Garcia, A. Riedo, S. Meyer, M. Tulej, M. B. Neuland, M. Mohos, C. Gutz, S. R. Waldvogek, P. Wurz and P. Broekmann, Anal. Chem., 2017, 89, 1632–1641 CrossRef CAS.
- M. H. He, Y. F. Meng, S. S. Yan, W. Hang, W. G. Zhou and B. L. Huang, Anal. Chem., 2017, 89, 565–570 CrossRef CAS.
- B. Fernandez and R. Pereiro, Anal. Bioanal. Chem., 2010, 396, 2723–2724 CrossRef CAS.
- B. Fernandez, R. Pereiro and A. Sanz-Medel, Anal. Chim. Acta, 2010, 679, 7–16 CrossRef CAS.
- B. Hattendorf, J. Pisonero, D. Gunther and N. Bordel, Anal. Chem., 2012, 84, 8771–8776 CrossRef CAS.
- A. Pelster, M. Korsgen, T. Kurosawa, H. Morita and H. F. Arlinghaus, Anal. Chem., 2016, 88, 9638–9646 CrossRef CAS.
- J. Pisonero, Anal. Bioanal. Chem., 2006, 384, 47–49 CrossRef CAS.
- J. Pisonero, J. Koch, M. Walle, W. Hartung, N. D. Spencer and D. Gunther, Anal. Chem., 2007, 79, 2325–2333 CrossRef CAS.
- J. Fietzke, V. Liebetrau, D. Guenther, K. Gurs, K. Hametner, K. Zumholz, T. H. Hansteen and A. Eisenhauer, J. Anal. At. Spectrom., 2008, 23, 955–961 RSC.
- J. Fietzke, V. Liebetrau, D. Gunther, A. Frische, K. Zumholz, T. H. Hansteen and A. Eisenhauer, Geochim. Cosmochim. Acta, 2008, 72, A267 CrossRef.
- V. N. Epov, S. Berail, M. Jimenez-Moreno, V. Perrot, C. Pecheyran, D. Amouroux and O. F. X. Donard, Anal. Chem., 2010, 82, 5652–5662 CrossRef CAS.
- M. Ivarsson, Biogeosciences, 2012, 9, 3625–3635 CrossRef CAS.
- M. Ivarsson, W. Bach, C. Broman, A. Neubeck and S. Bengtson, Geomicrobiol. J., 2018, 35, 460–467 CrossRef.
- M. Ivarsson, S. Bengtson, V. Belivanova, M. Stampanoni, F. Marone and A. Tehler, Geology, 2012, 40, 163–166 CrossRef CAS.
- S. McMahon, T. Bosak, J. P. Grotzinger, R. E. Milliken, R. E. Summons, M. Daye, S. A. Newman, A. Fraeman, K. H. Williford and D. E. G. Briggs, J. Geophys. Res.: Planets, 2018, 123, 1012–1040 CAS.
- S. McMahon, J. Parnell and N. J. F. Blamey, Int. J. Astrobiol., 2012, 11, 163–167 CrossRef CAS.
- R. Wiesendanger, M. Tulej, V. Grimaudo, A. C. Lopez, R. Lukmanov, A. Riedo and P. Wurz, J. Chemom., 2018, 1–10, DOI:10.1002/cem.3081.
- S. Meyer, A. Riedo, M. B. Neuland, M. Tulej and P. Wurz, J. Mass Spectrom., 2017, 52, 580–590 CrossRef CAS.
- M. B. Neuland, V. Grimaudo, K. Mezger, P. Moreno-Garcia, A. Riedo, M. Tulej and P. Wurz, Meas. Sci. Technol., 2016, 27, 035904 CrossRef.
- T. M. Seward, A. Williams-Jones and A. Migdisov, in Tratise on Geochemistry, Elsevier Ltd, 2013, vol. 13 Search PubMed.
- U. M. Graham and H. Ohmoto, Geochim. Cosmochim. Acta, 1994, 58, 2187–2202 CrossRef CAS.
- H. Ohmoto, K. Hayashi and Y. Kajisa, Geochim. Cosmochim. Acta, 1994, 58, 2169–2185 CrossRef CAS.
- M. Tulej, A. Neubeck, A. Riedo, R. Lukmanov, V. Grimaudo, N. Ligterink, M. Ivarsson, W. Bach and C. de Koning, J. Mass Spectrom., 2020, 55, e4660 CrossRef.
- N. Morimoto, Mineral. Mag., 1988, 52, 535–550 CrossRef CAS.
- http://geology.com/minerals/plagioclase.shtml .
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00390e |
| This journal is © The Royal Society of Chemistry 2021 |