An augmented (multi-descriptor) grouping algorithm to optimize chemical ordering in nanoalloys

Abstract

We propose the Augmented Grouping Approach (AugGA) and its deployment in the Augmented Grouping GO (AugGGO) scheme, for an efficient exploration of the chemical ordering (or compositional structure) of multi-component (alloyed) nanoparticles. The approach is based on a ‘grouping’ strategy (previously proposed for high-symmetry structures) by which the number of compositional degrees of freedom of the system is decreased by defining sets of atoms (groups, or orbits, or shells) that are constrained to be populated by the same element. Three fundamental advances are here included with respect to previous proposals: (i) groups are defined on the basis of descriptors (no point-group symmetry is assumed), (ii) bulk groups can exploit general chemical ordering patterns taken from databases, and (iii) sub-grouping is realized via a multi-descriptor strategy (here using two basic descriptors: the atomic energy and a few types of geometry patterns). The AugGGO approach is applied to two prototypical examples of binary nanoalloys: Pd–Pt and Ag–Cu, with a size between ≈500 and ≈1300 atoms, in different configurations, and the convex hull of the mixing energy as a function of composition is derived. It is shown how the three advances here proposed decisively extend the power and scope of the grouping approach: (i) making it applicable to any generic structural framework, (ii) achieving a thorough sampling of the core regions of nanoparticles, and (iii) catching exotic/unexpected chemical ordering arrangements, at a computational cost which is 1–2 orders of magnitude smaller than that of traditional Monte Carlo single-exchange techniques.

---

1. Introduction

Optimizing the properties (and thus the performance) of a given system by moving in the space of chemical variables¹ is a challenging task, due to the exponential increase in the number of possible structures and compositions.² The task can be restricted to exploring only the composition (stoichiometry) degrees of freedom of isomers sharing a fixed structural framework. This decreases the complexity of the problem, which however remains of combinatorial, and therefore non-algorithmic, complexity: the number of homotops equals M^N, where N is the total number of atoms and M is the number of components; this number corresponds to 2^N for binary systems, 3^N for ternary systems, etc. In the field of multi-component metallic nanoparticles or nanoalloys,^3,4 on which we focus in the present work, these isomers are named ‘homotops’,⁵ and the arrangement of the different elements in the given structural framework is named ‘chemical ordering’ or ‘compositional structure’. At the computational level, a systematic search over the full set of homotops is practically unfeasible only for systems with a number of atoms larger than a few tens, such that M^N remains computationally affordable. Developing methods to accelerate the exploration of the combinatorial phase space of larger systems still maintaining thoroughness over the physically and chemically significant isomers is mandatory to make simulations affordable and predictive.

Although a systematic exploration of all possible homotops is feasible only for smaller systems, for larger systems one can use Global Optimization (GO) techniques, in which a stochastic search over a selection of structures and transformation moves is performed. The GO search can be made as extensive as far as it is compatible with available computational resources, and the goal of GO methods is to direct the sampling towards low-energy isomers.⁶ Many variants of GO have been devised, typically differing in the choice of transformation moves. Popular techniques are the basin-hopping⁷ and genetic algorithm⁸ methods, in which transformation moves are accepted or rejected on the basis of a Metropolis⁹ criterion based on the difference in the energy (or some transformed function^7,10) between the starting and final configurations (see ref. 11 for a unified view of GO approaches). Possible approaches to GO in the chemical ordering space are traditionally based on individual-site moves, such as an exchange of two elements on two different sites of the structural framework,^12,13 or an exchange of an element on a given site with an external reservoir.¹⁴ GO based on these individual-site chemical-ordering moves however exhibits a slow convergence of the search to the global minimum.

An alternative way to achieve an effective acceleration of the chemical ordering search is based on collective moves, involving simultaneous changes of many atoms, as realized in the class of ‘grouping’ approaches.^15–17 In these approaches, atoms are grouped into equivalence sets (indifferently called ‘groups’ or ‘orbits’ or ‘shells’, but here we will mostly use the term ‘group’ to underline the generality of the approach), and the search is restricted to homotops in which the different groups are homogeneously populated, i.e., all the sites belonging to a given group, or orbit, or shell, are populated with the same element. If the number of orbits is N_orbs and the total number of atoms is N, the configurational space of a binary system is reduced from 2^N to 2^Norbs. Except for the fact that collective variables are used, the principles and techniques of structural exploration remain the usual ones: sampling can be conducted in an exhaustive way (i.e., systematic sampling),^15,16 or based on stochastic searches (the Grouping Global Optimization, GGO, approach,¹⁷ in the various variants and flavours of GO algorithms). GGO approaches have proven to be computationally efficient, enabling predictive sampling of the chemical ordering of systems composed of thousands of atoms when using empirical potentials, e.g., (Ag–Cu)₄₀₃₃,¹⁷ or hundreds of atoms when coupled with first-principles methods.¹⁸ Thus far, grouping techniques have been limited to high-symmetry structural frameworks, as the selection of orbits or shells was based on point-group symmetry, i.e., by grouping atoms equivalent by symmetry.^15–18 Additionally, the stability of the algorithm with respect to broken-symmetry perturbations was also envisaged by considering sub-groups, i.e., by partitioning orbits into sub-orbits as obtained by reducing the point-group symmetry with respect to a symmetry axis or spherical symmetry.¹⁷ Despite ensuring a huge increase in computational efficiency, the applicability of GGO grouping methods thus far has suffered from being limited to high-symmetry configurations, which represent only a tiny fraction of the exponential number of amenable structures, and possible issues in predicting ordered patterns in the core of nanoparticles. To accelerate the search for low-symmetry structures and exhaustively sample bulk patterns a more general approach is needed.

Here we propose just such an approach, the Augmented Grouping Approach (AugGA), and in particular its deployment in an Augmented Grouping GO (AugGGO) scheme. The AugGA approach is still based on a ‘grouping’ philosophy but including three basic advances: (i) groups (or orbits, or shells) here rely on general descriptors – in other words sites in the structural framework are grouped according to common values of a general descriptor function (at variance with equivalence based on point-group symmetry as used in our previous work¹⁷), (ii) grouping is generalized to include the possibility of populating groups with compositional arrangements taken from chemical ordering databases (at variance with populating groups each with a single-element as realized so far), and (iii) sub-grouping is realized via a multi-descriptor strategy (the present proof-of-principle investigation is limited to basically two descriptors at a time, but the approach can be extended to as many descriptors as needed). These three advances decisively extend the power and scope of the grouping methods. By the first advance (i), point-group symmetry is not invoked and the method is applicable to any generic structural framework, which enables its exploitation in basically all existing GO codes to deal with any system. By the second advance (ii), collective moves are further generalized to include transformations in which selected orbits are populated with chemical ordering motifs taken from a wide (potentially continuously updated) database (incidentally, this technique can also be seen as a form of pre-defined sub-grouping): this advance is particularly beneficial to achieve a thorough sampling of the core regions of nanoparticles, avoiding missing ordered compositional structures that are difficult to catch for entropic reasons (a tiny number of realizations) such as L1₀, etc.^19–21 By the third advance (iii), we formalize the previously defined combination of grouping and sub-grouping according to several (i.e., >1) descriptors or selection criteria: this significantly increases the thoroughness of the search especially in the case of exotic and unexpected surface chemical ordering arrangements, and is also very useful to catch and/or discover unusual chemical ordering motifs in the bulk of the particles.

In the following, we will demonstrate the power of the proposed Augmented Grouping Approach (AugGA), specifically in the form of the Augmented Grouping GO (AugGGO) scheme, by applying it to two prototypical examples of binary nanoalloys: Pd–Pt and Ag–Cu, deriving the convex hull¹⁶ of the mixing energy^15,22 as a function of composition. More specifically, for both Pd–Pt and Ag–Cu alloys, three different configurations have been investigated: one at size 609 atoms, corresponding to a high-symmetry motif, and two at size 500 atoms, corresponding to two low-symmetry motifs.

2. Methods

As discussed in the introduction, the Augmented Grouping GO (AugGGO) approach here developed includes three basic advances: (i) groups are defined on the basis of general descriptor functions; (ii) grouping moves are generalized to include transformations to compositional arrangements taken from chemical ordering databases; and (iii) sub-grouping is realized via a multi-descriptor strategy. Let us discuss these advances in sequence.

2.1 Descriptor-based groups (i)

The fundamental strategy of grouping consists in applying the same transformation (i.e., the same move) to atoms that share a common physics. This is by definition the case of atoms located on sites equivalent via operations of the point-group symmetry of the structural framework. In such a case, atoms within a given symmetry orbit will by definition also share common values of any, however-defined local descriptor function. In the case of low-symmetry structures, instead, none of the atoms is in principle exactly equivalent to any other atom (in the case of C₁ point-group symmetry of the structural framework), but, yet, it is usual to find many atoms that share a similar (although not exactly identical) physics up to some fuzziness criterion. It is then reasonable and technically easy to select a local descriptor function and generalize the grouping approach to define groups (sets of sites) in the structural framework according to a similar value of this descriptor function.

Let us give a definite example: the local descriptor function that we will use in the following is the atomic energy as defined via an empirical potential, the second-moment-approximation (SMA) potential.²³ Note in passing that when using the atomic energy as a descriptor to define groups we calculate atomic energies by freezing the structural framework, whereas when we calculate the total energy of each chemical ordering representation within successive GO runs we allow for local geometry relaxation. In the top-left of Fig. 1, we show a Leary tetrahedron (Leary Td) made of 609 atoms, while the top-right of the same figure reports the corresponding population (density) of its atomic energies. We stress that the choice of the Leary Td is taken as a specific example, but the approach is completely general. The class of Leary tetrahedra, found for the first time as the putative global minimum (GM) of the 98 atom Lennard-Jones cluster,²⁴ corresponds to a hybrid fcc-decahedral motif made of a crystalline core exhibiting a single (or double²⁵) tetrahedron on the faces of which further growth in a stacking-fault fashion gives rise to five-fold axes running parallel to the edges of the core. The resulting shape benefits from a reduced surface energy thanks to the local non-crystalline environment at the surface edges and by an overall quasi-spherical shape. It is pictorially apparent (and it is further clarified by the arrows in Fig. 1) how the local energies of the atoms in this structure group into well-distinct peaks according to their different physics, i.e., their position in the framework. Note that to calculate the atomic energies to define the orbits we do not necessarily need to relax the geometry (that we can assume has been extracted from a structural GO search for some pure or alloy nanoparticle or from some structural database): we populate all sites with the same element, we calculate the SMA atomic energies, we plot their density as in Fig. 1, and we distinguish the peaks thus defining the groups, and then we populate the groups with different elements using as the only constraint the criterion that the elemental population is constant within each orbit. The idea is that the difference in the local coordination environment implies that the corresponding atomic energies are different and therefore correctly distinguishes the relevant orbits. It should also be stressed that in the present proof-of-principle implementation we selected the atomic energy as the most natural choice of a descriptor, but one could use equally well other descriptors (or order parameters), such as those derived from a common-neighbour analysis (CNA).²⁶ Incidentally, we note that, in the CNA, one will have the option of distinguishing sites populated with different elements (the original formulation of the CNA does not distinguish elements but there is a clear advantage in distinguishing sites populated with different elements especially in the case of size-mismatched nanoalloys). Finally, peak recognition is here done manually, but visual recognition techniques²⁷ can of course be employed, especially useful to automate the AugGGO scheme within a general GO code.

Fig. 1 (Top) Illustration of the operation of generating groups for the 609-atom Leary tetrahedron. The atoms are coloured according to their different atomic (site) energy and the resulting groups are reported in the DOS (Density Of States) plot of atomic energies on the right-side. Below, a further partition of the groups according to a second (structural) descriptor is shown. (Bottom) Optimal orientation of the Leary structure according to the use of the C₄, C₅ or C₆ symmetry axis – the z-axis is perpendicular to the plane of the figure.

We also note in passing that the AugGA technique, similarly to the original grouping scheme, can exploit any given approach to the computation of the energy and its derivatives (forces, needed to optimize the structures), such as an empirical potential as in the present work,²³ but also more general machine-learning potentials,²⁸ or effective Hamiltonian methods,^13,29 or even first-principles methods such as Density-Functional Theory (DFT), as also done in our previous work.¹⁸ Indeed, the same descriptor here used, i.e., the atomic energy calculated via an empirical potential, can be used also in conjunction with DFT³⁰ or any other method to calculate the energy and forces. The underlying idea is that the descriptor is able to distinguish as precisely as possible the physics of the system and therefore the physically significant orbits; clearly, the more precisely this physics is described the more predictive the search will be, but in our experience simple empirical-potential (SMA) atomic energies are usually sufficient for the purpose. More precisely, according to SMA, the total energy of the i-th atom of the system is partitioned into an attractive many-body contribution, E_a(i), and a repulsive contribution, E_r(i), whose analytical expressions are the following:

In eqn (1) and (2), the parameters α and β correspond to the atomic species of the two components of the alloys. Parameters A, r₀, ξ, p and q are usually fitted to the experimental values of the cohesive energy, lattice parameters and independent elastic constants for the reference crystal structure of pure metals and bulk alloys at 0 K. To describe the homonuclear-interaction, the values of the parameters were taken from ref. 23, whereas, to describe the heteronuclear-interaction, the parameters of the homonuclear-interaction have been averaged.

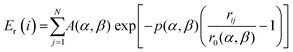2.2 Database-derived moves (ii) and multi-descriptor grouping (iii)

We describe advances (ii) and (iii) together since, in the present proof-of-principle investigation, our databases rely on symmetry recognition and we limit ourselves to two descriptors at a time: the atomic energy and an element of local symmetry, so that both databases (ii) and multi-descriptor (iii) involve local symmetry recognition, the topic of the following section.

2.2.1 Symmetry recognition. When investigating large nanoparticles, it is common to find – at least to some degree, i.e., for some portions of their sites/atoms – known structural motifs such as those based on crystal-like arrangements (fcc, hcp, bcc, etc.) or non-crystalline like ones (such as icosahedra, Ih, decahedra, Dh, etc.³¹). It is therefore useful to recognize these patterns and exploit them. At the bottom of Fig. 1 we pictorially illustrate our symmetry-recognition algorithm in a prototypical case, while the flow chart of the AugGA (AugGGO) scheme is shown in Fig. 2, whose main steps will be illustrated in the following. Our goal in this section is to recognize sets of atoms/sites belonging to known patterns based on local (to be stressed: not global) point-group symmetries (such as C_n local symmetry axes) and use them either to exploit chemical ordering motifs taken from databases, such as L1₀, L1₂, radial (multi-shell) symmetry, etc.,^19–21 or to partition selected groups (orbits) into sub-groups (sub-orbits) as a basis for chemical ordering transformation moves.

Fig. 2 Scheme of the grouping approach employing one or two descriptors.

A low-symmetry structure must be properly centred and re-oriented before grouping atoms. The protocol we use for this purpose is as follows. The central atom is selected on the basis of maximum spherical symmetry: each atom is scrutinized as the candidate centre of the cluster, the corresponding spherical groups (orbits, built by choosing the distance from the centre as a grouping criterion) are counted, and the atom corresponding to the minimum number of orbits is selected as the cluster centre. In general, the central atom is typically close to the centre of mass of the cluster and lies on a symmetry axis. After selecting the central atom, a proper orientation of the Cartesian axes is selected, an operation of pivotal importance to exploit grouping schemes based on symmetry breaking. Due to the presence of several possible different symmetry axes in the main structural motif, such as C₃ (or C₆), C₄ and C₅ axes (see for example Fig. 1, bottom panel, referring to the 609-atom Leary tetrahedron), orienting the z-axis along one of these axes achieves the optimal strategy for an efficient grouping. An angle sweeping in polar coordinates is used to estimate the presence of the symmetry axis for each sampled orientation and select the preferred one.

2.2.2 Selection of the descriptors and formation of the groups (orbits). Once geometric centring and re-orientation of the structure is achieved, the groups can be built on the basis of one or more descriptors. The use of a single descriptor corresponds to the strategy adopted in ref. 17 (with the difference here that the descriptor can be either energetic or geometric). As anticipated, in the present scheme we have implemented hierarchically two descriptors. The first is based on the atomic energy. This immediately distinguishes the atoms of the clusters into two ensembles, the surface and bulk atoms. Fig. 1 (top panel) pictorially illustrates the results of using the atomic energy descriptor for the 609-atom Leary tetrahedron, where the grey bulk atoms constitute a first large group and the surface atoms are automatically ordered and sub-grouped according to their reduced coordination (and thus their atomic energy). These groups can be further partitioned according to a second structural descriptor based on a geometric criterion, that in the present implementation can be spherical (i.e., distance from the centre) or cylindrical/layered (i.e., distance/projection from/onto a given symmetry axis), see Fig. S1 in the ESI.† Note that for surface atoms one can use sub-groups given by any of the two descriptors, i.e., either the atomic energy or local symmetry. Once the user has chosen the preferred grouping scheme, the atoms are partitioned according to an automatic quantitative screening of the descriptor(s), following a procedure aimed at achieving a well-balanced distribution of the size of the groups or orbits. This step is useful to get the “optimal” grouping scheme, i.e., that achieving an optimal compromise between the accuracy of the prediction and speed of the exploration of the lowest-energy chemical ordering pattern.

2.2.3 Selection of the moves for subgroups. The chemical ordering of the bulk orbits can be defined according to the subgroups given by the local-symmetry partitioning, or they can be projected onto chemical ordering motifs taken from a pre-defined database. As the local symmetry of the framework is known from Section 2.2.1, one can recognize the truncated octahedral (Oh), icosahedra (Ih), decahedra (Dh), etc.³¹ structural families and apply to the bulk sites known chemical ordering patterns, such as L1₀, L1₂, or Ih-like patterns, etc.¹⁹ The collective transformation moves corresponding to the database option change all the atoms in a bulk group according to a wide (potentially ever-increasing) database of motifs, and are useful to catch ordered compositional structures that are easy to miss for entropic reasons (the tiny number of realizations of, e.g., the L1₀ pattern). For clarity, it should be noted that in the case of pre-defined databases we allow the atoms in the given group to be populated not all by the same element, but by a multi-elemental pattern, which we claim is a useful generalization of the GGO approach.

2.2.4 Choice of GO technique. Once the groups are built and moves are selected, the search in the phase space of the chemical ordering patterns for any given composition can be performed using a variety of GO techniques. Note that in our implementation each chemical ordering pattern or configuration of the system is defined by a “string”, with length equal to the number of subgroups N_orbs, and made of 0s and 1s for binary systems, where 0 and 1 identify the occupation of a group by element A or B, respectively (this can be extended to ternaries by defining a string made of 0, 1, 2, and so on). In the present implementation of the AugGGO approach, we have used a BH (Basin Hopping) Monte Carlo technique,⁷ as also used in ref. 17. This entails randomly selecting a starting string, making a random move (modification of the string), and then accepting or rejecting the move according to the Metropolis criterion:⁹ if the move corresponds to an energy lowering, it is always accepted, otherwise the rate of acceptance follows a Boltzmann distribution involving a fictitious temperature which is externally tuned. To exploit parallel computing, in the present work we have implemented a version of the AugGGO code which automatically generates initial strings over a given fixed composition for each given walker, and exploits independent parallel computing (parallel walkers) to derive in one run several points along the mixing energy curve (convex hull) for a given structural framework. In other words, we use N processors, each one corresponding to one of N walkers, and each independent processor/walker screens a different composition (so we allow only moves for each walker that keep the composition constant). An alternative approach that we have exploited in our previous GGO approach¹⁷ consists in changing simultaneously both the chemical ordering and the composition, to quickly reach regions of low values of the mixing energy curve or simply to allow walkers more freedom: this approach is not yet implemented within AugGGO but it will be in a future version of the code. In short, both systematic sampling and stochastic explorations can be used within AugGA, and stochastic methods can work both for a given fixed composition via a Monte Carlo procedure exchanging the atom types of equivalence sets¹² or by defining a chemical potential¹⁴ and thus simultaneously spanning the whole range of compositions (this is beneficial for simulations exploiting a high level of parallel HPC), or focusing on finding the lowest mixing-energy composition(s).

Note in passing that the AugGGO exploration keeps track of all the patterns sampled by the algorithm (each one with its energy) and the so-accumulated database provides, for any size and composition, a spectrum of lowest-energy and higher-energy patterns which could be used in a statistical way to build up the partition function of the system and derive thermodynamic functions. Moreover, by performing AugGGO on different structural motifs with the same number of atoms one can investigate the competition among structural families, or one can also compare a range of different sizes and investigate the cross-over among structural families as a function of the number of atoms, as done in previous work.^15–17

To conclude this section, we underline that the present multi-descriptor approach, here deployed in the proof-of-principle case of only two descriptors at a time, can naturally be extended to exploit as many descriptors as useful. This is particularly promising if combined with structural searches within a general GO scheme and specifically within the Parallel-Walker (PW) approach.¹² Incidentally, to implement the PW approach, one needs to define a general function to recognize the similarity in chemical ordering between two configurations. We propose that a simple and effective recognition function corresponds to the scalar product between normalized ‘strings’, ranging between a maximum of 1 for the same string and a minimum of 0 when no sub-groups of the framework are populated with the same element.

2.2.5 Software implementation and distribution. The software used in this work is home-made and is written as a Fortran90 code. It performs all the operations described in Sections 2.2.1–2.2.4. The code has a flexible call to an external routine for the calculation of the energy and its first derivatives (the forces, which are essential in the optimization step of the algorithm), which, in the present implementation, has been taken from the software described in ref. 12. The software will be open-source distributed in the near future. Meanwhile, colleagues interested in using the code are invited to contact the authors, who will share the source code with no restrictions. Structures belonging to high-symmetry families (truncated-octahedra, decahedra and icosahedra) were generated using home-made codes that are also available for sharing.

3. Results and discussion

In the following, we will present two sets of results.

(1) The first set focuses on high-symmetry motifs: our goal in this set is to confirm the accuracy of the method by comparing with previous results on similar systems obtained using the original GGO approach, provide an estimate of its computational efficiency, and show that, even in the case of high-symmetry motifs, the database-including (ii) and multi-descriptor (iii) advances here proposed offer significant advantages over the original GGO.

(2) The second set focuses on low-symmetry motifs, to demonstrate that the descriptor-based-orbit advance (i) here proposed can be applied to generic structural frameworks without any symmetry or other restrictions.

For definitiveness, we will then focus on three structures: one at size 609 atoms, corresponding to the high-symmetry motif shown in Fig. 1, and two at size 500 atoms, corresponding to two low-symmetry motif configurations found as low-energy structures in unbiased structural searches conducted for the two nanoalloys.

We have chosen two different alloys, PdPt and AgCu (where the latter nano-alloy pair is immiscible in the bulk²⁰), that have two distinct behaviours at the nanoscale: PdPt exhibits a tendency to the formation of ordered mixing patterns,^18,32 whereas AgCu retains its tendency to segregation in the form of core–shell or Janus motifs.^33–36 These nanoalloys have attracted much attention in recent years thanks to their interesting catalytic properties.^37–44

The energy and forces are computed via the SMA (Second Moment Approximation) potential using parametrization schemes reported in the literature.^16,23

Before going into detail, let us recall two basic concepts in the nanoalloy field: the mixing energy^15,17,22 and the convex hull.¹⁶ The mixing energy is defined as:

Δ[N_A, N_B] = E_alloy[N_A, N_B] − N_AE_A[N]/N − N_BE_B[N]/N (3)

where E_alloy[N_A, N_B] is the energy of a nanoalloy cluster composed of N_A atoms of species A and N_B atoms of species B, N = N_A + N_B is the total number of atoms in the cluster, E_A[N] is the energy of a pure-A cluster of N atoms, and E_B[N] is the corresponding quantity for the B species. Negative values of the mixing energy are associated with a favourable tendency towards alloying, whereas positive values indicate a tendency towards segregation. This definition of the mixing energy is the same used in ref. 17, where a more extended discussion of the physical meaning of the different definition of mixing energy is given: the mixing energy measures the stability of an alloyed motif with respect to the corresponding motifs made of the two pure elements. Our present choice to freeze the same structural motif is a computational artefact aimed at disentangling structural and alloying effects, but has a drawback in that comparing mixing energy values between different motifs does not provide information on their relative stability, which must thus be taken as a separate piece of information. In contrast, in the usual definition of the mixing energy,^15,22E_alloy[N_A, N_B], E_A[N] and E_B[N] correspond to global minima; this is tantamount to modelling a system in which an ensemble of particles can exchange atoms keeping a fixed size (number of atoms) of the individual particles, but with no further constraints (see the discussion in ref. 17). In this work, instead, we will search for the GM in the phase space of homotops of a given structural framework;⁵ our lowest-energy structures are therefore constrained to be conformal to a pre-chosen configuration (incidentally this is closer to the original formulation of grouping methods¹⁵). It is important to underline that the goal of AugGGO approaches in general and thus of the present study is not to perform a full structural GO. Indeed, in AugGGO we use transformation moves on the variables related to chemical ordering, while allowing only for local relaxations of atomic coordinates. We therefore do not claim that some of the proposed structures correspond to global minima, and indeed we know for sure that in some cases they are not;⁴⁵ our goal is to accelerate the sampling of chemical ordering, so that it can be coupled to sampling in the phase space of structures to achieve a full and complete GO approach.¹²

Once the mixing energy is calculated for a set of compositions, its convex hull^46,47 can be estimated to derive nanoalloy phase diagrams.¹⁶ It can be noted in passing, in analogy with the theory of bulk alloy phase diagrams, that, when the envelope of lowest mixing energies as a function of composition has a concave (not convex) profile, the possibility of bistability and phase segregation exists.

3.1 High-symmetry motifs

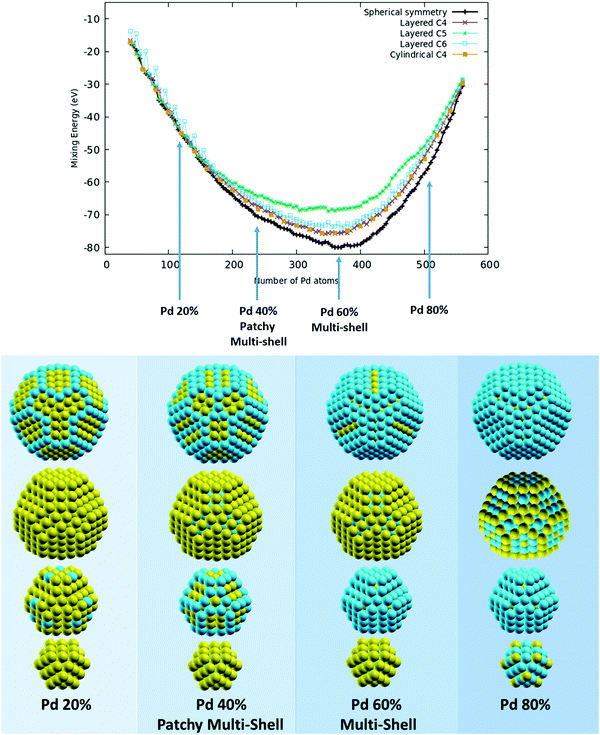
To investigate high-symmetry motifs, we have chosen to investigate chemical ordering in the same 609-atom Leary tetrahedron shown in Fig. 1. A partial fragment of this motif has been singled out in GO structural searches of a PdPt nanoalloy with 500 atoms (with various compositions) and manually completed at size 609 atoms to realize a high-symmetry structure. As already discussed, this hybrid motif has been already discussed in the literature for this alloy^16,25 and can be described as made of a crystalline (tetrahedral) core on the faces of which further growth in a stacking fault fashion gives rise to a local 5-fold axis along the directions of the six edges of its core. This combination of a crystalline core and surface 5-fold symmetry is effective in lowering the surface energy in both pure and alloyed systems, especially in the case of alloys made of elements (such as Pd and Pt) with a reduced size-mismatch (the experimental nearest-neighbour distances in the bulk are 2.75 and 2.77 Angstrom, respectively). For the AgCu alloy, which is characterized by a pronounced size mismatch (the experimental nearest-neighbour distances in the bulk are 2.88 and 2.49 Angstrom, respectively), this motif is not stable in the size range around 500 atoms. As we directly observed in an unbiased structural search of this alloy, highly non-crystalline motifs based on icosahedral units are stable instead.^35,45 Nevertheless, we decided to test the ordering in the Leary motif also for the AgCu alloy to demonstrate that the efficiency of the AugGGO approach is not limited to low-lying structural motifs. We will consider much more stable motifs for the AgCu alloy in the results on the low-symmetry motif structure in Section 3.2.

PdPt alloy In Fig. 3 (top panel) we have reported the mixing energy curves for the 609-atom Leary Td by considering 5 different grouping schemes: (a) one spherical (exploiting the full symmetry of the cluster, black line), (b) three layered on the basis of the values of the atom z-coordinates by choosing the three different orientations shown in the lower panel of Fig. 1 (purple line for C4, green line for C5 and cyan line for C6), and (c) one cylindrical on the basis of the distance of each atom from the z-axis (orange line). We have spanned a wide range of compositions from about 10% to about 90% in Pd content with a fine grid (the incremental Pd content between two consecutive points is 5 atoms). By looking at the curves, we can see that the lowest-energy one corresponds to spherical symmetry grouping; the other schemes tend to mimic (or reproduce) the spherical scheme with more success when choosing the orientation along the C₄ axis (for both layered and cylindrical schemes, which practically coincide) and give the worst result when orienting along the C₅ axis, due to the fact that C₅ axes are found only in peripheral regions of this structure. In the lower panel of Fig. 3 we have reported the lowest-energy patterns for compositions corresponding to a Pd content of 20%, 40%, 60% and 80%, by decomposing each structure in concentric layers. We can see that, in the whole compositional range, multi-shell arrangements dominate with the tendency of Pd to populate, at first, the cluster surface and then the internal layers. On the contrary, Pt has the tendency to occupy the most internal sites with a strong tendency to segregate in the sub-surface layer at high Pd content. This tendency to show a multi-shell arrangement, which is the typical mixing pattern of elements with a strong mixing tendency, is akin to the patchy multi-shell pattern which has been predicted for PdPt nanoalloys at smaller sizes and whose stability has been proven by first-principles calculations¹⁸ (actually, the tendency to show patchy multi-shell patterns is actually strengthened by first-principles approaches with respect to the less accurate SMA empirical potential); patchy patterns can indeed be easily recognized in the internal shells at both 40% and 80% Pd content. These results are in overall agreement with previous investigations on this nanoalloy and confirm the ability of the AugGGO approach in devising the preferred pattern of chemical ordering.

Fig. 3 (top) Excess energy curves for the PdPt alloy in the 609-atom Leary tetrahedron by invoking spherical symmetry (black) or broken symmetry according to a layering scheme by choosing the best C4 orientation (purple), C5 orientation (green) or C6 orientation (light blue); the curve corresponding to a cylindrical grouping scheme along a C4 orientation is also reported (orange). (bottom) Chemical ordering patterns corresponding to an increasing concentration of Pd; for each composition, each structure is decomposed in layers, see the main text for further details; Pd atoms in cyan, Pt atoms in yellow.

3.1.1 AgCu alloy. The behaviour of this alloy is remarkably different from that of the PdPt system, as can be observed when inspecting the mixing tendency in the same structural motif. We stress again that our purpose is not to predict the overall GM (Global Minimum) for this alloy, but to demonstrate the efficiency of the AugGGO algorithm in devising the chemical ordering of any given structural motif. By looking at the mixing-energy curves reported in the top panel of Fig. 4, we immediately note that: (a) the values of the mixing energy are smaller, thus showing a less pronounced tendency to alloying with respect to PdPt, and (b) the shape resulting from the envelope of the curves is not a convex hull, but it can rather be described as the combination of (i) a region with moderate tendency to mixing, presenting two distinct minima, the first located around 20% in Ag content and the second around 45% in Ag content, and (ii) a segregation region characterizing by an increase in mixing energy roughly proportional to the Ag content. When comparing the different grouping schemes employed, we observe that the spherical one (black line) is able to catch the lowest-energy mixing patterns only sporadically in the region of moderate mixing for those compositions that manage to form a (perfect) spherical core/shell arrangement with silver decorating the cluster surface, as can be seen in the structure achieved for a composition around 20% in Ag (see the bottom panel of Fig. 4). This type of pattern dominates the scenario up to 35% in Ag content and gives rise to the first minimum of the mixing energy envelope. When the Ag content surpasses 35%, the spherical scheme is no longer appropriate and the lowest-energy patterns are achieved by invoking other types of symmetry breaking. In the region of the second minimum (between 35% and 50% in Ag content), where we still observe a (moderate) tendency towards alloying, we single out low-symmetry structures whose stabilization is achieved via a distortion of the anti-Mackay-type shell forming a chiral structure (see the bottom panel of Fig. 4 for a composition with 40% in Ag content), whose formation and stabilization mechanism has been discussed for Ih-based structures of size-mismatched nanoalloys by Bochicchio et al.⁴⁸ The increase in the Ag content leads to the creation of pseudo-Janus patterns^34–36,49 where the copper core is off-centred and covered by a thin silver shell (see the bottom panel of Fig. 4 at 60% and 80% Ag content). The competition between off-centering in different directions is quite pronounced, as demonstrated by the closeness between the curves corresponding to C₄ and C₆ layered grouping schemes. Also for this alloy, the results of the present investigation are in perfect agreement with the literature.^33–35

Fig. 4 (top) Excess energy curves for the AgCu alloy in the 609-atom Leary tetrahedron by invoking spherical symmetry (black) or broken symmetry according to a layering scheme by choosing the best C4 orientation (purple), C5 orientation (green) or C6 orientation (light blue); the curve corresponding to a cylindrical grouping scheme along a C4 orientation is also reported (orange). (bottom) Chemical ordering patterns corresponding to an increasing concentration of Ag; for each composition, each structure is visualized by using big spheres (first row) and smaller balls for Ag to highlight the internal ordering of Cu. Ag atoms in white, Cu atoms in red.

From this section, we can conclude that the new implementation of the grouping algorithm has guaranteed (i) a synergic enhancement of the efficiency of the automatic grouping scheme generation, which in turn has led to (ii) a deeper comprehension of the physics of the investigated systems, highlighting for the PdPt alloy a competition between pure and patchy multi-shell ordering, whereas for AgCu the stabilization in the mixing region of core/shell regular (low Ag content) and distorted (chiral) structures (intermediate Ag content).

3.2 Low-symmetry motifs

3.2.1 PdPt alloy. In Fig. 5 (top panel) the results corresponding to two low-symmetry motifs of the PdPt alloy are reported in terms of mixing energy curves and preferred chemical ordering patterns. In order to focus on realistic structures at size 500, a large number of BH GO structural searches have been performed at that size, by choosing a variable composition of the seeds (between 25% and 75% in Pd content) and by applying explorations at several quite high temperatures between 1000 K and 2000 K. By inspecting the rich database so obtained, we have been able to classify the motifs in terms of structural families, according to a well-developed procedure.⁵⁰ At size 500, the landscape is dominated by the competition mainly between three motifs, i.e. (i) regular or slightly irregular crystalline motifs (in the form of incomplete truncated octahedra with or without hcp stacking fault planes); (ii) incomplete marks decahedra; and (iii) hybrid motifs, mainly of the fcc-Dh type (belonging to the same family as the 609-atom Leary tetrahedron) or Dh–Dh type (Dh characterized by a surface anti-Mackay growth mode). Ih-based motifs are quite absent, in agreement with previous results on this alloy.¹⁶ As the hybrid fcc-Dh motif was already analysed at the high-symmetry level, among these families we selected the two motifs reported in Fig. 5: a regular incomplete truncated octahedron, as an example of a crystalline type, and an incomplete marks decahedron, as an example of a non-crystalline motif. The convex hull shape of the mixing energy curves and the position of the minimum at about 60% in Pd content (for both motifs) are an immediate indication that the alloying process follows the same trends discussed for the high-symmetry Leary structure. In fact, by looking at the structures on the two sides of the plot corresponding to 40% and 60% in Pd content for the TO motif (left side) and Dh motif (right side), we observe the formation of a multi-shell type ordering with some irregularities due to the low symmetry of the structure. By looking at the central regular TO cores of 201 and 79 atoms on the left side, we can observe the insurgence of patchy motifs for both compositions, in agreement with the results already discussed in the previous section. In the case of the Dh family, the tendency towards the formation of patchy motifs appears less pronounced and we observe a strong tendency towards the formation of multi-(Marks-type)-shell patterns with the two elements alternating, segregating Pd at the surface and Pt in the central regions of the clusters.

Fig. 5 Excess energy curves for two selected low-symmetry structural motifs for both the PdPt alloy (for a 40% and 60% Pd composition, top panel) and the AgCu alloy (for a 40% and 80% Ag composition, bottom panel). The view style for the two alloys is the same used in Fig. 2 and 3, respectively.

3.2.2 AgCu alloy. When considering this second alloy, the GO runs aimed at collecting low-lying structural motifs were much more challenging, due to the stabilization of irregular structures, deriving from the size-mismatch and the consequent formation of disordered multi-poly-Ih⁵¹ structures. In order to perform an exhaustive sampling, we have thus performed both unbiased searches (following the same criteria used for the PdPt alloy) and biased searches by using as starting seeds the structural motifs singled out for the PdPt alloy. In summary, the AgCu system is dominated by Ih-based structures, both of pure type and mixed Ih–Dh (Ih with anti-Mackay growth). All the fcc-based families were remarkably destabilized and distorted, as confirmed by the broad segregation region and the low values of mixing energy characterizing the Leary tetrahedron observed in the previous section. For this reason, in Fig. 5 we have chosen to present the results of two Ih-based motifs, an almost perfect anti-Mackay (AM) Ih (the size of structural closure is 509 for this motif, left side) and a fragment of Mackay Ih (the size of structural closure is 561, right side). We can note that both motifs are characterized by negative values of the mixing energy in the whole composition range, highlighting a tendency towards mixing much more pronounced than in the case of the fcc-based motif of the previous section. Also, the lowest-energy values reached by the curves (between −15 and −30 eV) are much lower than those achieved for the Leary, also considering that the mixing energy (according to our definition) is an extensive quantity and the Leary is larger by a factor of about 20% in size. Regarding the evolution of the chemical ordering patterns as a function of the composition, we can say that for low Ag contents core/shell structures are stabilized: in the case of the anti-Mackay-Ih, the perfect core/shell is found at the minimum of the excess energy curve and the resulting structure presents a chiral distortion of the anti-Mackay overlayer discussed in ref. 48 and already observed in the anti-Mackay overlayer of the Leary motif at about 40% in Ag content; in the case of the Ih, for which the minimum of the curve is located at a slightly higher Ag content, the resulting structure is slightly distorted. After achieving the minimum in both curves, the mixing energy curves quickly increase, indicating a tendency towards segregation; the need of putting silver in the internal regions of the structures makes the copper core move to off-centre positions, as can be observed at 80% in Ag content for both motifs, and the structures lose the distortion developed at smaller Ag content, still in agreement with the behaviour of the Leary tetrahedron.

3.3 Assessment of the computational efficiency of the AugGGO approach

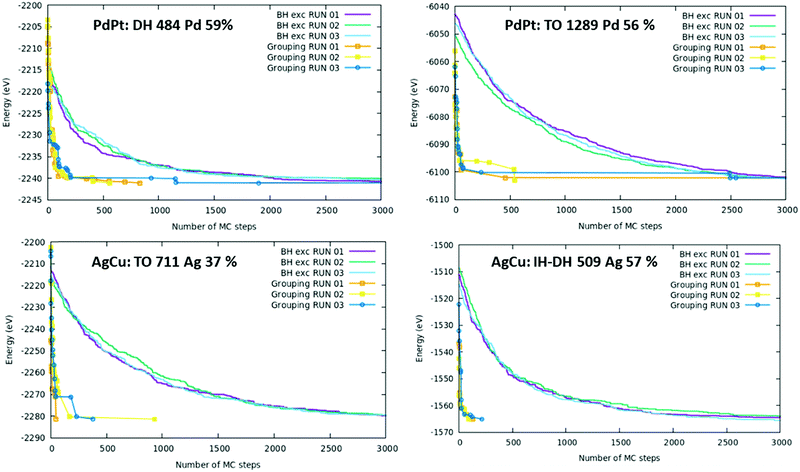
An important aspect of the present proposal regards the efficiency of the AugGGO algorithm. To assess it, we have compared the evolution of the total energy in GO runs using the AugGGO approach or a BH algorithm based on single exchange moves, as implemented in the code by Rossi et al.,¹² on selected structures, diverse in size, motif and type of alloy (note that, to make the comparison exhaustive, we included sizes and structures not previously discussed). The results of this comparison are shown in Fig. 6; in each plot the evolution of the total energy as a function of the number of GO steps is reported for the two approaches (AugGGO vs. BH exchange) in the case of four examples: two for PdPt and two for AgCu, at different sizes. In all four cases, the curves prove that a remarkable reduction in the number of BH steps needed to reach the low-energy regions of the PES (Potential Energy Surface) is achieved when using the new AugGGO approach. This reduction in the number of BH steps amounts to 1–2 orders of magnitude. The much increased efficiency of AugGGO is independent of the alloy nature, the size of the cluster and of the structural motif. The plots in Fig. 6 also implicitly contain a quantitative validation of our predictions. First, it can be observed that the AugGGO and the BH-exchange curves reach asymptotic values differing in energy by only 1–2 hundredths of an eV. Moreover, we add that the putative AugGGO and the BH-exchange global minima also correspond to the same chemical-ordering patterns (not shown). This technically validates the AugGGO approach, as it demonstrates that our approach is able to reproduce the global minimum (both energy and chemical order pattern) in the phase space of the chemical ordering produced by the BH exchange approach, an approach unbiased and free of grouping constraints. In terms of the physics, we recall once more that the goal of AugGGO is not to perform a full structural GO, but one limited to the variables related to chemical ordering, irrespective of whether the investigated structural framework pertains to the absolute global minimum (indeed we know for sure that in some cases it does not).

Fig. 6 Comparison of the performance of the AugGGO approach vs. the BH-exchange approach: plots of the energy of the systems as a function of the MC steps for selected structures of the PdPt alloy (top row) and of the AgCu alloy (bottom row) for different sizes and structural models. Three different BH runs and three different grouping runs are reported in each panel.

To conclude this section, we highlight the following points. (i) The AugGGO approach seems to be able to single out the preferred (global minimum) chemical ordering pattern of both high-symmetry and low-symmetry structures. Incidentally, we see in the investigated examples that the physics of the high- and low-symmetry structures is similar, implying that the high-symmetry configurations are good models to mimic real nanoclusters, although peculiar finite-size effects do occur when releasing the high-symmetry constraint. (ii) The computational efficiency of AugGGO is much improved with respect to other GO tools, such as BH-exchange, achieving the prediction of the global minimum chemical ordering in a few tens of MC steps, thus 1–2 orders of magnitude smaller than those needed in the BH-exchange algorithm. This makes the exploration of much larger structures and the simulation of complicated systems composed of several metallic elements computationally affordable and feasible.

4. Conclusions

Optimizing the functionalities of materials systems by changing their composition is an important part of any materials rational design strategy. To achieve this goal, efficient tools to explore the compositional space are strongly needed at both the experimental and computational levels, which is an extremely difficult task since this space is combinatorial, and thus exponentially increasing with the system size. Here we restrict ourselves to sampling at the computational level the stoichiometry degrees of freedom of isomers sharing a fixed structural framework (homotops) but with a different ‘chemical ordering’ or ‘compositional structure’: this sampling is still of combinatorial, and therefore non-algorithmic, complexity, as the number of homotops equals M^N, where N is the total number of atoms and M is the number of components. Within this constraint, we develop an original Augmented Grouping Approach (AugGA), specifically in the form of the Augmented Grouping GO (AugGGO) scheme.

The AugGA approach is based on a previously proposed ‘grouping’ philosophy, in which the number of compositional degrees of freedom of the system is decreased by defining sets of atoms (groups, or orbits, or shells) that are constrained to be populated by the same element. However, the power and scope of the grouping methods is here decisively extended by including three basic advances: (i) groups are defined on the basis of descriptors rather than point-group symmetry, (ii) chemical ordering patterns from databases are exploited, and (iii) sub-grouping is realized via a multi-descriptor strategy (here: the atomic energy and a few types of geometry pattern recognition). The first advance (i) makes the approach applicable to any generic structural framework, thus overcoming the major limitation of previous grouping methods. The use of descriptors in the definition of groups also makes the approach much more flexible and opens a wealth of possibilities in finely tuning the degrees of freedom of the proposed technique. The second advance (ii) improves the chance of achieving a thorough sampling of the core regions of nanoparticles. Finally, both the second (ii) and third (iii) advances improve the chance of catching exotic/unexpected chemical ordering arrangements, easily overlooked because they may be strongly penalized by entropic factors due to a tiny number of possible realizations, although energetically favoured.

By focusing on paradigmatic examples of two binary alloys, PdPt and AgCu, at sizes spanning from ≈500 to ≈1300 atoms, and exhibiting diverse structural motifs, here we show how AugGGO (i.e., AugGA using a Monte Carlo stochastic search in the compositional phase space) enables one to accelerate the exploration of the combinatorial phase space of large systems still maintaining thoroughness over the physically and chemically significant isomers – a mandatory step to make simulations affordable and predictive. Specifically, we demonstrate that AugGGO can predict the same global minimum compositional structure of all the investigated nanoalloys within a few tens of Monte Carlo steps and thus at a computational cost which is 1–2 orders of magnitude smaller than that of traditional Monte Carlo single-exchange techniques, i.e., the traditional approach based on individual-site moves.

Finally, we underline how the AugGA/AugGGO approach lends itself to interesting perspectives and possible further developments.

In particular, in the present work we have used the atomic energy calculated via an empirical potential as a descriptor function (or order parameter), but as discussed in Section 2 the approach is completely general and could employ any local function of atomic coordinates. This freedom will also facilitate the next development of AugGGO, that is, combining chemical ordering sampling with structural sampling into one general GO scheme¹² (work is in progress along these lines). In terms of other descriptor functions (or order parameters), one could use for example those derived from a common-neighbour analysis (CNA).²⁶

In this respect, it is interesting to note that CNA is usually applied to mono-elemental systems, but it could be easily generalized to binary or multicomponent systems.

A further, straightforward and promising perspective is the application of AugGGO to ternary, quaternary, etc. nanoalloys, high-entropy alloys,⁵² super-conductors,⁵³ quasi-crystals,⁵⁴etc.

The automated recognition of the best descriptor(s) to use in the definition of groups is finally a third promising advance for a user-friendly distribution of our code and to investigate physically very complex cases (this is also in progress in our lab).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Computational support from the Cineca Supercomputing Center within the ISCRA programme is gratefully acknowledged. A. F. gratefully acknowledges the contribution of the International Research Network IRN on Nanoalloys (CNRS).

Notes and references

1. P. Kirkpatrick and C. Ellis, Chemical space, Nature, 2004, 432, 823.
2. D. J. Wales and J. P. K. Doye, Energy landscapes applications clusters biomolecules and glasses, Cambridge University Press, 2003.
3. R. Ferrando, Structure and Properties of Nanoalloys, Elsevier, 2016.
4. F. Calvo, Nanoalloys – From Fundamentals to Emergent Applications, Elsevier, 2nd edn, 2020.
5. J. Jellinek and E. B. Krissinel, NinAlm alloy clusters: Analysis of structural forms and their energy ordering, Chem. Phys. Lett., 1996, 258, 283–292.
6. M. Sahimi and H. Hamzehpour, Efficient computational strategies for solving global optimization problems, Comput. Sci. Eng., 2010, 12, 74–82.
7. Z. Li and H. A. Scheraga, Monte Carlo-minimization approach to the multiple-minima problem in protein folding, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615.
8. R. L. Johnston, Evolving better nanoparticles: Genetic algorithms for optimising cluster geometries, Dalton Trans., 2003, 4193–4207.
9. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of State Calculations by Fast Computing Machines, J. Chem. Phys., 2004, 21, 1087.
10. J. P. K. Doye and D. J. Wales, Thermodynamics of global optimization, Phys. Rev. Lett., 1998, 80, 1357–1360.
11. G. Barcaro, L. Sementa, F. R. Negreiros, I. O. Thomas, S. Vajda and A. Fortunelli, in Oxide Materials at the Two-Dimensional Limit, ed. F. P. Netzer and A. Fortunelli, Springer, Berlin Heidelberg, 2016, vol. 234, pp. 39–90.
12. G. Rossi and R. Ferrando, Searching for low-energy structures of nanoparticles: a comparison of different methods and algorithms, J. Phys.: Condens. Matter, 2009, 21, 084208.
13. S. M. Kozlov, G. Kovács, R. Ferrando and K. M. Neyman, How to determine accurate chemical ordering in several nanometer large bimetallic crystallites from electronic structure calculations, Chem. Sci., 2015, 6, 3868–3880.
14. S. V. Karewar, N. Gupta, A. Caro and S. G. Srinivasan, A concentration dependent embedded atom method potential for the Mg-Li system, Comput. Mater. Sci., 2014, 85, 172–178.
15. A. Fortunelli and A. M. Velasco, THEOCHEM, 1999, 487, 251–266.
16. L. O. Paz-Borbón, T. V. Mortimer-Jones, R. L. Johnston, A. Posada-Amarillas, G. Barcaro and A. Fortunelli, Structures and energetics of 98 atom Pd-Pt nanoalloys: Potential stability of the Leary tetrahedron for bimetallic nanoparticles, Phys. Chem. Chem. Phys., 2007, 9, 5202–5208.
17. G. Barcaro, L. Sementa and A. Fortunelli, A grouping approach to homotop global optimization in alloy nanoparticles, Phys. Chem. Chem. Phys., 2014, 16, 24256–24265.
18. G. Barcaro, A. Fortunelli, M. Polak and L. Rubinovich, Patchy multishell segregation in Pd–Pt alloy nanoparticles, Nano Lett., 2011, 11, 1766–1769.
19. S. Bajaj, M. G. Haverty, R. Arróyave, W. A. Goddard and S. Shankar, Phase stability in nanoscale material systems: Extension from bulk phase diagrams, Nanoscale, 2015, 7, 9868–9877.
20. ASM Handbook, Volume 03 – Alloy Phase Diagrams, ed. H. Okamoto, M. E. Schlesinger and E. M. Mueller, ASM International, 2016.
21. P. J. Spencer, A brief history of CALPHAD, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2008, 32, 1–8.
22. R. Ferrando, A. Fortunelli and G. Rossi, Quantum effects on the structure of pure and binary metallic nanoclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085449.
23. F. Cleri and V. Rosato, Tight-binding potentials for transition metals and alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33.
24. R. H. Leary and J. P. K. Doye, Tetrahedral global minimum for the 98-atom Lennard-Jones cluster, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, R6320.
25. L. O. Paz-Borbón, R. L. Johnston, G. Barcaro and A. Fortunelli, A mixed structural motif in 34-atom Pd–Pt clusters, J. Phys. Chem. C, 2007, 111, 2936–2941.
26. J. D. Honeycutt and H. C. Andersen, Molecular dynamics study of melting and freezing of small Lennard-Jones clusters, J. Phys. Chem., 1987, 91, 4950–4963.
27. C. Steger, M. Ulrich and C. Wiedemann, Machine vision algorithms and applications, Wiley-VCH, 2018.
28. J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401.
29. L. Rubinovich, M. I. Haftel, N. Bernstein and M. Polak, Compositional structures and thermodynamic properties of Pd–Cu, Rh–Pd, and Rh–Pd–Cu nanoclusters computed by a combined free-energy concentration expansion method and tight-binding approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035405.
30. M. Jäger, R. Schäfer and R. L. Johnston, First principles global optimization of metal clusters and nanoalloys, Adv. Phys.: X, 2018, 3, 1077–1108.
31. L. D. Marks and L. D. Marks, Surface structure and energetics of multiply twinned particles, Philos. Mag. A, 1984, 49, 81–93.
32. Q. Yuan, Z. Zhou, J. Zhuang and X. Wang, Pd-Pt random alloy nanocubes with tunable compositions and their enhanced electrocatalytic activities, Chem. Commun., 2010, 46, 1491–1493.
33. C. Langlois, Z. L. Li, J. Yuan, D. Alloyeau, J. Nelayah, D. Bochicchio, R. Ferrando and C. Ricolleau, Transition from core–shell to Janus chemical configuration for bimetallic nanoparticles, Nanoscale, 2012, 4, 3381.
34. D. Bochicchio and R. Ferrando, Morphological instability of core-shell metallic nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165435.
35. I. Parsina and F. Baletto, Tailoring the structural motif of AgCo nanoalloys: Core/shell versus janus-like, J. Phys. Chem. C, 2010, 114, 1504–1511.
36. F. Baletto, Structural properties of sub-nanometer metallic clusters, J. Phys.: Condens. Matter, 2019, 31, 113001.
37. Z. Peng and H. Yang, Synthesis and oxygen reduction electrocatalytic property of Pt-on-Pd bimetallic heteronanostructures, J. Am. Chem. Soc., 2009, 131, 7542–7543.
38. A. X. Yin, X. Q. Min, W. Zhu, H. S. Wu, Y. W. Zhang and C. H. Yan, Multiply twinned Pt-Pd nanoicosahedrons as highly active electrocatalysts for methanol oxidation, Chem. Commun., 2012, 48, 543–545.
39. H. Zhang, M. Jin and Y. Xia, Enhancing the catalytic and electrocatalytic properties of Pt-based catalysts by forming bimetallic nanocrystals with Pd, Chem. Soc. Rev., 2012, 41, 8035–8049.
40. P. Zhang, Y. Hu, B. Li, Q. Zhang, C. Zhou, H. Yu, X. Zhang, L. Chen, B. Eichhorn and S. Zhou, Kinetically stabilized Pd@Pt core-shell octahedral nanoparticles with thin Pt layers for enhanced catalytic hydrogenation performance, ACS Catal., 2015, 5, 1335–1343.
41. A. Laghrissi and M. Es-Souni, Porous PtPd alloy nanotubes: Towards high performance electrocatalysts with low Pt-loading, Catal. Sci. Technol., 2019, 9, 4355–4364.
42. J. M. Conesa, M. V. Morales, C. López-Olmos, I. Rodríguez-Ramos and A. Guerrero-Ruiz, Comparative study of Cu, Ag and Ag-Cu catalysts over graphite in the ethanol dehydrogenation reaction: Catalytic activity, deactivation and regeneration, Appl. Catal., A, 2019, 576, 54–64.
43. K. Shin, D. H. Kim, S. C. Yeo and H. M. Lee, Catalysis Today, Elsevier, 2012, vol. 185, pp. 94–98.
44. X. Liu, D. Wang and Y. Li, Synthesis and catalytic properties of bimetallic nanomaterials with various architectures, Nano Today, 2012, 7, 448–466.
45. R. Ferrando, Symmetry breaking and morphological instabilities in core-shell metallic nanoparticles, J. Phys.: Condens. Matter, 2015, 27, 013003.
46. D. Hildebrandt and D. Glasser, Predicting phase and chemical equilibrium using the convex hull of the Gibbs free energy, Chem. Eng. J., 1994, 54, 187–197.
47. N. Perevoshchikova, B. Appolaire, J. Teixeira, E. Aeby-Gautier and S. Denis, A convex hull algorithm for a grid minimization of Gibbs energy as initial step in equilibrium calculations in two-phase multicomponent alloys, Comput. Mater. Sci., 2012, 61, 54–66.
48. D. Bochicchio and R. Ferrando, Size-dependent transition to high-symmetry chiral structures in AgCu, AgCo, AgNi, and AuNi nanoalloys, Nano Lett., 2010, 10, 4211–4216.
49. C. Langlois, Z. L. Li, J. Yuan, D. Alloyeau, J. Nelayah, D. Bochicchio, R. Ferrando and C. Ricolleauv, Transition from core-shell to Janus chemical configuration for bimetallic nanoparticles, Nanoscale, 2012, 4, 3381–3388.
50. A. Fortunelli and G. Barcaro, Density-Functional Theory of Free and Supported Metal Nanoclusters and Nanoalloys, in Metal Clusters and Nanoalloys, ed. M. M. Mariscal, O. A. Oviedo and E. P. Marcos Leiva, Springer, New York, NY, 2013, pp. 29–79.
51. G. Rossi, A. Rapallo, C. Mottet, A. Fortunelli, F. Baletto and R. Ferrando, Magic polyicosahedral core-shell clusters, Phys. Rev. Lett., 2004, 93, 105503.
52. Y. F. Ye, Q. Wang, J. Lu, C. T. Liu and Y. Yang, High-entropy alloy: challenges and prospects, Mater. Today, 2016, 19, 349–362.
53. P. Koželj, S. Vrtnik, A. Jelen, S. Jazbec, Z. Jagličić, S. Maiti, M. Feuerbacher, W. Steurer and J. Dolinšek, Discovery of a Superconducting High-Entropy Alloy, Phys. Rev. Lett., 2014, 113, 107001.
54. J.-M. Dubois, Properties- and applications of quasicrystals and complex metallic alloys, Chem. Soc. Rev., 2012, 41, 6760–6777.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03583e

---