 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modeling the impedance response and steady state behaviour of porous CGO-based MIEC anodes†
Philip
Marmet
 *a,
Lorenz
Holzer
a,
Jan G.
Grolig
b,
Holger
Bausinger
b,
Andreas
Mai
b,
Joseph M.
Brader
c and
Thomas
Hocker
a
*a,
Lorenz
Holzer
a,
Jan G.
Grolig
b,
Holger
Bausinger
b,
Andreas
Mai
b,
Joseph M.
Brader
c and
Thomas
Hocker
a
aZurich University of Applied Sciences, Institute of Computational Physics, Winterthur, Switzerland. E-mail: mame@zhaw.ch; Tel: +41 (0)58 934 70 80
bHexis AG, Winterthur, Switzerland
cDepartment of Physics, University of Fribourg, Fribourg, Switzerland
First published on 6th October 2021
Abstract
Mixed ionic and electronic conducting (MIEC) materials recently gained much interest for use as anodes in solid oxide fuel cell (SOFC) applications. However, many processes in MIEC-based porous anodes are still poorly understood and the appropriate interpretation of corresponding electrochemical impedance spectroscopy (EIS) data is challenging. Therefore, a model which is capable to capture all relevant physico-chemical processes is a crucial prerequisite for systematic materials optimization. In this contribution we present a comprehensive model for MIEC-based anodes providing both the DC-behaviour and the EIS-spectra. The model enables one to distinguish between the impact of the chemical capacitance, the reaction resistance, the gas impedance and the charge transport resistance on the EIS-spectrum and therewith allows its appropriate interpretation for button cell conditions. Typical MIEC-features are studied with the model applied to gadolinium doped ceria (CGO) anodes with different microstructures. The results obtained for CGO anodes reveal the spatial distribution of the reaction zone and associated transport distances for the charge carriers and gas species. Moreover, parameter spaces for transport limited and surface reaction limited situations are depicted. By linking bulk material properties, microstructure effects and the cell design with the cell performance, we present a way towards a systematic materials optimization for MIEC-based anodes.
1 Introduction
Solid oxide fuel cell (SOFC) technology is a promising solution for the efficient use of renewable fuels or natural gas for decentral heat and power generation. The most commonly used anode material in SOFCs is Ni-YSZ. Unfortunately, this material shows various types of degradation including Ni coarsening, carbon coking, sulfur poisoning and mechanical damage caused by redox cycling.1 Moreover, the electrochemical reaction is bound to the triple phase boundaries, which induces a specific microstructure limitation towards the electrochemical activity in Ni-YSZ cermet anodes. As an alternative anode concept, mixed ionic and electronic conductive (MIEC) materials are drawing much attention.2 An obvious advantage of MIEC materials is the fact that the fuel oxidation reaction can take place on the complete MIEC/pore interface. Furthermore, since it is a mixed conductor, only one contiguous solid phase is needed to enable transport of both charge carriers. In advanced materials concepts, MIECS are also often used as a basis for composite electrodes, whereby the MIEC is combined with an additional contiguous phase of superior electric conductivity. This combination leads to a reduction of the transport resistance. An additional variation of the anode concept is the infiltration of porous MIEC backbone with catalytically active metal particles, which leads to an enhancement of the electrochemical activity as e.g. shown by Primdahl et al.3,4 and Price et al.5 The optimization of these different anode concepts is the focus of ongoing research in the fuel cell community. Thereby, the type and chemistry of the MIEC material itself plays an important role. The most relevant MIECs for SOFC anodes are either perovskite-type materials with a wide range of elemental compositions or MIECs with fluorite structure. Ceria is the most prominent fluorite example.2 The importance of those materials is not restricted to fuel cells. They are also used as selective membranes to produce high purity oxygen,6 as electrode material in batteries, as sensors e.g. to measure the oxygen partial pressure based on the change in stoichiometry to mention but a few. A more complete overview of MIEC materials and their applications can be found in the Handbook of Solid State Electrochemistry of Bouwmeester et al.7In this study we present a comprehensive numerical model for MIEC-based SOFC anodes on the button cell level, using gadolinium doped ceria (CGO) represented by Ce0.9Gd0.1O1.95−δ. CGO is chosen as a reference system because it is widely used in commercial SOFC applications e.g. by Hexis AG8 and Sunfire GmbH9 due to its high performance and stability. However, similar or possibly even higher conductivities can be achieved by samarium doped ceria according to Koettgen et al.10 The importance of reliable models for the optimization of CGO-based anodes is emphasized here, because there are still many open questions regarding the underlying reaction mechanism and the rate limiting processes. A detailed physical model for MIEC anodes, such as the one presented in this study enables quantifying the resistive effects from different processes that are otherwise indistinguishably overlapping in EIS measurements. Furthermore, a model-based approach allows performing parametric studies for a wide range of parameters including microstructure and material properties, operating conditions and anode architectures. Such extensive parametric investigations would exceed by far the capacities and capabilities of conventional experimental approaches.
So far, the ceria-based anodes have been studied intensively and in great detail mainly in thin-film symmetric cell setups with transmission line (TL) and finite element (FE) models. TL-Models including corresponding measurements were presented by Lai et al.11 for SDC15 and by Nenning et al.2 for SrTi0.7Fe0.3O3−δ. FE-models for SDC15 thin film electrodes were presented by Ciucci et al.12 as a DC and by Chen et al.13 as an AC (EIS) model (these references are discussed in more detail in Section 2.2). Modeling studies for the case of porous high-performance electrodes with ceria as presented by Kishimoto et al.14 are less frequent. However, ceria-based anodes are now at the threshold of commercialization.8,9 The requirements of the market are improvements of performance and efficiency, longer lifetime and lower system costs. To reach these goals, a detailed understanding is required of the physico-chemical processes involved in ceria-based porous anodes. This is true for button cell, large area cell and stack levels. In this context it must be emphasized that only a suitable MIEC model – in combination with experiments – is capable to provide a fundamental understanding of the underlying mechanism, which is the basis for purposeful, knowledge-based optimization of different cell concepts and material systems.
In SOFC research, electrochemical impedance spectroscopy (EIS) is an essential characterization tool, which serves as a basis for materials optimization on the electrode, cell and stack levels. However, for CGO-based electrodes, there is no consensus how to interpret the impedance spectra yet. With EIS, the different processes in CGO-based anodes are often not distinguishable from each other because their frequency ranges overlap and because of their interdependencies. Especially for the low frequency arc(s) in impedance spectra of ceria-/CGO-based anodes, the resistive contributions from surface reaction resistance/chemical capacitance, gas diffusion impedance and charge transport resistance are often unclear. In addition, the impact of these processes may strongly depend on the cell architecture and type of electrode (e.g. dense thin-film electrode vs. porous anodes in button cells vs. large area cells). Hence, for the same anode material (i.e. CGO) different processes might become rate limiting in dependence of the cell architecture and electrode type, which explains the controversial interpretations of the corresponding impedance spectra in literature. A detailed discussion of this controversy is provided by Marmet et al.,15 who compared literature data of EIS-spectra for dense CGO-based anodes in thin-film electrodes, with the spectra of porous CGO-anodes in button cells and large area cells. The outcome of this comparison can be summarized as follows: In principle, it is well accepted (e.g. ref. 11, 16 and 17) that ceria-based electrodes exhibit a chemical capacitance, showing the ability of ceria to store energy by a change in its local stoichiometry. Hence, this process potentially controls the observed low-frequency arc. In fact, for ceria-based dense thin-film electrodes the low-frequency arc is identified as a surface reaction resistance/chemical capacitance process by Chueh et al.17 They employed conditions under which other effects like the gas impedance and transport resistance of the charge carriers are negligible. In contrast, for large area cells, there is strong evidence that the low frequency arc must be identified as a gas impedance process. Hence, large area cells exhibit a large gas conversion impedance due to the fuel consumption along the cell. This has been reported for a Hexis short stack with CGO-based anodes by Linder et al.18 For this case it must be noted that the (low frequency) contribution from the surface reaction resistance/chemical capacitance process is relatively small and therefore hidden within the dominant gas impedance arc. The third case of CGO-based anodes is represented by a button cell setup with an excess fuel flow rate. In this setup the gas impedance is much smaller compared to large area cells, which was reported by Riegraf et al.19 Hence, whether the low frequency arcs in button cells are dominated by the gas impedance, surface reaction resistance/chemical capacitance process or even by a different process like the transport resistance of the charge carriers, is usually not obvious in the experimental results. Consequently, different interpretations are found in the literature. In order to unravel this controversy, a model for MIEC/ceria-based anodes is presented in this study, which enables simulating the EIS-spectra for button cells, but also for other cell setups (e.g. thin films). Thus, the aim of this model (among others) is to reveal the different low frequency contributions on a quantitative level.
Another point of interest for SOFC developers is the contribution of the transport resistance of the charge carriers to the total area specific resistance (ASR). This contribution is closely linked to the extension of the reaction zone. Therefore, a quantitative description of the reaction zone and associated distribution of charge carriers are considered as important information for a controlled and knowledge-based optimization. Commonly it is suggested in the literature (e.g. by Primdahl et al.3 and Nakamura et al.20) that for MIEC anodes with a higher electronic than ionic conductivity, the reactive zone of the electrode will be localized at the electrolyte/anode interface. In some circumstances, however, the electrochemical conversion may spread over the entire anode layer or it can even take place preferentially in a zone adjacent to the current collector. A more detailed discussion of this topic can be found in Section 4.2. With our model operated in DC-mode, we also provide a quantitative description of the location of the reaction zone that gives new insight on the reaction mechanism of MIEC anodes. A reliable quantitative description of the extension of the reaction zone has, to the best of our knowledge, not been reported for porous CGO-based anodes so far.
From the discussion above it follows that reliable interpretations of impedance spectra and systematic optimizations of MIEC-based SOFC anodes require a detailed model, which captures (a) the relevant physico-chemical processes, (b) the associated material laws, (c) the influence of the microstructure and (d) the dependencies on varying operating conditions. Moreover, the possibility to run the model in both, AC and DC modes has great advantages. However, for porous MIEC/CGO electrodes, such combined AC/DC models are hardly available in the literature. This motivated us to develop a comprehensive model for a CGO-based anode on the button cell level enabling an appropriate interpretation of EIS-spectra and providing a thorough understanding of the complex physico-chemical processes involved.
This paper is structured as follows:
In Section 2 we present a thorough description of a 1D MIEC-anode model, which can be operated in DC as well as in AC modes. In a first stage, the model formulation focuses on general aspects of MIEC anodes (i.e. it describes processes that are common to all kinds of different MIEC materials). It also provides a quantitative description of the relationships between effective properties with the corresponding 3D microstructure characteristics. In this way, the 1D model is capable to capture in a reliable way the relevant microstructure effects based on input from 3D analysis. Furthermore, this first stage of model formulation also contains thorough descriptions of the following important processes and phenomena: charge transport in MIEC materials, hydrogen oxidation surface reaction, gas transport and gas concentration impedance. In a second stage, the model is then extended towards a specific MIEC material, which is Gd doped ceria (CGO10). Hence, CGO-specific material laws and phenomena are described, such as crystal chemistry and equilibrium density of charge carriers, nonstoichiometry, electric and ionic conductivities, surface reaction overpotential, exchange current density and chemical capacitance.
In Section 3 the results from DC- and AC-simulations with CGO-based anodes are presented. The DC-simulations provide profiles across the anode layer, which show for example local concentrations of charge carriers, and also the local reaction rates on the CGO surface. The AC-model enables to distinguish specific impedance contributions from different processes such as charge transport, gas transport and hydrogen oxidation surface reaction. In a first step, the simulations are performed for a specific set of parameters describing a standard button cell architecture, standard operating conditions, standard properties of CGO10 and a standard microstructure. In a second step, the DC- and AC-models are then used for parametric sweeps that illustrate e.g. the impact of anode layer thickness and microstructure variations on the cell performance.
The modeling results represent the basis for a detailed understanding of the overall reaction mechanism in CGO anodes, which is discussed in Section 4. The distribution of the reaction zone and associated current densities are discussed in the context of a complex interplay of different processes and associated resistances. The underlying mechanism of coupled processes and rate limiting effects are discussed specifically for charge transport, distribution of the reaction zone, gas impedance, surface reaction and chemical capacitance. Furthermore, the effect of parameter variations describing the anode architecture (e.g. layer thickness) and microstructure properties (e.g. porosity and surface area) are also discussed. The model thus allows us to distinguish and even quantify the overlapping impedance contributions from different processes.
Section 5 concludes with the lessons learned from combined DC- and AC-modeling of CGO anodes, with a special emphasis on the identification of rate limiting processes and their overlapping contributions to impedance spectra for different parameter constellations. The paper extends these aspects by providing an extensive illustration of simulated impedance spectra for different anode/cell architectures (i.e. model electrode, button cell, large are cell), different layer thicknesses and different microstructures (porous-dense-massive, coarse-fine). Together with the model-based identification of rate limiting processes, this overview helps solve the literature controversy about how to interpret the low frequency arcs in impedance spectra for MIEC/CGO-based anodes.
2 Model description
2.1 General properties of MIECs
MIECs exhibit both ionic and electronic conductivity. Ion transport occurs normally via interstitial sites or by vacancy motion, both caused by ionic defects. These ionic defects can be formed by thermal excitation, by change of stoichiometry or by doping.7 Electronic conductivity occurs via delocalized states in the conduction or valence bands or by localized states by a thermally assisted hopping mechanism.7 The electronic conductivity is generated by defects as well, but the mechanisms differ from those of the ionic conductivity. The conductivity depends on the mobility μ and the number density n of mobile charge carriers. As discussed for the case of CGO in the Section 2.4.1, immobile charge carriers are important to be considered for the electro-neutrality condition but do not contribute to the conductivity. The mobility generally depends on the crystal structure and the temperature T. The number of mobile charge carriers depends on the doping y and/or on the oxygen-nonstoichiometry δ, which is directly linked with oxygen vacancies. Especially when generated by reduction, the oxygen-nonstoichiometry depends strongly on the environmental conditions (oxygen partial pressure pO2) and temperature. Moreover, the transport of the charges in a MIEC is not simply governed by the drift in the electric field, but as well by diffusion due to concentration gradients of the charge carriers.11,16 Thereby, the mobility and the diffusivity of the charge carriers are related to each other according to the Nernst–Einstein relation eqn (7).As already mentioned, the simultaneous electronic and ionic conduction enables the electrochemical reaction at the MIEC/pore interface and is therefore not restricted to the three phase boundaries as in classical cermets. However, this does not mean that the whole MIEC/pore interface is electrochemically active to the same extent. Already Adler et al.21 concluded with their fundamental model for MIEC cathodes that the extension of the reaction zone is limited by the ionic conduction. Nakamura et al.20 and Primdahl et al.3 concluded from their experimental studies on MIEC anodes with a higher electronic than ionic conductivity that the active site of the electrode is nearby the electrolyte.
Another prominent feature of MIECs is their chemical capacitance, describing their ability of storing charges due to a change in the nonstoichiometry.11,13,16,22–24 Because the charges can be stored in the bulk, and not only as surface charges as in a dielectric capacitor, the chemical capacitance is a volumetric effect and can therefore be orders of magnitude higher than dielectric capacitance effects.
In the following, a MIEC anode model will be presented including the physical effects mentioned above. After a literature overview of MIEC anode models in Section 2.2, the model will at first be described in a general way, applicable for many MIEC materials in Section 2.3. In a second step, it will be specified and parametrized for Ce0.9Gd0.1O1.95−δ in Section 2.4.
2.2 Literature overview of MIEC anode models
For dense thin-film electrodes, a number of sophisticated models were reported. Ciucci et al.12 presented a 2D stationary simulation study with patterned metal current collectors to study the transport pathways of the charge carriers for symmetric thin-film electrodes. They concluded that the surface reaction rather than the migration of the charge carriers is the overall rate-limiting step for this particular cell setup. Chen et al.13 performed a linear perturbation study in the frequency domain to model the impedance response of samarium doped ceria (SDC) thin-film electrodes. They showed that depending on the spacing of the contacts on the SDC thin-film, either the surface reaction resistance or the transport resistance of the charge carriers become dominant. Based on these results they suggested the existence of a maximum electronic penetration depth.Jamnik and Maier16 developed a general transmission line model for thin-film MIEC electrodes and discussed the decisive materials parameters. The latter determine whether or not the impedance spectrum is of Warburg type i.e. dominated by transport limitations of the charge carriers. Lai and Haile11 presented a rigorous derivation of the impedance behaviour of mixed conducting materials using transmission lines and performed a case study for ceria. Nenning et al.2 presented a two-mode measurement setup for thin-film MIEC electrodes, which enables the determination of the ionic and electronic conductivities as well as the electrochemical reaction resistance by fitting the EIS-spectra to corresponding transmission line models. Their approach was tested for SrTi0.7Fe0.3O3−δ.
For porous MIEC high performance anodes, only few studies are available. Kishimoto et al.14 developed a one-dimensional numerical DC model of a nickel-infiltrated GDC anode. He especially studied the microstructure–performance relationship, where the microstructure information was obtained from focused ion beam tomography. However, a detailed analysis of the transport mechanisms of charge carriers and their interdependency with the surface reaction and the influence of the gas impedance was out of their scope.
2.3 Model formulation for a general MIEC anode on the button cell level
 | ||
| Fig. 1 Illustration of an SOFC button cell setup: eon = electrons, vac = oxygen ion vacancies, CCL = current collector layer. | ||
1D simulation setup. For this study, a 1D computational model is developed and implemented in the commercial software package COMSOL Multiphysics.25 The model consists of two computational domains as visualized schematically in Fig. 2. The domain x = [0,L] is the porous MIEC anode functional layer, where the hydrogen oxidation reaction (HOR), the transport of the charge carriers in the MIEC and the transport of the gas species in the porous media take place. As the pores and the MIEC phase are not spatially resolved, the effects of the porous microstructure are taken into account by using effective transport properties. They can be related to bulk material properties with a so called microstructure factor M for each phase as described in Section 2.3.2. The M-factor characterizes the considered microstructure by accounting for its phase volume fraction, tortuosity and constrictivity. The domain x = [−LStag,0] represents the stagnant gas layer at the interface between the gas flow channel and the anode functional layer. There, gas species diffusion corresponding to a button cell setup as depicted in Fig. 1 is taken into account.
Hydrogen oxidation reaction at the MIEC surface. In this contribution, humidified hydrogen is used as fuel. Due to the HOR, hydrogen is consumed and water, electrons and oxygen ion vacancies are produced at the MIEC/pore interface. The reaction kinetics depends on the actual material system and is formulated for CGO in Section 2.4.4. For CGO, the reaction kinetics especially depends on the concentration of electrons ceon and vacancies cvac. The surface reaction resistance in combination with chemical capacitance provoke the impedance contribution ZSR in the EIS-spectra. Note also that the production of an oxygen ion vacancy is equivalent to the consumption of an oxygen ion. Accordingly, the transport of an oxygen ion from the electrolyte to the MIEC/pore interface is equivalent to the transport of an oxygen ion vacancy in the opposite direction. In our model, we consider vacancies instead of the oxygen ions.
Charge transport. Electrons and vacancies are transported from the reaction site at the MIEC/pore interface throughout the MIEC to the CCL and to the electrolyte, respectively. The transport of the charge carriers is governed by drift and diffusion and is implemented based on the full Nernst Planck Poisson equation as described in Section 2.3.3. The charge transport losses in the MIEC provoke the impedance contribution Zchrgtpt in the EIS-spectra.
Gas transport. The gas species are transported from and to the reaction sites by convection and diffusion. The concentration changes along the gas supply cause a gas concentration impedance based on the Nernst equation (eqn (23)). Concentration gradients along the channel are caused by the fuel utilization (gas conversion impedance). This effect can be suppressed by an excess fuel supply, which is common practice for button cell experiments, as depicted in Fig. 1. Therefore, this effect is neglected in the current model. The gas transport in the gas channel is governed by convection. However, there exists a stagnant gas layer above the electrode as illustrated in Fig. 1, where the gas transport is governed by diffusion and not by convection of the excess fuel supply. In the domain x = [−LStag,0], the gas species diffusion in a stagnant gas layer is thus modeled. The thickness of this stagnant gas layer LStag depends on the actual button cell setup as discussed in further detail in Section 2.3.6. A Stefan–Maxwell formulation is used for the gas transport in the stagnant gas layer as described in Section 2.3.8.
The gas transport within the pores of the MIEC-electrode is governed by diffusion. However, for fine porous microstructures with pores in the range of sub-microns, the transport can no longer solely be described by ordinary bulk diffusion but is additionally affected by Knudsen diffusion. The latter describes the scattering events of the gas molecules with the pore walls. Fine porous microstructures are relevant because of their potentially high electrochemically activity associated with their high specific surface area. To capture the Knudsen effects, the well known dusty-gas model (DGM) is used. It has proven able to describe the combined transport mechanism by bulk and Knudsen diffusion appropriately, see Section 2.3.7 and Sections B, C of the ESI.†
The concentration gradients of the gas species in the stagnant gas layer and in the pores of the MIEC-electrode cause a gas diffusion impedance Zgas, as further discussed in Section 2.3.6.
By considering the gas transport and source terms from the reaction, the gas species concentrations are calculated. Moreover the oxygen partial pressure is calculated according to the dissociation of water. Therewith, oxygen partial pressure dependent material laws for the concentration and conductivity of electrons and vacancies and for the reaction kinetics can be used.
Model limitations. The described model entails some limitations. The electrolyte at x = L and the current collector layer (CCL) at x = 0 are modeled as boundary conditions and hence are not spatially resolved. The transport of electrons across the MIEC/CCL interface and the transport of vacancies across the MIEC/electrolyte interface are assumed to be lossless. In addition, the electrolyte and the CCL are modeled as ideal conductors. This means that the resistances of the CCL and the electrolyte are neglected and therefore do not induce any inhomogeneous in-plane current densities. In reality, losses from unfavourable in-plane conduction to the ribs of the interconnector might lead to electrochemically less active regions. According to the assumptions necessary for the 1D setup, the in-plane transport in y- and z-directions for the pore- and the MIEC-phase of the porous electrode is assumed to be ideal. However, this simplification is quite appropriate. On the one hand, there is no macroscopic in-plane charge carrier transport because of the assumption of an ideal current collector and an ideal electrolyte. In the same manner for the pore-phase, the assumption of an excess fuel supply leads to the absence of a concentration gradient in y- and z-directions. There are thus no macroscopic in-plane diffusion fluxes. On the other hand, for the pore-scale level of the MIEC-phase, the in-plane transport of the charge carriers happens only from the surface to the center of a sintered MIEC-particle. These distances are on the sub-micrometer scale. In a similar way, no steep in-plane concentration gradients are expected within the single pore bodies. Moreover, these in-plane pathways on pore-scale are not tortuous and no constrictions due to bottlenecks are present within one single grain or one local pore body (bulge). As a result, the effective transport properties are assumed to be very close to the intrinsic ones. Therefore, the in-plane transport resistance can be regarded as negligible for gas-transport in the pores as well as for charge-transport in the MIEC-phase. However, for transports in the through-plane direction, limitations from microstructure due to tortuosity and constrictivity (bottlenecks) become effective and must be considered in the model.
| Deff = M·Dbulk | (1) |
In (a) the M-factor is interpreted as a relative property (e.g. relative diffusivity M = Deff/Dbulk), which is indirectly derived from the knowledge of effective and intrinsic properties. In this work, the effective properties are determined by means of numerical simulations on the 3D geometry of the microstructure represented by a voxel grid using GeoDict27 software. The diffusion equation in the solid MIEC phase is solved to determine the effective diffusivity and therewith the M-factors for the diffusion of the charge carriers. The derived M-factor can be used for the drift and diffusion of the charge carriers, as the equations for transport by diffusion and drift (i.e. electric conduction) are mathematically equivalent, i.e. MsimMIEC = Deff/D0 = σeff/σ0. The diffusion equation in the pore space is solved to determine the effective diffusivity and therewith the M-factors Msimpore = Deff/D0 for the bulk diffusion of the gas species. Additionally, the gas flow permeability kflow for the parametrization of the Darcy law is determined by a flow simulation on the voxel grid. Moreover, an M-factor for the Knudsen diffusion is calculated. These M-factors for the pores space are needed for the parametrization of the dusty-gas model presented in Section 2.3.7. The used GeoDict solvers and their parametrization are documented in the results Section 3.6.
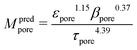
In (b) the M-factor is interpreted as a correction factor, which describes the limiting effects of microstructure and is directly obtained from microstructure characteristics. The M-factors for gas diffusion, as well as for conduction and diffusion of the charge carriers are additionally determined via such morphological analysis of the 3D microstructure data. Therewith, additional insight about the contribution of different microstructure effects on the transport properties can be achieved. Such methodologies have been developed and applied in previous publications by Holzer et al.,28–30 Gaiselmann et al.,31 Pecho et al.,32 Neumann et al.33,34 and Stenzel et al.35 Thereby, the M-factor includes the following microstructure effects: the phase fraction (e.g. porosity) ϕph, the tortuosity τ and the constrictivity β, relevant for drift and diffusion. A virtual materials testing (VMT) approach was applied in order to determine the M-factor empirically.26,31,35 Thereby a large number (>8000) of virtual 3D microstructures were created with a stochastic model. These structures cover a large range of values for ϕph, β and τ. For each 3D structure, the effective diffusivity Deff was determined by numerical simulation with GeoDict27 software. The following expression was then found by statistical error minimization:
 | (2) |
This equation for Mpred used in (b) was validated for different porous materials by comparing it with either results from simulation (Msim used in a) or from experiments (Mexp). Gaiselmann31 and Stenzel35 showed that the equation Mpred gives good results for all three phases in SOFC cermet electrodes. Furthermore, validations for this equation were also performed successfully by Holzer et al. for very different types of porous microstructures, such as sintered ceramic membranes,30 fibrous GDL in PEM fuel cell36 and even open cellular materials (Holzer, unpublished data). These successful validations confirm that the equation for Mpred has a global meaning, in the sense that it is capable to predict effective transport properties for all kinds of microstructures based on only three parameters (ϕph, β, τ).
For the solid MIEC-phase, the M-factor for the drift (i.e. electric conduction) and diffusion of the charge carriers within the MIEC yields:
 | (3) |
Likewise, for the bulk-diffusion of the gas species in the pore phase of the electrode the M-factor yields:
 | (4) |
Note that morphological analysis are also available for the gas flow permeability as e.g. reported by Holzer et al.30 and Neumann et al.33 As the results of the dusty-gas model (see Section 2.3.7) are less sensitive to the permeability as to the diffusivity, we only report the permeability extracted from the flow simulation on the voxel mesh.
| Jvac = −Dvac,eff∇cvac − zvacμvac,effFcvac∇ϕ, | (5) |
| Jeon = −Deon,eff∇ceon − zeonμeon,effFceon∇ϕ. | (6) |
 | (7) |
| Di,eff = MMIECDi | (8) |
 | (9) |
 | (10) |
 | (11) |
 | (12) |
Following Kishimoto et al.14iSR is expressed as a Butler–Volmer like expression with a surface reaction overpotential ηSR described below:
 | (13) |
Note that the Butler–Volmer formulation is also applied to traditional Ni-YSZ anodes, where the charge transfer process is assumed to occur at the three-phase boundaries. Thereby, the negatively charged oxygen ions are transported through the YSZ to the three-phase boundaries where they are consumed and two electrons are transferred over the phase boundary to the Ni-phase. This charge transfer can be associated with a well-defined overpotential between the YSZ- and the Ni-phase.39 However, MIEC-anodes do not exhibit a classical charge transfer process over a phase boundary like in Ni-YSZ anodes. Hence, oxygen ions are transported trough the MIEC to the MIEC/pore interface, where they are consumed. Electrons are produced at the MIEC/pore interface and have to be transported away from it. Oxygen ions (or vacancies respectively) and electrons are transported in the same MIEC-phase. However, the use of an overpotential formulation according to the Butler–Volmer equation is justified in the sense that an electrical double layer is formed at the MIEC/pore surface due to the charged surface reaction species. But the relation between the surface potential and the measurable overpotential of the surface reaction (or activation overpotential) ηSR can be complex, as derived by Fleig40 for a MIEC cathode. Moreover, the surface reaction overpotential cannot be directly associated to an electric potential difference within the same MIEC-phase. We therefore choose the approach that the surface reaction is driven by the chemical potential drop, which is associated with the surface reaction as suggested by Kishimoto et al.14 However, this surface reaction overpotential ηSR needs to be formulated appropriately in order to reflect the rate determining reaction step for the particular material system. An appropriate formulation for CGO is suggested in Section 2.4.4.
Note that the overall driving force for the HOR is the chemical potential difference between the reactants  and the product H2O. However, as we use a prescribed current density in our model formulation, we will directly account for the different overpotentials needed to drive this prescribed current. The available voltage of the fuel cell is then the chemical potential difference between reactants and product minus the sum of all overpotentials. Nonetheless, we will restrict our discussion on the overpotentials and ASR, because the discussion of current–voltage curves is out of the scope.
and the product H2O. However, as we use a prescribed current density in our model formulation, we will directly account for the different overpotentials needed to drive this prescribed current. The available voltage of the fuel cell is then the chemical potential difference between reactants and product minus the sum of all overpotentials. Nonetheless, we will restrict our discussion on the overpotentials and ASR, because the discussion of current–voltage curves is out of the scope.
Moreover, the Poisson equation needs to be fulfilled, i.e.
| ∇·(−ε0εr∇ϕ) = ρv | (14) |
| ρv = F(zeonceon + zvaccvac + zeonceon,imob). | (15) |
For CGO, a specific discussion of crystal chemistry and associated charge compensation mechanisms is given in Section 2.4.1.
 | ||
| Fig. 3 Illustration of gas concentration impedance with contributions from gas conversion and gas diffusion. | ||
Convective transport along the cell is limited in technically relevant systems in order to achieve a high fuel utilisation. This results in a concentration gradient along the cell (see Fig. 3) due to the consumption of hydrogen and the production of water vapour. This so-called gas conversion impedance41 is usually the dominant contribution to the gas concentration impedance for technically relevant large area cells and stacks. However, the gas conversion impedance can be suppressed in button cell configurations by using an excess fuel supply and is therefore neglected in our model.
Concentration gradients perpendicular to the electrode are because of diffusion limitations from different contributions and can be summarized by the term gas diffusion impedance.41 A possible diffusion limitation within the gas channel is associated with a stagnant gas layer, where the convective fuel flow does not contribute to mass transfer because of the no slip condition at the electrode surface (see Fig. 3). In contrast to the gas conversion impedance, there is no simple measure to avoid this effect. Nevertheless, Primdahl and Liu4 presented a setup with a MIEC-electrode mounted between auxiliary electrodes to avoid significant impedance contributions from gas diffusion outside the porous electrode structure. However, as our model intends to describe a classical button cell setup with an axial fuel supply as depicted in Fig. 1, a separate computation domain is introduced in the 1D-model for the stagnant gas layer. There, the gas diffusion is modeled with a Stefan–Maxwell approach, described in Section 2.3.8. At the boundary to the non-resolved gas channel region beyond the stagnant gas layer, the gas species concentrations are fixed, which mimics excess fuel supply without any concentration gradients along the button cell (i.e. the gas conversion impedance is suppressed).
Within the porous electrode, the gas transport is also dominated by diffusion and hence contributes to the gas diffusion impedance, which is illustrated in Fig. 2. In this simulation domain, the gas transport is modeled after the dusty gas model (DGM) which accounts for bulk and Knudsen diffusion, see Section 2.3.7 and Section B of the ESI.† The determination of the appropriate diffusion coefficients for the models is described in Section C of the ESI.†
Note that in button cells a metal mesh is often placed on top of the anode to ensure a good electric contact. This additional diffusion resistance is neglected in our model. Likewise, also the diffusion resistance in the not spatially resolved ideal CCL is neglected.
 | (16) |
 | (17) |
| R2 = −R1 = Rvac, | (18) |
For the molar flux densities N1 and N2, the effect of the porous microstructure needs to be considered. In nanoporous materials, gas diffusion is controlled by collision of gas molecules with the pore walls. In this case the mean free path of the gas molecules is longer than the characteristic length of the pores so that we enter the Knudsen diffusion regime. Modern high performance MIEC electrodes are usually very fine-grained in order to increase the specific surface area and associated reactivity. In most cases, the pore size in modern MIEC electrodes is in the mm to sub-mm scale, where both Knudsen and bulk diffusion become relevant. It is generally agreed14,42,43 that the dusty-gas model (DGM) is the most convenient approach for modeling combined bulk and Knudsen diffusion. Therefore, in our approach, the diffusion in the porous CGO-layer is modeled with the DGM. The DGM is an extension of the Stefan Maxwell model, where the pore phase (= “dust”) is treated as an additional, stationary species.42 In this work, an explicit version of the DGM for a binary system derived by Liu et al.44 is used. A detailed presentation and discussion of the used equations can be found in Section B of the ESI.†
The DGM needs to be parametrized appropriately. The bulk-diffusion contribution is governed by the effective binary diffusion coefficient D12,eff:
| D12,eff = MporeD12,0 | (19) |
The effect of the Knudsen diffusion is governed by the effective Knudsen diffusion coefficients for hydrogen D1Kn,eff and water D2Kn,eff, respectively:
| DiKn,eff = Mpore,KnDiKn,0. | (20) |
The relative contribution of the bulk and Knudsen diffusion on the overall diffusion resistance can be estimated by the Knudsen number, which is the ratio of the bulk and Knudsen diffusion coefficients. However, the bulk microstructure factor Mpore and the Knudsen microstructure factor Mpore,Kn might be similar, but not necessarily equal, as different processes are hindering the transport for the two transport mechanisms. Therefore, we distinguish two kinds of Knudsen numbers in this work: the intrinsic Knudsen number Kni,0 comparing the intrinsic properties and the effective Knudsen number Kni,eff comparing the effective properties. The definitions of both versions of the Knudsen number are presented and discussed in further detail in Section D of the ESI.†
Finally, the DGM includes a convective part, which is governed by the gas-flow permeability kflow of the microstructure and the dynamic viscosity of the gas mixture μvisc.
All the mentioned parameters needed for the DGM are tabulated in Tables 1 and 2. A detailed presentation of the equations and discussion of the binary and Knudsen diffusion coefficients can be found in Section C of the ESI.†
| Parameter | Value | Description | Ref. |
|---|---|---|---|
| a These parameters have been chosen according to illustrative aspects as discussed in Section 3.1. | |||
| L | 100 μm | CGO-layer thickness | |
| J charge | 2083 A m−2 | Prescribed current density | |
| D vac | 3.9228 × 10−9 m2 s−1 | Intrinsic diffusivity of vacancies | Estimated from Steele49 as documented in the ESI Section I |
| D eon | 3.3996 × 10−8 m2 s−1 | Intrinsic diffusivity of electrons | Estimated from Steele49 as documented in the ESI Section I |
| k 0 | 5.5 × 10−4 A m−2 | Surface specific exchange reaction rate constant | Estimated from Gerstl et al.57 as documented in the ESI Section J |
| L Stag | 0.2 mm | Stagnant gas layer thickness | Estimated for a reference setup documented in the ESI Section F |
| D 12,0 | 9.3363 × 10−4 m2 s−1 | Binary intrinsic diffusivity H2/H2O | Fuller et al.,45eqn (23) in Section C of the ESI |
| x 1,0 | 0.95 | H2 mole fraction in the fuel | |
| x 2,0 | 0.05 | H2O mole fraction in the fuel | |
| L Lattice | 5.422 Å | Lattice parameter of CGO | Li et al.52 |
| T | 850 °C | Temperature | Typical operating temperature18 for a high temperature SOFC |
| μ visc | 2.2 × 10−5 Pa s | Dynamic viscosity of hydrogen | Todd and Young64 |
| Microstructure parameter | Unit | MS1 | MS2 | MS3 | |
|---|---|---|---|---|---|
| a Input parameter. b Microstructure parameter determined from image analysis. c Microstructure parameter determined from transport simulation. The intrinsic and the effective Knudsen numbers are described in the ESI, Section D. | |||||
| Solid volume fraction | ϕ MIEC | — | 0.40 | 0.60 | 0.75 |
| Porosity | ε pore | — | 0.60 | 0.40 | 0.25 |
| Monosized particle diameter for the virtual powder | d mono | nm | 1000 | 800 | 400 |
| Voxel size | L voxel | nm | 50 | 20 | 10 |
| Cube size of the computation domain | L cube | μm | 25.6 | 10.24 | 5.12 |
| Simulated pore-phase M-factor | M simpore | — | 0.4324 | 0.2262 | 0.09292 |
| Simulated solid-phase M-factor | M simMIEC | — | 0.04660 | 0.2498 | 0.4826 |
| Simulated characteristic pore diameter | d pore | nm | 870.215 | 382.954 | 128.076 |
| Simulated Knudsen pore-phase M-factor | M simpore,Kn | — | 0.3600 | 0.1759 | 0.06465 |
| Simulated gas flow permeability | k simflow | m2 | 1.3349 × 10−14 | 1.5482 × 10−15 | 6.9714 × 10−17 |
| Specific surface area | S | μm2/μm3 | 1.7907 | 2.6793 | 5.0230 |
| Intrinsic Knudsen number for H2 | Kn1,0 | — | 0.69 | 1.56 | 4.67 |
| Intrinsic Knudsen number for H2O | Kn2,0 | — | 0.52 | 1.19 | 3.56 |
| Effective Knudsen number for H2 | Kn1,effc | — | 0.83 | 2.01 | 6.66 |
| Effective Knudsen number for H2O | Kn2,effc | — | 0.63 | 1.53 | 5.07 |
| Pore-phase geodesic tortuosity | τ pore | — | 1.0371 | 1.0678 | 1.1136 |
| Pore-phase tortuosity contribution to the predicted M-factor |
τ
pore
−4.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | 0.8521 | 0.7498 | 0.6236 |
| Pore-phase constrictivity | β pore | — | 0.7012 | 0.6045 | 0.4756 |
| Pore-phase constrictivity contribution to the predicted M-factor |
β
pore
0.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | 0.8769 | 0.8300 | 0.7596 |
| Porosity contribution to the predicted M-factor |
ε
pore
1.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | 0.5557 | 0.3487 | 0.2031 |
| Predicted pore-phase M-factor | M predpore | — | 0.4153 | 0.2170 | 0.09619 |
| Ratio predicted to simulated pore-phase M-factor | M simpore/Mpredpore | — | 1.0413 | 1.0423 | 0.9660 |
| Solid-phase geodesic tortuosity | τ MIEC | — | 1.2114 | 1.1054 | 1.0478 |
| Solid-phase tortuosity contribution to the predicted M-factor |
τ
MIEC
−4.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | 0.4309 | 0.6441 | 0.8145 |
| Solid-phase constrictivity | β MIEC | — | 0.2010 | 0.4515 | 0.6384 |
| Solid-phase constrictivity contribution to the predicted M-factor |
β
MIEC
0.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | 0.5523 | 0.7451 | 0.8470 |
| Solid volume fraction contribution to the predicted M-factor |
ϕ
MIEC
1.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | 0.3429 | 0.5552 | 0.7183 |
| Predicted solid-phase M-factor | M predMIEC | — | 0.08161 | 0.2664 | 0.4956 |
| Ratio predicted to simulated solid-phase M-factor | M simMIEC/MpredMIEC | — | 0.5710 | 0.9377 | 0.9921 |
The continuity equation for the stagnant gas layer reads:
 | (21) |
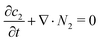 | (22) |
The molar fluxes densities N1 and N2 in the stagnant gas layer are modeled with the Stefan–Maxwell42 equations as documented in detail in Section E of the ESI.† Note that for the used simplified version of the Stefan–Maxwell model, the only governing parameter is the intrinsic binary diffusion coefficient as defined in eqn (23) in Section C of the ESI.†
The gas diffusion overpotential41ηgas can be calculated as follows:
 | (23) |
Boundary conditions for the drift-diffusion equation. At the MIEC/CCL interface at x = 0, the vacancies are blocked and there is a prescribed flux for electrons:
| Jvac(x = 0) = 0 | (24) |
 | (25) |
 | (26) |
| Jeon(x = L) = 0. | (27) |
Boundary conditions for the Poisson equation. The Poisson eqn (14) is coupled with the drift diffusion eqn (5) and (6) over the space charge density eqn (15). The voltage drop over the electrode therewith results from the drift transport losses of the charge carriers. Note that the total fluxes of the charge carriers are prescribed at the boundaries in eqn (24)–(27).
Per definition, we set the MIEC potential at the interface to the CCL to ground:
| ϕ(x = 0) = 0 | (28) |
 | (29) |
Boundary conditions for gas transport. The goal of the simplified model for the gas concentration impedance described in Section 2.3.6 is to mimic an ideal fuel supply, but respecting the diffusion limitations in the stagnant gas layer. Therefore, the concentrations at the end of the stagnant gas layer at x = −LStag are fixed to the given gas concentrations of the fuel supply of hydrogen c1,0 and water vapour c2,0:
| c1(x = −LStag) = c1,0 | (30) |
| c2(x = −LStag) = c2,0. | (31) |
| N1(x = L) = 0 | (32) |
| N2(x = L) = 0. | (33) |
Jcharge(t) = Ĵcharge + ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) charge charge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(jωt) exp(jωt) | (34) |
![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) charge is a small perturbation current density and Jcharge(t) is the total current density. This perturbation provokes a time dependent response of the dependent variables
charge is a small perturbation current density and Jcharge(t) is the total current density. This perturbation provokes a time dependent response of the dependent variables  and ci(t) = ĉi +
and ci(t) = ĉi + ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i
i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(jωt), where the variables with the
exp(jωt), where the variables with the  are the stationary solutions, the variables with the
are the stationary solutions, the variables with the  are the small perturbed components and i denotes eon, vac, 1 or 2, respectively.
are the small perturbed components and i denotes eon, vac, 1 or 2, respectively.
However, in our simulation approach a linear perturbation in the frequency domain is used in order to compute the EIS-spectra. Therefore, the equations are linearized around the stationary operating point ĉi,  . By substituting
. By substituting  and ci(t) = ĉi +
and ci(t) = ĉi + ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i
i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(jωt) in eqn (9), (10), (16), (17), (21) and (22) and calculating the first order Taylor expansions, a time-independent linear system for the perturbed components
exp(jωt) in eqn (9), (10), (16), (17), (21) and (22) and calculating the first order Taylor expansions, a time-independent linear system for the perturbed components ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i,
i, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) is obtained, which is solved for each frequency.47 For the linearized system, the perturbed components
is obtained, which is solved for each frequency.47 For the linearized system, the perturbed components ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i,
i, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) are the linear deviations from the linear perturbation. The boundary conditions for the perturbed system are obtained analogously. The linear perturbation of the current density is applied at the boundary conditions of eqn (25) and (26). The calculations are performed using the “Frequency Domain Perturbation” of the electrochemistry module of Comsol Multiphysics.48 For the DGM-model, the general form implementation of Comsol Multiphyiscs was used and the frequency domain perturbation terms were added as source terms, as the they are not included in the standard implementation of the general form.
are the linear deviations from the linear perturbation. The boundary conditions for the perturbed system are obtained analogously. The linear perturbation of the current density is applied at the boundary conditions of eqn (25) and (26). The calculations are performed using the “Frequency Domain Perturbation” of the electrochemistry module of Comsol Multiphysics.48 For the DGM-model, the general form implementation of Comsol Multiphyiscs was used and the frequency domain perturbation terms were added as source terms, as the they are not included in the standard implementation of the general form.
From the linear deviation results, the different impedance contributions can be computed. The impedance according to the charge transport is computed from the linear deviation of the electric potential at the interface to the electrolyte ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) (x = L) as the electric potential is set to zero at the CCL:
(x = L) as the electric potential is set to zero at the CCL:
 | (35) |
The surface reaction resistance/chemical capacitance impedance is calculated from the average surface reaction overpotential:
 | (36) |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) SR,avg is calculated from the local surface reaction overpotential
SR,avg is calculated from the local surface reaction overpotential ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) SR according to eqn (37) (derivation is documented in the ESI,† Section G):
SR according to eqn (37) (derivation is documented in the ESI,† Section G): | (37) |
The gas diffusion impedance is calculated from the average gas diffusion impedance overpotential from eqn (23):
 | (38) |
The total impedance of the anode is finally the sum of the three impedance contributions:
| Zanode,tot = Zchrgtpt + ZSR + Zgas | (39) |
2.4 Application of the model for CGO10
In Section 2.3, a general anode SOFC model valid for MIEC materials in general has been proposed. However, the corresponding material laws for the nonstoichiometry, the numbers of charge carriers, the charge transport and reaction mechanisms are specific to the considered MIEC material and material composition. In order to achieve a consistent model description, in the following, the general MIEC model is specified and parametrized for gadolinium doped ceria with the composition Ce0.9Gd0.1O1.95−δ, commonly abbreviated with CGO10. As has already been stated, the general model formulation is valid for many types of MIEC electrodes. If another MIEC electrode material is used, the formulation of this Section 2.4 needs to be adapted appropriately, which is further discussed in Section 2.4.7.| Ce1−yGdyO2−y/2−δ | (40) |
The crystal structure of CGO is schematically visualized in Fig. 4. Throughout this paper we use the concept of relative charges for the description of charge transport within the MIEC crystal. According to this concept it is not the actual charge of an ion which is counted. The charge of each species is always compared with the charge(s) of the species that is ‘normally’ occupying the considered lattice cite in a unit cell of an ideal crystal (i.e. in CeO2). For example, on each oxygen site two positive charges are attributed to the oxygen vacancy relative to O2−. In analogy, on the cation site, Ce3+ and Gd3+ have one negative charge relative to Ce4+. For more information about the relative charge concept see Kröger–Fink notation.50,51
 | ||
Fig. 4 Schematic visualization of the crystal structure of CGO, with cerium ions in oxidation states Ce4+ and Ce3+, gadolinium ions Gd3+, oxygen ions O2− and oxygen ion vacancies  . . | ||
In the following, we determine the equilibrium charge densities, i.e. the densities of charge carriers when no electric current is drawn. The crystal structure of CGO is schematically visualized in Fig. 4. As an intermediate step, the number density of cerium for pure ceria is expressed with the unit cell volume:
 | (41) |
 | (42) |
| neon,Gd,imob = nCey | (43) |
| nvac,red = nCeδ. | (44) |
| neon,eq = 2nCeδ | (45) |
 | (46) |
 | (47) |
| ceon,eq = 2cvac,red = 2cCeδ | (48) |
| ceon,Gd,imob = 2cvac,Gd | (49) |
| ρv = F(zeonceon + zvaccvac + zeonceon,Gd,imob) | (50) |
 | ||
| Fig. 5 Oxygen-nonstoichiometry of CGO10 as a function of temperature and oxygen partial pressure. Markers are manually extracted data from Wang et al.,54 the solid lines are the results of the fit function used in this work. | ||
 | ||
| Fig. 6 Central orthoslices of the virtual microstructures. The corresponding microstructure parameters are listed in Table 2. | ||
CGO is able to conduct double negatively charged oxygen ions for two reasons: due to oxygen vacancies introduced by the gadolinium doping and due to the oxygen-nonstoichiometry resulting from low oxygen partial pressures. The oxygen-nonstoichiometry also results in the presence of reduced Ce3+ ions, which are negatively charged with respect to the original Ce4+ ions. Via small polaron hopping, electrons can hop from Ce3+ to Ce4+ ions providing the MIEC's electronic conductivity (visualization in Fig. 4).
According to Steele49 the ionic (vacancy) conductivity σvac and electronic conductivity σeon of CGO10 can be approximated by the following equations:
 | (51) |
 | (52) |
The conductivity of the charge carriers is related to the mobility through:
| σi = μiF2ci | (53) |
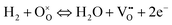 | (54) |
 do not influence the surface reaction overpotential:
do not influence the surface reaction overpotential: | (55) |
 | (56) |
| i0 = Sk0pO2−1/4 | (57) |
Moreover, it is reported in the literature that the reaction kinetics are enhanced for CGO-based anodes with increasing humidity. Riegraf et al.58 reported a power law of approximately pH2O0.08 for the reaction rate of an Ni–CGO10 symmetric anode button cell. Note that the oxygen partial pressure also increases for increasing humidity, which has a negative effect on the reaction kinetics according to the pO2−1/4-dependency. However, the positive effect of the humidity seems to be significantly stronger. This behaviour is also observed for dense SDC thin-film electrodes in the work of Chueh et al.,59 where a power low of pH2O0.3 was reported for the reaction kinetics with embedded platinum electrodes. The quantitative dependency of the surface reaction resistance on the water content thus needs to be determined experimentally for a specific material system, which is beyond the scope of the current study. Therefore, in this study we will hold the water friction constant for all simulations and just lump the effect of the water fraction in the rate constant k0. Moreover, positive effects of increasing water contents due to water vapour concentration gradients from gas diffusion processes are not considered.
The exchange current density can be strongly enhanced with the addition of catalyst metals. Often, CGO-based anodes are realized as a composite together with Ni.3,4,14,19 If the Ni-phase percolates, the electronic conductivity of composite is drastically enhanced, which cannot be described by the current model with one solid phase. Nonetheless, we suggest that Ni–CGO anodes with an Ni-phase far below the percolation threshold can be represented quite well with the current model by simply considering the effect of the Ni-phase by scaling the rate constant k0.
However, the role of Ni in Ni–CGO anodes is very complex and some selected literature references shall be briefly discussed here. Primdahl and Liu4 reported a decrease in the impedance by about a factor of 4 when adding a small amount of Ni of e.g. 2.5 wt% to a CGO40 anode. This drastic decrease of the reaction resistance cannot be explained by the variation of the microstructure and therefore was associated with the catalytic activity of Ni. However, in the work of Kleinlogel et al.,60 the positive effect of Ni was interpreted to origin from an improved microstructure, and the impact of Ni was explained as a sintering aid. A further interpretation of the role of Ni was presented by Primdahl and Mogensen,3 who reported for a Ni–CGO10 anode with a volume ratio of 60/40 that the impedance decreased about a factor of three after adding 3 wt% of additional fine dispersed Ni (i.e. Ni addition via impregnation of the porous, sintered composite). This implies that fine dispersed Ni particles on the surface of CGO show a higher catalytic activity than the “bulk” Ni phase, contacting the CGO only at the phase boundaries. However, the authors also suggested that this improvement might be because of an increase of the three-phase boundaries or possibly by an improved sintering of the contacts between Ni and CGO10.
For our model we assume that the non-percolating Ni-phase in the Ni–CGO anode has only a catalytic effect, which is considered by scaling the rate constant k0. However, it cannot be excluded that the addition of Ni might also add a small additional intermediate-frequency process. Such a process was e.g. reported by Riegraf et al.19 for Ni–CGO anodes in the range of 20–100 Hz. In the literature, this process is either interpreted as a charge transfer process3,61 or the oxygen ion transport across the MIEC/electrolyte interface.3 The latter effect is probably independent of the Ni-phase. However, both possible effects are neglected in our model.
 | (58) |
• Oxygen ion vacancies, abbreviated as vac with an elementary charge of zvac = +2. The corresponding number density can be expressed as nvac,eq = cvac,eqNA, where cvac,eq is the molar concentration of oxygen ion vacancies defined in eqn (47).
• Ce3+-Ions, abbreviated as eon with an elementary charge of zeon,eq = −1. The corresponding number density can be expressed as neon,eq = ceon,eqNA, where ceon,eq is the molar concentration of Ce3+-ions (electrons) defined in eqn (48).
Therewith, the chemical capacitance for the current CGO material system is given by:
 | (59) |
In addition to the chemical capacitance, there is also a surface capacitance present at the CGO/pore interface. Chen et al.13 included this surface capacitance in their model for SDC thin-film electrodes. They estimated the value of the surface capacitance on the basis of the experimental work about the capacitance in SDC thin-films of Chueh and Haile.17 They associated the capacitance independent of the electrode thickness to be the surface capacitance at the SDC/gas interface, assuming that a possible interface capacitance at the SDC/metal interface is negligible. However, as there is no specific data available for the surface capacitance of porous CGO, we do not consider this effect in the present study.
• The charge carrier concentrations as a function of the oxygen partial pressure (eqn (47)–(49)).
• Ionic and electronic conductivities as a function of pO2 (eqn (51) and (52)) to determine the mobility of the charge carriers as described in Section I of the ESI.†
• Formulation of the material specific surface reaction overpotential (eqn (55)).
• Dependency of the exchange current density on the pO2 and water content (eqn (57)).
The model can be easily applied for other ceria-based anodes like CGO20, CGO40 or Sm-doped ceria, as reaction and charge transport mechanisms are similar. For composite anodes where both phases contribute significantly to the charge transport (as e.g. for Ni–CGO anodes where both phases percolate), an additional transport-phase is needed in principle. However, effective conductivities of the composite structure might be used as a first approximation.
For other MIEC materials as e.g. titanate-based perovskite anodes like LST,63 LSCT,5 STFO2, etc., the material laws need to be adapted more carefully as additional physicochemical processes are expected. Burnat et al.63e.g. presented an additional process in the EIS-spectra of LST–CGO composite anodes, which was associated with an additional reaction pathway at the three phase boundaries.
3 Simulation results
The focus of this paper is the description of the mathematical model and the discussion of the complex physico-chemical processes in CGO-based anodes. We therefore do not compare our model results to experimental EIS-spectra of distinct cell setups, nor do we discuss in detail the dependency on the operating conditions. Both points are discussed conceptually in a previous publication (Marmet et al.15). However, realistic model parameters are used to match the order of magnitude for resistive/capacitive effects of the processes.3.1 Parameter values
Note: the parameters in Table 1 are the standard parameters used for the model. Most of these parameters are estimated based on literature data as referred in the reference-column. The anode layer thickness L and the operating conditions can vary in a wide range and are therefore chosen according to illustrative aspects. The relatively large anode layer thickness of L = 100 μm is chosen in order to illustrate the effects of gas and charge carrier transport. Note that the anode functional layer thickness is typically thinner (e.g. L < 30 μm19) for the commonly used Ni–CGO cermets, where the reaction resistance is lower due to the catalytic activity of Ni and the ionic conductivity is lower due to the lower CGO volume fraction. The current density is chosen according to an internal standard value (a current of 300 mA for an active button cell surface of 1.44 cm2). Parameters which are changed for parameter studies are mentioned separately in the subsequent text. The effective properties of the virtual microstructures MS1, MS2, and MS3 are listed in Table 2. All the listed properties are determined from the virtual microstructures according to microstructure analysis and simulations described in Section 2.3.2. The microstructure MS 2 is used for all the simulations where not otherwise specified.3.2 Steady state solution for an initial parameter set
Steady state results for the parameter set of Table 1 are obtained by solving the eqn (9), (10), (16), (17), (21) and (22) without the time dependent terms. In Fig. 7(a), the concentration of the double relative positive charged oxygen ion vacancies (hereafter simply called as vacancies) and the concentration of the single relative negative charged Ce3+-ions (hereafter simply called electrons) are plotted as a profile across a 100 mm thick anode layer. Note that there are less than twice as many mobile electrons as vacancies, because of the immobile negative charge of the Gd3+-ions. These charge carrier concentrations resulting for a prescribed current load deviate from the equilibrium at open circuit conditions. The deviation from the equilibrium, i.e. the difference of open circuit to an effectively drawn current, defined as Δci = ci − ci,eq (where ci,eq is the equilibrium concentration which is established at OCV) is plotted in Fig. 8(a). We can observe a negative deviation over the whole CGO-layer. According to the eqn (54) for the overall anode reaction, the products (i.e. electrons and vacancies) need to be depleted in order to drive the reaction. Moreover, it is – despite the very simplified reaction mechanism used in this study – in qualitative agreement with the in operando study of Feng et al.,55 where the response of surface oxygen vacancies and electrons were tracked using synchrotron-based ambient pressure X-ray photoelectron spectroscopy (APXPS). With these APXPS measurements, Feng et al. documented a depletion of oxygen vacancies and Ce3+-ions at the surface of the MIEC material under current load. Furthermore, Fig. 8(a) also illustrates that the deviation from equilibrium increases towards the CGO/CCL and CGO/electrolyte interfaces. This is in accordance with the distribution of the reaction along the CGO-layer as shown in Fig. 8(b), which is enhanced towards the CGO/CCL and the CGO/electrolyte interfaces. The distribution of the reaction is illustrated with the electron and vacancy source terms.As mentioned in Section 2.3.4, the overall driving force for the reaction is the chemical potential difference between the reactants  and the product H2O. This overall driving force then provokes the local driving forces for the different processes. In order to discuss the different driving forces for the charge carrier transport, the flux components due to drift and diffusion are plotted in Fig. 7(c) for the electrons and Fig. 7(d) for the vacancies. Note that only the total fluxes are physical and the separated drift and diffusion fluxes are virtual fluxes in order to illustrate the driving forces. The driving forces of the diffusive fluxes are the concentration gradients. A positive flux means that the charges are transported towards the electrolyte, which is characteristic for vacancies, whereas a negative flux (towards the current collector) is the overall direction for electrons. However, the total flux of each charge carrier is composed of drift and diffusion components. In this context it is important to note that the direction of diffusive flux components may be opposite to the overall transport direction for the same species, depending on the local concentration gradients. As shown in Fig. 7(a) the concentration profiles exhibit a maximum, so that the diffusive fluxes tend to go in the direction of the neighbouring interface (electrolyte or current collector, respectively). This is in contrast to the more constant potential gradient (Fig. 7(b)), which induces constant transport directions of the drift components (i.e. vacancies towards electrolyte, electrons towards current collector). This leads to a puzzling picture for the different transport species and components as illustrated in Fig. 7(c) and (d). For example, in the region close to the electrolyte, the negative concentration gradients for both species induce diffusive fluxes towards the electrolyte. For the electrons, the diffusive flux component in the region close to the electrolyte is opposite to the direction of the drift component. Therefore, close to the electrolyte, the diffusive flux component hinders the transport of electrons to the CCL. As a result, the total electronic current in this region is close to zero, consistent with the blocking boundary condition for electrons at the electrolyte (eqn (27)). Vice versa towards the CCL, the concentration gradients favor the diffusive transport of electrons to the CCL and hinder the diffusive transport of vacancies to the electrolyte. Therefore, in the region close to the CCL, the total flux of vacancies is almost zero, consistent with the blocking boundary condition for vacancies at the CCL (eqn (24)). The total flux of electrons is twice as big as the flux of the vacancies, because the vacancies carry two unit charges per charge carrier. However, the mobility of the electrons exceeds the mobility of the vacancies by approximately a factor of 10, depending on the oxygen partial pressure. As electrons and vacancies experience the same electric field, the concentration gradients are adjusted according to the energy minimization of the system to achieve low charge transport losses. Therefore, the zone, where the vacancy transport is favored by the concentration gradients is larger than the zone, where the electron transport is favoured. This explains the asymmetric shape of the concentration profile in Fig. 7(a). Of course, the charge transport resistance provide not the only energetic contribution but adds to the surface reaction resistance and gas impedance, which are all captured in the anode model.
and the product H2O. This overall driving force then provokes the local driving forces for the different processes. In order to discuss the different driving forces for the charge carrier transport, the flux components due to drift and diffusion are plotted in Fig. 7(c) for the electrons and Fig. 7(d) for the vacancies. Note that only the total fluxes are physical and the separated drift and diffusion fluxes are virtual fluxes in order to illustrate the driving forces. The driving forces of the diffusive fluxes are the concentration gradients. A positive flux means that the charges are transported towards the electrolyte, which is characteristic for vacancies, whereas a negative flux (towards the current collector) is the overall direction for electrons. However, the total flux of each charge carrier is composed of drift and diffusion components. In this context it is important to note that the direction of diffusive flux components may be opposite to the overall transport direction for the same species, depending on the local concentration gradients. As shown in Fig. 7(a) the concentration profiles exhibit a maximum, so that the diffusive fluxes tend to go in the direction of the neighbouring interface (electrolyte or current collector, respectively). This is in contrast to the more constant potential gradient (Fig. 7(b)), which induces constant transport directions of the drift components (i.e. vacancies towards electrolyte, electrons towards current collector). This leads to a puzzling picture for the different transport species and components as illustrated in Fig. 7(c) and (d). For example, in the region close to the electrolyte, the negative concentration gradients for both species induce diffusive fluxes towards the electrolyte. For the electrons, the diffusive flux component in the region close to the electrolyte is opposite to the direction of the drift component. Therefore, close to the electrolyte, the diffusive flux component hinders the transport of electrons to the CCL. As a result, the total electronic current in this region is close to zero, consistent with the blocking boundary condition for electrons at the electrolyte (eqn (27)). Vice versa towards the CCL, the concentration gradients favor the diffusive transport of electrons to the CCL and hinder the diffusive transport of vacancies to the electrolyte. Therefore, in the region close to the CCL, the total flux of vacancies is almost zero, consistent with the blocking boundary condition for vacancies at the CCL (eqn (24)). The total flux of electrons is twice as big as the flux of the vacancies, because the vacancies carry two unit charges per charge carrier. However, the mobility of the electrons exceeds the mobility of the vacancies by approximately a factor of 10, depending on the oxygen partial pressure. As electrons and vacancies experience the same electric field, the concentration gradients are adjusted according to the energy minimization of the system to achieve low charge transport losses. Therefore, the zone, where the vacancy transport is favored by the concentration gradients is larger than the zone, where the electron transport is favoured. This explains the asymmetric shape of the concentration profile in Fig. 7(a). Of course, the charge transport resistance provide not the only energetic contribution but adds to the surface reaction resistance and gas impedance, which are all captured in the anode model.
Our model thus provides a quantitative description of the distribution of charge carrier concentrations within the MIEC and allows to study the complex interplay with various transport components (drift, diffusion) and with the local distribution of surface reaction rates. In a similar way, the model also provides a quantitative description of species concentrations in the gas phase based on the coupled effects of transport and surface reaction. In Fig. 9, the molar fractions of hydrogen and water vapour are shown in the stagnant gas layer and in the pores of the CGO-layer. The concentrations are fixed at the end of the stagnant gas layer (left side), which reflects the ideal convective transport above the stagnant gas layer due to the excess fuel supply without concentration gradients, as introduced in Section 2.3.6. As hydrogen is consumed in the CGO-layer, the mole fraction decreases towards and within the CGO-layer and vice versa for water vapour. The concentration gradients are higher within the CGO-layer, because of the lower effective diffusivity in the porous media due to the “bulk” microstructure effects (M-factor Mpore) and the Knudsen diffusion resistance. Moreover, the concentration gradients are non-constant in the CGO-layer because transport and reaction (HOR) of gas species are both present. In contrast, the concentration gradients are constant within the stagnant gas layer because gas species are only transported (no reaction).
 | ||
| Fig. 9 Mole fractions of hydrogen x1 and water vapour x2 in the stagnant gas layer and in the porous CGO-layer. | ||
3.3 Frequency dependent results for an initial parameter set
The linear perturbation in the frequency domain enables the calculation of the impedance spectra. The impedance according to the surface reaction ZSR, the impedance due to the transport of the charge carriers in the CGO–MIEC Zchrgtpt, the gas concentration impedance Zgas and the sum of the three are plotted as Nyquist plot in Fig. 10(a) and the imaginary part of the impedance in Fig. 10(b).In the separate Nyquist plot Fig. 12(a), the charge transport impedance shows a characteristic mouse shape, which is the result of a frequency dependent optimization of the transport pathways illustrated in Fig. 12(b). The different aspects of this process are visible in more detail in Fig. 11, where profiles across the CGO-layer of the linear deviations from the dynamic equilibrium associated with the harmonic perturbation are presented for different frequencies for (a) electron reaction rate ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) eon, (b) electron concentration
eon, (b) electron concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) eon and (c) electron and vacancy fluxes
eon and (c) electron and vacancy fluxes  and
and  normalized by the fluxes at the interfaces to the CCL and electrolyte, respectively. The linear deviations of the reaction rate
normalized by the fluxes at the interfaces to the CCL and electrolyte, respectively. The linear deviations of the reaction rate ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) eon and of the electron concentration
eon and of the electron concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) eon show that the electrochemical activity is concentrated to the electrolyte interface with increasing frequencies. The transport pathways for electrons and vacancies are adapted, resulting in much lower average transport pathlength for the less mobile vacancies with increasing frequencies. A measure for the mean transport pathlengths for electrons and vacancies at a frequency of 500 Hz are the colored surface areas in Fig. 11(c). The mean pathlength for electrons is about a factor of 3 higher than for vacancies at a frequency of 500 Hz. In contrast, the mean pathlengths for electrons and vacancies are almost identical at low frequencies <0.1 Hz.
eon show that the electrochemical activity is concentrated to the electrolyte interface with increasing frequencies. The transport pathways for electrons and vacancies are adapted, resulting in much lower average transport pathlength for the less mobile vacancies with increasing frequencies. A measure for the mean transport pathlengths for electrons and vacancies at a frequency of 500 Hz are the colored surface areas in Fig. 11(c). The mean pathlength for electrons is about a factor of 3 higher than for vacancies at a frequency of 500 Hz. In contrast, the mean pathlengths for electrons and vacancies are almost identical at low frequencies <0.1 Hz.
 | ||
| Fig. 12 Visualization of the charge transport impedance process: (a) Nyquist plot of the charge transport impedance Zchrgtpt, (b) schematic illustration of the transport pathways of electrons and vacancies for low and high frequencies. At low frequencies, the reaction rate is almost homogeneously distributed over the CGO-layer, resulting in similar transport distances for electrons and vacancies. At high frequencies, only a small reaction zone in the vicinity of the electrolyte persists, resulting in longer transport distances of the more mobile electrons and therewith an increase of the total charge transport resistance. Note: the red and violet dots indicate typical locations of electron and ion sources (i.e. statistical mean values related to frequency dependent distributions, which are illustrated in Fig. 11). | ||
The mouse-shaped spectra of the charge transport process (Fig. 11(a)) ends with a nonzero real part for the plotted frequency range up to 1 MHz. In an experimental EIS measurement, this offset of the charge transport resistance is hard to distinguish from the electrolyte resistance. Another half circle process would add to the transport impedance due to the dielectric capacitance of the CGO-layer. However, this process has a peak frequency of about 100 GHz and is far beyond the frequency range normally used in EIS measurements. We thus plot the impedance spectra only up to 1 MHz and therewith this process is not visible in the plots of the simulation as well, even if its physics are included in the Poisson-eqn (14).
For the initial parameter set, the gas concentration resistance and the charge transport resistance are in the same range, while the surface reaction resistance is significantly higher than the other two effects. The gas concentration and the surface reaction impedance are in the same frequency range of about 0.05 Hz. From eqn (11)–(13), (16) and (17) it follows that the (perturbation of) sink and source terms for gas species are directly coupled to the surface reaction. Therefore both impedance-components ZSR and Zgas have the same peak frequency.
To illustrate the dependency of the gas diffusion impedance on the surface reaction resistance/chemical capacitance impedance, a decoupled simulation was performed for the gas diffusion impedance. Therefore, the gas diffusion impedance was calculated separately with the following homogeneous source terms in the porous layer:
 | (60) |
 | (61) |
3.4 Parameter set resulting in distinguishable gas impedance arc
To illustrate the relation of the gas impedance and the surface reaction resistance/chemical capacitance processes, a simulation with a parameter set where those processes can be distinguished (also in a simulation with full coupling) is performed.The parameter set is listed in Table 3. Only the parameters varied with respect to Table 1 are listed. The major changes are (a) the use of a huge stagnant gas layer thickness resulting in higher gas diffusion resistance and capacitance and (b) the reduction of the charge carrier equilibrium concentrations and a reduction of the MIEC-layer thickness, which results in a smaller chemical capacitance. This situation could be possibly observed experimentally for a large area cell with an anode based on a conductive backbone impregnated with CGO, which will be discussed in more detail in Section 4.3. The results for this parameter set are summarized with the Nyquist-plot in Fig. 13(a) and the imaginary part of the impedance in Fig. 13(b). Due to the choice of the parameters, the surface reaction resistance/chemical capacitance processes is shifted to higher frequencies and the gas diffusion impedance process is shifted to lower frequencies. The two processes are now distinguishable in the total impedance Zanode,tot. To judge the remaining coupling of the processes, the decoupled gas diffusion impedance Zgas,decoupled, calculated in the same manner as described in Section 3.3 with eqn (60) and (61), are plotted as well in both diagrams. The decoupled gas diffusion impedance has a characteristic mouse shape form, which is also visible to some extent for the coupled gas diffusion impedance process Zgas.
3.5 Parameter study with different CGO-layer thicknesses
We vary the CGO-layer thickness in a range of 10–800 μm to study its influence on surface reaction impedance, charge transport impedance, gas impedance, total impedance and the distribution of the reaction. Fig. 14 shows profiles across the CGO-layer with the source term of electrons, which illustrates the spatial distribution of the surface reaction rates for different anode layer thicknesses. The surface reaction rate varies only slightly along the CGO-layer for small CGO-layer thicknesses. The larger the CGO-layer thickness, the more the reaction is shifted towards the interfaces CGO/electrolyte and CGO/CCL. For large CGO-layer thicknesses (e.g. 400 μm) the reaction rate in the center of the CGO-layer is almost zero. | ||
| Fig. 14 Surface reaction rate (source term of electrons) across the CGO-layer for different CGO-layer thicknesses. | ||
In Fig. 15, the real parts of the different impedance contributions obtained by linear perturbation are summarized. The charge transport resistance ASRchrgtpt and the gas diffusion resistance ASRgas increase and the surface reaction resistance ASRSR decreases with growing CGO-layer thickness. There is a minimal total resistance for a thickness in the range of 100–200 μm, which is a specific finding for this anode and thus depending on the chosen parameter set and microstructure. For small CGO-layer thicknesses, the surface reaction resistance scales with 1/L. For larger thicknesses, there is a deviation from this law and the resistance does not decrease anymore with growing layer thickness, as illustrated in Fig. 15 by plotting the 1/L-behaviour.
In Fig. 16(a) the Nyquist plot and in Fig. 16(b) the imaginary impedance part of the total anode impedance are shown for selected CGO-layer thickness's L = [10,100,800] μm. For a small thickness, almost a perfect semi-circle results, while for a large thickness, a characteristic “mouse” shape can be observed.
 | ||
| Fig. 16 (a) Nyquist plot and (b) imaginary impedance plot of the total anode impedance for selected CGO-layer thicknesses. | ||
3.6 Parameter study with different microstructures
We now investigate the effect of microstructure on DC- and AC-performances. Changing the microstructure will affect the effective transport properties (ion- and electron-transport in the solid and gas transport in the pores) via the M-factors for MIEC- and pore-phase (see eqn (1)–(4)). For gas transport in fine-grained anodes, Knudsen diffusion is also directly affected by the pore radius (eqn (26) in Section C of the ESI†). Furthermore, varying the microstructure also has an impact on the exchange current density and associated reaction rates via the specific surface area (see eqn (57)). Experimentally, these effects are difficult to quantify separately because the underlying processes are interlinked with each other. For example, in coarse grained materials with low surface area it can be expected that the reaction is extended deeper into the anode layer in order to make use of more surface area. As a consequence also the transport distances of vacancies, electrons and gas species will change. Moreover, the same microstructure changes also have an impact on the M-factor of the MIEC- and pore-phase (e.g. effective diffusivities), which may increase or compensate the corresponding ASR-contributions. This example illustrates that microstructure effects in SOFC electrodes are always the result of a complex interplay. A thorough understanding of these coupled effects can be achieved with a modeling approach that combines DC-simulations, which provide distributions of currents and species concentrations across the anode layer, with AC-simulations, from which the different ASR-components can be extracted.In order to capture the influence of the microstructure, the performance of three anodes with different microstructures are presented. Virtual microstructure data are used in order to keep the focus on the model and for a better reproducibility of the simulation results. The virtual microstructures have been realized using GeoDict27 software using mono-sized spherical particles with a random seed of 45. The microstructure parameters are summarized in Table 2 and the corresponding orthoslices are shown in Fig. 6. Note that the virtual microstructures are isotropic and also the intrinsic conductivity of doped ceria is isotropic as stated by Koettgen et al.65 MS1 has a high porosity with a solid volume fraction of only ϕMIEC = 0.4 and is coarse grained with a monosized particle diameter of dmono = 1000 nm. MS3 is a dense (ϕMIEC = 0.75) and fine-grained (dmono = 400 nm) microstructure. MS2 is an intermediate microstructure (ϕMIEC = 0.6, dmono = 800 nm), which is used as standard microstructure for all simulations unless otherwise specified.
Effective transport properties for the different microstructures are determined in two ways: (a) indirectly, using numerical simulation on the voxel grid and (b) directly, via morphological analysis as described in Section 2.3.2. The results are listed in Table 2. For the direct numerical analysis on the voxel grid, GeoDict27 software was used. The M-factors for the effective diffusivity Msimpore and for the effective conductivity MsimMIEC were calculated with bulk (Laplace) diffusion using the DiffuDict-module. Note that the equations for the diffusion and drift (i.e. electric conduction) are mathematically equivalent. The M-factor for the effective Knudsen Diffusivity Msimpore,Kn and the characteristic pore diameter dpore for the Knudsen diffusion were calculated with a random walk algorithm of the DiffuDict module. The flow permeability ksimflow is calculated using the Stokes (LIR) solver of the FlowDict module with an in- and outflow region of 100 voxels.
The M-factors for the effective diffusivity in the pore and the MIEC-phase were determined in both ways, indirectly (a) and directly (b). The ratio's MsimMIEC/MpredMIEC and Msimpore/Mpredpore of the values extracted from simulations on the voxel mesh to the values predicted by morphological analysis are reported in Table 2. They show a deviation in the range of ±7%, except for MS 1 where a larger relative deviation is observed for the small absolute values of the MIEC-phase. For the parametrization of the FEM-model, the simulated properties were used because they are expected to provide the higher accuracy. However, the predicted M-factors are accurate enough to study the impact of different microstructure characteristics on the effective properties and thereby to identify the dominant microstructure effects. The microstructure properties τ, β, εpore and ϕMIEC and the corresponding components τ−4.39, β0.37, ϕMIEC1.15 and εpore1.15 for the computation of the M-factor according to eqn (2)–(4) are reported in Table 2.
The DC-results for three different microstructures are plotted in Fig. 17 as profiles across the porous CGO-layers showing distributions of (a) molar fraction of hydrogen, (b) potential drop and (c) reaction rates. The different contributions to the anode ASR as a function of the CGO-layer thickness obtained from AC simulations are plotted in Fig. 18. The highly porous and coarse grained MS1 shows the smallest gradient for the hydrogen molar fraction x1 (Fig. 17(a)) and the highest potential drop along the CGO-layer (Fig. 17(b)). In accordance, MS1 shows the smallest gas diffusion resistance ASRgas (Fig. 18(a)) and the largest charge transport resistance ASRchrgtpt (Fig. 18(b)) of the three studied microstructures. The dense and fine-grained MS3 shows the steepest gradient for the hydrogen molar fraction x1 (Fig. 17(a)) and the smallest potential drop along the CGO-layer (Fig. 17(b)). Accordingly, MS3 shows the largest ASRgas (Fig. 18(a)) and the smallest ASRchrgtpt (Fig. 18(b)).
The distribution of the reaction zone is shown in Fig. 17(c) for the different microstructures. For MS1, the electrochemical activity is enhanced towards the electrolyte and attenuated towards the CCL. The inverse behaviour can be observed for MS3. The surface reaction resistance ASRSR (Fig. 18(c)) is largest for MS1 and smallest for MS3, and therewith inverse proportional to their specific surfaces. In Fig. 18(d), the total area specific resistance ASRtot is plotted. The highly porous MS1 shows the largest ASRtot for all calculated CGO-layer thicknesses. The dense, fine-grained MS3 shows the smallest ASRtot up to a CGO-layer thickness of about L = 75 μm, while for larger CGO-layer thickness's the intermediate MS2 shows the lowest ASRtot.
In addition, the simulation MS2 + Ni is plotted along, where the rate constant k0 is increased by a factor of three, approximating the effect of additional fine dispersed but non-percolating Ni-particles on the surface of the CGO. This case shows the lowest surface reaction resistance ASRSR (Fig. 18(c)) and also the lowest total resistance ASRtot (Fig. 18(d)) for all the reported CGO-layer thicknesses. The ASRgas and ASRchrgtpt for MS2 with Ni differs only very slightly in comparison with MS2 without Ni and are therefore not shown.
4 Discussion
4.1 Charge transport resistance
The charge transport resistance is basically an ohmic resistance and therefore, one could expect to only observe a real impedance contribution. However, there is an imaginary component, because the transport pathways change with frequency, as illustrated in Fig. 12(b). With increasing frequency, the statistical mean transport pathlength for vacancies is minimized at the expense of a longer mean transport pathlength for the more mobile electrons. This results in a lower total charge transport resistance above the characteristic frequency of 0.45 Hz for the charge transport impedance. This can be explained with the nature of the chemical capacitance. The chemical capacitance is a volumetric effect in contrast to the dielectric capacitance, where the charges are stored at the interfaces. To access the chemical capacitance, the charge carriers need to travel for some distance into the bulk of the CGO-layer. Above the characteristic frequency of 0.04 Hz, the surface reaction is more and more bypassed by just buffering the charge carriers in the chemical capacitance of the CGO-layer. Note that the characteristic frequency of 0.45 Hz for the charge transport impedance is considerably higher than the characteristic frequency of 0.04 Hz for the surface reaction/chemical capacitance process as shown in Fig. 10(b).The different aspects of this processes can be discussed in more detail by considering the profiles across the CGO-layer of the linear deviations from the dynamic equilibrium associated with the harmonic perturbation for different frequencies in Fig. 11. In Fig. 11(b) the profiles of the linear deviation of the electron concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) eon, show a higher depletion towards the electrolyte. Also the deviation from the dynamic equilibrium of the surface reaction rate is higher towards the electrolyte as shown in Fig. 11(a). The change of the distribution of pathlengths for electrons and vacancies with increasing frequency is shown in Fig. 11(c) by the normalized deviations of the electron and vacancy fluxes
eon, show a higher depletion towards the electrolyte. Also the deviation from the dynamic equilibrium of the surface reaction rate is higher towards the electrolyte as shown in Fig. 11(a). The change of the distribution of pathlengths for electrons and vacancies with increasing frequency is shown in Fig. 11(c) by the normalized deviations of the electron and vacancy fluxes ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) eon,norm and
eon,norm and ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) vac,norm. The colored areas are measures for the mean transport pathlengths at a frequency of 500 Hz, which is about a factor of 3 higher for the electrons as for the vacancies. At low frequencies (f < 0.1 Hz), the pathlengths are approximately equal for electrons and vacancies. These results can be explained as follows. With increasing frequency, the chemical capacitance and associated storage of charges is shifted closer to the electrolyte interface. In this way, the mean transport distance for vacancies is reduced and at the same time, the surface reaction at longer distances from the electrolyte interface is suppressed.
vac,norm. The colored areas are measures for the mean transport pathlengths at a frequency of 500 Hz, which is about a factor of 3 higher for the electrons as for the vacancies. At low frequencies (f < 0.1 Hz), the pathlengths are approximately equal for electrons and vacancies. These results can be explained as follows. With increasing frequency, the chemical capacitance and associated storage of charges is shifted closer to the electrolyte interface. In this way, the mean transport distance for vacancies is reduced and at the same time, the surface reaction at longer distances from the electrolyte interface is suppressed.
By minimizing the transport pathlength of the less mobile vacancies associated with by-passing of the surface reaction, the transport resistance is decreased, resulting in a mouse-shaped spectrum for the charge transport impedance with a remaining real part for the plotted frequency range of up to 1 MHz (Fig. 12(a)). In a measured impedance spectrum, this remaining charge transport resistance (visible in the high frequency limit) might not be distinguishable from the other ohmic series resistances such as the resistance of the electrolyte. However, the frequency-dependent optimization of the charge transport pathways can only take place when the surface reaction is mainly bypassed and a smaller active part of the CGO-layer is needed to provide sufficient reaction surface and chemical capacitance. Therefore, the peak frequency of 0.45 Hz for the charge transport process is considerably higher than the peak frequency of 0.04 Hz for the surface reaction resistance/chemical capacitance process as shown in Fig. 10(b).
Note that the CGO-layer also owns a very small dielectric capacitance, where the charges are stored at the interfaces to the CCL and electrolyte respectively. To access this dielectric capacitance no transport into the bulk is necessary and therefore this additional charge transport process would end at zero in the high frequency limit. However, the characteristic frequency of this process is in the range of 100 GHz and therewith far beyond the frequency range measured in classical impedance spectroscopy and will not be observed in experiments.
The charge transport resistance depends also strongly on the microstructure. For the studied microstructures MS1–MS3, the microstructure factor varies in-between MMIEC = 0.04660–0.4826. Accordingly, the voltage drop differs remarkably for the different microstructures, as shown in Fig. 17(b).
4.2 Distribution of the reaction zone
The distribution of the reaction zone and associated concentration profiles are driven and controlled by the following coupled processes and effects:• Charge transport by drift and diffusion of electrons and vacancies in the CGO MIEC.
• Gas transport within the porous CGO-layer.
• Surface reaction resistance for the HOR.
The combined effects of gas and charge transport limitations (but also taking into account the coupled HOR resistance) can be illustrated by comparing the impact of microstructure variation on local distributions of species concentrations, electrical potential and surface reaction rates (Fig. 17). For the highly porous MS1, the gas transport in Fig. 17(a) is less limiting than the charge transport in Fig. 17(b). Therefore, there is a higher electrochemical activity towards the electrolyte in Fig. 17(c) in order to reduce the transport path for the less mobile vacancies. These results are in very good agreement with the study of Nakamura et al.,20 where a higher electrochemical activity towards the electrolyte in a CGO anode was reported from experiments in a semiquantitative way. For the very dense and micro-porous MS3, where the gas transport is essentially governed by Knudsen diffusion and the conductivity is comparably high, the situation is inverted. Accordingly, an electrochemical more active zone towards the CCL Fig. 17(c) is observed, where the transport distance for the gas is low. For MS2, the gas transport and charge transport resistances are in the same range, resulting in a similar electrochemical activity at both interfaces, CGO/CCL and CGO/electrolyte. However, the reaction is not homogeneously distributed but is enhanced towards the interfaces. This is because of the complex mechanism of the drift-diffusion transport of the charge carriers. The charge transport by diffusion is enhanced by the concentration gradient as visible in Fig. 7(a). Therewith, the ‘downhill’ transport of vacancies is very efficient towards the CGO/electrolyte interface. In contrast, the electrons needs to be transported “uphill” against the concentration gradient by the electric field Fig. 7(b). The same happens vice versa towards the CCL interface.
According to the reaction mechanism of our model assumptions formulated in eqn (55) and (56), the reaction is driven by a depletion of the charge carrier concentration, which are products of the HOR reaction. As a consequence, the zone in the center of the CGO-layer is less active because of the smaller depletion Δci of the charge carriers in the center as visible in Fig. 8(a). These effects vary depending on the magnitude of the involved driving forces, as can be illustrated by the variation of the CGO-layer thickness for MS2 in Fig. 14. For low CGO-layer thicknesses, the surface reaction resistance is limiting and therewith, the reaction is almost homogeneously distributed over the CGO-layer in order to use the whole available CGO-surface. With increasing CGO-layer thickness, the total CGO-surface increases and therewith the surface reaction resistance decreases, while the transport resistances increase at the same time. For large CGO-layer thicknesses, the center of the layer is therefore no more electrochemically active in order to limit the transport losses by using concentration gradients. While the surface reaction resistance decreases proportionally to 1/L for small layer thicknesses as shown in Fig. 15, it does not decrease anymore for larger CGO-layer thicknesses. This is because the electrochemically active region does not increase anymore, as can be seen in Fig. 14. In cases where the gas and charge transport properties are very different from each other, the reaction zone tends to be localized either only in the vicinity of the CCL or the electrolyte, respectively.
The present model-based study provides new aspects of the distribution patterns for the reaction zone and concentration profiles (asymmetric, bell-shaped form), which extends the picture reported in literature3,20,38 for similar MIEC anodes. In literature the distributions of reaction rates are usually characterized with a steady increase towards a maximum reaction rate at the electrolyte interface, which is more pronounced for larger electrode thicknesses and for much higher electronic than ionic conductivity. This behaviour is also observed in our simulation results for highly porous microstructures as MS1. In addition, our model suggest also an elevated electrochemical activity at the MIEC/CCL-interface because of the complex charge transport processes by drift and diffusion. Primdahl and Mogensen3 suggested qualitatively that the reaction rate increase towards a maximum at the MIEC/CCL interface in case of higher ionic than electronic conductivity. Our model suggests that this situation of maximal electrochemical activity towards the CCL might also be observed for the more common situation of higher electronic than ionic conductivity, if the gas diffusion in the pore phase is more limiting than the charge transport in the MIEC phase. This might be the case for very dense, fine-grained electrodes like MS3.
4.3 Gas concentration impedance and surface reaction impedance
The gas concentration impedance process can be classified by the following contributions:• Gas conversion impedance, especially relevant for large area cells.
• Gas diffusion impedance in the stagnant gas layer above the electrode.
• Gas diffusion impedance within the porous electrode, where bulk and Knudsen diffusion (described with dusty-gas model) can be relevant.
The gas conversion impedance is neglected in our study, as we aim to describe a button cell system with an excess hydrogen flow rate. However, a very large stagnant gas layer might have a similar effect as a gas conversion impedance, as will be discussed later in this section.
The magnitude of the gas diffusion impedance in the stagnant gas layer depends on the thickness of the stagnant gas layer and therewith on the button cell setup and the flowrate. For our standard simulations, a quite small stagnant gas layer thickness of LStag = 0.2 mm was used, which was estimated for a particular setup (see ESI,† Section F). The effect of a larger stagnant gas layer will be discussed later in this section.
The magnitude of the gas diffusion impedance in the porous electrode depends on the microstructure and on the thickness of the electrode. While the Knudsen diffusion coefficient is directly proportional to the pore size, the bulk diffusion depends on the dimension-less M-factor. Therefore, in contrast to the Knudsen diffusion, the bulk diffusion does not change when a certain microstructure is scaled (e.g. by changing the coarseness but at the same time maintaining volume fractions and particle and pore shapes). Both, pore sizes and M-factors vary strongly for the three microstructures and thus, these microstructure variations also have an impact on the effective Knudsen and bulk diffusivities. The Knudsen number reflects the ratio of bulk and Knudsen diffusion. We distinguish between the intrinsic Knudsen number Kn0 = D0/DKn,0, defined as the ratio of the unitary bulk diffusion coefficient to the intrinsic Knudsen diffusion coefficient and the effective Knudsen number Kneff = Deff/DKn,eff, defined as the ratio of the effective unitary bulk diffusion coefficient to the effective Knudsen diffusion coefficient (see ESI,† Section D). The intrinsic Knudsen diffusion coefficient Kn0 varies significantly for the three studied microstructures (Kn0 < 1 for MS, Kn0 > 1 for MS2 and Kn0 ≫ 1 for MS3). The Knudsen numbers are specific for different species and are listed in Table 2. Note that a Knudsen number of Kn0 = 1 would reflect an equal contribution of bulk and Knudsen diffusion to the gas diffusion resistance. As the microstructure hinders the transport by bulk and Knudsen diffusion in a different way, the effective Knudsen numbers Kneff are slightly larger than the intrinsic Knudsen numbers.
Our study suggests that in porous CGO anodes, the gas concentration impedance is only one of several processes that affect the low frequency spectrum. The RC-behavior of the chemical capacitance and surface reaction resistance might even be the larger contribution to the total impedance. These two low-frequency contributions (i.e. gas concentration impedance and surface reaction resistance/chemical capacitance impedance) are coupled with each other in two ways. There is a weak coupling between the two processes, as the concentration change due to the gas diffusion involves also a change in oxygen partial pressure, which impacts the exchange current density according to eqn (57). However, this effect is only significant if the gas diffusion limitation has a large impact on the pO2. This is the case for a very dry fuel supply, a setup with a large stagnant gas layer thickness or for thick, dense and fine porous electrodes. The second coupling becomes clear by comparing the characteristic frequencies of the processes. As already mentioned, the gas diffusion impedance and the surface reaction impedance show exactly the same characteristic frequency, which can be observed in Fig. 10(b). This can be understood in the way, these processes are coupled. An RC-like arc in an impedance spectrum always results by bypassing the resistance by just oscillating the charge in the capacitor. For the surface reaction impedance that means that the surface reaction resistance is bypassed above the characteristic frequency of the process. Significantly above the characteristic frequency there is no change in the surface reaction due to the applied perturbation at all, because the harmonic current is entirely stored in the chemical capacitance. If there is no effect on the reaction anymore, there is also no effect on the gas concentration at the electrode surface. Furthermore, if the concentration does not change anymore, also the gas diffusion impedance is bypassed. Due to this strong coupling associated with a frequency dependent bypassing, the two processes cannot be distinguished directly in an experimental EIS-spectra. For illustration, the decoupled gas diffusion process Zgas,decoupled is plotted in Fig. 10(b). The characteristic frequency f0 of a process is generally given by  with associated resistance R and capacitance C. Because the process is now not cut off by the vanishing surface reaction, the arc is built by the capacitance of the gas transport process itself, while the associated resistance of the gas diffusion remains the same. As the gas transport capacitance is much smaller than the chemical capacitance, the process Zgas,decoupled is located at a much higher characteristic frequency around 2 kHz compared to the coupled gas impedance Zgas. In Section K of the ESI,† experimental examples from literature illustrating this observation are discussed and the order of magnitude of the characteristic frequency is confirmed with an analytical estimation.
with associated resistance R and capacitance C. Because the process is now not cut off by the vanishing surface reaction, the arc is built by the capacitance of the gas transport process itself, while the associated resistance of the gas diffusion remains the same. As the gas transport capacitance is much smaller than the chemical capacitance, the process Zgas,decoupled is located at a much higher characteristic frequency around 2 kHz compared to the coupled gas impedance Zgas. In Section K of the ESI,† experimental examples from literature illustrating this observation are discussed and the order of magnitude of the characteristic frequency is confirmed with an analytical estimation.
With the parameter set of Section 3.4, a situation is constructed, where the gas diffusion impedance has a lower characteristic frequency than the chemical capacitance and associated surface reaction process. The huge stagnant gas layer results in a high ‘RC’ product for the gas diffusion process (larger diffusion resistance due to larger diffusion length and larger capacitance due to larger gas volume). In this situation, the two processes are clearly distinguishable from each other in the total anode impedance Zanode,tot in Fig. 13(a) and in Fig. 13(b), respectively. A weak coupling of the two processes still persists, which becomes clear by comparing Zgas with the decoupled Zgas,decoupled impedance in the imaginary part plot in Fig. 13(b). Between 10–100 Hz, Zgas,decoupled impedance still shows a small contribution, resulting in characteristic mouse shape in the Nyquist plot in Fig. 13(a), which is typical for diffusion limited processes. However, the coupled Zgas process is cut above 10 Hz because of the vanishing surface reaction in Fig. 13(b), which results in a distorted mouse shape in the Nyquist plot in Fig. 13(a).
The goal of the simulation with this parameter set was to illustrate ‘theoretically’ the dependency of the gas impedance with the surface reaction resistance/chemical capacitance process. However, the same simulation with this dedicated parameter set can also be used to briefly discuss the correspondence with two potentially existing physical cell setups, as follows:
(a) The huge stagnant gas layer thickness (which leads to a large Zgas with a relatively low characteristic frequency) could e.g. represent a flow-situation, where a button cell is clamped between two impermeable disks with an axial fuel supply. Therewith, the mass transport across the button cell needs to be largely achieved by diffusion. If a large amount of fuel is provided, the gas conversion impedance can be avoided, but a large gas diffusion impedance remains. Measurements with a setup of this kind have been reported by Aravind et al.66 However, the effect of this setup is similar to the gas conversion impedance, especially important for large area cells, where the order of magnitude of the impedance for this parameter set is easily reached.
(b) The lower charge carrier concentration and the associated lower chemical capacitance (with a relatively high characteristic frequency) could be realistic in a composite material, where e.g. a conductive matrix is impregnated by CGO. Because the chemical capacitance is a volumetric effect, the lower CGO volume fraction would then result in a lower capacitance. Of course, a lower charge carrier concentration could possibly also be observed for a different MIEC-materials. In summary, these hypothetical cases used for the illustration of the gas impedance process could possibly be observed in a large area cell or in an anode with different material composition.
In the following we will discuss how low frequency (LF) arcs in impedance spectra of MIEC anodes are interpreted in the literature. In general, there are two main LF processes, which are either associated with the gas concentration impedance or with the surface reaction resistance/chemical capacitance impedance. As will be discussed subsequently, depending on the authors but also depending on the cell architecture, the low frequency arc is usually interpreted as being either gas impedance or surface reaction impedance, but rarely as a mixture of both. For example, for studies with patterned thin-film electrodes as e.g. performed by Chueh et al.,22 the low frequency process is attributed to the surface reaction resistance/chemical capacitance impedance process. In thin-film electrodes (massive, no pores) the gas concentration impedance is negligible, simply because the surface area is relatively small and thus the surface reaction resistance is dominant. Additionally, as no net current is drawn in the symmetric cell setup, also the possible effect of pO2 change along with concentration changes due to gas diffusion is probably negligible for the whole common parameter range. Furthermore, in thin-film electrodes transport distances in the MIEC are usually very short so that also the charge transport resistance becomes negligible (unless especially designed to enforce a significant charge transfer contribution as e.g. studied by Chen et al.13). Therefore, thin-film electrodes typically exhibit EIS-spectra with a perfect semi-circle and low characteristic frequency.
Riegraf et al.19 suggested for their study of an Ni–CGO10 anode (4 × 4 cm2 active area) that there is a thermally activated electrode process in addition to a gas conversion process for the low frequency arc around 0.2 Hz. We suggest that this electrode process is the process of surface reaction resistance/chemical capacitance described in this work and hence in these anodes we are faced with a mixture of both LF processes.
Price et al.5 assigned the low frequency process in the impedance spectra of a button full cell (1 cm2 active area) with a CGO/Ni-impregnated LSCTA backbone anode as a gas concentration effect. Their argument is that the process is not thermally activated, which is in fact expected for a gas impedance process. However, in the work of Riegraf et al.19 with Ni–CGO anodes, the thermal activation was only visible in the low frequency arc for temperatures below 750 °C. So the thermal activation might just not be visible in the studied temperature range of 800–900 °C. Therefore, there might be a surface reaction resistance/chemical capacitance process included in the low frequency arc.
Burnat et al.63 performed a study with composite MIEC anodes of variable LST–CGO ratios (in button cells). The resulting low frequency effect was attributed to a chemical capacitance process, which in our nomenclature would be a surface reaction resistance/chemical capacitance process. They argued that this process depends on the LST–CGO ratio and also shows a thermal activation, which is very unlikely for a pure gas concentration impedance process. However, there will be for sure a gas concentration impedance effect included in the low frequency arc, but this effect might be small in comparison with the surface reaction resistance/chemical capacitance process. For the anode compositions with CGO contents above 50%, which show a good performance, the gas diffusion impedance may become significant. In such composite anodes with low surface resistance, the gas impedance can become even more significant when the nitrogen content in the fuel gas composition is increased, because this leads to a stronger gas diffusion impedance. However, the size of the gas diffusion impedance depends strongly on the actual test setup and cannot be judged here for the experiments by Burnat et al.63
Lomberg et al.67 performed EIS measurements for CGO10 anodes infiltrated with 14 wt% Ni. They interpreted a low frequency arc measured at T = 750 °C as a combination of gas diffusion impedance and chemical capacitance. The interpretations of Lomberg et al. are compatible with our model-based interpretations, according to which the low frequency arc would be attributed to surface reaction resistance/chemical capacitance process in combination with a gas diffusion process, where the latter is forced to the same frequency (i.e. Zgas), as explained before.
Aravind et al.66 measured the impedance spectra of a Ni–CGO anode using a setup with a large stagnant gas layer and identified a gas diffusion impedance process around a frequency of 0.5 Hz and a second, not further characterized process around 8 Hz. In this configuration, a low frequency process still persists, which therewith has to be attributed to the surface reaction resistance/chemical capacitance process.
Nakamura et al.38 performed EIS measurements for CGO10 anodes and associated the low frequency arc to a surface reaction resistance/chemical capacitance processes because of it's clear thermal activation. Although the effective transport properties of the microstructure were not characterized in detail within this publication, the reported SEM-pictures show a relatively high porosity with pores sizes about 1 μm. It thus seems reasonable that the gas impedance might be small compared to the surface reaction resistance/chemical capacitance process.
Using a special setup, Primdahl and Liu4 studied a Ce0.6Gd0.4O1.8 anode, mounted between auxiliary electrodes to avoid significant impedance contributions from gas diffusion outside the porous electrode structure. The remaining gas diffusion in the porous electrode was found to be negligible compared to the other processes. With this procedure, they assured the reliable interpretation of the EIS-spectra in an experimental way.
Riegraf et al.58 performed an EIS-study on symmetrical Ni–CGO10 electrodes for different temperatures and the gas compositions. They attributed a low frequency arc around 0.1–1 Hz as a combination of a surface process attributed to a charge transfer and a gas impedance process. The gas conversion and gas diffusion effects of the setup were quantified using another measurement set with Ni-YSZ anodes, where the gas impedance could well distinguished from other processes. The gas diffusion impedance within the electrode was assumed to be negligible, which might be appropriate for the relatively porous electrode with a thickness of 25 μm. For this particular case, they could isolate the surface reaction resistance/chemical capacitance process by using a simple model for the gas impedance.
Linder et al.18 performed EIS measurements for a Hexis short stack with Ni–CGO anodes for different fuel flow rates. The low frequency process <0.5 Hz is associated with a gas concentration process, as this process is strongly affected by a variation of the fuel amount. In the frequency range >0.5 Hz, two smaller not fully formed arcs are associated with the anode and cathode electrodes. This setup is comparable with our simulation with very large stagnant gas layer shown in Fig. 13 in Section 3.4. The very large stagnant gas layer has a similar effect like the gas conversion impedance due to fuel consumption along the cell in the setup of Linder et al.18 In contrast to our simulation study, which is parametrized in order to achieve well distinguishable gas and surface reaction resistance/chemical capacitance processes, the two processes largely overlap in the EIS-spectra of Linder et al.18 However, we suggest that the first small and incomplete arc in the frequency range >0.5 Hz can be associated with the surface reaction resistance/chemical capacitance process.
Overall, this short discussion of literature highlights that the interpretation of the low frequency arc for MIEC-based anodes (mostly CGO or CGO-composites) strongly depends on the cell architecture (i.e. thin-film electrodes, button cell, large area cell/stack). In thin-film electrodes, surface reaction resistance/chemical capacitance is the dominant LF phenomena and gas impedance tends to be negligible. In button cells, the LF-arc results in most cases from a combination of surface reaction resistance/chemical capacitance and gas impedance. Thereby the relative contribution of each process depends on several aspects, such as cell architecture, anode composition, microstructure and working conditions (fuel, temperature). Finally, in large area cells, the gas conversion impedance typically dominates over the surface reaction/chemical capacitance impedance.
4.4 EIS-spectra of CGO-based anodes for different applications
As demonstrated before, the CGO-anode arc, which appears as only one single process in the EIS-spectra, deconvolutes in three processes: (a) surface reaction resistance/chemical capacitance process, (b) gas diffusion impedance process and (c) charge carrier transport impedance process. Because of the strong coupling and overlapping of these processes, they can hardly be captured by analysing experimental EIS-spectra only. The contribution of the three processes to the total anode process depends on the actual cell design. In the following we provide some application examples and discuss the importance of the different contributions. Please note that the specified parameters are not absolute but depend on the actual material system and microstructure. If for example an additional catalyst like Ni or Pt is used, the surface reaction resistance will be considerably lower, and the transport of gas and charges will become important already at smaller CGO-layer thicknesses. The same is true for the different microstructures. For very dense and fine-grained microstructures with a relatively high surface area, the surface reaction resistance and the charge transport resistance decrease, while the gas diffusion resistance increases and will be relevant already for lower CGO-layer thicknesses and so on. Therefore, the different depicted cases will be observed for different absolute parameter ranges for different microstructures and material systems.(a) For very thin CGO-electrodes on the button cell level, the surface reaction resistance/chemical capacitance process dominates the anode process and the EIS-spectra will form an almost perfect semi-circle like in Fig. 16 for CGO-layer-thickness of L = 10 μm. The small impedance contribution from the gas and charge transport are negligible. An extreme case of this situation are thin-film electrodes.
(b) For CGO-electrodes with an intermediate thickness on the button cell level, the surface reaction resistance/chemical capacitance process still dominates the anode process, but the impedance contribution from the gas and charge carrier transport are no more negligible. However, the gas impedance is forced to the same frequency range because the gas impedance process is cut off when the surface reaction vanishes, which is the case above the characteristic frequency of the surface reaction resistance/chemical capacitance process. The two processes are not distinguishable by studying the total anode impedance experimentally. The small contribution of the transport resistance associated with relatively short transport pathways are usually not notable in the experimental spectra for high temperature applications in the range of T = 850 °C. However, for lower operating temperatures, the charge transport will be more significant according to the temperature dependency of the conductivity of eqn (51) and (52). If the anode EIS-spectra does not overlap with the cathode-process, a distortion of the arc-like process in a mouse-shaped end towards the higher frequencies might be visible like in Fig. 16 for CGO-layer-thickness of L = 100 μm. This configuration is typical for electrolyte supported button cells.
(c) For very thick CGO-electrodes, the transport resistances can become dominant because of the long transport ways for the charges and the gas species. For dense and very fine-grained electrodes, the gas impedance can already become limiting for intermediate layer thicknesses due to the transport limitation by Knudsen diffusion. It is worth noting that a part of the charge transport resistance is included in the anode process arc, while another part is only visible as an ohmic resistance as discussed in Section 4.1. This fact should be kept in mind if a MIEC-spectrum is analysed. However, the described behavior is only valid for the case of CGO-based anodes, where the CGO-phase is the only percolating phase in the composite. The EIS-spectra for this case will look like in Fig. 16 for CGO-layer thickness of L = 800 μm with a pronounced mouse shape and a large ohmic offset. This configuration might be important for anode supported button cells.
(d) For large area cells, the gas impedance process, which then is dominated by the gas conversion impedance, is usually the dominant part of the anode process. If the characteristic frequency of the gas impedance is below the characteristic frequency of the surface reaction resistance/chemical capacitance process, the two processes can even become distinguishable in experimental EIS-spectra, such as the one in Fig. 13. Note that for the case in Fig. 13(a), a dedicated parameter set for button cells is used, which is characterized by a huge stagnant gas layer. This case can be experimentally realized, but is not of importance for technical applications. However, the behaviour of this case is very similar to the gas conversion impedance configuration, relevant for SOFC large area cells.
4.5 Towards a systematic optimization of MIEC electrodes with digital materials design (DMD)
The optimization of MIEC electrodes is a very complex task with many parameters involved. As an example, in Fig. 18 different contributions to the anode ASR for different microstructures as a function of the layer thicknesses are shown.The total anode ASR is shown in Fig. 18(d) and is largest for MS1 for all CGO-layer thicknesses. For a CGO10 anode with MS1 microstructure, the surface reaction resistance is too high for the porous and coarse grained microstructure with its low specific surface area. With increasing thickness of the CGO-layer also the surface area increases and therewith the surface reaction resistance is reduced. At the same time, this causes a large charge transport resistance (Fig. 18(b)) because of the low M-factor for the MIEC (i.e. low effective ionic and electric conductivities) in combination with long transport pathways for charge carriers.
In contrast, the very dense and coarse grained MS3 has a large surface area and thus a low surface reaction resistance. For small CGO-layer thicknesses, MS3 therefore shows the best performance of the three microstructures. However, for the dense microstructure with Kn > 1, the gas diffusion resistance in the pores is very high even for intermediate CGO-layer thicknesses as can be seen in Fig. 18(a). Note that the gas diffusion resistance does not grow linearly with the CGO-layer thickness. This is because of the shift of the reaction zone towards the CCL as visible in Fig. 17(c), which limits the additional gas transport distance.
The intermediate microstructure MS2 shows a higher total ASR for small CGO-layer thicknesses (compared to MS3), because of its lower specific surface area resulting in higher surface reaction resistances. However, as the charge and gas transport resistance are both not too high the transport resistances increase moderately with increasing CGO-layer thickness as shown in Fig. 18(a) and (b). Therefore, the MS2 shows the lowest total ASR for L > 75 μm. Of course, the trade-off changes as well if the material system is changed. If for example a fine dispersed catalyst like Ni is added on the pore surface of the CGO-layer, the surface reaction resistance decreases, which also decreases the optimal layer thickness for the same microstructure (Fig. 18(d)).
The effective transport properties in the porous electrode can be described in a reliable way by running numerical simulations on the voxel mesh obtained from 3D imaging or from virtual microstructures. However, the effective properties (and the M-factors, respectively) do not provide a detailed understanding of the microstructure influence on the various transports. Additional information about possible optimization approaches can be deduced from morphological analysis described in Section 2.3.2. In order to illustrate the detailed level of morphological information, we compare in the following the various microstructure limitations for transport in the solid phase of MS1 with those in the pore phase of MS3. Apart from the rather intuitive dependency of the transport properties on the phase volume fraction, the constrictivity β and the tortuosity τ document additional transport restrictions due to bottlenecks and tortuous transport pathways, respectively. For example, the M-factor of the MIEC-phase MsimMIEC = 0.04660 for MS 1 with ϕMIEC = 0.4 shows a considerably lower value than the M-factor of the pore-phase Msimpore = 0.09292 for MS 3 with εpore = 0.25, despite the considerably larger phase volume fraction. This can be explained by the fact that the constrictivity βMIEC = 0.2010 of MS 1 is much lower than the constrictivity βpore = 0.4756 for MS 3. This is in agreement with the visual impression of limited connectivity of the only slightly overlapping particles in Fig. 6. In addition, the tortuosity τMIEC = 1.2114 of MS 1 is larger than the tortuosity τpore = 1.1136 of MS 3. This fact is less obvious from the visual impression from Fig. 6. Because of the different weights of the β0.37 and τ−4.37 in eqn (2), the tortuosity effect is even slightly higher for the transport limitation than the constrictivity effect as reported in Table 2.
Note that the virtual microstructures employed do not correspond to typical MIEC-electrodes. Such simplified microstructure were chosen for the purpose of illustration and easy reproduction. Realistic microstructure data can be obtained e.g. by FIB-tomography. Moreover, experimentally obtained microstructures can be varied by using microstructure simulation. For this purpose stochastic, digital twins of the experimental microstructures from tomography are created. They serve as a basis for a stochastic model (as e.g. performed by Neumann et al.68 for Ni-YSZ anodes), which is then capable to provide a large number of different virtual microstructures with realistic properties (e.g. parametric variations of porosity or particle sizes). The output from these microstructure simulations can then be combined with our numerical model for MIEC anodes, which opens new possibilities for virtual materials testing (VMT) and digital materials design (DMD). It must be emphasized that a systematic optimization of MIEC-anodes is only possible, if the material system with its associated bulk material properties, the microstructure and the design-parameters as e.g. the anode layer thickness are combined into a multiphysics model including all relevant physical processes. Such a systematic digital materials design (DMD) process for MIEC anodes could have the following procedure: the bulk properties of a specific material system are collected with literature data or measurements. Moreover, a specific cell-design and production process is chosen. A couple of button cells are then fabricated and characterized with EIS measurements, where the missing material parameters can be fitted. In a post mortem analysis, the microstructure can be reconstructed using 3D-tomography (e.g. FIB-tomography) and its effective properties can be determined using morphological analysis or direct simulation on the voxel microstructure using e.g. GeoDict.27 All the material and microstructure parameters can then be inserted in our MIEC model, which includes all relevant physical effects. The parametrized model can be validated and calibrated by comparison with the EIS-spectra. In the next step the numerical model can be combined with a microstructure model, which leads to a framework for digital materials design (DMD). Thereby, digital twins are deduced from the real microstructures as realistic start or edge-points for achievable microstructures. Virtual microstructures can then be used to vary microstructure properties and to analyze their impact on the cell performance (virtual materials testing VMT). Also the cell-design parameters (like e.g. the anode layer thickness, etc.) or the material system (e.g. different MIEC materials or addition of catalysts) can be varied. The MIEC model can then be used to predict the corresponding cell or anode performances. If one or more promising design-points are found, the realizability of these design points can be checked and validated by further experimental work.
5 Conclusions
A comprehensive model revealing the complex physico-chemical processes for CGO-based anodes on the button cell level is presented in this paper. The 1D-FE model can be operated in DC and AC mode and therewith the behaviour of the normal DC operation can be directly linked to the corresponding EIS-spectra. The fully implemented Nernst–Planck Poisson equations enables an appropriate description of the transport of electrons and vacancies in the CGO–MIEC. For fine-grained microstructures, the gas diffusion is limited by both, bulk and Knudsen diffusion. To capture these effects, a dusty-gas model is implemented, which is believed to be the most appropriate description for combined bulk and Knudsen diffusion. For the parametrization, literature data for CGO10 was used to estimate realistic values for the equilibrium charge carrier concentration, which has a strong influence on the chemical capacitance, the ionic and electronic conductivity and for the surface reaction resistance. It must be emphasized that it is beyond the scope of this paper to present a match with experimental measurements. Therefore, in the present paper, the microstructure effects are demonstrated on simple, well reproducible virtual structures.The CGO-anode arc, which appears as only one single process in the EIS-spectra, is shown to deconvolute in three processes (a) surface reaction resistance/chemical capacitance process, (b) gas diffusion impedance process and (c) charge carrier transport impedance process. Because of the strong coupling and overlap of these processes, they can hardly be captured by analysing experimental EIS-spectra only. Therefore, in the literature the anode arc, which typically has a low characteristic frequency (around 0.2–2 Hz), is often either depicted as gas impedance or as chemical capacitance process, without conclusive evidence. The contribution of the three processes to the total anode process depends on the cell design such as mechanical support (and associated thickness of anode layer) or design of gas distribution (and e.g. associated thickness of stagnant gas layer). In addition, also the microstructure and associated effective materials properties play an important role. This results in a large number of anode configuration, whereby the same material concept (i.e. CGO-based MIEC anode) can reveal very different performances characterized with different impedance spectra. The controversial interpretation of rate limiting processes in literature indicates that experimental methods alone may not be suitable for a reliable interpretation of such EIS-spectra from different anode configurations. Fortunately, our numerical model can be used to simulate the EIS-spectra for all these different MIEC/CGO-based anode configurations. In addition, the model also enables us to identify the limiting effects and/or quantifying the resistive/capacitive contributions from different processes. The model can thus be used to illustrate the impact of different CGO-anode configurations (i.e. microstructure and associated effective properties, anode layer thickness, gas distribution system and stagnant gas layer thickness). Fig. 19 provides an overview of the simulated EIS-spectra and identifies the limiting processes for many different configurations discussed throughout this paper at an operating temperature of T = 850 °C. In the following we briefly emphasize four specific configurations, which represent the most important cases in context with the controversial literature on the topic of LF-arcs in CGO anodes:
• For very low CGO-layer thicknesses in button cells or for thin-film electrodes, the surface reaction resistance is dominant.
• For intermediate electrode thicknesses, which are e.g. used for electrolyte supported button cells, the surface reaction resistance is still dominant, but the resistances due to gas and charge transport are no more negligible, even if they are hardly distinguishable in measured EIS-spectra.
• For larger CGO-layer thicknesses, which might be used for anode supported cells, the resistances for gas or charge transport – dependent on the actual material system and microstructure – might be dominant.
• For large area cells, the gas impedance process, which then is dominated by the gas conversion impedance, is usually the dominant part of the anode EIS-spectra and might be even distinguishable if the gas process shows a considerably lower characteristic frequency than the surface reaction resistance/chemical capacitance process.
Although the impedance according to the transport of electrons and ions is basically an ohmic effect, it shows a mouse-shaped arc with a non-zero ohmic contribution at the high frequency limit as a result of changing transport pathways for higher frequencies (in combination with by-passing of the surface reaction). A part of the transport resistance is included in the anode process arc, while another part is only visible as an ohmic resistance adding to the electrolyte resistance. This behaviour should be kept in mind for an appropriate interpretation of experimental EIS-spectra for MIEC (CGO) electrodes.
With our MIEC model in DC mode, the extension of the reaction zone for different CGO-layer thicknesses can be illustrated. It is observed that thick CGO layers are also characterized by a large inactive zone. A good qualitative agreement with experimental studies from literature could be shown and a more precise mechanism for the electrochemically active region could be suggested. For very dense fine-grained microstructures, the electrochemical most active zone might be found towards the CCL while for porous, course-grained microstructures, it might be found towards the electrolyte. The extension of the reaction zone can have a direct impact on the anode optimization in order to reduce the ASR. It is obvious that a too small CGO-layer thickness will posses a very high surface reaction resistance and a too large CGO-layer thickness will own a very high transport resistance. The optimal layer thickness in between will depend on how the extension of the reaction zone will behave with increasing CGO-layer thickness. The optimal thickness thus depends on various effects and coupled processes, which can be predicted reliably with our MIEC–CGO model.
Our simulation study enables the appropriate interpretation of the EIS-spectra and the understanding of the complex physico-chemical processes, which is a crucial prerequisite for a systematic materials optimization for CGO-based anodes. The model thereby serves as a platform for the integration of information from bulk material properties, fabrication parameters, microstructure effects, material laws and operating conditions and relates them to the cell performance on button cell level. Hence, with the integration of detailed physico-chemical properties into a single model framework, findings from basic and applied research, from theoretical models and experimental characterization can be directly used for a systematic optimization of CGO-based anodes.
We also discussed the methods of digital materials design (DMD) for the efficient optimization of anode materials and microstructures. In such a DMD framework, the MIEC (CGO) anode model is combined with other analytical and simulation methods (tomography, image analysis, stochastic microstructure modeling and characterization e.g. with impedance spectroscopy). The DMD framework allows virtual testing of a very large parameters space (e.g. many different virtual microstructures, different anode architectures/thicknesses, etc.) and predicting the corresponding anode performances. Such extensive parameter studies would not be achievable with experimental methods only. As a perspective for the future, the DMD approach that includes our MIEC-model will enable a systematic, fast and cost-effective research and development process for MIEC-anodes with improved properties. However, the DMD approach is not limited to fuel cells, but can be adapted for any application where microstructure effects are important, like e.g. batteries, filter materials, sensors, porous membranes, etc.
In a nutshell, the most important conclusions are the following:
• EIS-impedance only on experimental evidence is difficult to interpret. The presented model helps to understand important effects in MIEC- and especially CGO-based anodes and to distinguish different limiting processes as e.g. the gas impedance and the surface reaction resistance/chemical capacitance process. The model shows that the dynamics of these two processes are coupled and hence occur in the same frequency range.
• Based on the model it can be illustrated that configurations with the same anode material but with different cell architectures (thin film, button cell, large area cell/stack) result in very different impedance signatures.
• The model implies that the extension of the reaction zone also depends on the transport limitations. If the charge transport is limiting (e.g. for highly porous and course microstructures), the most reactive zone is towards the electrode/electrolyte interface. If the gas transport is limiting (e.g. for very dense and fine-grained electrodes), the most reactive zone is towards the electrode/CCL interface.
• Using effective properties from microstructures (e.g. impact of tortuosity) and intrinsic properties from materials (e.g. MIEC intrinsic conductivities, impact of catalyst on reaction kinetics) as input, the model provides a basis for a systematic anode optimization. Thereby it turns out that the microstructure needs to be optimized specifically for a given architecture and material system. E.g. for a thick anode the microstructure optimization needs to face the transport limitations, whereas in thin anodes sufficient reaction surface has to be provided.
List of symbols
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the Swiss Federal Office of Energy (SFOE) is gratefully acknowledged (project number SI/501792-01).Notes and references
- M. S. Khan, S. B. Lee, R. H. Song, J. W. Lee, T. H. Lim and S. J. Park, Ceram. Int., 2016, 42, 35–48 CrossRef CAS.
- A. Nenning, A. K. Opitz, T. M. Huber and J. Fleig, Phys. Chem. Chem. Phys., 2014, 16, 22321–22336 RSC.
- S. Primdahl and M. Mogensen, Solid State Ionics, 2002, 152–153, 597–608 CrossRef CAS.
- S. Primdahl and Y. L. Liu, J. Electrochem. Soc., 2002, 149, A1466 CrossRef CAS.
- R. Price, M. Cassidy, J. G. Grolig, A. Mai and J. T. S. Irvine, J. Electrochem. Soc., 2019, 166, F343–F349 CrossRef CAS.
- C. Li, J. J. Chew, A. Mahmoud, S. Liu and J. Sunarso, J. Membr. Sci., 2018, 567, 228–260 CrossRef CAS.
- H. Bouwmeester and P. Gellings, Handbook of Solid State Electrochemistry, 1997 Search PubMed.
- A. Mai, J. G. Grolig, S. Venkatesh, M. Dold and A. Schuler, 14th European SOFC & SOE Forum, EFCF, Luzern, 2020, p. A0303 Search PubMed.
- C. Walter, K. Schwarze, M. Boltze, K. Herbrig and A. Surrey, 14th European SOFC & SOE Forum, EFCF, Luzern, 2020, p. A0301 Search PubMed.
- J. Koettgen and M. Martin, J. Am. Ceram. Soc., 2020, 103, 3776–3787 CrossRef CAS.
- W. Lai and S. M. Haile, J. Am. Ceram. Soc., 2005, 88, 2979–2997 CrossRef CAS.
- F. Ciucci, W. C. Chueh, D. G. Goodwin and S. M. Haile, Phys. Chem. Chem. Phys., 2011, 13, 2121–2135 RSC.
- C. Chen, D. Chen, W. C. Chueh and F. Ciucci, Phys. Chem. Chem. Phys., 2014, 16, 11573–11583 RSC.
- M. Kishimoto, M. Lomberg, E. Ruiz-Trejo and N. P. Brandon, Electrochim. Acta, 2016, 190, 178–185 CrossRef CAS.
- P. Marmet, T. Hocker, J. G. Grolig, H. Bausinger, A. Mai, J. M. Brader and L. Holzer, 14th European SOFC & SOE Forum, EFCF, Luzern, 2020, p. A1514 Search PubMed.
- J. Jamnik and J. Maier, J. Electrochem. Soc., 1999, 146, 4183–4188 CrossRef CAS.
- W. C. Chueh and S. M. Haile, Phys. Chem. Chem. Phys., 2009, 11, 8144–8148 RSC.
- M. Linder, T. Hocker, C. Meier, L. Holzer, K. A. Friedrich, B. Iwanschitz, A. Mai and J. A. Schuler, J. Power Sources, 2015, 288, 409–418 CrossRef CAS.
- M. Riegraf, V. Yurkiv, R. Costa, G. Schiller and K. A. Friedrich, ChemSusChem, 2017, 10, 587–599 CrossRef CAS PubMed.
- T. Nakamura, K. Yashiro, A. Kaimai, T. Otake, K. Sato, T. Kawada and J. Mizusaki, J. Electrochem. Soc., 2008, 115(12), B1244–B1250 CrossRef.
- S. B. Adler, J. Electrochem. Soc., 1996, 143, 3554–3564 CrossRef CAS.
- W. C. Chueh, W. Lai and S. M. Haile, Solid State Ionics, 2008, 179, 1036–1041 CrossRef CAS.
- W. Lai and S. M. Haile, Phys. Chem. Chem. Phys., 2008, 10, 865–883 RSC.
- C. I. Priyadharsini, G. Marimuthu, T. Pazhanivel, P. M. Anbarasan, V. Aroulmoji, S. Prabhu and R. Ramesh, Ionics, 2020, 26, 3591–3597 CrossRef CAS.
- COMSOL Multiphysics, v. 5.5, http://www.comsol.com, COMSOL AB, Stockholm, Sweden, 2019.
- O. Stenzel, O. Pecho, L. Holzer, M. Neumann and V. Schmidt, AIChE J., 2016, 62, 1834–1843 CrossRef CAS.
- GeoDict, Math2Market GmbH, 2019, http://www.geodict.com.
- L. Holzer, B. Münch, B. Iwanschitz, M. Cantoni, T. Hocker and T. Graule, J. Power Sources, 2011, 196, 7076–7089 CrossRef CAS.
- L. Holzer, B. Iwanschitz, T. Hocker, L. Keller, O. Pecho, G. Sartoris, P. Gasser and B. Muench, J. Power Sources, 2013, 242, 179–194 CrossRef CAS.
- L. Holzer, O. Stenzel, O. Pecho, T. Ott, G. Boiger, M. Gorbar, Y. de Hazan, D. Penner, I. Schneider, R. Cervera and P. Gasser, Mater. Des., 2016, 99, 314–327 CrossRef CAS.
- G. Gaiselmann, M. Neumann, V. Schmidt, O. Pecho, T. Hocker and L. Holzer, AIChE J., 2014, 60, 1983–1999 CrossRef CAS.
- O. M. Pecho, O. Stenzel, B. Iwanschitz, P. Gasser, M. Neumann, V. Schmidt, M. Prestat, T. Hocker, R. J. Flatt and L. Holzer, Materials, 2015, 8, 5554–5585 CrossRef CAS PubMed.
- M. Neumann, O. Stenzel, F. Willot, L. Holzer and V. Schmidt, Int. J. Solids Struct., 2020, 184, 211–220 CrossRef.
- M. Neumann, O. Furat, D. Hlushkou, U. Tallarek, L. Holzer and V. Schmidt, Communications in Computer and Information Science, 2018, pp. 145–158 Search PubMed.
- O. Stenzel, O. Pecho, L. Holzer, M. Neumann and V. Schmidt, AIChE J., 2017, 63, 4224–4232 CrossRef CAS.
- L. Holzer, O. Pecho, J. Schumacher, P. Marmet, O. Stenzel, F. N. Büchi, A. Lamibrac and B. Münch, Electrochim. Acta, 2017, 227, 419–434 CrossRef CAS.
- COMSOL Multiphysics, Batteries & Fuel Cells Module, v. 5.5. COMSOL AB, Stockholm, Sweden, 425.
- T. Nakamura, T. Kobayashi, K. Yashiro, A. Kaimai, T. Otake, K. Sato, J. Mizusaki and T. Kawada, J. Electrochem. Soc., 2008, 155, B563–B569 CrossRef CAS.
- P. Costamagna, P. Costa and V. Antonucci, Electrochim. Acta, 1998, 43, 375–394 CrossRef CAS.
- J. Fleig, Phys. Chem. Chem. Phys., 2005, 7, 2027–2037 RSC.
- W. G. Bessler, J. Electrochem. Soc., 2006, 153, A1492–A1504 CrossRef CAS.
- R. Krishna and J. A. Wesselingh, Chem. Eng. Sci., 1997, 52, 861–911 CrossRef CAS.
- A. Bertei and C. Nicolella, J. Power Sources, 2015, 279, 133–137 CrossRef CAS.
- S. Liu, W. Kong and Z. Lin, J. Power Sources, 2009, 194, 854–863 CrossRef CAS.
- E. N. Fuller, P. D. Schettler and J. C. Giddings, Ind. Eng. Chem., 1966, 58, 18–27 CrossRef CAS.
- J. Becker, C. Wieser, S. Fell and K. Steiner, Int. J. Heat Mass Transfer, 2011, 54, 1360–1368 CrossRef CAS.
- D. Bernhardsgrütter and M. M. Schmid, J. Phys. Chem. C, 2019, 123, 30077–30087 CrossRef.
- COMSOL Multiphysics, Reference Manual, v. 5.5. COMSOL AB, Stockholm, Sweden, 2019.
- B. C. Steele, Solid State Ionics, 2000, 129, 95–110 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 3, 307–435 Search PubMed.
- C. B. Carter and M. G. Norton, Ceramic materials: Science and engineering, 2013 Search PubMed.
- X. Li, Z. Feng, J. Lu, F. Wang, M. Xue and G. Shao, Ceram. Int., 2012, 38, 3203–3207 CrossRef CAS.
- H. L. Tuller, Nonstoichiometric Oxides, Academic Press, New York, 1981 Search PubMed.
- S. Wang, H. Inaba, H. Tagawa, M. Dokiya and T. Hashimoto, Solid State Ionics, 1998, 107, 73–79 CrossRef CAS.
- Z. A. Feng, F. El Gabaly, X. Ye, Z. X. Shen and W. C. Chueh, Nat. Commun., 2014, 5, 1–9 Search PubMed.
- A. N. Tabish, H. C. Patel, J. Schoonman and P. V. Aravind, Electrochim. Acta, 2018, 283, 789–797 CrossRef CAS.
- M. Gerstl, A. Hutterer, J. Fleig, M. Bram and A. K. Opitz, Solid State Ionics, 2016, 298, 1–8 CrossRef CAS.
- M. Riegraf, R. Costa, G. Schiller, K. A. Friedrich, S. Dierickx and A. Weber, J. Electrochem. Soc., 2019, 166, F865–F872 CrossRef CAS.
- W. C. Chueh, Y. Hao, W. Jung and S. M. Haile, Nat. Mater., 2012, 11, 155–161 CrossRef CAS PubMed.
- C. Kleinlogel and L. Gauckler, ECS Proc., 1999, 99, 225–232 CrossRef.
- P. Kim, D. J. Brett and N. P. Brandon, J. Power Sources, 2009, 189, 1060–1065 CrossRef CAS.
- J. Jamnik and J. Maier, Phys. Chem. Chem. Phys., 2001, 3, 1668–1678 RSC.
- D. Burnat, G. Nasdaurk, L. Holzer, M. Kopecki and A. Heel, J. Power Sources, 2018, 385, 62–75 CrossRef CAS.
- B. Todd and J. B. Young, J. Power Sources, 2002, 110, 186–200 CrossRef CAS.
- J. Koettgen, S. Grieshammer, P. Hein, B. O. Grope, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2018, 20, 14291–14321 RSC.
- P. V. Aravind, J. P. Ouweltjes and J. Schoonman, J. Electrochem. Soc., 2009, 156, B1417–B1422 CrossRef CAS.
- M. Lomberg, E. Ruiz-Trejo, G. Offer and N. P. Brandon, J. Electrochem. Soc., 2014, 161, F899–F905 CrossRef CAS.
- M. Neumann, J. Staněk, O. M. Pecho, L. Holzer, V. Beneš and V. Schmidt, Comput. Mater. Sci., 2016, 118, 353–364 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: With further documentation of the model components and parametrization of the material laws. See DOI: 10.1039/d1cp01962g |
| This journal is © the Owner Societies 2021 |









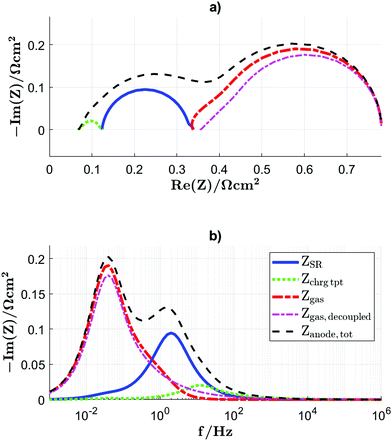




![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)

