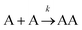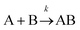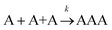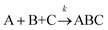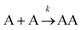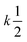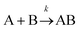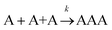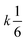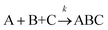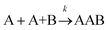Open Access Article
Open Access ArticleDichotomy between heterotypic and homotypic interactions by a common chemical law
Jérôme J.
Lacroix

Graduate College of Biomedical Sciences, Western University of Health Sciences, 309 E 2nd St, Pomona, CA 91709, USA. E-mail: jlacroix@westernu.edu
First published on 9th July 2021
Abstract
It is now well established that chemical systems evolve as a function of the frequency at which their individual chemical components interact. This notion is seemingly embedded into a ubiquitous chemical law which proposes that the rate of elementary chemical interactions is proportional to the Product of Interactant Concentrations (PIC) by a rate constant. Here, it is shown that, while the PIC is always proportional to the frequency at which interactants simultaneously collide (Interactant Collision Frequency, or ICF), the coefficient of proportionality between PIC and ICF diverges as a function of the number of identical interactants, a property hereby defined as “homo-molecularity”. To eliminate the divergence between heterotypic and homotypic chemical interactions, the PIC must be divided by the factorial of homo-molecularity. Although this correction may not be practically essential for studies in which the homo-molecularity of chemical interactions is unchanged, it becomes critical when the goal is to compare interaction rates between similar chemical systems differing by their homo-molecularity, such as when interactants are purposefully modified for de novo design of heterotypic interactions, or when the goal is to compare theoretically-predicted rates of homotypic interactions with those that are empirically-determined by varying interactant concentrations.
Introduction
The formation of chemical complexes is essential for the advancement of chemical reactions. The vast majority of chemical complexes form in elementary steps in which two chemical species physically collide or interact with each other (bimolecular interactions), although few elementary chemical reactions occur as a result of simultaneous interactions between three individual interactants (termolecular interactions). The importance of inter-molecular collisions also bears true for unimolecular reactions, i.e., in which products form from a single, isolated reactant. Indeed, in most theories of unimolecular reactions, including those developed by Lindemann, Hinshelwood, Rice, Ramsperger, Kassel, and Marcus, individual reactants become “activated” upon collisions with surrounding solvent molecules.1–4It is now commonly assumed that the rate at which molecular complexes form in chemical systems should be proportional to the rate at which individual interactants collide. This proportionality between the rate of molecular complex formation and the Interactant Collision Frequency (ICF) is a central tenet of chemistry that is encompassed into a classical rate law established over 150 years ago by Guldberg and Waage (and independently few years later by van't Hoff).5–7 This law posits that the rate of any elementary chemical reaction must be equal to the Product of Interactant Concentrations (PIC) multiplied by a rate constant, conventionally represented by the lower-case letter “k”. Table 1 summarizes the rate law for elementary chemical reactions of varying molecularity.
This paper presents several thought experiments to reveal that the proportionality between PIC and ICF changes as a function of the number of identical interactants occurring in elementary chemical interactions. A simple and general correction of the rate law to keep the proportionality between PIC and ICF constant for any arbitrary elementary chemical interaction is presented.
Results
Illustration of the divergence using a thought experiment
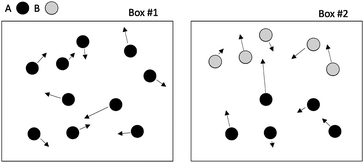
Let us imagine two identical boxes of same volume V containing molecules that randomly move and collide due to thermal agitation. Box #1 is filled with 2N molecules A, whereas Box #2 is filled with N molecules A and N molecules B (Fig. 1). Let us also assume that molecules A and B are physically and chemically equivalent, i.e., they are indistinguishable except by the label “A” or “B” affixed to them. We will also assume that collisions between any two molecules (A or B) lead to the formation of bimolecular complexes. Since A and B are equivalent, it is reasonable to assume that the formation of any bimolecular complexes (AA, BB, or AB) is governed by the same intrinsic rate constant. Let us call it k′.Since the total number of molecules in both boxes is the same (2N), the frequency of bimolecular collisions in both boxes is predicted to be identical. Therefore, the rate at which any bimolecular complex forms, regardless of the nature of the complex (AA for box #1; AA, BB, or AB for box #2) should be identical in both boxes. Let us calculate this rate using the rate law shown in Table 1. Since box #1 only contains molecules A, the rate of bimolecular complex formation in this box is equal to the rate of formation of AA complexes:
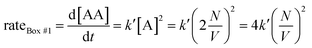 | (1) |
Since box #2 contain both molecules A and B, the rate of bimolecular complex formation is equal to the sum of the rate of formation of all possible bimolecular complexes, i.e., AA, BB, and AB:
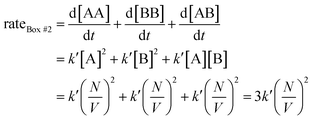 | (2) |
The rate eqn (1) systematically gives a higher value than rate eqn (2). This is in contrast with aforementioned assumptions which suggest both rates should be equal.
Divergence between homotypic and heterotypic bimolecular interactions
Let us use a more quantitative approach to compare the ICF between homotypic and heterotypic bimolecular interactions. For the sake of simplicity, we will solely focus on box #2. In this box, the frequency of homotypic AA collisions can be compared relatively to the frequency of heterotypic AB collisions by comparing the probability of AA vs. AB collisions to occur. The probability PAA of any bimolecular AA collision to happen can be approximated by calculating the probability of two (and only two) molecules A to occupy the same small collisional sub-volume v (v ≤ V) (this approach is, of course, an approximation since molecules are hereby considered volumeless). To calculate this probability, we must employ the rules of combinatorics. These rules state that this probability must be equal to the probability of any two molecules A to be located within v multiplied by the probability of all other molecules to be located outside v. In a mathematical form, this translates to: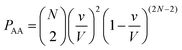 | (3) |
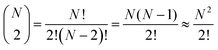 | (4) |
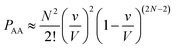 | (5) |
Let us now use the same method to calculate the probability PAB of exactly one molecule A and one molecule B to occupy the collisional volume v:
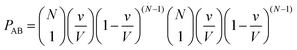 | (6) |
Which simplifies to:
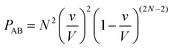 | (7) |
When comparing eqn (5) and (7), we have the relation:
| PAB ≈ 2PAA | (8) |
Eqn (8) means there are about twice as many AB collisions as there are AA collisions in box #2. This result does not seem very surprising. Box #2 contains the same number of molecules A and B. AB collisions happen when A collides with B or when B collides with A. In contrast AA collisions only occur when A collides with another A. When N is large, there are thus approximately twice as many AB collisions as there are AA collisions. Under our assumption that the intrinsic rate constant underlying the formation of AA and AB complexes is identical, the overall rate of AB complex formation should be twice that of AA complex formation. However, application of the rate law would invariably conclude that both rates are identical:
| rateAA = k′[A]2 = k′N2 | (9) |
| rateAB = k′[A][B] =k′N2 | (10) |
To further prove the validity of our probabilistic approach, let us compare the absolute ICF for AA and AB interactions in box #2. According to the kinetic collision theory, the frequency of bimolecular AB collisions in box #2, ZAB (s−1 m−3), is calculated by multiplying the relative mean velocity between colliding molecules, a collision cross-section surface, and the interactant concentrations:8
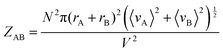 | (11) |
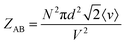 | (12) |
On the other hand, for homotypic biomolecular interactions, the ICF is commonly calculated using a slightly different equation that includes a ½ factor:
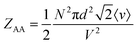 | (13) |
Comparing eqn (10) and (11) leads to:
| ZAB = 2ZAA | (14) |
Eqn (14) mirrors the differences between the probability of AA and AB collisions shown in eqn (8).
Elimination of the divergence between homotypic and heterotypic interactions
Eqn (8)–(14) show that the proportionality between ICF and PIC is not the same between homotypic and heterotypic interactions. Specifically, the proportionality coefficient between PIC and ICF is systematically 2-fold larger for homotypic bimolecular interactions relative to heterotypic bimolecular interactions.Another way to underscore this dichotomy is to realize that the ICF for bimolecular interactions is a function of the number of combinations of dyads that can form in the system: the higher the number of dyads, the higher the chance for them to form randomly, and thus the higher the frequency at which they occur. For example, in box #2, the total number of combinations of AB dyads is:
| number of AB dyads = NA × NB = N2 | (15) |
In contrast, the total number of combinations of AA dyads in the same box is mathematically equivalent to a binomial coefficient:
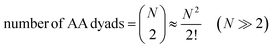 | (16) |
Whereas the PIC for heterotypic AB interactions exactly corresponds to the number of AB dyads shown in eqn (15), the PIC for homotypic AA interactions is 2-fold greater than the number of AA dyads shown in eqn (16). Therefore, to eliminate the dichotomy between heterotypic and homotypic interactions, the PIC for homotypic bimolecular interactions should be divided by 2.
Beyond bimolecular interactions
Let us assume that three molecules A or B simultaneously interact to form termolecular complexes in box #2. Since termolecular interactions may contain 2 or 3 identical interactants, the number of identical interactants will be defines as “homo-molecularity” to distinguish it from the total number of interactants (molecularity). For termolecular interactions with a homo-molecularity of 3, such as A + A + A → AAA, the number of combinations of AAA triads in box #2 is: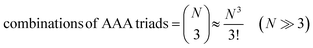 | (17) |
For termolecular interactions with a homo-molecularity of 2, such as A + A + B → AAB, the number of combinations of AAB triads in box #2 is:
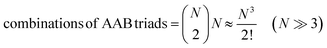 | (18) |
Therefore, when the number of molecules is very large compared to the homo-molecularity, as in most experimental systems, the divergence between PIC and ICF is generally corrected by dividing the PIC by the factorial of homo-molecularity. Table 2 summarizes the corrected rate for various examples of interactions with various molecularity and homo-molecularity values.
Let us use the corrected rates depicted in Table 2 to our first thought experiment, in which the rate of bimolecular complex formation in boxes #1 and #2 calculated using the uncorrected law differs despite both boxes having the same total number of molecules (eqn (1) and (2)):
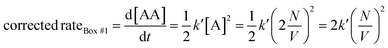 | (19) |
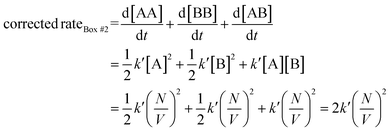 | (20) |
Whit this correction, the rate of bimolecular complex formation agrees between the two boxes, yielding the same value of 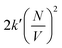 (eqn (19) and (20)).
(eqn (19) and (20)).
Discussion
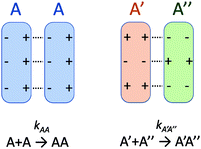
There is no doubt that many of us studying molecular systems have previously figured out the dichotomy resulting from the application of the empirical rate law between homotypic and heterotypic interactions. To many, correcting this dichotomy may seem trivial. There is some credit to support this thought. The rate of most elementary chemical reactions is almost always empirically determined by varying reactant concentrations and measuring how these variations affect the rate of product formation: the rate constant simply corresponds to the proportionality coefficient between the observed reaction rate and PIC. In homotypic reactions, the dichotomy appears as an additional constant (equal to the factorial of the homo-molecularity of the reaction) that is multiplied by the intrinsic rate constant of the reaction to form an apparent rate constant. This additional constant does not change the order of the reaction and remains constant as long as the homo-molecularity of the reaction remains unchanged.However, one can envision few applications when correcting this dichotomy would seem absolutely critical. One such application is the modification of homotypic interactants to engineer desired heterotypic systems. Fig. 2 illustrates a hypothetical example inspired from a recently-designed thermal bioswitch.9 In this example, a naturally occurring protein A interacts with another protein A via 3 thermolabile homotypic electrostatic interactions mediated by charged residues. Changing the charge polarity of some of these residues, for instance by substituting a glutamate with a lysine and vice versa, leads to two variants called A′ and A′′. Due to these changes, the formation of homotypic A′A′ or A′′A′′ complexes is now unfavorable due to negative–negative or positive–positive electrostatic repulsions. However, heterotypic A′A′′ interactions are predicted to lead to the formation of stable complexes with 3 positive-negative electrostatic interactions, similar to how two unmodified A proteins interact to form a stable AA dimer. Assuming that the intrinsic rate constants, kAA and kA'A'', mainly depend on the number of positive–negative interactions between two monomers, one could hypothesize that 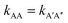 . To test this prediction, one would need to experimentally calculate rate constants by varying interactant concentrations and measuring the rate at which AA and A′A′′ complexes form, for example using a spectroscopic method. Assuming both intrinsic rate constants are indeed equal
. To test this prediction, one would need to experimentally calculate rate constants by varying interactant concentrations and measuring the rate at which AA and A′A′′ complexes form, for example using a spectroscopic method. Assuming both intrinsic rate constants are indeed equal 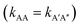 , application of the rate law to uncorrected experimental data would invariably lead to the wrong conclusion that
, application of the rate law to uncorrected experimental data would invariably lead to the wrong conclusion that 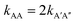 .
.
Another potential application is the comparison between experimentally-observed and theoretically-predicted intrinsic rate constants10–14 and binding affinities.15 If the homo-molecularity of these chemical reactions, or interactions, is >1, the correction presented in Table 2 would need to be implemented to the rates and affinities that are experimentally determined to make sure that the proportionality between PIC and ICF remains strictly a function of the size and speed of colliding molecules as shown in eqn (11) and (13).
Conclusions
In conclusion, this study uncovers a dichotomy in a commonly-used rate law between homotypic and heterotypic elementary chemical interactions. The proposed correction will be useful for specific applications in which the number of identical interactants, a quantity defined here as homo-molecularity, varies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
I thank my colleague Dr Yun Luo for critical reading of the manuscript.References
- F. A. Lindemann, S. Arrhenius, I. Langmuir, N. R. Dhar, J. Perrin and L. W. C. McC, Trans. Faraday Soc., 1922, 17, 598 RSC.
- H. R. Oscar Rice, J. Am. Chem. Soc., 1927, 49, 1617 CrossRef.
- F. Di Giacomo, J. Chem. Educ., 2015, 92, 476 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1952, 20, 359 CrossRef CAS.
- C. M. Guldberg and P. Waage, Journal für praktische Chemie, 1879, 19, 69 CrossRef CAS.
- C. M. Guldberg and P. Waage, Forhandelinger: Videnskabs-Selskabet i Christiana, 1864, 35 Search PubMed.
- J. H. van 't Hoff, Berichte der Deutschen Chemischen Gesellschaft zu Berlin, 1877, 10, 669 CrossRef.
- M. Trautz, Zeitschrift für anorganische und allgemeine Chemie, 1916, 96, 1 CrossRef CAS.
- D. I. Piraner, Y. Wu and M. G. Shapiro, ACS Synth. Biol., 2019, 8, 2256 CrossRef CAS PubMed.
- S. H. Li, J. J. Guo, R. Li, F. Wang and X. Y. Li, J. Phys. Chem. A, 2016, 120, 3424 CrossRef CAS PubMed.
- A. L. Kaledin, M. C. Heaven and K. Morokuma, J. Chem. Phys., 2001, 114, 215 CrossRef CAS.
- Z. F. Xu, R. S. Zhu and M. C. Lin, J. Phys. Chem. A, 2003, 107, 3841 CrossRef CAS.
- C. Leng, H. M. Qin, Y. B. Si and Y. Zhao, J. Phys. Chem. C, 2014, 118, 1843 CrossRef CAS.
- Y. Y. Zhang, T. X. Xie, Z. R. Li, Y. Shi and M. X. Jin, Chin. Phys. B, 2015, 24, 038201 CrossRef.
- E. Gallicchio and R. M. Levy, Adv. Protein Chem. Struct. Biol., 2011, 85, 27 CAS.
| This journal is © the Owner Societies 2021 |