Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlling radiolysis chemistry on the nanoscale in liquid cell scanning transmission electron microscopy†
Juhan
Lee
 a,
Daniel
Nicholls
a,
Daniel
Nicholls
 a,
Nigel D.
Browning
abc and
B. Layla
Mehdi
a,
Nigel D.
Browning
abc and
B. Layla
Mehdi
 *a
*a
aDepartment of Mechanical, Materials and Aerospace Engineering and Department of Physics, University of Liverpool, Liverpool, L69 3GH, UK. E-mail: b.l.mehdi@liverpool.ac.uk
bSivananthan Laboratories, 590 Territorial Drive, Bolingbrook, IL 60440, USA
cPhysical and Computational Science Directorate, Pacific Northwest National Laboratory, Richland, WA 99352, USA
First published on 9th March 2021
Abstract
When high-energy electrons from a scanning transmission electron microscope (STEM) are incident on a liquid, the vast majority of the chemical reactions that are observed are induced by the radiolysis breakdown of the liquid molecules. In the study of liquids, the radiolysis products of pure water are well known, and their rate of formation for a given flux of high-energy electrons has been studied intensively over the last few years for uniform TEM illumination. In this paper, we demonstrate that the temporal and spatial distribution of the electron illumination can significantly affect the final density of radiolysis products in water and even change the type of reaction taking place. We simulate the complex array of possible spatial/temporal distributions of electrons that are accessible experimentally by controlling the size, the scan rate and the hopping distance of the electron probe in STEM mode and then compare the results to the uniformly illuminated TEM mode of imaging. By distributing the electron dose both spatially and temporally in the STEM through a randomised “spot-scan” mode of imaging, the diffusion overlap of the radiolysis products can be reduced, and the resulting reactions can be more readily controlled. This control allows the resolution of the images to be separated from the speed of the induced reaction (which is based on beam current alone) and this facet of the experiment will allow a wide range of chemical reactions to be uniquely tailored and observed in all liquid cell STEM experiments.
In the last decade, liquid cell electron microscopy has emerged as a unique technology for understanding nanoscale structures and processes in liquids or at the liquid/solid interface.1–5 In particular, in situ liquid cell (scanning) transmission electron microscopy ((S)TEM), has brought new insights and perspectives into various disciplines, for instance, observation of nucleation and growth,6–9 electrochemical reactions,3,10,11 and investigation of oxidation states12 and electronic structure of the electrodes.13,14 However, despite these significant contributions, liquid cell electron microscopy has several outstanding challenges. Firstly, due to the restricted space of the TEM microscope column, the sample volume has to be greatly miniaturised, which presents itself with technological limitations for further modifications. This creates a challenge for liquid-phase TEM community when trying to correlate experimental results with the realistic conditions of the bulk setup. For example, it is not possible to engineer commercial battery consisting of a current collector, active-electrode materials, conductive additives, and binder; and instead, the setup is limited to a small piece of an active electrode only.15 Secondly, the interaction between the electron beam and the liquid sample cannot be completely avoided, and this can have a significant effect on the kinetics of the reactions being observed.1,16,17 In all studies reported so far, chemical interactions through radiolysis appear to be the predominant effect of the electron beam. Understanding and controlling it is therefore of great importance to the development of more controlled observations using liquid cell (S)TEM.1,18
In general, radiolysis in electron microscopy is understood as decomposition of molecules caused by electron–electron interactions. For example, in the case of water, water molecules will interact with the high energy electron and undergo ionisation (H2O+, e−) and excitation (H2O*) processes on the femtosecond timescale. Picoseconds after the initial energy transfer, these species are further converted to H3O+, solvated electrons eh−, hydroxyl radical OH˙, and hydrogen radical H˙. As time continues, these products start clustering together (spurs), diffusing randomly, reacting to form secondary products such as H2O2 and OH−, and eventually become homogeneously distributed.19 The radiolysis yields at the homogeneous stage, ∼10−6 s after the initial energy transfer to the water molecules are represented as primary yields and expressed conventionally as G-values.16 The G-values are dependent on the energy of the initial fast electron and the chemistry of the liquid sample and often quoted as the number of molecular yield per 100 eV absorbed energy.20,21 For instance, the G-values of water radiolysis for 300 keV electron beam obtained by Hill and Smith are:
 | (1) |
Recently, an intriguing experimental indication has been reported by Biskupek et al.22 that the direct knock-on collisions caused by the electron beam are the main driving force for dissociating water molecules in a specific case of molecular confinement in a sub-nanometre space. They also addressed that the dissociation processes caused by electron–electron interactions such as radiolysis are quickly reversed due to the confined space. Their results imply the necessity of modifying the conventional approach of applying G-values in exceptional circumstances such as encapsulated water in fullerenes or carbon nanotubes. Nonetheless, despite the fundamental importance, these conditions are accompanied by rare cases for limited applications, the conventional approach with the G-value is still considered as the most relevant modelling element for general cases of radiolysis simulations.
Radiolysis by ionising radiation such as neutrons, photons, and γ-rays, has been intensively studied for applications in food preservation, nuclear energy, and medicine.16 However, only a few studies have been reported so far concerning the fundamental principles behind electron beam-induced radiation chemistry for in situ liquid (S)TEM. Pioneering work by Grogan et al.18 simulating the spatial and temporal variation of radiolytic byproducts in water was further developed by Schneider et al.16 considering the degree of aeration and pH of the water. These simulations,23 however, are limited to static conventional TEM acquisition conditions and ignore the effects of modifying the spatial/temporal profile of the electron beam that can be achieved with a STEM.
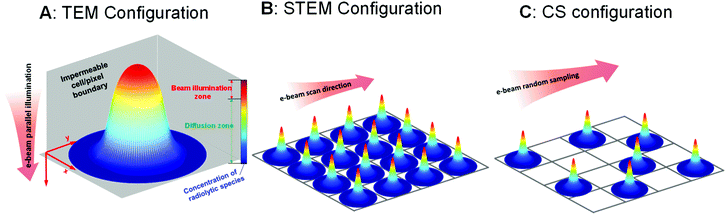
Inside the (S)TEM various beam configurations controlling the spot size24,25 and the electron dose rate17,26,27 can be applied, and different illumination schemes can be used, such as regular scanning,28 spot-scan,29 and sub-sampling with compressive sensing.30,31 The full range of these beam configurations, which can control the number of electrons on the picosecond to microsecond timescales (i.e. the same timescales over which the radiolysis products equilibrate) is shown in Fig. 1. Specifically, when an electron beam hits a thin liquid sample, radiolysis occurs primarily in the beam-exposed zone. As a result of the localised radiolysis process, the concentrations of the chemical species will not be homogeneous throughout the cell and diffusion is expected to take place. As illustrated in Fig. 1A, a diffusion zone will thus arise around the edge of the beam-exposed zone. Depending on the characterisation scheme being used, either TEM or STEM, the electron beam can then be moved to another area of interest either by manually changing the sample position or by using a pre-set beam movement scheme. In these cases, if the diffusion of the species from the first beam position is fast/far enough, they will influence radiolysis in the second beam position. Depending on how large the beam size is, how long it is stationary, how many electrons illuminate the beam area, how far the beam jumps to the next position (distance between illuminated pixels), and how fast the diffusion processes are, we can use these movement schemes to change the overall distribution of the radiolysis products within the (S)TEM liquid cell. Here, we examine all these possibilities based on a reaction–diffusion model to determine the underlying phenomena controlling the distribution of radiolysis products and determine the optimal controls for performing high-resolution liquid cell analyses.
One of the easiest observations to make in liquid cell TEM is the formation of bubbles – more often than not this is the first experiment that everyone performs simply by turning the beam on under standard illumination conditions. Understanding beam-induced gas bubble formation is critical for fundamental aspects of liquid dynamics, such as the formation kinetics of hydrogen nanobubbles,32,33 and also for preventing undesired influences on the kinetics of other liquid cell experiments (the formation of bubbles means the liquid is consumed). While the generation of gas bubbles by the electron irradiation of water could be due to the formation of hydrogen and/or oxygen gas,33 recent theoretical work indicates that O2 is less likely to induce bubble nucleation.16,18 For the nucleation of hydrogen (H2) gas bubbles, one of the key criteria is the saturation concentration;18 bubbles form if the concentration of the dissolved hydrogen gas is significantly higher than this level. To study the influence of the beam on the distribution of H2 and the formation of bubbles, here we use an equivalent dose rate of 1 e Å−2 s−1 (equivalent to 3.78 × 106 Gy s−1) for all simulations. To include the confinement effect of the constrained TEM liquid cell, the illuminated volume for TEM shown in Fig. 1A is surrounded with a constrained volume that is both chemically-inert and impermeable. The set-up for STEM in Fig. 1B considers each of these cells to be an individual pixel, and the pixels are arranged over the area of the liquid cell exposed to the electron beam. For all of the simulations, the irradiation in a cylindrical exposed zone at the centre of the cell was maintained for t = 104 s, corresponding to a typical in situ experiment.
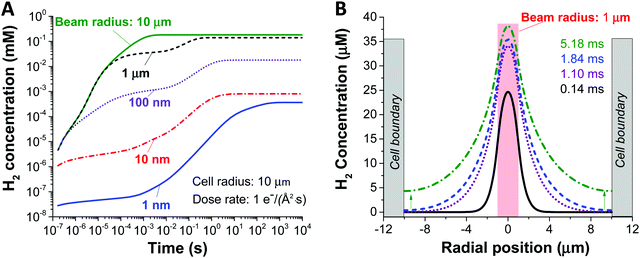
Fig. 2, shows the effect of increasing the beam size (1–1000 nm), as represented by the beam radius of the cylindrical geometry, relative to the constrained cell size (in this case 1 micron) on the concentration of H2 created by radiolysis (the concentration profiles of other chemical species such as H2O2, H3O+ (or H+), and O2 are shown in ESI,† Fig. S1). From these simulations we can immediately observe that the H2 concentration increases as a function of irradiation time for all beam sizes. Thus, reducing the irradiation time is a general solution for preventing the formation of hydrogen gas bubbles (this would mean a short dwell time for STEM and a short exposure time for TEM). Also, we observe that less H2 is produced for smaller beam size, simply because the total integrated dose is reduced for the smaller beam size under equivalent dose rate condition. Another noticeable feature from Fig. 2A is the appearance of a plateau regime for cases when the beam radius is smaller than the cell radius, and a longer time before the H2 concentration saturates. This can be understood as a confinement effect that is related to the speed of diffusion of the chemical species involved. When the beam size is the same as the cell size, there is a homogeneous distribution, no diffusion and a quick saturation in concentration. However, when the beam size is smaller than the cell size, diffusion is expected to arise due to the heterogeneous spatial concentration and the plateau corresponds to the time for the chemical species to diffuse enough and start interacting with the cell walls. Consequently, the concentration surges after this time, until it stabilises again when the steady state has been reached. The details of this interaction are shown in Fig. 2B.
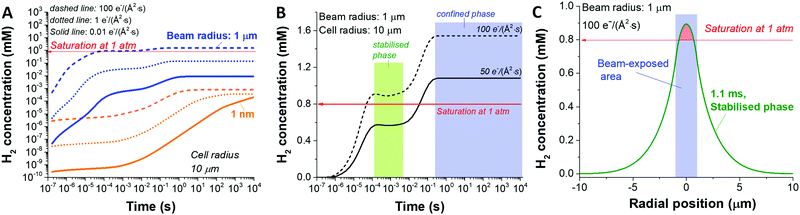
Another key parameter to consider in the formation of H2 bubbles is the dose rate. In Fig. 2 where the dose rate was defined as 1 e Å−2 s−1, the maximum concentration of H2 was observed to be below the gas saturation concentration of 0.79 mM at 1 atm. This saturation concentration value was calculated by applying Henry's law with the Henry's law constant for H2 of 0.00078 mol kg−1 bar−1.34 At a higher dose rate, however, the maximum H2 concentration may exceed the saturation concentration. For this particular analysis, we carried out simulations for 1 nm and 1000 nm beam radius by varying the electron dose rate from 0.001 to 100 e Å−2 s−1 with the same cell radius of 10 μm. At first glance, we see that more H2 is generated at higher dose rates in both cases (Fig. 3). Also, while the H2 concentration for the small beam size (1 nm) was kept below the H2 saturation concentration (0.8 mM at 1 atm) in the range of the applied dose rate, the concentration for the large beam size (1000 nm) exceeds the saturation concentration at the dose rate of 100 e Å−2 s−1. For a detailed analysis of the latter case, we compared the temporal concentration profiles for the beam radius of 1000 nm with the dose rate of 100 and 50 e Å−2 s−1. Shortly after the irradiation, the H2 concentration starts rising and becomes stabilised, subsequently contributing to the first plateau in Fig. 3; within this time frame, the H2 has not reached the system boundary by diffusion.16 Assuming that the system has a sufficient volume so that the H2 concentration does not reach the boundary in a given time frame, the concentration maximum in the stabilised regime can be a useful criterion regarding the formation of H2 bubbles. As indicated by higher values than H2 saturation concentration in the stabilised regime, H2 bubbles are more likely to be formed for the dose rate of 100 e Å−2 s−1 than that of 50 e Å−2 s−1. The spatial profile of the former (Fig. 3C) further implies that H2 bubble may form most probably at the beam centre where the concentration exceeds its saturation value of 0.8 mM at 1 atm.
So far, we have analysed the possibility of H2 bubble formation within the time frame of the stabilised regime and ignored the influence of confined cell volume. However, from an experimental point of view, we see the great importance of considering the size of the cell volume within a timeframe of the measurement. In particular cases like graphene liquid cells (system radius <1 μm)23,35 or commercially available liquid sample holder with microwells (<20 μm),36,37 the confined liquid volume is not large enough to assume that the concentration will stay in the stabilised regime. Fig. S2 (ESI†) shows three concentration profiles at the dose rate of 50 e Å−2 s−1 at different irradiation times considering the stabilised, confined, and transition regimes. Our data imply that the H2 bubble is less likely to be formed when a sufficiently large cell volume is applied, i.e. when the Vcell/Vbeam ≫ 1. However, when the cell volume is insufficient, H2 bubbles can be formed as the concentration exceeds its saturation value. Also, it is worth noting that there is a huge concentration surge during the transition from the stabilised to the confined phase.
This result may correspond to the formation of large explosive bubbles by Grogan et al.18 while investigating the liquid cell containing 20 mM HAuCl4 aqueous solution by STEM mode with a beam radius of 0.5–1.5 nm in the beam current range of 0.05–1.2 nA. In particular, they found that the bubble formation by STEM mode appeared on a time scale from minutes to hours after the beam exposure. However, the bubble formation in the TEM mode was on a second scale for the beam current range of 1–10 nA. According to our simulation, the onset of the confined phase depends greatly on the ratios of the beam size to the size of the liquid cell (Fig. S4, ESI†); for instance, in the case of fixed cell size, the confined phase appears earlier for the larger beams in TEM mode than that for the smaller beams in STEM mode. Considering a vast difference in the area ratios of ca. 10−5 and 10−12 for the TEM and STEM mode from work by Grogan et al.,18 their observed difference in bubble formation kinetics potentially indicate similar behaviour to the confinement effect in our work.
While the experimental set-up in the TEM is not to have the beam size the same as the cell size, we can understand many of the differences between broad beam TEM illumination vs focused probe STEM illumination from these simulations. If you consider the case where we have two pixels side by side, where each is illuminated with the same beam current/area, the chemical species will diffuse to the interface between the pixels in the same way giving rise to no mass flow across the pixel boundaries and in effect forming an impermeable barrier. The smaller the pixel size in TEM, the closer these impermeable barriers will be and the larger the effect of the homogeneous distribution of chemical species will be. In the STEM mode of operation, this can be reduced simply by increasing the distance between each sampling position, i.e. the ratio of beam size to beam hopping distance must be small. In the STEM mode of operation this is accomplished by simply turning down the magnification.
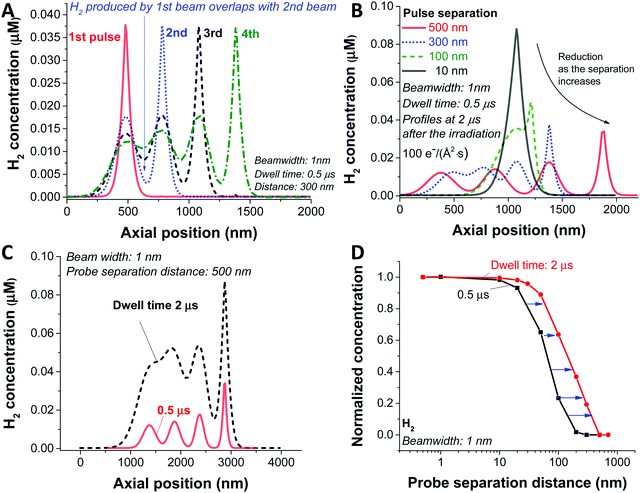
In the analysis so far, we have simulated a static beam condition. For realistic STEM applications, the beam will be moved with given pixel size and dwell time. To study the dynamic aspect of STEM imaging, we carried out a particular simulation with 4 beam positions at different spots and a dose rate of 100 e Å−2 s−1. For the simplicity of the simulation, we applied a slab symmetry by assuming 1 dimensional diffusion along the direction of the scan (schematic illustration in Fig. S3A, ESI†); therefore, from now on, the term ‘beamwidth’ will be used to represent the beam size. For this particular case, the H2 gas is generated as a result of beam overlap between the pulses which are in close proximity as shown in Fig. 4A with a probe separation distance of 300 nm for a dwell time of 0.5 μs. Since this overlaps occurs as a result of diffusion generated by the species between the pulses, the level of overlap is expected to be dependent on the probe separation distance. In Fig. 4B, the H2 concentration profiles with various separation distances are shown. In a case of 10 nm probe separation, we observe the highest H2 concentration due to direct overlap of consecutive pulses, similar to the static beam exposure with the large beam. As we increase the distance to 100 nm we observe beam overlap creating an additional shoulder, which increases the diffusion zone and creates a new reaction mixing zone between two consecutive probe areas. As a result, the maximum concentration of H2 gets lower as the probe distance increases as shown in Fig. 4B. Particularly, in the case of 500 nm probe separation, the high concentration of the reactants in the centre of the beam does not overlap and has time to diffuse away minimising the probability of generating new reactant mixing zone, and therefore, a less chance for H2 bubbling formation (Fig. S3B, ESI†).
Next, we investigated the influence of dwell time for the given 1 nm beam width, 100 e Å−2 s−1 dose rate, and probe separation of 500 nm (Fig. 4C). Similarly, to the distance of each consecutive probe scans, the longer the electron beam interacts with each pixel (the longer the dwell time), the higher concentration of radiolytic species which increases the probability of H2 generation and formation of mixing zones leading to poor baseline separation. As shown in Fig. 4D, the influence of dwell time and probe separation distance on the H2 concentration is summarised as the data were normalised by subtracting the non-overlapping portion of the H2 concentration (Fig. S3C, ESI†), which is the minimum value in the graph, and normalised by the maximum value.
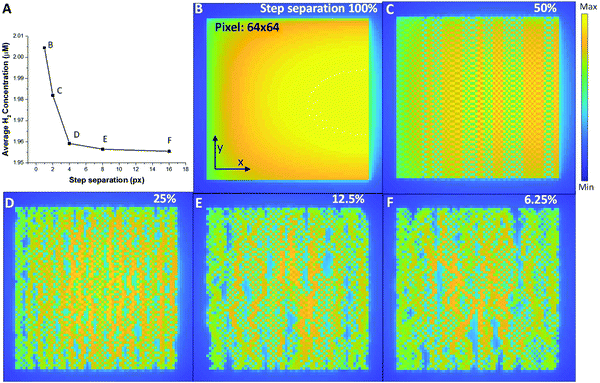
Now that we have the diffusion profiles for an individual probe location, we can simulate what the distribution of H2 looks like for a range of different STEM scans. Fig. 5 shows a series of STEM scans where the total dose and dose rate for the entire area was kept constant, and the only variable was the dose overlap, i.e. the distance between successive scan positions. In this analysis, the final H2 concentration in the imaging area is calculated by the sum of the concentration in each pixel divided by the number of pixels. Important in the control of the overall radiolysis chemistry in the cell, we can use this analysis to see the relative effects of diffusion compared to simply creation of the products (see methods section for the equations). A finite element method is used to simulate a 2-D plane to represent the product during the electron–water interaction. For the simulated images in Fig. 5, diffusion of H2 occurs at every coordinate in the 2-D plane simultaneously, and the product creation term occurs only at a coordinate [x,y] determined by the sampling scheme and input parameters. The images in Fig. 5 demonstrate that simply by moving the beam farther between pixels, i.e. increasing the spatial and temporal distance between connected sampling locations, the overall concentration of hydrogen can be reduced for identical dose and dose rates. Interestingly from Fig. 5A, we can determine a minimum separation above which the formation of H2 is significantly reduced (corresponding to the plateau region). Although this calculation is demonstrated for H2 production, each of the radiolysis products that is created will have a different profile based on creation, diffusion and conversion, so that the methodology described above can be used to determine a scan separation that will create one type of product preferentially over another.
We have simulated water radiolysis under various experimental (scanning) transmission electron microscope conditions, using reaction–diffusion equations to understand how the distribution of incoming fast electrons affects the overall reaction dynamic. Selecting one particular radiolysis product, hydrogen gas, allowed the analysis to identify the fundamental control parameters behind bubble formation (which can be extended to the other radiolysis products). Our data reproduces the well-known bubble control mechanism of keeping the illumination to a low dose rate or short irradiation time. Also, we found that H2 bubble formation has a higher probability when a large volume is illuminated compared to a small volume, indicating that a small probe STEM illumination may make it easier to avoid bubble formation completely. For the small probe illumination, our data show clear evidence that the proximity of probe positions and diffusion induced beam-overlap can increase the H2 gas concentration. For STEM, this means that the deleterious effect of beam radiolysis can be significantly reduced by working at lower magnification or using a sub-sampled imaging approach, e.g. compressed sensing.9 Using these models, we can predict the distribution of radiolysis products for a range of different illumination and sub-sampling conditions, allowing the beam to be used to create well-controlled reactive environments in the constrained in situ liquid cells used in (S)TEM. These controls can be applied to any liquid system (not just water) greatly increasing the number of chemical experiments that can be performed in the microscope. Furthermore, when adopting advanced elements such as beam broadening,38 more precise and subtle controls will also be available.
Methods
Simulation for liquid-beam interaction
Our simulation work was carried out based on the kinetic model developed by Schneider et al. considering 79 reactions and reaction rate constants as well as diffusion coefficients of each species.16 The details of the approach and the validation of their model can be found in ref. 16. The model by Schneider et al. assumes that the water acts as a solvent and mass of the water remains constant throughout the process. By solving the following reaction–diffusion equation, the concentration of various chemical species can be obtained as a function of time and space: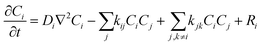 | (2) |
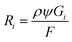 | (3) |
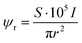 | (4) |
Electron dose rate calculation
The electron dose rate (e− (Å2 s)−1) was calculated from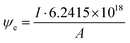 | (5) |
Conflicts of interest
The authors state no conflict of interest.Acknowledgements
This work was supported in part by the UK Faraday Institution under the Degradation (FIRG01), Recycling (FIRG05) and Characterisation (FIRG013) projects and by a Laboratory Directed Research and Development (LDRD) Program at the Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated by Battelle for the U.S. Department of Energy (DOE) under Contract DE-AC05-76RL01830.References
- N. de Jonge and F. M. Ross, Electron microscopy of specimens in liquid, Nat. Nanotechnol., 2011, 6, 695, DOI:10.1038/nnano.2011.161.
- E. Ruska, Beitrag zur übermikroskopischen Abbildung bei höheren Drucken, Kolloid-Z., 1942, 100(2), 212–219, DOI:10.1007/bf01519549.
- M. J. Williamson, R. M. Tromp, P. M. Vereecken, R. Hull and F. M. Ross, Dynamic microscopy of nanoscale cluster growth at the solid–liquid interface, Nat. Mater., 2003, 2(8), 532–536, DOI:10.1038/nmat944.
- J. M. Grogan, N. M. Schneider, F. M. Ross and H. H. Bau, The nanoaquarium: a new paradigm in electron microscopy, J. Indian Inst. Sci., 2012, 92(2), 295–308 Search PubMed.
- S. Thiberge, A. Nechushtan, D. Sprinzak, O. Gileadi, V. Behar, O. Zik, Y. Chowers, S. Michaeli, J. Schlessinger and E. Moses, Scanning electron microscopy of cells and tissues under fully hydrated conditions, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(10), 3346–3351, DOI:10.1073/pnas.0400088101.
- H. Zheng, R. K. Smith, Y.-W. Jun, C. Kisielowski, U. Dahmen and A. P. Alivisatos, Observation of single colloidal platinum nanocrystal growth trajectories, Science, 2009, 324(5932), 1309–1312 Search PubMed.
- T. J. Woehl, J. E. Evans, I. Arslan, W. D. Ristenpart and N. D. Browning, Direct in Situ Determination of the Mechanisms Controlling Nanoparticle Nucleation and Growth, ACS Nano, 2012, 6(10), 8599–8610, DOI:10.1021/nn303371y.
- D. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. De Yoreo, Direction-Specific Interactions Control Crystal Growth by Oriented Attachment, Science, 2012, 336(6084), 1014–1018, DOI:10.1126/science.1219643.
- B. L. Mehdi, A. Stevens, L. Kovarik, N. Jiang, H. Mehta, A. Liyu, S. Reehl, B. Stanfill, L. Luzi, W. Hao, L. Bramer and N. D. Browning, Controlling the spatio-temporal dose distribution during STEM imaging by subsampled acquisition: In situ observations of kinetic processes in liquids, Appl. Phys. Lett., 2019, 115(6), 063102, DOI:10.1063/1.5096595.
- M. T. McDowell, I. Ryu, S. W. Lee, C. Wang, W. D. Nix and Y. Cui, Studying the Kinetics of Crystalline Silicon Nanoparticle Lithiation with In Situ Transmission Electron Microscopy, Adv. Mater., 2012, 24(45), 6034–6041, DOI:10.1002/adma.201202744.
- B. L. Mehdi, A. Stevens, J. Qian, C. Park, W. Xu, W. A. Henderson, J. G. Zhang, K. T. Mueller and N. D. Browning, The Impact of Li Grain Size on Coulombic Efficiency in Li Batteries, Sci. Rep., 2016, 6, 34267, DOI:10.1038/srep34267.
- R. R. Unocic, L. Baggetto, G. M. Veith, J. A. Aguiar, K. A. Unocic, R. L. Sacci, N. J. Dudney and K. L. More, Probing battery chemistry with liquid cell electron energy loss spectroscopy, Chem. Commun., 2015, 51(91), 16377–16380, 10.1039/C5CC07180A.
- M. E. Holtz, Y. Yu, D. Gunceler, J. Gao, R. Sundararaman, K. A. Schwarz, T. A. Arias, H. D. Abruña and D. A. Muller, Nanoscale Imaging of Lithium Ion Distribution During In Situ Operation of Battery Electrode and Electrolyte, Nano Lett., 2014, 14(3), 1453–1459, DOI:10.1021/nl404577c.
- M. E. Holtz, Y. Yu, J. Gao, H. D. Abruña and D. A. Muller, In Situ Electron Energy-Loss Spectroscopy in Liquids, Microsc. Microanal., 2013, 19(4), 1027–1035, DOI:10.1017/S1431927613001505.
- B. Layla Mehdi, M. Gu, L. R. Parent, W. Xu, E. N. Nasybulin, X. Chen, R. R. Unocic, P. Xu, D. A. Welch, P. Abellan, J.-G. Zhang, J. Liu, C.-M. Wang, I. Arslan, J. Evans and N. D. Browning, In Situ Electrochemical Transmission Electron Microscopy for Battery Research, Microsc. Microanal., 2014, 20(2), 484–492, DOI:10.1017/S1431927614000488.
- N. M. Schneider, M. M. Norton, B. J. Mendel, J. M. Grogan, F. M. Ross and H. H. Bau, Electron–Water Interactions and Implications for Liquid Cell Electron Microscopy, J. Phys. Chem. C, 2014, 118(38), 22373–22382, DOI:10.1021/jp507400n.
- P. Abellan, T. J. Woehl, L. R. Parent, N. D. Browning, J. E. Evans and I. Arslan, Factors influencing quantitative liquid (scanning) transmission electron microscopy, Chem. Commun., 2014, 50(38), 4873–4880, 10.1039/C3CC48479C.
- J. M. Grogan, N. M. Schneider, F. M. Ross and H. H. Bau, Bubble and Pattern Formation in Liquid Induced by an Electron Beam, Nano Lett., 2014, 14(1), 359–364, DOI:10.1021/nl404169a.
- M. Spotheim-Maurizot, M. Mostafavi, T. Douki and J. Belloni, Radiation chemistry: from basics to applications in material and life sciences, EDP Sciences, 2008 Search PubMed.
- A. J. Elliot and D. R. McCracken, Computer modelling of the radiolysis in an aqueous lithium salt blanket: Suppression of radiolysis by addition of hydrogen., Fusion Eng. Des., 1990, 13(1), 21–27, DOI:10.1016/0920-3796(90)90028-5.
- M. A. Hill and F. A. Smith, Calculation of initial and primary yields in the radiolysis of water, Radiat. Phys. Chem., 1994, 43(3), 265–280, DOI:10.1016/0969-806X(94)90190-2.
- J. Biskupek, S. T. Skowron, C. T. Stoppiello, G. A. Rance, S. Alom, K. L. Y. Fung, R. J. Whitby, M. H. Levitt, Q. M. Ramasse, U. Kaiser, E. Besley and A. N. Khlobystov, Bond Dissociation and Reactivity of HF and H(2)O in a Nano Test Tube, ACS Nano, 2020, 14(9), 11178–11189, DOI:10.1021/acsnano.0c02661.
- C. Wang, T. Shokuhfar and R. F. Klie, Precise In Situ Modulation of Local Liquid Chemistry via Electron Irradiation in Nanoreactors Based on Graphene Liquid Cells, Adv. Mater., 2016, 28(35), 7716–7722, DOI:10.1002/adma.201602273.
- D. A. Muller, Structure and bonding at the atomic scale by scanning transmission electron microscopy, Nat. Mater., 2009, 8, 263, DOI:10.1038/nmat2380.
- W. Denk and H. Horstmann, Serial Block-Face Scanning Electron Microscopy to Reconstruct Three-Dimensional Tissue Nanostructure, PLoS Biol., 2004, 2(11), e329, DOI:10.1371/journal.pbio.0020329.
- J. P. Buban, Q. Ramasse, B. Gipson, N. D. Browning and H. Stahlberg, High-resolution low-dose scanning transmission electron microscopy, Microscopy, 2009, 59(2), 103–112, DOI:10.1093/jmicro/dfp052.
- P. Abellan, B. L. Mehdi, L. R. Parent, M. Gu, C. Park, W. Xu, Y. Zhang, I. Arslan, J.-G. Zhang, C.-M. Wang, J. E. Evans and N. D. Browning, Probing the Degradation Mechanisms in Electrolyte Solutions for Li-Ion Batteries by in Situ Transmission Electron Microscopy, Nano Lett., 2014, 14(3), 1293–1299, DOI:10.1021/nl404271k.
- N. D. Browning, J. P. Buban, M. Chi, B. Gipson, M. Herrera, D. J. Masiel, S. Mehraeen, D. G. Morgan, N. L. Okamoto, Q. M. Ramasse, B. W. Reed and H. Stahlberg, The Application of Scanning Transmission Electron Microscopy (STEM) to the Study of Nanoscale Systems, in Modeling Nanoscale Imaging in Electron Microscopy, ed. T. Vogt; W. Dahmen and P. Binev, Springer, US: Boston, MA, 2012, pp. 11–40 Search PubMed.
- K. H. Downing, Spot-Scan Imaging in Transmission Electron Microscopy, Science, 1991, 251(4989), 53–59 Search PubMed.
- A. Stevens, L. Luzi, H. Yang, L. Kovarik, B. L. Mehdi, A. Liyu, M. E. Gehm and N. D. Browning, A sub-sampled approach to extremely low-dose STEM, Appl. Phys. Lett., 2018, 112(4), 043104, DOI:10.1063/1.5016192.
- A. Stevens, H. Yang, L. Carin, I. Arslan and N. D. Browning, The potential for Bayesian compressive sensing to significantly reduce electron dose in high-resolution STEM images, Microscopy, 2013, 63(1), 41–51, DOI:10.1093/jmicro/dft042.
- T.-W. Huang, S.-Y. Liu, Y.-J. Chuang, H.-Y. Hsieh, C.-Y. Tsai, W.-J. Wu, C.-T. Tsai, U. Mirsaidov, P. Matsudaira, C.-S. Chang, F.-G. Tseng and F.-R. Chen, Dynamics of hydrogen nanobubbles in KLH protein solution studied with in situ wet-TEM, Soft Matter, 2013, 9(37), 8856–8861, 10.1039/C3SM50906K.
- Y. Tomo, Q.-Y. Li, T. Ikuta, Y. Takata and K. Takahashi, Unexpected Homogeneous Bubble Nucleation near a Solid–Liquid Interface, J. Phys. Chem. C, 2018, 122(50), 28712–28716, DOI:10.1021/acs.jpcc.8b09200.
- W. Kamolpornwijit and L. Liang, Investigation of gas production and entrapment in granular iron medium, J. Contam. Hydrol., 2006, 82(3), 338–356, DOI:10.1016/j.jconhyd.2005.10.009.
- J. M. Yuk, J. Park, P. Ercius, K. Kim, D. J. Hellebusch, M. F. Crommie, J. Y. Lee, A. Zettl and A. P. Alivisatos, High-Resolution EM of Colloidal Nanocrystal Growth Using Graphene Liquid Cells, Science, 2012, 336(6077), 61–64, DOI:10.1126/science.1217654.
- E. S. Pohlmann, K. Patel, S. Guo, M. J. Dukes, Z. Sheng and D. F. Kelly, Real-Time Visualization of Nanoparticles Interacting with Glioblastoma Stem Cells, Nano Lett., 2015, 15(4), 2329–2335, DOI:10.1021/nl504481k.
- A. Cameron Varano, A. Rahimi, M. J. Dukes, S. M. Poelzing, S. McDonald and D. F. Kelly, Visualizing virus particle mobility in liquid at the nanoscale, Chem. Commun., 2015, 51(90), 16176–16179, 10.1039/C5CC05744B.
- D. Nicholls, J. Lee, H. Amari, A. J. Stevens, B. L. Mehdi and N. D. Browning, Minimising damage in high resolution scanning transmission electron microscope images of nanoscale structures and processes, Nanoscale, 2020, 12(41), 21248–21254, 10.1039/D0NR04589F.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06369j |
| This journal is © the Owner Societies 2021 |