 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comment on “On the thermodynamic stability of bubbles, immiscible droplets, and cavities” by G. S. Manning, Phys. Chem. Chem. Phys., 2020, 22, 17523
Lasse
Makkonen
and
Tapio
Vehmas
 *
*
VTT Technical Research Centre of Finland, Box 1000, 02044 VTT, Espoo, Finland. E-mail: tapio.vehmas@vtt.fi; Tel: +358 207224618
First published on 25th May 2021
Abstract
In this comment, the thermodynamic analysis of the stability of nanobubbles is discussed in reference to the recent paper by Manning (G. S. Manning, On the Thermodynamic Stability of Bubbles,Immiscible Droplets, and Cavities, Phys. Chem. Chem. Phys., 2020, 22, 17523–17531). It is argued that Manning's critcism on the classical Epstein–Plesset model of bubble stability is unwarranted, and that the Young–Laplace-equation must be understood as a fundamental law of the pressure difference across a curved interface regardless of the reaction of the gas in the bubble. Consequently, the internal pressure and the radius of a bubble are inherently linked, so that the net force considered in Manning's stability analysis does not exist.
Recently in this journal, Manning1 presented a paper “On the thermodynamic stability of bubbles, immiscible droplets, and cavities” where he concluded that the Epstein–Plesset model of bubble dissolution is inapplicable and claimed to give a direct proof that nanobubbles are unstable if the surface tension is assumed independent of sphere radius. These conclusions were described as representing “a sharper understanding of the Laplace equation and the physics underlying it”. We find Manning's analysis and his interpretation of the Young–Laplace equation misleading and, therefore, wish to submit the following comments.
First, we would like to emphasize that Manning's stability analysis1 has very little to do with the Epstein–Plesset model,2 which deals with dissolution of gas from a bubble to the surrounding liquid. The Epstein–Plesset model is a diffusion calculation and does not take a stand on bubble stability criteria. Results similar to Epstein and Plesset were obtained by Lunggren and Eriksson,3 who made calculations related more specifically to nanosized bubbles.
Manning1 analyses the stability of a bubble from which no gas escapes. This, of course, rules out the applicability of the Epstein–Plesset diffusion model, which predicts stable bubbles when assuming zero gas solvability. Manning's1 argument is that, since the pressure gradient is discontinuous across the gas–liquid interface, the concentration gradient cannot be continuous, and, therefore, Henry's law does not relate the internal gas pressure of a bubble to the dissolved gas concentration just outside the bubble. However, such an assumption is not necessary for the calculations by Epstein and Plesset or Ljunggren and Eriksson. Rather, the assumption is that the system is in chemical equilibrium, i.e. “Full contact equilibrium prevails and the chemical potentials are the same everywhere”, as stated by Ljunggren and Eriksson.3
A theoretical framework of a bubble in chemical equilibrium was given by Ward et al.4 In order to derive equations for the bubble behaviour, four different chemical potentials must be considered. These are the chemical potential of water outside the bubble (μ1′), vapour pressure inside the bubble (μ1′′), dissolved gas concentration outside the bubble (μ2′) and pure gas pressure inside the bubble (μ2′′). These four chemical potentials can be derived from the standard chemical potentials of the water (μ01(P∞,T)) and gas (μ02(P′,T)):
| μ1′ = μ01(P∞,T) + ν1′(p0 − p∞) | (1) |
 | (2) |
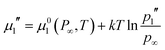 | (3) |
 | (4) |
In chemical equilibrium, chemical potential of the water and vapour must be equal. Chemical potential of the vapour inside the bubble reduces to the Kelvin factor η (eqn (5)). Moreover, the chemical potential of the gas phase is the same inside and outside the bubble (eqn (6)).
 | (5) |
 | (6) |
 | (7) |
According to Laplace–Young equation, the pressure inside the bubble depends on the surface tension σ and bubble radius r:
 | (8) |
 | (9) |
Our second comment concerns the fundamental understanding of the Young–Laplace equation. Manning1 refers to the basic thermodynamic derivation of the Young–Laplace equation. However, there exists also a mechanical derivation,5,6 the implications of which need to be understood. The normal stress balance for fluids meeting at an interface is
| ΔP = ∇·ñ = γ·H = γ(1/R1 + 1/R2) | (10) |
| ΔP = 2γ/R | (11) |
As pointed out above, the mechanical derivation of Young–Laplace equation has nothing to do with how the gas in a bubble behaves. Accordingly, the force exerted by the gas in the bubble to the liquid is not an active force that could affect the realization of eqn (11) in any way. It is a reaction force for the radial surface tensional force exerted on the bubble.
By the third law of Newton's classical mechanics, all forces occur in pairs such that, if one object exerts a force on another object, then the second object exerts an equal and opposite reaction force on the first.7 However, the terms ‘action’ and ‘reaction’ have the misleading suggestion of causality. It is, therefore, easy to think of the second force as being there because of the first, and even happening some time after the first. This is incorrect; the forces are simultaneous, and are there for the same reason.8
An essential ingredient of Manning's1 analysis is “the net force exerted by the surroundings of a bubble, including the surface, on the interior of the bubble”. Of that concept, he writes: “If this net force is directed inwards, the bubble shrinks. If it is directed outwards, the bubble expands. If it vanishes, the bubble is in a state of mechanical equilibrium. The Laplace equation, eqn (6), is the condition for vanishing net force. From this condition, we recognize that the net zero force is the resultant of two competing tendencies.” As pointed out above, this way of thinking is misleading. The action force and the reaction force are inherently linked and simultaneous, even in a dynamic situation. Therefore, no such net force, as postulated by Manning,1 can exist.
For the same reason, “an arbitrary constant pressure difference, independent of R”, used by Manning1 in the derivation of the stability condition, is an inappropriate concept. The pressure difference cannot be arbitrary, because it is set by eqn (11) exactly at all times.
Manning1 presents his eqn (2) for the change in the Helmholtz free energy F as
| dF = −PwdVw − PbdVb + γ(R) dA | (12) |
| dF = −ΔPdVb + γ(R)dA | (13) |
| dF/dR = −4πR2ΔP + 8πRγ(R) | (14) |
| γ(R) − R (dγ/dR) < 0 | (15) |
Manning's1eqn (2), i.e. our eqn (12) above, includes both the term γ(R)dA and the term −PbdVb, as if they were separate free energies. This represents double-counting of the surface free energy of the bubble. A way to demonstrate this error is to insert eqn (11) into eqn (14), giving dF/dR = 0. This suggests that the free energy of a volume of liquid including a bubble is independent of the size of the bubble. Clearly, this cannot be correct.
When the erroneous second term on the right hand side of eqn (12) is removed, the variable −ΔP will change to the variable Pw, and the stability criterion in eqn (15) changes to
| PwR + γ(R) + R(dγ/dR) > 0 | (16) |
Notwithstanding the criticism above, we agree with Manning1 in his assertion that the “Laplace Pressure Bubble Catastrophe” has no physical basis. A high pressure inside a bubble cannot logically be the cause of dissolving it, because in that case the pressure should decrease when the gas in the bubble dissolves and the bubble gets smaller while, according to the Young–Laplace equation, the pressure then increases. The bubble stability problem must be solved by considering the thermodynamics of a complete liquid, gas, vapour system while properly treating the free energy of the interface, and considering the energy barriers that may lead to metastable nanobubbles.11
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Academy of Finland, grant no. 297278.References
- G. S. Manning, On the Thermodynamic Stability of Bubbles, Immiscible Droplets, and Cavities, Phys. Chem. Chem. Phys., 2020, 22(31), 17523–17531, 10.1039/D0CP02517H.
- P. S. Epstein and M. S. Plesset, On the Stability of Gas Bubbles in Liquid-Gas Solutions, J. Chem. Phys., 1950, 18(11), 1505–1509, DOI:10.1063/1.1747520.
- S. Ljunggren and J. C. Eriksson, The Lifetime of a Colloid-Sized Gas Bubble in Water and the Cause of the Hydrophobic Attraction, Colloids Surf., A, 1997, 129–130, 151–155, DOI:10.1016/S0927-7757(97)00033-2.
- C. A. Ward, P. Tikuisis and R. D. Venter, Stability of Bubbles in a Closed Volume of Liquid-gas Solution, J. Appl. Phys., 1982, 53(9), 6076–6084, DOI:10.1063/1.331559.
- L. Makkonen, On the Methods To Determine Surface Energies, Langmuir, 2000, 16(20), 7669–7672, DOI:10.1021/la990815p.
- L. Dufour and R. Defay, Thermodynamics of Clouds, Acad. Press., New York-London, 1963, p. 69 Search PubMed.
- J. R. Taylor, et al., Classical Mechanics, University Science Books, 2005 Search PubMed.
- D. E. Brown, Students’ Concept of Force: The Importance of Understanding Newton's Third Law, Phys. Educ., 1989, 24(6), 353 CrossRef.
- Y. A. Lei, T. Bykov, S. Yoo and X. C. Zeng, The Tolman Length: Is It Positive or Negative?, J. Am. Chem. Soc., 2005, 127(44), 15346–15347 CrossRef CAS PubMed.
- S. Burian, M. Isaiev, K. Termentzidis, V. Sysoev and L. Bulavin, Size dependence of the surface tension of a free surface of an isotropic fluid, Phys. Rev. E, 2017, 95, 062801, DOI:10.1103/PhysRevE.95.062801.
- T. Vehmas and L. Makkonen, Metastable Nanobubbles, ACS Omega, 2021, 6, 8021–8027, DOI:10.1021/acsomega.0c05384.
| This journal is © the Owner Societies 2021 |
