X-ray stability and degradation mechanism of lead halide perovskites and lead halides

Abstract

Lead halide perovskites have become a leading material in the field of emerging photovoltaics and optoelectronics. Significant progress has been achieved in improving the intrinsic properties and environmental stability of these materials. However, the stability of lead halide perovskites to ionising radiation has not been widely investigated. In this study, we investigated the radiolysis of lead halide perovskites with organic and inorganic cations under X-ray irradiation using synchrotron based hard X-ray photoelectron spectroscopy. We found that fully inorganic perovskites are significantly more stable than those containing organic cations. In general, the degradation occurs through two different, but not mutually exclusive, pathways/mechanisms. One pathway is induced by radiolysis of the lead halide cage into halide salts, halogen gas and metallic lead and appears to be catalysed by defects in the perovskite. The other pathway is induced by the radiolysis of the organic cation which leads to formation of organic degradation products and the collapse of the perovskite structure. In the case of Cs_0.17FA_0.83PbI₃, these reactions result in products with a lead to halide ratio of 1 : 2 and no formation of metallic lead. The radiolysis of the organic cation was shown to be a first order reaction with regards to the FA⁺ concentration and proportional to the X-ray flux density with a radiolysis rate constant of 1.6 × 10⁻¹⁸ cm² per photon at 3 keV or 3.3 cm² mJ⁻¹. These results provide valuable insight for the use of lead halide perovskite based devices in high radiation environments, such as in space environments and X-ray detectors, as well as for investigations of lead halide perovskites using X-ray based techniques.

---

Introduction

The invention of lead halide perovskite solar cells about a decade ago has been a revolution in the field of emerging photovoltaics due to their low cost starting materials,¹ excellent optoelectronic properties,² and simple deposition techniques.¹ Lead halide perovskites emerged in 2009 from the field of dye-sensitised solar cells with the usage of MAPbI₃ as a photo absorber, where MA is methylammonium (CH₃NH₃⁺).³ During the last decade lead halide perovskite solar cells have developed into their own research field with efficiencies comparable to that of silicon solar cells.⁴ This has, in part, been achieved through the development of significantly more complex and stable compositions such as Cs_XFA_YMA_1−X−YPbBr_ZI_1−Z, where FA is formamidinium (NH₂CHNH₂⁺).⁵ However, the long-term stability of these materials remains a significant obstacle for commercialisation. Lead halide perovskites are sensitive to high humidity, elevated temperature, and oxygen, especially during illumination.⁶ These are issues that need to be resolved before the widespread implementation of commercial lead-halide perovskite devices.

For certain applications, the stability to ionising radiation becomes one of the most important factors. One such application is the deployment of solar cells for powering spacecrafts where the requirements are quite different from terrestrial deployment. Most significant being the lack of atmosphere (and therefore no moisture or oxygen), extreme temperature variations, and of course significantly higher exposure to ionizing radiation. Another example is the usage as radiation detectors, where early studies indicate that the performance of wide bandgap lead halide perovskites is competitive to currently used materials,⁷ and with the additional benefit that they can be deposited on flexible substrates.⁸ The most promising candidates for this kind of applications appear to be MAPbBr₃^9,10 and CsPbBr₃.^11–13

Studies using high energy photon (i.e. gamma/X-rays) or proton irradiation have been carried out on perovskite solar cells. The perovskites demonstrated remarkable radiation resistance, often better than for the substrate and significantly better than for silicon, partially attributed the perovskites self-healing ability.^14–17 Boldyreva et al. studied a large number of hybrid organic–inorganic and inorganic perovskites composition under up to 500 krad of 662 keV gamma rays. They found that inorganic perovskites as well as MAPbI₃ have excellent radiation hardness and self-healing ability. More complex mixed cation perovskites showed poorer radiation stability which was attributed to the inhibition of the reactions responsible for self-healing.

Several studies have also been carried out on the effect of electron radiation with variations in perovskite composition, temperature, and electron energy. Both hybrid organic–inorganic (MAPbBr₃/MAPbI₃) and inorganic (CsPbBr₃/CsPbI₃) lead halide perovskite have been shown to rapidly degrade under electron beam irradiation. Electron beam irradiation has been found to induce the formation of nanometre sized metallic lead particles (Pb⁰) and voids in the lead-halide crystal.^18,19 However, the direct effect of high-energy photons, i.e. X-ray and gamma radiation, on perovskites structure and composition is still relatively unknown. The effects are expected to be similar to those from electron beams due to the generation of, and damage induced by, secondary electrons. The X-ray stability of these materials is highly relevant for the interpretation of the results from X-ray photoelectron spectroscopy (XPS) and other X-ray based techniques commonly used for characterisation of lead halide perovskites. Knowledge of the indicators of degradation also allows researchers to detect X-ray damage, and understanding the degradation mechanisms could aid in designing experiments to minimize the effect of X-rays.

X-ray damage during XPS measurements on lead-halide perovskite has previously been reported. MAPbI₃ and FA_0.83MA_0.17PbBr_0.51I_2.49 perovskites have been showed to form Pb⁰ during X-ray irradiation at both elevated temperatures²⁰ and at room temperature.^21,22 Pb⁰ has also been observed before X-ray irradiation of perovskite^23–25 as well as been shown to form during visible light illumination.^26,27 Furthermore, most lead halide perovskite compositions contain an organic component which is expected to be sensitive to ionizing radiation.^28,29

The aim of this study was to investigate how X-ray radiation affects the composition and electronic properties of both hybrid organic–inorganic and inorganic lead halide perovskites and to determine how the degradation depends on X-ray fluence or flux density. The study was carried out using synchrotron light sources where the X-ray flux density and photon energy can be carefully controlled. This allows the X-rays to be used as a probe by detecting the outgoing photoelectrons using hard X-ray photoelectron spectroscopy (HAXPES) which gives insight concerning changes in both chemical and electronic properties.

Experimental section

The perovskites and lead halide thin film samples were deposited on FTO/TiO₂ substrates prepared in the following way: the FTO glass was cleaned in an ultrasound bath in three 30 minutes steps with RBS 50 detergent, ethanol, and finally acetone. The substrates were subsequently treated in a UV-ozone cleaner for 10 minutes. An electron transport layer of TiO₂ was deposited on the cleaned FTO substrates using spray pyrolysis. The spray solution consisted of ethanol, acetyl acetone and titanium diisopropoxide (30% in isopropanol) in the proportions of 90 : 4 : 6 by volume with air at a base pressure of 1 bar as a carrier gas. The FTO substrates were heated to 450 °C on a hotplate and kept at that temperature for 15 minutes prior to the spraying. A 10 ml of spray solution was used to cover 200 cm² of substrates giving a compact layer of anatase with a thickness of around 20–30 nm. On top of the compact layer, a mesoporous scaffold of TiO₂ nanoparticles was deposited by spin-coating. TiO₂ paste (30 NR-D) and was dissolved in ethanol at a concentration of 150 mg ml⁻¹. On each substrate (1.5 × 2.5 cm), 50 μl of the TiO₂ solution was applied and spin-coated at 4000 rpm, with an acceleration of 2000 rpm s⁻¹, for 10 s. Both the compact and mesoporous TiO₂ layers were sintered at 450 °C in air on a hot plate/oven for 30 minutes after deposition and then slowly cooled to ambient temperature.

Perovskite precursor solutions were prepared in a glovebox with an argon atmosphere. Stock solutions of PbI₂ and PbBr₂ were prepared in advance, whereas the final precursor solutions were prepared just before perovskite deposition with anhydrous DMF : DMSO in the proportion 4 : 1 used as the solvent. The PbI₂ and PbBr₂ solutions were close to the saturation point, and to ensure that the lead salts were completely dissolved, the solutions were heated under stirring on hotplate at 100 °C for 20 min, and then cooled down to room temperature just before use. For the perovskite with composition FA_0.83MA_0.17PbBr_0.51I_2.49 (MAFA-Mix), two master solutions were prepared, (a) 1.35 M PbI₂ and 1.24 M FAI, (b) 1.35 M PbBr₂ and 1.24 M MABr. Those were mixed in the proportion a : b = 83 : 17 to give the final precursor solution. For the perovskite with the composition Cs_0.17FA_0.83PbBr_0.51I_2.49 (CsFA-Mix), three master solutions where prepared: (a) 0.9 M PbI₂ and 0.9 M FAI, (b) 0.9 M PbBr₂ and 0.9 M FABr, (c) 0.9 M PbI₂ and 0.9 M CsI. Those were mixed in the proportion a : b : c = 66 : 17 : 17. The CsI does not dissolve easily and therefore solution (a) and (b) where poured into (c) in the right proportion. For the perovskite with composition Cs_0.17FA_0.83PbI₃ (CsFA-I), two master solutions were prepared, (a) 0.9 M PbI₂ and 0.9 M FAI, (b) 0.9 M PbI₂ and 0.9 M CsI in a proportion a : b = 83 : 17. As for CsFA-Mix, solution (a) was added to solution (b). In the case of the pure inorganic CsPbBr₃ perovskite, the final solution was prepared by dissolving 0.33 mol of PbBr₂ and 0.40 mol of CsBr in Dimethyl sulfoxide (DMSO) (121 mg ml⁻¹ PbBr₂ and 85.7 mg ml⁻¹ CsBr). The solutions were heated under stirring on a hotplate at 50 °C for 30 min, after that the solutions were cooled down and filtered through a 0.22 μm PTTA filter right before the deposition. The MA and FA salts were bought from Dyesol, the lead salts from TCI, solvents from Fisher, and the remaining chemicals from Sigma Aldrich. All chemicals were used as received without further treatment.

The perovskite precursor solutions were spin-coated in a glove box with an inert atmosphere. For the MAFA-Mix and CsFA-Mix 35 μl precursor solution and for the CsFA-I and CsPbBr₃ 75 μl precursor solution was spread over the substrate (1.5 × 2.5 cm), which thereafter was spin-coated using a two-step program. The first step was a spreading step using a rotation speed of 1000 rpm with an acceleration of 200 rpm s⁻¹ for 10 s. That step was immediately (without pause) followed by the second step where the films were spun at 4000 rpm for 20 s using an acceleration of 2000 rpm s⁻¹ for the FA_0.83MA_0.17PbBr_0.51I_2.49 (MAFA-Mix) and Cs_0.17FA_0.83MA_0.17PbI₃ (CsFA-I) perovskite and 6000 rpm for 15 s using an acceleration of 2000 rpm s⁻¹ for the Cs_0.17FA_0.83PbBr_0.51I_2.49 (CsFA-Mix) perovskite. During the second step, when approximately 5 seconds of the program remained, 100 μl of anhydrous chlorobenzene was dropped on the spinning film with a handheld automatic pipette. This last step, known as the anti-solvent method, has a large impact on film morphology. Directly after spin-coating, the films were placed on a hotplate at 100 °C where they were annealed for 30–70 min. The pure inorganic CsPbBr₃ perovskite was spin-coated using the same two steps program described previously but without the use of the anti-solvent method. PbI₂ and PbBr₂ thin films samples were prepared by spin-coating 0.8 M solutions of the materials in DMF using a one step program and a rotation speed of 3500 rpm with an acceleration of 3500 rpm s⁻¹ for 20 s. This was followed by 30 min of annealing at 70 °C.

The measurements were carried out on 3 different occasions, twice at the GALAXIES beamline at the SOLEIL synchrotron³⁰ and once at the I09 beamline at the Diamond light source.³¹ All the measurements were carried out at a photon energy of 3000 eV. The X-ray flux density was controlled by transmission filters at the GALAXIES beamline and by detuning the undulator at the I09 beamline. All measurements were carried out at room temperature and at pressures below 10⁻⁹ mbar. The average X-ray flux densities were estimated from the maximum photon flux, the ring current, the spot size, and the incidence angle to the sample. To cover a greater range of intensities, the X-ray flux densities were varied exponentially. The probing depth of the HAXPES measurements was calculated to be 19.3 nm for the valence band and 15.6 nm for the deepest core levels (Cs3d and I3d).³²

At the I09 beamline, Diamond light source, the X-rays were generated using the U27 undulator and monochromated using a Si(111) double-crystal monochromator with a secondary monochromator using back-reflecting Si(111), Si(011) and Si(001) channel cuts. The beam was defocused in order to reduce the X-ray flux density. The maximum intensity was estimated to 1.0 × 10¹³ photons per s and the defocused beam forms a circle with a diameter of 300 μm, giving it an area of 70 700 μm². However, the beam hits the sample at a grazing angle of 11 degrees resulting in a spot size of 37 000 μm² and an actual flux density of about 2.7 × 10¹⁵ photons per s per cm². The intensity was reduced by detuning the undulator gap, resulting in a lower X-ray intensity as measured by the mirror current, see Table S1 (ESI†).

At the GALAXIES beamline at the SOLEIL synchrotron, the measurements were carried out at two different occasions, and the synchrotron was operating at two different modes and with two different ring currents: 8 bunch mode with a ring current of 100 mA and hybrid mode with a ring current of 450 mA. The full beam intensity was estimated to 3.4 × 10¹³ and 7.6 × 10¹² photons per s at ring currents of 450 and 100 mA, respectively. The beam has a size of about 30 μm (H) × 80 μm (V), giving an area of 1885 μm². However, sample is at an angle of 2 degrees relative to the incoming beam which increases the spot size to 54 000 μm². This results in a flux density of 6.3 × 10¹⁶ and 1.40 × 10¹⁶ photons per s per cm² at a beam current of 450 and 100 mA, respectively. The beam intensities were reduced using the transmission filters available at the beamline, resulting in the intensities shown in Table S2 (ESI†).

The photoelectrons at both beamlines were detected using a Scienta Omicron EW4000 HAXPES hemispherical analyser. The measured core levels were fitted using a pseudo-Voigt function with a polynomial, a Herrera-Gomez,³³ and a Shirley background³⁴ as deemed appropriate. The intensity of the core levels derived by the Voigt fit was normalised by photoionization cross section,³⁵ and an homogeneous distribution was assumed to attain the relative fractions of the different species. However, due to the exponential decrease in the escape probability of the photoelectrons, the atomic density obtained is dominated by the surface layer and for non-homogeneous materials, this will affect the obtained values.

The X-rays and secondary radiation will affect the samples mainly in three ways: through ionisation (e.g. bond breaking), the excitation of charge carriers, and by heating. Due to the small spot sizes used, no significant heating is expected as even the highest X-ray intensities (672 mW cm⁻²) would increase the temperature by less than 3 °C, see ESI† for details. The excitation of charge carries from the X-rays and the secondary radiation could, however, be significant as the X-ray intensities approach or even exceed an irradiance of 100 mW cm⁻² (2.0 × 10¹⁵ photons per s per cm² at 3000 eV), i.e. the same power as 1 sun illumination.

Results and discussion

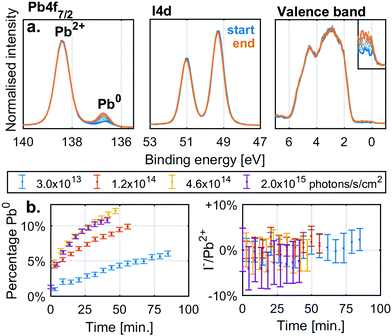
Before investigating the detailed effect of X-rays on two specific, single anion lead halide perovskites, we studied the simpler lead halide compounds and general degradation trends in mixed cation and anion perovskites. Fig. 1a shows the changes in the Pb4f_7/2 and I4d core levels as well as the valence band of a thin film sample of PbI₂ under X-ray irradiation with a flux density of 4.6 × 10¹⁴ photons per s per cm². Initially there is a single Pb4f signal associated with Pb²⁺ at 138.4 eV while the I4d spectra show a single spin orbit split doublet associated with I⁻ (I4d_5/2 at 49.3 eV). However, during irradiation a new Pb4f signal associated with Pb⁰ appears at 136.6 eV with a Fermi edge signal appearing in the valence band. The I4d spectra show no new signals during X-ray irradiation and no clear shift or intensity changes relative to the Pb4f signal coming from Pb²⁺. Equivalent measurements carried out at additional X-ray intensities are supplied in the ESI† (Fig. S2a).

Fig. 1 (a) The Pb4f, I4d and valence band (Fermi edge enlarged) spectra recorded for a PbI₂ sample at an X-ray flux density of 4.6 × 10¹⁴ photons per s per cm² as a function of time (blue: start, orange: end). Energy calibrated and intensity normalised against the Pb²⁺ component of Pb4f. Measured at the I09 beamline at the Diamond light source with a photon energy of 3000 eV. (b) The contribution of Pb⁰ to the total Pb4f signal and I⁻/Pb²⁺ signal ratio relative to the initial ratio as a function of time at different X-ray flux densities.

Fig. 1b shows the percentage of the total Pb4f signal intensity associated with the Pb⁰ signal (left) and the relative change in the I⁻/Pb²⁺ ratio relative to the initial value (right). The values were determined from curve fitting of the individual spectra as a function of time. The fraction of Pb⁰ increases with time and with a higher rate at higher X-ray flux densities, but there is no significant change in the I⁻/Pb²⁺ ratio with irradiation. Similar behaviour was observed for PbBr₂ (Fig. S2c and d, ESI†). X-Ray irradiation of lead halides (PbI₂ and PbBr₂) appears to induce the formation of Pb⁰ but very little change in the halide/Pb²⁺ ratio indicating the loss of halide (I⁻ or Br⁻) in relation to total lead. This agrees with the following reaction

PbX₂(s) → Pb⁰(s) + X₂(g)

where X is I or Br and which has previously been observed in lead halides under excitation with visible light.^26,27,36 At the surface under vacuum conditions the halogens (I₂ or Br₂) would then escape into vacuum as gasses leaving Pb⁰ and any remaining lead halide.

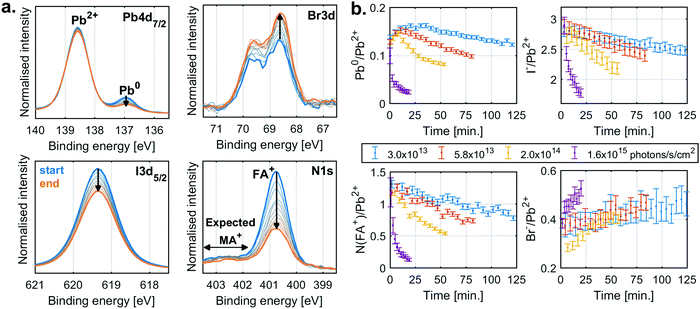
The behaviour for typical mixed anion and cation perovskite compositions under X-ray irradiation becomes significantly more complex, suggesting several competing reactions. Fig. 2a shows the changes in core level spectra for such a perovskite thin film with a composition of FA_0.83MA_0.17PbBr_0.51I_2.49 (MAFA-Mix), during X-ray irradiation with a flux density of 2.0 × 10¹⁴ photons per s per cm². The Pb4f_7/2 signal shows two contributions, one peak at 138.6 eV associated with Pb²⁺ and one peak at 137.0 eV associated with Pb⁰. Initially, there is a significant fraction of Pb⁰, most likely formed during sample fabrication²³ or due to exposure to light^26,27 afterwards. During X-ray exposure we observe a decrease in the relative Pb⁰ concentration. Simultaneously, we see a decrease in FA⁺ and I⁻ and an increase in Br⁻. This is quantified by the N1s signal at 400.8 eV, attributed to the formamidinium (FA⁺) cation, and the I3d_5/2 component at 619.3 eV, attributed to I⁻, which decrease significantly in intensity, while the Br3d signal at 68.6 eV, attributed to Br⁻, increases. We would also expect a signal from the N1s core level of methylammonium (MA⁺) cation at around 402.5 eV. However, due to the low nitrogen concentration, we are unable to reliably quantify this species.

Fig. 2 (a) The Pb4f_7/2, N1s, I3d_5/2 and Br3d spectra of recorded for a MAFA-Mix sample at an X-ray flux density of 2.0 × 10¹⁴ photons per s per cm² as a function of time (blue: start, orange: end) energy calibrated and intensity normalised against Pb²⁺ component of Pb4f. Measured at the GALAXIES beamline at SOLEIL synchrotron, ring current of 100 mA, with a photon energy of 3000 eV. (b) The contribution of Pb⁰/Pb²⁺, N(FA)/Pb²⁺, I⁻/Pb²⁺, Br⁻/Pb²⁺ ratio as a function time at different X-ray flux densities.

The detailed analysis of measurements carried out at several X-ray flux densities (Fig. S3, ESI†) shows that the Pb⁰ contribution initially increases but then decreases, with the decrease occurring earlier and faster at higher X-ray flux densities. Simultaneously, the N(FA⁺)/Pb²⁺ ratio decreases from about 1.3 to almost 0.1, while the I⁻/Pb²⁺ ratio decreases from 2.8 to 1.8, and the Br⁻/Pb²⁺ ratio increases only slightly. Similar behaviour was also observed for measurements of a perovskite with a composition Cs_0.17FA_0.83PbBr_0.51I_2.49 (CsFA-Mix) but with the difference that no initial formation of Pb⁰ was observed (Fig. S4, ESI†).

To summarise, the MAFA-Mix initially show a significant fraction of Pb⁰ which increases at the start of X-ray irradiation similar to what was observed for the pure lead halides. As the X-ray exposure continues, there is, however, a reversion in the trend and with a significant decrease in Pb⁰. There is simultaneously loss of both FA⁺ and I⁻. This would suggest radiolysis of FA⁺ and the degradation of the perovskite. There is also an increase in Br⁻, which could be related to ion movement or phase segregation.^37–40 The behaviour of MA⁺ is unknown, which further complicates the analysis. Overall, this suggests several competing reactions.

The mechanisms and kinetics of the cation radiolysis and Pb⁰ formation can be investigated in detail, by exploration of similar systems where some processes (such as phase segregation) cannot occur. We therefore explored the behaviour of two perovskites with simpler compositions, i.e. the hybrid organic–inorganic perovskite Cs_0.17FA_0.83PbI₃, referred to as CsFA-I, and the inorganic perovskite CsPbBr₃. Both perovskite compositions are known to be relatively stable, in part due to the exclusion of MA⁺, which is thought of as a degradation trigger, and because they contain only one type of halide, preventing halide phase-segregation. Furthermore, each core level can be clearly assigned to one perovskite component in the analysis, which enables us to follow the evolution of each ion in the perovskite structure.

X-ray degradation of hybrid organic–inorganic Cs_0.17FA_0.83PbI₃

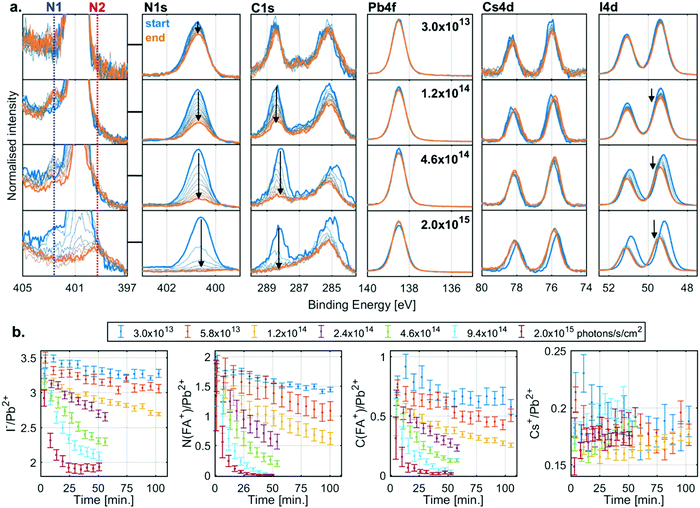
The evolution of the core level spectra of the CsFA-I sample during irradiation at different X-ray flux densities is shown in Fig. 3a. The Pb4f_7/2 core level spectra show no initial Pb⁰, and no formation of it either (expected between 136 and 138 eV). The presence of Cs⁺ is observed through the Cs4d core level, which shows little change in intensity during X-ray irradiation. On the other hand, the intensity of the I4d core level decreases during irradiation. However, the most significant changes are in the C1s and N1s core levels. The C1s core levels show an adventitious carbon signal at about 285.0 eV and an FA⁺ signal at 288.5 eV with the corresponding FA⁺ signal in the N1s core level being found at about 400.7 eV. During irradiation we observe a decrease in intensity of both FA⁺ signals. While the intensity only drops by a small amount for low flux densities, these changes occur faster with increasing flux densities with the FA⁺ signal intensity decreasing to zero at the highest X-ray flux density.

Fig. 3 (a) The N1s, C1s, Pb4f, Cs4d and I4d spectra recorded for a CsFA-I sample at different X-ray flux densities function of time (blue: start, orange: end) energy calibrated and intensity normalised to the Pb²⁺ component of Pb4f. A zoomed-in version of the N1s spectra showing the formation of two new nitrogen species, one higher binding energy (N1) and one lower binding energy (N2). Measured at the I09 beamline at the Diamond light source with a photon energy of 3000 eV. (b) The I⁻/Pb²⁺ (left), N(FA⁺)/Pb²⁺ (middle left), C(FA⁺)/Pb²⁺ (middle right) and Cs⁺/Pb²⁺ (right) ratio of a CsFA-I samples as a function of time at different X-ray flux densities.

In addition to the decreases in the FA⁺ signals, we also observe two new nitrogen signals (marked N1 and N2) during irradiation. The first new nitrogen signal (N1) appears early during irradiation at about 402.6 eV but disappears over time, which is most clearly seen at higher X-ray flux densities. The second new nitrogen signal (N2) appears at higher X-ray flux densities at about 399.6 eV and appears to stem from a less volatile species, as it remains even after all the FA⁺ has degraded, most clearly seen at the highest flux density. In addition to the changes in intensity, there is also a shift in the position of the I4d and Cs4d core levels relative to Pb²⁺ during irradiation, which indicates a change in the chemical environment. However, the exact nature of these shifts is difficult to determine as will be discussed below.

Measurements carried out at additional X-ray flux densities (Fig. S5, ESI†) show similar trends as Fig. 3a. All the core level spectra were curve fitted to obtain quantitative information. Fig. 3b shows the resulting I⁻/Pb²⁺ (left), N(FA⁺)/Pb²⁺ (middle left), C(FA⁺)/Pb²⁺ (middle right) and Cs⁺/Pb²⁺ (right) intensity ratios as a function of irradiation time. During X-ray irradiation with the highest flux densities, the I⁻/Pb²⁺ ratio decreases from about 3.5 to about 2.0, the N(FA⁺)/Pb²⁺ ratio decreases from about 1.8 to close to 0, the C(FA⁺)/Pb²⁺ ratio decreases from about 0.8 to close to 0, while the Cs⁺/Pb²⁺ stays relative constant around 0.2. These ratios indicate that the degradation of the perovskite results in PbI₂ that remains in the film and the loss of almost all of the organic component, with the volatile components leaving as gas into vacuum.

Typically, variations in binding energies would be used for assignment of changes in chemical states. However, binding energies of semiconductors/insulators are often energy calibrated with respect to the position of the Fermi level in the band gap which can vary significantly, especially if the defect density varies as a consequence of irradiation. A useful approach is to use the relative binding energy of the core levels, which we refer to as core-to-core difference, and which is largely independent of changes in the Fermi level. Using this metric, we find that the core-to-core difference of Pb4f (Pb²⁺) to I4d (I⁻) of both PbI₂ and CsFA-I are almost identical (Table S4, ESI†). Since we observe a shift of the I4d (I⁻) position relative to the Pb4f (Pb²⁺) during the degradation, this suggest that we are not forming crystalline PbI₂. Furthermore, at these X-ray flux densities it should degrade by forming Pb⁰ similarly to the pristine PbI₂ films, but we do not observe any traces of Pb⁰. On the contrary, the MAFA-Mix and CsFA-Mix samples show a decrease in the amount of Pb⁰ during irradiation, not an increase, suggesting a reaction that consumes Pb⁰ faster than it is formed.

A similar process allowed encapsulated MAPbI₃ to reform after decomposition under gamma radiation as proposed by Boldyreva et al.¹⁵ The new nitrogen species observed during radiolysis of the organic cation are very likely, in part, responsible for this self-healing process. Radiolysis of ammonium halide salts and alkylammonium halide salts has been shown to result in the production of halide containing radicals.^41,42 Some of these degradation products could likely react with Pb⁰, reforming the Pb²⁺, and even remain bound to the film resulting in a more amorphous PbI₂. This could also help passivate defects and slowing the degradation of PbI₂ to Pb⁰. Regardless, even if all the FA⁺ at the surface is decomposed, there is likely ongoing FA⁺ decomposition in the bulk that could help prevent the formation Pb⁰.

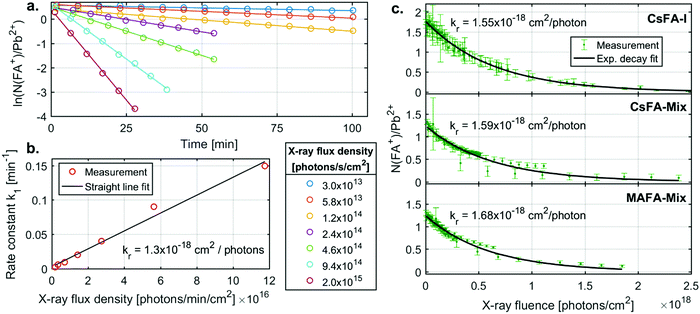
We now turn to the specific kinetics of the radiolysis of the FA⁺ cation. The N(FA⁺)/Pb²⁺ ratios can be shown to decrease exponentially with X-ray fluence (number of photons absorbed per area sample). This is a first order reaction with regards to the FA⁺ concentration and the X-ray flux density. The first order behaviour with regards to the FA⁺ concentration is observed through plotting the logarithm of (N(FA⁺)/Pb²⁺) ratio vs time (Fig. 4a). These graphs give straight lines from which first order rate constants (k₁) with units of min⁻¹ can be extracted for different X-ray flux densities. These rate constants are proportional to the X-ray flux density (Fig. 4b) and an overall radiolysis rate constant (k_r) with units of cm² per photon can then be extracted. This constant can also be determined by fitting a plot of the chemical ratios (R) vs. the X-ray fluence (photons per cm²) to an exponential decay according to the equation

R(x) = R₀e^−k_rx (1)

where R₀ is the initial ratio (more details in ESI†). This 2nd procedure is shown in Fig. 4c and was repeated for the CsFA-Mix and MAFA-Mix samples in addition to the CsFA-I sample.

Fig. 4 (a) The N(FA⁺)/Pb²⁺ decay profile at all X-ray flux densities for the CsFA-I sample. Straight line fit to determine rate constant k₁ shown. (b) The rate constant for the decay of the N(FA⁺)/Pb²⁺ ratio of the CsFA-I sample as a function of X-ray flux density. (c) The exponential decay fit N(FA⁺)/Pb²⁺ ratio of the CsFA-I, CsFA-Mix and MAFA-Mix samples.

For CsFA-I, k_r determined by the first method has a value of 1.3 × 10⁻¹⁸ cm² per photon, while a value of 1.55 × 10⁻¹⁸ cm² per photon was obtained from the 2nd method. As all data points are fitted together in the 2nd method, we regard this radiolysis rate constant as more accurate, while the first method clearly shows that the reaction rate is first order with regards to the FA⁺ concentration and proportional to the X-ray flux density on the sample.

The radiolysis rate constants determined with the 2nd method are similar for the different samples. A similar fitting procedure was also carried out for C(FA⁺)/Pb²⁺ for the CsFA-I sample (Fig. S6 and Table S5, ESI†), yielding a rate constant very close to that for N(FA⁺)/Pb²⁺. Fitting procedures of I⁻/Pb²⁺ had to include a constant ratio to which the signal decreases as a large fraction of the iodide ions remains in the sample (see ESI†) and yielded slightly lower constants than those for N(FA⁺)/Pb²⁺ for all samples. These findings indicate that the radiolysis of the FA⁺ cation is driving these changes and that this process is unaffected by tweaking the composition by the addition of Br⁻ or the replacement of Cs⁺ with MA⁺. This is expected as the bonds between the FA⁺ cation and the lead halide cage are strongly ionic, i.e. lead halide cage does not affect the internal bonds in the cation. Taking the average of the radiolysis rate constants determined from the N(FA⁺)/Pb²⁺ ratio using the 2nd method gives a value of 1.6 × 10⁻¹⁸ cm² per photon or, when converted to energy deposited, 3.3 cm² mJ⁻¹. A radiolysis rate constant of 1.6 × 10⁻¹⁸ cm² per photon should be accurate for photon energies close to 3000 eV, while for larger deviations, 3.3 cm² mJ⁻¹ could be a reasonable first estimate as radiation damage often depends on the deposited energy.

Comparing these results with literature, a study by Hodes and co-workers⁴³ found that the current generated by a TiO₂/MAPbI₃/spiro-MeOTAD solar cell exposed to a 3 keV electron beam decayed exponentially with respect to electron fluence, although with a different radiolysis rate constant. On the other hand, Milosavljevic et al.⁴⁴ using low energy electron beams (10 eV) on MAPbI₃ found a logarithmic decrease of the N/Pb and I/Pb ratio. The damage varied with the electron energy (between 4.5–60 eV) with little damage at 4.5 eV and but increasing damage at the higher energies. This indicates that different radiolysis pathways might be available depending on the energy.

X-ray stability and degradation of the inorganic CsPbBr₃

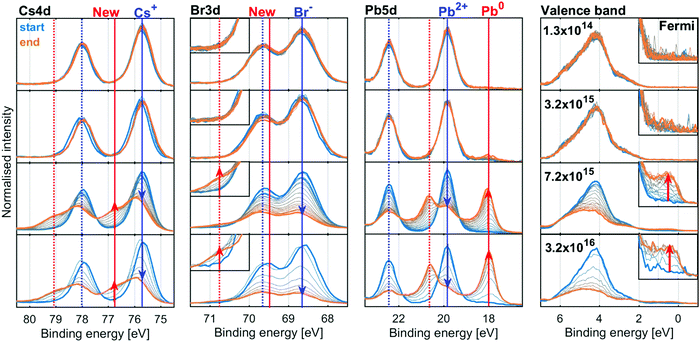
We now turn to the inorganic perovskite CsPbBr₃, where we do not expect any radiolysis of the monovalent cation. Fig. 5 shows the evolution of the Cs4d, Br3d, Pb4d core levels and valence band of the CsPbBr₃ sample at four X-ray flux densities (additional X-ray flux densities shown in Fig. S9 and S10, ESI†). The intensity was normalised to total Pb, as the amount of Pb is assumed to be constant over time due to the relative immobility of the Pb atoms.

Fig. 5 The Cs4d, Br3d (new feature enlarged), Pb5d and valence band (Fermi level enlarged) spectra of recorded for a CsPbBr₃ sample as a function of time (blue: start, orange: end) energy calibrated against the Pb²⁺ component and intensity normalised to total intensity of Pb5d. Measured using the GALAXIES beamline at SOLEIL synchrotron with a ring current of 450 mA.

The core level spectra initially show the spin orbit doublets expected for the perovskite: a Pb5d doublet (19.8 and 22.4 eV) associated with Pb²⁺, a Br3d doublet associated with Br⁻ (68.6 and 69.6 eV) and a Cs4d doublet (75.7 and 78.0 eV) associated with the Cs⁺ cation. In the spectra at low X-ray flux densities, there is little change in these core levels over time.

At higher X-ray flux densities, all original core levels decrease in intensity and simultaneously new doublets appear, which increase in intensity: a new lower binding energy doublet of Pb5d (18.0 and 20.6 eV), associated with Pb⁰, a new higher binding energy Br3d doublet (69.8 and 70.8 eV, most clearly visible as a higher energy shoulder in the inset) and a new higher binding energy doublet of Cs4d (76.8 and 79.1 eV). Furthermore, signal appears at the Fermi edge in the valence band spectra, which is associated with the formation of metallic states in the material. The initial Br3d doublet shifts by +0.1 eV and the initial Cs4d doublet shifts by +0.2 eV relative to the Pb²⁺ contribution of Pb5d core level, indicating a change in the chemical environment.

The spectra at all intensities were fitted to extract the positions and relative intensities of the core levels. At higher X-ray flux densities, the new components were included in the model and typical fits including both components are shown in Fig. S11 (ESI†). The top row of Fig. 6 shows the intensity changes of the Pb²⁺, Br⁻ and Cs⁺ components initially found, and the bottom row shows the intensity of the emerging components determined from the Pb4f (left), Br3d (middle) and Cs4d (right) core levels normalised to the total intensity of the Pb4f signal as a function of X-ray fluence. The same data is shown in Fig. S12 (ESI†) as a function of time and on a logarithmic X-ray fluence scale. For Br3d and Cs4d, the initial intensity ratios relative to Pb are set to 3 and 1, respectively. For all these components, no changes are observed until the X-ray fluence reaches about 10¹⁹ photons per cm² and therefore no degradation is observed at the two lowest X-ray flux densities. However, at higher fluence the reaction initially starts slowly and then accelerates until it is slowed again. This suggests that a certain amount of fluence (i.e. damage) is required to initiate the degradation, which in turn appears to catalyse further degradation, meaning that degradation could be limited or avoided by reducing the X-ray fluence. Additionally, at 3.2 × 10¹⁵ photons per s per cm² the formation of metallic lead is significantly slower than at higher intensities, indicating that the reaction behaves differently at lower X-ray flux densities. Therefore, the same total fluence can give less damage at lower X-ray flux densities suggesting that the X-ray stability is improved by limiting the maximum X-ray flux density.

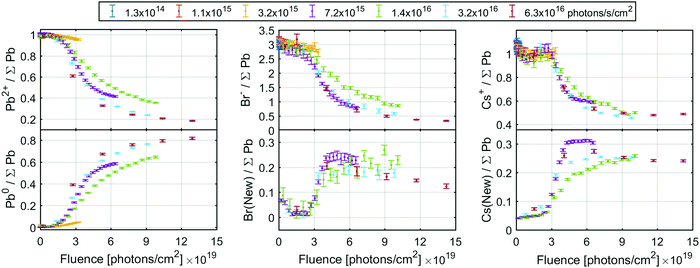Fig. 6 The ratio of the initial signals (top row) and new signals (bottom row) of the Pb4f (left column), Br3d (middle column) and Cs4d (right column) core levels intensity normalised to total Pb4f core level. The Br3d and Cs4d signals were calibrated by setting the initial Br/Pb and Cs/Pb ratio to 3 and 1, respectively. See Fig. S12 (ESI†) for the same data as a function of fluence (log scale) or time.

The conversion of Pb²⁺ to Pb⁰ determined from the Pb4f signal reaches about 80% at the highest fluences (Fig. 6, left), indicating that very little CsPbBr₃ perovskite remains. The Br⁻ component decreases from about 3.0 to about 0.4 Br/Pb, while the new signal only increases to about 0.25 Br/Pb (Fig. 6, middle), resulting in a significant decrease of the total Br/Pb ratio from 3 to about 0.65. Finally, a decrease in the Cs⁺/Pb from about 1 to about 0.5 was observed, while the Cs(New)/Pb increases from 0 to about 0.25 (Fig. 6, right). Overall, this signifies a small decrease in total Cs/Pb ratio from 1 to about 0.75, which could be explained by a preference of Pb⁰ to accumulate at the surface.¹⁸ Additionally, the new Br and the new Cs appear to track each other with a ratio close to 1 : 1 (Fig. S13a, ESI†), suggesting the formation of CsBr. This is roughly in agreement with studies using electron beams which show a loss of Br⁻ by about 2/3 but not Pb or Cs with increased electron fluence.¹⁸ Using the Fermi level independent core-to-core difference we find a Br3d (New) to Cs4d (New) difference of 7.16 eV and the Br3d (New) to Cs3d (New) difference of 656.23 eV. This is close to that of a CsBr reference sample which shows a Br3d to Cs4d difference of 7.12 eV and Br3d to Cs3d difference of 656.13 eV (Table S6 and Fig. S14, ESI†).

There is a significant decrease in bromide in relation to the other components at the surface of the CsPbBr₃ sample. This loss of bromide is not fully balanced by the loss of Pb²⁺, as the Br(initial)/Pb²⁺ ratio decreases from about 3 to 2 (i.e. there remains just enough Br⁻ to charge balance Pb²⁺) while the Cs⁺/Pb²⁺ ratio increases significantly, see Fig. S13b (ESI†). This means that not enough Br⁻ is available to charge balance the Cs⁺, indicating that it is either balanced by another species (adventitious carbon being one candidate) or has lost its positive charge.

To summarise, we observe the conversion of Pb²⁺ to Pb⁰, a significant of loss Br, and the formation of CsBr. This can be explained by the following reaction

CsPbBr₃ → Pb⁰(s) + CsBr(s) + Br₂(g)

with the Br₂ escaping into vacuum. This involves the excitation of an electron from the halide dominated valence band edge to the lead dominated conduction band edge² and therefore a transfer of electron density from the halide to Pb. The reaction has been shown to be catalysed by the high defect (trap) density^45,46 in the perovskite. This could explain why the reaction only starts after a certain fluence, specifically after 10¹⁹ photons per cm², as the reaction requires the build-up of defects in the film. The concentration and formation of defects could be affected by cation or halide ratio as well as the manufacturing technique. While the formation of Pb⁰ was not observed for CsFA-I, the formation of metallic lead has been detected in other hybrid organic–inorganic perovskites under X-ray irradiation.^21,46 When a similar reaction was caused by the excitation with visible light,^26,27 it was found that even small amounts of Cs⁺ reduced the formation of Pb⁰ thus suggesting that CsPbBr₃ could be more resistant to the formation of Pb⁰. Given previous studies on CsBr^47–49 and other caesium halides,⁵⁰ one would also expect the degradation of CsBr during irradiation according the following reaction

CsBr → Cs⁰ + 1/2Br₂(g)

with Br₂ escaping into vacuum. This is supported by the decrease of the CsBr species at the highest X-ray fluences and the apparent lack of counter-ions for Cs⁺ after degradation. However, the formation of Cs⁰ should give rise to new Cs4d signals at about 77.4 and 79.7 eV^51,52 and Cs3d signals at 726.3 and 740.3 eV⁵² with a characteristic Cs3d plasmon at about 729 and 743 eV.⁵² None of these indications of metallic Cs are observed. One explanation could be alloying Cs⁰ with Pb⁰ resulting in CsPb, as observed under electron irradiation at cryogenic temperatures.⁴⁷ The Cs3d plasmon is suppressed in similar alloys (CsAu), while the Cs core levels are shifted to lower binding energies.⁵³ However, CsPb is a semiconductor with an estimated band gap between 0.5–0.8 eV, depending on phase, and would not contribute to a Fermi edge signal.⁵⁴ Furthermore, there is no indication of any new lead signal associated with this compound.

Comparison between the compounds

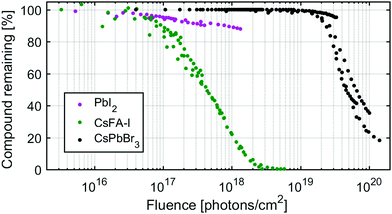
To compare the X-ray stability of the different samples, the amount of PbI₂, CsFA-I and CsPbBr₃ remaining as a function of X-ray fluence is shown in Fig. 7. These amounts were determined from the percentage Pb²⁺ of total lead in the PbI₂ and CsPbBr₃ samples and from the percentage of N(FA⁺)/Pb²⁺ relative to the initial in the CsFA-I sample for all measurements at different X-ray flux densities. We find that the onset of degradation occurs significantly earlier for lead iodide and for the hybrid organic–inorganic perovskites (between 10¹⁶ and 10¹⁷ photons per cm²) than for the inorganic perovskite (at about 10¹⁹ photons per cm²). The kinetics are also different with the CsFA-I degradation following an exponential decay (first order) as shown previously, while the CsPbBr₃ degradation appears to be initiated and catalysed by X-ray damage. PbI₂, unlike CsPbBr₃, begins degrading at the onset of X-ray irradiation but degrades significantly slower than CsFA-I but not CsPbBr₃ (the larger slope of the later is due to the logarithmic scale).

Fig. 7 Percentage of PbI₂ or perovskite remaining as a function of X-ray fluence. Determined by percentage of Pb²⁺ to total Pb for the PbI₂ and CsPbBr₃ and by N(FA⁺)/Pb²⁺ ratio relative to the initial ratio for the CsFA-I, using all the measurements at different X-ray flux densities.

Conclusions

We have investigated the X-ray stability of lead halide perovskites with a particular focus on two different, relatively stable, perovskite compositions. For these two compositions, the inorganic CsPbBr₃ is significantly more stable under X-ray irradiation as damage is only observed at fluences over 10¹⁹ photons per cm² compared to 10¹⁶–10¹⁷ photons per cm² for the hybrid organic–inorganic FA⁺ based perovskite. Comparing the two perovskites in detail, we found two different X-ray degradation reactions, of which only one was observed for each. However, in other perovskite compositions, both reactions might occur simultaneously.

In the case of CsPbBr₃, X-rays cause the formation of metallic lead and CsBr with a significant loss of bromide. This mechanism is also observed in lead halides such as PbI₂ or PbBr₂, but which are significantly more sensitive to degradation by X-rays than CsPbBr₃. The reaction appears to be initiated, and then catalysed, by the accumulation of defects (e.g. defects induces by radiation damage) in the perovskite meaning that degradation only becomes pronounced after a certain X-ray fluence. There also appears to be a threshold of X-ray flux density (photons per s per cm²) below which the radiation damage of CsPbBr₃ per photon is reduced, compared to flux densities above this threshold.

For Cs_0.17FA_0.83PbI₃, the X-rays cause degradation of the organic cation (FA⁺) resulting in a Pb to I ratio of 1 : 2 but no formation of metallic lead. Instead, the degradation appears to consume metallic lead, as observed in similar compositions. Furthermore, we have been able to show that the radiolysis of the organic cation FA⁺ is a first order reaction (exponential decay) with regards to the FA⁺ concentration and proportional to the X-ray flux density, i.e. the damage induced by a photon is independent of flux density. The reaction has a radiolysis rate constant of 1.6 × 10⁻¹⁸ cm² per photon at 3000 eV or 3.3 cm² mJ⁻¹ and does not appear to be affected by small variations in the anion or cation compositions. The radiolysis rate constant of 3.3 cm² mJ⁻¹ could be a reasonable first estimate for FA⁺ radiolysis at other photon energies as radiation damage usually depends on the deposited energy. Other organic cations, e.g. methylammonium and guanidinium, might behave similar to FA⁺, although the radiolysis rate constant is likely to be different. Radiolysis constants for these cations could be determined in future studies.

Author contributions

Conceptualization: Sebastian Svanström, Alberto García Fernández and Ute B. Cappel. Software, formal analysis, visualization and writing – original draft: Sebastian Svanström. Investigation: Sebastian Svanström, Alberto García Fernández, Tamara Sloboda and Ute B. Cappel. Resources: Alberto García Fernández and T. Jesper Jacobsson. Supervision, funding acquisition and project administration: Håkan Rensmo and Ute B. Cappel. Writing – review and editing: all contributors.

Conflicts of interest

There are no conflicts to declare

Acknowledgements

We acknowledge research funding from the Swedish Research Council (Grant No. VR 2018-04125, VR 2018-04330, VR 2018-06465), Swedish Energy Agency (P50626-1), the Göran Gustafsson foundation, the Swedish Foundation for Strategic Research (project no. RMA15-0130), and the Carl Tryggers foundation (Grant No. CTS 18:59). We acknowledge SOLEIL for provision (proposal number: 20180483, 20191506) of synchrotron radiation facilities and we would like to thank Rueff Jean-Pascal and Ceolin Denis for their assistance in using the Galaxies beamline. This work was carried out with the support of Diamond Light Source, (proposal SI24192) and we would like to thank Tien-Lin Lee and Pardeep Kumar Thakur for their assistance at the I09 beamline. The research leading to this result has been supported by the project CALIPSOplus under the Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. We thank Mats Jonsson for discussions about chemical kinetics and radiation chemistry.

References

1. Z. Song, C. L. McElvany, A. B. Phillips, I. Celik, P. W. Krantz, S. C. Watthage, G. K. Liyanage, D. Apul and M. J. Heben, Energy Environ. Sci., 2017, 10, 1297–1305.
2. J. S. Manser, J. A. Christians and P. V. Kamat, Chem. Rev., 2016, 116, 12956–13008.
3. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
4. NREL, Best Research-Cell Efficiency Chart, https://www.nrel.gov/pv/cell-efficiency.html (accessed 31 March 2021).
5. M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. Khaja Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Energy Environ. Sci., 2016, 9, 1989–1997.
6. C. C. Boyd, R. Cheacharoen, T. Leijtens and M. D. McGehee, Chem. Rev., 2019, 119, 3418–3451.
7. H. Wei and J. Huang, Nat. Commun., 2019, 10, 1066.
8. J. Zhao, L. Zhao, Y. Deng, X. Xiao, Z. Ni, S. Xu and J. Huang, Nat. Photonics, 2020, 14, 612–617.
9. H. Wei, Y. Fang, P. Mulligan, W. Chuirazzi, H.-H. Fang, C. Wang, B. R. Ecker, Y. Gao, M. A. Loi, L. Cao and J. Huang, Nat. Photonics, 2016, 10, 333–339.
10. W. Wei, Y. Zhang, Q. Xu, H. Wei, Y. Fang, Q. Wang, Y. Deng, T. Li, A. Gruverman, L. Cao and J. Huang, Nat. Photonics, 2017, 11, 315–321.
11. C. C. Stoumpos, C. D. Malliakas, J. A. Peters, Z. Liu, M. Sebastian, J. Im, T. C. Chasapis, A. C. Wibowo, D. Y. Chung, A. J. Freeman, B. W. Wessels and M. G. Kanatzidis, Cryst. Growth Des., 2013, 13, 2722–2727.
12. D. N. Dirin, I. Cherniukh, S. Yakunin, Y. Shynkarenko and M. V. Kovalenko, Chem. Mater., 2016, 28, 8470–8474.
13. Y. He, L. Matei, H. J. Jung, K. M. McCall, M. Chen, C. C. Stoumpos, Z. Liu, J. A. Peters, D. Y. Chung, B. W. Wessels, M. R. Wasielewski, V. P. Dravid, A. Burger and M. G. Kanatzidis, Nat. Commun., 2018, 9, 1609.
14. S. Yang, Z. Xu, S. Xue, P. Kandlakunta, L. Cao and J. Huang, Adv. Mater., 2019, 31, 1805547.
15. A. G. Boldyreva, L. A. Frolova, I. S. Zhidkov, L. G. Gutsev, E. Z. Kurmaev, B. R. Ramachandran, V. G. Petrov, K. J. Stevenson, S. M. Aldoshin and P. A. Troshin, J. Phys. Chem. Lett., 2020, 11, 2630–2636.
16. F. Lang, N. H. Nickel, J. Bundesmann, S. Seidel, A. Denker, S. Albrecht, V. V. Brus, J. Rappich, B. Rech, G. Landi and H. C. Neitzert, Adv. Mater., 2016, 28, 8726–8731.
17. O. Malinkiewicz, M. Imaizumi, S. B. Sapkota, T. Ohshima and S. Öz, Emerg. Mater., 2020, 3, 9–14.
18. Z. Dang, J. Shamsi, F. Palazon, M. Imran, Q. A. Akkerman, S. Park, G. Bertoni, M. Prato, R. Brescia and L. Manna, ACS Nano, 2017, 11, 2124–2132.
19. X. Chen and Z. Wang, Micron, 2019, 116, 73–79.
20. B. Philippe, B.-W. Park, R. Lindblad, J. Oscarsson, S. Ahmadi, E. M. J. Johansson and H. Rensmo, Chem. Mater., 2015, 27, 1720–1731.
21. J. D. McGettrick, K. Hooper, A. Pockett, J. Baker, J. Troughton, M. Carnie and T. Watson, Mater. Lett., 2019, 251, 98–101.
22. T. J. Jacobsson, S. Svanström, V. Andrei, J. P. H. Rivett, N. Kornienko, B. Philippe, U. B. Cappel, H. Rensmo, F. Deschler and G. Boschloo, J. Phys. Chem. C, 2018, 122, 13548–13557.
23. G. Sadoughi, D. E. Starr, E. Handick, S. D. Stranks, M. Gorgoi, R. G. Wilks, M. Bär and H. J. Snaith, ACS Appl. Mater. Interfaces, 2015, 7, 13440–13444.
24. J. Chun-Ren, Ke, A. S. Walton, D. J. Lewis, A. Tedstone, P. O’Brien, A. G. Thomas and W. R. Flavell, Chem. Commun., 2017, 53, 5231–5234.
25. B. Conings, L. Baeten, C. De Dobbelaere, J. D’Haen, J. Manca and H.-G. Boyen, Adv. Mater., 2014, 26, 2041–2046.
26. U. B. Cappel, S. Svanström, V. Lanzilotto, F. O. L. Johansson, K. Aitola, B. Philippe, E. Giangrisostomi, R. Ovsyannikov, T. Leitner, A. Föhlisch, S. Svensson, N. Mårtensson, G. Boschloo, A. Lindblad and H. Rensmo, ACS Appl. Mater. Interfaces, 2017, 9, 34970–34978.
27. S. Svanström, T. J. Jacobsson, T. Sloboda, E. Giangrisostomi, R. Ovsyannikov, H. Rensmo and U. B. Cappel, J. Mater. Chem. A, 2018, 6, 22134–22144.
28. S. B. Dhiman and J. A. LaVerne, J. Nucl. Mater., 2013, 436, 8–13.
29. O. I. Shadyro, A. A. Sosnovskaya and O. N. Vrublevskaya, Int. J. Radiat. Biol., 2003, 79, 269–279.
30. D. Céolin, J. M. Ablett, D. Prieur, T. Moreno, J.-P. Rueff, T. Marchenko, L. Journel, R. Guillemin, B. Pilette, T. Marin and M. Simon, J. Electron Spectrosc. Relat. Phenom., 2013, 190, 188–192.
31. T.-L. Lee and D. A. Duncan, Synchrotron Radiat. News, 2018, 31, 16–22.
32. S. Tanuma, C. J. Powell and D. R. Penn, Surf. Interface Anal., 2003, 35, 268–275.
33. A. Herrera-Gomez, M. Bravo-Sanchez, F. S. Aguirre-Tostado and M. O. Vazquez-Lepe, J. Electron Spectrosc. Relat. Phenom., 2013, 189, 76–80.
34. D. A. Shirley, Phys. Rev. B: Solid State, 1972, 5, 4709.
35. J. H. Shofield, Theoretical photoionization cross sections from 1 to 1500 keV, California University, Livermore, Lawrence Livermore Lab, 1973, vol. no. UCRL-51326.
36. R. Dawood, A. Forty and M. Tubbs, Proc. R. Soc. London, Ser. A, 1965, 284, 272–288.
37. C. G. Bischak, C. L. Hetherington, H. Wu, S. Aloni, D. F. Ogletree, D. T. Limmer and N. S. Ginsberg, Nano Lett., 2017, 17, 1028–1033.
38. M. C. Brennan, S. Draguta, P. V. Kamat and M. Kuno, ACS Energy Lett., 2018, 3, 204–213.
39. T. Duong, H. K. Mulmudi, Y. Wu, X. Fu, H. Shen, J. Peng, N. Wu, H. T. Nguyen, D. Macdonald, M. Lockrey, T. P. White, K. Weber and K. Catchpole, ACS Appl. Mater. Interfaces, 2017, 9, 26859–26866.
40. E. T. Hoke, D. J. Slotcavage, E. R. Dohner, A. R. Bowring, H. I. Karunadasa and M. D. McGehee, Chem. Sci., 2015, 6, 613–617.
41. J. B. Raynor and I. J. Rowland, J. Chem. Soc., Faraday Trans., 1991, 87, 571–577.
42. F. W. Patten, Phys. Rev., 1968, 175, 1216–1227.
43. N. Klein-Kedem, D. Cahen and G. Hodes, Acc. Chem. Res., 2016, 49, 347–354.
44. A. R. Milosavljević, W. Huang, S. Sadhu and S. Ptasinska, Angew. Chem., Int. Ed., 2016, 55, 10083–10087.
45. A. Kirakosyan, N. D. Chinh, M. R. Sihn, M.-G. Jeon, J.-R. Jeong, D. Kim, J. H. Jang and J. Choi, J. Phys. Chem. Lett., 2019, 10, 4222–4228.
46. X. Tang, M. Brandl, B. May, I. Levchuk, Y. Hou, M. Richter, H. Chen, S. Chen, S. Kahmann, A. Osvet, F. Maier, H.-P. Steinrück, R. Hock, G. J. Matt and C. J. Brabec, J. Mater. Chem. A, 2016, 4, 15896–15903.
47. Z. Dang, J. Shamsi, Q. A. Akkerman, M. Imran, G. Bertoni, R. Brescia and L. Manna, ACS Omega, 2017, 2, 5660–5665.
48. M. T. E. Halliday, A. G. Joly, W. P. Hess and A. L. Shluger, J. Phys. Chem. C, 2015, 119, 24036–24045.
49. M. T. E. Halliday, A. G. Joly, W. P. Hess, P. V. Sushko and A. L. Shluger, J. Phys. Chem. C, 2013, 117, 13502–13509.
50. P. V. Galiy, Radiat. Meas., 1999, 30, 41–50.
51. C. Y. Su, I. Lindau, P. W. Chye, S.-J. Oh and W. E. Spicer, J. Electron Spectrosc. Relat. Phenom., 1983, 31, 221–259.
52. G. Ebbinghaus and A. Simon, Chem. Phys., 1979, 43, 117–133.
53. J. A. Rodriguez, J. Hrbek, M. Kuhn and T. K. Sham, Surf. Sci., 1993, 293, 260–274.
54. J. Fortner, M.-L. Saboungi and J. E. Enderby, Phys. Rev. Lett., 1995, 74, 1415–1418.

---

Footnote

† Electronic supplementary information (ESI) available: XPS spectra, chemical ratios, kinetic analysis and core to core differences of CsBr, lead halides and lead halide perovskites. Heating model of X-ray spot. X-ray intensities, flux densities, irradiance and pass energies used at the different beamlines. See DOI: 10.1039/d1cp01443a

---