Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conformational energies and equilibria of cyclic dinucleotides in vacuo and in solution: computational chemistry vs. NMR experiments†
Ondrej
Gutten
 *a,
Petr
Jurečka
*a,
Petr
Jurečka
 b,
Zahra
Aliakbar Tehrani‡
b,
Zahra
Aliakbar Tehrani‡
 a,
Miloš
Buděšínský
a,
Miloš
Buděšínský
 a,
Jan
Řezáč
a,
Jan
Řezáč
 a and
Lubomír
Rulíšek
a and
Lubomír
Rulíšek
 *a
*a
aInstitute of Organic Chemistry and Biochemistry of the Czech Academy of Sciences, Flemingovo náměstí 2, 166 10, Praha 6, Czech Republic. E-mail: gutten@uochb.cas.cz; rulisek@uochb.cas.cz
bDepartment of Physical Chemistry, Faculty of Science, Palacky University Olomouc, 17. listopadu 12, 771 46, Olomouc, Czech Republic
First published on 22nd March 2021
Abstract
Performance of computational methods in modelling cyclic dinucleotides – an important and challenging class of compounds – has been evaluated by two different benchmarks: (1) gas-phase conformational energies and (2) qualitative agreement with NMR observations of the orientation of the χ-dihedral angle in solvent. In gas-phase benchmarks, where CCSD(T) and DLPNO-CCSD(T) methods have been used as the reference, most of the (dispersion corrected) density functional approximations are accurate enough to justify prioritizing computational cost and compatibility with other modelling options as the criterion of choice. NMR experiments of 3′3′-c-di-AMP, 3′3′-c-GAMP, and 3′3′-c-di-GMP show the overall prevalence of the anti-conformation of purine bases, but some population of syn-conformations is observed for guanines. Implicit solvation models combined with quantum-chemical methods struggle to reproduce this behaviour, probably due to a lack of dynamics and explicitly modelled solvent, leading to structures that are too compact. Molecular dynamics simulations overrepresent the syn-conformation of guanine due to the overestimation of an intramolecular hydrogen bond. Our combination of experimental and computational benchmarks provides “error bars” for modelling cyclic dinucleotides in solvent, where such information is generally difficult to obtain, and should help gauge the interpretability of studies dealing with binding of cyclic dinucleotides to important pharmaceutical targets. At the same time, the presented analysis calls for improvement in both implicit solvation models and force-field parameters.
1. Introduction
Cyclic dinucleotides (CDNs) are an intriguing class of molecules that act as second messengers in prokaryotes and vertebrates.1,2 In vertebrates they bind to the stimulator of interferon genes (STING), a protein involved in the innate immune system.3 The role of CDNs in defense against pathogens as well as sensing of tumor cells render them important for understanding, and potentially for treatment, of a number of autoimmune diseases,4–6 cancers,7 and viral diseases, as well as having potential as adjuvants in vaccines.8,9 For these reasons, CDNs have attracted a lot of interest which resulted in the design of various analogues that could improve the affinity, bioavailability, and pharmacokinetic properties of the parent compounds.10–12 The importance of these efforts is highlighted by a number of registered patents,13–15 and even some of the candidate molecules entering clinical trials.16,17Understanding the processes that involve this class of compounds and development of new derivatives have been greatly assisted by computational chemistry. These studies include molecular dynamics simulations of protein:ligand complexes,18–21 as well as modelling of the free ligand in solvent.20,22–25 Studies on modelling the free ligand can provide valuable information about the propensity of a ligand to adapt a bound-like conformation, which has been shown to be a relevant consideration for studying protein:ligand interactions.26,27 Some form of molecular dynamics is typically used for generating structures, followed either by directly comparing relative populations with certain structural features22,23 or by identifying the most relevant ones using e.g. density functional theory (DFT) for calculation of conformational energies.23,24 Alternatively, the obtained conformations can be used as a starting point for ensemble docking.25 Recently, we have shown that the difference in binding to STING between a series of ‘natural’ CDNs and their difluorinated analogues is a subtle interplay between ligand conformational strain and the loss of conformational entropy.20 In addition, combination of QM/MM and ‘QM-in-solvent’ methodology has been used to rationalize effect of single-point mutations in STING on binding of selected CDNs.21
The need for the accurate description of the conformational flexibility of CDNs is further highlighted by the variety of conformations found in various protein:CDN complexes.28 This raises the question of how accurate are the underlying quantum chemical (and/or solvation) methods. The choice of an appropriate computational method is dependent not only on the problem at hand,29,30 but may change dramatically from one class of compounds to another. This is reflected by the high number of data sets that aim to evaluate the accuracy of conformational energies in different contexts.29,31–51 The data set most relevant to CDNs is the UPU46 data set,47 which examines non-cyclic dinucleotides as models for representative RNA backbone families. Similarly to this data set, CDNs require an accurate description of weak dispersion forces, due to the presence of purine bases. The overall charge is increased by the presence of an additional phosphate group, which increases the need for treatment of polarization, especially in a solvent environment. Perhaps most importantly, the macrocyclic nature of CDNs renders them challenging to the accurate description of torsions. Torsional angles and their role in conformational equilibria of nucleic acids are a subject of active research, e.g. A/B-DNA,52 BI/BII-DNA,53 ZI/ZII-DNA,54 or α/γ equilibria in RNA.55 However, the question of the transferability of force-field parameters remains relevant, due to significant internal stresses and shifts of values of optimal dihedral angles that commonly occur in the macrocyclic compounds.
In summary, CDNs represent a complex and highly relevant case, both for their potential application and their complexity. Moreover, the availability of experimental data, reported both previously23 and herein, describing the structural features of molecules in solvent provides a benchmarking opportunity beyond the usual gas-phase CCSD(T) testing.
The aim of this study is comprehensive analysis of CDN conformational energies and equilibria, both in vacuo and in solvent, by employing a range of computational chemistry methods (including molecular mechanics, semiempirical quantum-mechanical (SQM) methods, popular DFT functionals, and wave-function methods up to gold standard CCSD(T) benchmarks) and NMR experiments. First, we perform gas-phase benchmarks to establish the level of accuracy of DFT, SQM, and wave-function methods. These serve as a starting point for examining modelling in a solvent environment, which we explore by looking at NMR measurements of three selected CDNs (3′3′-c-di-AMP, 3′3′-c-GAMP, and 3′3′-c-di-GMP) in solvent. We specifically focus on distinguishing between the anti- and syn-orientation of purine bases – a structural feature that is in fine equilibrium, providing a very enticing, albeit qualitative, experimental benchmark. Finally, we compare these observations with predictions of molecular dynamics simulations and with QM methods in combination with some available solvation methods. It needs to be mentioned that observation of multiple conformers implies free-energy separation of at most units of kcal mol−1. Such a small difference is an immensely difficult test case for systems where modelling of aspects across a wide range of strengths (“weak” dispersion vs. “strong” polarization of charged groups) and scales (“local” torsional angles vs. “global” solvent–solute interactions) is required.
2. Computational details
2.1 Systems and structures
We use two separate sets of structures – one to address the overall accuracy of computational methods for predicting gas-phase conformational energies (CDN set), and the other is employed to reproduce experimentally observed structural features of CDNs (syn-/anti-set).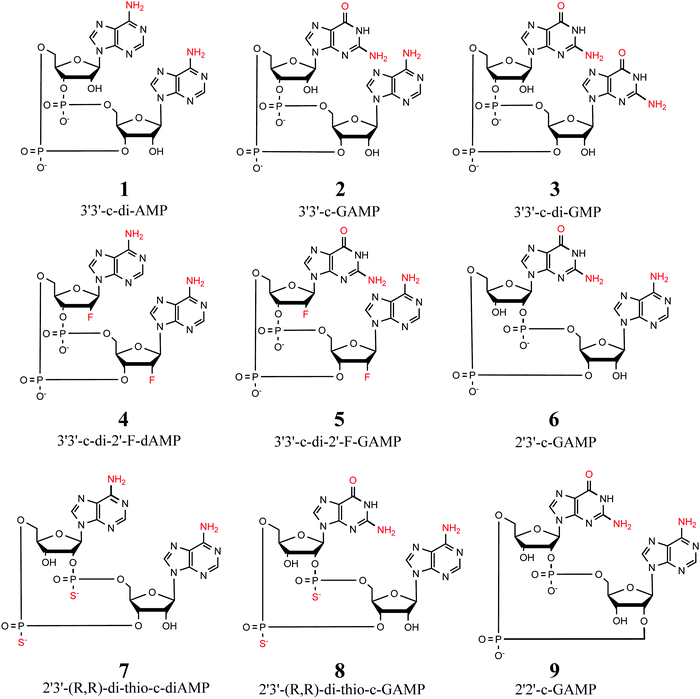 | ||
| Fig. 1 Selection of 9 cyclic dinucleotides studied herein. All CDNs are considered in their doubly-deprotonated state, i.e. with a total charge of −2. | ||
For each of the nine compounds we selected 20 conformers by the following procedure: (1) each compound was first subjected to conformational sampling by the Prime algorithm56 as implemented in Schrodinger 2017-1 suite.57 (2) From the obtained set of several hundreds of initial conformers (ranked by their force field energies), 20 conformers were selected for each system. The only selection criterion was to cover the energy spectrum of the sets (ca. 35 kcal mol−1), in order to avoid bias towards low-energy conformers. (3) The selected structures were then optimized using the BP86+D3(0)/def-TZVP/COSMO(ε = 80) method (vide infra) to obtain structures relevant for water environments.
The two main orientations of the χ-dihedral angle allow for several combinations of the two bases, namely anti-/anti-, syn-/anti-, anti-/syn- or syn-/syn- (further denoted as classes). Therefore, we conceived the syn-/anti-set comprising the energetically most favorable conformers within each χ-dihedral class for the 3′3′-c-di-AMP, 3′3′-c-GAMP, and 3′3′-c-di-GMP compounds. This set contains up to three energetically most favorable candidates (obtained from conformational sampling described above in Section 2.1.1, ranked by the BP86+D3(0)/COSMO-RS energy values) for each class of each of the three selected CDNs. At the same time, we request that the conformational energy of any member (conformer) of the syn-/anti-set is not higher than 10 kcal mol−1 above the global minimum of the particular compound. This trimmed final selection to 8 conformers for 3′3′-c-di-AMP, 9 for 3′3′-c-GAMP, and 9 for 3′3′-c-di-GMP (yielding 26 conformers in syn-/anti-set, in total).
2.2 Computational methods
| Egp = ECBS + Ehoc | (1) |
Specifically, we use the following setup for obtaining reference energies:50
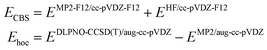 | (2) |
It can be mentioned that the MP2-F12 method60–62 is computationally more demanding than canonical MP2 but converges faster to the complete basis set limit. The DLPNO-CCSD(T) method is used with the TightPNO thresholds. The mean difference between MP2-F12 and a Helgaker extrapolation formula63 to CBS limit based on triple-ζ/quadruple-ζ (aug-cc-pVXZ basis set) for a subset of 20 studied conformers was 0.11 kcal mol−1, with a maximum absolute value of 0.26 kcal mol−1.
The choice of these methods is driven by computational cost. Using full CCSD(T) for Ehoc, and triple-ζ to quadruple-ζ basis set extrapolation using canonical MP263 is too demanding for CDNs molecule (ca. 70 atoms). Still, we benchmarked DLPNO approximation (vs. full CCSD(T)) on a set of fragments taken from studied CDNs (described in detail in Section S1 of the ESI†). This allowed us to estimate mean unsigned error for CDNs between our reference (eqn (2) and the “gold standard” (CCSD(T)+MP2/CBS) to be ca. 0.2 kcal mol−1.
All of the functionals are tested employing a triple-ζ basis set (def2-TZVPD84,85). Basis set dependence is further tested by calculating conformational energies for a subset of functionals with double-ζ (specifically DZVP-DFT basis set86) and quadruple-ζ (def2-QZVP87) basis sets. In a few specifically discussed cases we also test the triple-ζ basis set without the additional diffuse functions, i.e. def2-TZVP.85
Effects of dispersion are tested by employing several correction parametrizations: D3 with zero, D3(0),88 or Becke–Johnson damping, D3(BJ),89 and D4.90 A reparametrized version of D3(BJ) and D3(0) for use with a small DZVP-DFT basis set was reported previously91 and, therefore, we further test its transferability to the CDN test set.
Default grid sizes were used for most of the DFT calculations, with the exception of SCAN and double-hybrid functionals B2PLYP and PWPB95. Detailed information about the grids used is listed in Table S1 (ESI†). The effects of changing a grid size were examined for several functionals and are shown in Table S2 (ESI†).
Semiempirical PM6, RM1, PM7 calculations and their variants with corrections for non-covalent interactions were carried out using MOPAC2016.113 DFTB3 calculations were performed using the DFTB+ program,114 which now also implements all the corrections for non-covalent interactions used herein. For GFN-xTB and GFN-XTB2 calculations, we used the software provided by the authors of the method.115
MD simulations were carried out using PMEMD for the CUDA program116 of the AMBER 16 software package117 and trajectory analysis was performed using CPPTRAJ software.118
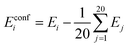 | (3) |
In our previous study50 we found this definition more convenient than setting Eglobal minimum = 0. We use this definition for obtaining several statistics:
Mean Unsigned Error (MUE):
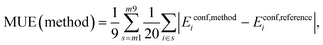 | (4) |
Maximum Absolute Deviation (MAD):
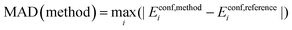 | (5) |
The maximum absolute deviation across all 180 conformers is reported.
Root Mean Square Error (RMSE):
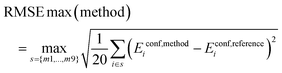 | (6) |
Thus, we calculate the root mean square error for each of the 9 subsets of 20 conformers and report the maximum of these values.
Mean Signed Error (MSE):
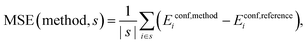 | (7) |
2.3 Experimental methods
1H and 13C NMR spectra of CDNs were measured on a Bruker AVANCE-600 spectrometer (1H at 600 MHz and 13C at 150.9 MHz frequency) and 31P NMR spectra on a Bruker AVANCE-500 instrument (31P at 202.4 MHz) in D2O at 25 °C. The homonuclear 2D-H,H-COSY, 2D-H,H-ROESY, and heteronuclear 2D-H,C-HSQC, 2D-H,C-HMBC spectra were recorded and used for the structural assignment of proton and carbon signals. The 2D-H,H-ROESY spectra were measured with a spinlock mixing time of 300 ms. Proton-coupled 13C NMR spectra of CDNs were used for estimation of J(C,H) values of adenine and guanine carbon atoms. Experimental proton and carbon-13 NMR parameters are summarized in Tables S4 and S5 (ESI†). The 1H and 13C chemical shifts were referenced to dioxane as the internal standard and recalculated to TMS using δH (dioxane) = 3.75 ppm and δC (dioxane) = 69.3 ppm; 31P chemical shifts are referenced to H3PO4 as the external standard.3. Results and discussion
3.1 Gas-phase conformational energies (CDN set)
We evaluate the accuracy of gas-phase conformational energies by employing a range of DFT and semi-empirical methods on 9 × 20 conformers of the “CDN” set (see Section 2.1.1). These will serve as a starting point for examining modelling of CDNs in solvent in later sections of this work. The reference is provided by the DLPNO-CCSD(T)/MP2-F12 composite scheme (see eqn (2)). This represents an affordable compromise to a “gold standard” CCSD(T)+MP2-CBS composite scheme (see the discussion in Section S1 of the ESI†), which is computationally prohibitive for CDN systems of ∼70 atoms. The estimated MUE between the two composite schemes (DLPNO-CCSD(T)/MP2-F12 vs. full CCSD(T)/MP2-CBS) for CDN systems is expected to be 0.2 kcal mol−1, based on a fragmentation scheme that we explain in detail in the ESI.†A summary of comparison among different DFT functionals is shown in Table 1. The best performing GGA functionals include B-LYP+D3(0)/D4 and B-97D+D3(BJ) with MUE of 0.7 kcal mol−1. However, even the worst GGA result, the OLYP+D3(0) functional, shows MUE of ca. 1.2 kcal mol−1. This corresponds to only about 4% of the energy range. These values are reasonably low and suggest that for modelling of gas-phase conformational energies of CDNs the choice of the functional is actually not critical. Still, while the MUE values are comparable, the MAD and RMSEmax values suggest better performance of e.g. B-LYP over PBE and OLYP functionals, see Tables S6 and S7 (ESI†). Among meta-GGA, SCAN+D3(BJ) deserves a special mention as it marginally outperforms all the other functionals, with MUE of 0.4 kcal mol−1, which is close to the error of DLPNO-CCSD(T) NormalPNO/MP2-F12 (which is around 0.2 kcal mol−1). We can recommend this functional for single-point evaluations. However, geometry optimizations proved to be problematic even with finer integration grids.
| Functional | Jacob's ladder class | No dispersion correction | D3(0) | D3(BJ) | D4 |
|---|---|---|---|---|---|
| B-LYP | GGA | 6.2 | 0.7 | 0.8 | 0.7 |
| B-P | GGA | 5.3 | 1.0 | 1.0 | 0.9 |
| B97-D | GGA | 6.9 | 0.9 | 0.7 | n.a. |
| OLYP | GGA | 9.1 | 1.2 | 0.9 | 1.0 |
| PBE | GGA | 4.4 | 0.9 | 1.0 | 0.9 |
| revPBE | GGA | 6.9 | 0.9 | 0.7 | 0.9 |
| M06-L | Meta-GGA | 0.6 | 1.0 | n.a. | n.a. |
| revTPSS | Meta-GGA | 3.8 | n.a. | n.a. | 0.8 |
| SCAN | Meta-GGA | 1.5 | 0.5 | 0.4 | 0.5 |
| TPSS | Meta-GGA | 5.2 | 0.7 | 0.9 | 0.8 |
| B3-LYP | Hybrid | 5.3 | 0.5 | 0.6 | 0.6 |
| BH-LYP | Hybrid | 4.2 | 0.5 | 0.6 | 0.6 |
| M06 | Hybrid | 0.6 | 1.6 | n.a. | n.a. |
| M06-2X | Hybrid | 0.6 | 0.7 | n.a. | n.a. |
| PBE0 | Hybrid | 4.0 | 0.6 | 0.7 | 0.7 |
| PW6B95 | Hybrid | 2.7 | 0.6 | 0.6 | 0.7 |
| TPSSH | Hybrid | 5.0 | 0.7 | 0.7 | 0.7 |
| ωB-97X | Hybrid | 1.4 | 0.9 | 1.0 | n.a. |
| B2PLYP | Double-hybrid | 1.4 | 1.6 | 1.6 | 1.9 |
| PWPB95 | Double-hybrid | 1.0 | 1.7 | 1.4 | 1.2 |
| MP2/aug-cc-pVTZ | 2.6 |
Hybrid functionals provide satisfactory results, with MUE values between 0.5 and 1.0 kcal mol−1. The best performer is B3-LYP+D3(0) and BH-LYP+D3(0) with MUE of 0.5 kcal mol−1, although only by a very small margin to other functionals. However, the B3-LYP+D3(0) combination exhibits the overall lowest MAD value of only 1.6 kcal mol−1, while the typical value of this statistic was in between 2–3 kcal mol−1 (see Table S6, ESI†). On the other hand, the long-range corrected ωB-97X shows good overall performance with MUE of 0.9 kcal mol−1, but some of the highest MAD values among all tested calculations (5–6 kcal mol−1).
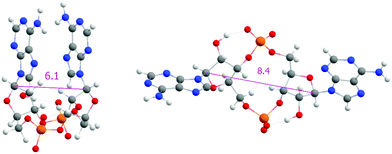
The importance of dispersion correction for our dataset is exacerbated by relative orientation of bases (i.e. “open” and “closed”, see Fig. 3), which interact primarily via dispersion. However, the rather discrete distribution of base distances renders our dataset unsuitable for in-depth testing of different dispersion corrections. Indeed, combination of tested DFT functionals with D3(0), D3(BJ), and D4 corrections exhibit differences below our established error of 0.2 kcal mol−1.
However, there are a few exceptions. In our tests, the (empirical dispersion)_non-corrected versions of Minnesota functionals (M06, M06L, M06-2X) perform better compared to the D3(0) corrected versions. For M06-2X the difference is mild, but for M06 and M06L the decrease in performance is notable, from MUE of circa 0.6 kcal mol−1 for both M06 and M06L, to 1.6 and 1.0 kcal mol−1 after addition of D3(0) correction, respectively. This decrease in performance is even more notable in MAD and RMSEmax statistics shown in Tables S6 and S7 (ESI†). The problematic relationship between Minnesota functionals and their ability to capture non-covalent interactions has been discussed before.29,119
Surprisingly, the most underwhelming performance is exhibited by both tested double-hybrid functionals, PWPB95 and B2PLYP. In both cases, adding dispersion correction actually degrades their MUE values to 1.6 and 1.2 kcal mol−1, way behind even the worst GGA functionals. This result is surprising, as double-hybrid functionals have been recommended as superior for conformational energies.29
A more detailed inspection suggests that the culprit lies in the evaluation of interaction of the bases. Closed conformers (i.e. conformers with stacked purine bases, see Fig. 3), which interact primarily via dispersion, are greatly overstabilized if dispersion correction is included, leading to higher errors compared to dispersion-uncorrected versions of these functionals. We show this by examining mean signed errors (MSE, see eqn (7), for a subset of closed |s| = 74 conformers). We present these values for some of the methods in Table 2, while the full list can be found in Table S8 (ESI†).
Table 2 and Table S8 (ESI†) show that the dispersion-uncorrected functionals under-stabilize the closed conformers, leading to positive MSE values. Adding the empirical dispersion remedies the situation in most cases. The exceptions include the Minnesotta functionals and the double-hybrids, where it leads to significant overstabilization of these conformers, i.e. negative MSE values. This behaviour is similar to regular MP2, which is added for comparison.
| Functional | Jacob's ladder class | No dispersion correction | D3(0) | D3(BJ) | D4 |
|---|---|---|---|---|---|
| B-P | GGA | 6.0 | −0.8 | −0.5 | −0.3 |
| TPSS | Meta-GGA | 5.9 | 0.6 | 0.7 | 0.5 |
| B3-LYP | Hybrid | 5.8 | 0.0 | −0.1 | 0.0 |
| M06 | Hybrid | 0.1 | −1.8 | n.a. | n.a. |
| B2PLYP | Double-hybrid | 1.2 | −1.7 | −1.8 | −2.1 |
| PWPB95 | Double-hybrid | 0.6 | −1.7 | −1.5 | −1.2 |
| MP2/aug-cc-pVTZ | −2.9 |
Surprisingly, removing the diffuse basis functions, i.e. using the def2-TZVP basis, remedies the situation, bringing the MUE values of both double-hybrid functionals down to ca. 0.5 kcal mol−1. It is worth mentioning that for several other functionals (B-P, B-LYP, SCAN) the removal of diffuse basis functions has a very minor effect. These values are listed in Table S9–S12 (ESI†).
Concerning basis set effects, all of the previous discussion on DFT was based on using triple-ζ basis set def2-TZVPD. For a few selected functionals we test the use of quadruple-ζ and double-ζ basis sets. Using a quadruple-ζ basis set (def2-QZVP) produces virtually identical results, changing MUE by less than 0.1 kcal mol−1 in all cases, see Table S13 (ESI†). Thus, triple-ζ basis set results can be considered as essentially converged for the purpose of obtaining accurate conformational energies.
A more interesting case is the use of the cheaper double-ζ basis set, DZVP-DFT. In combination with standard D3 or D4 empirical corrections this does lead to a significant decrease in performance (by ca. 0.5 to 1 kcal mol−1). However, the performance can be recovered by use of reparametrized DZVP-D3 corrections91 instead. This leads to MUE values which are comparable to the much more expensive triple-ζ basis set, see Table S14 (ESI†). We also confirm the equalizing effect of this dispersion correction reported previously.50 All of the 7 tested functionals (B-LYP, B-P, B97-D, PBE, PBE0, B3-LYP, TPSS) show MUE between 0.7 and 0.9 kcal mol−1, and RMSEmax values between 1.1 and 1.4 kcal mol−1. It is also worth mentioning that most of the bias regarding closed/open subset division is eliminated using this reparametrization (compare to Tables S8 and S17, ESI†). Thus, the setup consisting of any of these functionals in combination with the DZVP-DFT basis set and DZVP-D3 reparametrization can be recommended as the most cost-effective approach for calculation of conformational energies. This extends the previous observations of good transferability50 of these methods to CDN systems as well.
In conclusion, most of the tested DFT functionals, when paired with proper dispersion correction, perform with MUE of approximately 1 kcal mol−1, which correspond to ca. 3% of the energy range of the conformers in the dataset. The SCAN functional stands out as a cheap and very accurate option. Possibility of using a small DZVP-DFT basis set with DZVP-D3 reparametrization offers a very fast and accurate computational setup as well.
| Method | MUE [kcal mol−1] |
|---|---|
| PM6 | 4.9 |
| PM6-D3 | 3.9 |
| PM6-D3H4 | 3.6 |
| PM7 | 4.1 |
| RM1-D3H4 | 4.0 |
| DFTB3 | 4.2 |
| DFTB3-D3H4 | 2.1 |
| DFTB3-D3H5 | 3.2 |
| GFN-xTB | 2.7 |
| GFN2-xTB | 2.3 |
| HF-3c | 1.9 |
| PBEh-3c | 1.0 |
| B97-3c | 0.8 |
Most of the semiempirical methods provide very unsatisfactory results, with MUE values reaching up to 5 kcal mol−1. Only two of them, DFTB3-D3H4 and GFN2-xTB, approach the accuracy of 2 kcal mol−1. The HF-3c method based on HF calculation in a minimal basis set, the cheapest one among the “3c” methods, is only slightly better with MUE of 1.9 kcal mol−1. The remaining triple-correction (“3c”) methods, PBEh-3c and B97-3c yield MUE around 1 kcal mol−1, which is comparable to DFT results obtained for larger basis sets.
The errors of the semiempirical methods observed here are comparable to previous tests on conformational energies of non-cyclic dinucleotides47 and other compound classes that include small peptides50 or sugars.35 The approximations involved in these methods lead to an inaccurate description of torsional profiles,120 and in the charged systems studied here, further errors may result from limitations in the description of electrostatic induction.
Evaluating conformational energies with force-field methods is in principle possible, but not very informative. Force-fields are very sensitive to minor structural changes, rendering conformational energies on structures not optimized with respect to a given energy function dominated by deviations from optimal bond lengths and angles rather than by interplay of structural features. Moreover, force-fields are developed to reproduce dynamical behavior of the system and its free-energy landscape, rather than conformational energies specifically. For these reasons, we examine a force-field approach in Section 3.3.2 by correlating MD simulations to the measured experimental data.
3.2 Experimental benchmarks
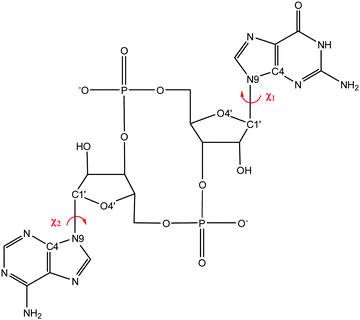
We are ultimately interested in the behaviour of CDNs in a water environment, where accurate reference conformational energies are not available. Instead, we focus specifically on the χ-dihedral angle (i.e. O4′–C1′–N9–C4), a structural feature that distinguishes between significantly populated conformers. The orientation of this angle is accessible to multiple NMR experimental setups. These features promise a less quantitative, but challenging and relevant benchmark for modelling of these systems in solution.We focused on three molecules, 3′3′-c-di-AMP, 3′3′-c-GAMP, and 3′3′-c-di-GMP (see Fig. 1.1-3), selected for the syn-/anti-dataset. Information about the orientation of χ-dihedral can be discerned from comparison of 3J(H1′,C8) and 3J(H1′,C4) coupling constants Fig. S2 (ESI†). The relative magnitude of coupling constants 3J(H1′,C8) > 3J(H1′,C4) indicates anti-orientation; 3J(H1′,C8) < 3J(H1′,C4) indicates syn-orientation. Our observed values of 3J(H1′,C8) = 2.1 to 3.0 Hz and 3J(H1′,C4) < 1 Hz therefore indicate anti-orientation. Alternatively, correlation of measured and calculated 1H chemical shifts also suggest prevalence of the anti-/anti-conformation, see Table S19 (ESI†).
This conclusion is further supported by transient NOE signals between a purine proton (e.g. H8) and a ribose proton (e.g. H1′), see Table S20 (ESI†). In line with conclusions presented by Wang et al.,23 we observe that for all three molecules, these measurements clearly suggest a dominant population of anti-conformers.
Even more detailed information may be provided by relative NOE signals from 2D-ROESY spectra. Here too, the relative intensities of cross-peaks indicate a general preference for the anti-conformation. However, the weak observed cross-peaks H2/H2′ and H2/H3′ may indicate the presence of a certain population of syn-conformations. Selected observed NOEs together with calculated “inter-proton” distances are summarized in Table S21 (ESI†).
Moreover, the 1/r6 decay of the signals and their relative strength to proton pairs with known mutual distance (such as H1′–H2′ ribose proton pair) may be used to asses compliance of a candidate structure with the measured signals. We focus on the relative strength of the H8/H1′ signal. According to MD simulations, this proton pair provides well separated peaks of distance distributions (see Fig. S3, ESI†), which allows for distinguishing between anti- and syn-conformations.
Experimental ROESY signals of H8/H1′ as well as hypothetical signal strengths of the lowest-energy conformers of the syn-/anti-data set are shown in Table 4. In the case of 3′3′-c-GAMP and 3′3′-c-di-GMP, the observed values are not consistent with any of the considered conformers. An intermediate χ-conformer (corresponding to χ ≈ 140° or χ ≈ −20°) would justify observed signal strength, but such a conformer was not found in a conformational search. Hence, we interpret this as an indication of a mixed population of anti- and syn-conformers, which can be estimated from a linear combination of signals of individual conformers. Such an estimate is underdetermined, but permissible solutions are in a narrow range (see Table 5).
| CDN | ROESY | Anti-/anti- | Syn-/anti- | Anti-/syn- | Syn-/syn- |
|---|---|---|---|---|---|
| a Syn-/anti- and anti-/syn-designations refer to the same conformers for these molecules. | |||||
| 3′3′-c-di-AMPa | 0.19 | 0.17 | 1.48 | 1.48 | 3.04 |
| Adenine of 3′3′-c-GAMP | 0.30 | 0.14 | 0.15 | 2.79 | 2.81 |
| Guanine of 3′3′-c-GAMP | 0.43 | 0.17 | 2.21 | 0.17 | 2.99 |
| 3′3′-c-di-GMPa | 0.52 | 0.17 | 1.44 | 1.44 | 2.68 |
| CDN | Syn-/anti-dataset | MD ensembles |
|---|---|---|
| 3′3′-c-di-AMP | 98–99% | 98% |
| Adenine of 3′3′-c-GAMP | 94% | 90% |
| Guanine of 3′3′-c-GAMP | 87–91% | 81% |
| 3′3′-c-di-GMP | 72–86% | 74% |
Alternatively, we may use an ensemble of χ-conformers from MD trajectories (see below) for calculating hypothetical signal strength and compare them to their experimental counterparts. This leads to very similar conclusions regarding the population of purely anti-conformations. This is because the H8/H1′ signal strength is primarily determined by the value of χ-dihedral and thus even if the QM structures and/or MD ensembles are not entirely accurate, the result of the analysis is robust.
3.3 Accuracy of modelling structural features in solvent (syn-/anti-set and MD simulations)
| CDN | χ-Conformer class | Reference Egpa/COSMO-RS | B-LYP/COSMO-RS | B-LYP/COSMO | B-LYP/SMD | B-LYP (gas-phase) |
|---|---|---|---|---|---|---|
| a DLPNO-CCSD(T) TightPNO/MP2-F12 used as reference gas-phase energies, see eqn (2). | ||||||
| 3′3′-c-di-AMP | Anti-/anti- | 0.9 | 0.4 | 0.0 | 0.0 | 0.0 |
| Syn-/anti- | 0.0 | 0.0 | 2.3 | 2.9 | 10.9 | |
| Syn-/syn- | 2.9 | 2.4 | 5.9 | 5.8 | 22.6 | |
| 3′3′-c-GAMP | Anti-/anti- | 2.3 | 2.9 | 2.1 | 1.6 | 17.1 |
| Anti-/syn- | 0.0 | 0.0 | 4.7 | 4.8 | 27.6 | |
| Syn-/anti- | 0.3 | 0.6 | 0.0 | 0.0 | 0.0 | |
| Syn-/syn- | 2.5 | 2.9 | 2.0 | 2.5 | 13.3 | |
| 3′3′-c-di-GMP | Anti-/anti- | 2.1 | 2.7 | 2.0 | 0.0 | 18.3 |
| Syn-/anti- | 0.0 | 0.0 | 0.8 | 0.0 | 10.3 | |
| Syn-/syn- | 3.9 | 3.9 | 0.0 | 0.6 | 0.0 | |
In all cases, the gas-phase energy strongly prefers the syn-orientation for the guanine base as this allows for formation of an intramolecular hydrogen bond. This results in a very straightforward ranking of conformers for all electronic structure methods (only the B-LYP functional is shown here), where adenines prefer anti-orientation, while guanines prefer syn-orientation.
Including solvation treatment flattens the energy range of conformer classes down to mere units of kcal mol−1. Indeed, the solvation treatment largely counteracts the preference for the intramolecular hydrogen bond.
The NMR experiments presented in the previous section showed two qualitative trends – a higher propensity for the syn-conformation of guanine and predominant anti-/anti-orientation for all three studied molecules. Although the details vary across the methods and both of these trends can be recognized to some extent, none of the methods/solvation models reproduce both of these trends at the same time.
Observed differences of 1–3 kcal mol−1 between anti-/anti- and syn-/anti-conformers in Table 6 make it unlikely for the electronic structure methods to be responsible for the disagreement, as these are observed even for DLPNO-CCSD(T) TightPNO/MP2-F12(+COSMO-RS) for which the estimated error is one order of magnitude smaller.
A potential reason for the incorrect relative free energies are inaccurate structures. In Section 3.1 we showed that some of the methods show systematic bias by over- or under-stabilizing closed structures. Table 6 shows the results for structures optimized with B-P/COSMO, which showed a bias for over-stabilizing the closed structures. For this reason, we reoptimized the structures in the syn-/anti-dataset with TPSS (which showed an under-stabilizing bias for closed structures) and B3-LYP (which was bias free), see Table 2. We combined both methods with CPCM and SMD solvation models and reevaluated the relative free conformational energies. The results are shown in Table S22 (ESI†), which shows that the situation is not remedied by optimization by other methods. Even with structures obtained with different approaches, none of the methods consistently reproduce both of the trends observed in the NMR experiments.
Another potential reason for underestimating anti-conformers are the entropic contributions, which have been neglected so far. We have performed normal-mode analysis on all 26 structures of the syn-/anti-data set. Inclusion of the thermal contributions and zero-point vibrational energies do not, however, reverse the observed trends. A more detailed look into the magnitude of these terms can be found in Table S23 (ESI†). Moreover, normal-mode analysis only provides “local” entropic information, not accounting for (co)existence of other conformers.
| CDN | χ-Conformer | MD population % | MD population syn-/anti-ratio % | Estimates for ROESY % |
|---|---|---|---|---|
| 3′3′-c-di-AMP | Anti-/anti- | 57 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77 77 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 98 98 |
| Syn-/anti- | 40 | |||
| Syn-/syn- | 3 | |||
| 3′3′-c-GAMP | Anti-/anti- | 18 | G: 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 27 |
G: 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81 81 |
| Gsyn-/Aanti- | 61 | A: 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79 79 |
A: 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 90 |
|
| Ganti-/Asyn- | 9 | |||
| Syn-/syn- | 12 | |||
| 3′3′-c-di-GMP | Anti-/anti- | 8 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 23 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 74 |
| Syn-/anti- | 31 | |||
| Syn-/syn- | 61 |
The most prominent feature in Table 7 is the different preference for syn-/anti-conformations of guanine and adenine. Similarly to the result provided by gas-phase conformational energies (Table 6), guanine does show higher preference for syn-, the syn- to anti-ratio being approximately 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. On the other hand, adenine prefers the anti-conformation by about the same margin, i.e. 1
1. On the other hand, adenine prefers the anti-conformation by about the same margin, i.e. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. This points to strong overestimation of the syn-conformations for guanine (e.g., syn-conformation for 3′3′-c-di-GMP is 77% in MD compared to less than 25% estimate from ROESY spectra), but not so much for adenine. We traced this to an overly stable hydrogen bond, which occurs between the amino group of guanine and phosphate oxygen that is present only when guanine is in the syn-orientation. It has recently been pointed out that this type of base-phosphate hydrogen bond appears to be too stable in current amber force fields,121,122 and therefore we consider this inaccuracy to be a consequence of a known force field artifact. It is worth noting that the orientation of bases in the MD simulations are mostly independent of each other. Assuming the probability of the anti-conformation to be 76% for adenine and 22% for guanine describes the overall conformer population reasonably well, see Table S24 (ESI†).
3. This points to strong overestimation of the syn-conformations for guanine (e.g., syn-conformation for 3′3′-c-di-GMP is 77% in MD compared to less than 25% estimate from ROESY spectra), but not so much for adenine. We traced this to an overly stable hydrogen bond, which occurs between the amino group of guanine and phosphate oxygen that is present only when guanine is in the syn-orientation. It has recently been pointed out that this type of base-phosphate hydrogen bond appears to be too stable in current amber force fields,121,122 and therefore we consider this inaccuracy to be a consequence of a known force field artifact. It is worth noting that the orientation of bases in the MD simulations are mostly independent of each other. Assuming the probability of the anti-conformation to be 76% for adenine and 22% for guanine describes the overall conformer population reasonably well, see Table S24 (ESI†).
Thus, while higher propensity of guanine for syn-compared to adenine is reproduced by both the QM single-point approach and by force-field MD simulations, this trait usually overshadows the overall observed preference for the anti-conformation in all three molecules. The rare case where the anti-/anti-conformation is correctly reproduced to be prevalent is in MD simulations of 3′3′-c-di-AMP, but even here the prevalence is marginal over the syn-/anti-conformation, while the experiments indicate the strongest presence of anti-conformations. Although the BLYP/SMD solvation model prefers anti-/anti- for 3′3′-c-di-AMP as well, it is at the expense of the other qualitative trend, i.e. higher propensity for the syn-conformation of the guanine base. Thus, both QM and MD underestimate the anti-/anti-conformation in all three cases, albeit to a varying extent.
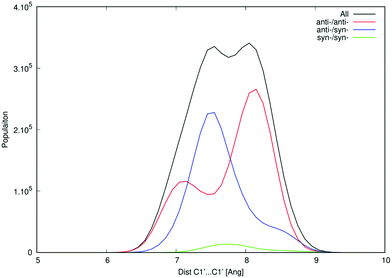
One of the apparent differences between structures provided by DFT/COSMO optimization (the syn-/anti-dataset) and structures from MD trajectories is the openness of the macrocycle, see Fig. 3. Even a small deformation of several backbone angles is enough to open the structure and expose both sides of the bases to the solution. For the force-field, the distributions of the backbone angles in the closed form are shifted slightly outside their usual energy minima, which leads to its lower thermodynamic stability. This is reflected by the C1′–C1′ distances obtained for 3′3′-c-di-AMP in Fig. 4. It remains unclear whether predominance of the open form is natural or whether it is a force field artifact. However, both of the distribution peaks in Fig. 4 are significantly higher than corresponding distances obtained in the syn-/anti-dataset (ca. 6 Å for anti-/anti-conformers of 3′3′-c-di-AMP, compared to peaks of ca. 7 Å and 8 Å in MD populations).
We can obtain some insight about the openness of the structure (discussed above in terms of C1′–C1′ distances) by looking at the torsion angles of the macrocycle. We refrain from exhaustive comparison of structural parameters and focus instead on two torsion angles, namely β and ε (see Fig. S4, ESI†), which highlight the issue. For both angles, MD populations show better agreement with values obtained from NMR than the QM structures of the syn-/anti-dataset (see Tables S26 and S27, ESI†). Moreover, a restrained optimization of the QM structures that pushes C1′–C1′ further apart does force β and ε torsions towards the experimental values (data not shown). This indicates that QM structures obtained by optimization in implicit solvent are inaccurate, leading to slight deformations of the macrocycle and geometries that are too closed, which contributes to inaccurate prediction of relative conformational energies.
4. Conclusions
In this work, we evaluated the performance of modelling approaches by two different benchmarks: (1) gas-phase conformational energies referenced to a DLPNO-CCSD(T)/MP2-F12 composite scheme and (2) qualitative prediction of a structural feature (orientation of the purine base) in solvent vs. NMR experiment.First, we have shown that most of the density functional approximations provide conformational energies with good accuracy, provided that a dispersion correction is used. A typical mean unsigned error is below 1 kcal mol−1, which represents around 3% of the conformational energy range in the dataset. Hybrid functionals outperform GGA and meta-GGA functionals by only a very small margin (ca. 0.1 kcal mol−1 in mean unsigned error). Thus, computational cost and compatibility with other modelling options are recommended as the criteria of choice. In particular, use of the economical DZVP-DFT basis set even in combination with a GGA functional gives results comparable to the best DFT setups that come at significantly higher computational cost. However, use of DZVP-DFT is only efficient in combination with reparametrized dispersion correction.91 On the other hand, semi-empirical methods do not provide a satisfactory approximation for conformational energies. A typical error of tested MNDO methods and tight-binding schemes is on the order of several units of kcal mol−1.
Second, we addressed the conformational behavior of cyclic dinucleotides in solvent (water), which represents a more realistic setup. NMR experiments, carried out for 3′3′-c-di-AMP, 3′3′-c-GAMP, and 3′3′-c-di-GMP, unequivocally identified the dominant anti-orientation of the purine bases. Presence of a certain population of the syn-conformer is, however, apparent for the two systems containing guanine.
While higher occurrence of the syn-conformation for guanine is recognized by most approaches, the overall dominance of the anti-conformation for all molecules is not. Nevertheless, the differences still provide valuable insights.
Guanine's propensity for the syn-conformation is most likely due to the intramolecular hydrogen bond with a phosphate. This interaction is, unsurprisingly, very strong in a gas-phase context and is weakened to a limited extent by introduction of solvent. In MD simulations the interaction remains over-stabilized, leading to incorrectly predicting the syn-conformation to be dominant for guanine. Population of the χ-conformation in MD simulations is largely determined by the base, suggesting that improving the description of this specific interaction might improve the results significantly. For quantum-mechanical methods the reasons behind the discrepancy are not straightforward. Lack of explicit solvent and dynamical interactions with solvent likely lead to geometries that are too compact, which leads to inaccuracies in relative free-energies.
It should be reiterated that the chosen structural feature – the syn-/anti-equilibrium of the purine bases – remains an extremely challenging case for modelling. Despite the observed shortcomings, computational methods do provide useful insights into identifying relative trends (adenine vs. guanine preferences), less sensitive structural features (such as ribose phase angles), or interpretation of experimental data (e.g. H8/H1′ distances obtained from MD for the interpretation of ROESY spectra). By pointing to some of the inaccuracies provided by a range of available approaches we attempted to gauge the interpretability of the results in context where estimating computational “error bars” is often difficult.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was supported by the Grant Agency of the Czech Republic (17-16107S to P. J. and 20-08772S to L. R.). Computer time at the IT4I supercomputer center (project LM2018140 of the MSMT CR) is gratefully acknowledged.References
- O. Danilchanka and J. J. Mekalanos, Cyclic Dinucleotides and the Innate Immune Response, Cell, 2013, 154, 962–970 CrossRef CAS.
- U. Römling, M. Y. Galperin and M. Gomelsky, Cyclic di-GMP: the First 25 Years of a Universal Bacterial Second Messenger, Microbiol. Mol. Biol. Rev., 2013, 77, 1–52 CrossRef.
- X. Cai, Y.-H. Chiu and Z. J. Chen, The cGAS-cGAMP-STING Pathway of Cytosolic DNA Sensing and Signaling, Mol. Cell, 2014, 54, 289–296 CrossRef CAS.
- R. Fang, C. Wang, Q. Jiang, M. Lv, P. Gao, X. Yu, P. Mu, R. Zhang, S. Bi, J.-M. Feng and Z. Jiang, NEMO–IKKβ Are Essential for IRF3 and NF-κB Activation in the cGAS–STING Pathway, J. Immunol., 2017, 199, 3222–3233 CrossRef CAS PubMed.
- Q. Chen, L. Sun and Z. J. Chen, Regulation and function of the cGAS–STING pathway of cytosolic DNA sensing, Nat. Immunol., 2016, 17, 1142–1149 CrossRef CAS PubMed.
- J. Papinska, H. Bagavant, G. B. Gmyrek, M. Sroka, S. Tummala, K. A. Fitzgerald and U. S. Deshmukh, Activation of Stimulator of Interferon Genes (STING) and Sjögren Syndrome, J. Dent. Res., 2018, 97, 893–900 CrossRef CAS PubMed.
- M. Musella, G. Manic, R. De Maria, I. Vitale and A. Sistigu, Type-I-interferons in infection and cancer: Unanticipated dynamics with therapeutic implications, Oncoimmunology, 2017, 6, e1314424 CrossRef PubMed.
- X.-D. Li, J. Wu, D. Gao, H. Wang, L. Sun and Z. J. Chen, Pivotal Roles of cGAS-cGAMP Signaling in Antiviral Defense and Immune Adjuvant Effects, Science, 2013, 341, 1390–1394 CrossRef CAS PubMed.
- G. N. Barber, STING: infection, inflammation and cancer, Nat. Rev. Immunol., 2015, 15, 760–770 CrossRef CAS PubMed.
- B. Novotná, L. Vaneková, M. Zavřel, M. Buděšínský, M. Dejmek, M. Smola, O. Gutten, Z. A. Tehrani, M. Pimková Polidarová, A. Brázdová, R. Liboska, I. Štěpánek, Z. Vavřina, T. Jandušík, R. Nencka, L. Rulíšek, E. Bouřa, J. Brynda, O. Páv and G. Birkuš, Enzymatic Preparation of 2′–5′,3′–5′-Cyclic Dinucleotides, Their Binding Properties to Stimulator of Interferon Genes Adaptor Protein, and Structure/Activity Correlations, J. Med. Chem., 2019, 62, 10676–10690 CrossRef PubMed.
- H. Zhang, Q.-D. You and X.-L. Xu, Targeting Stimulator of Interferon Genes (STING): A Medicinal Chemistry Perspective, J. Med. Chem., 2020, 63, 3785–3816 CrossRef CAS PubMed.
- T. Lioux, M.-A. Mauny, A. Lamoureux, N. Bascoul, M. Hays, F. Vernejoul, A.-S. Baudru, C. Boularan, J. Lopes-Vicente, G. Qushair and G. Tiraby, Design, Synthesis, and Biological Evaluation of Novel Cyclic Adenosine–Inosine Monophosphate (cAIMP) Analogs That Activate Stimulator of Interferon Genes (STING), J. Med. Chem., 2016, 59, 10253–10267 CrossRef CAS PubMed.
- J. Chang, F. Guo, T. M. Block and J.-T. Guo, Use of Sting Agonists to Treat Chronic Hepatitis B Virus Infection, US pat., US10045961B2, 2018 Search PubMed.
- T. Ebensen, M. Morr and C. A. Guzman, Cyclic-Dinucleotides and Its Conjugates as Adjuvants and Their Uses in Pharmaceutical Compositions, US pat., US9597391B2, 2017 Search PubMed.
- F. Vernejoul, G. Tiraby and T. Lioux, Fluorinated Cyclic Dinucleotides for Cytokine Induction, World Intellectual Property Organization Patent, WO2016096174A1, 2016 Search PubMed.
- Study of MK-1454 Alone or in Combination With Pembrolizumab (MK-3475) in Participants With Advanced/Metastatic Solid Tumors or Lymphomas (MK-1454-001) - Full Text View - ClinicalTrials.gov, https://clinicaltrials.gov/ct2/show/NCT03010176, accessed May 5, 2020.
- Safety and Efficacy of MIW815 (ADU-S100) +/- Ipilimumab in Patients With Advanced/Metastatic Solid Tumors or Lymphomas - Full Text View - ClinicalTrials.gov, https://clinicaltrials.gov/ct2/show/NCT02675439, accessed May 5, 2020.
- J. Guo, J. Wang, J. Fan, Y. Zhang, W. Dong and C.-P. Chen, Distinct Dynamic and Conformational Features of Human STING in Response to 2′3′-cGAMP and c-di-GMP, ChemBioChem, 2019, 20, 1838–1847 CAS.
- B. Tang, B. Li, B. Li, Z. Li, J. Qin, X. Zhou, Y. Qiu, Z. Wu and M. Fang, The effect of V155M mutation on the complex of hSTING and 2′3′-cGAMP: an in silico study case, RSC Adv., 2017, 7, 39185–39196 RSC.
- M. Smola, O. Gutten, M. Dejmek, M. Kožíšek, T. Evangelidis, Z. Aliakbar Tehrani, B. Novotná, R. Nencka, G. Birkuš, E. Boura and L. Rulíšek, Ligand Strain and Its Conformational Complexity Is a Major Factor Determining Binding of Cyclic Dinucleotides to STING Protein, Angew. Chem., Int. Ed., 2021 DOI:10.1002/anie.202016805.
- Z. Vavřina, O. Gutten, M. Smola, M. Zavřel, Z. Aliakbar Tehrani, V. Charvát, M. Kožíšek, E. Boura, G. Birkuš and L. Rulíšek, Protein-Ligand Interactions in the STING Binding Site Probed by Rationally Designed Single-Point Mutations: Experiment and Theory, Biochemistry, 2021, 60, 607–620, DOI:10.1021/acs.biochem.0c00949.
- X. Che, J. Zhang, Y. Zhu, L. Yang, H. Quan and Y. Q. Gao, Structural Flexibility and Conformation Features of Cyclic Dinucleotides in Aqueous Solutions, J. Phys. Chem. B, 2016, 120, 2670–2680 CrossRef CAS PubMed.
- B. Wang, Z. Wang, U. Javornik, Z. Xi and J. Plavec, Computational and NMR spectroscopy insights into the conformation of cyclic di-nucleotides, Sci. Rep., 2017, 7, 16550 CrossRef PubMed.
- H. Shi, J. Wu, Z. J. Chen and C. Chen, Molecular basis for the specific recognition of the metazoan cyclic GMP-AMP by the innate immune adaptor protein STING, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 8947–8952 CrossRef CAS PubMed.
- X. Che, J. Zhang, H. Quan, L. Yang and Y. Q. Gao, CDNs–STING Interaction Mechanism Investigations and Instructions on Design of CDN-Derivatives, J. Phys. Chem. B, 2018, 122, 1862–1868 CrossRef CAS PubMed.
- E. Perola and P. S. Charifson, Conformational Analysis of Drug-Like Molecules Bound to Proteins: An Extensive Study of Ligand Reorganization upon Binding, J. Med. Chem., 2004, 47, 2499–2510 CrossRef CAS PubMed.
- D. L. Mobley and K. A. Dill, Binding of Small-Molecule Ligands to Proteins: “What You See” Is Not Always “What You Get, Structure, 2009, 17, 489–498 CrossRef CAS PubMed.
- J. He, W. Yin, M. Y. Galperin and S.-H. Chou, Cyclic di-AMP, a second messenger of primary importance: tertiary structures and binding mechanisms, Nucleic Acids Res., 2020, 48, 2807–2829 CrossRef CAS PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- L. Goerigk and S. Grimme, A General Database for Main Group Thermochemistry, Kinetics, and Noncovalent Interactions – Assessment of Common and Reparameterized (meta-)GGA Density Functionals, J. Chem. Theory Comput., 2010, 6, 107–126 CrossRef CAS PubMed.
- L. Goerigk, A. Karton, J. M. L. Martin and L. Radom, Accurate quantum chemical energies for tetrapeptide conformations: why MP2 data with an insufficient basis set should be handled with caution, Phys. Chem. Chem. Phys., 2013, 15, 7028–7031 RSC.
- L.-J. Yu, F. Sarrami, A. Karton and R. J. O’Reilly, An assessment of theoretical procedures for π-conjugation stabilisation energies in enones, Mol. Phys., 2015, 113, 1284–1296 CrossRef CAS.
- D. Folmsbee and G. Hutchison, Assessing conformer energies using electronic structure and machine learning methods, Int. J. Quantum Chem., 2021, 121, e26381 CrossRef CAS.
- M. Marianski, A. Supady, T. Ingram, M. Schneider and C. Baldauf, Assessing the Accuracy of Across-the-Scale Methods for Predicting Carbohydrate Conformational Energies for the Examples of Glucose and α-Maltose, J. Chem. Theory Comput., 2016, 12, 6157–6168 CrossRef CAS PubMed.
- Y. Li, S. Zhang, J. Z. H. Zhang and X. He, Assessing the performance of popular QM methods for calculation of conformational energies of trialanine, Chem. Phys. Lett., 2016, 652, 136–141 CrossRef CAS.
- M. K. Kesharwani, A. Karton and J. M. L. Martin, Benchmark ab Initio Conformational Energies for the Proteinogenic Amino Acids through Explicitly Correlated Methods. Assessment of Density Functional Methods, J. Chem. Theory Comput., 2016, 12, 444–454 CrossRef CAS PubMed.
- S. Kozuch, S. M. Bachrach and J. M. L. Martin, Conformational equilibria in butane-1,4-diol: a benchmark of a prototypical system with strong intramolecular H-bonds, J. Phys. Chem. A, 2014, 118, 293–303 CrossRef CAS PubMed.
- J. J. Wilke, M. C. Lind, H. F. Schaefer, A. G. Császár and W. D. Allen, Conformers of Gaseous Cysteine, J. Chem. Theory Comput., 2009, 5, 1511–1523 CrossRef CAS PubMed.
- D. Manna, M. K. Kesharwani, N. Sylvetsky and J. M. L. Martin, Conventional and Explicitly Correlated ab Initio Benchmark Study on Water Clusters: Revision of the BEGDB and WATER27 Data Sets, J. Chem. Theory Comput., 2017, 13, 3136–3152 CrossRef CAS PubMed.
- A. Mládek, P. Banáš, P. Jurečka, M. Otyepka, M. Zgarbová and J. Šponer, Energies and 2′-Hydroxyl Group Orientations of RNA Backbone Conformations. Benchmark CCSD(T)/CBS Database, Electronic Analysis, and Assessment of DFT Methods and MD Simulations, J. Chem. Theory Comput., 2014, 10, 463–480 CrossRef PubMed.
- G. I. Csonka, A. D. French, G. P. Johnson and C. A. Stortz, Evaluation of Density Functionals and Basis Sets for Carbohydrates, J. Chem. Theory Comput., 2009, 5, 679–692 CrossRef CAS PubMed.
- A. Karton and J. M. L. Martin, Explicitly correlated benchmark calculations on C8H8 isomer energy separations: how accurate are DFT, double-hybrid, and composite ab initio procedures?, Mol. Phys., 2012, 110, 2477–2491 CrossRef CAS.
- V. K. Prasad, A. Otero-de-la-Roza and G. A. DiLabio, PEPCONF, a diverse data set of peptide conformational energies, Sci. Data, 2019, 6, 1–9 CrossRef PubMed.
- D. Gruzman, A. Karton and J. M. L. Martin, Performance of Ab Initio and Density Functional Methods for Conformational Equilibria of CnH2n + 2 Alkane Isomers (n = 4–8), J. Phys. Chem. A, 2009, 113, 11974–11983 CrossRef CAS PubMed.
- H. Kruse, M. Havrila and J. Šponer, QM Computations on Complete Nucleic Acids Building Blocks: Analysis of the Sarcin–Ricin RNA Motif Using DFT-D3, HF-3c, PM6-D3H, and MM Approaches, J. Chem. Theory Comput., 2014, 10, 2615–2629 CrossRef CAS PubMed.
- H. Kruse, A. Mladek, K. Gkionis, A. Hansen, S. Grimme and J. Sponer, Quantum Chemical Benchmark Study on 46 RNA Backbone Families Using a Dinucleotide Unit, J. Chem. Theory Comput., 2015, 11, 4972–4991 CrossRef CAS PubMed.
- D. Řeha, H. Valdés, J. Vondrášek, P. Hobza, A. Abu-Riziq, B. Crews and M. S. de Vries, Structure and IR Spectrum of Phenylalanyl–Glycyl–Glycine Tripetide in the Gas-Phase: IR/UV Experiments, Ab Initio Quantum Chemical Calculations, and Molecular Dynamic Simulations, Chem. – Eur. J., 2005, 11, 6803–6817 CrossRef PubMed.
- U. R. Fogueri, S. Kozuch, A. Karton and J. M. L. Martin, The Melatonin Conformer Space: Benchmark and Assessment of Wave Function and DFT Methods for a Paradigmatic Biological and Pharmacological Molecule, J. Phys. Chem. A, 2013, 117, 2269–2277 CrossRef CAS PubMed.
- J. Řezáč, D. Bím, O. Gutten and L. Rulíšek, Toward Accurate Conformational Energies of Smaller Peptides and Medium-Sized Macrocycles: MPCONF196 Benchmark Energy Data Set, J. Chem. Theory Comput., 2018, 14, 1254–1266 CrossRef PubMed.
- J. M. L. Martin, What Can We Learn about Dispersion from the Conformer Surface of n-Pentane?, J. Phys. Chem. A, 2013, 117, 3118–3132 CrossRef CAS PubMed.
- M. Zgarbová, P. Jurečka, J. Šponer and M. Otyepka, A- to B-DNA Transition in AMBER Force Fields and Its Coupling to Sugar Pucker, J. Chem. Theory Comput., 2018, 14, 319–328 CrossRef PubMed.
- M. Zgarbová, F. J. Luque, J. Šponer, T. E. Cheatham, M. Otyepka and P. Jurečka, Toward Improved Description of DNA Backbone: Revisiting Epsilon and Zeta Torsion Force Field Parameters, J. Chem. Theory Comput., 2013, 9, 2339–2354 CrossRef PubMed.
- M. Zgarbová, J. Šponer, M. Otyepka, T. E. Cheatham, R. Galindo-Murillo and P. Jurečka, Refinement of the Sugar–Phosphate Backbone Torsion Beta for AMBER Force Fields Improves the Description of Z- and B-DNA, J. Chem. Theory Comput., 2015, 11, 5723–5736 CrossRef PubMed.
- M. Zgarbová, P. Jurečka, P. Banáš, M. Havrila, J. Šponer and M. Otyepka, Noncanonical α/γ Backbone Conformations in RNA and the Accuracy of Their Description by the AMBER Force Field, J. Phys. Chem. B, 2017, 121, 2420–2433 CrossRef PubMed.
- D. Sindhikara, S. A. Spronk, T. Day, K. Borrelli, D. L. Cheney and S. L. Posy, Improving Accuracy, Diversity, and Speed with Prime Macrocycle Conformational Sampling, J. Chem. Inf. Model., 2017, 57, 1881–1894 CrossRef CAS PubMed.
- Maestro Release 2017-1, Schrödinger LLC, New Yor, NY, 2017 Search PubMed.
- J. S. Richardson, B. Schneider, L. W. Murray, G. J. Kapral, R. M. Immormino, J. J. Headd, D. C. Richardson, D. Ham, E. Hershkovits, L. D. Williams, K. S. Keating, A. M. Pyle, D. Micallef, J. Westbrook and H. M. Berman, RNA backbone: Consensus all-angle conformers and modular string nomenclature (an RNA Ontology Consortium contribution), RNA, 2008, 14, 465–481 CrossRef CAS PubMed.
- J. E. Sokoloski, S. A. Godfrey, S. E. Dombrowski and P. C. Bevilacqua, Prevalence of syn nucleobases in the active sites of functional RNAs, RNA, 2011, 17, 1775–1787 CrossRef CAS PubMed.
- A. J. May and F. R. Manby, An explicitly correlated second order Møller-Plesset theory using a frozen Gaussian geminal, J. Chem. Phys., 2004, 121, 4479–4485 CrossRef CAS PubMed.
- D. P. Tew and W. Klopper, New correlation factors for explicitly correlated electronic wave functions, J. Chem. Phys., 2005, 123, 074101 CrossRef PubMed.
- R. A. Bachorz, F. A. Bischoff, A. Glöβ, C. Hättig, S. Höfener, W. Klopper and D. P. Tew, The MP2-F12 method in the TURBOMOLE program package, J. Comput. Chem., 2011, 32, 2492–2513 CrossRef CAS PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- N. C. Handy and A. J. Cohen, Left-right correlation energy, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- Y. Zhang and W. Yang, Comment on “Generalized Gradient Approximation Made Simple”, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Workhorse Semilocal Density Functional for Condensed Matter Physics and Quantum Chemistry, Phys. Rev. Lett., 2009, 103, 026403 CrossRef PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- L. Goerigk and S. Grimme, Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- D. Rappoport and F. Furche, Property-optimized Gaussian basis sets for molecular response calculations, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Optimization of Gaussian-type basis sets for local spin density functional calculations. Part I. Boron through neon, optimization technique and validation, Can. J. Chem., 1992, 70, 560–571 CrossRef CAS.
- F. Weigend, F. Furche and R. Ahlrichs, Gaussian basis sets of quadruple zeta valence quality for atoms H–Kr, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A generally applicable atomic-charge dependent London dispersion correction, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- J. Hostaš and J. Řezáč, Accurate DFT-D3 Calculations in a Small Basis Set, J. Chem. Theory Comput., 2017, 13, 3575–3585 CrossRef PubMed.
- J. J. P. Stewart, Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- G. B. Rocha, R. O. Freire, A. M. Simas and J. J. P. Stewart, RM1: A reparameterization of AM1 for H, C, N, O, P, S, F, Cl, Br, and I, J. Comput. Chem., 2006, 27, 1101–1111 CrossRef CAS PubMed.
- J. Řezáč and P. Hobza, Advanced Corrections of Hydrogen Bonding and Dispersion for Semiempirical Quantum Mechanical Methods, J. Chem. Theory Comput., 2012, 8, 141–151 CrossRef PubMed.
- J. J. P. Stewart, Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- M. Gaus, A. Goez and M. Elstner, Parametrization and Benchmark of DFTB3 for Organic Molecules, J. Chem. Theory Comput., 2013, 9, 338–354 CrossRef CAS PubMed.
- M. Gaus, X. Lu, M. Elstner and Q. Cui, Parameterization of DFTB3/3OB for Sulfur and Phosphorus for Chemical and Biological Applications, J. Chem. Theory Comput., 2014, 10, 1518–1537 CrossRef CAS.
- M. Gaus, Q. Cui and M. Elstner, DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB), J. Chem. Theory Comput., 2012, 7, 931–948 CrossRef PubMed.
- V. M. Miriyala and J. Řezáč, Description of non-covalent interactions in SCC-DFTB methods, J. Comput. Chem., 2017, 38, 688–697 CrossRef CAS PubMed.
- J. Řezáč, Empirical Self-Consistent Correction for the Description of Hydrogen Bonds in DFTB3, J. Chem. Theory Comput., 2017, 13, 4804–4817 CrossRef PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- R. Sure and S. Grimme, Corrected small basis set Hartree-Fock method for large systems, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, Consistent structures and interactions by density functional theory with small atomic orbital basis sets, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, B97-3c: a revised low-cost variant of the B97-D density functional method, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- C. W. Hopkins, S. Le Grand, R. C. Walker and A. E. Roitberg, Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning, J. Chem. Theory Comput., 2015, 11, 1864–1874 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- T. E. C. III, P. Cieplak and P. A. Kollman, A Modified Version of the Cornell et al. Force Field with Improved Sugar Pucker Phases and Helical Repeat, J. Biomol. Struct. Dyn., 1999, 16, 845–862 CrossRef.
- A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham, C. A. Laughton and M. Orozco, Refinement of the AMBER Force Field for Nucleic Acids: Improving the Description of α/γ Conformers, Biophys. J., 2007, 92, 3817–3829 CrossRef PubMed.
- M. Zgarbová, M. Otyepka, J. Sponer, A. Mládek, P. Banáš, T. E. Cheatham and P. Jurečka, Refinement of the Cornell et al. Nucleic Acids Force Field Based on Reference Quantum Chemical Calculations of Glycosidic Torsion Profiles, J. Chem. Theory Comput., 2011, 7, 2886–2902 CrossRef PubMed.
- M. Zgarbová, M. Otyepka, J. Šponer, F. Lankaš and P. Jurečka, Base Pair Fraying in Molecular Dynamics Simulations of DNA and RNA, J. Chem. Theory Comput., 2014, 10, 3177–3189 CrossRef.
- J. J. P. Stewart, MOPAC2016, Stewart Computational Chemistry, Colorado Springs, CO, USA, 2016 Search PubMed.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, DFTB+, a software package for efficient approximate density functional theory based atomistic simulations, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS PubMed.
- XTB, Grimme lab, 2020 Search PubMed.
- A. W. Götz, M. J. Williamson, D. Xu, D. Poole, S. Le Grand and R. C. Walker, Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born, J. Chem. Theory Comput., 2012, 8, 1542–1555 CrossRef.
- D. Case, R. Betz, D. S. Cerutti, T. Cheatham, T. Darden, R. Duke, T. J. Giese, H. Gohlke, A. Götz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T.-S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko and P. Kollman, Amber 16, University of California, San Francisco., 2016 Search PubMed.
- D. R. Roe and T. E. Cheatham, PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, How Accurate Are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Composed of Main-Group Elements?, J. Chem. Theory Comput., 2016, 12, 4303–4325 CrossRef CAS.
- B. D. Sellers, N. C. James and A. Gobbi, A Comparison of Quantum and Molecular Mechanical Methods to Estimate Strain Energy in Druglike Fragments, J. Chem. Inf. Model., 2017, 57, 1265–1275 CrossRef CAS PubMed.
- C. Bergonzo and T. E. Cheatham, Improved Force Field Parameters Lead to a Better Description of RNA Structure, J. Chem. Theory Comput., 2015, 11, 3969–3972 CrossRef CAS PubMed.
- P. Kührová, R. B. Best, S. Bottaro, G. Bussi, J. Šponer, M. Otyepka and P. Banáš, Computer Folding of RNA Tetraloops: Identification of Key Force Field Deficiencies, J. Chem. Theory Comput., 2016, 12, 4534–4548 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05993e |
| ‡ Currently at the Institute of Biotechnology of the Czech Academy of Sciences, BIOCEV, Průmyslová 595, 252 50 Vestec, Czech Republic. |
| This journal is © the Owner Societies 2021 |