Convergence behaviour of solvation shells in simulated liquids

Abstract

A convenient way to analyse solvent structure around a solute is to use solvation shells, whereby solvent position around the solute is discretised by the size of a solvent molecule, leading to multiple shells around the solute. The two main ways to define multiple shells around a solute are either directly with respect to the solute, called solute-centric, or locally for both solute and solvent molecules alike. It might be assumed that both methods lead to solvation shells with similar properties. However, our analysis suggests otherwise. Solvation shells are analysed in a series of simulations of five pure liquids of differing polarity. Shells are defined locally working outwards from each molecule treated as a reference molecule using two methods: the cutoff at the first minimum in the radial distribution function and the parameter-free Relative Angular Distance method (RAD). The molecular properties studied are potential energy, coordination number and coordination radius. Rather than converging to bulk values, as might be expected for pure solvents, properties are found to deviate as a function of shell index. This behaviour occurs because molecules with larger coordination numbers and radius have more neighbours, which make them more likely to be connected to the reference molecule via fewer shells. The effect is amplified for RAD because of its more variable coordination radii and for water with its more open structure and stronger interactions. These findings indicate that locally defined shells should not be thought of as directly comparable to solute-centric shells or to distance. As well as showing how box size and cutoff affect the non-convergence, to restore convergence we propose a hybrid method by defining a new set of shells with boundaries at the uppermost distance of each locally derived shell.

---

1 Introduction

Quantifying the molecular structure and interactions of liquids, solutions and mixtures is important in understanding their thermodynamic properties such as solubility, miscibility, colloidal stability and activity^1–4 as well as answering such questions as the range of solvent–solute interactions^5–10 The molecular structure of solvated systems is complicated because of the high-dimensional and highly variable distribution of configurations of all the participating molecules, ranging from crystalline order all the way to random disorder. Various methods are needed to simplify and reduce the dimensionality of the data and make it more comprehensible or tractable to further processing. The most widely used structural quantities for liquids are the particle coordinate distribution functions. The first-order one is molecular density but gives no molecular detail. The second-order one is the pairwise radial distribution function, g(r), which expresses the measured density of one species at a distance r from another species relative to the average density.¹¹ As well as being a highly intuitive quantity, it provides many points of comparison between simulation and experiment, whether it be g(r) itself, the entropy of liquids and dilute solutions,^12–15 or numerous other thermodynamic properties, such as isothermal compressibility or chemical potential via Kirkwood–Buff integrals of g(r).^16–21 For small, rigid, near-radially symmetric molecules, g(r) captures much structural information of interest along the single radial coordinate r. However, given its spherical nature, the validity and usefulness of g(r) diminishes for non-spherical solutes, and for spherical molecules it is unable to capture aspherical inhomogeneities. Partial solutions are using energy-derivative information to improve convergence,^22–25 multiple g(r)s relative to each solute atom,²⁶ angular information,^14,15 a three-dimensional grid centred on the solute,^27,28 or multiple grids localized on different solute atoms.²⁹ However, this makes them more complex, slower to converge, and still insensitive to inhomogeneities beyond the coordinates used.

An alternative way to analyse solution structure, motivated by the discrete size of molecules and the oscillatory structure typically seen in g(r), is to coarse-grain the distribution of the solvent around the solute into discrete shells.^30–32 Being based on molecular topology rather than distance, shells have the advantages of being statistically better defined, simpler to manipulate and interpret, more adaptable to fluctuations and lower symmetry, and better able to capture multibody effects based on molecular connectivity. The topological network of molecules in shells can be conveniently analysed using the tools of graph theory.³³ All this makes shells more amenable to complex, multi-component, flexible systems such as electrolytes, ionic liquids, liquid crystals, polymers, and biomolecules. The most commonly used shell is the one adjacent to the solute. Called the first shell or coordination shell, it represents the immediate environment of the solute and contains the solvent that is most perturbed by the solute, having the strongest interactions with it. Beyond this lie the second shell, the third shell and so on out to the edge of the system.

There is no unique way to define solvation shells, but two general classes of method exist. Shells may be defined with boundaries at every maximum in the g(r) relative to the solute, with multiple maxima leading to multiple shells. This is essentially a coarse-graining of g(r) which becomes less well-defined at longer range due to the smoother g(r). Alternatively, shells may be built locally with the first around the solute, the second shell around those molecules in the solute's first shell, the third shell around those molecules in the solute's second shell, and so on. Because local methods require knowing the environment of each individual solvent molecule, they are only accessible by simulation.^34–37 Each shell may be constructed from the g(r)-derived first shell of each molecule, using fixed cutoff parameters, or a fixed number of nearest neighbours.^38–43 Cutoffs assume mean-field, radially symmetric structure and require either well-defined g(r)s averaged over multiple configurations or multiple, arbitrary cutoff parameters, features that make them less suitable for systems of greater complexity. Alternatively, shells may be defined using topological methods which are parameter-free and directly applicable to individual configurations.^43–45 The most widely used method, Voronoi tesselation, identifies neighboring molecules as those that share polyhedra faces.^46,47 The number of Voronoi neighbors in the first shell of a molecule is typically overestimated^47,48 with respect to g(r), even for crystals because spurious second-shell molecules are included. However, these may be removed by adopting additional geometric criteria.^49–51 More recent methods based on blocking include the SANN algorithm⁵² (Solid-Angle Nearest Neighbor) which allows nearest neighbors up to a solid-angle threshold 4π and the RAD algorithm (Relative Angular Distance)^53,54 which defines blocking based on collinearity and inverse-square distance. RAD produces shells in close agreement with those using cutoffs at the first g(r) minimum⁵³ and is better able to handle the complexities of mixtures.⁵⁴ The advantages of topological methods are that they can resolve local density fluctuations and non-spherical symmetry and a particular property of them is that shells are always built locally rather than solute-centrically.

Despite the practical, intuitive nature and widespread use of solvation shells to analyse solvent structure, we encountered a number of properties of locally defined shells relating to their long-range convergence that are not well recognised and may not be immediately obvious. These properties concerned the inhomogeneity between different shells and inhomogeneity within each shell. To make clear this behaviour, we focus on shells in pure liquids rather than for solutes in a liquid so as to remove the perturbing effect of solutes,^5–10 which would otherwise obscure perturbations arising from other causes. Two local shell methods are used: the fixed cutoff at the first minimum in g(r) and RAD. Five liquids are chosen differing in their degree of polarity, namely water, ammonia, hydrogen sulfide, methane and argon. The properties examined are potential energy, coordination number and coordination radius, and they are analysed as a function of both distance and shell index from the reference molecule. Our main finding is that average bulk behaviour is not reached with increasing shell index, contrary to what is seen using solute-centric shells or g(r). The cause of this is that molecules with larger coordination number and radii have a higher probability to lie in lower-index shells. Our second finding is that within each shell, molecules with a smaller coordination number tend to lie closer to the reference molecule because of their smaller coordination radii. Both deviations are stronger for RAD than for the fixed-cutoff method but nonetheless are inherent to both methods. A third finding is that the direction of trends for potential energy are found to depend on the hydrogen-bond propensity of the liquid because stable energy correlates with low coordination for hydrogen-bonded liquids but high coordination for non-polar liquids. This non-convergence of locally defined shells shows that they should be used with care when analysing solvent structure in any system. To remedy this, we present a hybrid solute-centric and local way to define solvation shells that brings about long-range convergence. This is done by reassigning molecules to closer local shells at a certain distance from the solute. Going beyond the pure liquids studied here, this method can be readily generalised to solvent structure around any solute.

2 Methods

2.1 Shell definitions

The first shell of a designated reference molecule is assigned using two methods: Relative Angular Distance (RAD)⁵³ and the g(r) cutoff (GC) method with the cutoff at the first minimum in g(r). The RAD shell of molecule i is defined as containing those molecules j for which no other molecule k blocks that interaction and no other closer molecule is blocked. Blocking by k occurs ifwhere r_ij and r_ik are the distances from i to j and i to k, and θ_jik is the angle subtended at i by j and k. Roughly speaking, molecule k blocks if r_ik is smaller than r_ij and θ_jik is near zero. RAD is implemented in the symmetric version whereby each molecule must have the other molecule as a neighbor. The GC distance cutoffs are in line with g(r)s derived elsewhere, making allowances for the different temperatures, and are 3.5 Å for water,^55,56 4.0 Å for ammonia,^57–60 4.7 Å for hydrogen sulfide,⁶¹ 5.8 Å for methane,⁶² and 5.1 Å for argon.⁶³ Molecules in the second shell of the reference molecule are defined as all the molecules in the first shell of those molecules in the first shell of the reference molecule, excluding the reference molecule and any molecules that are already in its first shell. This is repeated iteratively to assign further shells until all molecules are assigned to a shell, ignoring periodic molecules.^{37,41,43,45,64} An example assignment of molecules to shells using RAD and GC for one configuration of liquid argon is depicted in Fig. 1a and b.

Fig. 1 Snapshot of liquid argon (5 Å thick cross-section) with atoms colored by their shell index defined using (a) RAD, (b) GC, (c) RAD-hybrid or (d) GC-hybrid methods (made in VMD⁶⁵).

2.2 Molecular properties

The following properties are used to assess the shells:

(1) Shell index ϕ ranks the shells. It ranges from 0 for the reference molecule up to the maximum shell index in the simulation box, avoiding periodicity.

(2) Molecular distance r is between a molecule and the reference molecule, with the heavy atom of each molecule defining its position.

(3) Molecular potential energy U is the sum of the potential energies of all the atoms in the molecule (see Simulation Protocol for more details).

(4) Coordination number N₁ is the number of molecules in the first shell of the molecule.

(5) Coordination radius r₁ is the average distance between a molecule and all its first-shell molecules using the heavy atom as the position of each molecule.

2.3 Simulation protocol

Molecular dynamics simulations of each of the five liquids are conducted with 600 molecules per box. The force-field parameters are those of Michels et al. for argon,⁶⁶ SPC/E for water⁵⁵ and GAFF for hydrogen sulfide, methane and ammonia.⁶⁷ Initial molecular geometries are created using Avogadro⁶⁸ and initial box geometries are created using Packmol,⁶⁹ where molecules are randomly assigned with a distance tolerance of 2 Å in cubic simulation boxes with length 26 to 32 Å. Three additional larger simulations are created for water containing 2134, 7200 and 24 300 water molecules to assess the affect of box size. System topology files are generated using the leap module of AMBER 18 (Assisted Model-Building and Energy Refinement)⁷⁰ and minimised for 500 steps of steepest-descent using sander.

The simulations thereafter are conducted using LAMMPS (Large-Scale Atomic/Molecular Massive Parallel Simulator)⁷¹ which prints out atomic potential-energy trajectories. AMBER topology and minimised coordinate files are converted into LAMMPS input files using InterMol.⁷² The system is equilibrated for 0.2 ns at NVT conditions (number, volume, temperature) and for 1 ns at NPT conditions (number, pressure, temperature), followed by 10 ns of NPT data collection. The temperatures used are 298 K for water, 240 K for ammonia, 213 K for hydrogen sulfide, 112 K for methane, and 87 K for argon. The pressure is 1 bar for all systems. Temperature and pressure are controlled using a Nosé–Hoover thermostat and barostat, respectively. Non-bonded interactions are truncated at 9 Å and long-range electrostatic interactions are calculated using particle–particle–particle–mesh (PPPM).⁷³ Atomic potential energies are calculated using the pe/atom command in LAMMPS. For the potential energy, the two-body and three-body energy terms are partitioned evenly over all contributing atoms and the long-range PPPM contribution is calculated using the method of Heyes.⁷⁴ The SHAKE algorithm constrains all bonds and angles to hydrogen atoms.⁷⁵ Trajectories of coordinates and potential energy for each atom are saved at 100 ps intervals, giving 100 frames for analysis, which are sufficient when averaged over 600 identical molecules, each in turn treated as the reference ‘solute’, totaling 60 000 data points for each system. Output files are read using the MDAnalysis Python library⁷⁶ and analysed using an in-house Python program. Plots are made with the matplotlib Python library.⁷⁷

3 Results

3.1 Average potential energy of shells

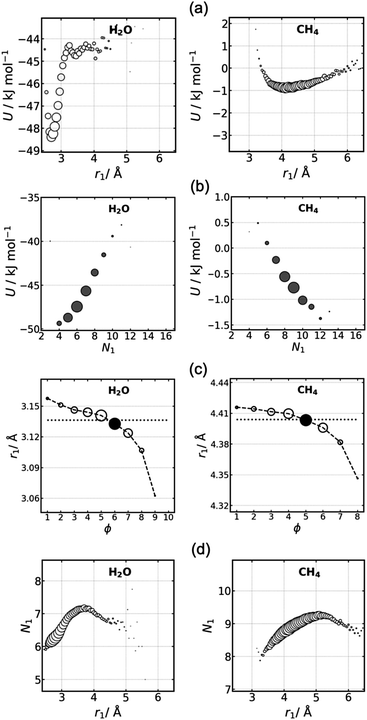
The average potential energy U of molecules in each shell defined with RAD and GC is plotted in Fig. 2. U is seen to deviate from the average value across shells for both methods at short and long ranges. The deviation is larger for RAD than GC, and largest in water compared to the less-polar liquids. Fig. S1 (ESI†) makes clear that the trends are converged with respect to the number of frames used, and Fig. S2 (ESI†) indicates that the total system energy has leveled off at the start of data collection.

Fig. 2 Potential energy U versus shell index ϕ (circles and dashed) and averaged over the whole system (dotted) for each liquid with shells defined by (a) RAD and (b) GC. The circle size indicates the number of molecules in the shell and the most common shell for each system is filled in.

This trend contrasts with the dependence of U on r, shown in Fig. 3. As expected, U shows some short-range fluctuation, reflecting local solvent structure, but then converges to a constant bulk value at long range for all liquids. If we look at how U varies within each shell as a function of distance r from the reference molecule, U shows a strong dependence on r in all liquids, with larger differences in U apparent in shells of more polar liquids. For RAD shells, U increases from the closer part of the shell to the outer part of the shell for water and ammonia, the trend is reversed for argon, while hydrogen sulfide and methane are more symmetric with both edges of the shell having a higher U and with a weaker dependence on distance. GC shells have more symmetric distributions of U for water and ammonia but more monotonic and decreasing for the other liquids. Of note is that the GC cutoff strongly influences the U distribution within a shell, as seen in Fig. S3 (ESI†), which shows that the trend for water goes from having a negative slope with cutoff 3 Å to a positive slope with cutoff 4 Å.

Fig. 3 Potential energy U of a molecule in a particular shell ϕ and distance r from the reference molecule for shells defined by (a) RAD or (b) GC. Averaged energy by distance is shown with a black dashed-line. Each marker represents an r bin value of 0.5 Å that is colored and shaped according to the shell index and sized according to its population.

3.2 Effect of coordination number and radius

To better understand the non-convergence of U, the influence of a molecule's coordination number and radius on potential energy is analysed. We focus on water and methane in Fig. 4 as representative polar and non-polar liquids, with results for all liquids being presented in Fig. S4–S7 (ESI†). First, as expected, the potential energy is sensitive to coordination radius, r₁ (Fig. 4a). There is a stable minimum at r₁ = 2.7 Å for water and 4.1 Å for methane with higher, less favorable energy at smaller and larger radii. The width of the minimum depends on the strength of interactions, with water having the sharpest minimum due to its hydrogen bonds compared to the broader minimum for methane with its weaker interactions. This sensitive dependence of U on r₁ for water makes clear why U deviates more for its solvation shells. Another observation is that at larger r₁ for RAD in the sparser region beyond the GC cutoff of 3.5 Å, U varies little for water but continues to increase for methane beyond its GC cutoff of 5.8 Å, indicating that water's hydrogen bonds are less affected by the lower density than are non-polar interactions. These trends are similar for all shells, as made clear by plots of U versus N₁ and r for each individual shell in Fig. S8 (ESI†) and its averaged version Fig. S9 (ESI†).

Fig. 4 Effect of (a) coordination radius and (b) number N₁ on potential energy U, (c) r₁versus ϕ, and (d) N₁versus r₁ for water (column 1) and methane (column 2) RAD shells. Marker size represents the population of molecules at each value.

Potential energy is also sensitive to coordination number (Fig. 4b). The trend is positive for water but negative for methane. Evidently, the lower N₁ of 4–7 for water is a consequence of its 3–5 hydrogen bonds and small number of interstitial molecules. Fewer neighbors means stronger hydrogen bonds tending to the stable tetrahedral arrangement and lower U. On the other hand, indicative of normal close-packed liquids, the negative trend for methane occurs because the greater number of 7–11 neighbors brings about more van der Waals interactions and thus a lower U. The trends are similar for the other three liquids according to their polarity (Fig. S5, ESI†). Hydrogen sulfide and argon are like methane, while ammonia with its weak hydrogen bonds lies in between, with U being lowest when there are nine neighbors. The trends are similar for RAD and GC, although RAD better picks out the anomalous reverse behavior for water and ammonia than GC.

Turning to Fig. 4c, molecules with closer neighbours are seen to be more common in more distant shells. This can also be understood as molecules with fewer neighbours being more common in more distant shells because we see in Fig. 4d that r₁ and N₁ are closely correlated for all but the highest values of r₁. This trend is important to explain the non-converging U in local shell assignment because N₁ relates to connectivity and thus ϕ while r₁ to U, thereby relating U to ϕ.

The final trend of interest is r₁versus r, shown in Fig. S10 (ESI†). This shows a clear increase in r₁versus r for all shells, liquids and methods, demonstrating that this appears to be a universal property of locally defined shells. Smaller shells lie at closer distances and larger shells at further distances.

3.3 Model to explain non-convergence with shell index

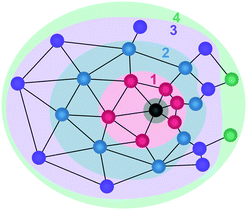
We next construct a model to explain the non-convergence of properties with shell index. Fig. 5 illustrates the shells around a solute, showing regions of molecules separated by larger and smaller distances. When assigning shells locally, what matters is not the separating distance to the solute, as in a solute-centric approach, but the number of intervening molecules. Molecules that have more neighbours have further neighbours and vice versa for fewer neighbours. Molecules with further neighbours themselves lie further distances away from other molecules, including the reference molecule. In addition, molecules with more neighbours are more likely to be more closely connected by fewer shells. Thus a region containing molecules that are more closely spaced has more intervening shells than a region containing fewer molecules, while molecules with more neighbours have fewer intervening shells. Given the dependence of coordination size and number on shell index, this makes other properties such as energy depend on shell index, particularly for polar solvents because they have a larger energetic dependence on the number of neighbours and distance between neighbours.

Fig. 5 Schematic to illustrate the non-convergence of properties as a function of shell index. Molecules are coloured by shell index and black lines link molecules in each other's coordination shells. Closer proximity on the right brings out the two effects: it causes molecules at a given distance to be assigned to more distant shells, and it causes molecules in a given shell to lie at a shorter distance within the shell.

3.4 Methods to reduce the non-convergence

We finally look at how locally derived shells can be converted into another set of shells that do have convergence in their properties. The boundaries of the new shells are placed at the uppermost distance of each locally derived shell. The dependence of U with shell index using the new shells is plotted in Fig. 6 for all liquids and both methods, now labelled as RAD-hybrid and GC-hybrid. It can be seen that rapid convergence of U to the average value occurs for all liquids and methods, similar to what is seen for U as a function of r. Evidently, this reassignment redistributes the molecules between and within locally derived shells to even out their properties. This thus provides a way to define solvation shells that have convergence of properties but without the need for defining shell thickness. Another possible way to bring about property convergence is to vary the size of the simulation box. However, boxes with larger side lengths of 40, 60 and 90 Å for water using RAD are seen to still show a similar non-convergent trend (Fig. S11, ESI†), but the size of the deviation is smaller in larger boxes. Yet another possible approach to bring about property convergence applicable to the GC method is to vary the GC cutoff. The effect of this on convergence may be seen in Fig. S12 (ESI†) which shows the dependence of r₁ on ϕ and r for three different cutoffs of 3, 3.5 and 4 Å. When the cutoff is 3 Å, which is near the g(r) maximum, the non-convergence is substantially reduced, suggesting that having smaller shells that are more homogeneous in size makes them less susceptible to this behaviour. However, even with this cutoff, Fig. S10 (ESI†) shows that U is still not converged versus ϕ.

Fig. 6 As for Fig. 2 but using the hybrid RAD and GC methods whereby boundaries are defined by the largest distances of the locally derived shells.

The resulting set of shells are illustrated in Fig. 7 for both methods and all liquids. This shows the U distribution of each locally derived shell as in Fig. 3 but coloured according to the new shell definition. It creates solvation shells that are slightly thicker closer to the reference molecule.

Fig. 7 As in Fig. 3, but using the hybrid RAD and GC methods whereby boundaries are defined by the largest distances of the locally derived shells.

4 Discussion

Solvation shells provide an intuitive model to simplify and represent the structure of a liquid around a central solute molecule. They are especially useful for larger, intricate, flexible molecules, for which Cartesian coordinate-based methods become too complex or intractable. Shells better adapt to the flexible structure of both solute and solvent molecules than coordinate-based methods. While the general idea is to discretise shells based on the size of the solvent molecule, there is no unique way to define them. Here we show that for shells defined locally in a pure liquid, their properties do not converge to bulk values at long range either in terms of distance or shell index. In particular, molecules in more distant shells are found to have lower coordination number and radius than those in closer shells. Moreover, molecules in the inner edge of a shell have lower coordination number and radius than those in the outer edge. The explanations for these two trends are geometrical, as illustrated in Fig. 5. The first trend reflects a greater probability for molecules with larger coordination number and radius to end up in shells closer to the reference molecule because their greater number of neighbours gives them more connections with neighbouring molecules and because their larger size means there are fewer separating neighbours between them and the reference molecule. Conversely, molecules with smaller coordination number and radius are more likely to end up in more distant shells. The second trend arises because molecules with smaller coordination number and radius are more likely to lie closer to their neighbours, while those with larger values lie further away. RAD is more sensitive to this effect because its coordination radii are more variable than those of GC which has a fixed cutoff, especially for water with its open structure, but even GC is not immune. However, RAD still has the advantages that it resolves instantaneous structure, it reveals structure beyond the GC cutoff, and it better resolves the anomalous structure in the hydrogen-bonded liquids.

It is interesting that the shell effect analysed here affects potential energy differently, depending on the liquid. Higher coordination brings about less stable energy for the hydrogen-bonding liquids of water and ammonia but more stable energy for the close-packed liquids of methane and argon. This reflects the well-known behaviour of hydrogen-bonded liquids such as water⁷⁸ and to a lesser extent ammonia^57–60 to have a low coordination because the directionality of hydrogen bonds limits the number of neighbors. On the other hand, molecules in close-packed liquids are dominated by van der Waals interactions, whose non-directional nature permits multiple interactions, so enabling higher coordination to bring about more stable energy. Within each shell, potential energy may increase or decrease with increasing distance, depending on the method and liquid.

Considering possible ways to reduce the non-convergence, using a larger box helps somewhat (Fig. S11, ESI†). Going further away from the reference molecule and including molecules in periodic images would bring about further softening but only as an artifact of periodicity. Using a smaller GC cutoff also reduces the effect (Fig. S12, ESI†). Other solutions not attempted here could be to allocate a molecule to a new shell if more than one neighbor belongs to the preceding shell, or to allow shells to get thicker further away from the reference molecule, a limit of which would be having only the first shell with the rest of the solvent as bulk, as is commonly done. Recourse could always be made to the solute-centric option of defining shells from multiple peaks in g(r) using the solute as a common reference point, effectively a molecular-level coarse-graining of g(r). This avoids the non-convergence behaviour by angular averaging but struggles to resolve shells at larger distances in the flatter g(r) arising from the diminishing correlation with the solute, reflecting the reduced structuring further from the solute. In contrast, there is no such reduction of long-range structure in the graph of connections generated locally for every molecule, but instead there is long-range non-convergence. As one way to combine the features of both methods, we present an approach that suppresses non-convergence by defining shell boundaries at the maximum distance of each locally derived shell but at the cost of radial averaging. This results in shells having converged potential energies as a function of shell index in the same manner as solute-centric shells or g(r) itself.

5 Conclusions

An analysis of the properties of solvation shells defined locally in pure liquids has revealed that properties do not converge to the bulk values, either averaged over each shell or within each shell. Coordination number and radius are found to decrease in more distant shells and to increase from the inner to the outer part of each shell. The reason for these trends is that the properties of larger coordination number and radius make such molecules more likely to lie in closer shells and at the outer part of each shell. The shell dependence is greater for RAD than GC because of the greater variability of RAD coordination, but RAD reveals instantaneous structure, structure beyond the GC cutoff and the anomalous structure in the hydrogen-bonded liquids. The effect on potential energy differs for each liquid. Hydrogen-bonded water and ammonia have smaller coordination and lower potential energy whereas non-polar hydrogen sulfide, methane and argon have larger coordination and higher potential energy. We examine approaches to reduce the non-convergence and show how a hybrid method with cutoffs at the maximum distance of locally derived shells restores long-range convergence. These effects for pure liquids will inevitably carry over to solutions and complex mixtures of larger and more flexible molecules. Our analysis reinforces the complexity of analysing liquid structure, which is part-discrete, suitable to shell approaches and part-continuous, suitable to g(r) approaches. Which approach one uses largely depends on the complexity of the system, whether molecular distance or molecular topology is more important, and whether one wishes to detect aspherical inhomogeneities or ensure long-range convergence.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Research IT of the University of Manchester for access to and support with using the Computational Shared Facility. J. K. was supported by the EPSRC under grant codes EP/L015218/1 and EP/N025105/1.

References

1. S. v. Bülow, M. Siggel, M. Linke and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9843–9852.
2. K. D. Collins, Quart. Rev. Biophys., 2019, 52, e11.
3. C. C. Bannan, G. Calabró, D. Y. Kyu and D. L. Mobley, J. Chem. Theory Comput., 2016, 12, 4015–4024.
4. G. Duarte Ramos Matos, G. Calabrò and D. L. Mobley, J. Chem. Theory Comput., 2019, 15, 3066–3074.
5. K. D. Collins, G. W. Neilson and J. E. Enderby, Biophys. Chem., 2007, 128, 95–104.
6. R. Mancinelli, A. Botti, F. Bruni, M. A. Ricci and A. K. Soper, Phys. Chem. Chem. Phys., 2007, 9, 2959–2967.
7. D. Paschek and R. Ludwig, Angew. Chem., Int. Ed., 2011, 50, 352–353.
8. S. J. Irudayam and R. H. Henchman, J. Chem. Phys., 2012, 137, 034508.
9. Y. X. Chen, H. I. Okur, N. Gomopoulos, C. Macias-Romero, P. S. Cremer, P. B. Petersen, G. Tocci, D. M. Wilkins, C. W. Liang, M. Ceriotti and S. Roke, Sci. Adv., 2016, 2, e1501891.
10. P. Jungwirth and D. Laage, J. Phys. Chem. Lett., 2018, 9, 2056–2057.
11. J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548.
12. D. C. Wallace, J. Chem. Phys., 1987, 87, 2282–2284.
13. A. Baranyai and D. J. Evans, Phys. Rev. A, 1989, 40, 3817–3822.
14. T. Lazaridis and M. Karplus, J. Chem. Phys., 1996, 105, 4294–4316.
15. T. Lazaridis and M. E. Paulaitis, J. Phys. Chem., 1992, 96, 3847–3855.
16. J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777.
17. M. B. Gee and P. E. Smith, J. Chem. Phys., 2009, 131, 165101.
18. E. A. Ploetz, N. Bentenitis and P. E. Smith, J. Chem. Phys., 2010, 132, 164501.
19. P. Ganguly and D. E. R. van, J. Chem. Theory Comput., 2013, 9, 1347–1355.
20. A. A. Galata, S. D. Anogiannakis and D. N. Theodorou, Fluid Phase Equil., 2018, 470, 25–37.
21. N. Dawass, P. Krüger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, J. M. Simon and T. J. H. Vlugt, Mol. Simul., 2018, 44, 599–612.
22. P. Kruger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, T. J. H. Vlugt and J. M. Simon, J. Phys. Chem. Lett., 2013, 4, 235–238.
23. D. Borgis, R. Assaraf, B. Rotenberg and R. Vuilleumier, Mol. Phys., 2013, 111, 3486–3492.
24. A. J. Schultz, S. G. Moustafa, W. S. Lin, S. J. Weinstein and D. A. Kofke, J. Chem. Theory Comput., 2016, 12, 1491–1498.
25. D. de las Heras and M. Schmidt, Phys. Rev. Lett., 2018, 120, 218001.
26. P. K. Mehrotra and D. L. Beveridge, J. Am. Chem. Soc., 1980, 102, 4287–4294.
27. I. M. Svishchev and P. G. Kusalik, J. Chem. Phys., 1993, 99, 3049–3058.
28. P. G. Kusalik and I. M. Svishchev, Science, 1994, 265, 1219–1221.
29. R. H. Henchman and J. A. McCammon, J. Comput. Chem., 2002, 23, 861–869.
30. H. G. Hertz, Angew. Chem., Int. Ed. Engl., 1970, 9, 124–138.
31. R. W. Impey, P. A. Madden and I. R. McDonald, J. Phys. Chem., 1983, 87, 5071–5083.
32. Y. Marcus, Chem. Rev., 2009, 109, 1346–1370.
33. F. Rao, S. Garrett-Roe and P. Hamm, J. Phys. Chem. B, 2010, 114, 15598–15604.
34. T. M. Raschke and M. Levitt, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6777–6782.
35. N. Bhattacharjee and P. Biswas, J. Phys. Chem. B, 2011, 115, 12257–12265.
36. S. S. Ribeiro, N. Samanta, S. Ebbinghaus and J. C. Marcos, Nat. Rev. Chem., 2019, 3, 552–561.
37. V. Zeindlhofer, M. Berger, O. Steinhauser and C. Schröder, J. Chem. Phys., 2018, 148, 193819.
38. A. Luzar and D. Chandler, Phys. Rev. Lett., 1996, 76, 928–931.
39. S. J. Irudayam and R. H. Henchman, J. Phys.: Condens. Matter, 2010, 22, 284108.
40. S. J. Irudayam and R. H. Henchman, Mol. Phys., 2011, 109, 37–48.
41. F. Persson, P. Söderhjelm and B. Halle, J. Chem. Phys., 2018, 148, 215101.
42. T. J. Yoon, M. Y. Ha, W. B. Lee and Y.-W. Lee, J. Chem. Phys., 2018, 149, 014502.
43. H. Tanaka, H. Tong, R. Shi and J. Russo, Nat. Rev. Phys., 2019, 1, 333–348.
44. V. P. Voloshin, N. N. Medvedev, N. Smolin, A. Geiger and R. Winter, Phys. Chem. Chem. Phys., 2015, 17, 8499–8508.
45. G. Neumayr, T. Rudas and O. Steinhauser, J. Chem. Phys., 2010, 133, 084108.
46. G. Voronoi, J. Reine Angew. Math., 1908, 134, 97–178.
47. J. L. Finney, Proc. R. Soc. London Ser. A, 1970, 319, 479–493.
48. A. Rahman, J. Chem. Phys., 1966, 45, 2585–2592.
49. A. Geiger, N. N. Medvedev and Y. I. Naberukhin, J. Struct. Chem., 1992, 33, 226–234.
50. R. Abseher, H. Schreiber and O. Steinhauser, Proteins, 1996, 25, 366–378.
51. A. Malins, S. R. Williams, J. Eggers and C. P. Royall, J. Chem. Phys., 2013, 139, 234506.
52. J. A. van Meel, L. Filion, C. Valeriani and D. Frenkel, J. Chem. Phys., 2012, 136, 234107.
53. J. Higham and R. H. Henchman, J. Chem. Phys., 2016, 145, 084108.
54. J. Higham and R. H. Henchman, J. Comput. Chem., 2018, 39, 699–703.
55. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
56. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960.
57. M. A. Ricci, M. Nardone, F. P. Ricci, C. Andreani and A. K. Soper, J. Chem. Phys., 1995, 102, 7650–7655.
58. M. Diraison, G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 111, 1096–1103.
59. A. D. Boese, A. Chandra, J. M. L. Martin and D. Marx, J. Chem. Phys., 2003, 119, 5965–5980.
60. I. Vyalov, M. Kiselev, T. Tassaing, J. C. Soetens and A. Idrissi, J. Phys. Chem. B, 2010, 114, 15003–15010.
61. S. Riahi and C. N. Rowley, J. Phys. Chem. B, 2013, 117, 5222–5229.
62. S.-W. Chao, A. H.-T. Li and S. D. Chao, J. Comput. Chem., 2009, 30, 1839–1849.
63. B. J. Yoon, M. S. Jhon and H. Eyring, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 6588–6591.
64. S. Y. Cheng, H. V. Duong, C. Compton, M. W. Vaughn, H. Nguyen and K. H. Cheng, Biophys. Chem., 2015, 198, 22–35.
65. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 , 27–28.
66. A. Michels, H. Wijker and H. Wijker, Physica, 1949, 15, 627–633.
67. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
68. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminform., 2012, 4, 17.
69. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
70. D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzerio, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, T. Kurtzman, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, D. J. Luo, R. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. Salomon-Ferrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER 2018, University of California, San Francisco, 2018.
71. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
72. M. R. Shirts, C. Klein, J. M. Swails, J. Yin, M. K. Gilson, D. L. Mobley, D. A. Case and E. D. Zhong, J. Comput. Aided Mol. Des., 2017, 31, 147–161.
73. R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, 1988.
74. D. M. Heyes, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 755–764.
75. J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
76. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
77. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
78. L. G. M. Pettersson, R. H. Henchman and A. Nilsson, Chem. Rev., 2016, 13, 7459–7462.

---

Footnote

† Electronic supplementary information (ESI) available: This contains figures on the effect of box size and GC cutoff on shell dependence, energy convergence as a function of time and energy dependence on shell properties. See DOI: 10.1039/d0cp05903j

---